§ 13. НЕВОЗМОЖНОСТЬ АЛГОРИТМА ДЛЯ ПРОБЛЕМЫ ЭКВИВАЛЕНТНОСТИ СЛОВ

В этом параграфе доказывается невозможность алгоритма для распознавания эквивалентности слов в любом исчислении. Это доказательство проводится в два этапа.

На первом этапе (п. 1 этого параграфа) рассматриваются ассоциативные исчисления с ориентированными

подстановками вила Для таких исчислений, которые можно называть односторонними, рассматривается проблема переводимости слов. Слово считается переводимым в слово если существует дедуктивная цепочка.

где есть есть а стрелка означает, что предыдущее слово переходит в последующее в результате разового применения ориентированной подстановки. Устанавливается, что не существует алгоритма распознавания переводимости слов в произвольном одностороннем исчислении. Наряду с исчислениямибудем рассматривать исчисления Исчисление получается из соответствующего путем замены каждой из односторонних подстановок вида на двухсторонние подстановки вида

Очевидно, если из двух слов одно переводимо в другое в то эти слова эквивалентны в Обратное утверждение, вообще говоря, не верно, ибо при установлении эквивалентности допускаются и такие дедуктивные цепочки, в которых наряду с данными подстановками вида допускаются и подстановки вида Поэтому получаемый результат для односторонних исчислений не распространяется автоматически на любые исчисления.

На втором этапе этого параграфа) доказательства как раз и преодолевается эта трудность и устанавливается теорема неразрешимости для проблемы эквивалентности.

1. Невозможность алгоритма распознавания переводимости слов.

Теорема 1. Не существует алгоритма, позволяющего выяснить для любой пары слов в произвольном исчислении, переводимо или нет.

Доказательство теоремы 1 осуществляется путем сведения проблемы переводимости для машин Тьюринга к проблеме переводимости для односторонних исчислений. Поскольку первая является алгоритмически неразрешимой, то таковой является и вторая. Приводимые ниже понятия и конструкции предназначены как раз для сведения первой проблемы ко второй.

Расмотрим некоторую конфигурацию машины Тьюринга. Условимся называть активными в данной конфигурации следующие ячейки:

а) обозреваемую ячейку;

б) ячейки, заполненные буквами (отличными от пустого знака Л);

в) всякую ячейку, левее и правее которой имеются ячейки типа а) или б).

Совокупность всех активных ячеек образует сплошную часть ленты — ее активную часть. На рис. 26 изображены некоторые конфигурации и отмечены соответствующие активные части ленты. В конфигурации рис. 26, а обозреваемая ячейка не является крайней, т. е. левее и правее ее все еще имеются ячейки активной части ленты.

Рис. 26.

Такую конфигурацию будем называть глубинной, в отличие от конфигураций типа рис. 26, б, рис. 26, в, рис. 26, г, которые будем называть соответственно левой, правой, одиночной.

Предположим, что внешний алфавит машины такой:

а внутренний алфавит такой:

Введем еще в рассмотрение букву (не входящую в указанные алфавиты) и предназначенную для обозначения краев активной части ленты.

Всякую конфигурацию можно обозначить в виде слова где слово, составленное так, как это было сделано в § 11. Эти слова будем называть К-словами (конфигурационными). Например, конфигурациям

рис. 26 соответствуют слова

Сопоставим теперь машине исчисление следующим образом:

1. Алфавит жсостоит из буквы и всех букв алфавитов машины Заметим, что в то время как всякое -слово является словом в исчислении не всякое слово является конфигурационным. Так, например, в слове дважды встречается внутренняя буква чего не может быть в -слове.

2. Подстановки (ориентированные) в строятся так, чтобы они обеспечивали в точности такие преобразования -слов, которые соответствуют преобразованиям конфигураций в машине согласно ее командам. Поясним подробнее, как это делается.

Рассмотрим команду вида

при которой не происходит смены обозреваемой ячейки. Легко понять, что в результате такой команды активная часть ленты не меняется. Если сравнить -слова до и после применения команды, то оказывается, что пара букв просто заменяется парой букв В соответствии с этим команде (1) машины Тьюринга сопоставляем в исчислении ориентированную подстановку

Если же брать команду со сдвигом, то в зависимости от характера конфигурации (глубинная, левая и т. п.) и сдвига (влево, вправо) могут происходить изменения активной части ленты. По этой причине для команды не удается указать в исчислении такой единственной ориентированной подстановки, которая была бы ей равноценна (в том смысле, как это было сделано для команды (1)). Однако, как будет показано ниже, можно указать конечную систему подстановок, которая в своей совокупности равноценна данной команде.

Пример. В соответствии с командой

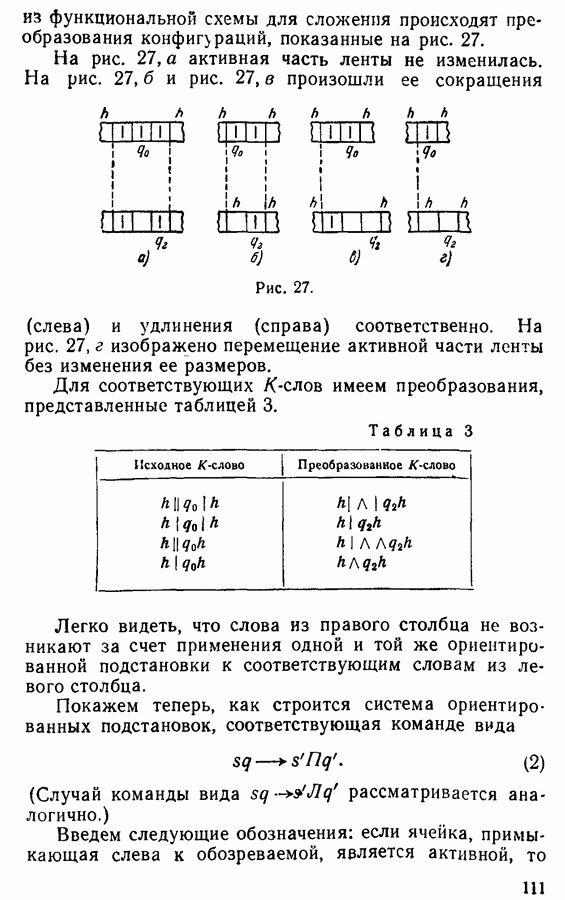
из функциональной схемы для сложения происходят преобразования конфигураций, показанные на рис. 27.

На рис. 27, а активная часть ленты не изменилась. На рис. 27, б и рис. 27, в произошли ее сокращения (слева) и удлинения (справа) соответственно.

Рис. 27.

На рис. 27, г изображено перемещение активной части ленты без изменения ее размеров.

Для соответствующих -слов имеем преобразования, представленные таблицей 3.

Таблица 3 (см. скан)

Легко видеть, что слова из правого столбца не возникают за счет применения одной и той же ориентированной подстановки к соответствующим словам из левого столбца.

Покажем теперь, как строится система ориентированных подстановок, соответствующая команде вида

(Случай команды вида рассматривается аналогично.)

Введем следующие обозначения: если ячейка, примыкающая слева к обозреваемой, является активной, то

букву, помещенную в ней, обозначим через о; аналогично, обозначает букву, помещенную в соседней ячейке справа, если она активна; при этом не исключено, что о или или обе одновременно — пустые знаки.

Подстановки, соответствующие команде (2), удобно классифицировать по типам конфигураций:

1. Глубинная конфигурация. В К-слове имеются вхождения вида Каждому такому вхождению произвольные внешние буквы машины) соответствует подстановка

2. Левая конфигурация. В К-словах имеются вхождения вида Им соответствуют подстановки вида

Последняя подстановка отражает тот факт, что ячейка, содержавшая перестает быть активной (см. рис. 28).

Рис. 28.

Рис. 29.

Рис. 30.

3. Правая конфигурация. В -словах имеются вхождения вида которым соответствуют подстановки

отражающие факт удлинения справа активной части ленты (см. рис. 29).

4. Одиночная конфигурация В -словах имеются вхождения которым соответствуют подстановки

Последняя подстановка отражает факт перемещения единственной активной ячейки (см. рис. 30).

Этим и завершается перечень ориентированных подстановок, соответствующих в исчислении машинной команде вида (2).

Пример. Построить для машины Тьюринга реализующей сложение (см. § 9), соответствующее исчисление

Алфавит

Команде соответствует подстановка

Команде соответствуют подстановки:

Точно так же можно указать подстановки, соответствующие остальным командам.

Отметим теперь следующие свойства исчисления построенного по заданной машине М:

Утверждение 1. Всякое -слово для машины является словом в

Утверждение 2 Если есть -слово, описывающее конфигурацию то в к нему применима не более чем одна подстановка. Эта подстановка преобразует в -слово для конфигурации , в которую машина перерабатывает

Утверждение 3. Если является заключительной конфигурацией машины то к не применима никакая подстановка.

Из этих утверждений непосредственно вытекает, что вопрос о том, переводима ли в машине какая-нибудь конфигурация в другую конфигурацию , равносилен вопросу о том, переводимо ли в исчислении К-слово в -слово . Иными словами, проблема распознавания переводимости для машин Тьюринга сводится к проблеме распознавания переводимости для исчислений с ориентированными подстановками. Этим и завершается доказательство теоремы 1.

Если в качестве 58 берутся лишь заключительные конфигурации в машине то из отмеченной выше сводимости вытекает

Теорема 2. Не существует алгоритма, позволяющего установить для любого исчисления с ориентированными подстановками и для любой пары слов и , из которых второе является заключительным, переводимо в или нет.

2. Неразрешимость проблемы эквивалентности. Пусть два -слова в исчислении Если переводимо в ориентированными подстановками, то тем более эквивалентны в Появятся ли новые эквивалентности, если объявить подстановки в неориентированными? Ответ на этот вопрос дается в следующей лемме:

Лемма. Если есть заключительное -слово и эквивалентно (допускаются неориентированные подстановки), то переводимо в одними лишь ориентированными подстановками.

Из этой леммы непосредственно вытекает возможность алгоритма для решения проблемы эквивалентности слов в ассоциативных исчислениях. Действительно, такой алгоритм решал бы одновременно и проблему переводимости слов посредством ориентированных подстановок в заключительные слова. Теорема 2 утверждает невозможность такого алгоритма.

Доказательство леммы. Если то существует дедуктивная цепочка, ведущая от

Пусть два смежных слова в этой цепочке. Если переход от осуществляется путем применения ориентированной подстановки вида то будем писать если же этот переход осуществляется путем замены в вхождения правой части допустимой подстановки на левую (или, что то же самое, переходит в путем применения ориентированной подстановки), то будем писать Рассмотрим теперь следующие возможные случаи для тройки слов в цепочке (3):

В силу утверждения 2 слова и в случае (4) совпадают, ибо к слову применима лишь единственная подстановка. Поэтому обнаружение такой тройки в дедуктивной цепочке позволяет сократить ее путем изъятия двух слов (например, В случае же (5) слова могут быть в самом деле различными; в терминах машины Тьюринга это соответствует тому обстоятельству, что по данной конфигурации машины предшествующая ей конфигурация однозначно не восстанавливается.

Вернемся теперь к цепочке (3). Поскольку является заключительной конфигурацией, то (см. утверждение 3) может быть лишь Если в данной цепочке все стрелки являются правыми, то лемма уже установлена. Если же существуют левые стрелки, то пусть последняя встречается перед словом. Тогда

имеется тройка

которая может быть сокращена на 2 слова, и мы получаем более короткую дедуктивную цепь, ведущую от Продолжая эту процедуру сокращения цепочки, мы дойдем до цепочки, которую больше сокращать нельзя, потому что в ней все стрелки ориентированы вправо. Итак, переводимо в ориентированными подстановками.