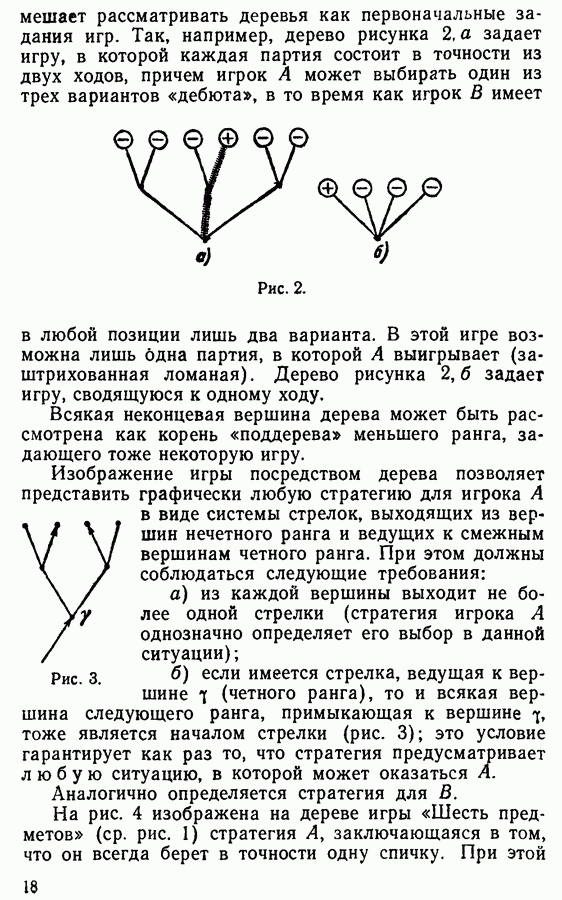
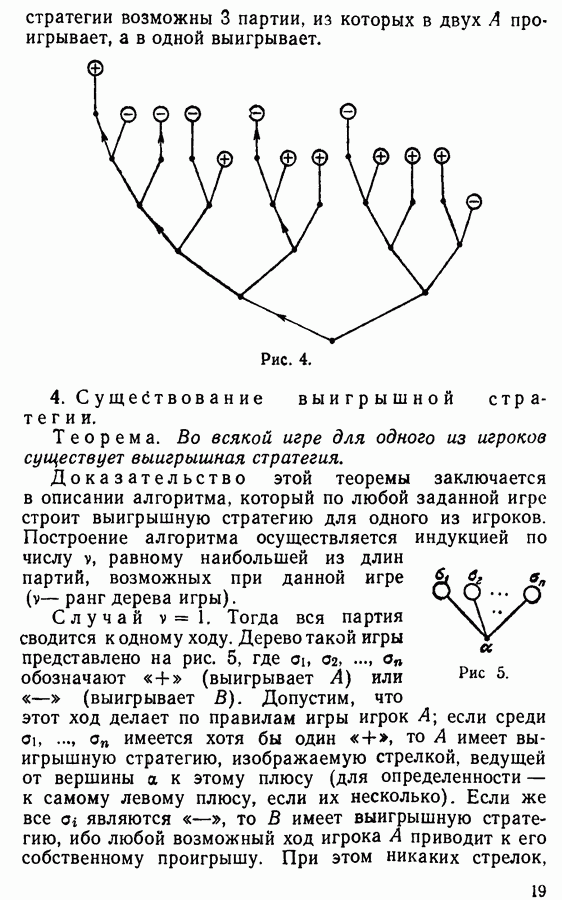
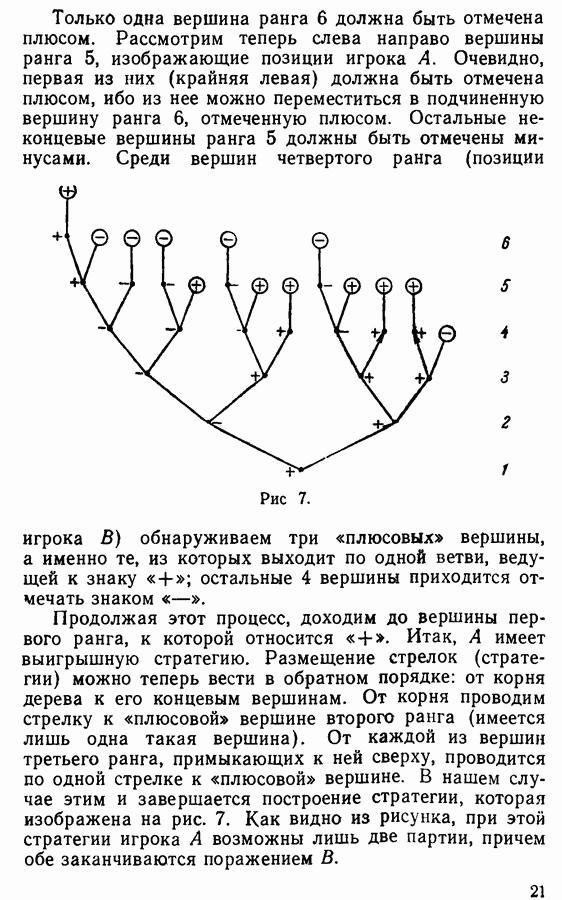
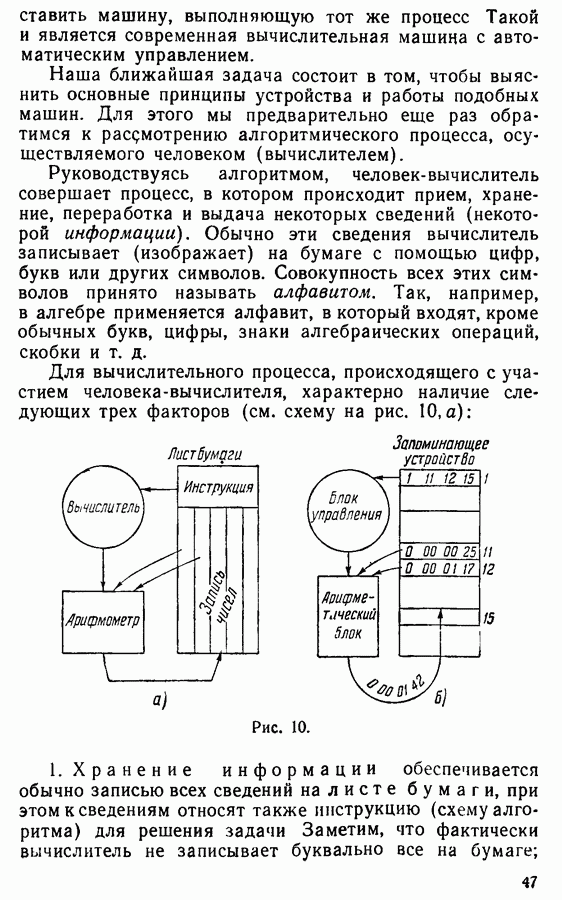
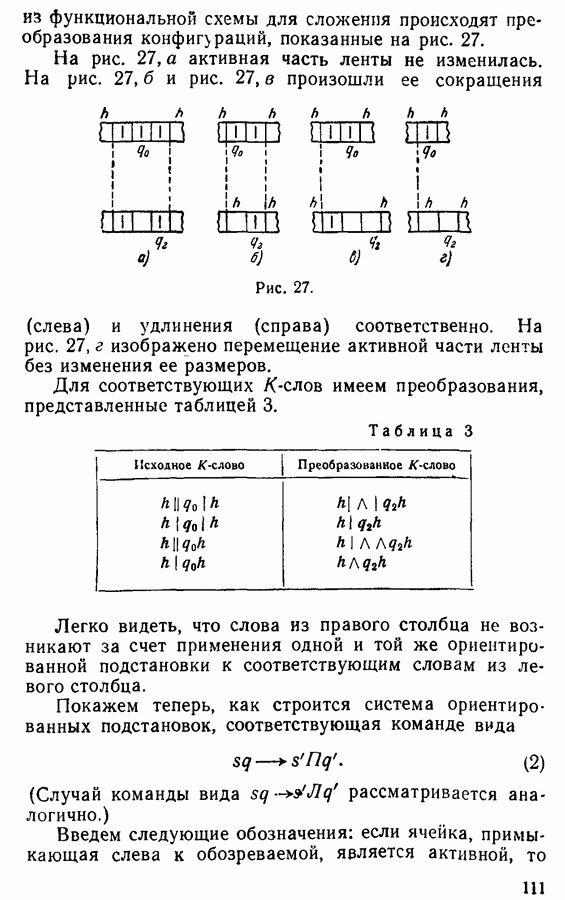
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. ПРОБЛЕМА СЛОВ
Проблема слов представляет собою далеко идущее обобщение поисков Тезея. Если поиски Тезея могут происходить в произвольном, но конечном лабиринте, то проблема слов является в определенном смысле проблемой поиска в бесконечном лабиринте. Проблема слов возникла в специальных разделах современной алгебры, называемых теорией ассоциативных систем и теорией групп, однако ее значение выходит за рамки этих специальных теорий. Разные варианты этой проблемы были с успехом исследованы выдающимися советскими математиками Андреем Андреевичем Марковым и Петром Сергеевичем Новиковым, а также их учениками.
Введем сперва некоторые предварительные понятия:
Алфавитом будем называть любую конечную систему попарно различных знаков, называемых буквами этого алфавита. Так, например, можно рассматривать алфавит  состоящий из греческой буквы а, русской
состоящий из греческой буквы а, русской  латинской
латинской  и вопросительного знака. Словом в данном алфавите называется любая последовательность букв этого алфавита. Например,
и вопросительного знака. Словом в данном алфавите называется любая последовательность букв этого алфавита. Например,  и ЬЬас являются словами в алфавите
и ЬЬас являются словами в алфавите  Если слово
Если слово  является частью слова
является частью слова  то будем говорить о вхождении слова
то будем говорить о вхождении слова  в слово
в слово  Так, например, в слове
Так, например, в слове  имеются два вхождения слова
имеются два вхождения слова  одно начиная со второй буквы, а другое — с четвертой. Мы будем рассматривать преобразования одних слов в другие посредством некоторых допустимых подстановок, которые задаются в виде
одно начиная со второй буквы, а другое — с четвертой. Мы будем рассматривать преобразования одних слов в другие посредством некоторых допустимых подстановок, которые задаются в виде

где  два слова в том же алфавите
два слова в том же алфавите
Применение ориентированной подстановки  к слову
к слову  возможно в том случае, когда в нем имеется хотя бы одно вхождение левой части
возможно в том случае, когда в нем имеется хотя бы одно вхождение левой части  оно заключается в замене любого одного такого вхождения соответствующей правой частью
оно заключается в замене любого одного такого вхождения соответствующей правой частью  Применение же неориентированной подстановки
Применение же неориентированной подстановки  допускает как замену вхождения левой части правой, так и замену вхождения правой части левой. Начиная с этого места, мы будем рассматривать преимущественно неориентированные подстановки, называя их просто подстановками, там, где это не вызывает недоразумений.
допускает как замену вхождения левой части правой, так и замену вхождения правой части левой. Начиная с этого места, мы будем рассматривать преимущественно неориентированные подстановки, называя их просто подстановками, там, где это не вызывает недоразумений.
Пример 1. Подстановка  применима четырьмя способами к слову
применима четырьмя способами к слову  замена каждого из двух вхождений
замена каждого из двух вхождений  дает слова:
дает слова:

а замена каждого из двух вхождений  дает слова:
дает слова:

К слову же  эта подстановка неприменима.
эта подстановка неприменима.
Условимся называть ассоциативным исчислением совокупность всех слов в некотором алфавите вместе с какой-нибудь конечной системой допустимых подстановок.
Для того чтобы задать ассоциативное исчисление, достаточно указать соответствующие алфавит и систему подстановок.
Если слово  может быть преобразовано в слово
может быть преобразовано в слово  посредством однократного применения допустимой подстановки, то и
посредством однократного применения допустимой подстановки, то и  может быть преобразовано в
может быть преобразовано в  таким же путем; в таком случае
таким же путем; в таком случае  будем называть смежными словами. Последовательность слов
будем называть смежными словами. Последовательность слов

таких, что  смежны,
смежны,  смежны,
смежны,  смежны, будем называть дедуктивной цепочкой, ведущей от
смежны, будем называть дедуктивной цепочкой, ведущей от  Если существует дедуктивная цепочка, ведущая от слова
Если существует дедуктивная цепочка, ведущая от слова  к слову
к слову  то, очевидно, существует и дедуктивная цепочка, ведущая от
то, очевидно, существует и дедуктивная цепочка, ведущая от  в таком случае слова будем называть эквивалентными и обозначать это так:
в таком случае слова будем называть эквивалентными и обозначать это так:  Ясно также, что если
Ясно также, что если  и
и  то
то  В дальнейшем нам понадобится еще следующая теорема.
В дальнейшем нам понадобится еще следующая теорема.
Теорема. Пусть  тогда, если в каком-либо слове
тогда, если в каком-либо слове  имеется вхождение
имеется вхождение  то в результате подстановки вместо него
то в результате подстановки вместо него  получается слово, эквивалентное
получается слово, эквивалентное 
Доказательство. В условиях теоремы слово  удобно представить в виде
удобно представить в виде  где
где  — часть слова
— часть слова  предшествующая вхождению
предшествующая вхождению  и
и  часть, следующая за ним, а преобразованное слово в виде
часть, следующая за ним, а преобразованное слово в виде  Далее, в силу эквивалентности
Далее, в силу эквивалентности  существует дедуктивная цепочка
существует дедуктивная цепочка

Но в таком случае, как легко видеть, последовательность слов

является дедуктивной цепочкой, ведущей от  (т. е.
(т. е.  к
к  (т. е. к преобразованному слову). Теорема доказана.
(т. е. к преобразованному слову). Теорема доказана.
Пример 2. Рассмотрим ассоциативное исчисление, которое было изучено Г. С. Цейтиным
Алфавит:

Система допустимых подстановок:

В этом исчислении к слову  применима только третья подстановка и оно имеет только одно смежное слово
применима только третья подстановка и оно имеет только одно смежное слово  Далее имеет место эквивалентность:
Далее имеет место эквивалентность:  как видно из следующей дедуктивной цепочки:
как видно из следующей дедуктивной цепочки:

Если же взять слово  то к нему неприменима ни одна из подстановок и поэтому оно не имеет никаких
то к нему неприменима ни одна из подстановок и поэтому оно не имеет никаких
смежных слов; тем более не существует слов, отличных от  которые были бы ему эквивалентны.
которые были бы ему эквивалентны.
Для каждого ассоциативного исчисления возникает своя специальная проблема эквивалентности слов. Она заключается в следующем:
Для любых двух слов в данном исчислении требуется узнать, эквивалентны они или нет.
Поскольку различных слов в любом исчислении найдется бесчисленное множество, то фактически здесь имеется бесконечная серия однотипных задач, а решение мыслится в виде алгоритма, распознающего эквивалентность или неэквивалентность любой пары слов.
Может создаться впечатление, что проблема слов представляет собой искусственно надуманную головоломку, и следовательно, нахождение такого алгоритма не представляет собою особого практического или теоретического интереса. На самом же деле это далеко не так; можно показать, что эта проблема является весьма естественной и имеет большое теоретическое и практическое значение, вполне оправдывающее усилия, направленные на построение соответствующего алгоритма. Однако на данной стадии изложения мы воздержимся пока от обсуждения этого вопроса по существу и перейдем к рассмотрению некоторых конкретных фактов.
Во-первых, укажем на связь проблемы эквивалентности слов с проблемой Тезея. Если построить для каждого слова свою «площадку» и для каждой пары смежных слов — коридор, соединяющий соответствующие площадки, то ассоциативное исчисление предстанет перед нами в виде лабиринта с бесконечным числом площадок и коридоров, в котором от каждой площадки расходится только конечное число коридоров (правда, здесь возможны и такие площадки, из которых не выходит ни одного коридора: см. слово  в примере 2). При этом дедуктивная цепочка, ведущая от какого-либо слова
в примере 2). При этом дедуктивная цепочка, ведущая от какого-либо слова  к слову
к слову  будет представлять собою путь в лабиринте, ведущий от одной площадки к другой. Значит эквивалентности слов соответствует взаимная достижимость каждой из площадок, если отправляться от другой. Наконец, при такой трактовке сама пррблема слов становится проблемой поиска пути в бесконечном лабиринте.
будет представлять собою путь в лабиринте, ведущий от одной площадки к другой. Значит эквивалентности слов соответствует взаимная достижимость каждой из площадок, если отправляться от другой. Наконец, при такой трактовке сама пррблема слов становится проблемой поиска пути в бесконечном лабиринте.
Для того чтобы лучше уяснить специфику тех трудностей, которые здесь возникают, рассмотрим
предваригельно ограниченную проблему слов, которая заключается в следующем:
Для любых двух слов  в данном ассоциативном исчислении требуется узнать, можно ли преобразовать одно в другое последовательным применением не более чем
в данном ассоциативном исчислении требуется узнать, можно ли преобразовать одно в другое последовательным применением не более чем  раз допустимых подстановок
раз допустимых подстановок  произвольное, но фиксированное натуральное число).
произвольное, но фиксированное натуральное число).
При такой постановке проблемы алгоритм строится легко: именно, можно пользоваться уже известным нам алгоритмом перебора, при котором просматривается список всех слов, начиная со слова  переходя ко всем его смежным словам, потом к смежным для смежных и так далее
переходя ко всем его смежным словам, потом к смежным для смежных и так далее  раз. Ответ на поставленный вопрос будет положительным или отрицательным в зависимости от того, будет ли обнаружено слово
раз. Ответ на поставленный вопрос будет положительным или отрицательным в зависимости от того, будет ли обнаружено слово  в этом списке или нет.
в этом списке или нет.
Однако если вернуться к неограниченной проблеме слов, то там положение существенно иное. Поскольку длина дедуктивной цепочки, ведущей от  к
к  (если такая существует), может оказаться сколь угодно большой, то, вообще говоря, неизвестно, когда следует считать законченным процесс перебора. Пусть, например, мы уже продолжили процесс перебора до
(если такая существует), может оказаться сколь угодно большой, то, вообще говоря, неизвестно, когда следует считать законченным процесс перебора. Пусть, например, мы уже продолжили процесс перебора до  и уже располагаем списком всех слов, которые можно получить из
и уже располагаем списком всех слов, которые можно получить из  при помощи многократных применений подстановок, общее число которых не превосходит
при помощи многократных применений подстановок, общее число которых не превосходит  , и пусть в этом списке слова
, и пусть в этом списке слова  не оказалось. Дает ли это нам какое-либо основание для заключения о неэквивалентности слов
не оказалось. Дает ли это нам какое-либо основание для заключения о неэквивалентности слов  Разумеется, нет, ибо не исключена возможность, что
Разумеется, нет, ибо не исключена возможность, что  эквивалентны, но минимальная дедуктивная цепочка, соединяющая их, еще длиннее.
эквивалентны, но минимальная дедуктивная цепочка, соединяющая их, еще длиннее.
Для получения желаемых результатов здесь приходится отказаться от простого перебора; необходимо привлекать другие идеи, основанные на анализе самого механизма преобразования одних слов в другие посредством допустимых подстановок. Попытаемся, например, выяснить, эквивалентны ли в исчислении Цейтлина (см. пример 2) слова  и
и  Отрицательный ответ на этот вопрос вытекает из следующих соображений: в каждой из допустимых подстановок этого исчисления левая и правая части содержат одно и то же число вхождений буквы а (или же вовсе не содержат этой буквы); поэтому в любой дедуктивной цепочке
Отрицательный ответ на этот вопрос вытекает из следующих соображений: в каждой из допустимых подстановок этого исчисления левая и правая части содержат одно и то же число вхождений буквы а (или же вовсе не содержат этой буквы); поэтому в любой дедуктивной цепочке
все слова должны содержать одно и то же число вхождений буквы а. Поскольку в предложенных двух словах число вхождений буквы а не одинаково, то эти слова не эквивалентны.
Обнаружение подобных дедуктивных инвариантов. т. е. свойств, остающихся неизменными для всех слов дедуктивной цепочки, и позволяет в некоторых случаях находить искомые разрешающие алгоритмы.
Пример 3.
Алфавит

Система допустимых подстановок:

Эти допустимые подстановки не изменяют количества вхождений каждой буквы в слове, меняется только порядок букв в слове. Непосредственно ясно, что два слова эквивалентны в том и только в том случае, когда в них одинаковое число вхождений каждой буквы. Поэтому алгоритм распознавания эквивалентности весьма прост и сводится к подсчету числа вхождений букв в каждое из этих слов и сравнению этих чисел.
Мы разберем ниже подробно более сложный пример, но предварительно условимся о следующем обобщении понятий «слово» и «допустимая подстановка». Именно, будем рассматривать, кроме обычных слов, в данном алфавите и пустое слово, не содержащее ни одной буквы, и примем для него обозначение  Вместе с тем будем допускать и подстановки вида
Вместе с тем будем допускать и подстановки вида

При этом замена левой части пустым словом означает просто, что из преобразуемого слова выбрасывается вхождение слова  Замена же правой части левой означает, что между двумя какими-либо буквами преобразуемого слова или впереди него, или за ним вставляется слово
Замена же правой части левой означает, что между двумя какими-либо буквами преобразуемого слова или впереди него, или за ним вставляется слово 
Пример 4. Дано ассоциативное исчисление в алфавите  с системой подстановок:
с системой подстановок:

Требуется найти разрешающий алгоритм для проблемы эквивалентности слов в этом исчислении.
Построим один вспомогательный алгоритм — алгоритм приведения, который указывает для любого слова эквивалентное ему слово специального вида — приведенное слово. Для этого рассмотрим упорядоченную систему ориентированных подстановок

и условимся, что в применении к какому-либо слову  алгоритм работает так: берется первая по порядку подстановка (ориентированная) из этого списка, которая применима к слову
алгоритм работает так: берется первая по порядку подстановка (ориентированная) из этого списка, которая применима к слову  и при наличии нескольких вхождений ее левой части в слове
и при наличии нескольких вхождений ее левой части в слове  подстановку применяют к первому, самому левому, вхождению; для полученного таким образом слова
подстановку применяют к первому, самому левому, вхождению; для полученного таким образом слова  опять берется первая в этом списке подстановка, которая к нему применима, и она тоже применяется к самому левому вхождению своей левой части; если после конечного числа таких шагов получается слово 5, к которому ни одна из этих подстановок уже неприменима, то говорят, что алгоритм применим к слову
опять берется первая в этом списке подстановка, которая к нему применима, и она тоже применяется к самому левому вхождению своей левой части; если после конечного числа таких шагов получается слово 5, к которому ни одна из этих подстановок уже неприменима, то говорят, что алгоритм применим к слову  и перерабатывает его в слово
и перерабатывает его в слово 
Мы покажем, что каково бы ни было слово  алгоритм приведения применим к нему и перерабатывает его в одно из следующих восьми слов (приведенных слов):
алгоритм приведения применим к нему и перерабатывает его в одно из следующих восьми слов (приведенных слов):

Действительно, если в слове  имеются вхождения буквы
имеются вхождения буквы  то сначала будет применяться первая подстановка, исключающая
то сначала будет применяться первая подстановка, исключающая  и заменяющая его на
и заменяющая его на  до тех пор, пока не останется ни одного
до тех пор, пока не останется ни одного  Далее заработает вторая подстановка, перемещающая букву а левее буквы с до тех пор, пока не останется ни одного а, непосредственно следующего правее буквы с, иными словами, пока все а не окажутся впереди всех с. Наконец, начнется процесс вычеркивания пар соседних а и четверок соседних с, до тех пор пока не появится слово, содержащее не более одного а и не более трех с; таких же слов может быть всего восемь, и они как раз и были перечислены выше.
Далее заработает вторая подстановка, перемещающая букву а левее буквы с до тех пор, пока не останется ни одного а, непосредственно следующего правее буквы с, иными словами, пока все а не окажутся впереди всех с. Наконец, начнется процесс вычеркивания пар соседних а и четверок соседних с, до тех пор пока не появится слово, содержащее не более одного а и не более трех с; таких же слов может быть всего восемь, и они как раз и были перечислены выше.
Очевидно, каждое слово эквивалентно своему приведенному слову, поэтому два слова эквивалентны в том и только в том случае, когда им соответствует одно и то же приведенное слово, или два эквивалентных приведенных слова. Мы докажем ниже, что все 8 приведенных слов попарно неэквивалентны. Отсюда будет следовать, что два слова эквивалентны в том и только в том случае, когда им соответствует одно и то же приведенное слово. Вместе с тем будет построен и алгоритм для поставленной проблемы слов. Он будет заключаться в применении алгоритма приведения к каждому из двух рассматриваемых слов с последующим сравнением получаемых приведенных слов.
Пусть, например, даны слова  и
и  Находим приведенные слова:
Находим приведенные слова:

Вывод: слова  и
и  неэквивалентны, ибо получились два различных приведенных слова:
неэквивалентны, ибо получились два различных приведенных слова: 
Доказательство попарной неэквивалентности восьми приведенных слов. Во-первых, заметим, что если дана дедуктивная цепочка, ведущая от какого-либо слова  не содержащего буквы
не содержащего буквы  к слову
к слову  также не содержащему этой буквы, то можно из нее извлечь дедуктивную цепочку, ведущую от
также не содержащему этой буквы, то можно из нее извлечь дедуктивную цепочку, ведущую от  но такую, что в промежуточных словах цепочки не встречается буква
но такую, что в промежуточных словах цепочки не встречается буква  Действительно, если во всех словах данной дедуктивной цепочки заменить каждое вхождение буквы
Действительно, если во всех словах данной дедуктивной цепочки заменить каждое вхождение буквы  словом
словом  то получится последовательность слов, в которой каждые два рядом стоящие слова являются смежными (в смысле исчисления) или просто одинаковыми. Если удалить теперь лишние повторяющиеся слова (из рядом стоящих), то получится нужная дедуктивная цепочка. В дедуктивных цепочках этого типа совсем не участвует подстановка
то получится последовательность слов, в которой каждые два рядом стоящие слова являются смежными (в смысле исчисления) или просто одинаковыми. Если удалить теперь лишние повторяющиеся слова (из рядом стоящих), то получится нужная дедуктивная цепочка. В дедуктивных цепочках этого типа совсем не участвует подстановка  .
.
Далее, в каждой из оставшихся допустимых подстановок число вхождений буквы а в левой части и число вхождений в правой части либо одновременно четны, либо одновременно нечетны. Аналогичное утверждение справедливо и для буквы с. Значит четность числа вхождений буквы а (или буквы с) является дедуктивным инвариантом для дедуктивных цепочек вышеуказанного вида. Отсюда сразу вытекает, что ни одно из четырех приведенных слов, содержащих по одному вхождению буквы а, не эквивалентно ни одному из четырех приведенных слов, не содержащих вовсе таких вхождений. Точно так же ни одно из приведенных слов, содержащих одно или три вхождения буквы с, не эквивалентно какому-либо слову, содержащему два таких вхождения или не содержащему ни одного вхождения. Поэтому остается еще убедиться в неэквивалентности следующих пар слов:

Если бы имела место эквивалентность хотя бы одной из первых трех пар, то, как следствие из теоремы этого параграфа, имела бы место и эквивалентность четвертой. Достаточно поэтому установить неэквивалентность пары  ассс; и к этому мы сейчас и переходим.
ассс; и к этому мы сейчас и переходим.
Условимся в следующих терминах.
Индексом какого-либо вхождения буквы а в слове  называется число всех вхождений буквы с,
называется число всех вхождений буквы с,
встречающихся правее этого вхождения буквы а. Индексом слова  называется сумма индексов всех вхождений буквы а. Каждая из подстановок
называется сумма индексов всех вхождений буквы а. Каждая из подстановок  и
и  не меняет четности индекса слова. Действительно, при подстановке
не меняет четности индекса слова. Действительно, при подстановке  вместо пустого слова индекс слова увеличивается на сумму равных между собою индексов этих двух вхождений буквы а, т. е. на четное число; при замене же вхождения
вместо пустого слова индекс слова увеличивается на сумму равных между собою индексов этих двух вхождений буквы а, т. е. на четное число; при замене же вхождения  пустым словом индекс слова уменьшается на четное число.
пустым словом индекс слова уменьшается на четное число.
При подстановке сссс индексы некоторых вхождений а увеличиваются на четыре, индексы других же не изменяются; в целом индексе слово увеличивается на четное число. Аналогично при зачеркивании  . Подстановка
. Подстановка  очевидным образом не меняет четности индекса слова.
очевидным образом не меняет четности индекса слова.
Наконец, покажем, что подстановка  изменяет четность индекса слова. Для этого сравним слова
изменяет четность индекса слова. Для этого сравним слова

индекс каждого вхождения а в часть  слова
слова  изменяется ровно на 2, а индекс вхождения а в
изменяется ровно на 2, а индекс вхождения а в  не изменяется. Что же касается индекса единственного вхождения а между
не изменяется. Что же касается индекса единственного вхождения а между  то он изменяется в точности на 3. В целом индекс слова изменяется на нечетное число.
то он изменяется в точности на 3. В целом индекс слова изменяется на нечетное число.
Слова  и
и  оба имеют индексы одной и той же четности; поэтому, если они эквивалентны, то в соответствующей дедуктивной цепочке (можно считать, что в ней буква
оба имеют индексы одной и той же четности; поэтому, если они эквивалентны, то в соответствующей дедуктивной цепочке (можно считать, что в ней буква  не встречается, см. выше) может быть лишь четное число подстановок
не встречается, см. выше) может быть лишь четное число подстановок  .
.
Однако такое предположение приводит к противоречию, как видно из следующих рассуждений. Каждое применение подстановки  меняет число вхождений буквы с на 2, поэтому четное число ее применений меняет число вхождений буквы с на число, кратное четырем. Очевидно, подстановка
меняет число вхождений буквы с на 2, поэтому четное число ее применений меняет число вхождений буквы с на число, кратное четырем. Очевидно, подстановка  меняет число вхождений буквы с в точности на 4, а подстановка
меняет число вхождений буквы с в точности на 4, а подстановка  совсем не меняет этого числа. Подведя итог всему сказанному, мы должны заключить, что если
совсем не меняет этого числа. Подведя итог всему сказанному, мы должны заключить, что если  , то количества вхождений буквы с в них отличаются на
, то количества вхождений буквы с в них отличаются на
число, кратное четырем, чего на самом деле нет Итак, слова  неэквивалентны. Вместе с тем мы завершили обоснование предложенного алгоритма.
неэквивалентны. Вместе с тем мы завершили обоснование предложенного алгоритма.
Приведенное в примере 4 подробное решение проблемы слов для конкретного ассоциативного исчисления во многом характеризует понятия и методы, возникающие и при исследовании проблемы слов для других исчислений.

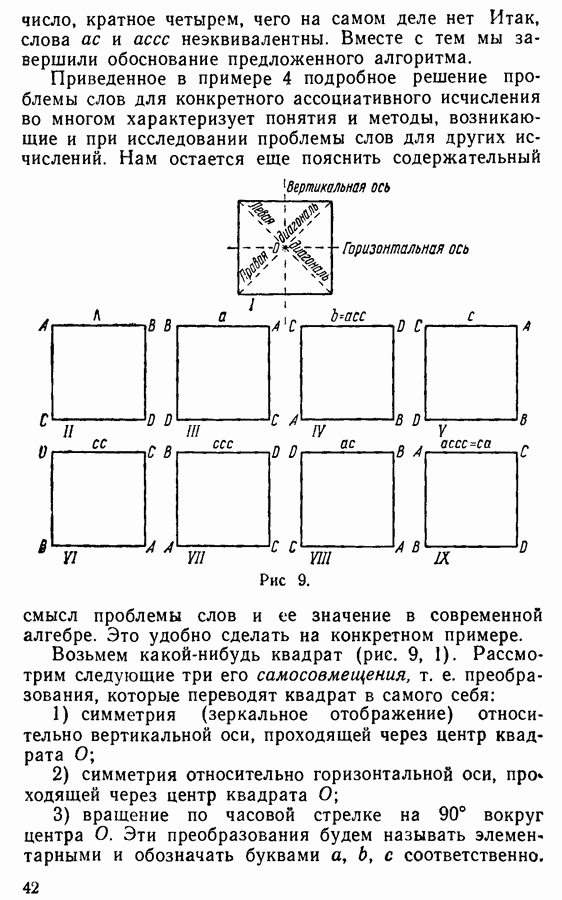
Рис. 9.
Нам остается еще пояснить содержательный смысл проблемы слов и ее значение в современной алгебре. Это удобно сделать на конкретном примере.
Возьмем какой-нибудь квадрат (рис. 9, 1). Рассмотрим следующие три его самосовмещения, т. е. преобразования, которые переводят квадрат в самого себя:
1) симметрия (зеркальное отображение) относительно вертикальной оси, проходящей через центр квадрата 
2) симметрия относительно горизонтальной оси, проходящей через центр квадрата 
3) вращение по часовой стрелке на 90° вокруг центра О. Эти преобразования будем называть элементарными и обозначать буквами  с соответственно.
с соответственно.
На рис. 9 (III-IV-V) показано, как изменяется расположение вершин квадрата (II) при каждом из элементарных преобразований.
Заметим, что в результате последовательного осуществления каких бы то ни было двух или нескольких самосовмещений квадрата происходит также самосовмещение квадрата. Будем придерживаться общепринятого определения, согласно которому умножить два заданных преобразования (в частности — два самосовмещения квадрата) — значит последовательно произвести их одно-за другим. Условимся еще для операции умножения преобразований сохранить обычную систему обозначений, а также термин произведение для результирующего преобразования. Так, например, произведение  есть результат двух последовательных вращений по 90°, т. е. вращение на 180°; произведение
есть результат двух последовательных вращений по 90°, т. е. вращение на 180°; произведение  результат симметрии относительно вертикальной оси с последующим поворотом на 90° — равносильно симметрии относительно левой диагонали (см. рис 9, I). Произведение же
результат симметрии относительно вертикальной оси с последующим поворотом на 90° — равносильно симметрии относительно левой диагонали (см. рис 9, I). Произведение же  двух предыдущих произведений равносильно симметрии относительно правой диагонали (см. рис. 9, I).
двух предыдущих произведений равносильно симметрии относительно правой диагонали (см. рис. 9, I).
Наше умножение не является переместительным; на рисунке  изображены два различных расположения вершин квадрата, которые возникают при самосовмещениях:
изображены два различных расположения вершин квадрата, которые возникают при самосовмещениях:  исходного квадрата
исходного квадрата  Однако его роднит с арифметическим умножением свойство ассоциативности (сочетательности): каковы бы ни были преобразования
Однако его роднит с арифметическим умножением свойство ассоциативности (сочетательности): каковы бы ни были преобразования  имеет место тождество
имеет место тождество  Благодаря этому в произведениях можно пренебрегать расстановкой скобок; так, например
Благодаря этому в произведениях можно пренебрегать расстановкой скобок; так, например  дают одно и то же. самосовмещение квадрата, а именно симметрию относительно левой диагонали.
дают одно и то же. самосовмещение квадрата, а именно симметрию относительно левой диагонали.
Объектом наших последовательных рассмотрений будет совокупность  состоящая из элементарных преобразований
состоящая из элементарных преобразований  с и всех самосовмещений квадрата, которые могут быть представлены как произведения конечного (но произвольного) числа элементарных преобразований. Благодаря ассоциативности умножения при символической записи элементов из
с и всех самосовмещений квадрата, которые могут быть представлены как произведения конечного (но произвольного) числа элементарных преобразований. Благодаря ассоциативности умножения при символической записи элементов из  можно опустить скобки и ограничиться записью в соответствующем порядке букв, изображающих соответствующие элементарные самосовмещения, например
можно опустить скобки и ограничиться записью в соответствующем порядке букв, изображающих соответствующие элементарные самосовмещения, например  и
и 
Это означает, что всякое произведение изобразится в виде слова в алфавите 
Из ассоциативности умножения вытекает также, что если к слову  приписать справа слово
приписать справа слово  так, чтобы получилось одно слово
так, чтобы получилось одно слово  то оно будет изображать произведение самосовмещений, изображенных словами
то оно будет изображать произведение самосовмещений, изображенных словами  соответственно; так, например, слово
соответственно; так, например, слово  изображает произведение самосовмещений, изображаемых словами
изображает произведение самосовмещений, изображаемых словами 
Очевидно, графически различных (т. е. различных по своему начертанию) слов в алфавите  существует бесчисленное множество; однако графически различные слова могут изображать одно и то же самосовмещение из
существует бесчисленное множество; однако графически различные слова могут изображать одно и то же самосовмещение из  В этом случае естественно слова считать равными и обозначать такое равенство обычным образом. Читатель легко проверит справедливость равенств:
В этом случае естественно слова считать равными и обозначать такое равенство обычным образом. Читатель легко проверит справедливость равенств:

Для этого достаточно сравнить расположения вершин квадрата, которые возникают в результате преобразований из левой и правой частей этих равенств. Далее, легко видеть, что каждое из слов:  сссс задает одно и то же самосовмещение, а именно так называемое тождественное преобразование, при котором все вершины остаются на прежних местах. Поскольку это преобразование ничего не меняет, целесообразно его изображать также пустым словом
сссс задает одно и то же самосовмещение, а именно так называемое тождественное преобразование, при котором все вершины остаются на прежних местах. Поскольку это преобразование ничего не меняет, целесообразно его изображать также пустым словом  Итак, имеют место и равенства
Итак, имеют место и равенства

Сопоставление равенств (1) — (5) с допустимыми подстановками ассоциативного исчисления примера 4 подсказывает следующее предложение, устанавливающее связь между этим исчислением и рассматриваемой системой преобразований квадрата:
Два произведения элементарных самосовмещений квадрата задают одно и то же преобразование в том и только в том случае, когда изображающие их слова эквивалентны в исчислении примера 4,
В самом деле из равенств (1) — (5) вытекает, что при каждом применении любой допустимой подстановки к любому слову  оно переходит в равное слово. Например, применяя подстановку
оно переходит в равное слово. Например, применяя подстановку  к слову
к слову  , получаем слово
, получаем слово  но ведь в силу ассоциативности умножения мы можем писать: Ьсас
но ведь в силу ассоциативности умножения мы можем писать: Ьсас  и Ьасссс
и Ьасссс  правые части равны как произведения соответственно равных множителей, значит, и левые равны между собой. Итак, любые два смежных слова равны.
правые части равны как произведения соответственно равных множителей, значит, и левые равны между собой. Итак, любые два смежных слова равны.
Теперь уже легко понять, что эквивалентность двух слов в нашем ассоциативном исчислении влечет за собой их равенство (т. е. одинаковость самосовмещений, задаваемых ими). Действительно, если  то в соответствующей цепочке всякие два смежных элемента равны, а значит, и
то в соответствующей цепочке всякие два смежных элемента равны, а значит, и 
Имеет место и обратное утверждение: если слова равны, то они эквивалентны. Действительно, если два слова равны, то равны и соответствующие им приведенные слова (это вытекает из прямого утверждения). Вместе с тем непосредственно можно проверить, что все восемь приведенных слов задают попарно различные самосовмещения (см. рисунки 9, II—IX, где изображены расположения вершин квадрата (рис. 9, II) при самосовмещениях, соответствующих восьми приведенным словам). Поэтому, если два слова равны, то им соответствует одно и то же приведенное слово, а значит, по ранее доказанному они эквивалентны.
Таким образом, формальная эквивалентность двух слов в нашем исчислении получает конкретный геометрический смысл и распознавание эквивалентности двух слов приобретает значение решения конкретной геометрической задачи. Вместе с тем описанный нами алгоритм предстает перед нами как общий метод решения любой геометрической задачи данного типа.
Аналогично обстоит дело и с другими исчислениями, в которых формальная эквивалентность также допускает конкретное геометрическое, алгебраическое или иное истолкование. Без преувеличения можно сказать, что во всякой области математики имеются теоремы, которые могут быть сформулированы после некоторой обработки в виде утверждений об эквивалентности двух слов в некотором исчислении. В этой книжке нет возможности разобрать этот круг вопросов; некоторые
пояснения будут даны еще по ходу дальнейшего изложения (см. § 7).
Заметим еще, что, исходя из того геометрического истолкования, которое мы дали проблеме слов в рассмотренном исчислении, можно теперь построить алгоритм непосредственно и даже несколько проще. Именно, достаточно для каждого из двух предлагаемых произведений фактически осуществить последовательность соответствующих самосовмещений (хотя бы на чертеже) и сравнить результаты.
Упражнение. Решить проблему слов для ассоциативного исчисления, заданного в алфавите  с допустимыми подстановками:
с допустимыми подстановками:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. ЧИСЛЕННЫЕ АЛГОРИТМЫ
- § 2. АЛГОРИТМЫ ИГР
- § 3. АЛГОРИТМЫ ПОИСКА ПУТИ В ЛАБИРИНТЕ
- § 4. ПРОБЛЕМА СЛОВ
- § 5. ВЫЧИСЛИТЕЛЬНАЯ МАШИНА С АВТОМАТИЧЕСКИМ УПРАВЛЕНИЕМ
- § 6. ПРОГРАММА (машинный алгоритм)
- § 7. НЕОБХОДИМОСТЬ УТОЧНЕНИЯ ПОНЯТИЯ АЛГОРИТМА
- § 8. МАШИНА ТЬЮРИНГА
- § 9. РЕАЛИЗАЦИЯ АЛГОРИТМА В МАШИНЕ ТЬЮРИНГА
- § 10. ОСНОВНАЯ ГИПОТЕЗА ТЕОРИИ АЛГОРИТМОВ
- § 11. УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА
- § 12. АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ
- § 13. НЕВОЗМОЖНОСТЬ АЛГОРИТМА ДЛЯ ПРОБЛЕМЫ ЭКВИВАЛЕНТНОСТИ СЛОВ
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ