§ 12. АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ

Переход от расплывчатого понятия алгоритма к точному понятию машины Тьюринга, которая может быгь задана своим шифром, позволяет уточнить и вопрос об алгоритмической (или машинной) разрешимости того или иного круга задач. Именно, теперь этот вопрос следует понимать так: существует ли машина Тьюринга, решающая данный класс задач, или же такой машины не существует? (Что значит «машина Тьюринга решает некоторый класс задач» — см. § 8.)

На этот вопрос теория алгоритмов в ряде случаев дает отрицательный ответ. Один из первых результатов такого типа, установленный американским математиком Чёрчем в 1936 году, относится к проблеме распознавания выводимости в математической логике (см. § 7).

Теорема Чёрча. Проблема распознавания выводимости алгоритмически неразрешима.

Тем самым не только выясняется причина безуспешности всех прошлых попыток создания соответствующих алгоритмов, но и обнаруживается полная бессмысленность таких попыток.

Доказательствам невозможности, приводимым в теории алгоритмов, присуща та же математическая строгость, что и доказательствам невозможности, приводимым в других областях математики (например, невозможность трисекции угла с помощью циркуля и линейки, или невозможность определения общей меры для

стороны квадрата и его диагонали) Эскиз такого доказательства мы приведем ниже для проблемы распознавания самоприменимости.

Пусть в машине Тьюринга зафиксирована какая-нибудь конфигурация. Возможны два случая: 1) машина применима к этой конфигурации, т. е. срабатывая в этой конфигурации машина после конечного числа тактов останавливается в заключительной конфигурации, подавая сигнал об остановке; 2) машина не применима к этой конфигурации, т. е. сигнал об остановке никогда не наступает и машина впадает в бесконечный процесс. Возникает следующая массовая проблема:

Проблема распознавания применимости. Заданы функциональная схема какой-нибудь машины и конфигурация в ней; узнать, применима машина к этой конфигурации или нет. Это — типичная задача на построение алгоритма, ибо для ее решения надо найти общий метод (алгоритм или машину), позволяющий автоматически решать вопрос о применимости любой заданной машины к любой заданной конфигурации.

Предположим теперь, что на ленте машины Тьюринга изображен ее же собственный шифр (т. е. шифр функциональной схемы), записанный в алфавите машины. Если машина применима к такой конфигурации, то будем называть ее самоприменимой, в противном случае — несамоприменимой. Тогда можно сформулировать следующую массовую проблему:

Проблема распознавания самоприменимости. По любому заданному шифру установить, к какому классу относится машина, зашифрованная им: к классу самоприменимых или несамоприменимых?

Теорема. Проблема распознавания самоприменимости алгоритмически неразрешима.

Очевидно, из этой теоремы немедленно вытекает и алгоритмическая неразрешимость более общей проблемы применимости.

Доказательство. Предположим, напротив, что такая машина А существует. Тогда в А всякий самоприменимый шифр перерабатывается в какой-то символ а (имеющий смысл утвердительного ответа на поставленный вопрос о самоприменимости), а всякий несамоприменимый шифр — в другой символ (имеющий

смысл отрицательного ответа на поставленный вопрос). В таком случае можно было бы построить и такую машину В, которая по-прежнему перерабатывает несамоприменимые шифры в -с, в то время как к самоприменимым шифрам В уже не применима. Этого можно было бы добиться путем такого изменения схемы машины А, чтобы после появления символа о вместо сигнала об остановке машина стала бы неограниченно повторять этот же символ.

Итак, В применима ко всякому несамоприменимому шифру (вырабатывая при этом символ и не применима к самоприменимым шифрам. Однако это приводит к противоречию. Действительно,

1) пусть эта машина В самоприменима, тогда она применима к своему шифру В и перерабатывает его в символ но ведь появление этого символа как раз и должно означать, что В несамоприменима;

2) пусть В несамоприменима, тогда она применима к В, что должно означать как раз, что самоприменима.

Полученное противоречие доказывает теорему.

На основании доказанной теоремы удается установить алгоритмическую неразрешимость и некоторых других массовых проблем, возникающих в теории машин Тьюринга. При этом широко применяется метод сводимости, заключающийся в следующем.

Пусть для каждой единичной задачи входящей в серию задач эффективно указана единичная задача входящая в серию и такая, что коль скоро известно решение задачи то из него извлекается, и решение задачи В таком случае естественно говорить, что массовая проблема сведена к массовой проблеме При этих условиях ясно также, что если имеется алгоритм для решения задач то его можно перестроить в алгоритм, решающий серию задач Если же ранее было установлено, что серия задач алгоритмически неразрешима, то отсюда вытекает и алгоритмическая неразрешимость серии Такая ситуация как раз и используется часто для установления алгоритмической неразрешимости; именно для исследуемой проблемы отыскивают проблему которая заведомо алгоритмически неразрешима, но вместе С тем сводится к проблеме ,

Приведем пример сводимости проблем из теории машин Тьюринга.

Для произвольной машины Тьюринга можно построить другую машину которая связана с ней следующим образом. Пусть К — какая-нибудь конфигурация в тогда и в ей сопоставлена конфигурация К с соблюдением двух условий:

1) если не применима к К, то и не применима к К,

2) если применима к К, то тоже применима к К, причем перерабатывает ее в некоторую фиксированную заключительную конфигурацию (например, в обозреваемой ячейке вписана буква а все остальные ячейки пусты).

Проблема распознавания переводимости. Для любой заданной машины Тьюринга и любых двух конфигураций в ней требуется выяснить: если в качестве начальной конфигурации взята то перейдет ли машина (после конечного числа тактов) в конфигурацию или нет?

Пользуясь введенными выше терминами, можно сказать, что проблема применимости сводится к проблеме переводимости. Действительно, для распознавания применимости машины к конфигурации К достаточно выяснить, переводима ли в машине конфигурация К к стандартной конфигурации Отсюда вытекает, что проблема переводимости тоже алгоритмически неразрешима.

Более того, проблема переводимости остается алгоритмически неразрешимой, если в качестве брать только такие конфигурации, которые заведомо являются заключительными.

Впервые алгоритмическая неразрешимость была установлена для проблем, возникающих в самой математической логике (проблема выводимости) и в теории алгоритмов (например, проблемы применимости, переводимости и т. п.). Однако позднее выяснилось, что подобные явления имеют место и для некоторых, казалось бы, более узких проблем, возникающих в самых разнообразных специальных разделах математики. В первую

очередь здесь следует указать на ряд алгебраических проблем, приводящих к различным вариантам проблемы слов, которые исследовались советскими математиками.

Проблема эквивалентности слов для ассоциативных исчислений (см. § 4) была сформулирована еще в 1914 году норвежским математиком Туэ. Им же был предложен алгоритм для распознавания эквивалентности слов в некоторых ассоциативных исчислениях специального вида. С тех пор предпринимались многие попытки построить такой общий алгоритм, который для любого ассоциативного исчисления и для любой пары слов в нем позволили бы установить, эквивалентны эти слова или нет.

В 1946 и 1947 годах советский математик Андрей Андреевич Марков и американский математик Эмиль Пост, независимо один от другого, построили конкретные примеры ассоциативных исчислений, для каждого из которых проблема эквивалентности слов алгоритмически неразрешима. Тем более не существует алгоритма для распознавания эквивалентности слов в любом исчислении. Впоследствии на основе этого результата А. А. Марков и его ученики установили невозможность распознавания алгоритмов для широкого класса свойств ассоциативных исчислений.

В следующем параграфе приводится один из вариантов доказательства теоремы о невозможности алгоритма для распознавания эквивалентности слов в любом ассоциативном исчислении.

Большое впечатление произвел в математическом мире опубликованный в 1955 году результат Петра Сергеевича Новикова, доказавшего алгоритмическую неразрешимость проблемы тождества теории групп Эта проблема заключается в распознавании эквивалентности слов для ассоциативных исчислений специального вида: рассматриваются лишь такие ассоциативные исчисления, в которых для каждой буквы а алфавита в списке допустимых подстановок исчисления имеется подстановка вида

где а — какая-либо буква того же алфавита (возможно,

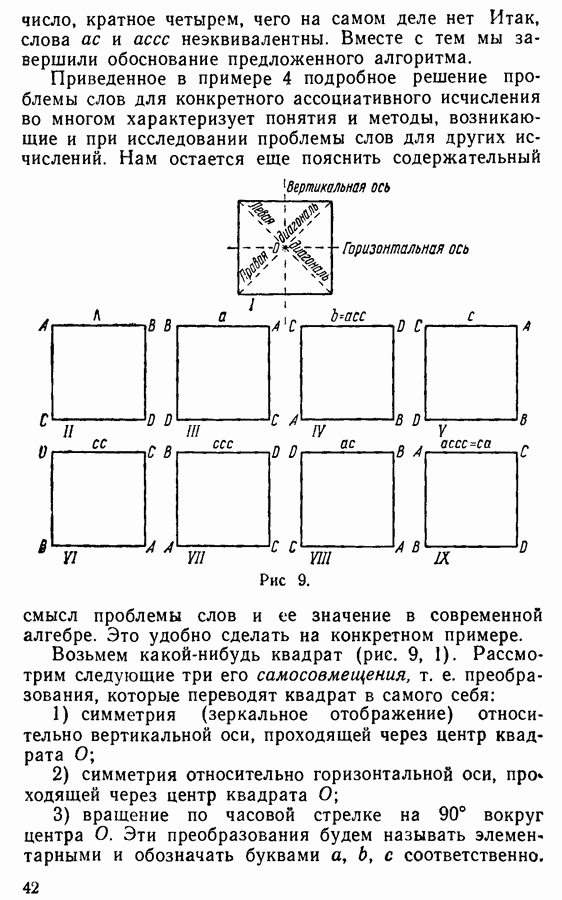
совпадающая с а). Содержательный смысл этого требования становится понятным, если, по аналогии с примером 4 из § 4, истолковать слова в любом ассоциативном исчислении как некоторые сложные преобразования, получаемые путем умножения элементарных преобразований, задаваемых соответствующими буквами, образующими это слово. В таком случае пустое слово задает тождественное преобразование, ничего не изменяющее (сравни с § 4), а наличие допустимых подстановок вида означает, что для каждого элементарного преобразования (задаваемого буквой а) существует элементарное преобразование (задаваемое буквой а) такое, что последовательное их осуществление дает тождественное преобразование. Не вдаваясь в дальнейшие подробности, отметим лишь, что рассмотрение таких множеств преобразований, называемых группами преобразований, представляет исключительно большой теоретический и практический интерес, а само понятие группы является одним из самых основных понятий современной математики.

Теперь нам нужно уяснить себе, что весьма важный результат Маркова — Поста, отмеченный выше, сам по себе не позволяет делать никаких выводов по существу проблемы тождества теории групп. Дело в том, что те индивидуальные ассоциативные исчисления, для которых А. А. Марков и Э. Пост установили алгоритмическую неразрешимость проблемы эквивалентности, как раз не удовлетворяют требованию, отмеченному выше, которое является существенным при постановке проблемы тождества теории групп. Поэтому возможность алгоритма для этой последней проблемы не исключается результатами Маркова — Поста. Надежда на создание этого алгоритма еще не была полностью утрачена, и поиски его еще продолжались, когда стал известен результат П. С. Новикова, согласно которому такого алгоритма не существует. П. С. Новиков построил индивидуальный пример ассоциативного исчисления, удовлетворяющего указанному требованию, для которого невозможен алгоритм, распознающий эквивалентность; тем более невозможен единый алгоритм для всех рассматриваемых групп.

Первые примеры, построенные А. А. Марковым и П. С. Новиковым для опровержения алгоритмической

разрешимости исследуемых проблей, оказались весьма громоздкими и насчитывали сотни допустимых подстановок. Была поставлена задача построения по возможности более простых примеров. В этом направлении блестящий успех был достигнут молодым ленинградским математиком Г. С. Цейтиным; для приведенного в § 4 исчисления, построенного Цейтиным и насчитывающего всего лишь семь допустимых подстановок, проблема эквивалентности слов также алгоритмически неразрешима.

Обнаружение алгоритмически неразрешимых проблем создало в науке такую ситуацию, когда математик, стремящийся к построению желаемого алгоритма, должен считаться с тем, что такого алгоритма может и не существовать. Поэтому параллельно с усилиями, направленными на поиски желаемого алгоритма, приходится прилагать усилия на доказательство невозможности такого алгоритма. В зависимости от того, на каком из этих направлений будет достигнут успех, и выяснится окончательно картина: либо будет найден разрешающий алгоритм, либо будет установлена алгоритмическая неразрешимость проблемы.

В § 1 была сформулирована проблема Гильберта о диофантовых уравнениях. В течение полувека велись односторонние, причем безуспешные, исследования с целью построить желаемый алгоритм. В последнее время проводятся исследования и в противоположном направлении, и хотя окончательного результата пока еще нет, но в свете частичных результатов, которые уже получены, кажется правдоподобным, что проблема Гильберта также является алгоритмически неразрешимой.