| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
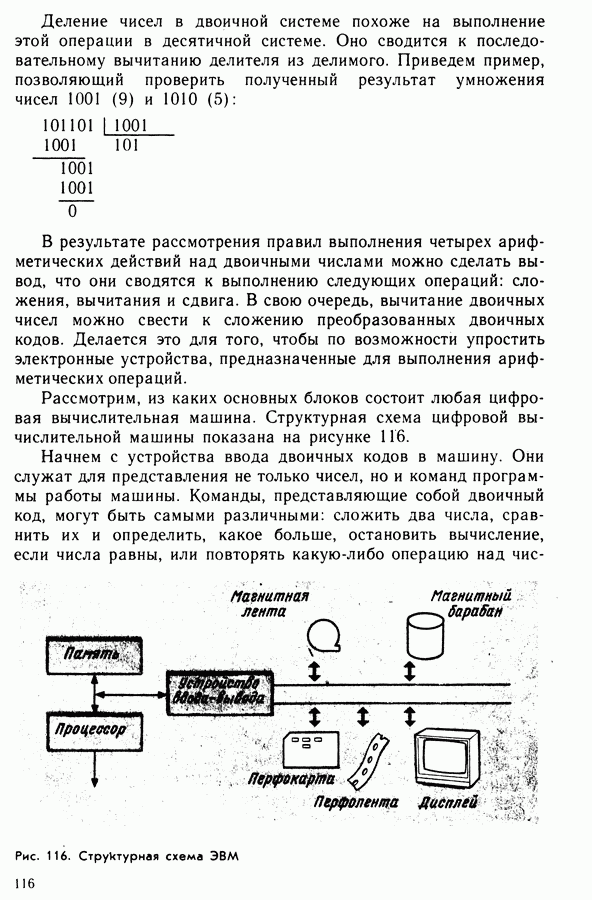
26. Способы представления информации в ЭВМ
Понятие ЭВМ стало привычным для нас. Сравнительно недавно им пользовались только специалисты. За это время машины, как уже говорилось, изменились до неузнаваемости. Но при этом произошло еще одно малозаметное изменение: исчезла буква Ц в их прошлом названии — ЭЦВМ. Однако электронные цифровые вычислительные машины (ЭЦВМ) не изменили свою «цифровую природу». Произошло их широкое распространение и вытеснение машин другого типа — аналоговых ЭВМ, или АВМ. В аналоговых и цифровых машинах используются различные способы представления информации. Это различие, характерное не только для вычислительных машин, носит настолько важный характер, что в радиоэлектронике различают аналоговую и цифровую технику. С аналоговыми устройствами — усилителями звуковых сигналов, радиоприемными и автоматическими устройствами — мы уже познакомились в первой части книги. Теперь познакомимся с цифровыми устройствами, используемыми, в частности, в цифровых вычислительных машинах.
Цифровая техника нисколько не сложнее аналоговой, может быть, даже проще для понимания и практического использования. Во-первых, электронные цепи, используемые в цифровой технике, не нужно налаживать подбором элементов; во-вторых, процесс конструирования заметно упрощается из-за возможности собирать практически любые сложные устройства с помощью готовых функциональных узлов, выполненных в виде интегральных микросхем. Изучение электроники мы начали с айалоговой техники потому, что она более привычна и совсем простые устройства, типа электронного телефона или детекторного радиоприемника, могут сразу найти практическое применение.
Особенности различных способов представления информации рассмотрим на некоторых конкретных примерах. Так, в аналоговых вычислительных машинах математические операции — сложения, вычитания, умножения, интегрирования и другие — выполняются над величинами, представляемыми различными напряжениями, которые являются аналогами математических величин. Например, операцию сложения двух чисел 5 и 2 можно выполнять путем измерения напряжений на резисторе, к которому подводится напряжение 5 В и 2 В.
Схема простого электронного устройства, способного моделировать выполнение операции сложения двух чисел от 0 до 9, показана на рисунке 114. Она состоит из источника питания 9 В (две батареи от карманного фонаря, соединенные

Рис. 114. Электрическое устройство для сложения чисел от 0 до 9
последовательно), двух многоступенчатых делителей напряжения, каждый из которых состоит из девяти последовательно соединенных резисторов сопротивлением в 100 Ом, общего нагрузочного сопротивления и вольтметра. Напряжение питания и сопротивления делителей выбраны так, что с резисторов можно снимать напряжение от 0 до 9 В через 1 В. Расчет делителя проводится по закону Ома для участка цепи. Общее сопротивление делителя равно сумме всех сопротивлений, соединенных последовательно, т. е. 900 Ом.
Сила тока в цепи равна  . В этом случае напряжение на каждом резисторе
. В этом случае напряжение на каждом резисторе 
Напряжения с делителей снимаются с помощью переключателей  и через резисторы подаются на общее сопротивление. Напряжение на нем будет равно примерно сумме подаваемых напряжений (слагаемых). На примере этой простой электрической цепи хорошо видны основные достоинства и недостатки аналоговых вычислительных устройств: простота и вместе с тем невысокая точность. Действительно, в схеме имеется небольшое число деталей. Принцип работы схемы очень простой — суммирование цифр заменено суммированием напряжений. Невысокая точность выполнения операции суммирования связана с рядом причин: ограниченной точностью показаний вольтметра, погрешностями при установке напряжения, погрешностями, связанными с неизбежным отклонением величины сопротивлений резисторов от заданного значения. Кроме того, при подключении напряжений, снимаемых с делителей, к общему резистору
и через резисторы подаются на общее сопротивление. Напряжение на нем будет равно примерно сумме подаваемых напряжений (слагаемых). На примере этой простой электрической цепи хорошо видны основные достоинства и недостатки аналоговых вычислительных устройств: простота и вместе с тем невысокая точность. Действительно, в схеме имеется небольшое число деталей. Принцип работы схемы очень простой — суммирование цифр заменено суммированием напряжений. Невысокая точность выполнения операции суммирования связана с рядом причин: ограниченной точностью показаний вольтметра, погрешностями при установке напряжения, погрешностями, связанными с неизбежным отклонением величины сопротивлений резисторов от заданного значения. Кроме того, при подключении напряжений, снимаемых с делителей, к общему резистору
происходит перераспределение токов в цепях, в результате меняется сила тока в делителях и, следовательно, меняются значения самих «слагаемых». Эти изменения можно уменьшить, вводя резисторы в цепи, по которым напряжение подается на общий резистор нагрузки. Чем больше сопротивления этих резисторов по сравнению с сопротивлениями делителя, тем меньше взаимное влияние цепей. В рассматриваемом устройстве используются резисторы сопротивлением  Оказывается, точность суммирования зависит и от величины «слагаемых», т. е. от значений напряжений, снимаемых с деталей..
Оказывается, точность суммирования зависит и от величины «слагаемых», т. е. от значений напряжений, снимаемых с деталей..
Покажем на примере, как проявляются два последних из перечисленных источников погрешности измерения. Для этого упростим схему устройства, заменив последовательно соединенные резисторы одним с соответствующим сопротивлением. Такая упрощенная схема для сложения чисел 8 и 2 показана на рисунке 115. Когда к делителям не подключены резисторы  и
и  то есть они, как принято говорить, не нагружены, то в точках
то есть они, как принято говорить, не нагружены, то в точках  делителей устанавливаются напряжения 8 и 2 В с определенной точностью.
делителей устанавливаются напряжения 8 и 2 В с определенной точностью.
При подключении цепи суммирования произойдет перераспределение токов и напряжений делителей. Так, параллельно резистору  подключаются резисторы
подключаются резисторы  и
и  Новое сопротивление
Новое сопротивление  этого участка цепи равно:
этого участка цепи равно:

Приведенный расчет показывает, что в результате подключения суммирующей цепи сопротивление участка делителя уменьшается с  до
до  соответственно, уменьшается напряжение первого слагаемого с 0,8 В до 0,737 В. По той же причине изменится второе слагаемое с 0,2 В до 0,195 В. В первом случае погрешность оказалась равной 0,063 В, во втором случае — 0,005 В, что составляет соответственно 7,8% и 2,5%. Таким образом, величина погрешности зависит от величины слагаемых: она тем больше, чем меньше сопротивление суммирующей цепи.
соответственно, уменьшается напряжение первого слагаемого с 0,8 В до 0,737 В. По той же причине изменится второе слагаемое с 0,2 В до 0,195 В. В первом случае погрешность оказалась равной 0,063 В, во втором случае — 0,005 В, что составляет соответственно 7,8% и 2,5%. Таким образом, величина погрешности зависит от величины слагаемых: она тем больше, чем меньше сопротивление суммирующей цепи.

Рис. 115. Электрическая цепь при сложении чисел
Отмеченные выше недостатки простейшего аналогового суммирующего устройства присущи и сложным аналоговым вычислительным устройствам, точность вычислений которых гораздо выше, хотя их источники погрешностей имеют тот же характер.
В цифровых машинах числа представляются в виде кодов, например в виде двоичного кода, состоящего из единиц и нулей. Подобный код используется, например, в азбуке Морзе, когда каждой букве алфавита соответствует определенный набор точек и тире. Двоичный код удобен для технической реализации. Например, единице можно сопоставить наличие одного уровня (высокого) напряжения, а нулю — другой (низкий) уровень напряжения. Тогда последовательностью импульсов напряжения разных уровней можно будет представить или закодировать любое число. Подобный способ задания чисел имеет преимущества перед аналоговым в точности. Очевидно, что если, например, закодировано число 5, то оно и будет воспринято электронным усройством как именно это число, а не как, допустим, число 5,1, которое имеет другой код. В цифровых машинах операции над десятичными числами заменены операциями над двоичными кодами, представленными двумя уровнями напряжения, т. е. набором единиц и нулей. Выполнение операций проводится по определенным правилам, так же как мы выполняем сложение десятичных чисел. Например, числа 5 и 2 цифровая машина сложит абсолютно точно, без каких-либо погрешностей.
Итак, цифровые ЭВМ более сложны, чем аналоговые, но обладают значительно большей точностью. Другим ценным свойством их является высокое быстродействие: они могут выполнять миллионы операций в секунду. Цифровые машины значительно больше распространены, чем аналоговые. Микрокалькулятор, например, является цифровым вычислительным устройством.
Важно также знать, что ЭВМ, как цифровые, так и аналоговые, в настоящее время все больше выполняют функции управления, например в станках с ЧПУ, в гибком автоматизированном производстве и во многих других областях промышленности, связи и транспорта. В последнее время получили распространет ние гибридные вычислительные машины, соединяющие в себе достоинства ЭВМ и АВМ.
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть I. ОСНОВЫ РАДИОЭЛЕКТРОНИКИ И АВТОМАТИКИ
- Глава 1. ОСНОВНЫЕ РАДИОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 2. Безопасные приемы работы с электроцепями и электроприборами
- 3. Монтаж электроцепей
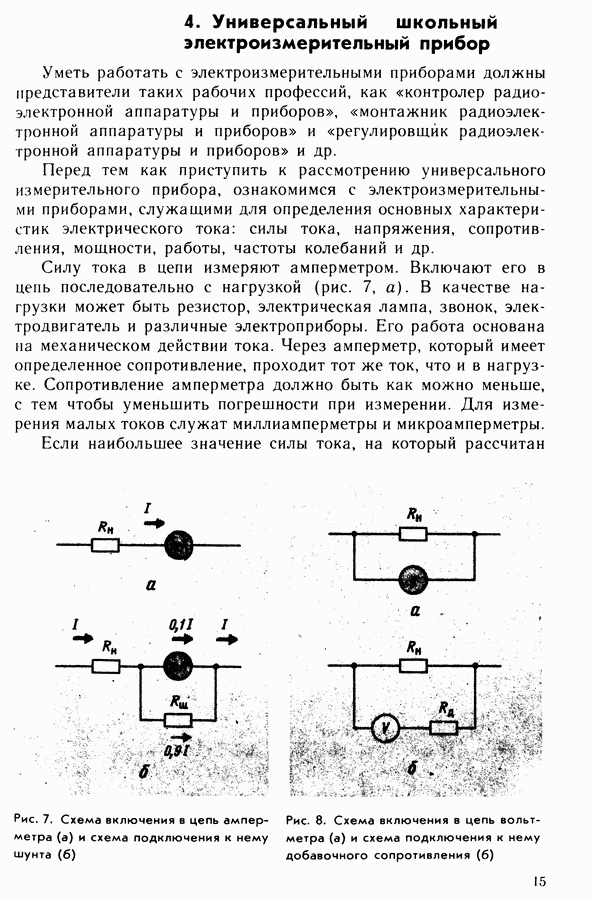
- 4. Универсальный школьный электроизмерительный прибор
- 5. Электронные осциллографы
- 6. Школьные звуковые генераторы
- 7. Источники тока
- Глава 2. РАДИОЭЛЕМЕНТЫ — СОСТАВНЫЕ ЧАСТИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 8. Резисторы
- 9. Конденсаторы
- 10. Детали с катушками индуктивности
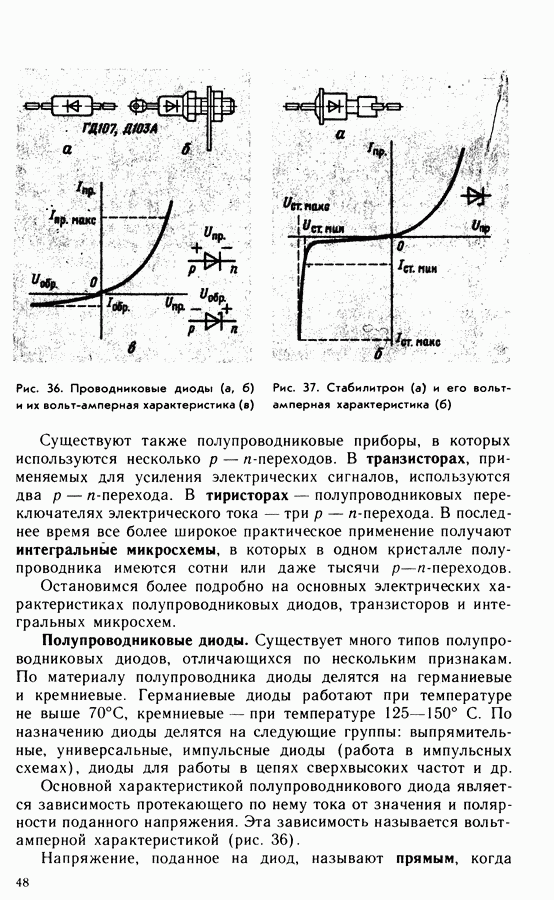
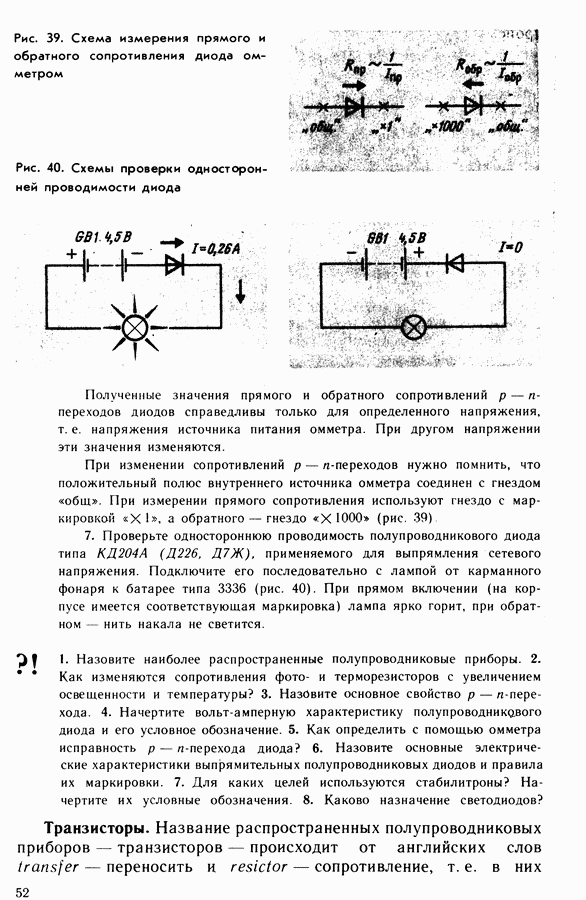
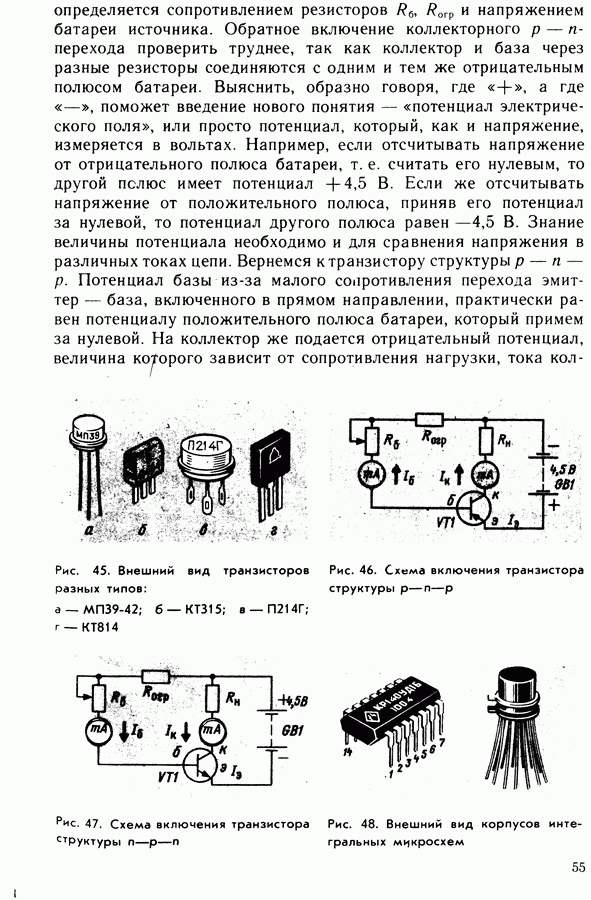
- 11. Полупроводниковые приборы
- 12. Выключатели, кнопки и переключатели
- Глава 3. ОСНОВНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
- 13. Делитель напряжения и мост сопротивлений
- 14. Фильтрующие цепи
- 15. Колебательный контур
- Глава 4. ОСНОВНЫЕ ЭЛЕКТРОННЫЕ УСТРОЙСТВА
- 16. Выпрямители
- 17. Усилители
- 18. Генераторы электрических колебаний
- Глава 5. ЭЛЕКТРОННЫЕ МОДЕЛИ И ПРИБОРЫ ЮНОГО КОНСТРУКТОРА
- 19. Приемы радиолюбительского конструирования
- 20. Прибор для проверки транзисторов
- 21. Простые автоматы
- 22. Электронные переговорные и радиоприемные устройства
- 23. Электронная музыка
- 24. Источник электропитания
- Часть II. Элементы цифровой техники и ЭВМ
- 25. Из истории развития электронной вычислительной техники
- 26. Способы представления информации в ЭВМ
- 27. Двоичная арифметика и структура ЭВМ
- Глава 7. ЭЛЕМЕНТЫ И УЗЛЫ ЦИФРОВОЙ ТЕХНИКИ
- 28. Логические схемы
- 29. Триггеры
- 30. Цифровые интегральные микросхемы
- 31. Индикаторные приборы
- 32. Шифраторы и дешифраторы
- 33. Сумматоры
- 34. Регистры
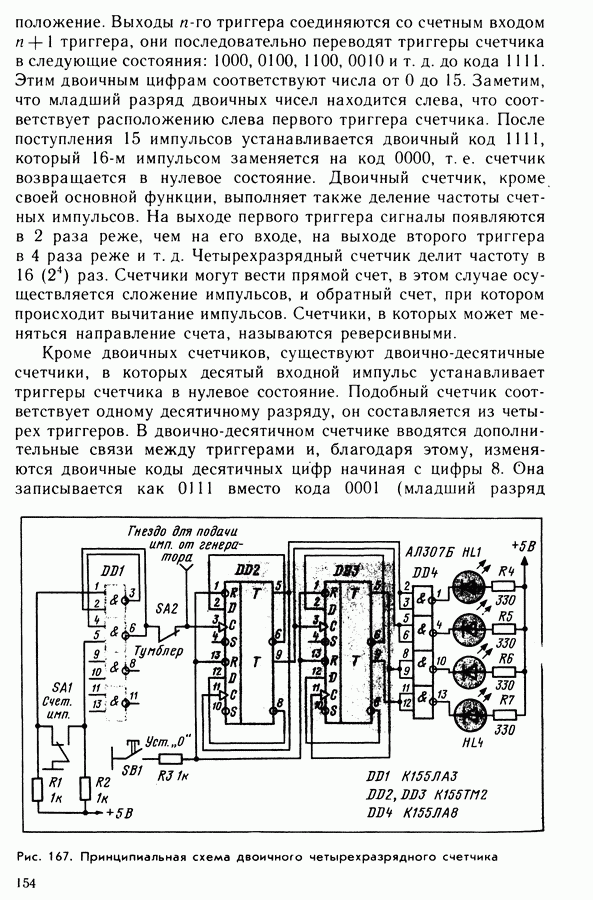
- 35. Счетчики электрических импульсов
- Глава 8. МОДЕЛИ ЦИФРОВЫХ АВТОМАТОВ
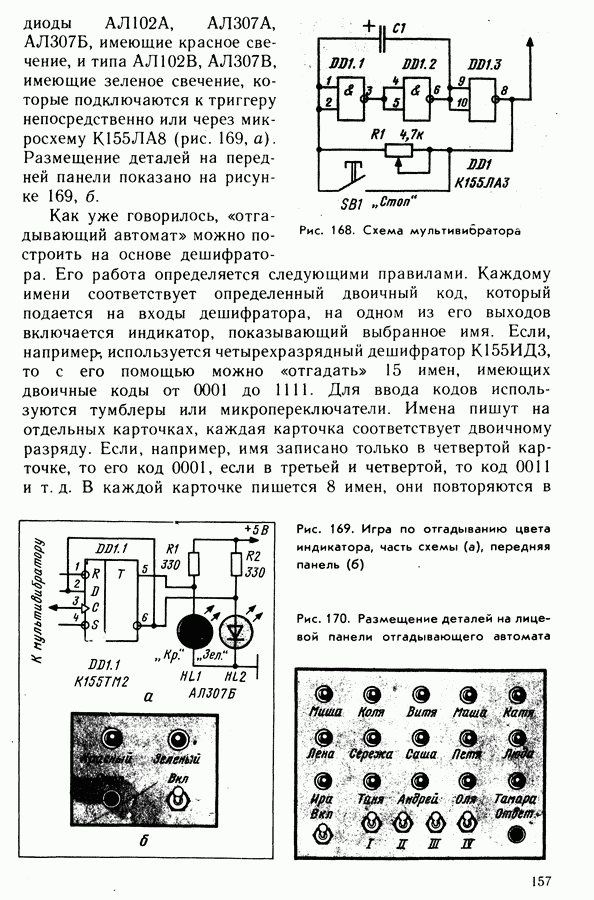
- 36. Игровые автоматы и кодовые замки
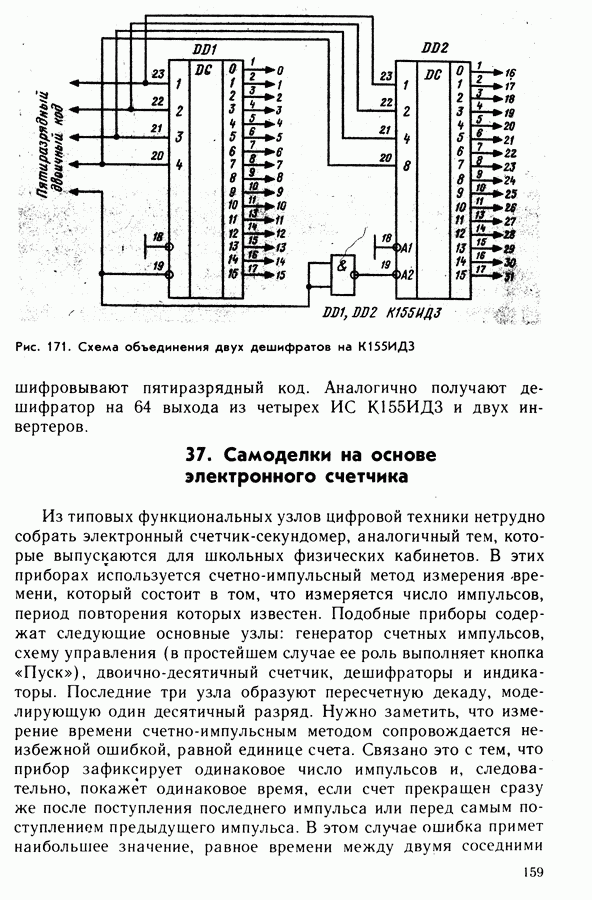
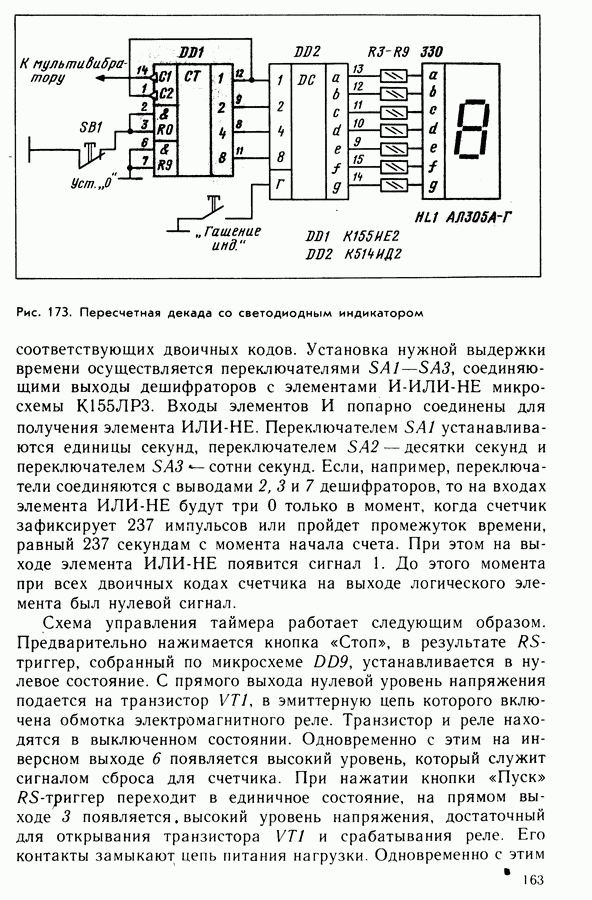
- 37. Самоделки на основе электронного счетчика
- 38. Модель «бегущие огни» световой рекламы и новогодней елочки
- Заключение
- СЛОВАРЬ ОСНОВНЫХ ТЕРМИНОВ