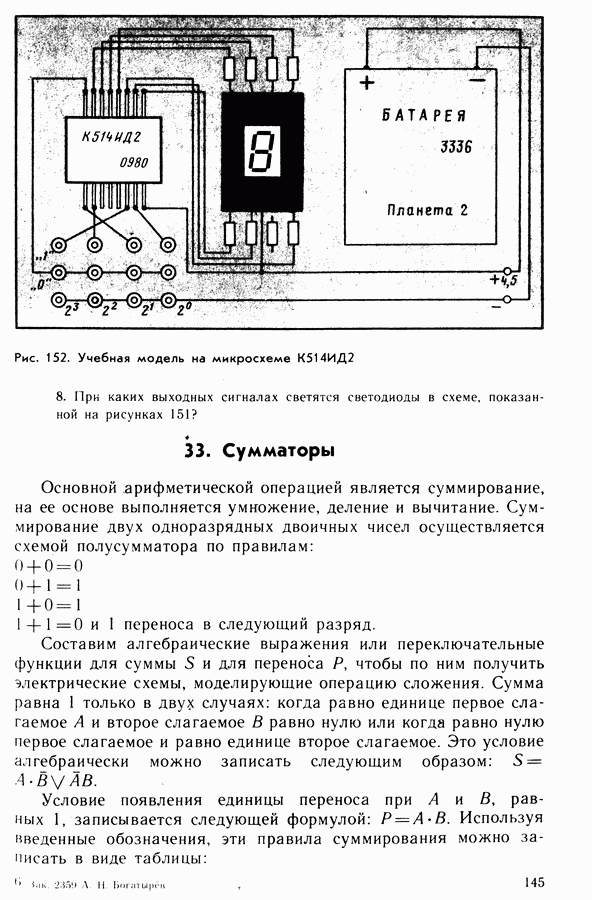
33. Сумматоры

Основной арифметической операцией является суммирование, на ее основе выполняется умножение, деление и вычитание. Суммирование двух одноразрядных двоичных чисел осуществляется схемой полусумматора по правилам:

1 + 1 = 0 и 1 переноса в следующий разряд.

Составим алгебраические выражения или переключательные функции для суммы 5 и для переноса чтобы по ним получить электрические схемы, моделирующие операцию сложения. Сумма равна 1 только в двух случаях: когда равно единице первое слагаемое А и второе слагаемое В равно нулю или когда равно нулю первое слагаемое и равно единице второе слагаемое. Это условие алгебраически можно записать следующим образом: .

Условие появления единицы переноса при А к В, равных 1, записывается следующей формулой: Используя введенные обозначения, эти правила суммирования можно записать в виде таблицы:

По этой таблице и по формулам для функций можно составить электрическую схему, моделирующую сложение двоичных чисел. Схема, составленная непосредственно по формуле для двоичной функции показана на рисунке 153. Переменным А и. В соответствуют замыкающие контакты, а переменным размыкающие контакты.

Упрощенная схема с переключающими контактами показана на рисунке 154. Схема, моделирующая образование суммы 5 и переноса называется полусумматором (рис. 155). Она, в соответствии с формулой для суммы 5, состоит из двух элементов НЕ, двух элементов И и элемента ИЛИ. Элемент НЕ инвертирует слагаемые, т. е. меняет их код на противоположный. На элементы И поступают слагаемые, представленные в прямом и обратном кодах, т. е. выходные сигналы подаются на элемент ИЛИ. Для получения единицы переноса служит элемент И, на который непосредственно подаются слагаемые Упрощенный вариант этой структурной схемы показан на рисунке 156. Условное обозначение полусумматора показано на рисунке 157.

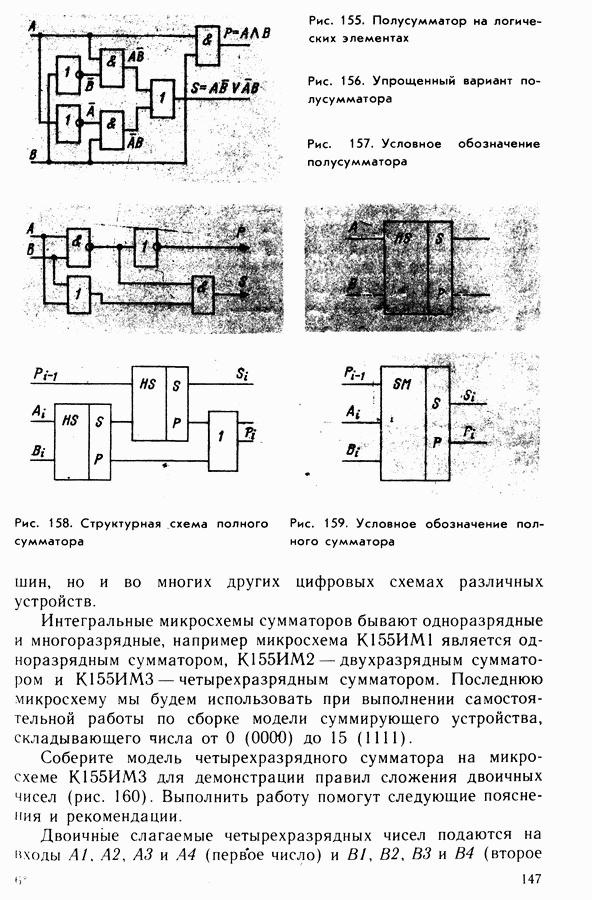
Сложение многоразрядных чисел осуществляется с помощью полных сумматоров, в которых суммируются не только слагаемые, но и единицы переноса из предыдущих разрядов, если они образуются при сложении. Полный одноразрядный сумматор состоит из двух полусумматоров. Структурная схема и условное обозначение одноразрядного сумматора показаны на рисунках 158 и 159.

Сумматоры, являющиеся типовым узлом ЭВМ, применяются не только в арифметических устройствах вычислительных

Рис. 153. Схема суммирующего устройства, составленная по формуле

Рис. 154. Схема суммирующего устройства с использованием переключающих контактов

Рис. 155. Полусумматор на логических элементах

Рис. 156. Упрощенный вариант полусумматора

Рис. 157. Условное обозначение полусумматора

Рис. 158. Структурная схема полного сумматора

Рис. 159. Условное обозначение полного сумматора

машин, но и во многих других цифровых схемах различных устройств.

Интегральные микросхемы сумматоров бывают одноразрядные и многоразрядные, например микросхема является одноразрядным сумматором, двухразрядным сумматором и четырехразрядным сумматором. Последнюю микросхему мы будем использовать при выполнении самостоятельной работы по сборке модели суммирующего устройства, складывающего числа от 0 (0000) до 15 (1111).

Соберите модель четырехразрядного сумматора на микросхеме для демонстрации правил сложения двоичных чисел (рис. 160). Выполнить работу помогут следующие пояснения и рекомендации.

Двоичные слагаемые четырехразрядных чисел подаются на входы (первое число) и и (второе

Рис. 160. Учебная модель для сложения чисел с использованием микросхемы

число). В каждом разряде образуется сумма и сигнал переноса в следующий разряд . В схеме сумматора имеется возможность учитывать сигнал переноса из предыдущего, младшего разряда (вход РО). В нашем случае являются младшими разрядами слагаемых чисел, поэтому на вход должен подаваться нулевой сигнал, который в схеме соединяется с общим проводом источника. Двоичные числа на вход подаются с помощью переключателей, как и в схеме интегрального дешифратора. Схема включения индикаторных диодов другая по сравнению с дешифратором так как у микросхемы выходы прямые, т.е. если сумма равна единице, то на выходе.

Рис. 161. Схема расположения переключателей и индикаторов на учебной модели

сигнал единица. Вывод 12 микросхемы соединяется с общим зажимом источника, а к выводу 5 подается напряжение +4,5 или +5 В.

Для наглядности переключатели (тумблеры) и светодиоды можно расположить, как при сложении «столбиком» (рис. 161, а). Еще лучше использовать светодиоды и для индикации входных сигналов, как это было в схеме дешифратора (см. рис. 151). Необходимые изменения в схему модели суммирующего устройства внесите сами. В этом случае светодиоды складываемых разрядов и суммы располагают, как показано на рисунке 161, б. Модель будет более привлекательна, если использовать светодиоды разного цвета.

(см. скан)