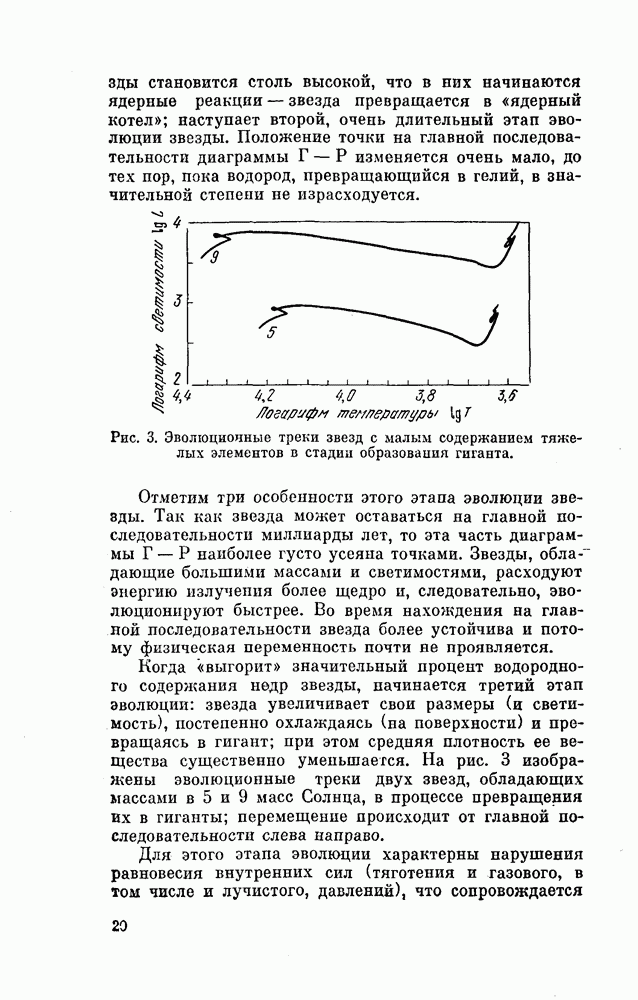
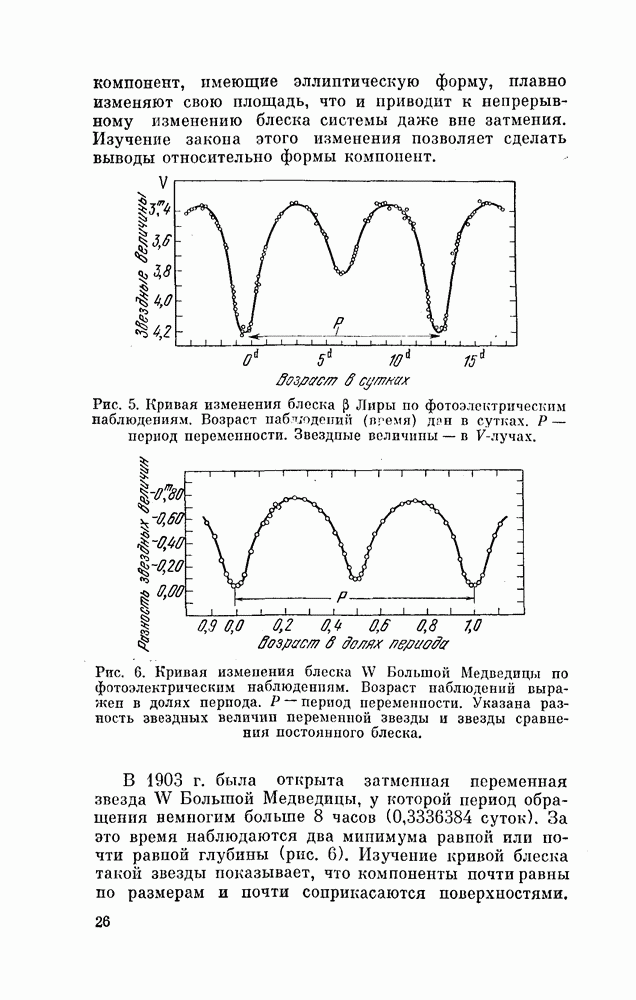
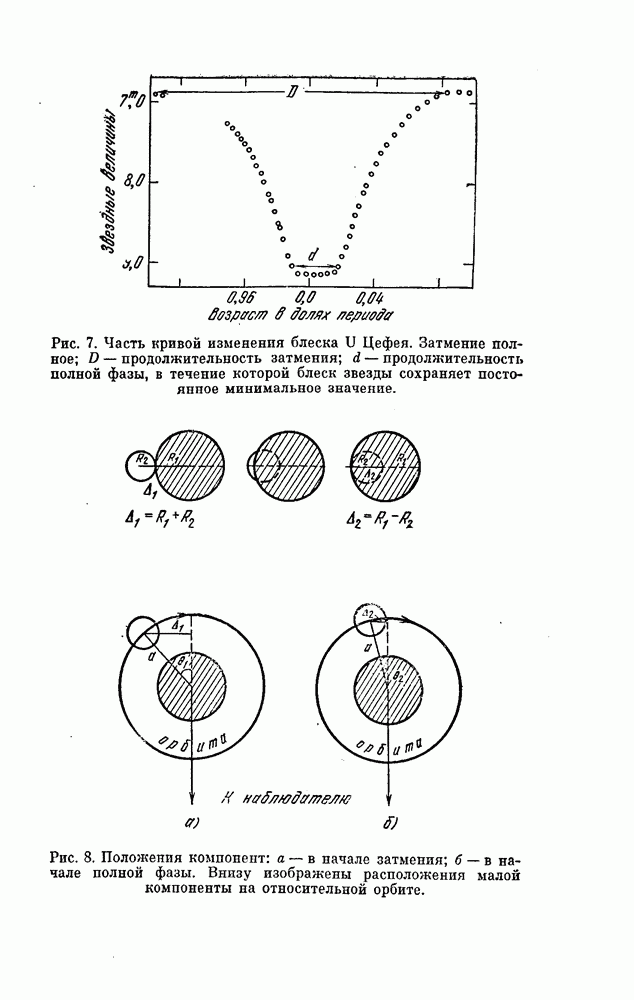
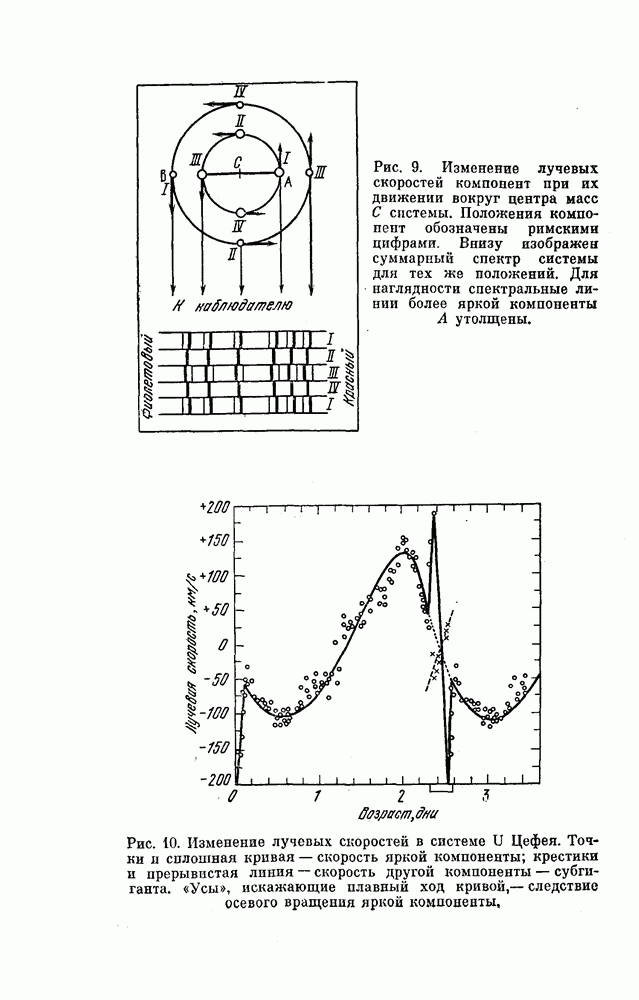
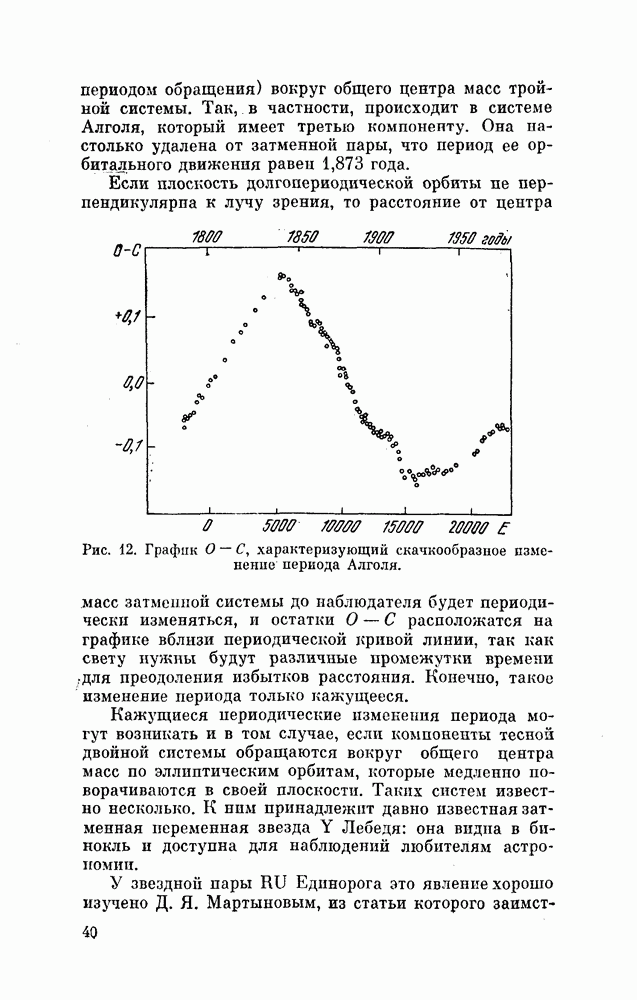
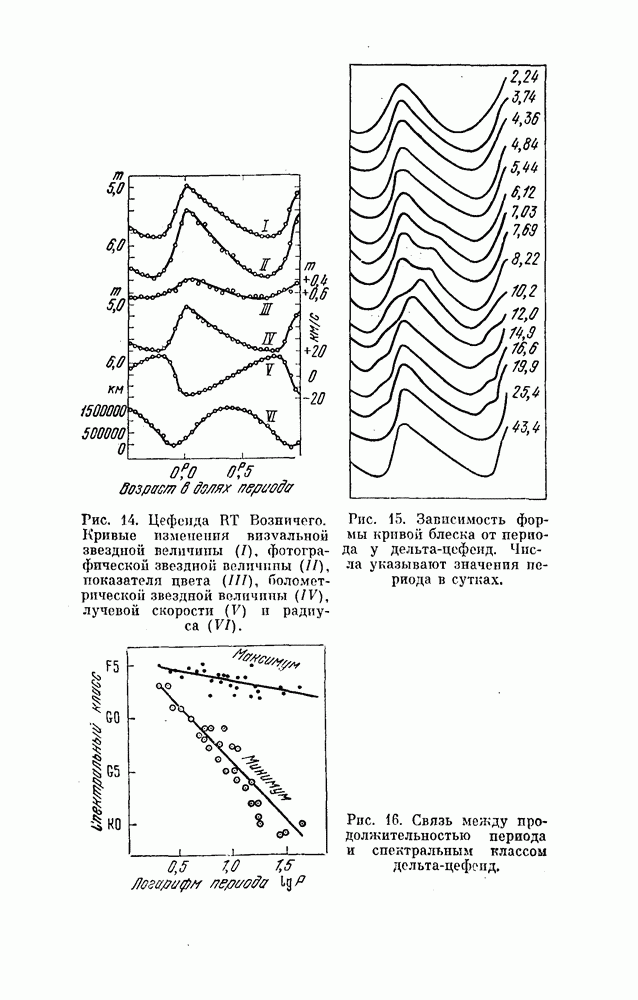
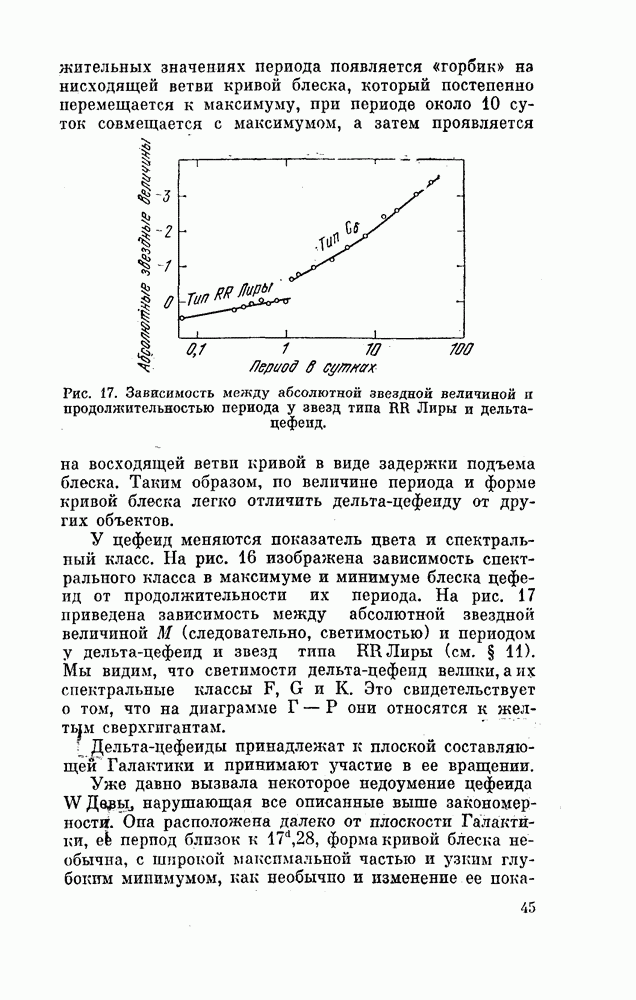
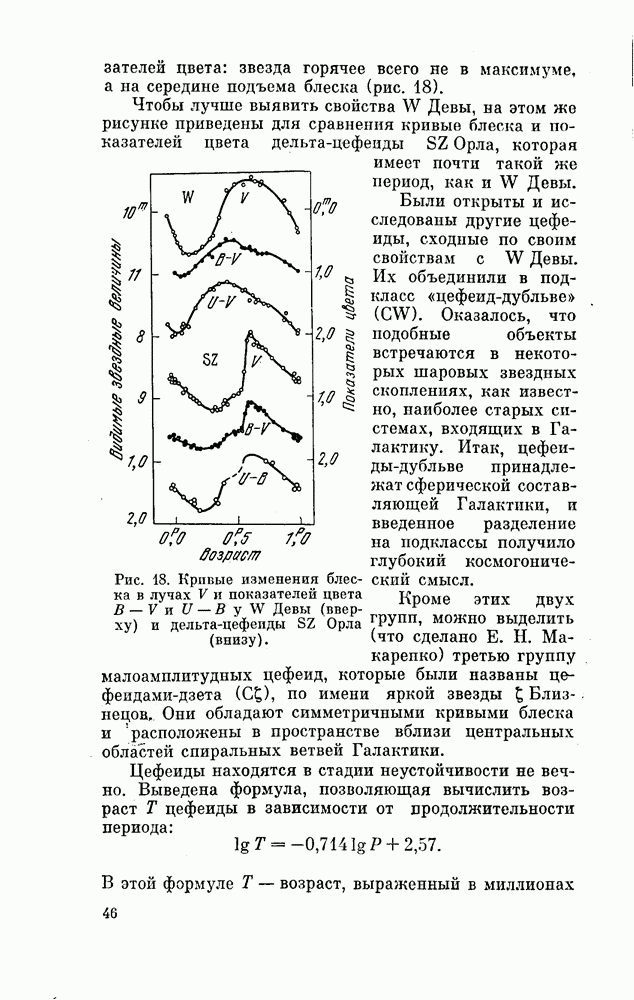
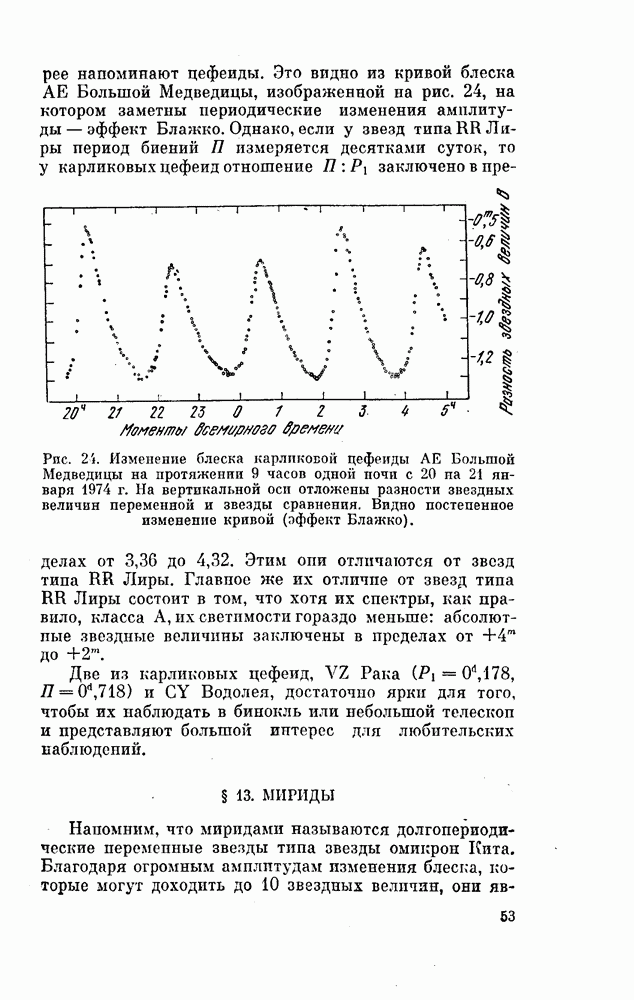
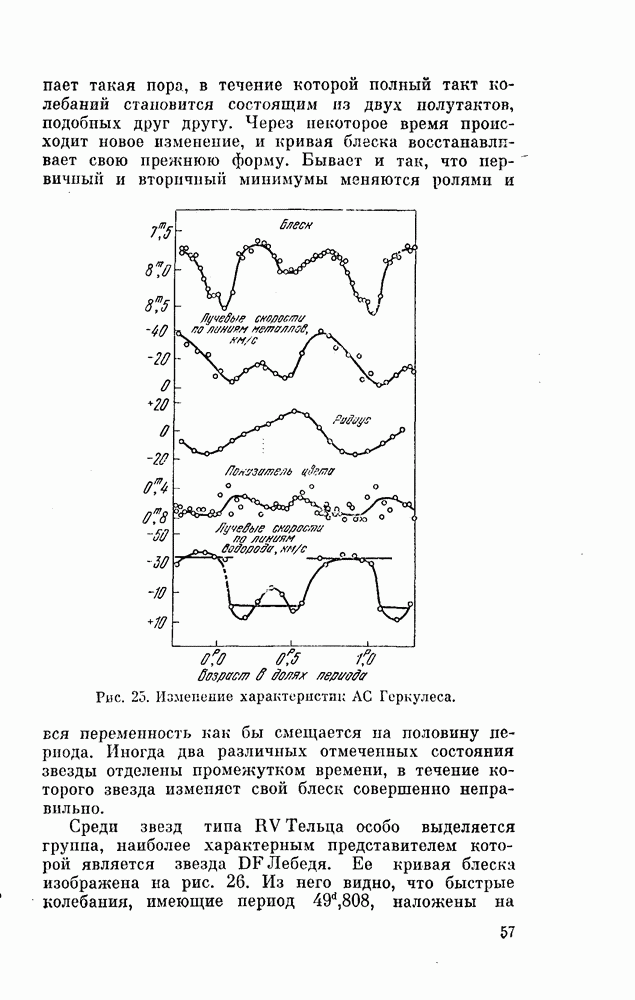
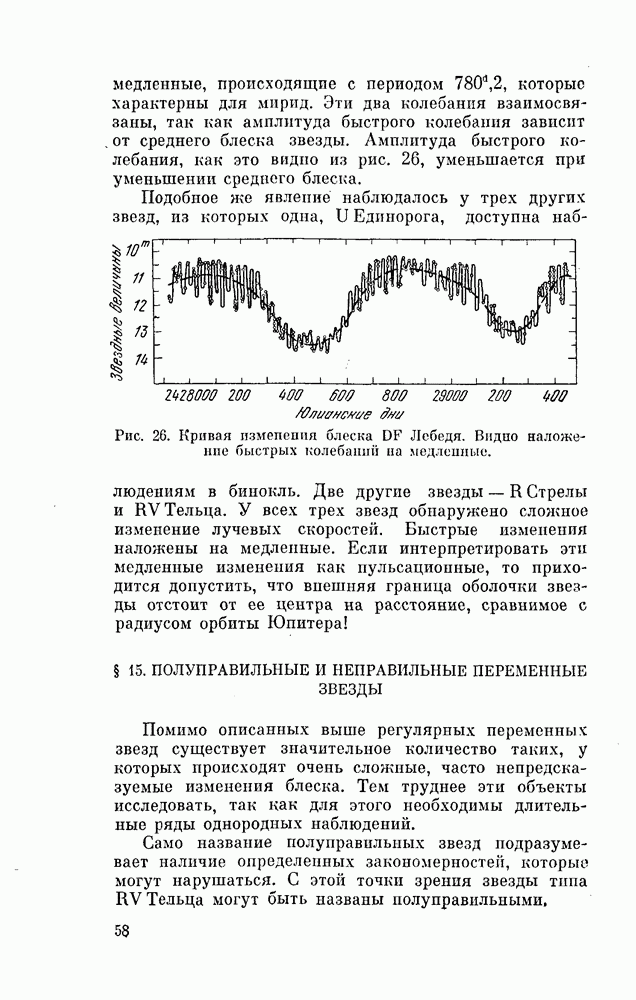
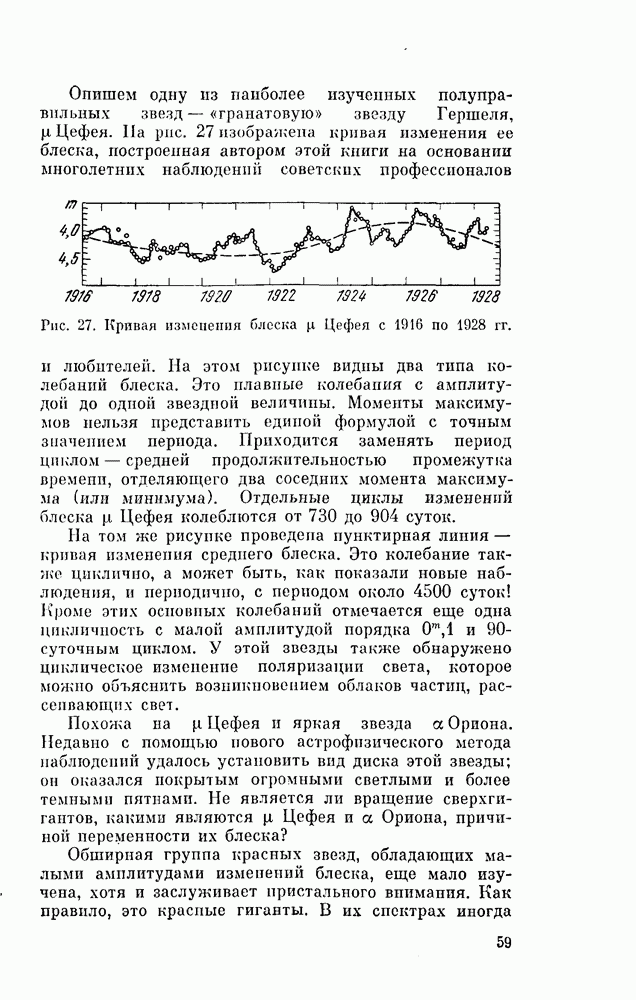
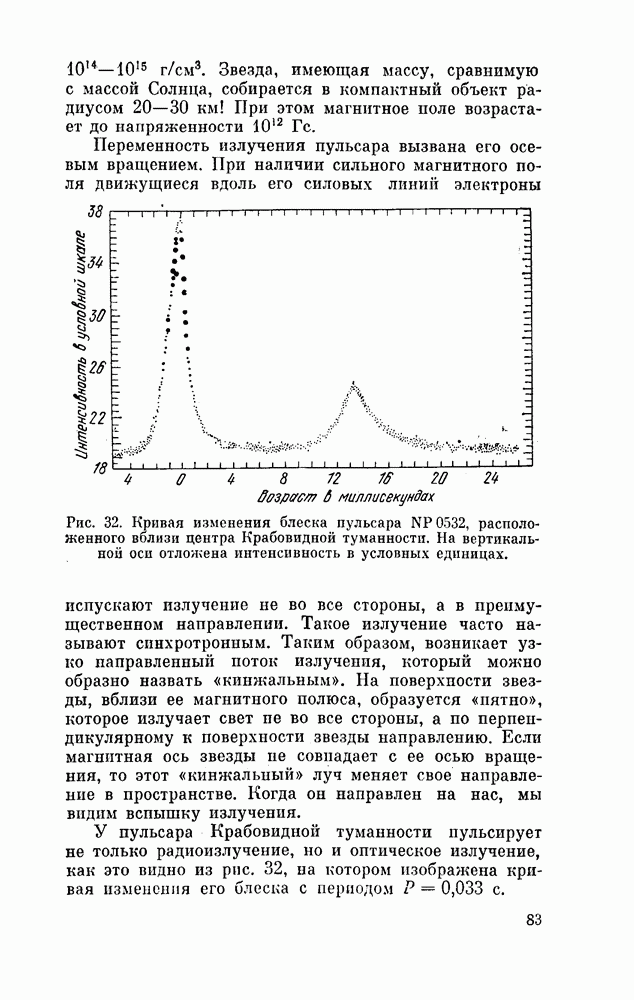
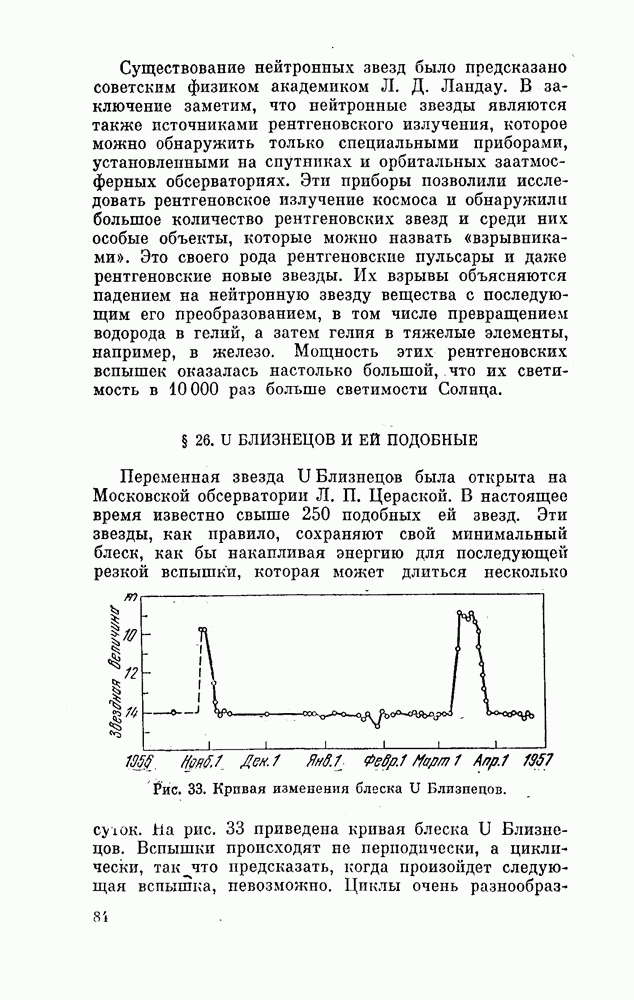
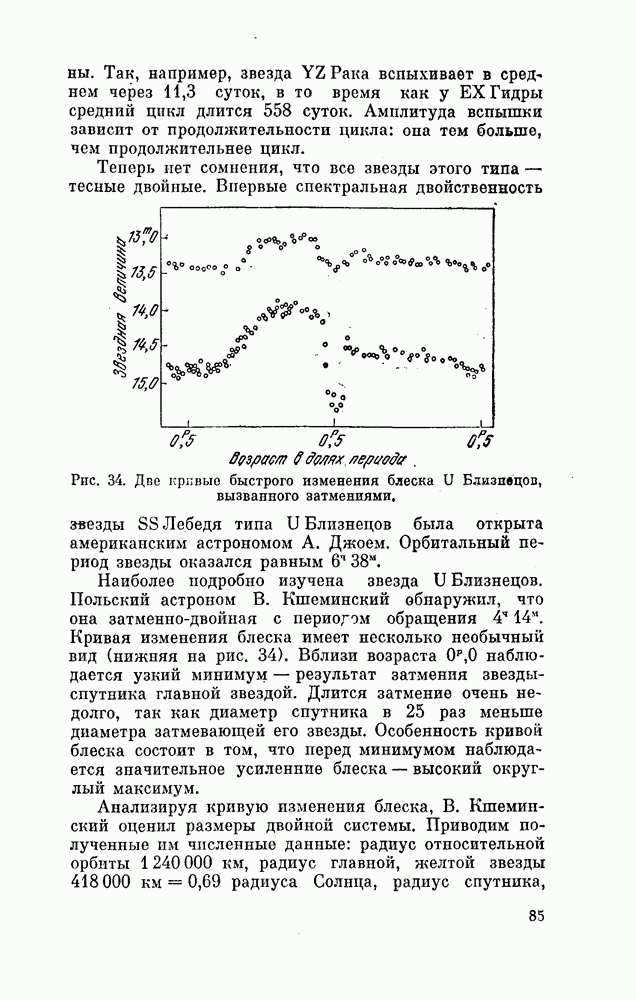
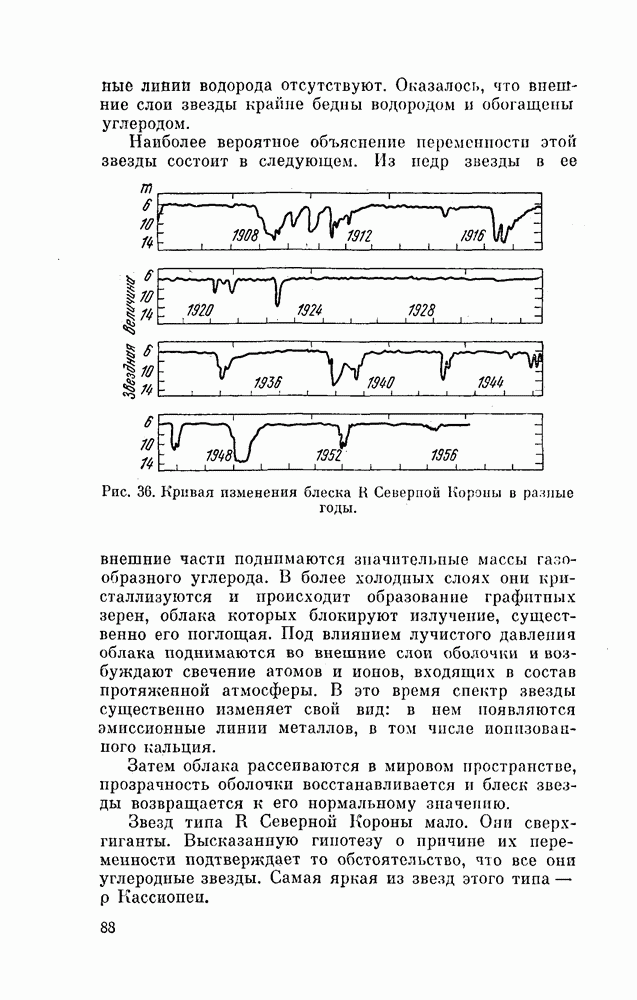
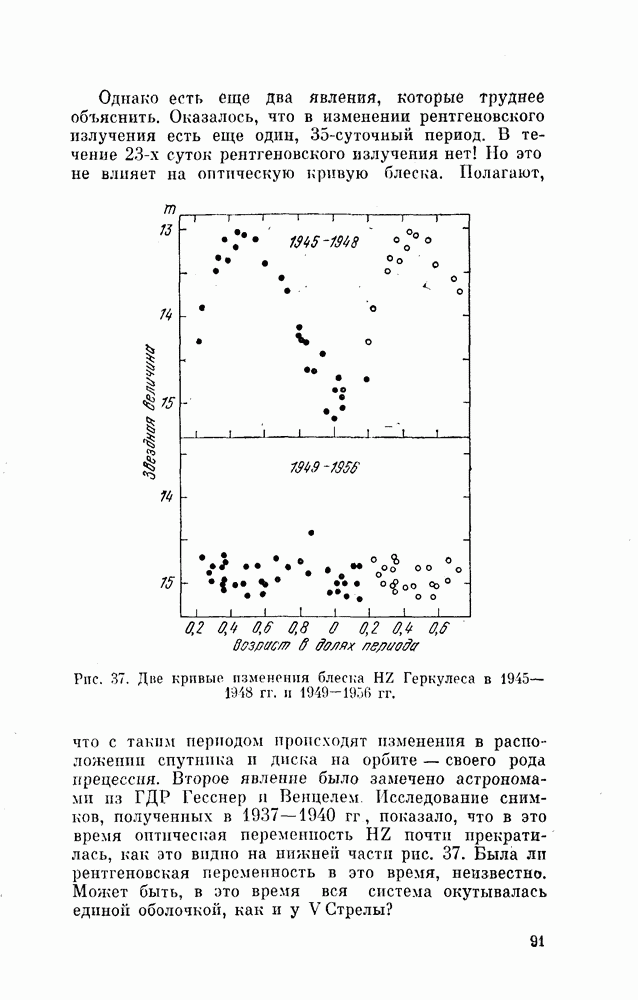
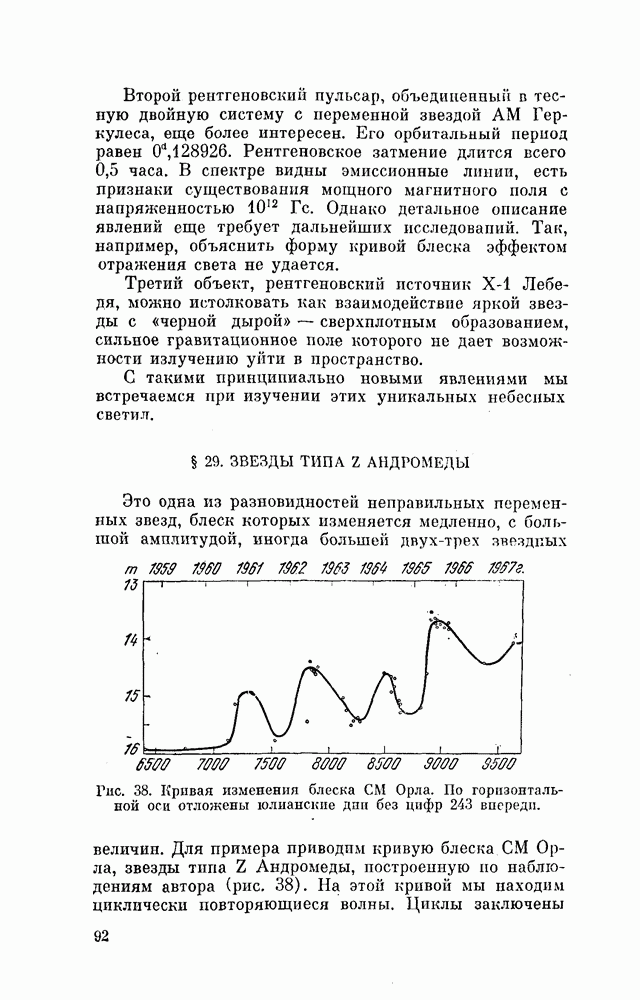
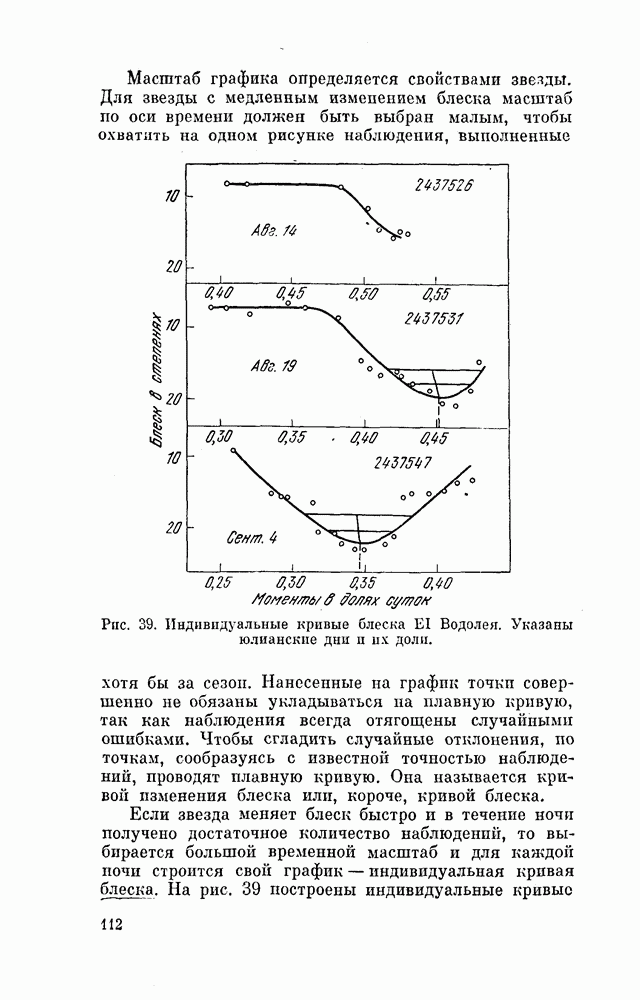
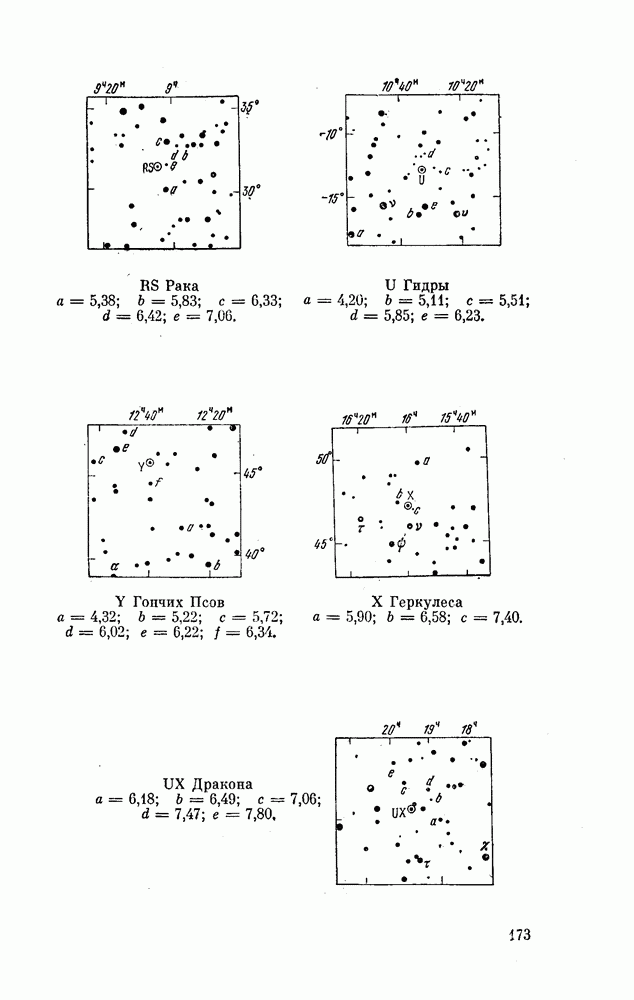
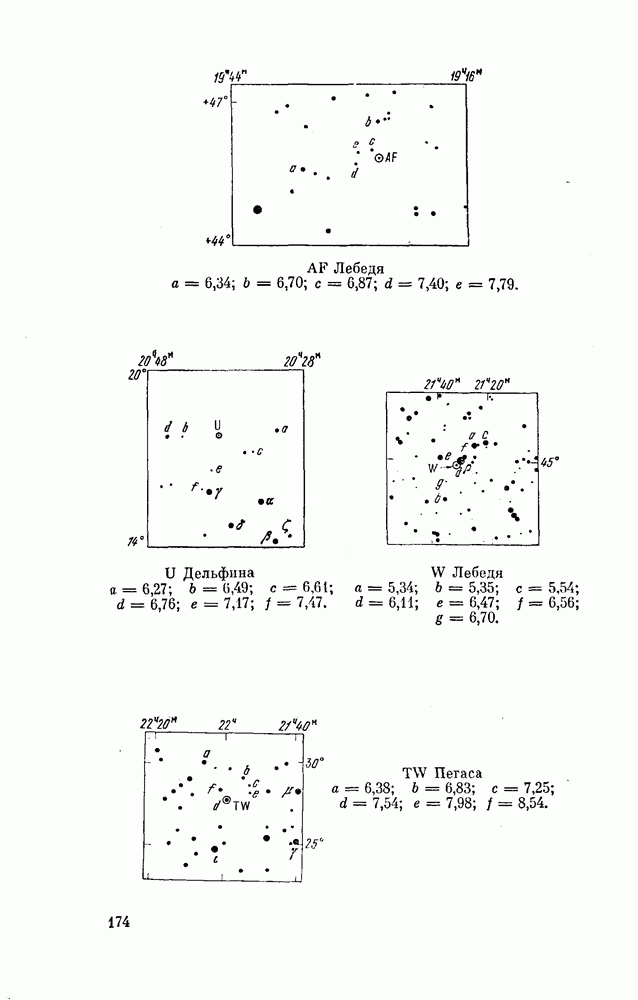
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 32 РЕДУКЦИЯ ШКАЛ
Несмотря на то, что отдельная оценка блеска может быть не очень точной, выведенная из многих оценок шкала блеска звезд сравнения, как показывает практика, очень устойчива, т. е. гораздо точнее отдельного наблюдения. Здесь берет свое массовость определений, которая сглаживает случайные ошибки. Поэтому метод Нейланда — Блажко можно считать наилучшим из трех описанных способов наблюдений даже в том случае, если известны каталожные (взятые из каталога) звездные величины, определенные фотометрами.
Допустим, что наблюдатель произвел длительные ряды наблюдений одной и той же переменной звезды, пользуясь теми же самыми звездами сравнения. Естественно, что за время наблюдений его опыт увеличился, и цена степени могла измениться. Из наблюдений, полученных в два сезона, выведены две различные шкалы. Как их связать друг с другом?
Положим в основу допущение, что шкалы связаны между собой линейной зависимостью, т. е. удовлетворяют уравнению

где  — блеск в прежней,
— блеск в прежней,  — в новой шкале, а — значение нуль-пункта новой шкалы и b — переводный коэффициент.
— в новой шкале, а — значение нуль-пункта новой шкалы и b — переводный коэффициент.
Для каждой звезды составляется такое уравнение, и система с избыточным числом условных уравнении решается по способу наименьших квадратов (см. Дополнение 1), для чего составляются два нормальных уравнения. Их решение по правилам алгебры дает значения неизвестных а и b, которые обозначим через 
Тогда уравнение (21) становится эмпирической формулой для перехода от старой шкалы  к новой
к новой 

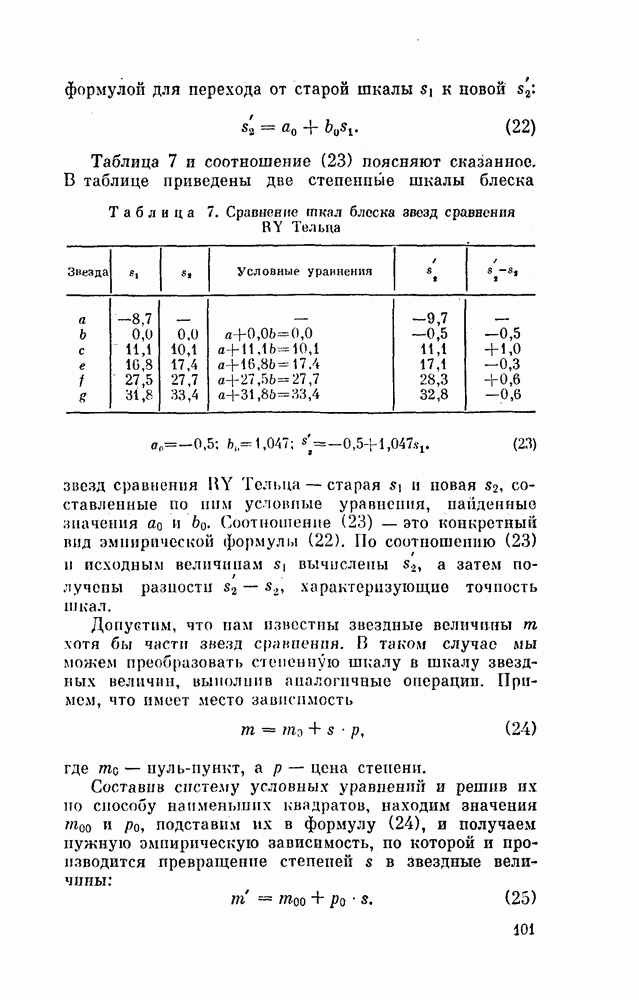
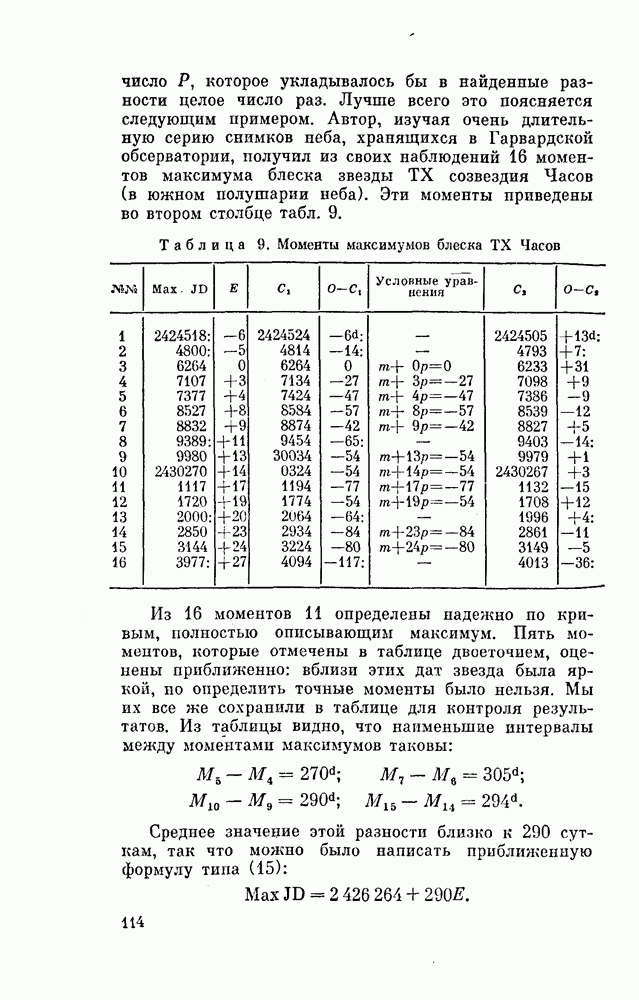
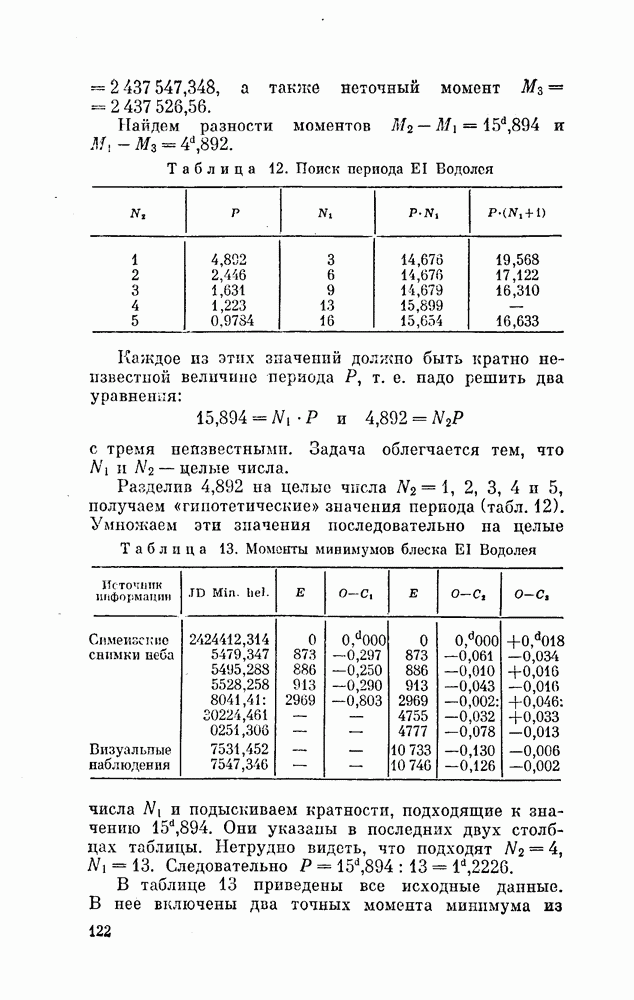
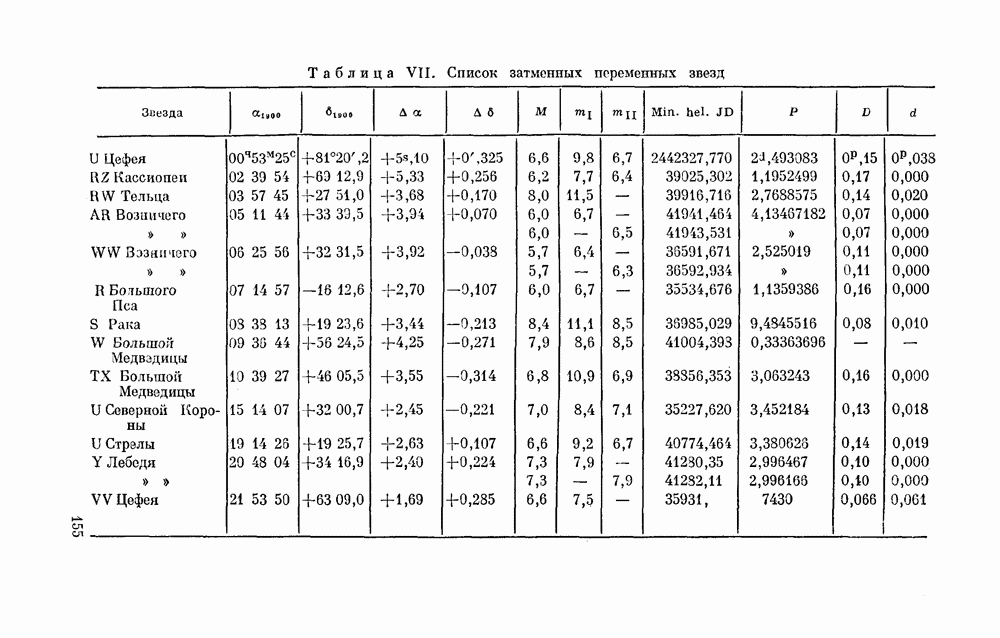
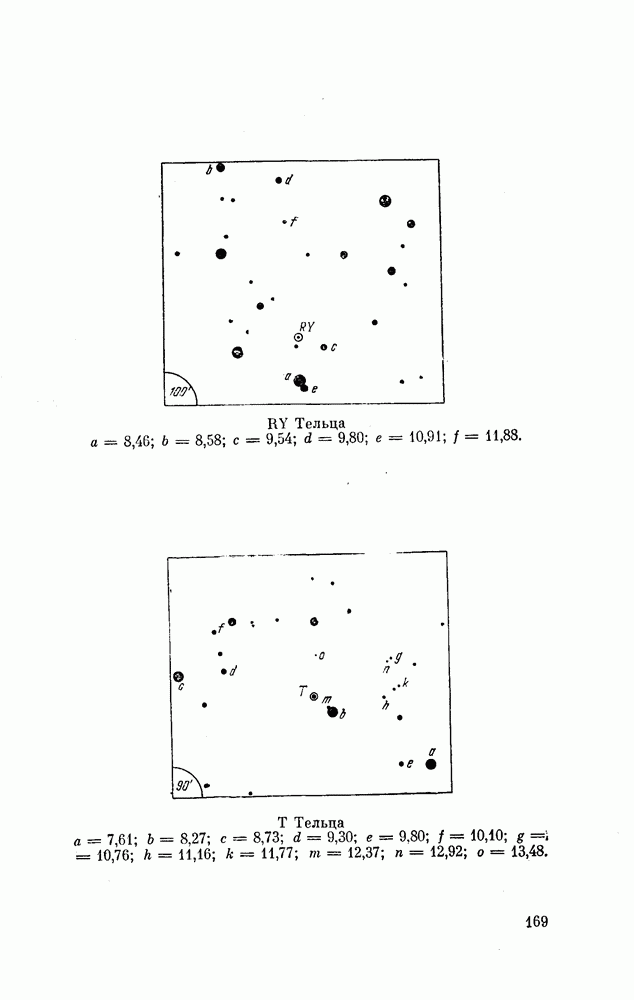
Таблица 7 и соотношение (23) поясняют сказанное. В таблице приведены две степенные шкалы блеска
Таблица 7. Сравнение шкал блсска звезд сравнения RY Тельца


звезд сравнения НУ Тельца — старая s] и новая  составленные по ним условные уравнения, найденные значения
составленные по ним условные уравнения, найденные значения  . Соотношение (23) — это конкретный вид эмпирической формулы (22). По соотношению (23) и исходным величинам s 1 вычислены
. Соотношение (23) — это конкретный вид эмпирической формулы (22). По соотношению (23) и исходным величинам s 1 вычислены  а затем получены разности
а затем получены разности  характеризующие точность шкал.
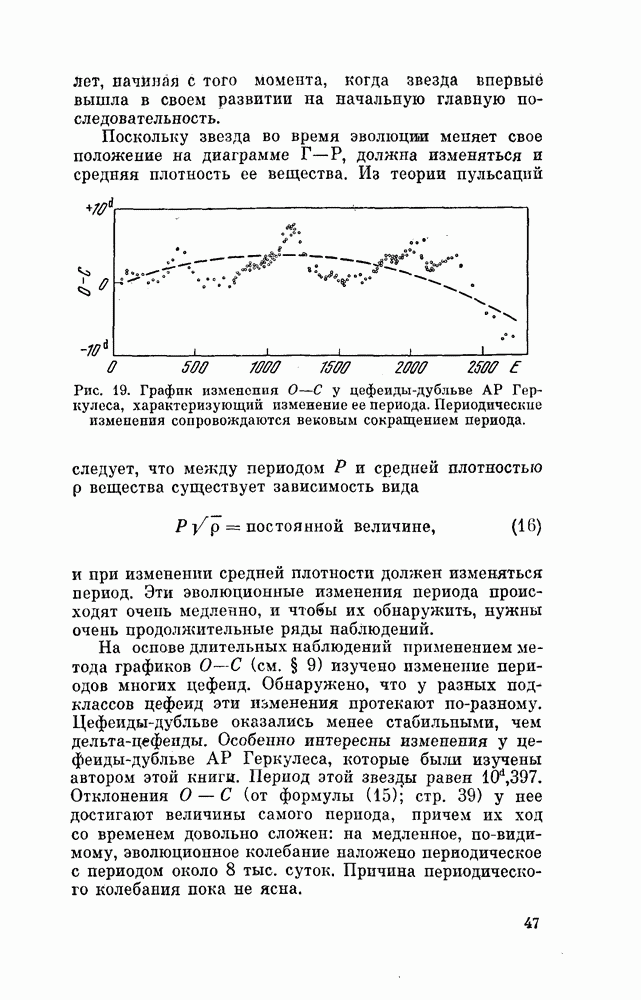
характеризующие точность шкал.
Допустим, что нам известны звездные величины  хотя бы части звезд сравнения. В таком случае мы можем преобразовать степенную шкалу в шкалу звездных величин, выполнив аналогичные операции. Примем, что имеет место зависимость
хотя бы части звезд сравнения. В таком случае мы можем преобразовать степенную шкалу в шкалу звездных величин, выполнив аналогичные операции. Примем, что имеет место зависимость

где  — нуль-пункт, а
— нуль-пункт, а  — цена степени.
— цена степени.
Составив систему условных уравнений и решив их по способу наименьших квадратов, находим значения  подставим их в формулу (24), и получаем нужную эмпирическую зависимость, по которой и производится превращение степеней s в звездные величипы:
подставим их в формулу (24), и получаем нужную эмпирическую зависимость, по которой и производится превращение степеней s в звездные величипы:

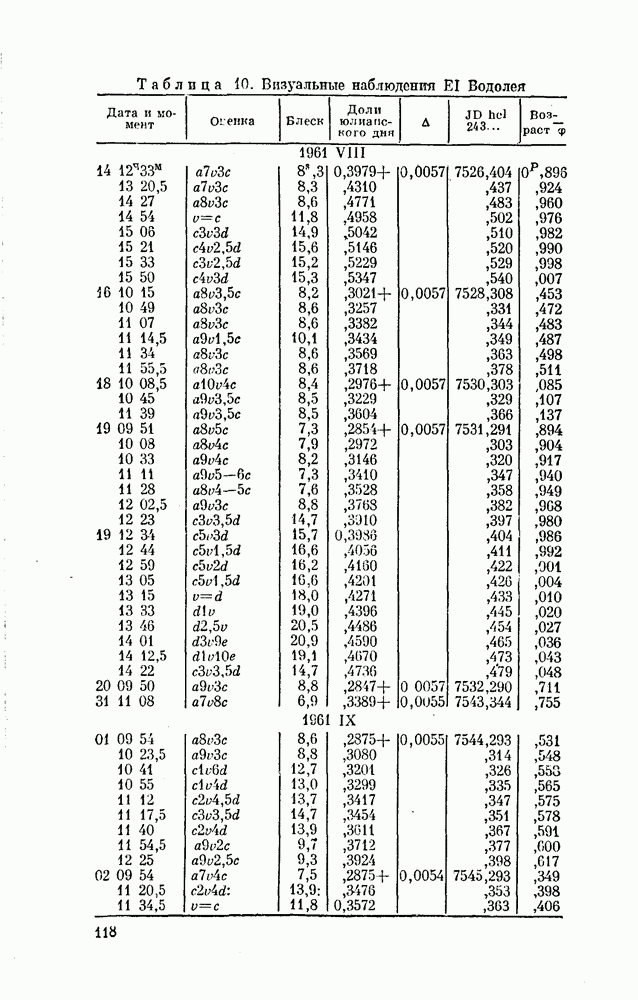
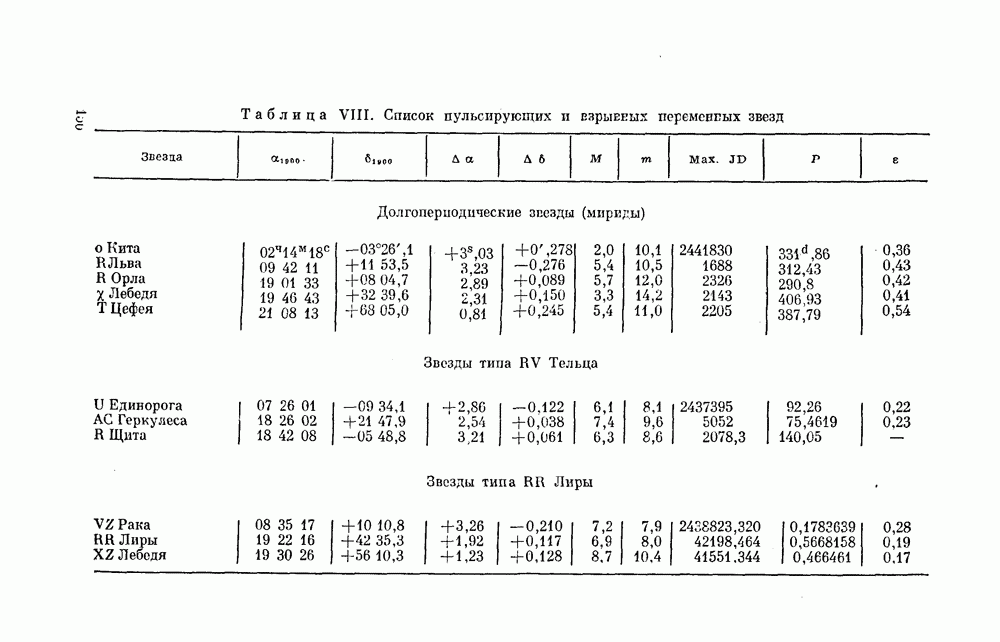
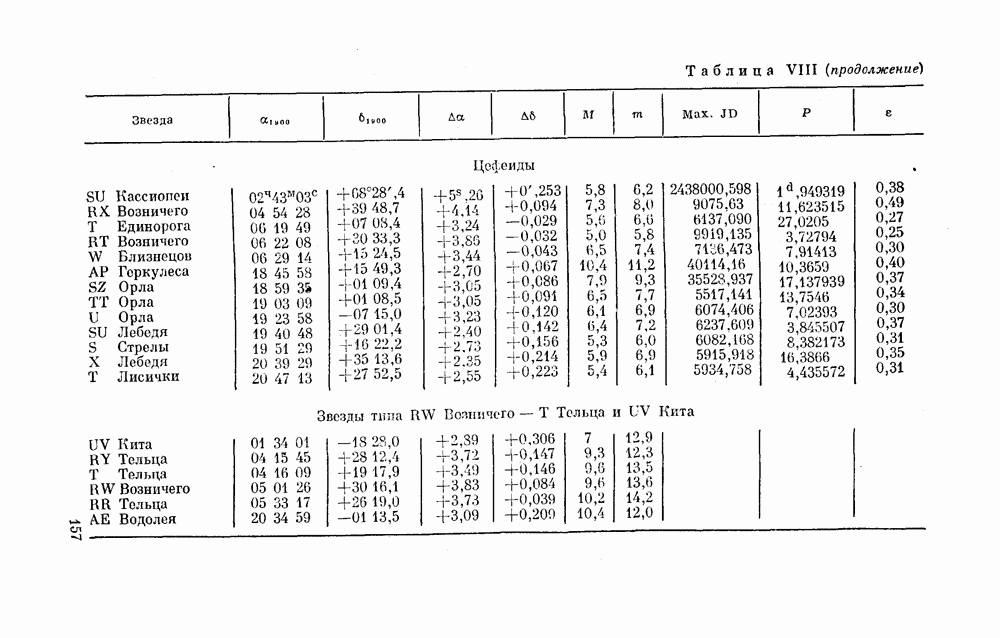
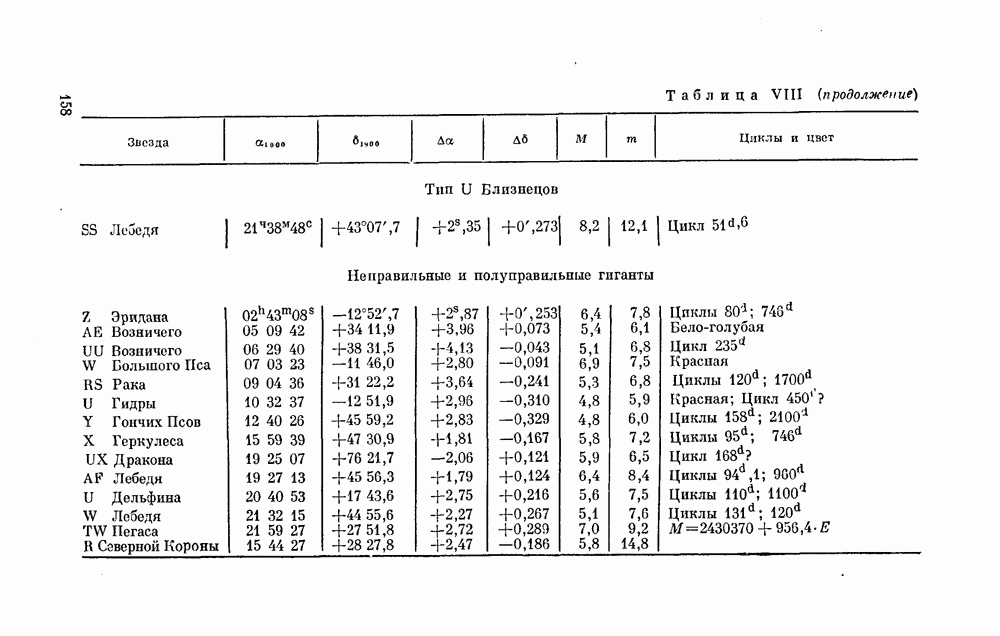
В таблице 8 приведен численный пример. Заданы та же (см. табл. 7) шкала блеска звезд сравнения RY Тельца и их звездные величины. Написаны условные уравнения, по ним составлены нормальные уравнения, получено их решение  и в результате найдена формула (26) для вычисления звездных величин
и в результате найдена формула (26) для вычисления звездных величин  .
.
Таблица 8. Преобразование степенной шкалы звезд сравнения RY Тельца в звездные величины

Описанный процесс привязки степенной шкалы к шкале звездных величин приближенный. Он требует некоторых уточнений.
Дело в том, что цветоощущение глаз различных наблюдателей разное, в каждый наблюдатель, определяет «свои» звездные величины. Они могут не совпадать со звездными величинами каталога. Поэтому при переходе от степенной шкалы к звездным величинам следует учесть и цвет звезд сравнения, который определяется показателем цвета С (или B-V). Формула связи имеет вид

По этой формуле составляются для каждой звезды условные уравнения по типу предыдущих; они содержат три подлежащих определению неизвестных:  . Неизвестное с — цветовой коэффициент системы звездных величин наблюдателя.
. Неизвестное с — цветовой коэффициент системы звездных величин наблюдателя.
Решаются эти условные уравнения также по способу наименьших квадратов.
Все сказанное относится в равной мере как к визуальным, так и к фотографическим наблюдениям. Фотоматериалы также обладают различной, отнюдь не стандартной цветочувствительностью.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ВВЕДЕНИЕ
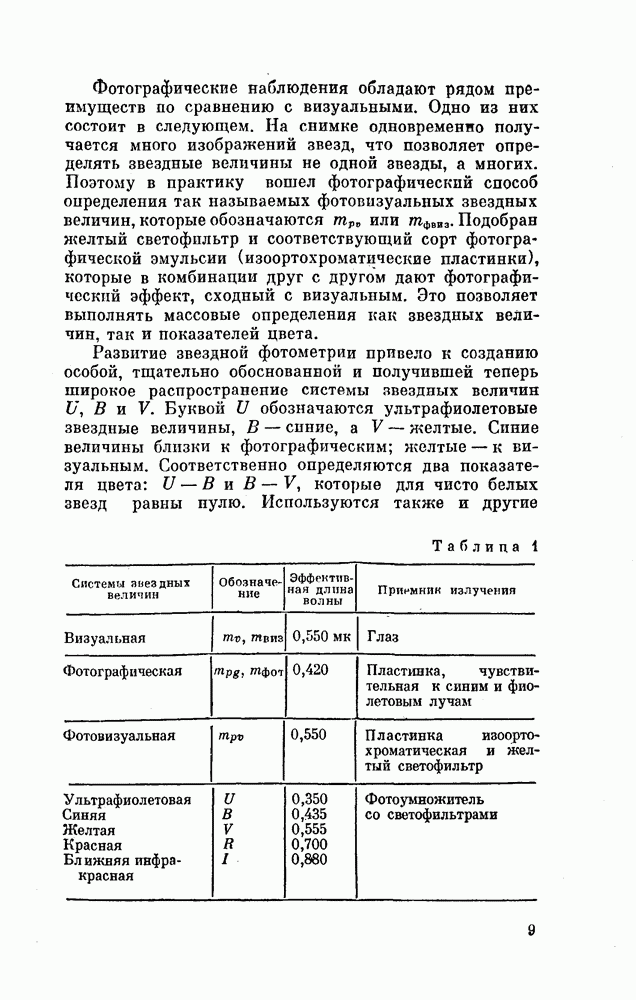
- § 1. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ЦВЕТА
- § 2. СВЕТИМОСТИ И РАДИУСЫ ЗВЕЗД
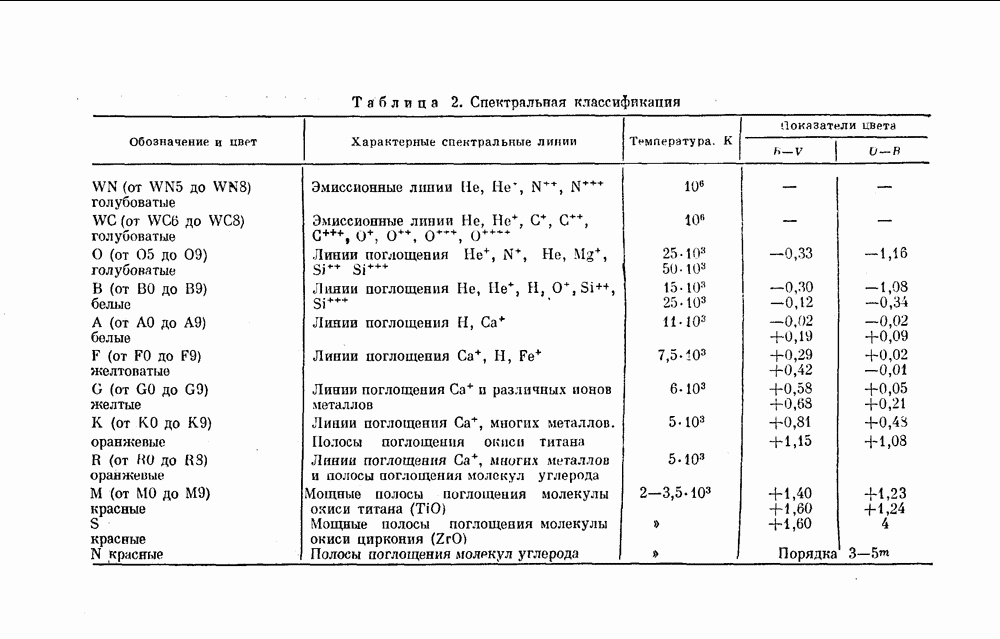
- § 3. СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ И ЛУЧЕВЫЕ СКОРОСТИ
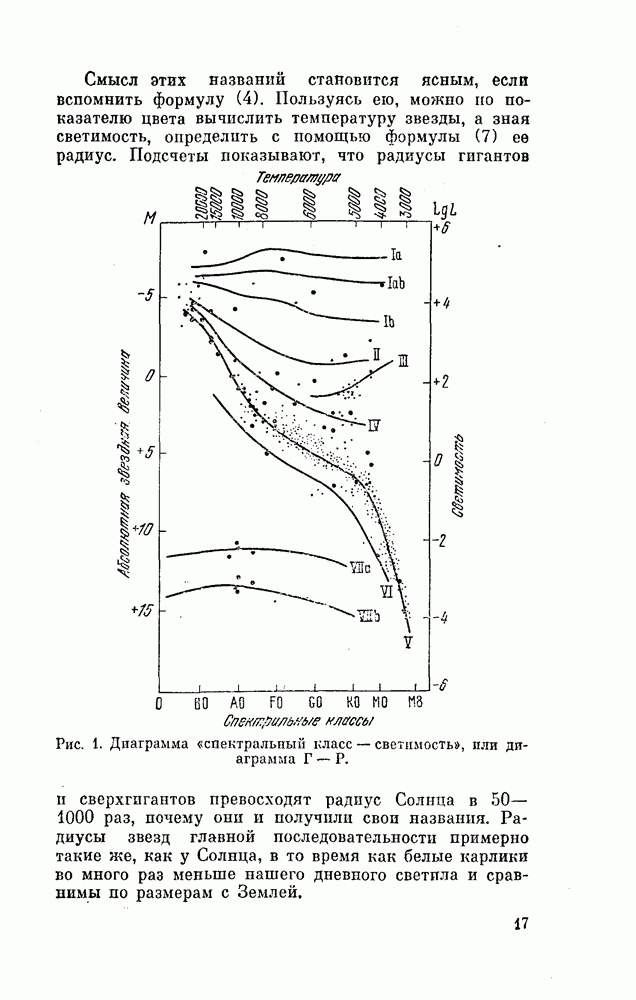
- § 4. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- § 5. ТИПЫ ЗВЕЗДНОГО НАСЕЛЕНИЯ
- ГЛАВА II. ЗАТМЕННЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 6. КЛАССИФИКАЦИЯ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
- § 7. ЧТО ДАЕТ ИЗУЧЕНИЕ КРИВОЙ БЛЕСКА ЗВЕЗДЫ ТИПА АЛГОЛЯ?
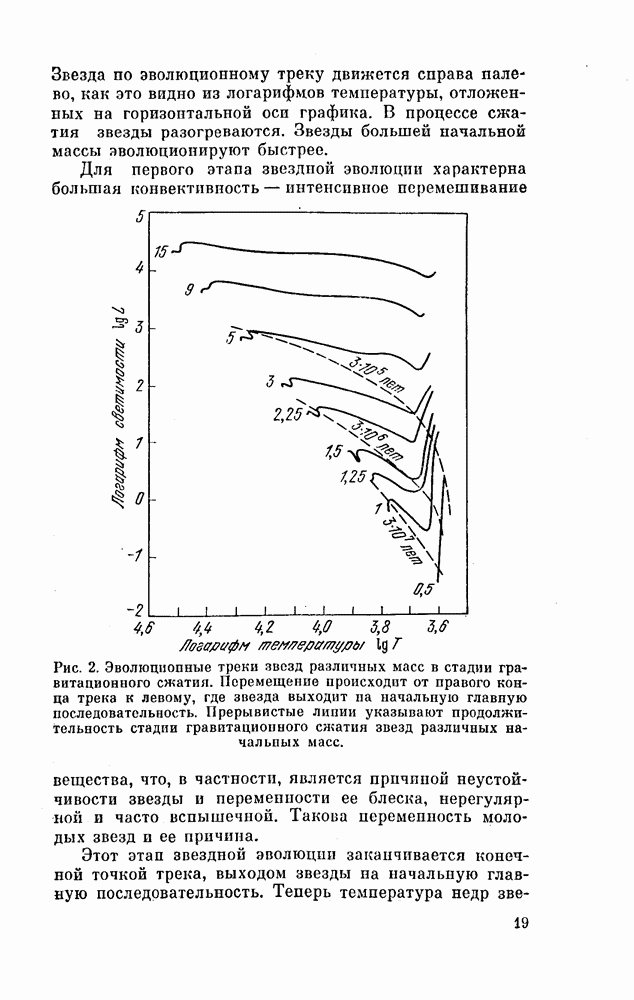
- § 8. ЭВОЛЮЦИЯ ТЕСНОЙ ДВОЙНОЙ ЗВЕЗДЫ
- § 9. ИЗМЕНЕНИЕ ПЕРИОДОВ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
- ГЛАВА III. ПУЛЬСИРУЮЩИЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 10. ЦЕФЕИДЫ, ИЛИ ЗВЕЗДЫ ТИПА б ЦЕФЕЯ
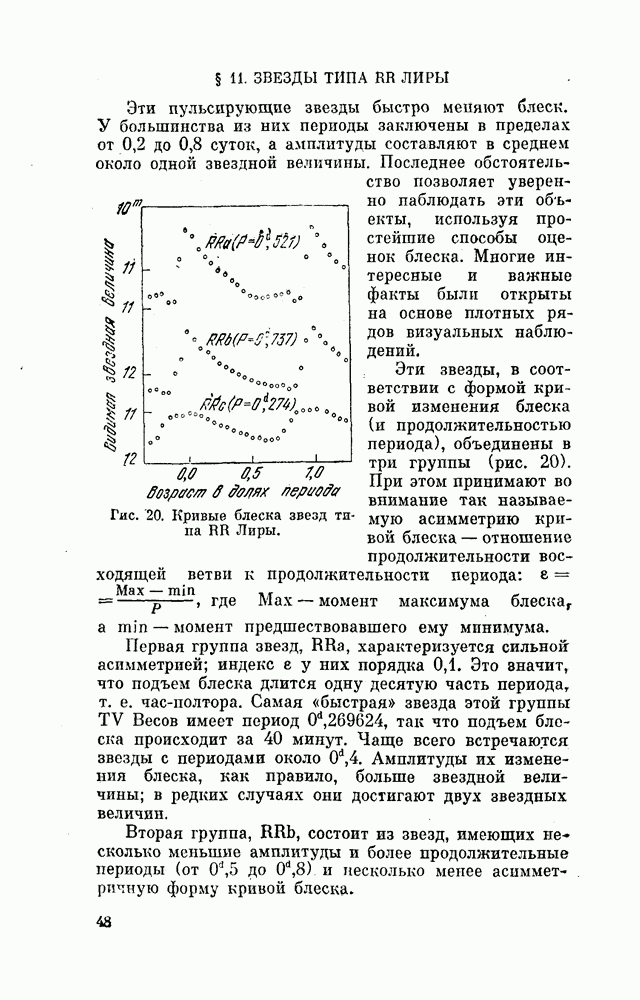
- § 11. ЗВЕЗДЫ ТИПА RR ЛИРЫ
- § 12. КАРЛИКОВЫЕ ЦЕФЕИДЫ
- § 13. МИРИДЫ
- § 14. ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА
- § 15. ПОЛУПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
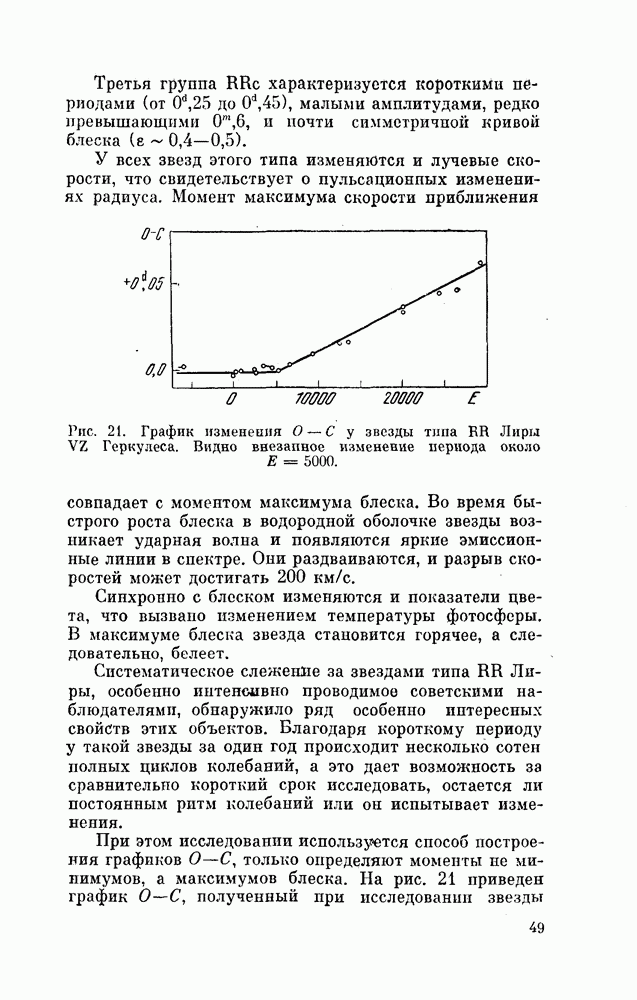
- § 16. ПЕРЕМЕННЫЕ ЗВЕЗДЫ, ОБЛАДАЮЩИЕ МАЛЫМИ АМПЛИТУДАМИ
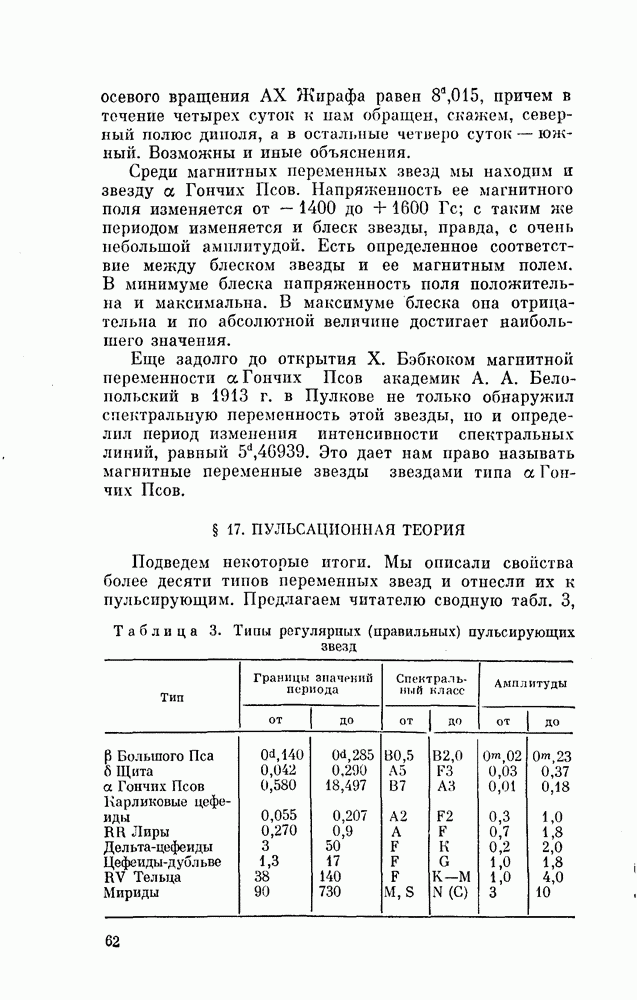
- § 17. ПУЛЬСАЦИОННАЯ ТЕОРИЯ
- ГЛАВА IV. ПЕРЕМЕННОСТЬ МОЛОДЫХ ЗВЕЗД
- § 18. ЗВЕЗДЫ ТИПА UV КИТА
- § 19. ВСПЫШЕЧНЫЕ ЗВЕЗДЫ
- § 20. ЗВЕЗДЫ ТИПА RW ВОЗНИЧЕГО — Т ТЕЛЬЦА
- § 21. ФУОРЫ И АНТИФУОРЫ
- ГЛАВА V. ВЗРЫВАЮЩИЕСЯ ЗВЕЗДЫ
- § 22. ТИПЫ ВЗРЫВАЮЩИХСЯ ЗВЕЗД
- § 23. ЯВЛЕНИЯ, ПРОИСХОДЯЩИЕ ПРИ ВСПЫШКЕ НОВОЙ ЗВЕЗДЫ
- § 24. ЗАГАДКА DQ ГЕРКУЛЕСА
- § 25. «ЗВЕЗДА-ГОСТЬЯ» В СОЗВЕЗДИИ ТЕЛЬЦА
- § 26. U БЛИЗНЕЦОВ И ЕЙ ПОДОБНЫЕ
- § 27. ТИХИЕ ВЗРЫВЫ
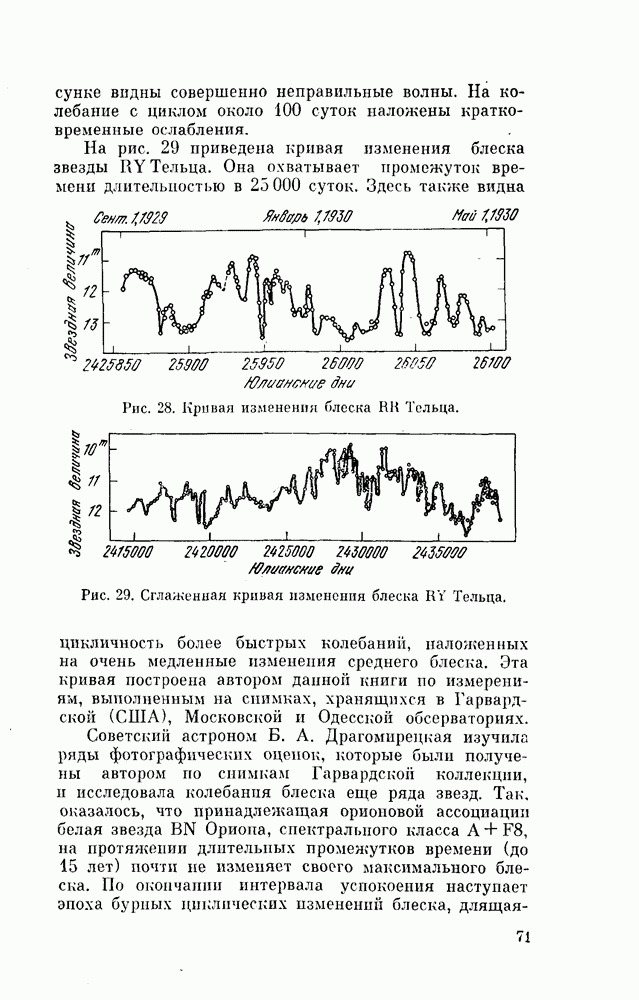
- § 28. РЕНТГЕНОВСКИЕ ПУЛЬСАРЫ В ДВОЙНЫХ ЗВЕЗДНЫХ СИСТЕМАХ
- § 29. ЗВЕЗДЫ ТИПА Z АНДРОМЕДЫ
- ГЛАВА VI. ОПРЕДЕЛЕНИЯ БЛЕСКА ПЕРЕМЕННЫХ ЗВЕЗД И СПОСОБЫ ИХ ОБРАБОТКИ
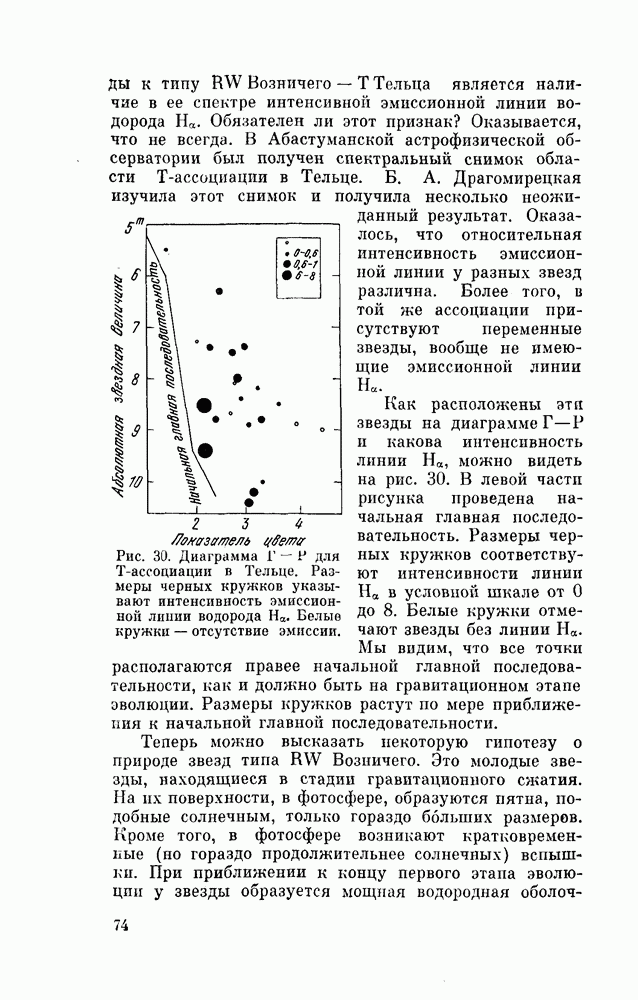
- § 30. ГЛАЗОМЕРНЫЕ ОЦЕНКИ БЛЕСКА
- § 31. СТЕПЕННАЯ ШКАЛА БЛЕСКА ЗВЕЗД СРАВНЕНИЯ
- § 32 РЕДУКЦИЯ ШКАЛ
- § 33. СИСТЕМАТИЧЕСКИЕ ОШИБКИ НАБЛЮДЕНИЙ БЛЕСКА
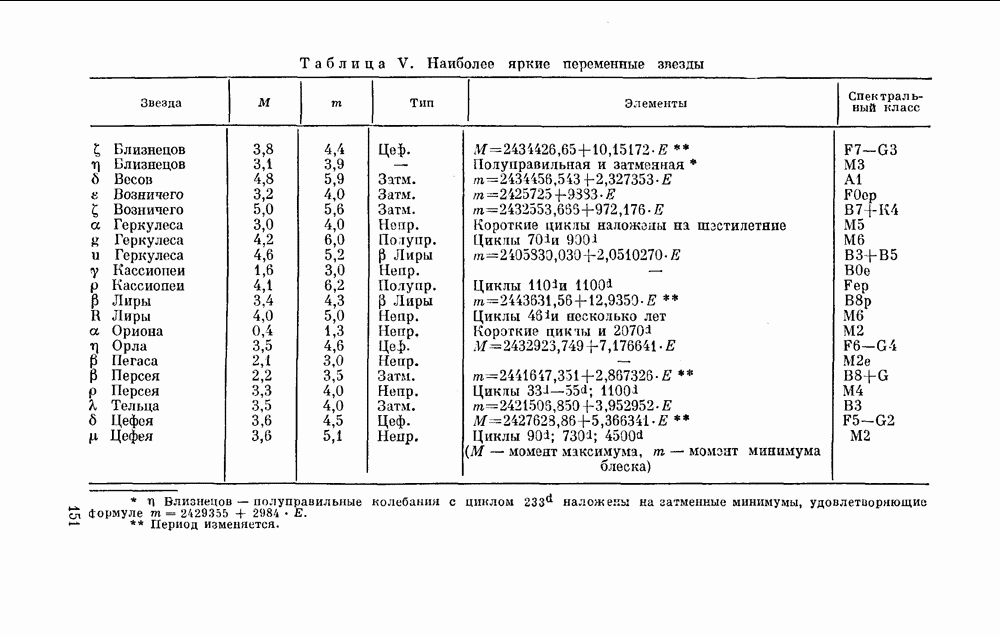
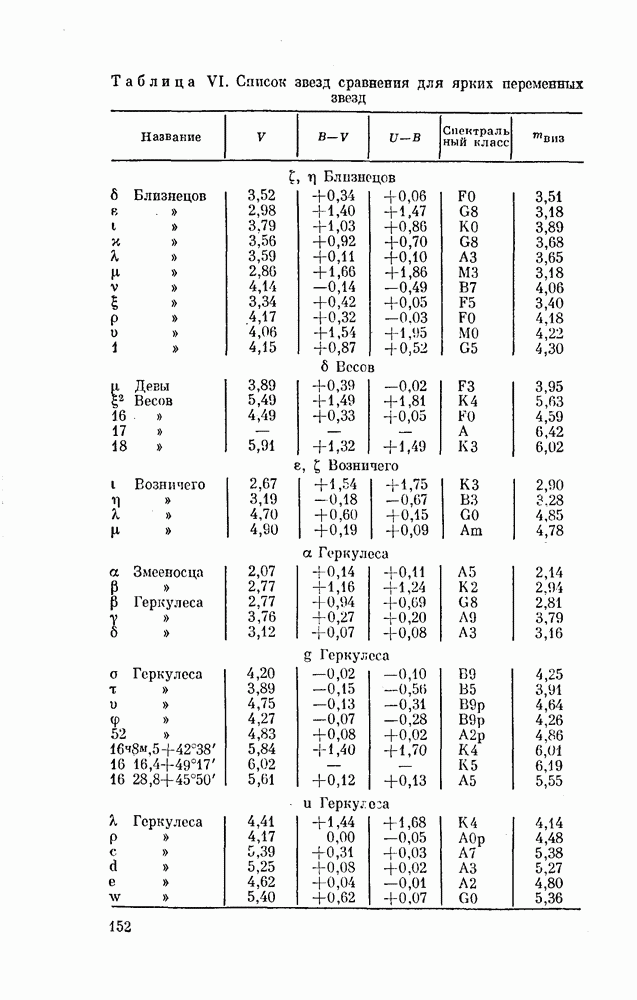
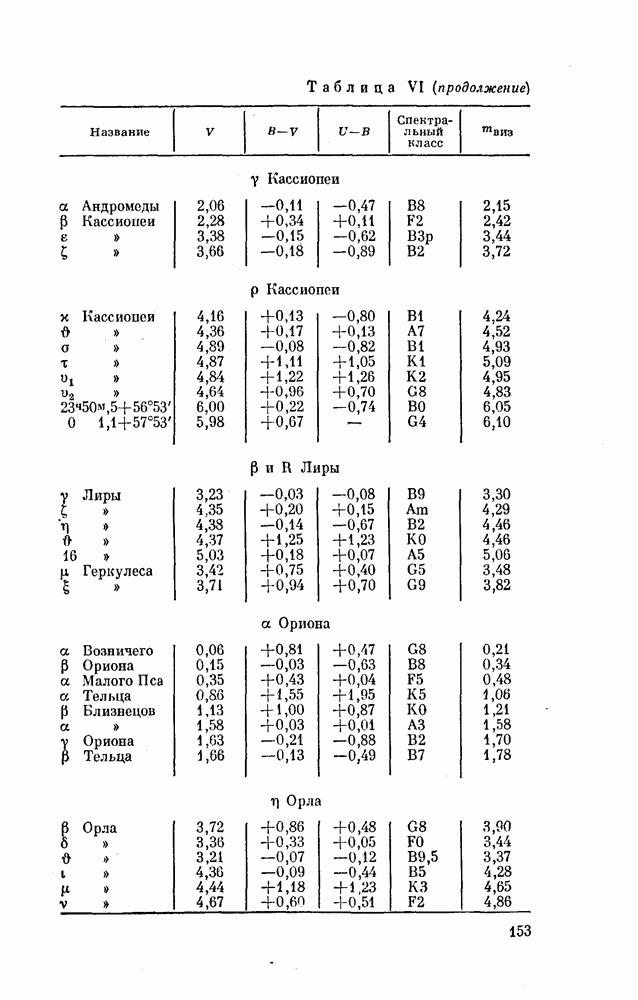
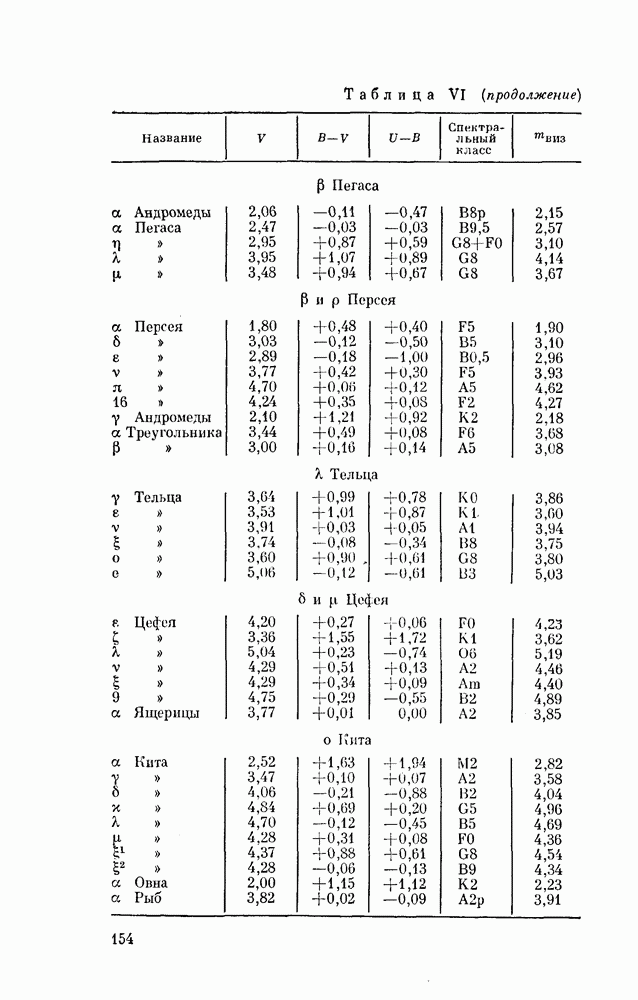
- § 34. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ ЗВЕЗД СРАВНЕНИЯ
- § 35. ПЕРВИЧНАЯ ОБРАБОТКА МОМЕНТОВ НАБЛЮДЕНИЙ
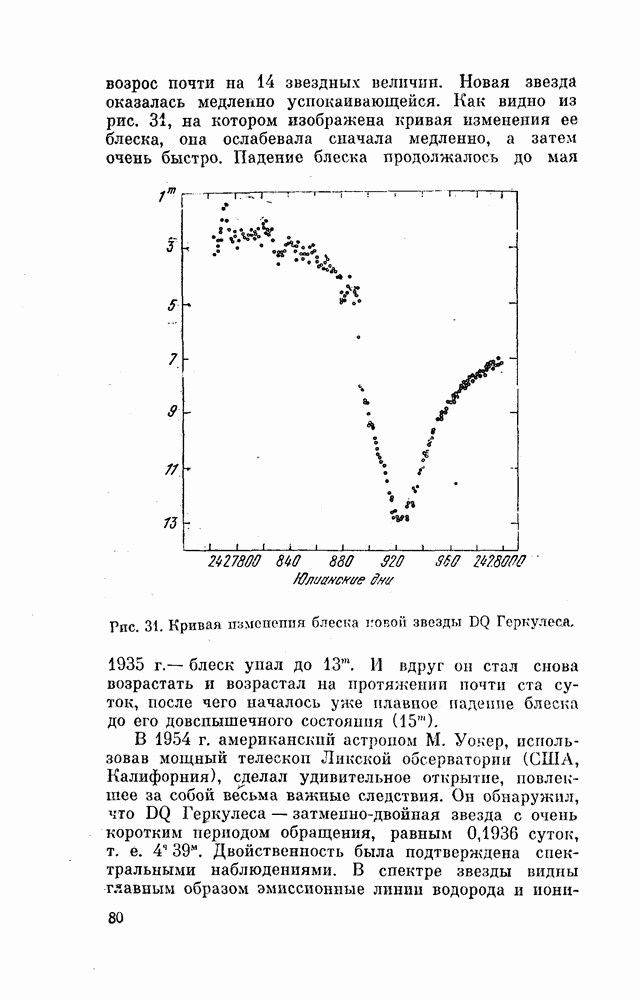
- § 36. КРИВАЯ ИЗМЕНЕНИЯ БЛЕСКА
- § 37. ИССЛЕДОВАНИЕ МИРИД
- § 38. СРЕДНЯЯ КРИВАЯ БЛЕСКА
- § 39. ИССЛЕДОВАНИЕ КОРОТКОПЕРИОДИЧЕСКИХ ЗВЕЗД. ПОИСКИ ПЕРИОДА
- § 40. УСКОРЕННОЕ ВЫЧИСЛЕНИЕ ВОЗРАСТОВ
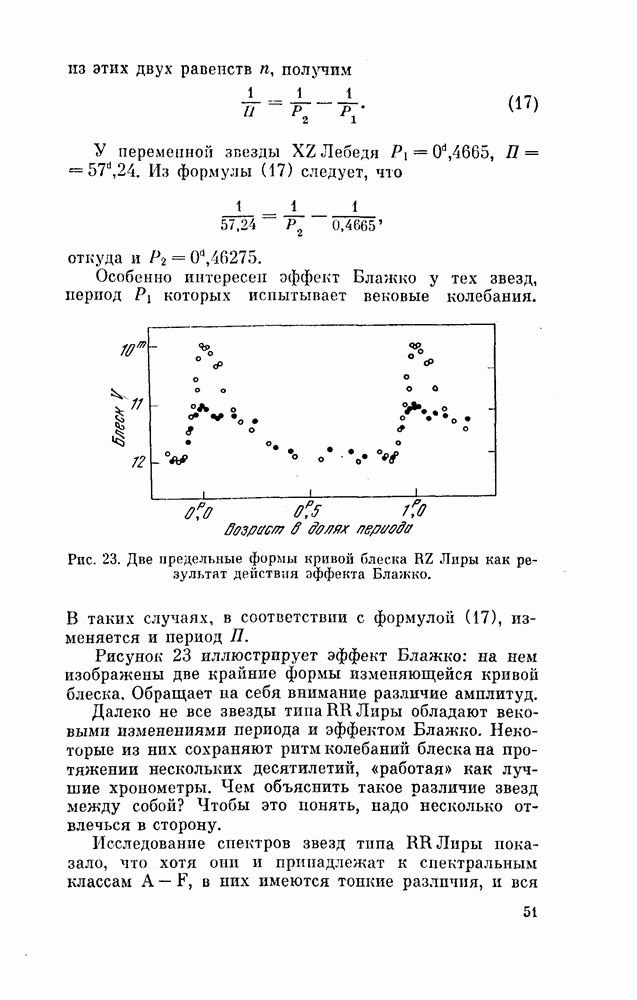
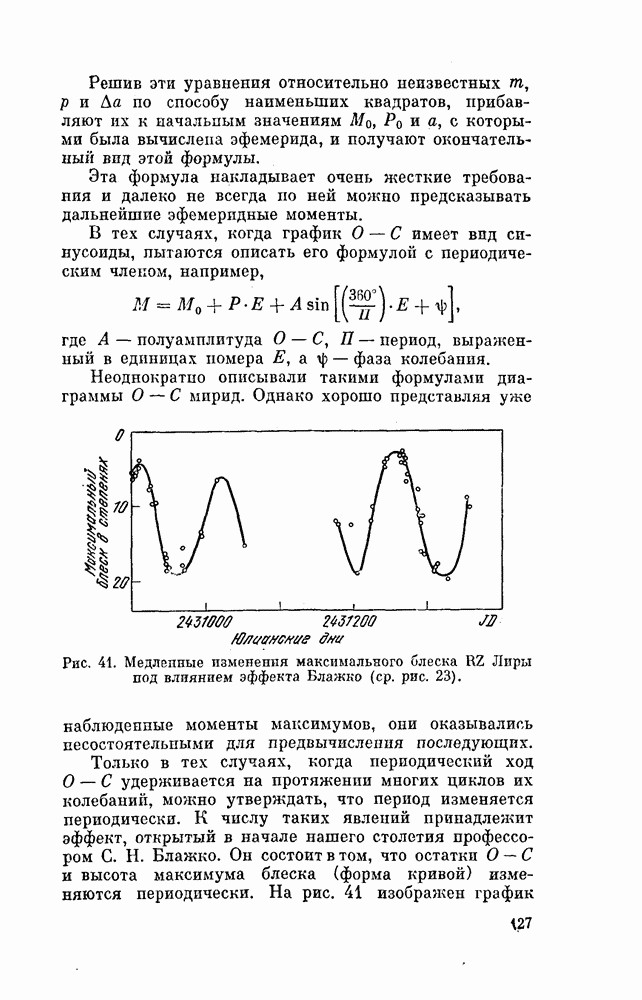
- § 41. ИЗМЕНЕНИЕ ПЕРИОДОВ И ЭФФЕКТ БЛАЖКО
- § 42. ОРГАНИЗАЦИЯ НАБЛЮДЕНИЙ
- § 43. РЕКОМЕНДАЦИИ НАБЛЮДАТЕЛЯМ
- ДОПОЛНЕНИЯ
- Дополнение 1. СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
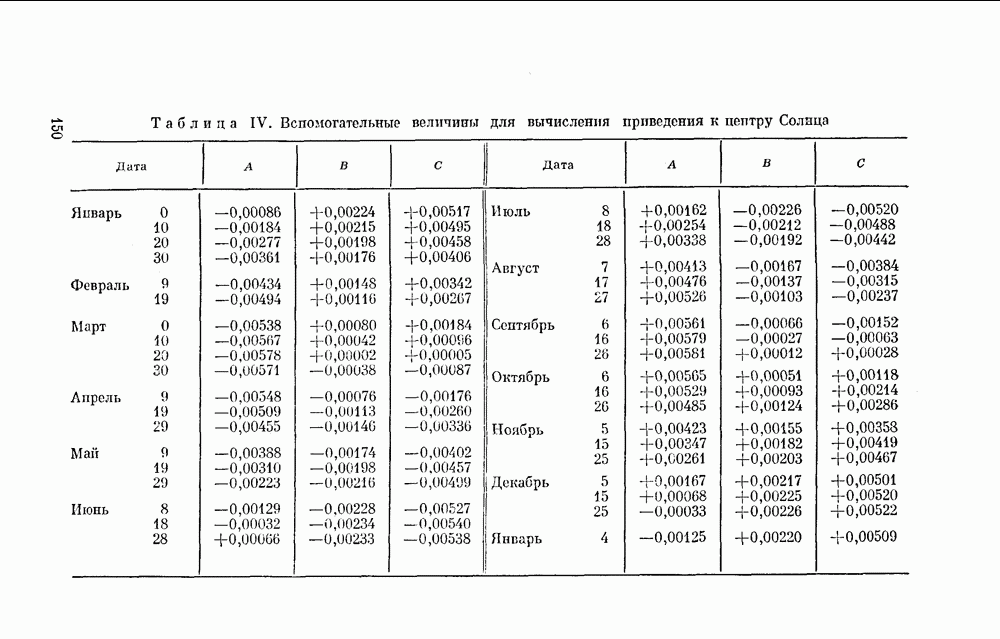
- Дополнение 2. ПРИВЕДЕНИЕ МОМЕНТОВ ВРЕМЕНИ К ЦЕНТРУ СОЛНЦА
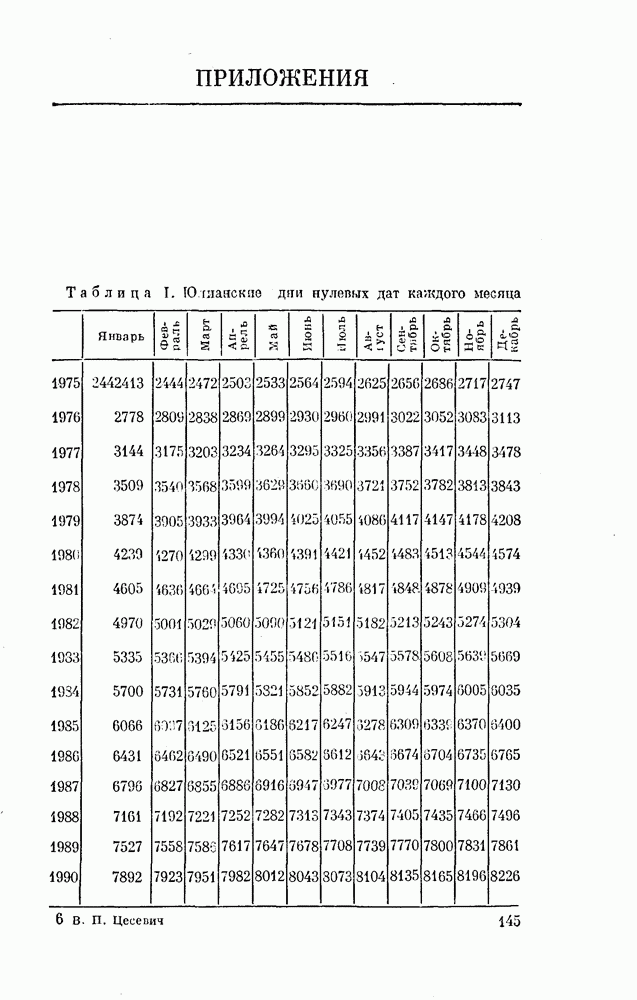
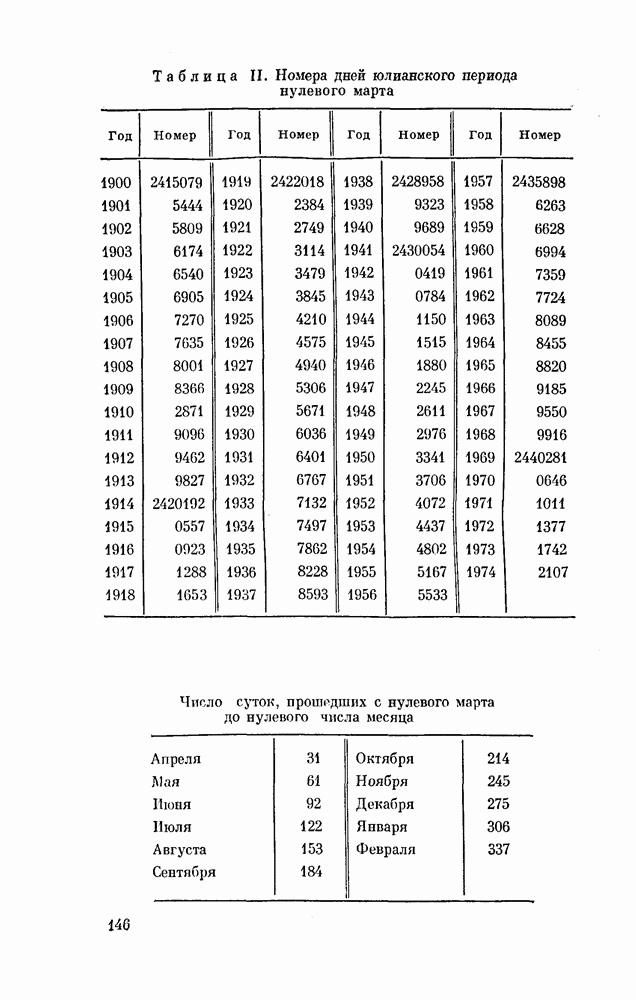
- ПРИЛОЖЕНИЯ