| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДОПОЛНЕНИЯ
Дополнение 1. СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
При обработке наблюдений приходится решать системы «нестрогих», так называемых условных уравнеппй вида

или

в которых число уравнений превышает число неизвестных.
Надо найти такие значения пеизвестпых х, у(х, у и z), которые наилучшим образом удовлетворяют совокупности уравнений. Так как наблюдения, использованные для составления этих уравнений, содержат неизбежные погрешности, то каждое уравнение является пестрогим. Обозначив эту погрешность уравнения через  можно написать уравнение (28) в виде
можно написать уравнение (28) в виде

В способе наименьших квадратов предполагается, что наилучшими или наиболее вероятными значениями неизвестных будут такие, которые придадут сумме квадратов  меньшее значение. Этот способ описан во многих книгах; его элементарное обоснование подробно изложено в книге автора «Что и как наблюдать на небе» (М.: Наука, — 5-е изд., 1979, с. 279). Не вдаваясь в подробности, укажем, как пользоваться этим способом на практике.
меньшее значение. Этот способ описан во многих книгах; его элементарное обоснование подробно изложено в книге автора «Что и как наблюдать на небе» (М.: Наука, — 5-е изд., 1979, с. 279). Не вдаваясь в подробности, укажем, как пользоваться этим способом на практике.
Из совокупности условных уравнений составляются нормальные уравнения, число которых равно числу неизвестных (при двух неизвестных псобходимы два нормальпых уравнения, а при трех неизвестных — три и т. д.). Чтобы получить первое нормальное уравнение, умножают каяодое из условных уравнений на свой коэффициент  при первой неизвестной и суммируют все результаты умпожений.
при первой неизвестной и суммируют все результаты умпожений.
Затем умножают каждое условное уравнение на свой коэффициент  при втором неизвестном и тоже суммируют все результаты. Так получается второе нормальное уравнение. Если неизвестных три, то умножают каждое условное уравнение на свой коэффициент с, - при третьем неизвестном и суммируют результаты. Так получается третье нормальное уравнение.
при втором неизвестном и тоже суммируют все результаты. Так получается второе нормальное уравнение. Если неизвестных три, то умножают каждое условное уравнение на свой коэффициент с, - при третьем неизвестном и суммируют результаты. Так получается третье нормальное уравнение.
Применяются следующие обозначения:
сумма произведений  на
на  т. е. обозначается
т. е. обозначается 
сумма произведений  на
на  т. е.
т. е.  обозначается
обозначается  и т. д.
и т. д.
Таким образом, при двух неизвестных имеем два нормальных уравнения

и

а при трех неизвестных — три нормальных уравнения

и

Эти уравнения решают обычными приемами элементарной алгебры. После подстановки найденных вероятнейших значений неизвестных в условные уравнения находят остатки  характеризующие точность исходных данных наблюдений.
характеризующие точность исходных данных наблюдений.
Численные примеры применения способа наименьших квадратов приведены в §§ 32 и 37,
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ВВЕДЕНИЕ
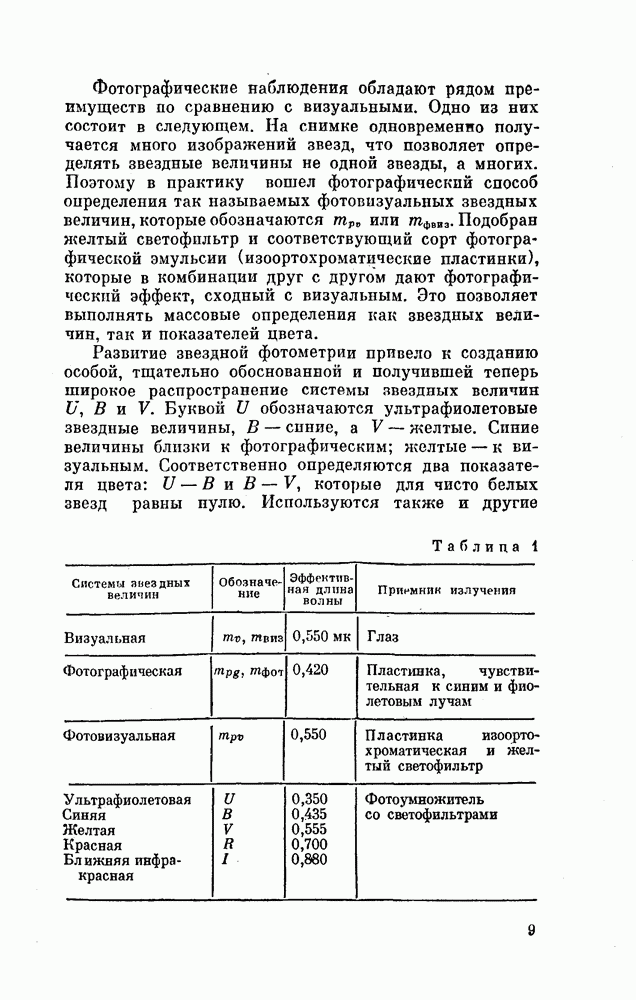
- § 1. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ЦВЕТА
- § 2. СВЕТИМОСТИ И РАДИУСЫ ЗВЕЗД
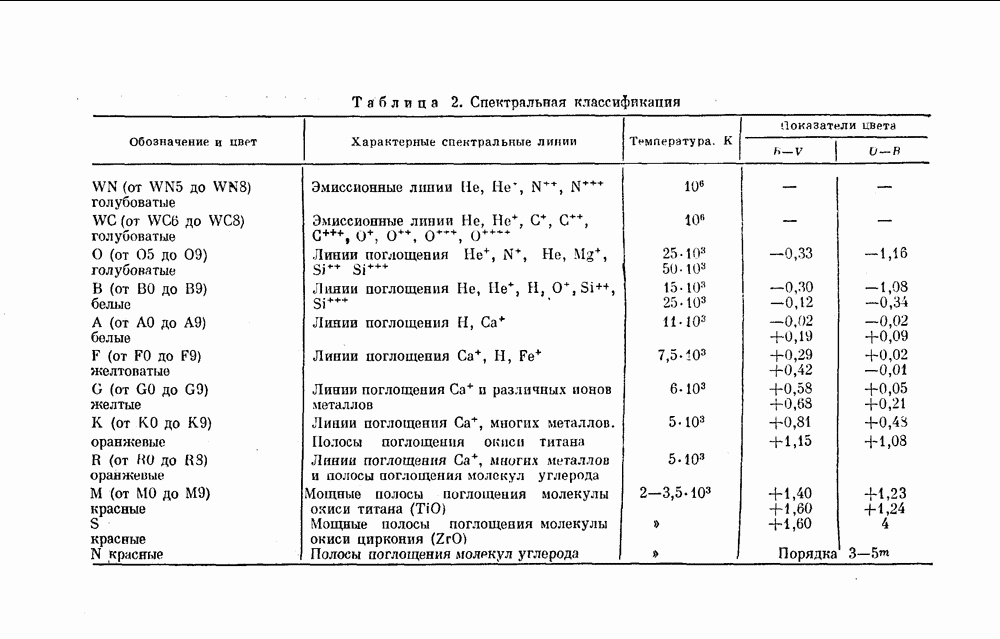
- § 3. СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ И ЛУЧЕВЫЕ СКОРОСТИ
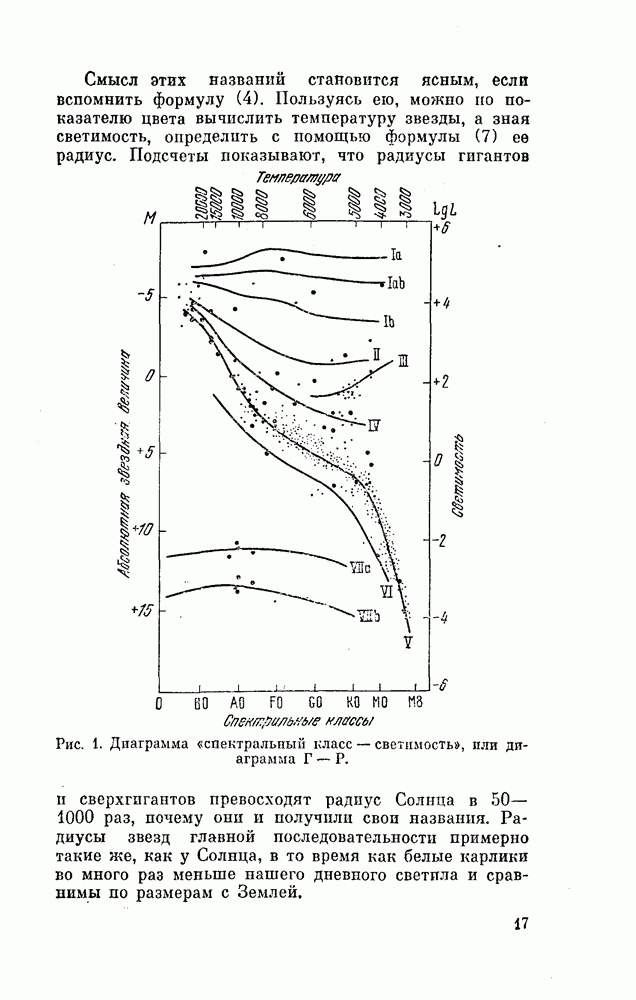
- § 4. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- § 5. ТИПЫ ЗВЕЗДНОГО НАСЕЛЕНИЯ
- ГЛАВА II. ЗАТМЕННЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 6. КЛАССИФИКАЦИЯ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
- § 7. ЧТО ДАЕТ ИЗУЧЕНИЕ КРИВОЙ БЛЕСКА ЗВЕЗДЫ ТИПА АЛГОЛЯ?
- § 8. ЭВОЛЮЦИЯ ТЕСНОЙ ДВОЙНОЙ ЗВЕЗДЫ
- § 9. ИЗМЕНЕНИЕ ПЕРИОДОВ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
- ГЛАВА III. ПУЛЬСИРУЮЩИЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 10. ЦЕФЕИДЫ, ИЛИ ЗВЕЗДЫ ТИПА б ЦЕФЕЯ
- § 11. ЗВЕЗДЫ ТИПА RR ЛИРЫ
- § 12. КАРЛИКОВЫЕ ЦЕФЕИДЫ
- § 13. МИРИДЫ
- § 14. ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА
- § 15. ПОЛУПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 16. ПЕРЕМЕННЫЕ ЗВЕЗДЫ, ОБЛАДАЮЩИЕ МАЛЫМИ АМПЛИТУДАМИ
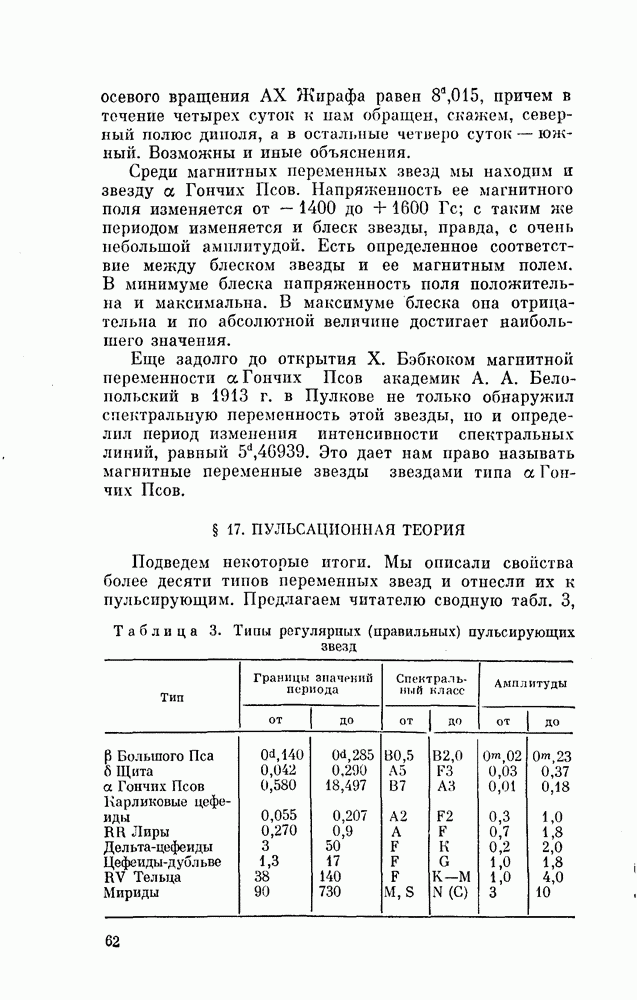
- § 17. ПУЛЬСАЦИОННАЯ ТЕОРИЯ
- ГЛАВА IV. ПЕРЕМЕННОСТЬ МОЛОДЫХ ЗВЕЗД
- § 18. ЗВЕЗДЫ ТИПА UV КИТА
- § 19. ВСПЫШЕЧНЫЕ ЗВЕЗДЫ
- § 20. ЗВЕЗДЫ ТИПА RW ВОЗНИЧЕГО — Т ТЕЛЬЦА
- § 21. ФУОРЫ И АНТИФУОРЫ
- ГЛАВА V. ВЗРЫВАЮЩИЕСЯ ЗВЕЗДЫ
- § 22. ТИПЫ ВЗРЫВАЮЩИХСЯ ЗВЕЗД
- § 23. ЯВЛЕНИЯ, ПРОИСХОДЯЩИЕ ПРИ ВСПЫШКЕ НОВОЙ ЗВЕЗДЫ
- § 24. ЗАГАДКА DQ ГЕРКУЛЕСА
- § 25. «ЗВЕЗДА-ГОСТЬЯ» В СОЗВЕЗДИИ ТЕЛЬЦА
- § 26. U БЛИЗНЕЦОВ И ЕЙ ПОДОБНЫЕ
- § 27. ТИХИЕ ВЗРЫВЫ
- § 28. РЕНТГЕНОВСКИЕ ПУЛЬСАРЫ В ДВОЙНЫХ ЗВЕЗДНЫХ СИСТЕМАХ
- § 29. ЗВЕЗДЫ ТИПА Z АНДРОМЕДЫ
- ГЛАВА VI. ОПРЕДЕЛЕНИЯ БЛЕСКА ПЕРЕМЕННЫХ ЗВЕЗД И СПОСОБЫ ИХ ОБРАБОТКИ
- § 30. ГЛАЗОМЕРНЫЕ ОЦЕНКИ БЛЕСКА
- § 31. СТЕПЕННАЯ ШКАЛА БЛЕСКА ЗВЕЗД СРАВНЕНИЯ
- § 32 РЕДУКЦИЯ ШКАЛ
- § 33. СИСТЕМАТИЧЕСКИЕ ОШИБКИ НАБЛЮДЕНИЙ БЛЕСКА
- § 34. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ ЗВЕЗД СРАВНЕНИЯ
- § 35. ПЕРВИЧНАЯ ОБРАБОТКА МОМЕНТОВ НАБЛЮДЕНИЙ
- § 36. КРИВАЯ ИЗМЕНЕНИЯ БЛЕСКА
- § 37. ИССЛЕДОВАНИЕ МИРИД
- § 38. СРЕДНЯЯ КРИВАЯ БЛЕСКА
- § 39. ИССЛЕДОВАНИЕ КОРОТКОПЕРИОДИЧЕСКИХ ЗВЕЗД. ПОИСКИ ПЕРИОДА
- § 40. УСКОРЕННОЕ ВЫЧИСЛЕНИЕ ВОЗРАСТОВ
- § 41. ИЗМЕНЕНИЕ ПЕРИОДОВ И ЭФФЕКТ БЛАЖКО
- § 42. ОРГАНИЗАЦИЯ НАБЛЮДЕНИЙ
- § 43. РЕКОМЕНДАЦИИ НАБЛЮДАТЕЛЯМ
- ДОПОЛНЕНИЯ
- Дополнение 1. СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
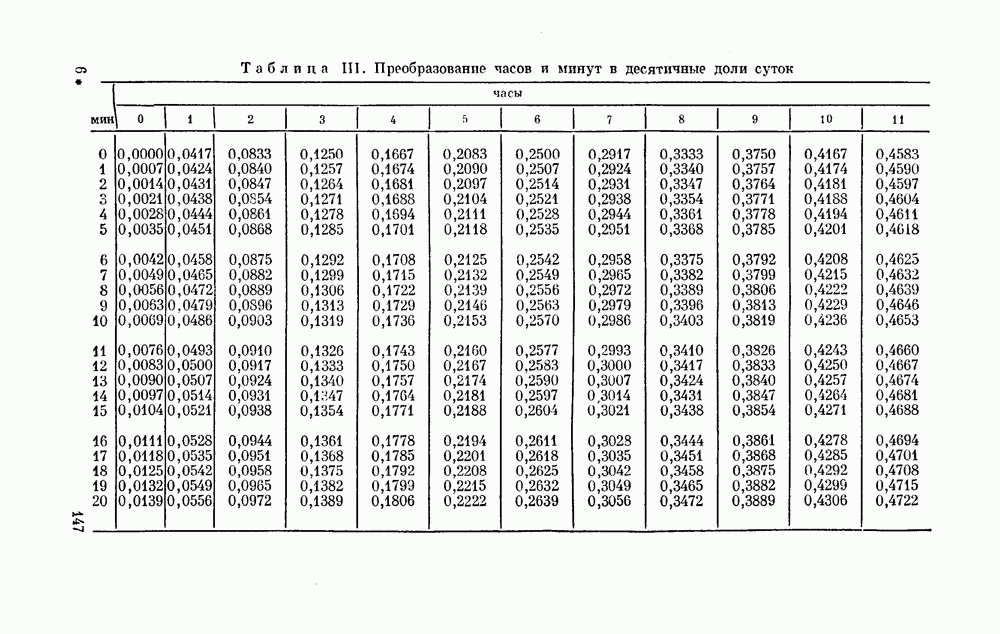
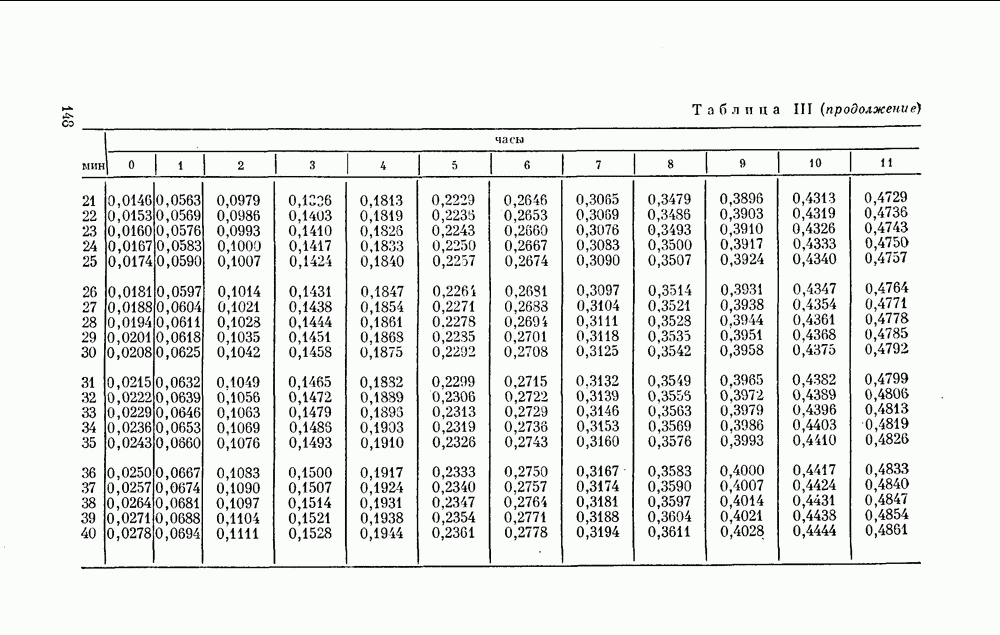
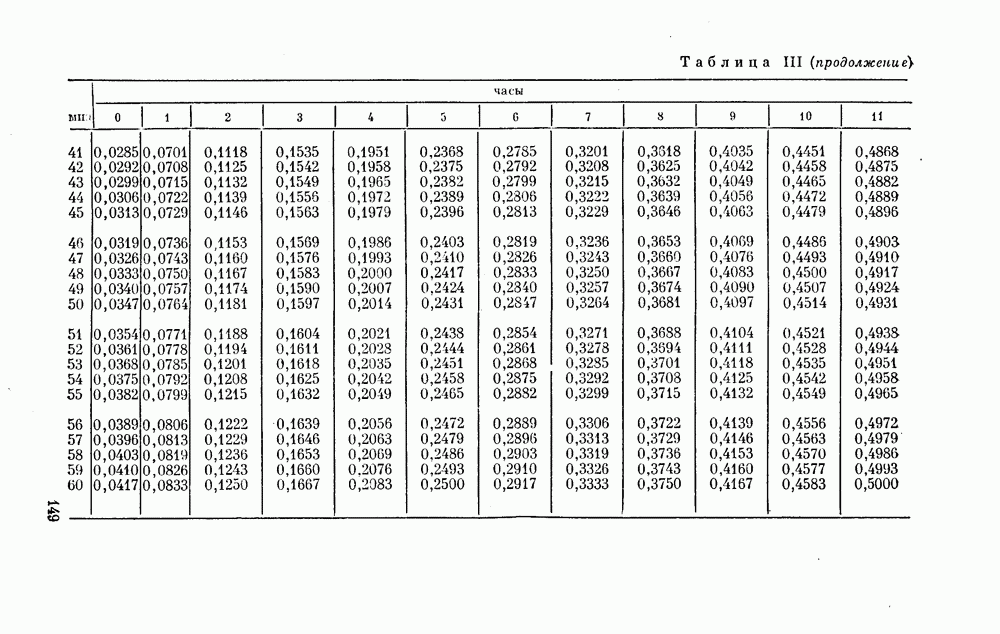
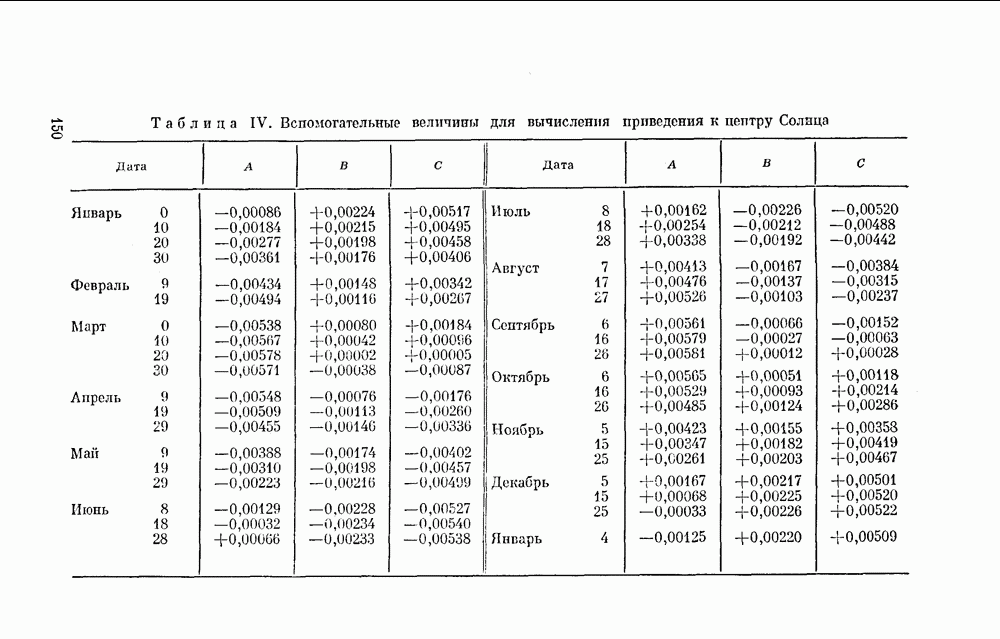
- Дополнение 2. ПРИВЕДЕНИЕ МОМЕНТОВ ВРЕМЕНИ К ЦЕНТРУ СОЛНЦА
- ПРИЛОЖЕНИЯ