| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
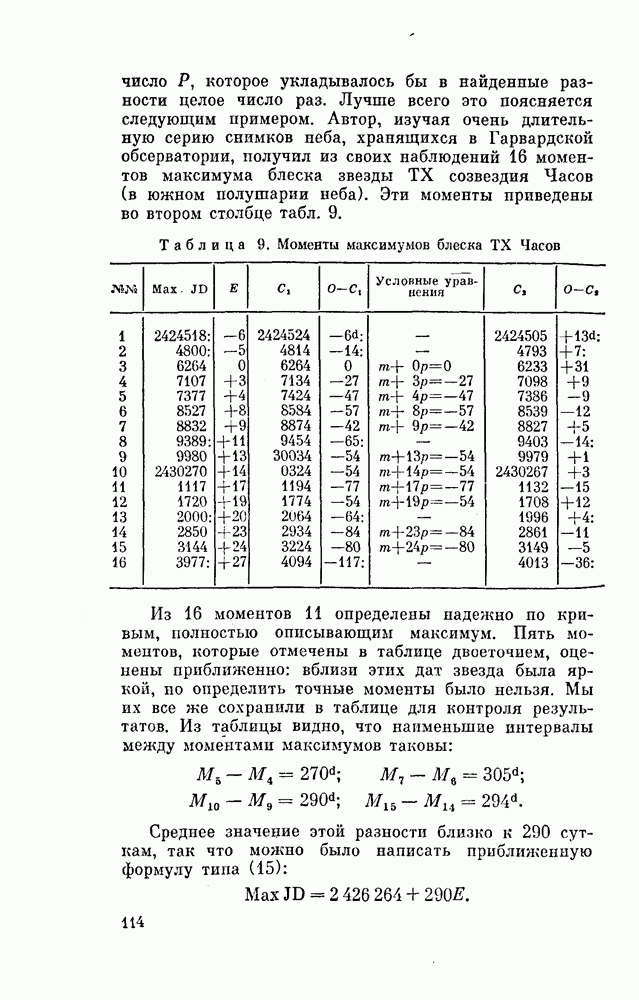
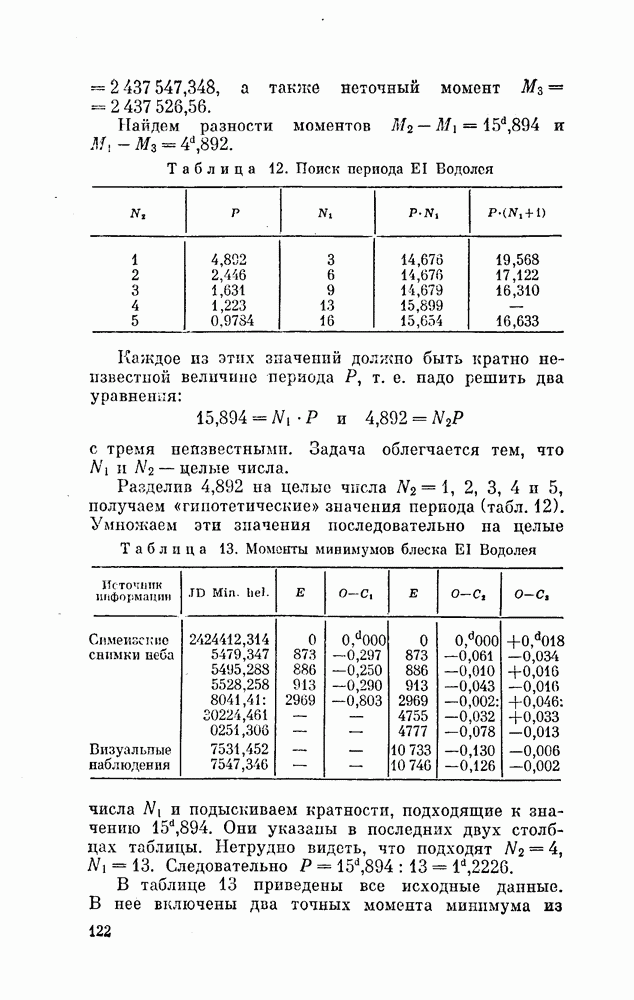
Дополнение 2. ПРИВЕДЕНИЕ МОМЕНТОВ ВРЕМЕНИ К ЦЕНТРУ СОЛНЦА
Некоторые переменные звезды меняют свой блеск столь быстро, что нужно отмечать момент наблюдения с точностью до минуты. В таком случае необходимо вводить в моменты поправку, называемую приведением к центру Солпца. Эта необходимость вызывается тем, что при годовом обращении Земли вокруг Солнца расстояние звезды от Земли, с которой проводятся наблюдения, немного изменяется, но не более, чем на удвоенное расстояние Земли от Солнца, т. е. на  . Но скорость света
. Но скорость света  и поэтому расстояние
и поэтому расстояние  свет пройдет за интервал времени
свет пройдет за интервал времени

Таким образом, если этого не учитывать, то при наблюдениях одной и той же звезды, разделенных промежутком в полгода, ошибка в моментах времени может достичь  в то время как требуемая точность должна быть не меньше 1 мин. Чтобы избежать такой ошибки, условились все моменты времени наблюдений приводить к центру Солнца, т. е. вычислять их для наблюдателя, как бы находящегося в этом центре.
в то время как требуемая точность должна быть не меньше 1 мин. Чтобы избежать такой ошибки, условились все моменты времени наблюдений приводить к центру Солнца, т. е. вычислять их для наблюдателя, как бы находящегося в этом центре.

Рис. 42. К выводу формулы для приведения к центру Солнца.
Поправка приведения к центру Солнца зависит не только от положения Земли на ее орбите, но от положения звезды относительно плоскости земной орбиты. Изобразим на чертеже (рис. 42) земную орбиту NMN, Солнце S в ее центре (небольшой эллиптичностью земной орбиты можно пренебречь) и направление SQ от него на звезду Q.
Пусть в некоторый момент времепи Земля занимает на своей орбите положение М, так что расстояние  км. Это положение определяется угловым расстоянием
км. Это положение определяется угловым расстоянием  от точки весеннего равноденствия Y, отсчитываемым в направлении движения Земли и называемым гелиоцентрической долготой Земли. Положение звезды Q на небе относительно плоскости земной орбиты (NMN) определяется двумя координатами — эклиптической долготой
от точки весеннего равноденствия Y, отсчитываемым в направлении движения Земли и называемым гелиоцентрической долготой Земли. Положение звезды Q на небе относительно плоскости земной орбиты (NMN) определяется двумя координатами — эклиптической долготой  и эклиптической широтой
и эклиптической широтой  Опустим из положения Земли М на направление SQ перпендикуляр МК, который отметит отрезок SK. При движении Земли вокруг Солнца длина отрезка SK меняется, и поэтому в разные дни года свет проходит этот отрезок за несколько различающиеся интервалы времепи. При перемещении Земли в положение N длина отрезка SK достигает наибольшего значения
Опустим из положения Земли М на направление SQ перпендикуляр МК, который отметит отрезок SK. При движении Земли вокруг Солнца длина отрезка SK меняется, и поэтому в разные дни года свет проходит этот отрезок за несколько различающиеся интервалы времепи. При перемещении Земли в положение N длина отрезка SK достигает наибольшего значения  . При любом ином положении Земли, например, в точке М, длина отрезка
. При любом ином положении Земли, например, в точке М, длина отрезка  что следует из раздела математики называемого сферической тригонометрией. Следовательно, искомая поправка приведения к Солнцу
что следует из раздела математики называемого сферической тригонометрией. Следовательно, искомая поправка приведения к Солнцу

а так как

ТО

и получается в минутах времени.
Значения гелиоцентрической долготы Земли  для разпых дней года публикуются в Астрономическом календаре-ежегоднике Всесоюзного астрономо-геодезического общества. В Астрономическом ежегоднике СССР, издаваемом Институтом теоретической астрономии Академии паук СССР, публикуются ежедневные значения геоцетрической долготы Солнца
для разпых дней года публикуются в Астрономическом календаре-ежегоднике Всесоюзного астрономо-геодезического общества. В Астрономическом ежегоднике СССР, издаваемом Институтом теоретической астрономии Академии паук СССР, публикуются ежедневные значения геоцетрической долготы Солнца  также отсчитываемой от точки весеннего равподепствия V по наблюдениям с Земли. Так как положения Земли и Солнца в пространстве всегда диаметрально противоположны, то
также отсчитываемой от точки весеннего равподепствия V по наблюдениям с Земли. Так как положения Земли и Солнца в пространстве всегда диаметрально противоположны, то

и поэтому в минутах

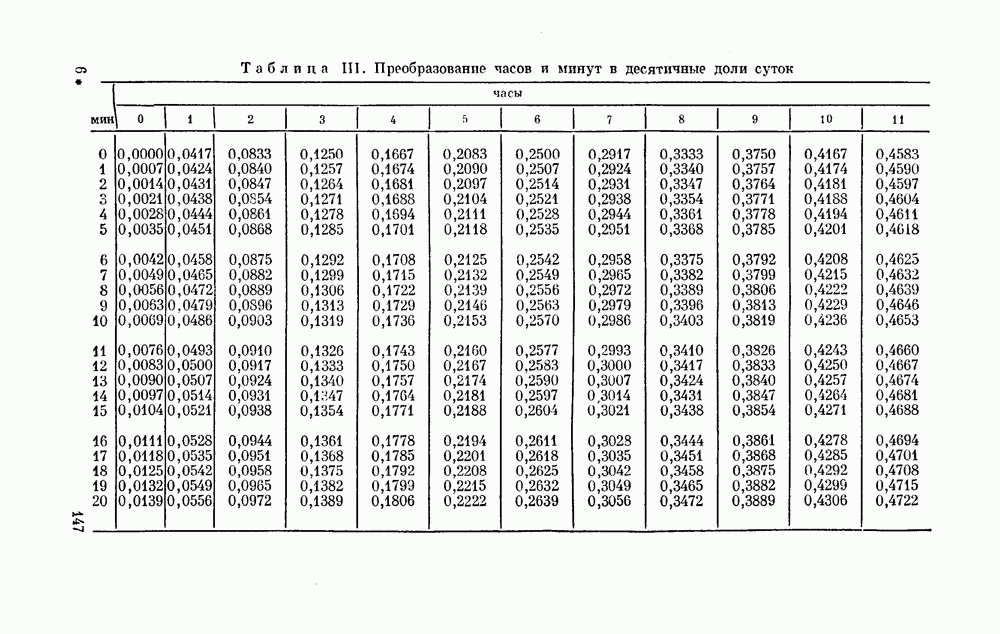
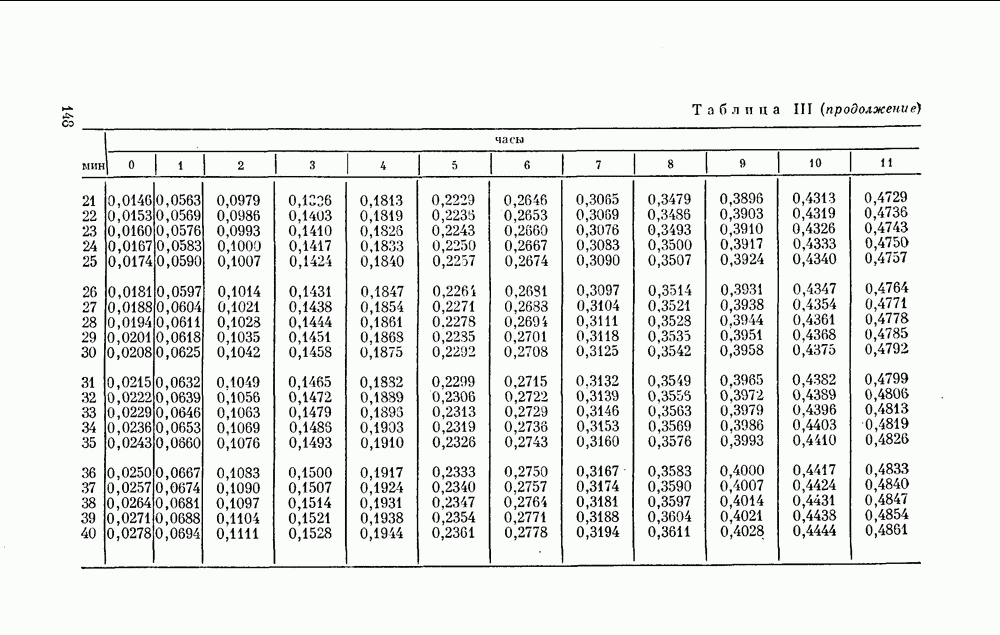
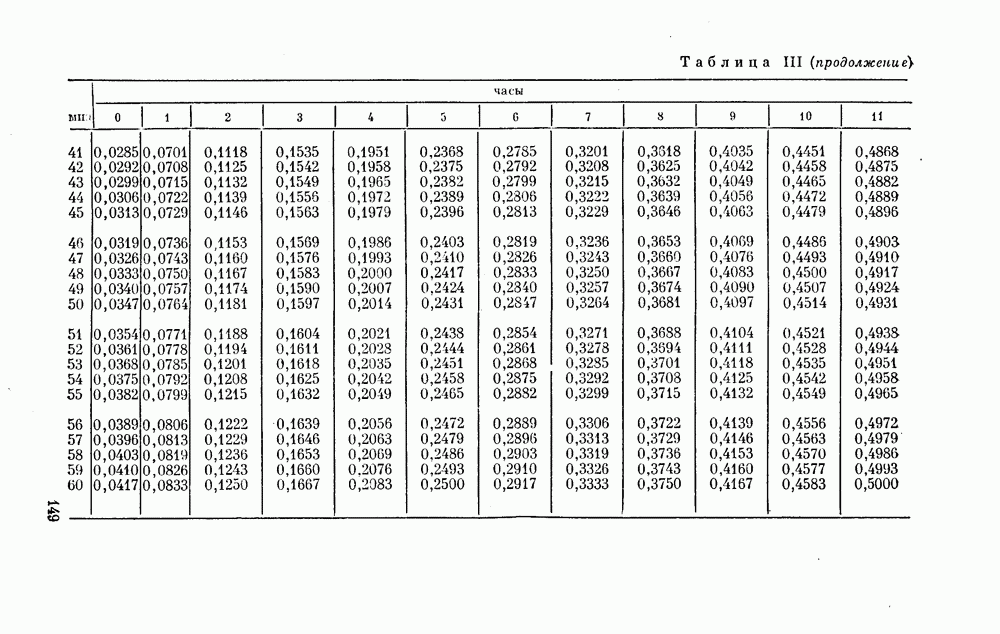
Чтобы выразить  в долях суток, следует
в долях суток, следует  заменить на
заменить на 
Следовательно, если из наблюдений короткопериодической переменной звезды определен момент  , то приведенный к центру Солнца момент, называемый гелиоцентрическим моментом, будет
, то приведенный к центру Солнца момент, называемый гелиоцентрическим моментом, будет

где, в зависимости от использования  или
или  значение поправки
значение поправки  (в минутах или долях суток) определяется соответственно по формуле (29) или (30). Гелиоцентрические моменты, как уже указывалось, обозначаются индексом
(в минутах или долях суток) определяется соответственно по формуле (29) или (30). Гелиоцентрические моменты, как уже указывалось, обозначаются индексом 
В формулы (29) и (30) входят эклиптические координаты  звезды, которые вычисляются по их экваториальным координатам — прямому восхождению а и склонению
звезды, которые вычисляются по их экваториальным координатам — прямому восхождению а и склонению  , публикуемым в списках (каталогах) ззезд. Сферическая тригонометрия дает соответствующие формулы:
, публикуемым в списках (каталогах) ззезд. Сферическая тригонометрия дает соответствующие формулы:

в которых наклонение плоскости небесного экватора к плоскости земной орбиты  (для 1900 г.
(для 1900 г.  ).
).
Вычисления эклиптических координат звезды довольно сложны, но их можпо упростить. Для этого представим формулу (30) в виде

где коэффициенты А, В и С связаны с положением Солнца и изменяются со временем

со звездой связаны величины

которые для избранной звезды вычисляются один раз.
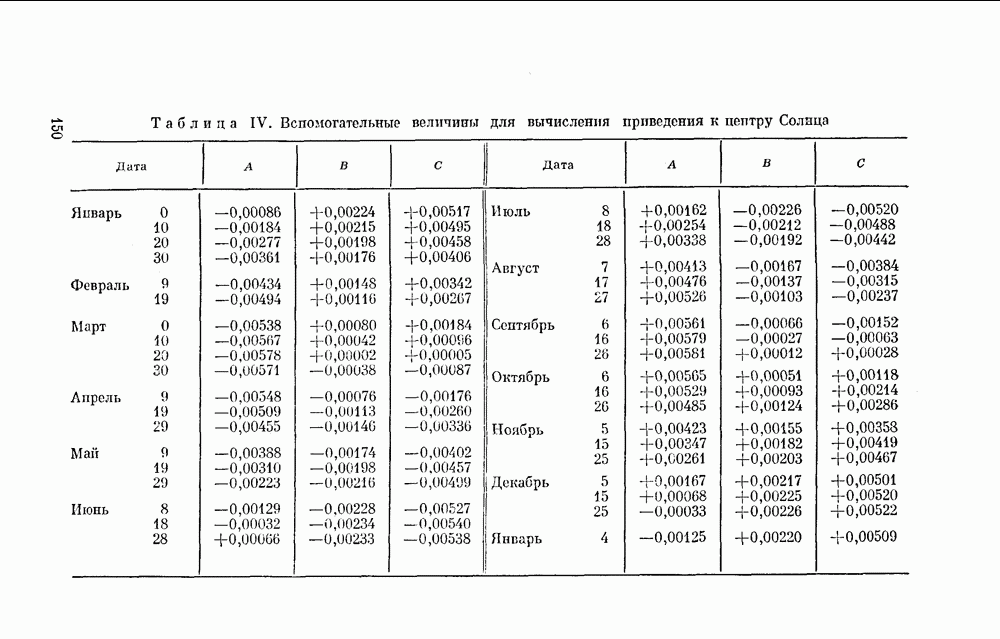
Коэффициенты А, В и С могут с определенной степенью точности считаться повторяющимися из года в год в одни и те же календарные даты (небольшая неточность, которой можно пренебречь, вызвана чередованием простых и високосных годов). Они приведены в табл. IV, с. 150) и их использование дает  в долях суток.
в долях суток.
Покажем, как пользоваться этой таблицей. Пусть координаты звезды  По таблицам тригонометрических функций находим
По таблицам тригонометрических функций находим  По формулам (31) вычисляем
По формулам (31) вычисляем 
Предположим, что надо найти значение Д для 24 января. По табл. IV находим значения А, В в С для 20 и 30 января:

Интерполируя, находим для 24 января

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ВВЕДЕНИЕ
- § 1. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ЦВЕТА
- § 2. СВЕТИМОСТИ И РАДИУСЫ ЗВЕЗД
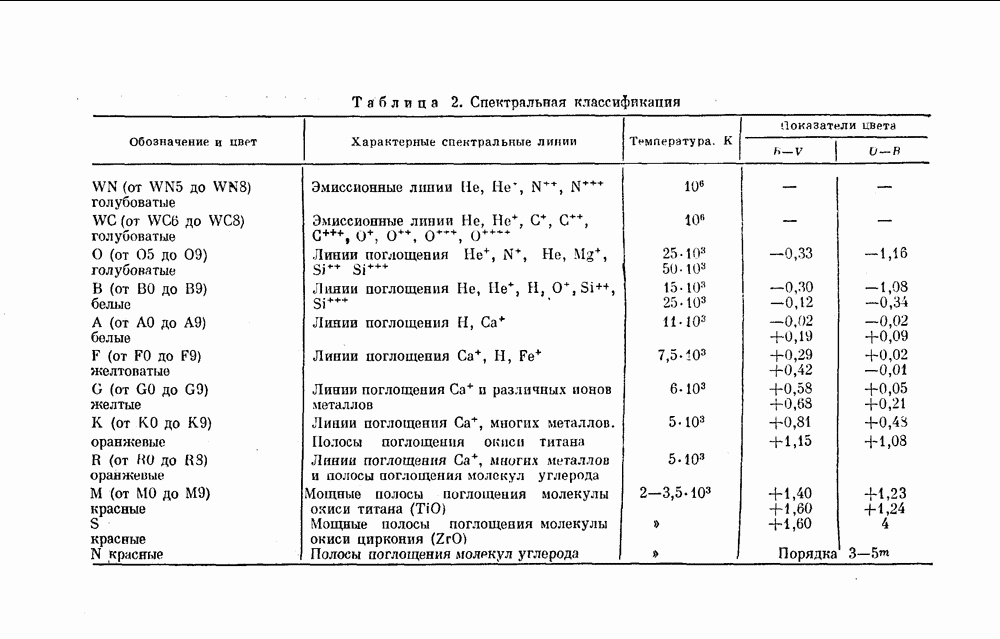
- § 3. СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ И ЛУЧЕВЫЕ СКОРОСТИ
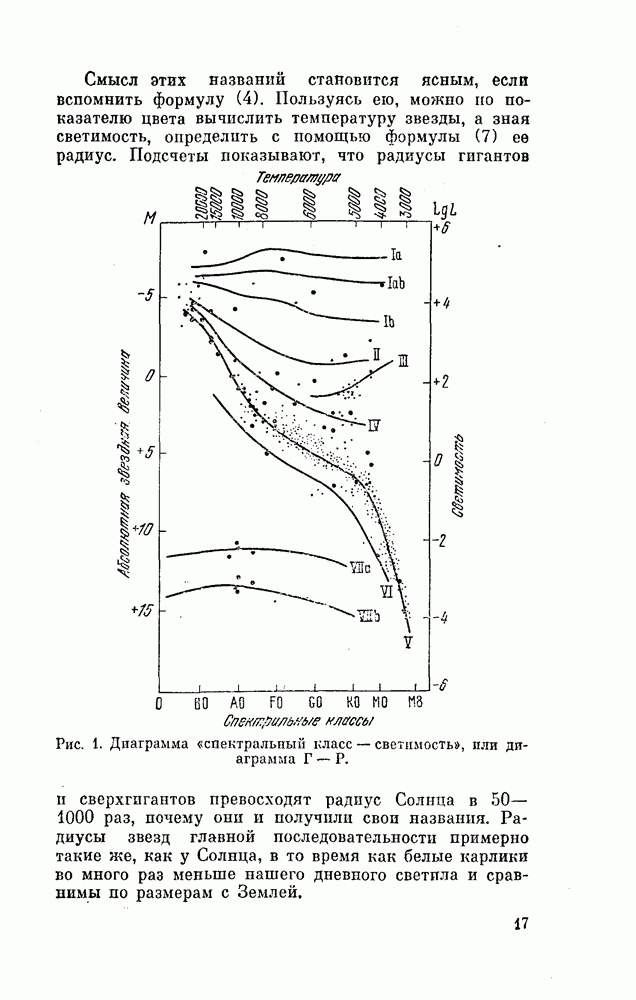
- § 4. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- § 5. ТИПЫ ЗВЕЗДНОГО НАСЕЛЕНИЯ
- ГЛАВА II. ЗАТМЕННЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 6. КЛАССИФИКАЦИЯ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
- § 7. ЧТО ДАЕТ ИЗУЧЕНИЕ КРИВОЙ БЛЕСКА ЗВЕЗДЫ ТИПА АЛГОЛЯ?
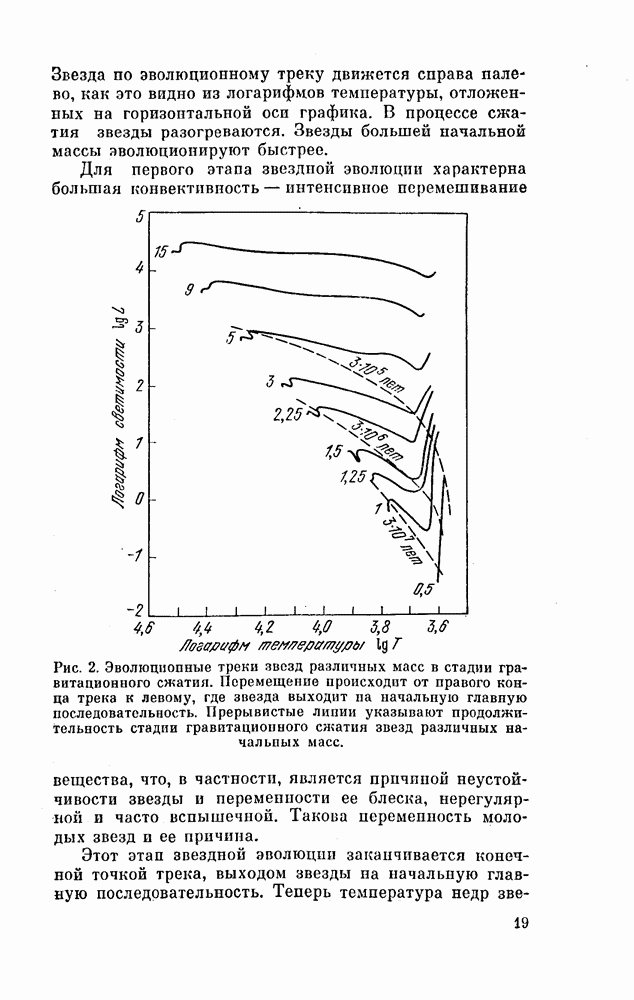
- § 8. ЭВОЛЮЦИЯ ТЕСНОЙ ДВОЙНОЙ ЗВЕЗДЫ
- § 9. ИЗМЕНЕНИЕ ПЕРИОДОВ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
- ГЛАВА III. ПУЛЬСИРУЮЩИЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 10. ЦЕФЕИДЫ, ИЛИ ЗВЕЗДЫ ТИПА б ЦЕФЕЯ
- § 11. ЗВЕЗДЫ ТИПА RR ЛИРЫ
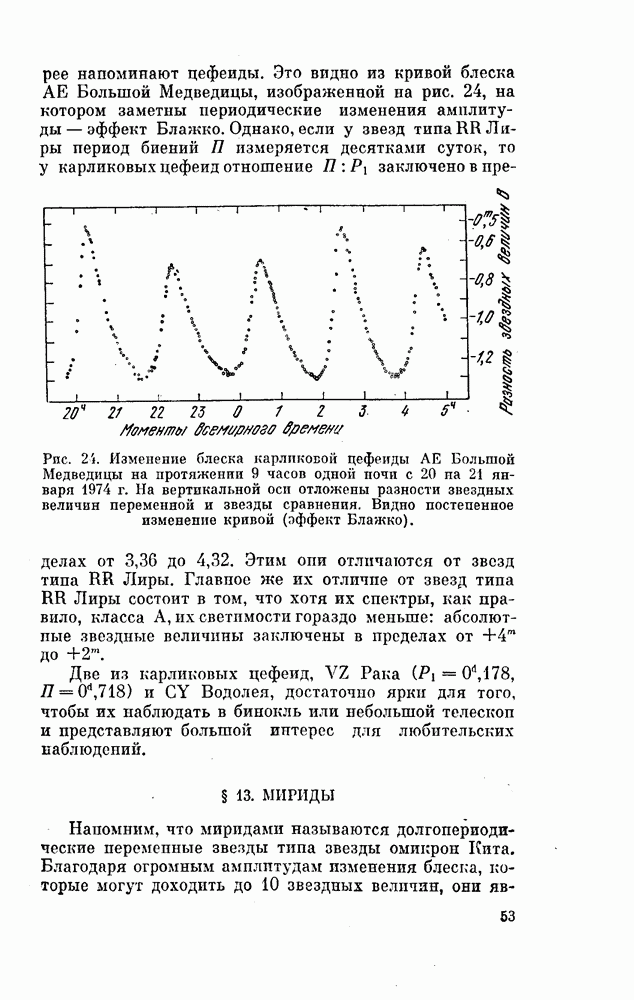
- § 12. КАРЛИКОВЫЕ ЦЕФЕИДЫ
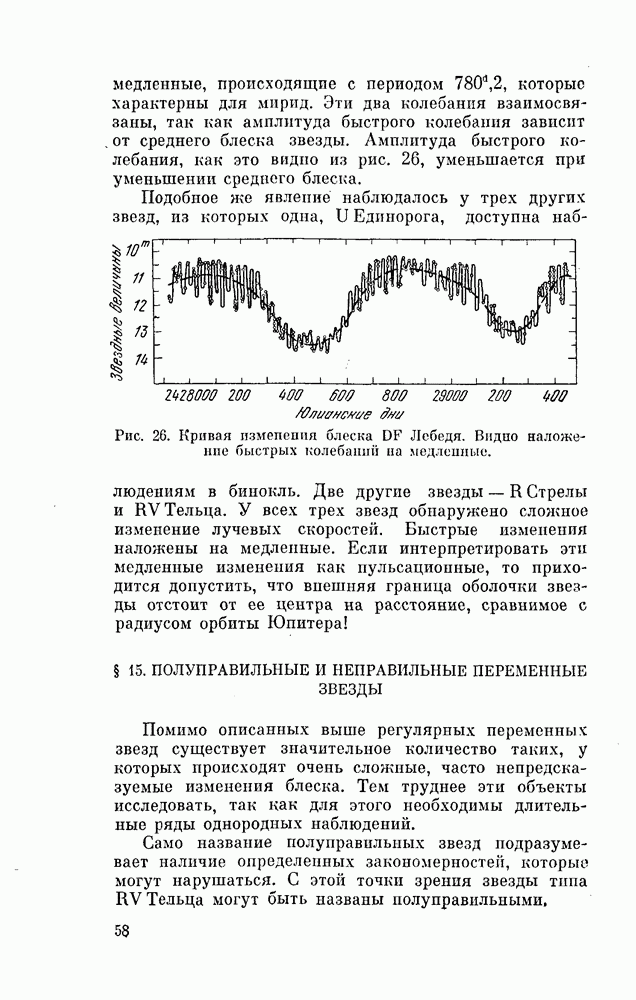
- § 13. МИРИДЫ
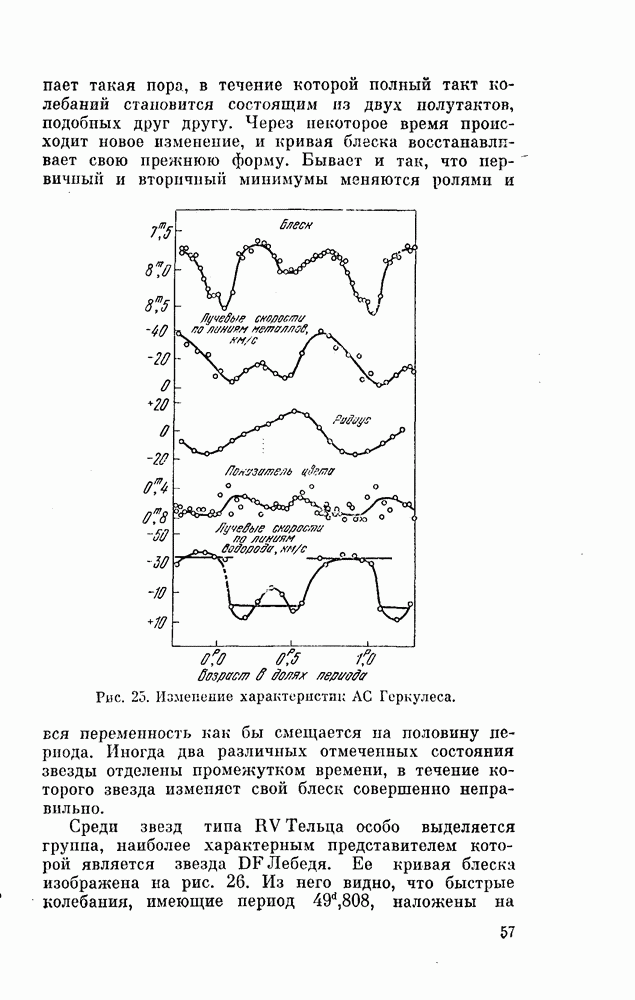
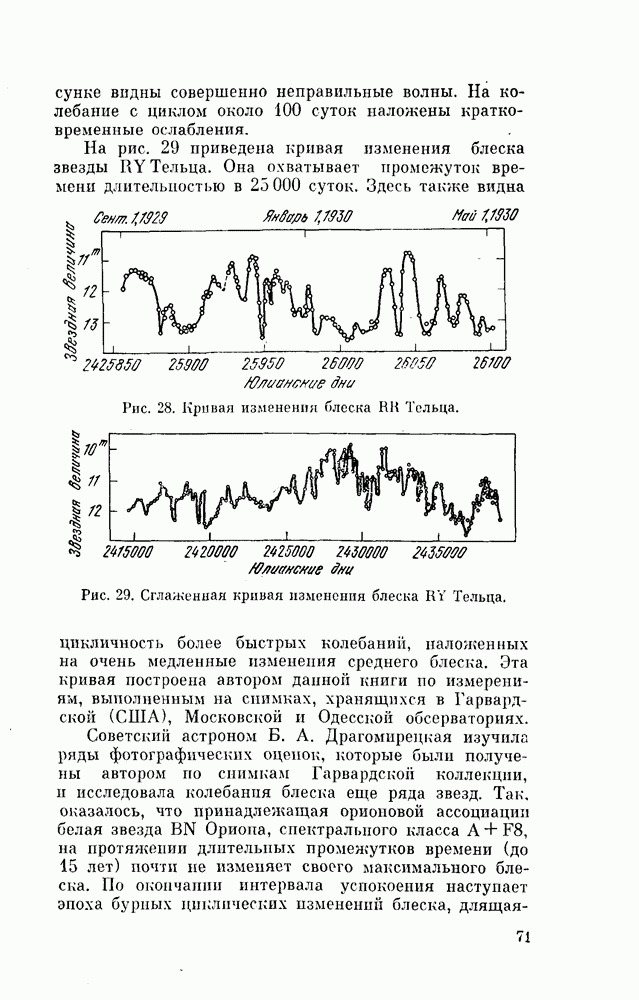
- § 14. ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА
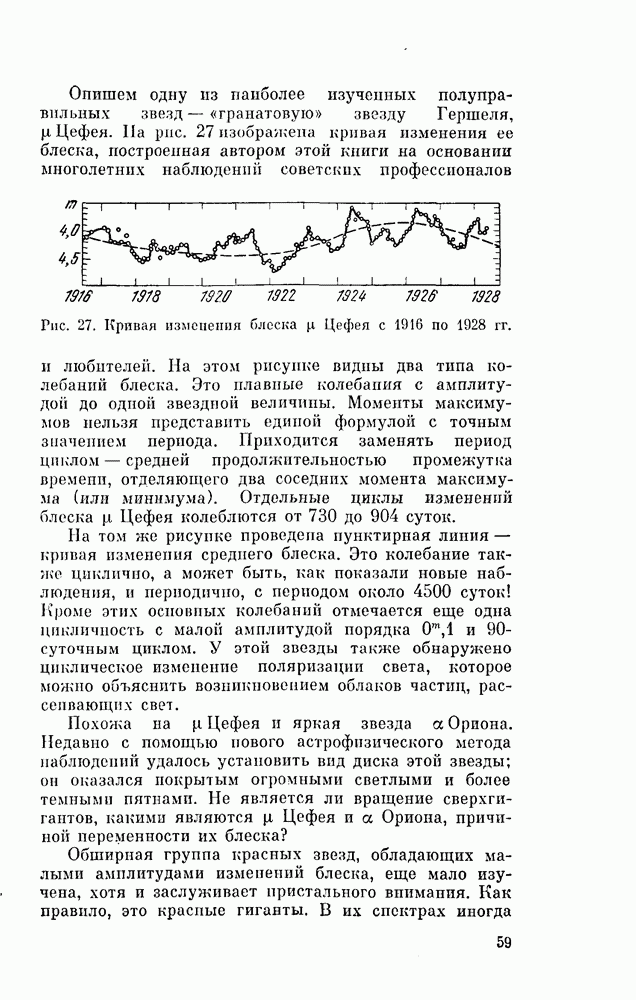
- § 15. ПОЛУПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 16. ПЕРЕМЕННЫЕ ЗВЕЗДЫ, ОБЛАДАЮЩИЕ МАЛЫМИ АМПЛИТУДАМИ
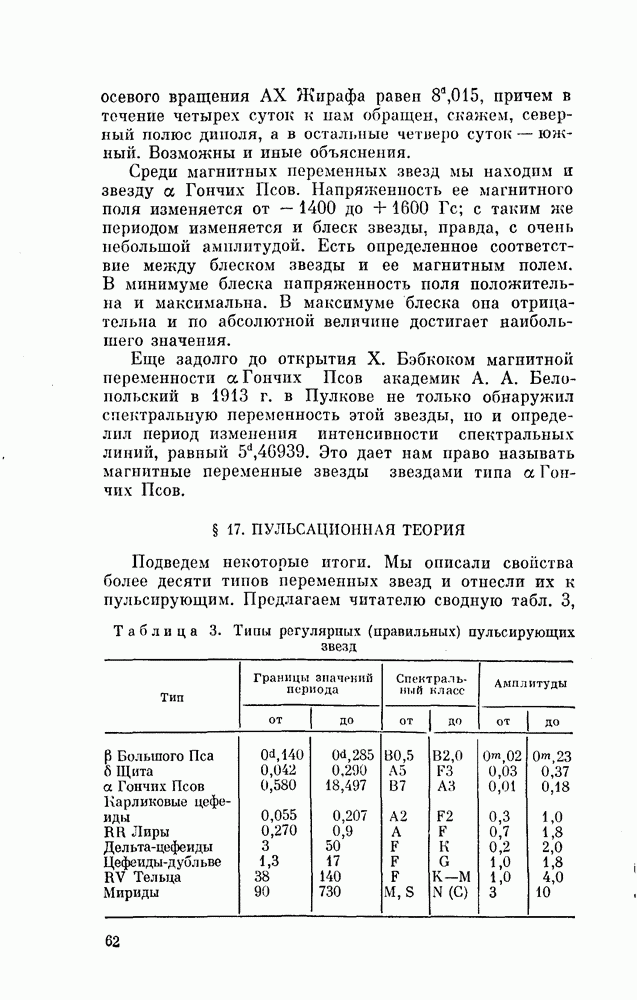
- § 17. ПУЛЬСАЦИОННАЯ ТЕОРИЯ
- ГЛАВА IV. ПЕРЕМЕННОСТЬ МОЛОДЫХ ЗВЕЗД
- § 18. ЗВЕЗДЫ ТИПА UV КИТА
- § 19. ВСПЫШЕЧНЫЕ ЗВЕЗДЫ
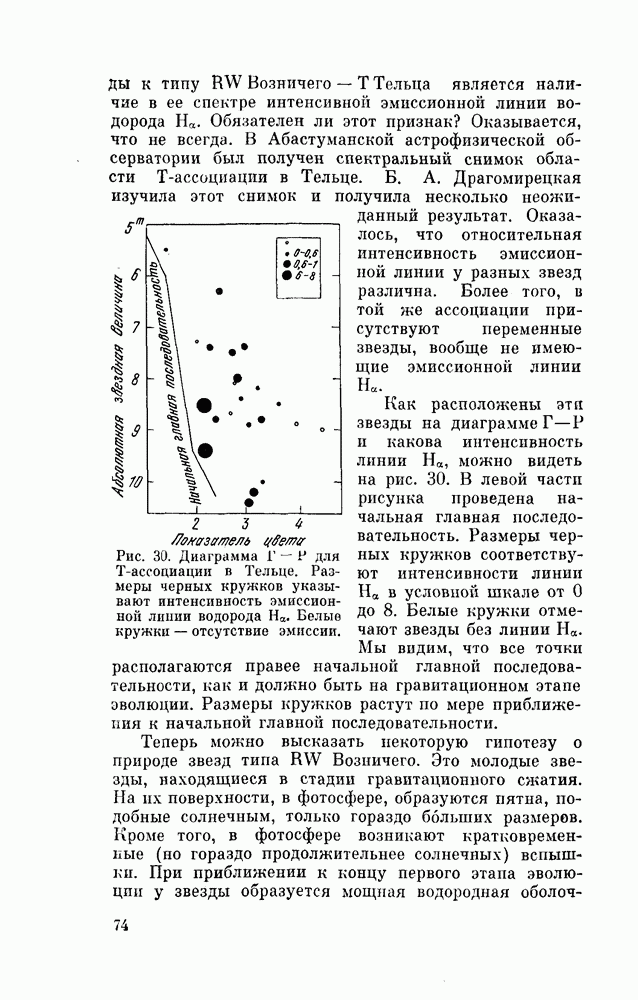
- § 20. ЗВЕЗДЫ ТИПА RW ВОЗНИЧЕГО — Т ТЕЛЬЦА
- § 21. ФУОРЫ И АНТИФУОРЫ
- ГЛАВА V. ВЗРЫВАЮЩИЕСЯ ЗВЕЗДЫ
- § 22. ТИПЫ ВЗРЫВАЮЩИХСЯ ЗВЕЗД
- § 23. ЯВЛЕНИЯ, ПРОИСХОДЯЩИЕ ПРИ ВСПЫШКЕ НОВОЙ ЗВЕЗДЫ
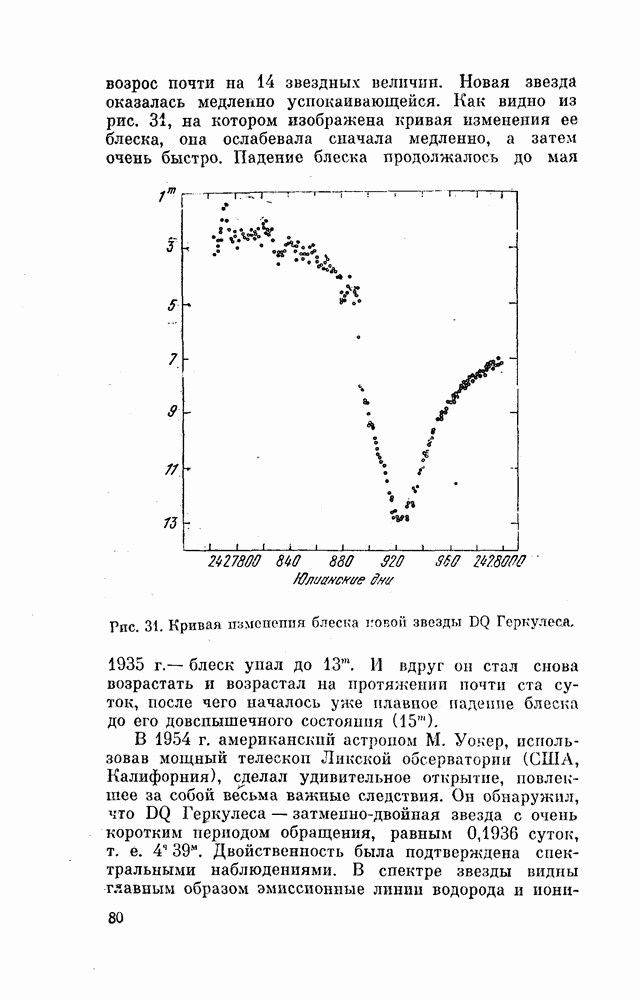
- § 24. ЗАГАДКА DQ ГЕРКУЛЕСА
- § 25. «ЗВЕЗДА-ГОСТЬЯ» В СОЗВЕЗДИИ ТЕЛЬЦА
- § 26. U БЛИЗНЕЦОВ И ЕЙ ПОДОБНЫЕ
- § 27. ТИХИЕ ВЗРЫВЫ
- § 28. РЕНТГЕНОВСКИЕ ПУЛЬСАРЫ В ДВОЙНЫХ ЗВЕЗДНЫХ СИСТЕМАХ
- § 29. ЗВЕЗДЫ ТИПА Z АНДРОМЕДЫ
- ГЛАВА VI. ОПРЕДЕЛЕНИЯ БЛЕСКА ПЕРЕМЕННЫХ ЗВЕЗД И СПОСОБЫ ИХ ОБРАБОТКИ
- § 30. ГЛАЗОМЕРНЫЕ ОЦЕНКИ БЛЕСКА
- § 31. СТЕПЕННАЯ ШКАЛА БЛЕСКА ЗВЕЗД СРАВНЕНИЯ
- § 32 РЕДУКЦИЯ ШКАЛ
- § 33. СИСТЕМАТИЧЕСКИЕ ОШИБКИ НАБЛЮДЕНИЙ БЛЕСКА
- § 34. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ ЗВЕЗД СРАВНЕНИЯ
- § 35. ПЕРВИЧНАЯ ОБРАБОТКА МОМЕНТОВ НАБЛЮДЕНИЙ
- § 36. КРИВАЯ ИЗМЕНЕНИЯ БЛЕСКА
- § 37. ИССЛЕДОВАНИЕ МИРИД
- § 38. СРЕДНЯЯ КРИВАЯ БЛЕСКА
- § 39. ИССЛЕДОВАНИЕ КОРОТКОПЕРИОДИЧЕСКИХ ЗВЕЗД. ПОИСКИ ПЕРИОДА
- § 40. УСКОРЕННОЕ ВЫЧИСЛЕНИЕ ВОЗРАСТОВ
- § 41. ИЗМЕНЕНИЕ ПЕРИОДОВ И ЭФФЕКТ БЛАЖКО
- § 42. ОРГАНИЗАЦИЯ НАБЛЮДЕНИЙ
- § 43. РЕКОМЕНДАЦИИ НАБЛЮДАТЕЛЯМ
- ДОПОЛНЕНИЯ
- Дополнение 1. СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
- Дополнение 2. ПРИВЕДЕНИЕ МОМЕНТОВ ВРЕМЕНИ К ЦЕНТРУ СОЛНЦА
- ПРИЛОЖЕНИЯ