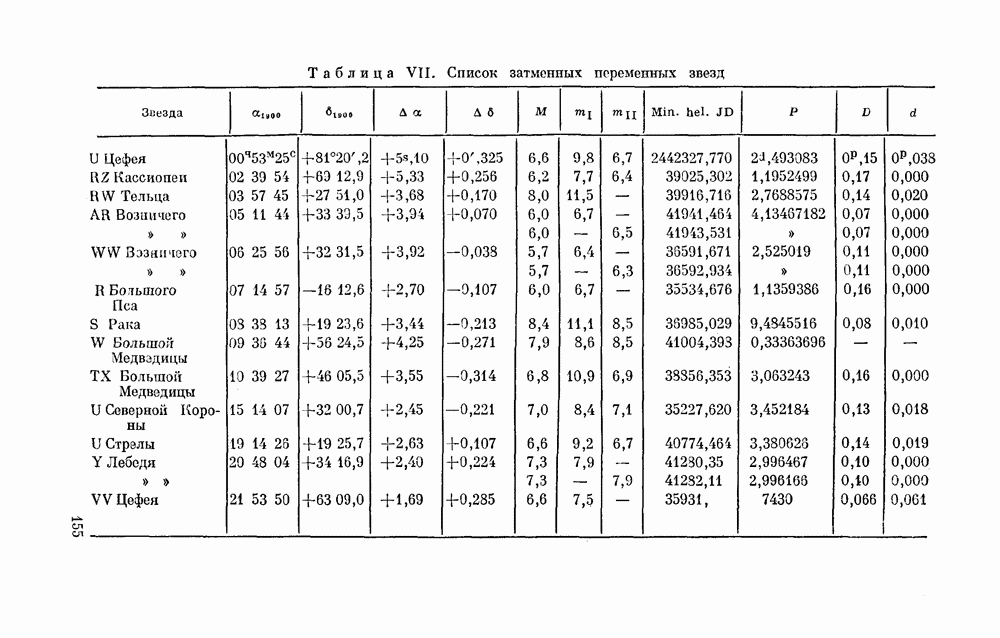
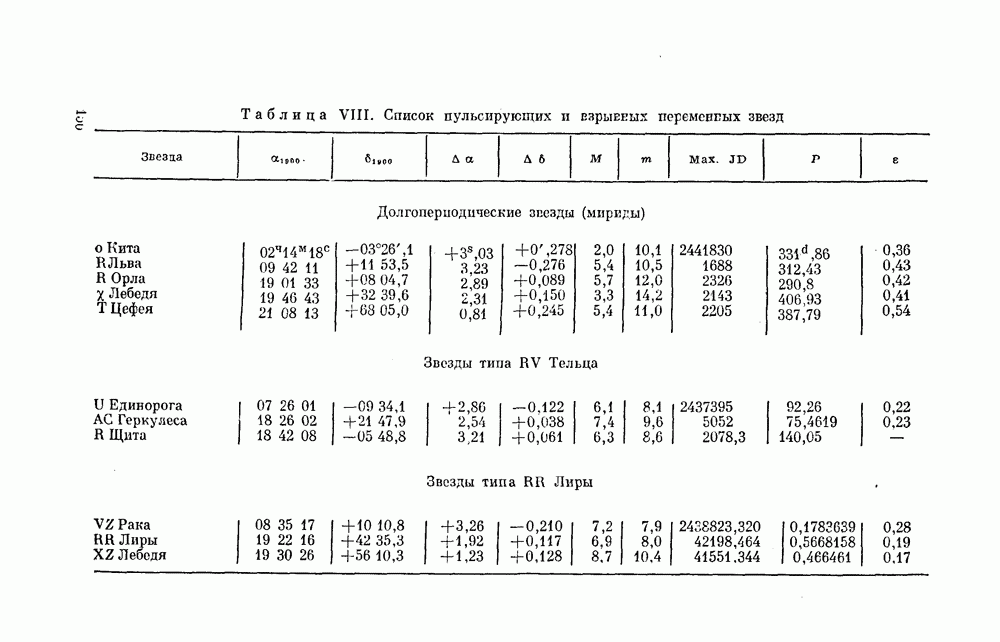
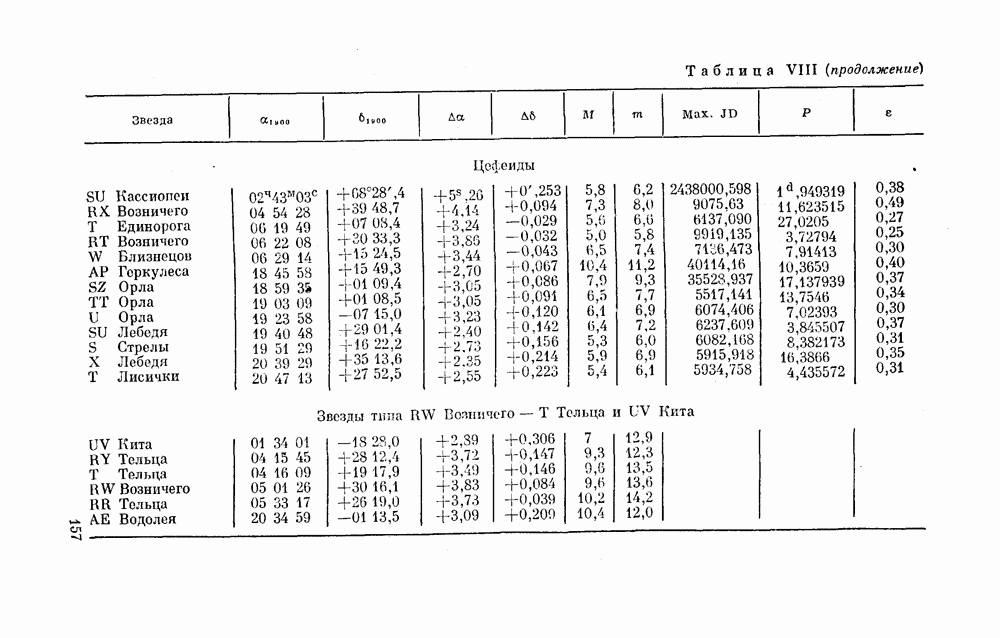
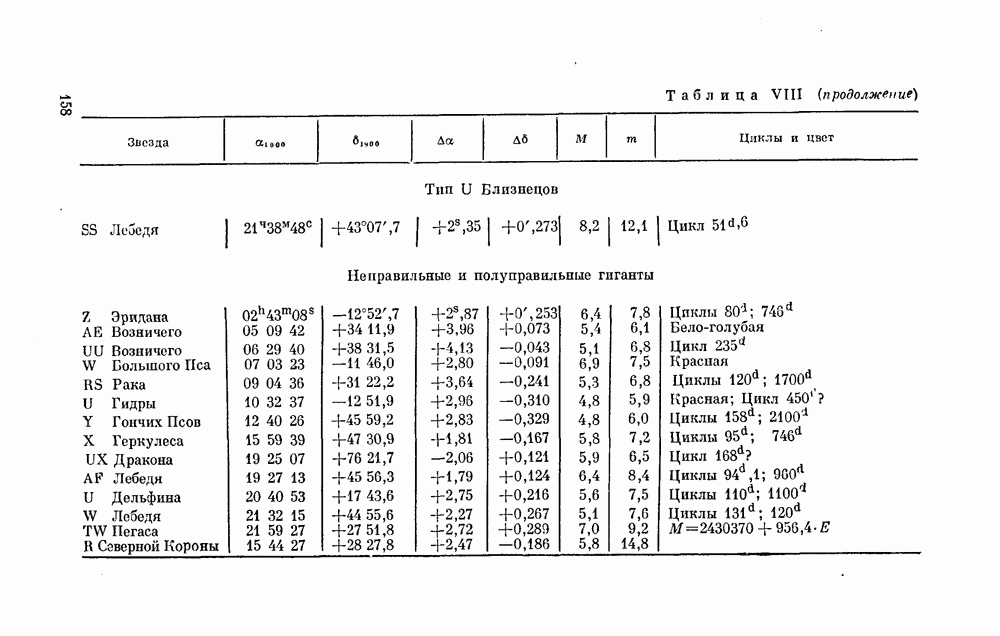
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
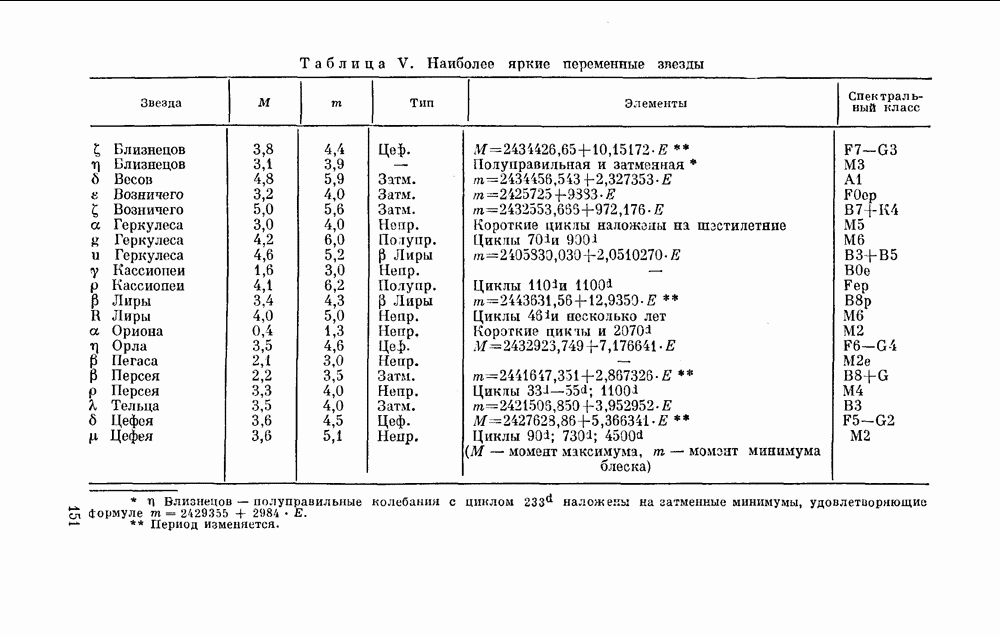
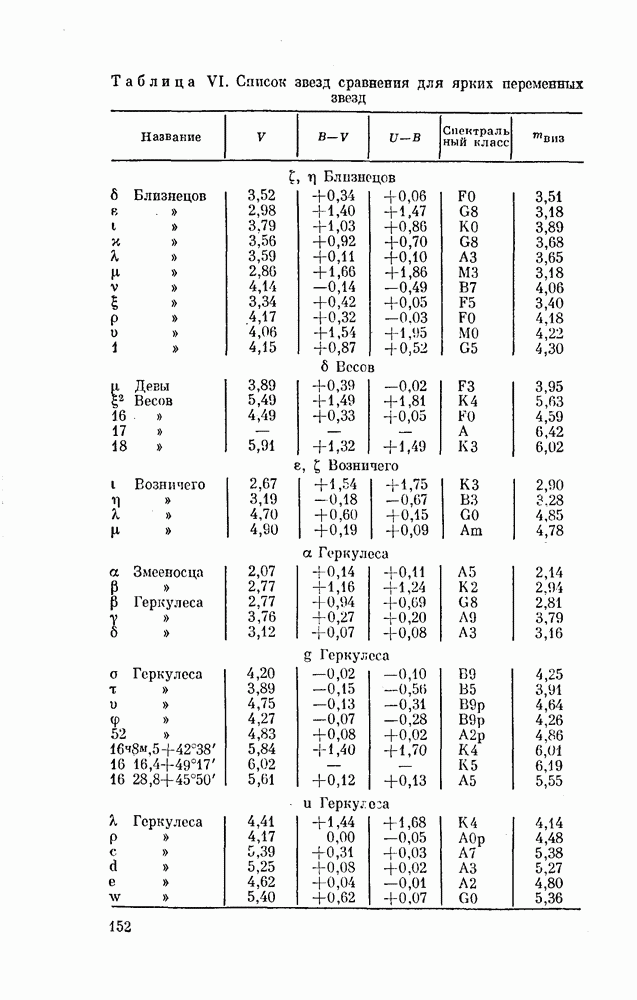
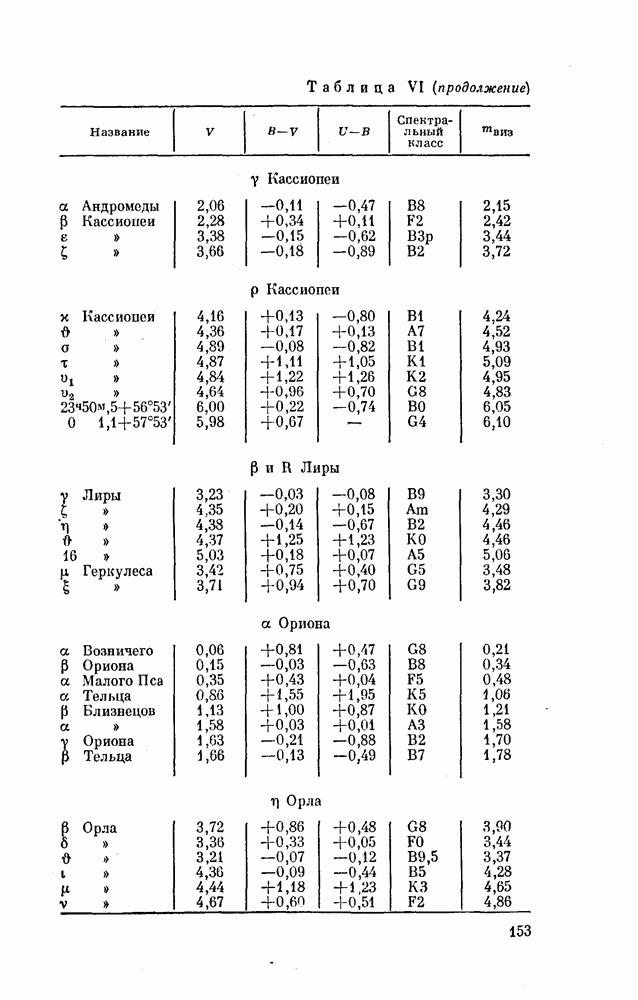
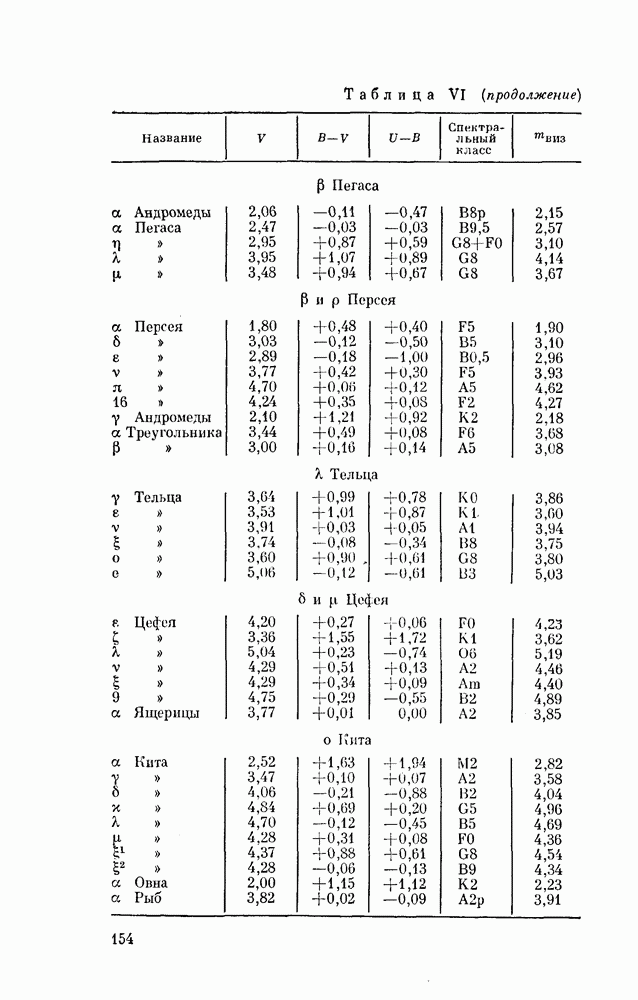
§ 37. ИССЛЕДОВАНИЕ МИРИД
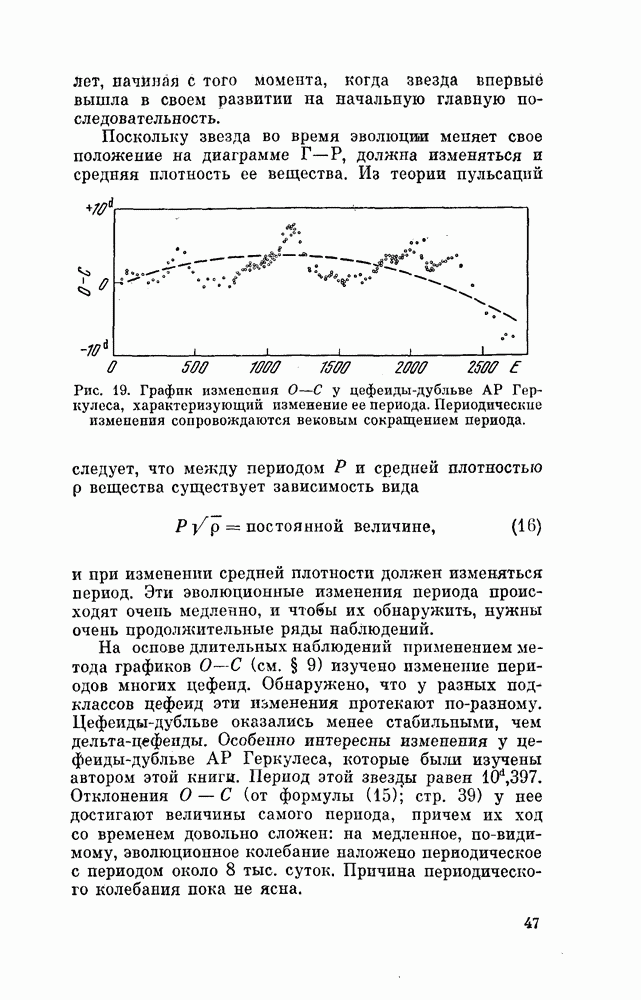
Большинство ярких мирид хорошо изучено. Так как это периодические переменные звезды, моменты максимумов их блеска представляются формулой вида (15)

где  — начальный момент максимума, Р — период, а Е — целое число (порядковый номер максимума МЕ). Исследователь строит по своим наблюдениям кривую блеска и но ней определяет момент максимума. Затем по формуле (15) вычисляет эфемериду и сравнивает наблюденный момент с вычисленным, т. е. находит остаток О — С. Он также сможет определить величину максимального блеска переменной.
— начальный момент максимума, Р — период, а Е — целое число (порядковый номер максимума МЕ). Исследователь строит по своим наблюдениям кривую блеска и но ней определяет момент максимума. Затем по формуле (15) вычисляет эфемериду и сравнивает наблюденный момент с вычисленным, т. е. находит остаток О — С. Он также сможет определить величину максимального блеска переменной.
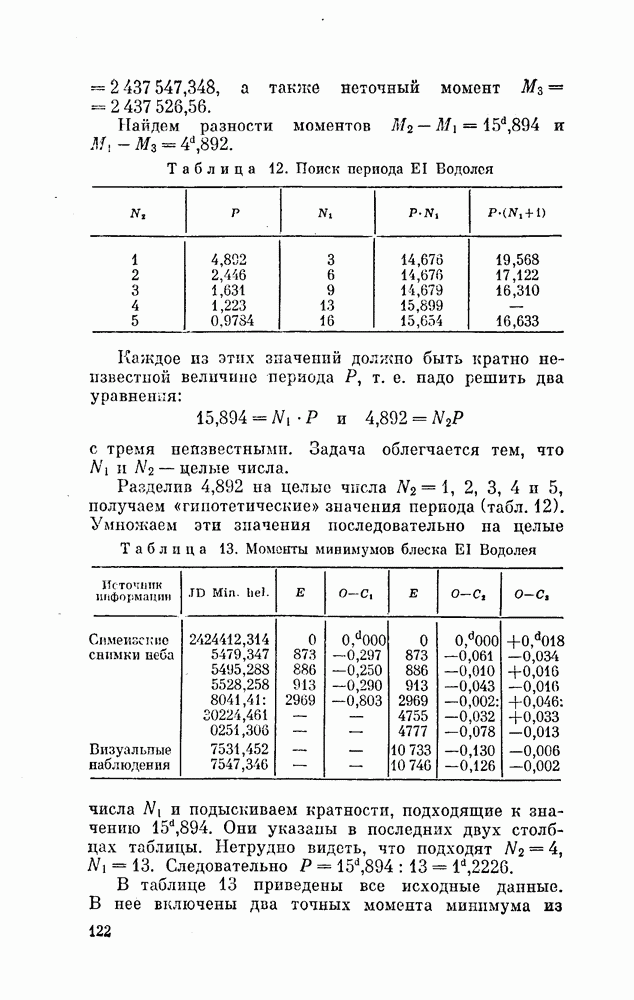
Допустим, что мы наблюдали еще не исследованную мириду. В результате наших наблюдений мы нашли совокупность моментов максимума и хотим вывести из нее конкретный вид формулы, (15). Задача сводится к следующему. Образовав разности последовательных моментов максимума, надо подыскать такое число Р, которое укладывалось бы в найденные разности целое число раз.
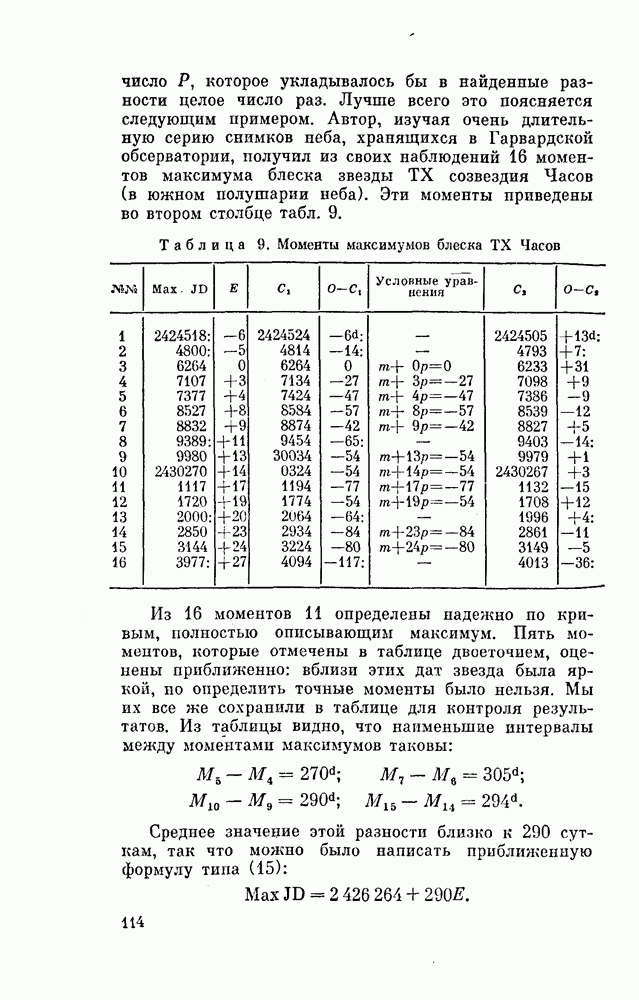
Лучше всего это поясняется следующим примером. Автор, изучая очень длительную серию снимков неба, хранящихся в Гарвардской обсерватории, получил из своих наблюдений 16 моментов максимума блеска звезды ТХ созвездия Часов (в южном полушарии неба). Эти моменты приведены во втором столбце табл. 9.
Таблица 9. Моменты максимумов блеска ТХ Часов

Из 16 моментов 11 определены надежно по кривым, полностью описывающим максимум. Пять моментов, которые отмечены в таблице двоеточием, оценены приближенно: вблизи этих дат звезда была яркой, но определить точные моменты было нельзя. Мы их все же сохранили в таблице для контроля результатов. Из таблицы видно, что наименьшие интервалы между моментами максимумов таковы:

Среднее значение этой разности близко к 290 суткам, так что можно было написать приближенную формулу типа (15):

С этой формулой была вычислена эфемерида  и в той же таблице указаны остатки
и в той же таблице указаны остатки  Указаны также и номера максимумов Е, Мы видим, что остатки отрицательны и нарастают по абсолютной величине с ростом номера Е. Это означает, что предварительная формула требует исправления, что можно сделать по способу наименьших квадратов.
Указаны также и номера максимумов Е, Мы видим, что остатки отрицательны и нарастают по абсолютной величине с ростом номера Е. Это означает, что предварительная формула требует исправления, что можно сделать по способу наименьших квадратов.
Для получения нужных условных уравнений вернемся к формуле (15). Обозначим истинное значение периода через Р, а приближенное через Р, истинное значение начального момента максимума через  а приближенное через
а приближенное через  Тогда можно написать
Тогда можно написать

где тир — поправки. Истинный момепт максимума должен удовлетворять формуле

где  — момент, вычисленный по приближенной формуле.
— момент, вычисленный по приближенной формуле.
Итак,

даст нужное условное уравнение. В табл. 9 паходпм необходимые для составления условных уравнений величины  эти уравнения показаны в той же таблице, но для неточных моментов (№№ 1, 2, 8, 13 и 16) они не составлены. По способу, описанному в Дополнении 1, составляем нормальные уравнения:
эти уравнения показаны в той же таблице, но для неточных моментов (№№ 1, 2, 8, 13 и 16) они не составлены. По способу, описанному в Дополнении 1, составляем нормальные уравнения:

и

Решив эти уравнения, находим  . Придав эти поправки к величинам
. Придав эти поправки к величинам  и Р исходной формулы, получаем окончательную формулу:
и Р исходной формулы, получаем окончательную формулу:

По этой формуле вычислены значения и остатки  приведенные в последних столбцах табл. 9. Сумма значений последних близка к нулю (как и должно быть при применении способа наименьших квадратов).
приведенные в последних столбцах табл. 9. Сумма значений последних близка к нулю (как и должно быть при применении способа наименьших квадратов).
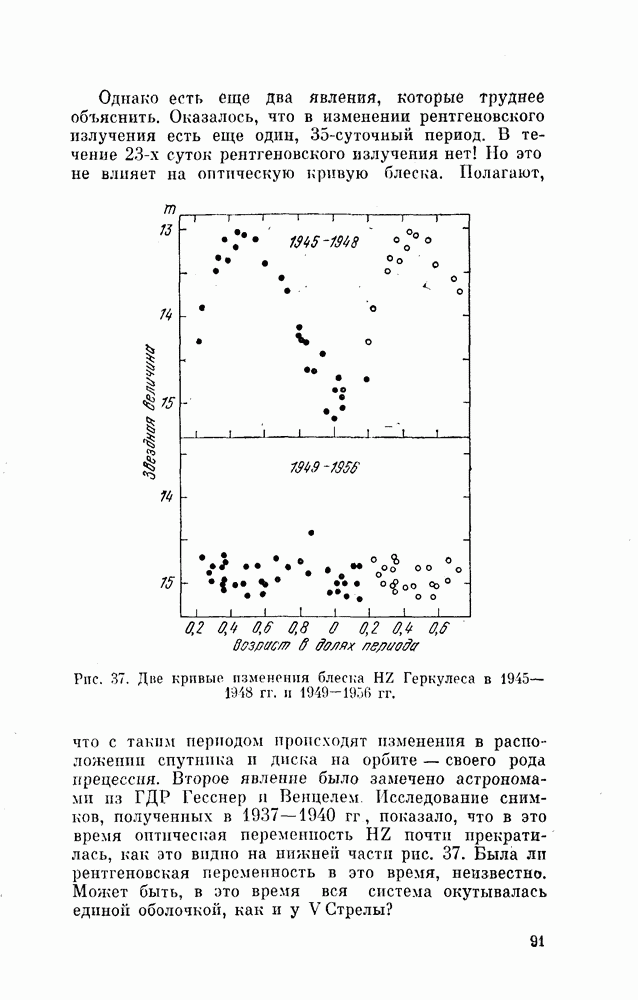
Их величины не показывают никакого систематического хода с номером Е. - Это позволяет считать, что период сохранял свое постоянное значение.
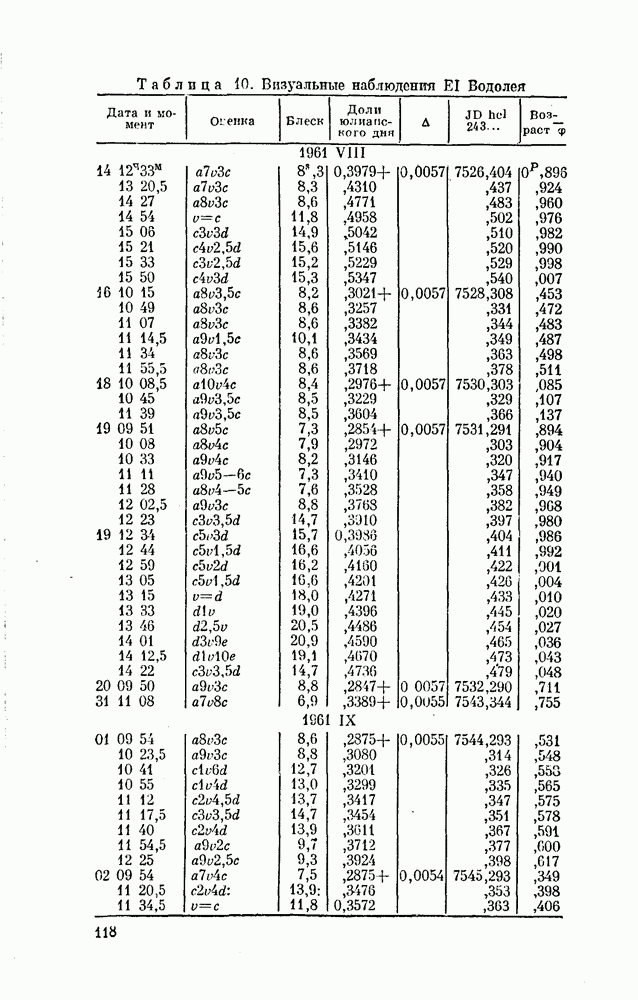
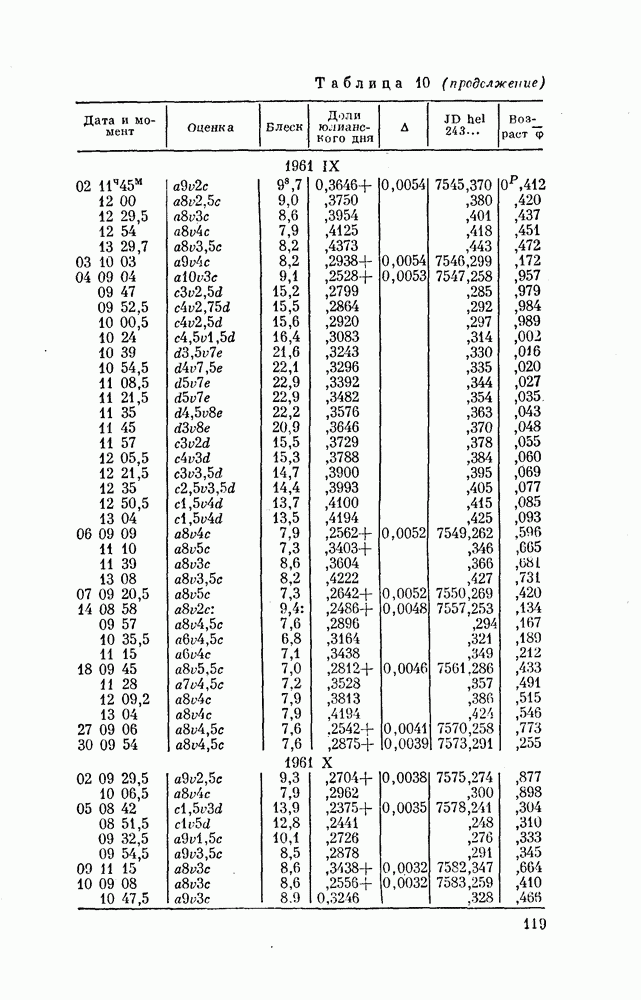
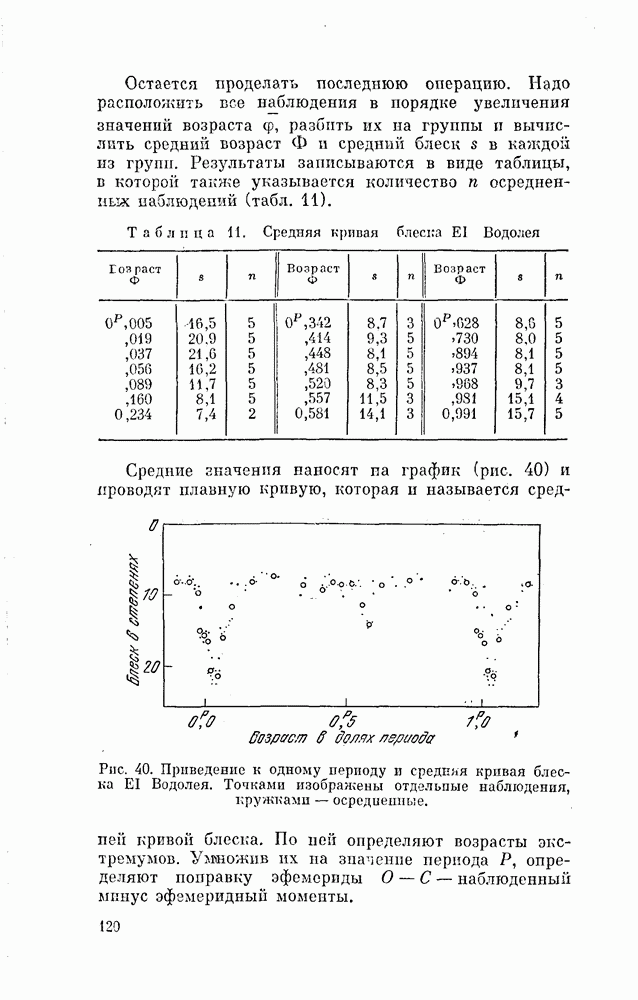
Теперь можно построить среднюю кривую блеска.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ВВЕДЕНИЕ
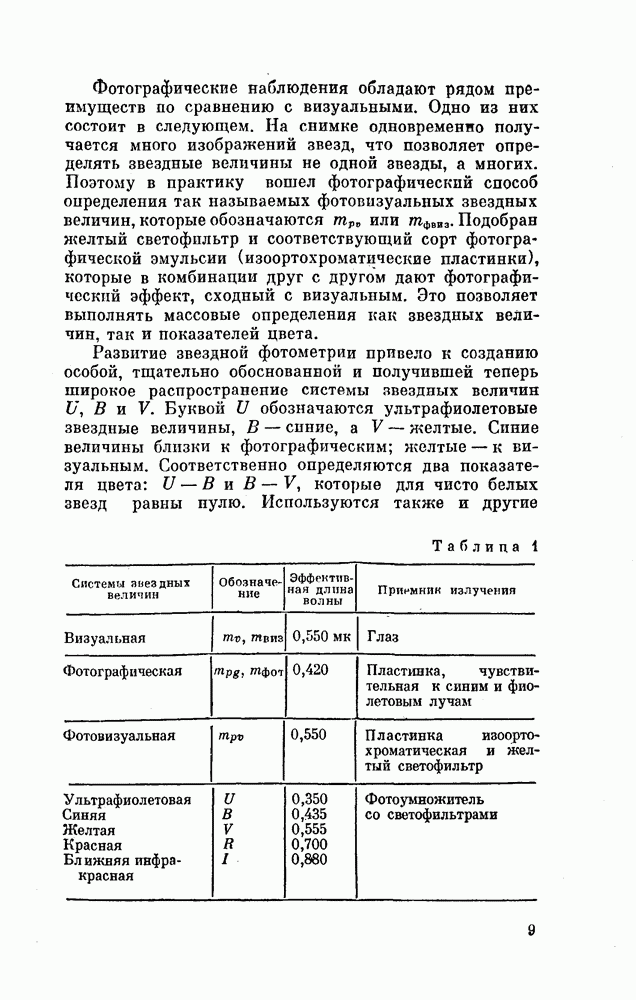
- § 1. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ЦВЕТА
- § 2. СВЕТИМОСТИ И РАДИУСЫ ЗВЕЗД
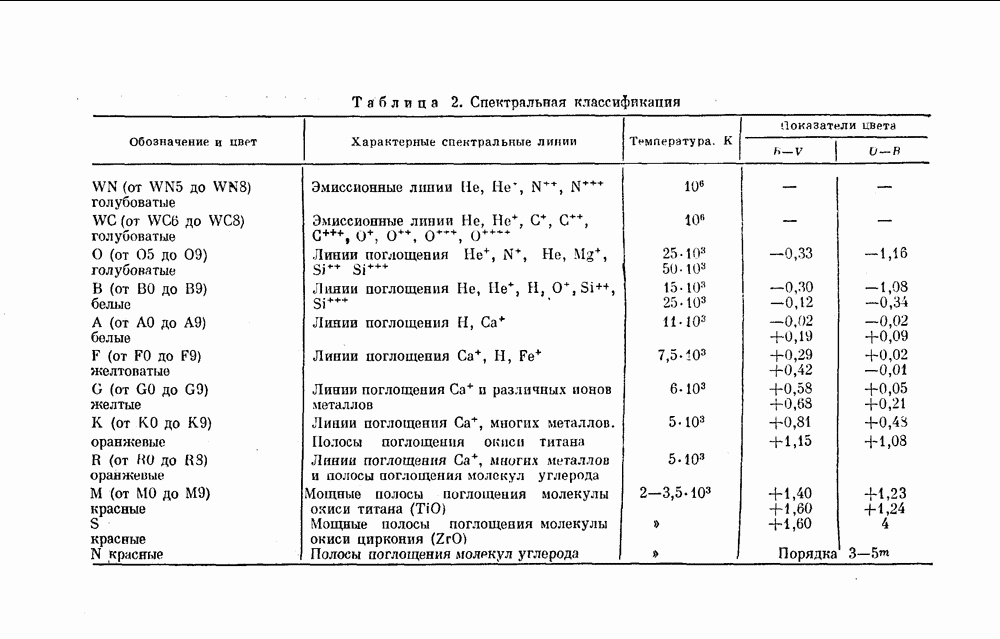
- § 3. СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ И ЛУЧЕВЫЕ СКОРОСТИ
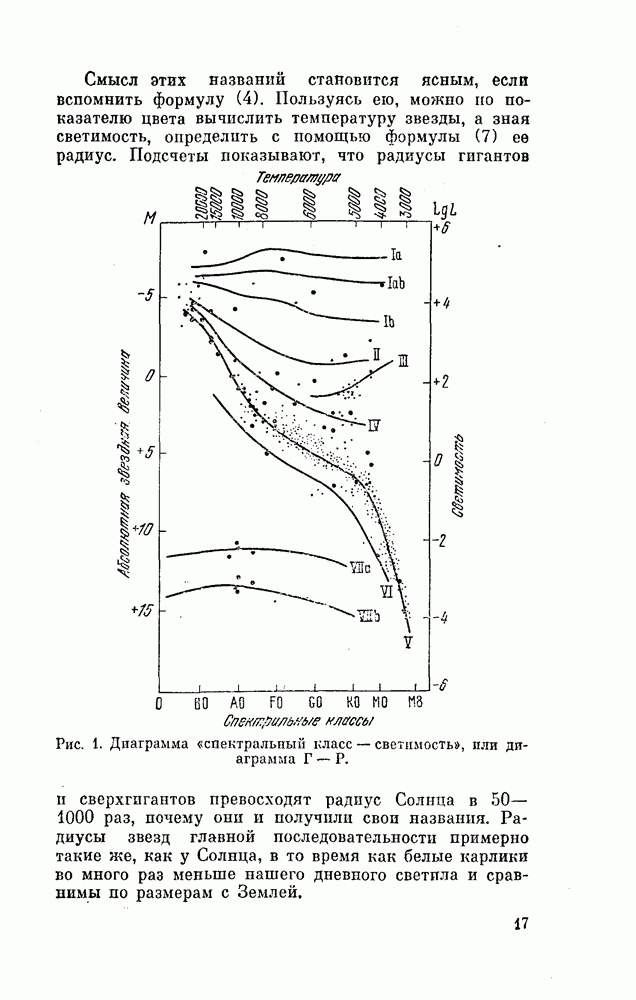
- § 4. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- § 5. ТИПЫ ЗВЕЗДНОГО НАСЕЛЕНИЯ
- ГЛАВА II. ЗАТМЕННЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 6. КЛАССИФИКАЦИЯ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
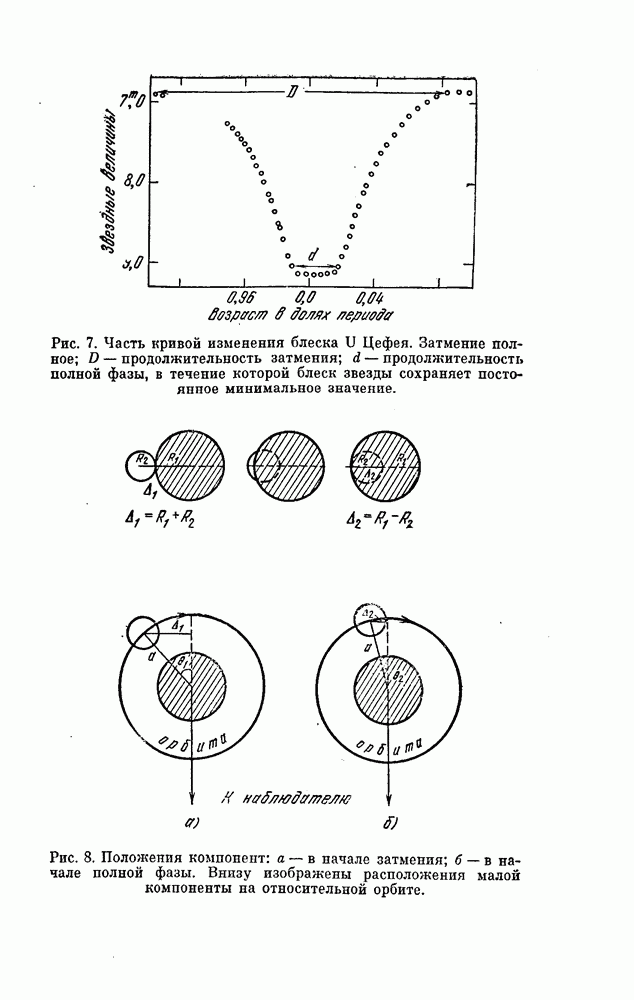
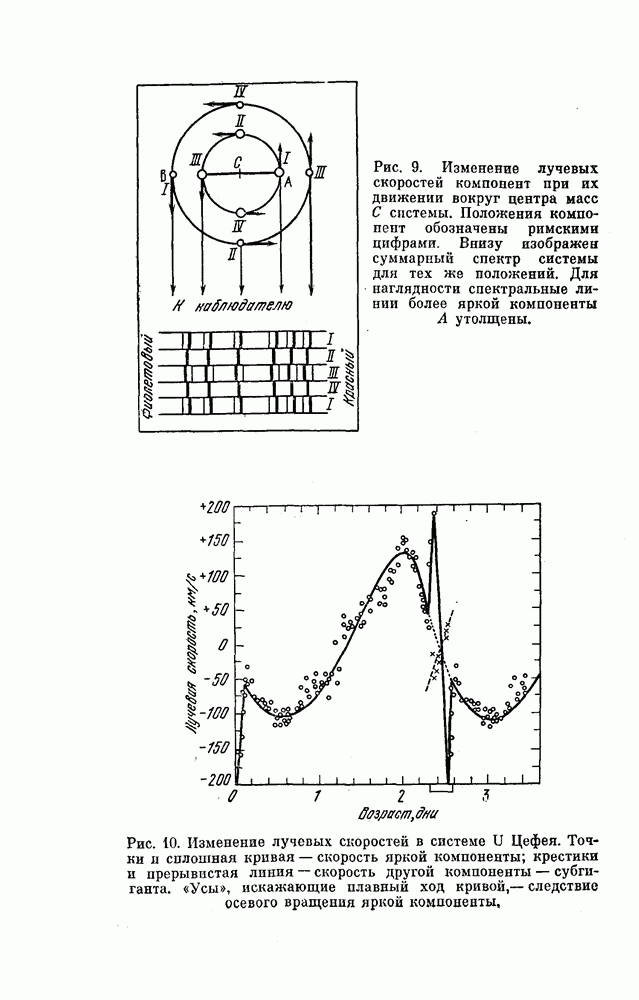
- § 7. ЧТО ДАЕТ ИЗУЧЕНИЕ КРИВОЙ БЛЕСКА ЗВЕЗДЫ ТИПА АЛГОЛЯ?
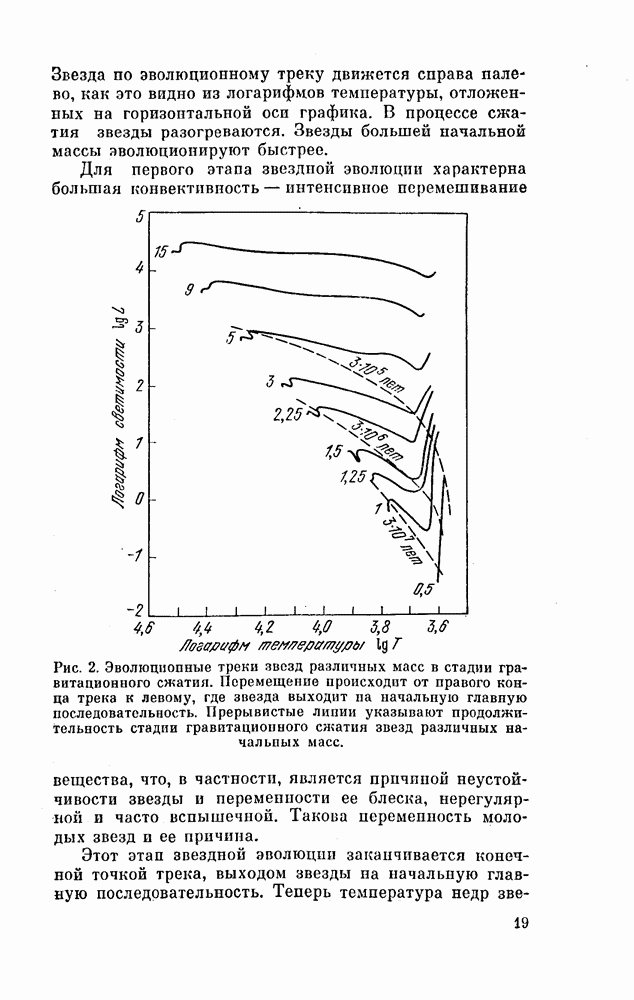
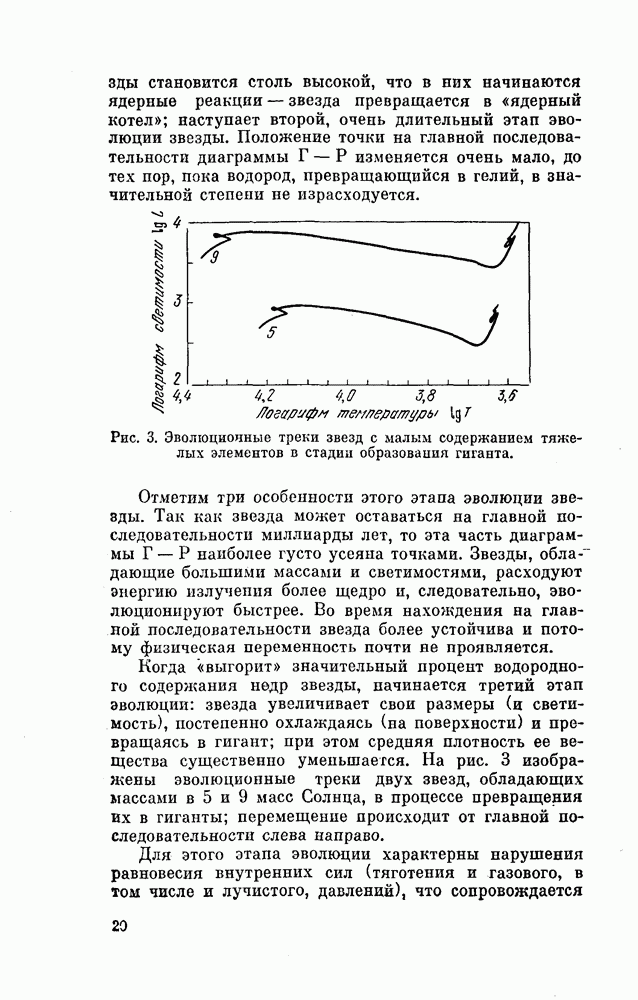
- § 8. ЭВОЛЮЦИЯ ТЕСНОЙ ДВОЙНОЙ ЗВЕЗДЫ
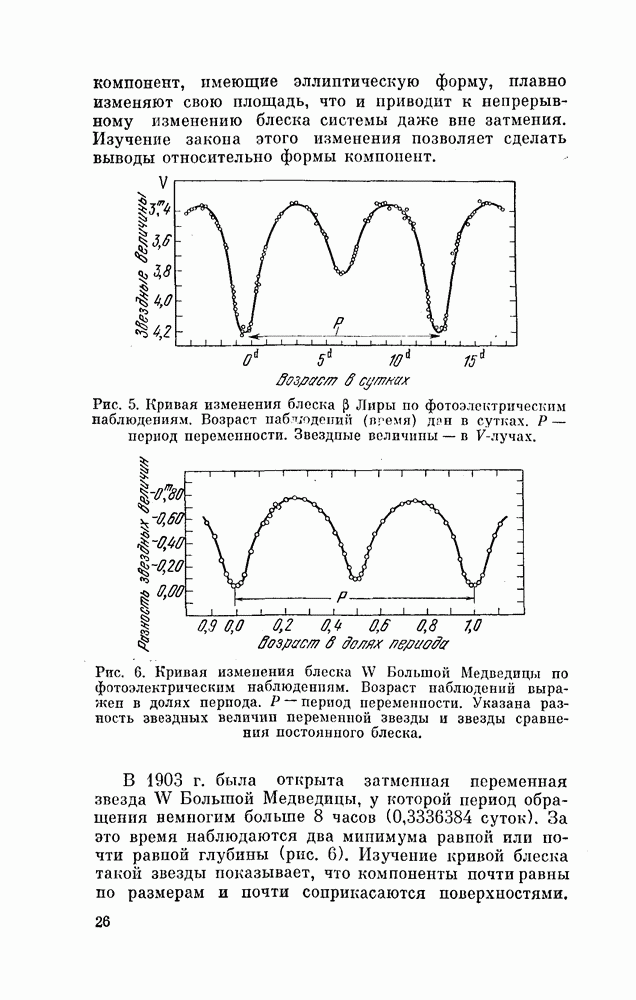
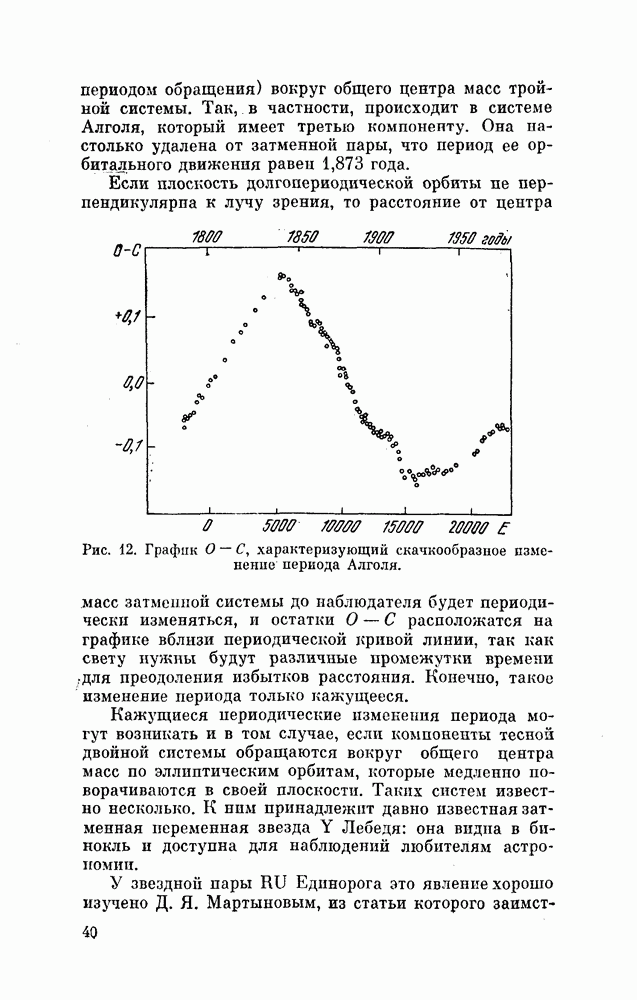
- § 9. ИЗМЕНЕНИЕ ПЕРИОДОВ ЗАТМЕННЫХ ПЕРЕМЕННЫХ ЗВЕЗД
- ГЛАВА III. ПУЛЬСИРУЮЩИЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
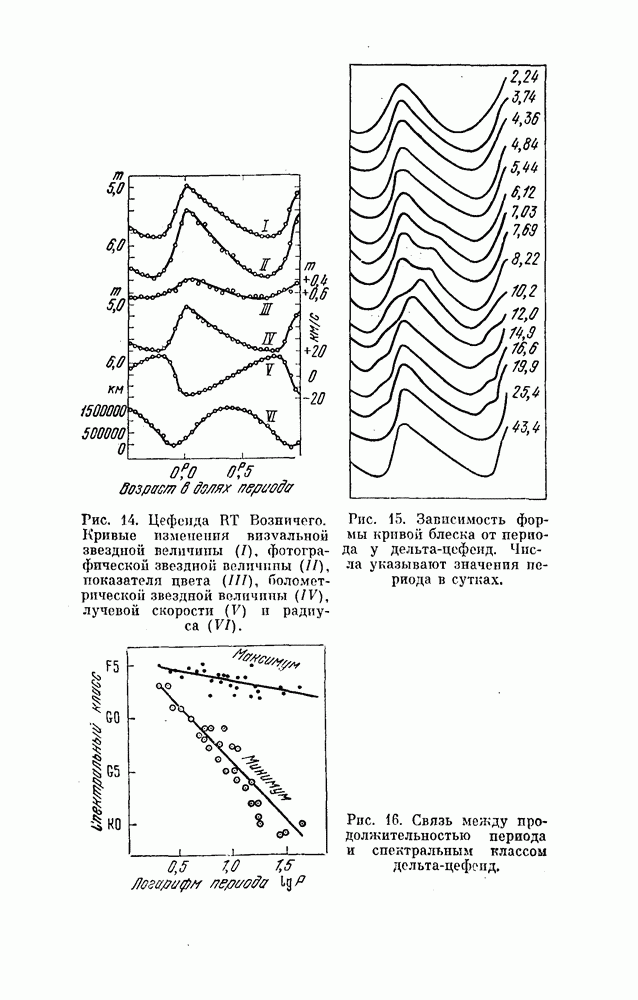
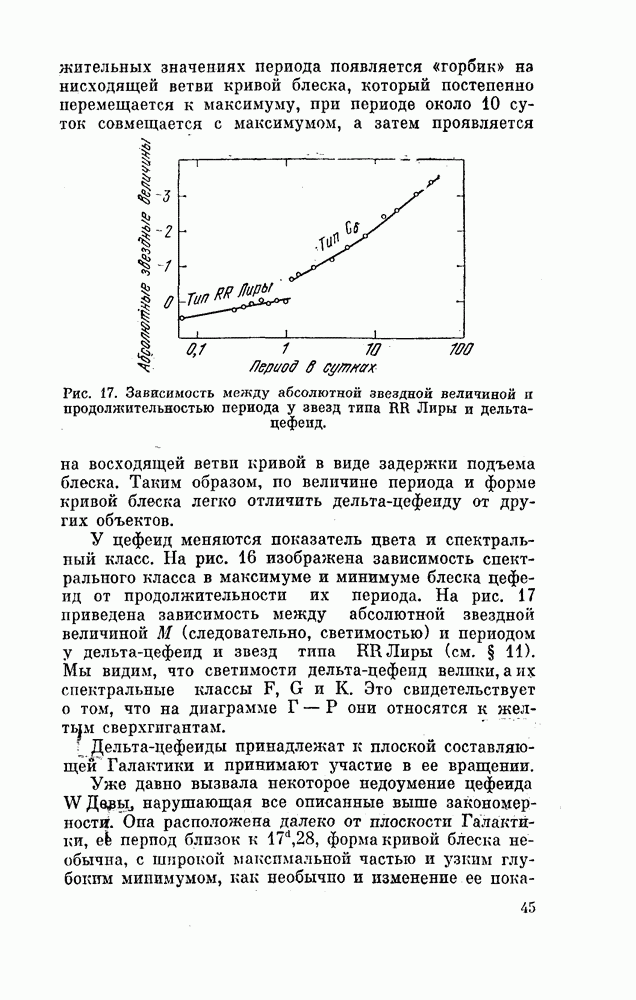
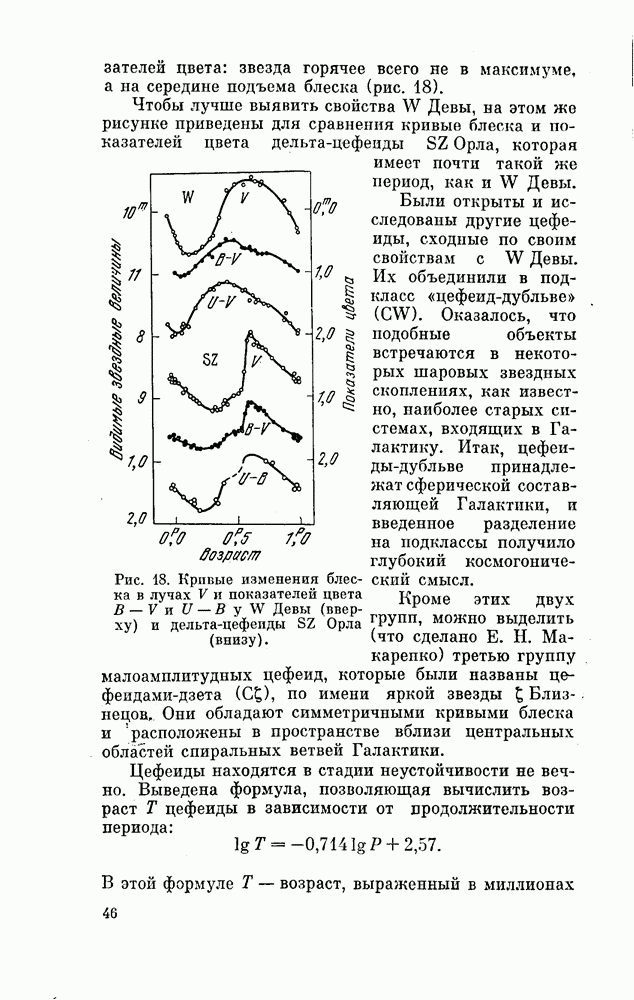
- § 10. ЦЕФЕИДЫ, ИЛИ ЗВЕЗДЫ ТИПА б ЦЕФЕЯ
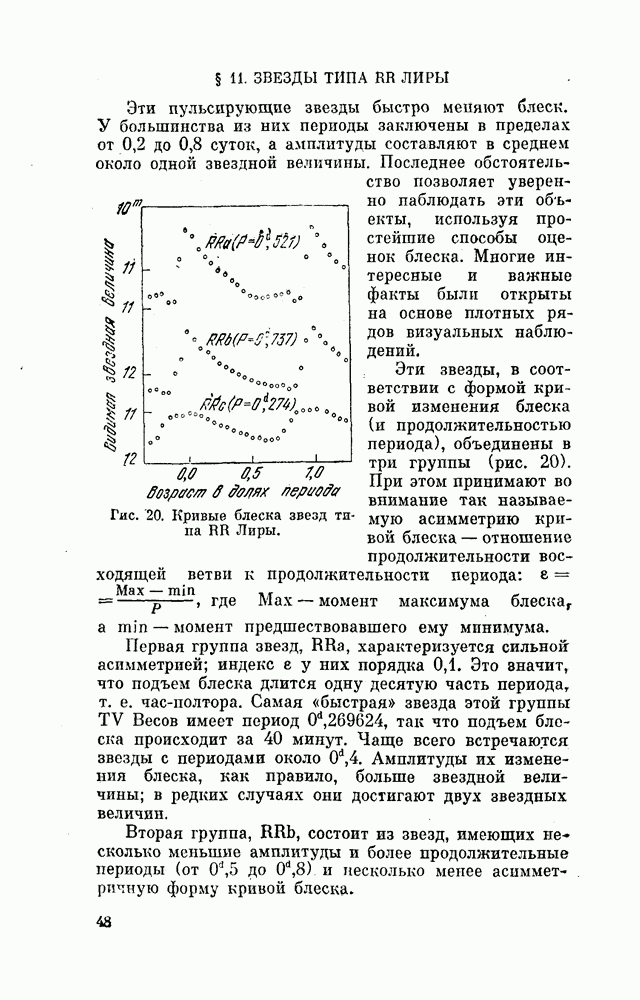
- § 11. ЗВЕЗДЫ ТИПА RR ЛИРЫ
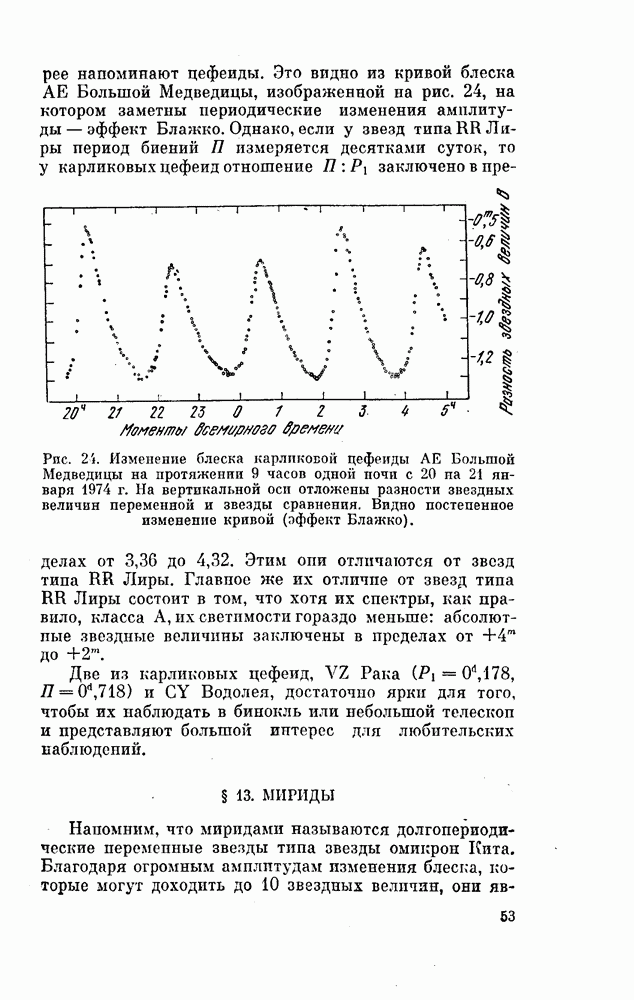
- § 12. КАРЛИКОВЫЕ ЦЕФЕИДЫ
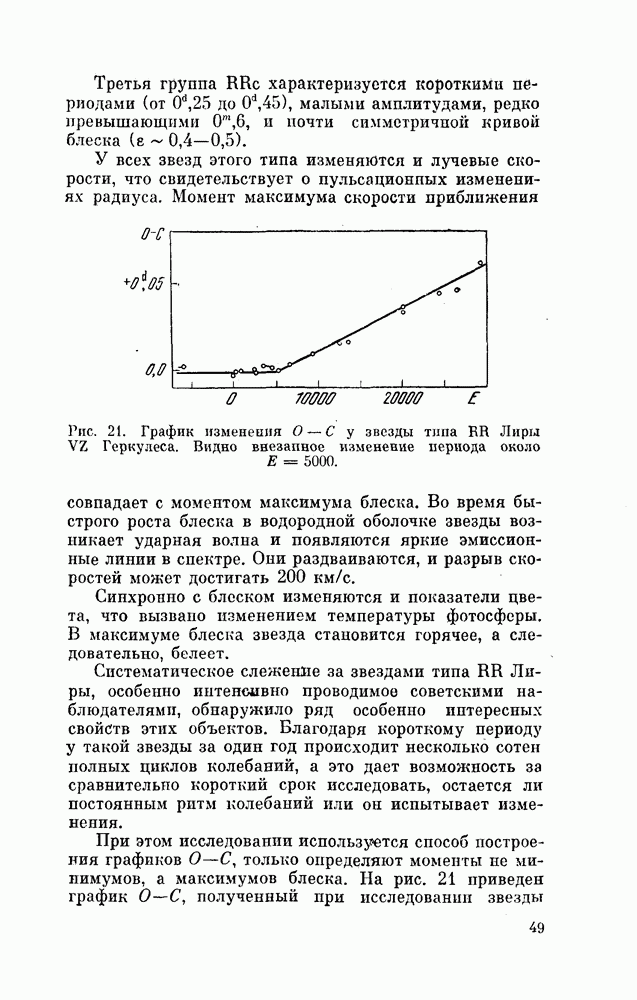
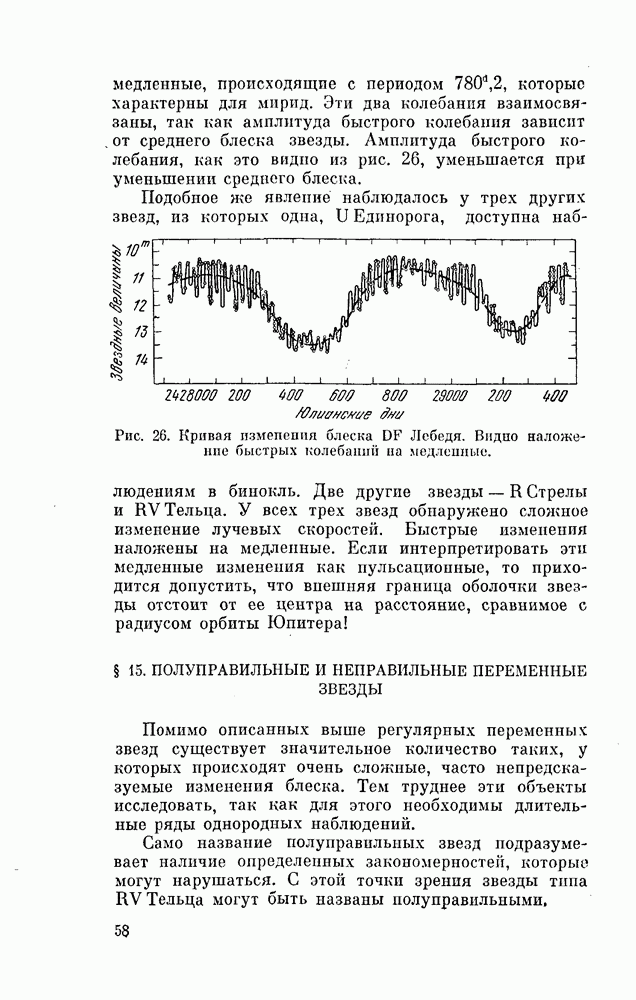
- § 13. МИРИДЫ
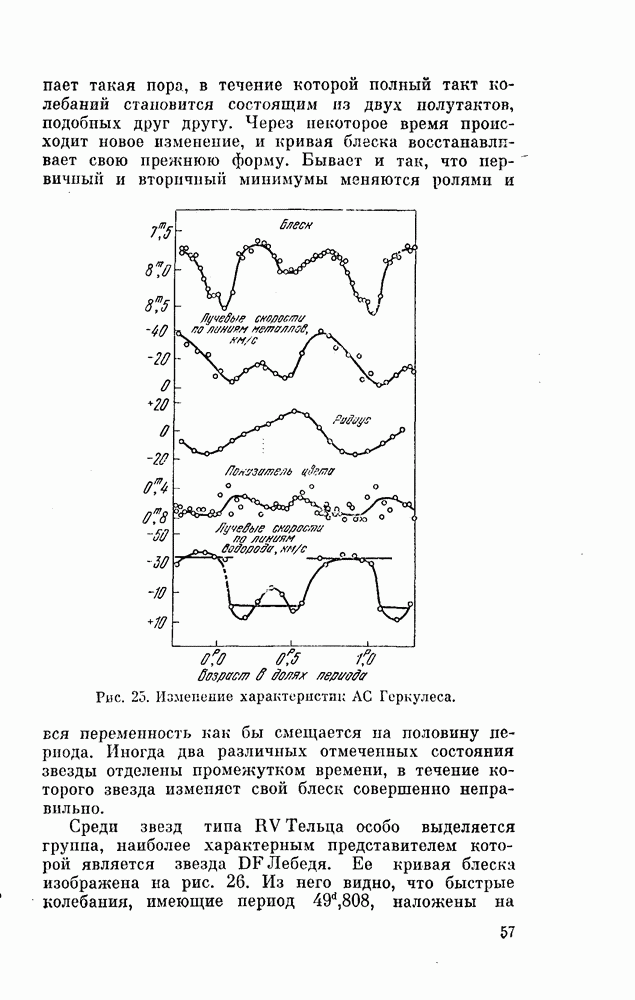
- § 14. ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА
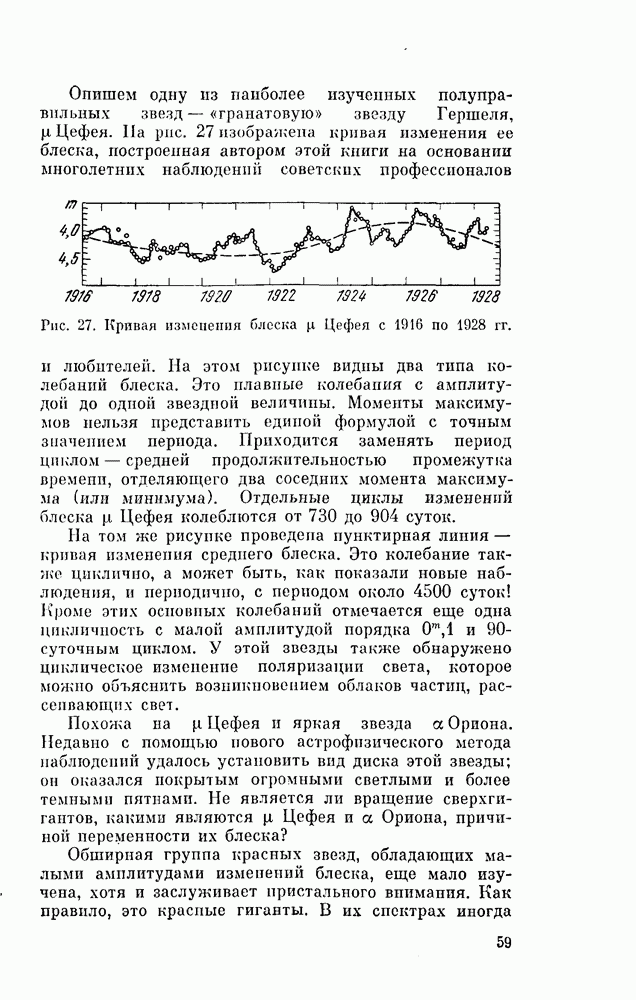
- § 15. ПОЛУПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- § 16. ПЕРЕМЕННЫЕ ЗВЕЗДЫ, ОБЛАДАЮЩИЕ МАЛЫМИ АМПЛИТУДАМИ
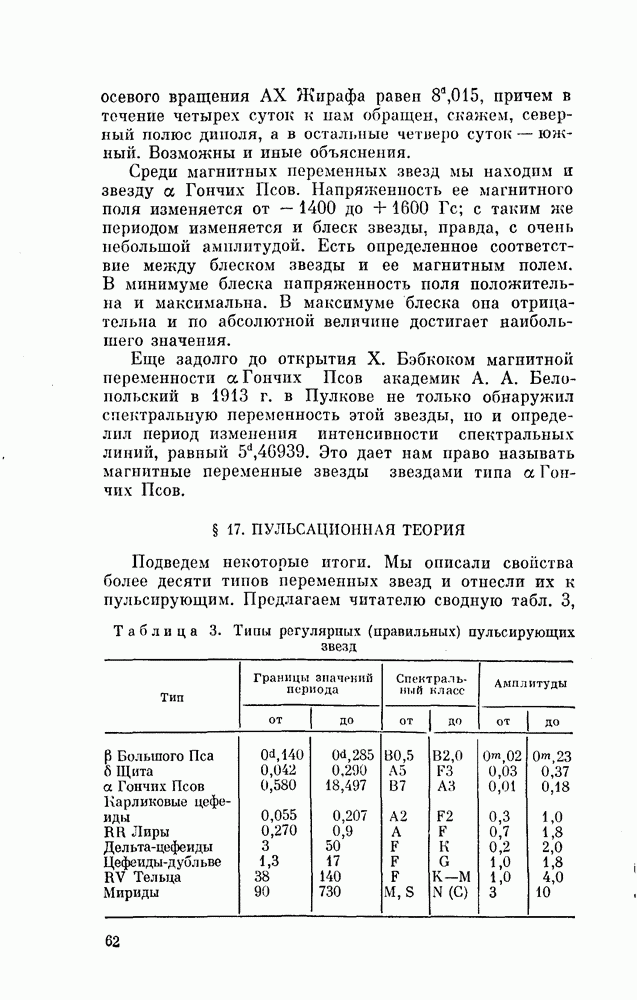
- § 17. ПУЛЬСАЦИОННАЯ ТЕОРИЯ
- ГЛАВА IV. ПЕРЕМЕННОСТЬ МОЛОДЫХ ЗВЕЗД
- § 18. ЗВЕЗДЫ ТИПА UV КИТА
- § 19. ВСПЫШЕЧНЫЕ ЗВЕЗДЫ
- § 20. ЗВЕЗДЫ ТИПА RW ВОЗНИЧЕГО — Т ТЕЛЬЦА
- § 21. ФУОРЫ И АНТИФУОРЫ
- ГЛАВА V. ВЗРЫВАЮЩИЕСЯ ЗВЕЗДЫ
- § 22. ТИПЫ ВЗРЫВАЮЩИХСЯ ЗВЕЗД
- § 23. ЯВЛЕНИЯ, ПРОИСХОДЯЩИЕ ПРИ ВСПЫШКЕ НОВОЙ ЗВЕЗДЫ
- § 24. ЗАГАДКА DQ ГЕРКУЛЕСА
- § 25. «ЗВЕЗДА-ГОСТЬЯ» В СОЗВЕЗДИИ ТЕЛЬЦА
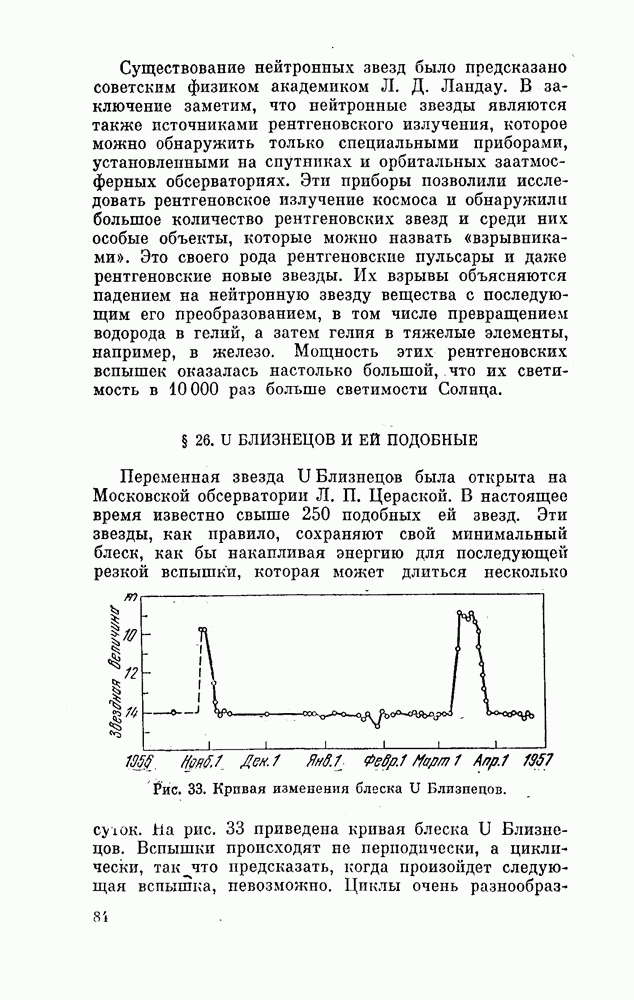
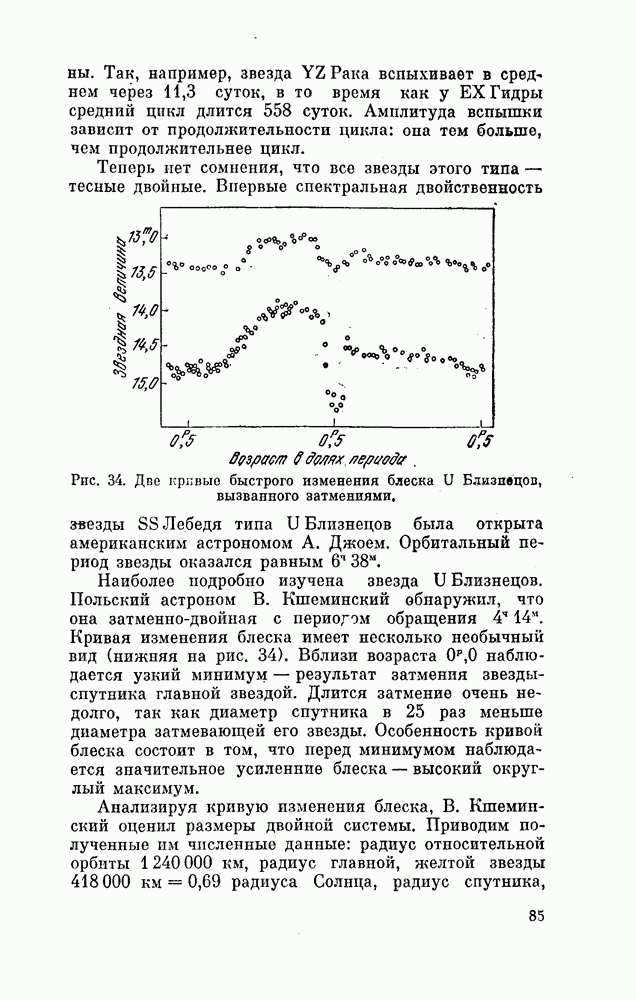
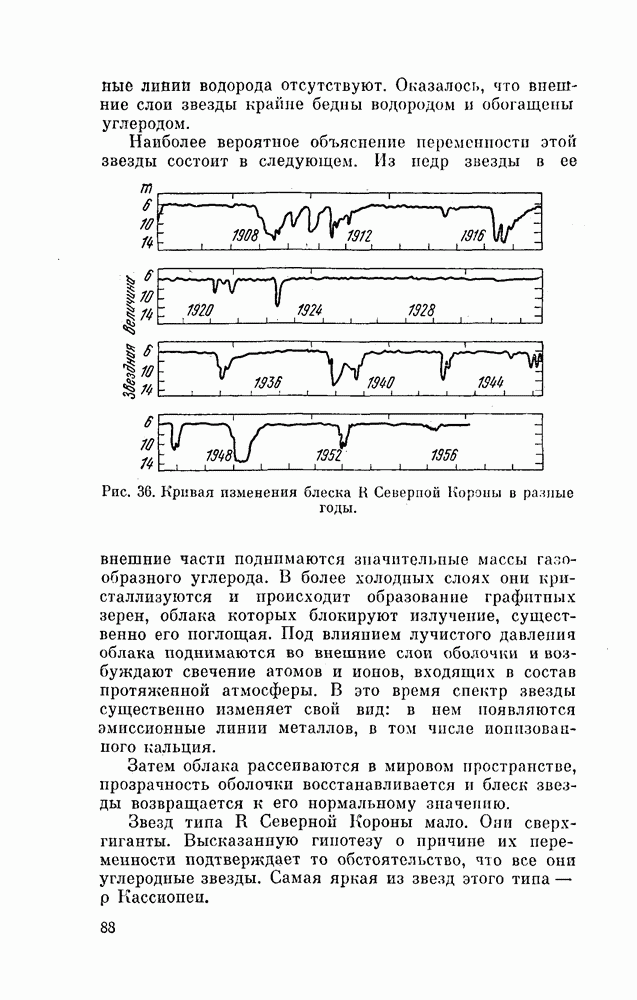
- § 26. U БЛИЗНЕЦОВ И ЕЙ ПОДОБНЫЕ
- § 27. ТИХИЕ ВЗРЫВЫ
- § 28. РЕНТГЕНОВСКИЕ ПУЛЬСАРЫ В ДВОЙНЫХ ЗВЕЗДНЫХ СИСТЕМАХ
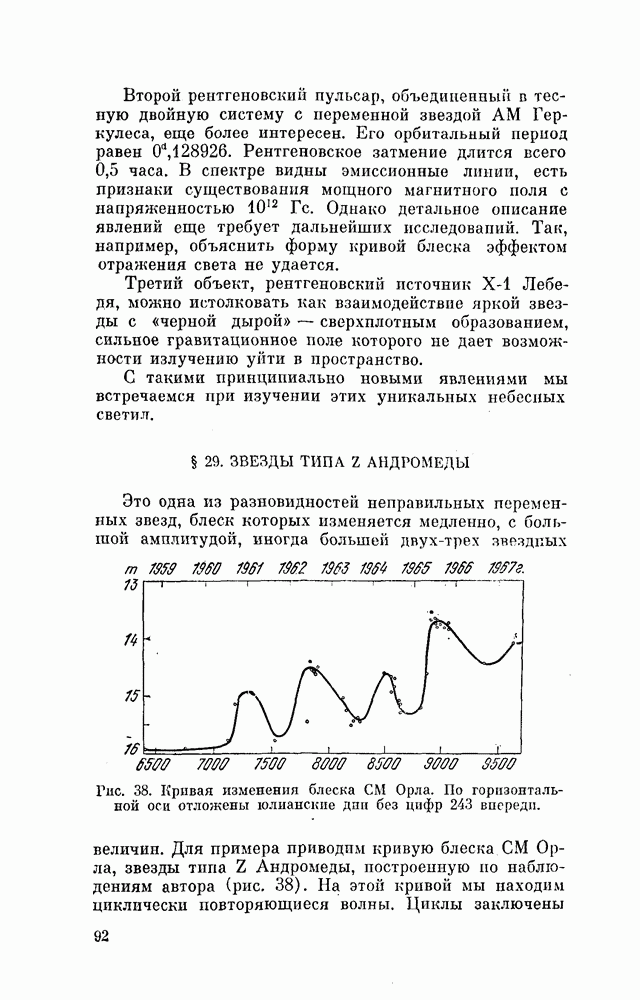
- § 29. ЗВЕЗДЫ ТИПА Z АНДРОМЕДЫ
- ГЛАВА VI. ОПРЕДЕЛЕНИЯ БЛЕСКА ПЕРЕМЕННЫХ ЗВЕЗД И СПОСОБЫ ИХ ОБРАБОТКИ
- § 30. ГЛАЗОМЕРНЫЕ ОЦЕНКИ БЛЕСКА
- § 31. СТЕПЕННАЯ ШКАЛА БЛЕСКА ЗВЕЗД СРАВНЕНИЯ
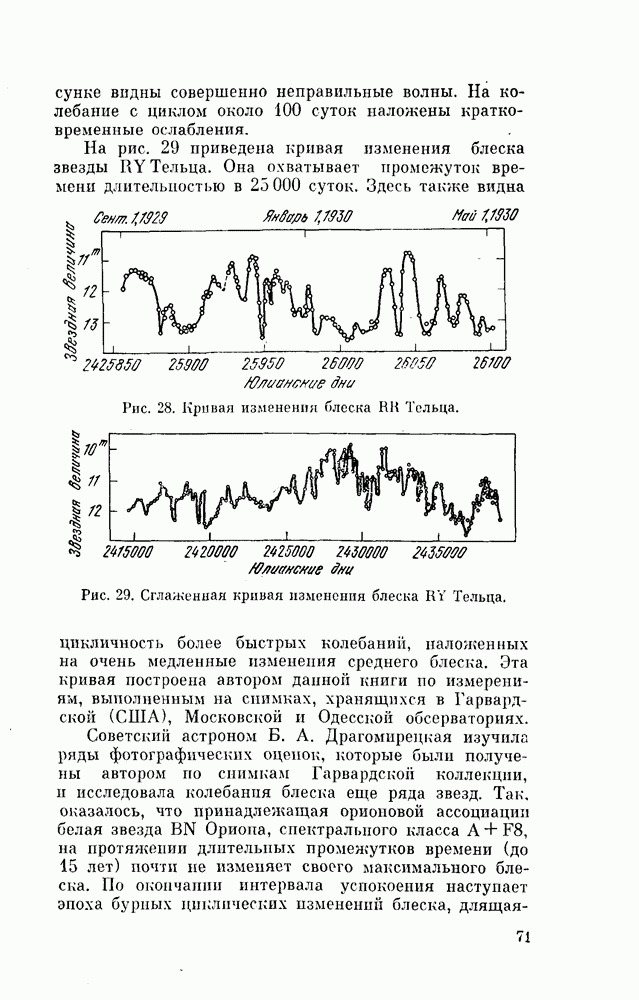
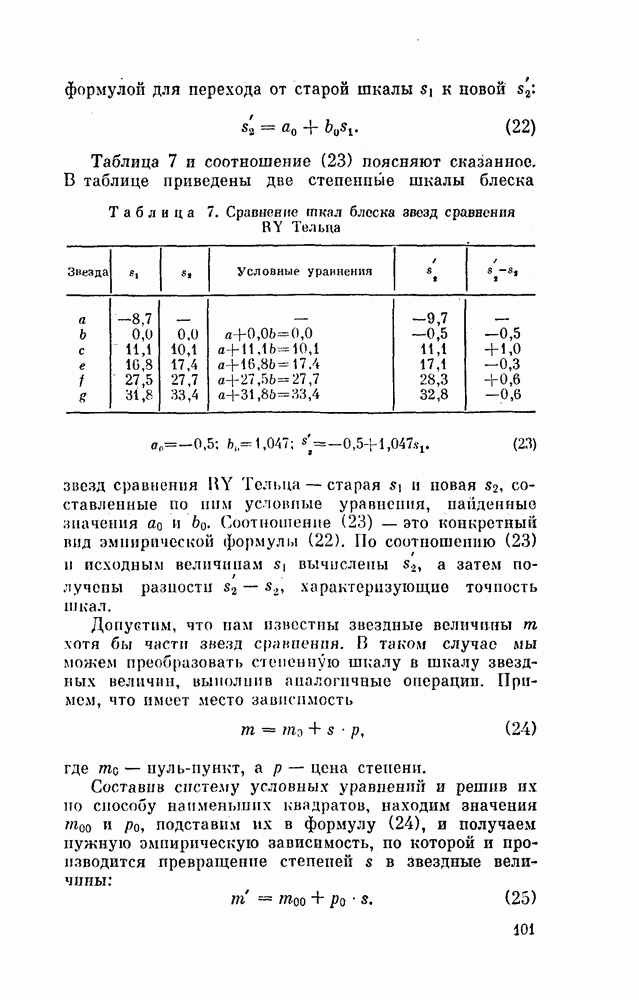
- § 32 РЕДУКЦИЯ ШКАЛ
- § 33. СИСТЕМАТИЧЕСКИЕ ОШИБКИ НАБЛЮДЕНИЙ БЛЕСКА
- § 34. ЗВЕЗДНЫЕ ВЕЛИЧИНЫ ЗВЕЗД СРАВНЕНИЯ
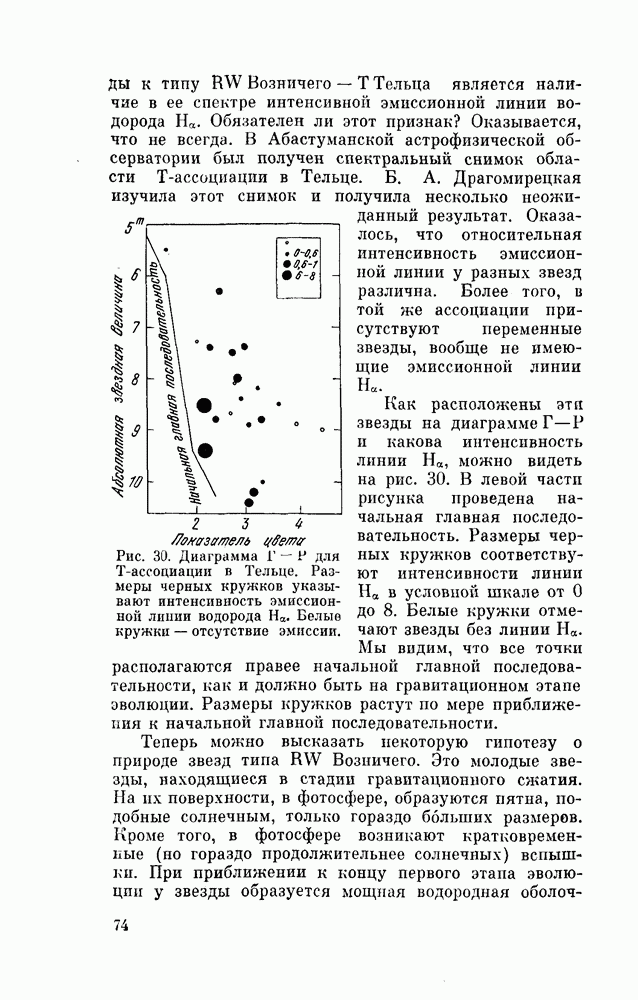
- § 35. ПЕРВИЧНАЯ ОБРАБОТКА МОМЕНТОВ НАБЛЮДЕНИЙ
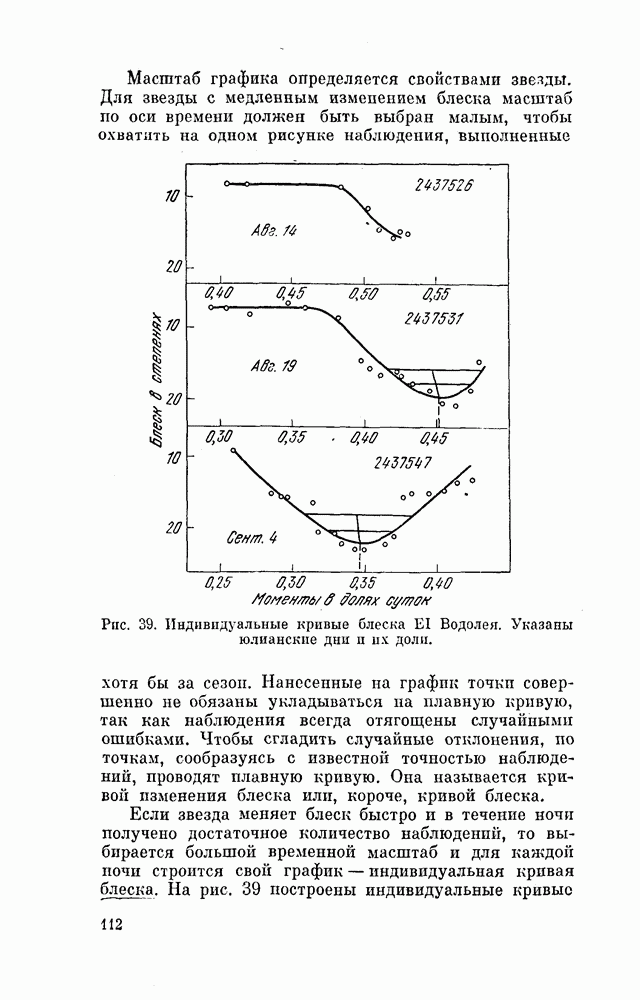
- § 36. КРИВАЯ ИЗМЕНЕНИЯ БЛЕСКА
- § 37. ИССЛЕДОВАНИЕ МИРИД
- § 38. СРЕДНЯЯ КРИВАЯ БЛЕСКА
- § 39. ИССЛЕДОВАНИЕ КОРОТКОПЕРИОДИЧЕСКИХ ЗВЕЗД. ПОИСКИ ПЕРИОДА
- § 40. УСКОРЕННОЕ ВЫЧИСЛЕНИЕ ВОЗРАСТОВ
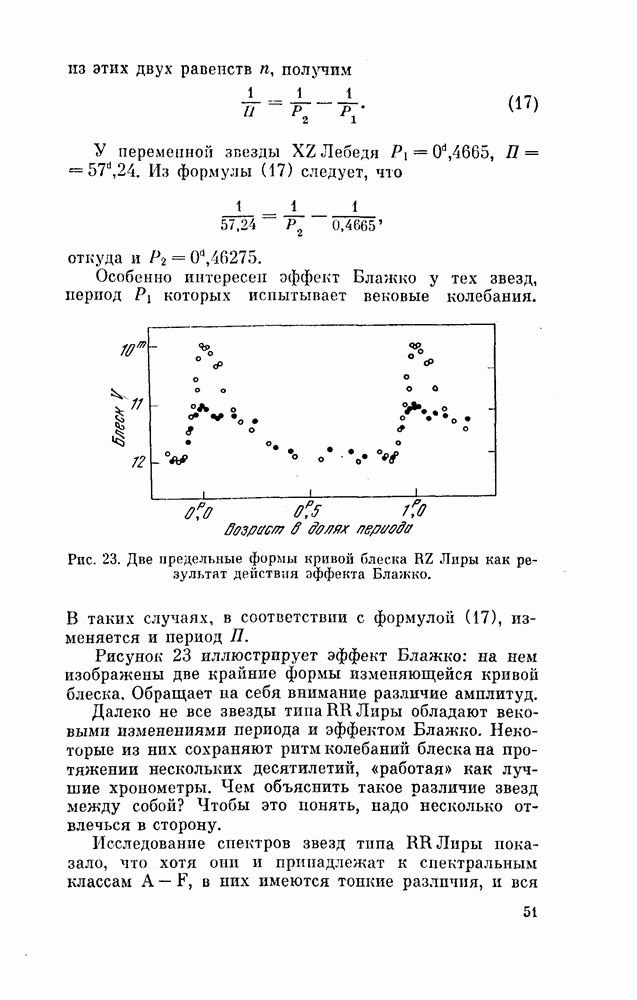
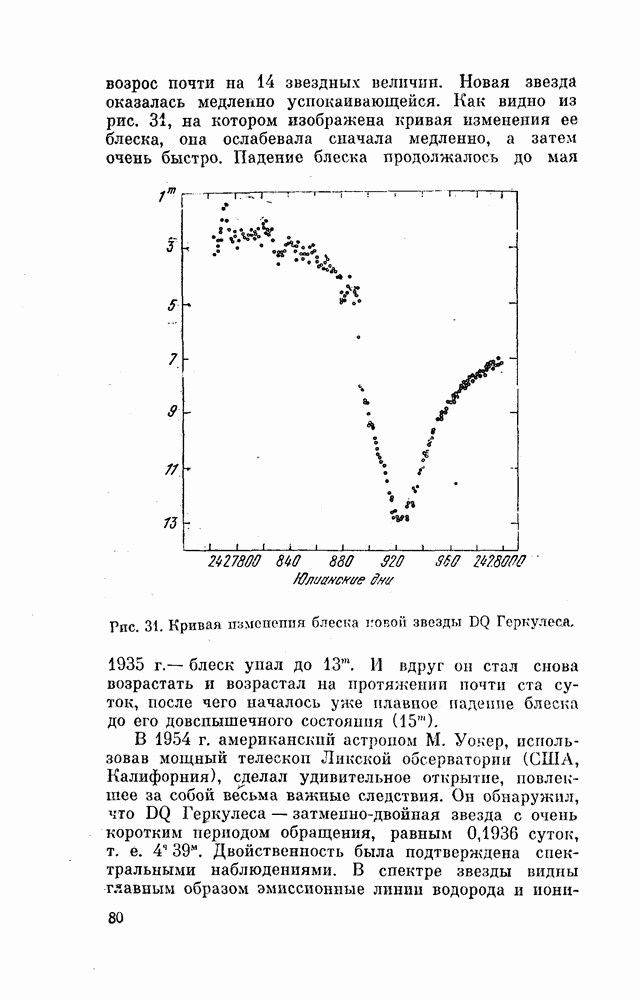
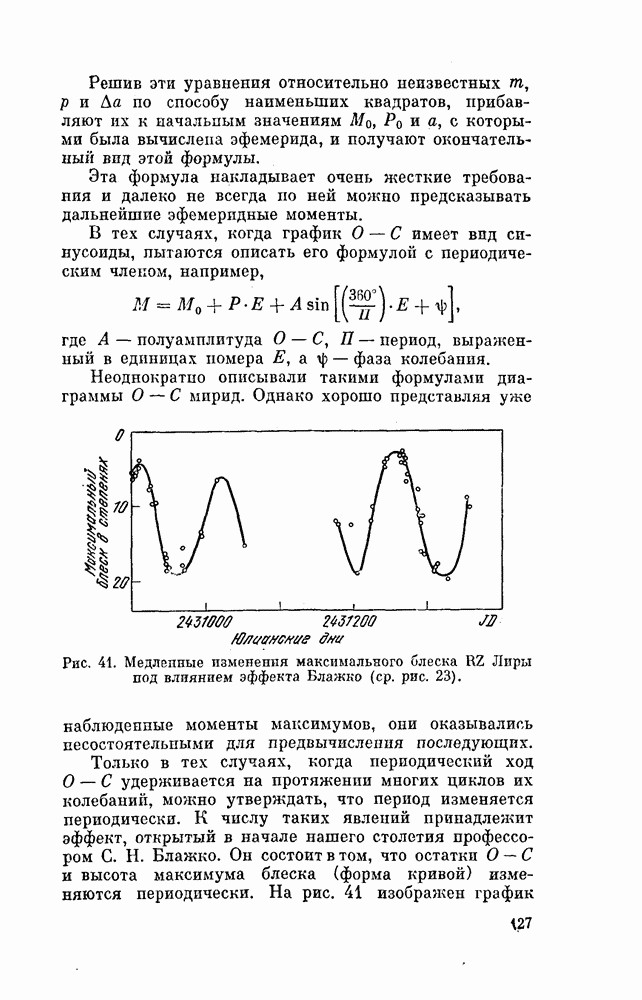
- § 41. ИЗМЕНЕНИЕ ПЕРИОДОВ И ЭФФЕКТ БЛАЖКО
- § 42. ОРГАНИЗАЦИЯ НАБЛЮДЕНИЙ
- § 43. РЕКОМЕНДАЦИИ НАБЛЮДАТЕЛЯМ
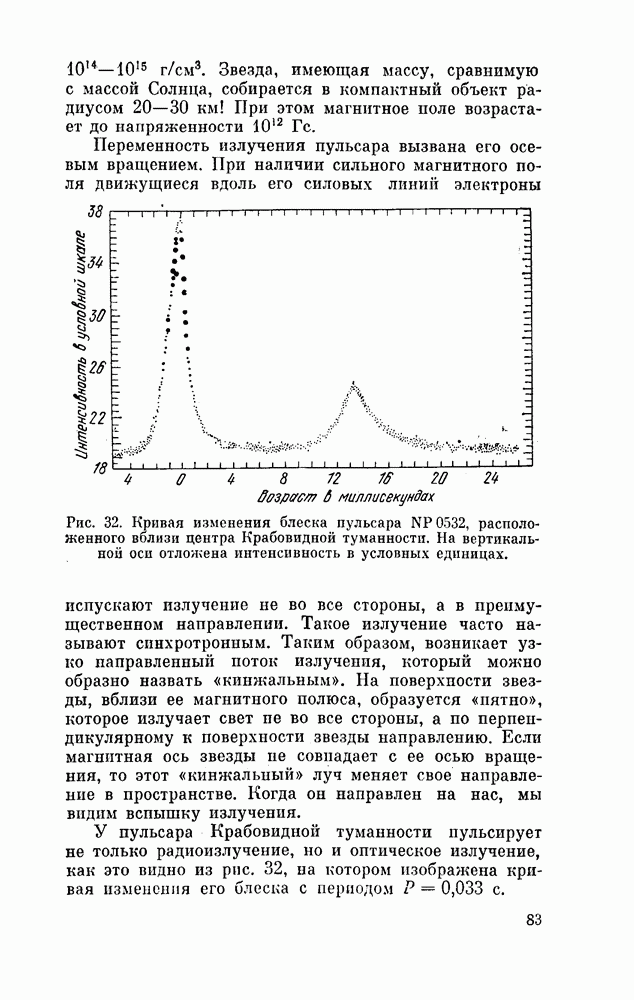
- ДОПОЛНЕНИЯ
- Дополнение 1. СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
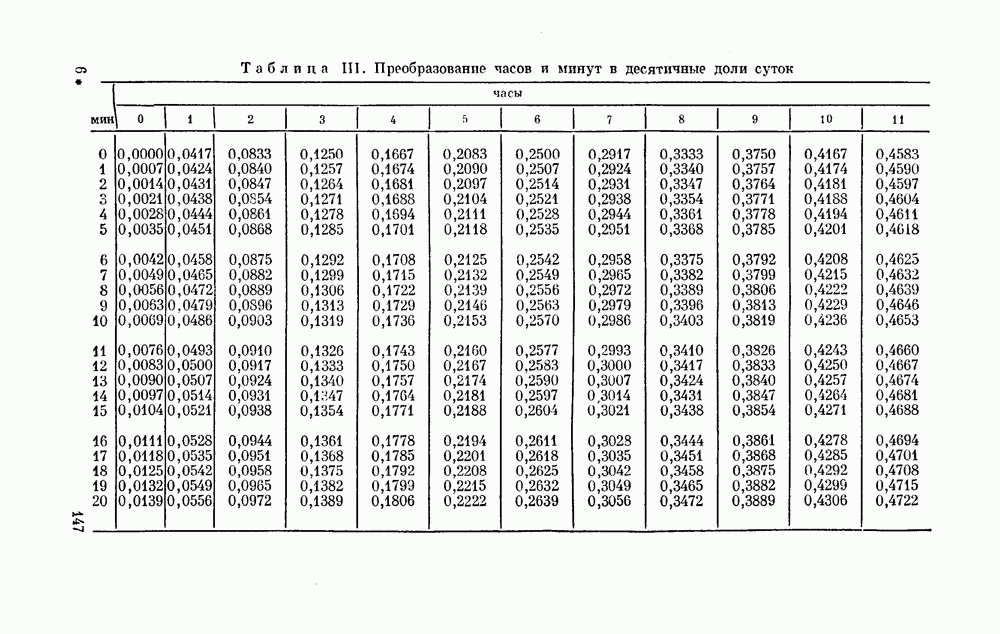
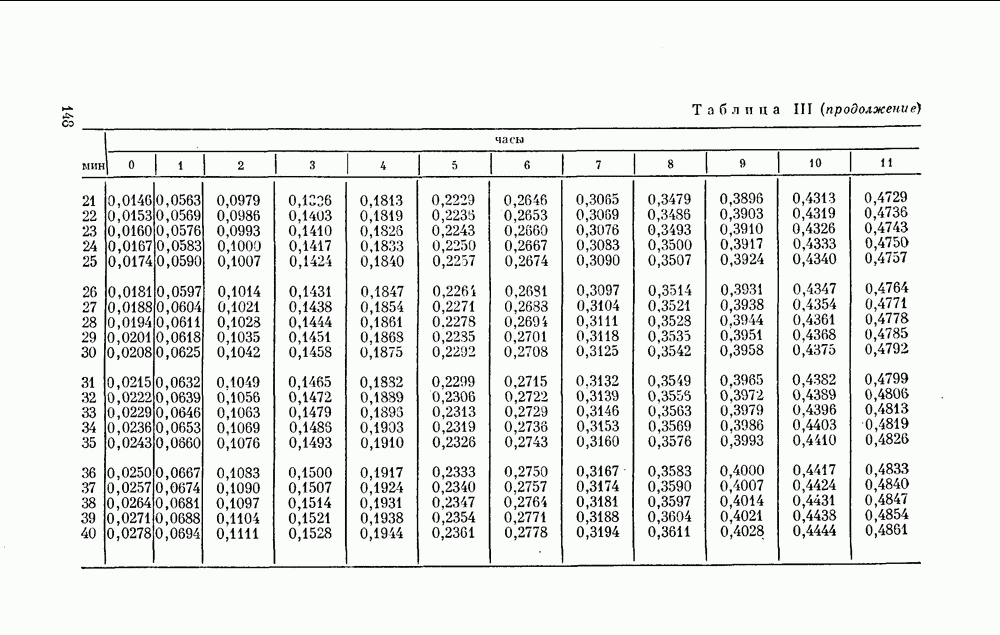
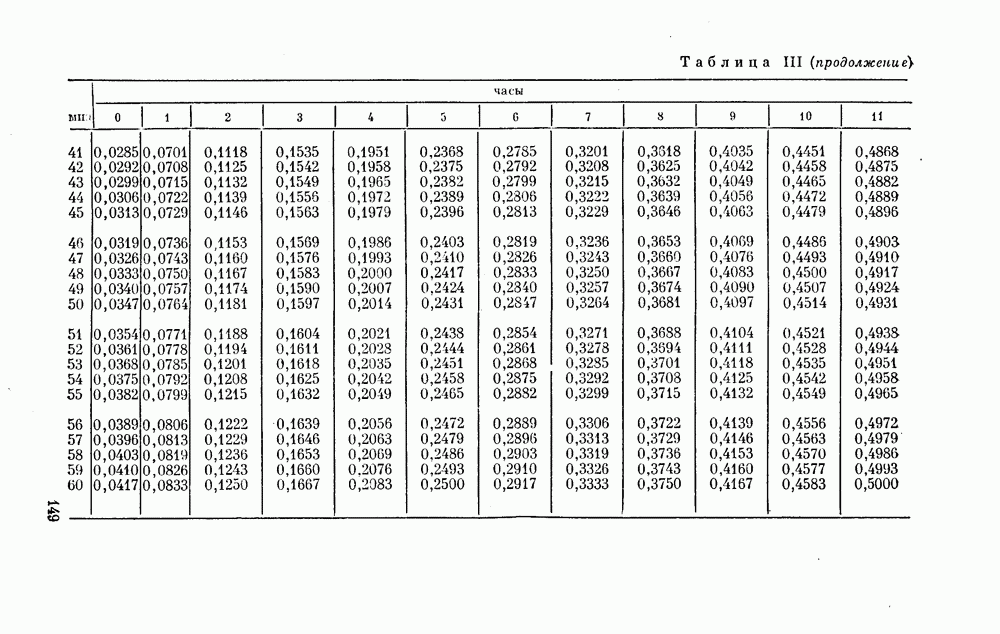
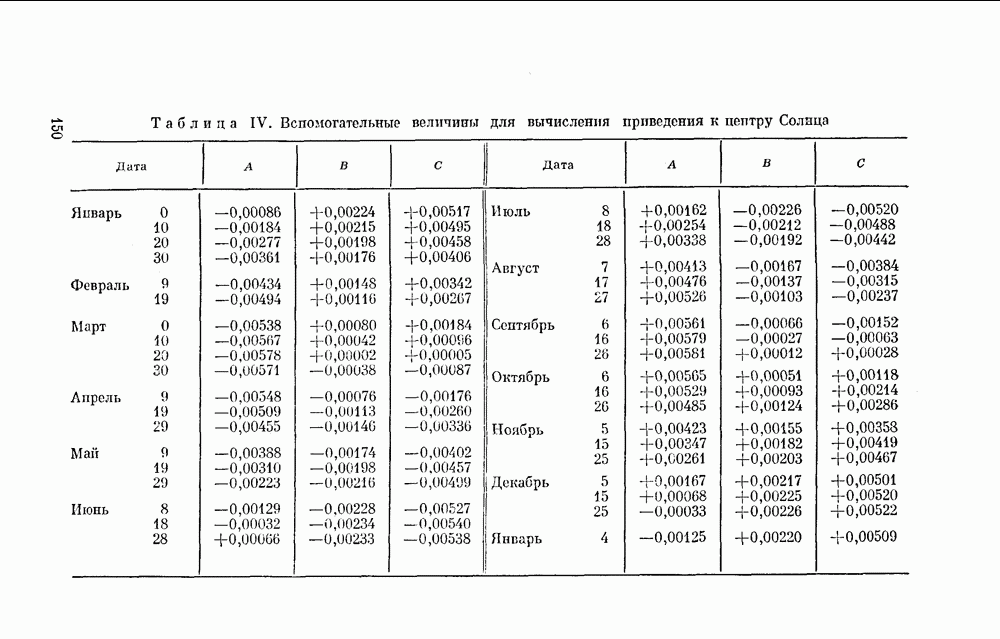
- Дополнение 2. ПРИВЕДЕНИЕ МОМЕНТОВ ВРЕМЕНИ К ЦЕНТРУ СОЛНЦА
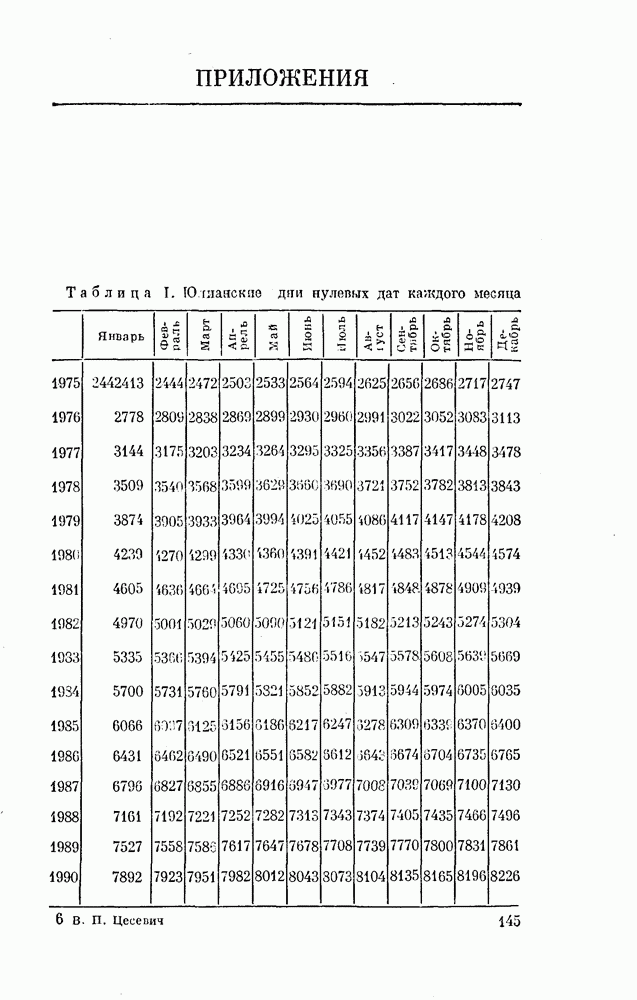
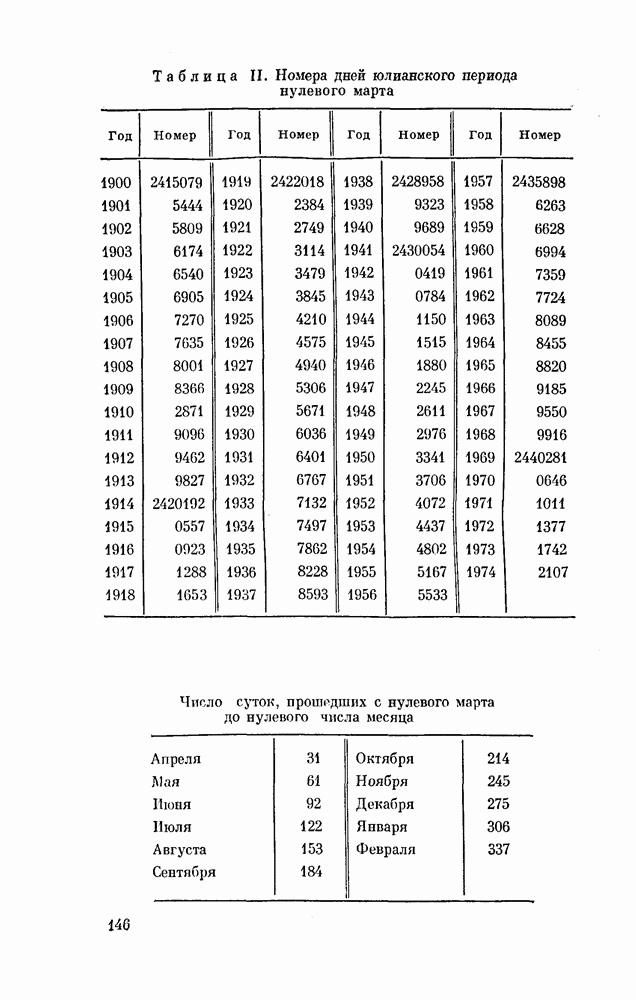
- ПРИЛОЖЕНИЯ