| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
С учетом вышеупомянутых предположений дискретизованное изображение можно описать функцией
![]() (4.2.1)
(4.2.1)
где дискретизирующая функция
![]() (4.2.2)
(4.2.2)
состоит из ![]() одинаковых импульсов
одинаковых импульсов ![]() , образующих
решетку с шагом
, образующих
решетку с шагом ![]() .
Для упрощения обозначений пределы суммирования выбраны симметричными. Будем
считать, что дискретизирующие импульсы нормированы так, что
.
Для упрощения обозначений пределы суммирования выбраны симметричными. Будем
считать, что дискретизирующие импульсы нормированы так, что
 (4.2.3)
(4.2.3)
При анализе можно полагать, что
дискретизирующая функция была получена пропусканием конечного набора
дельта-функций ![]() через
линейный фильтр с импульсным откликом
через
линейный фильтр с импульсным откликом ![]() . Таким образом,
. Таким образом,
![]() (4.2.4)
(4.2.4)
где
![]() (4.2.5)
(4.2.5)
Подставив выражение (4.2.2) в (4.2.1), получим формулу для дискретизованного изображения
![]() (4.2.6)
(4.2.6)
Спектр этой функции имеет вид
![]() (4.2.7)
(4.2.7)
где ![]() - результат преобразования Фурье
функции
- результат преобразования Фурье
функции ![]() .
Преобразование Фурье конечной решетки дискретизирующих импульсов описывается
следующим соотношением [5, стр. 105]:
.
Преобразование Фурье конечной решетки дискретизирующих импульсов описывается
следующим соотношением [5, стр. 105]:
 (4.2.8)
(4.2.8)
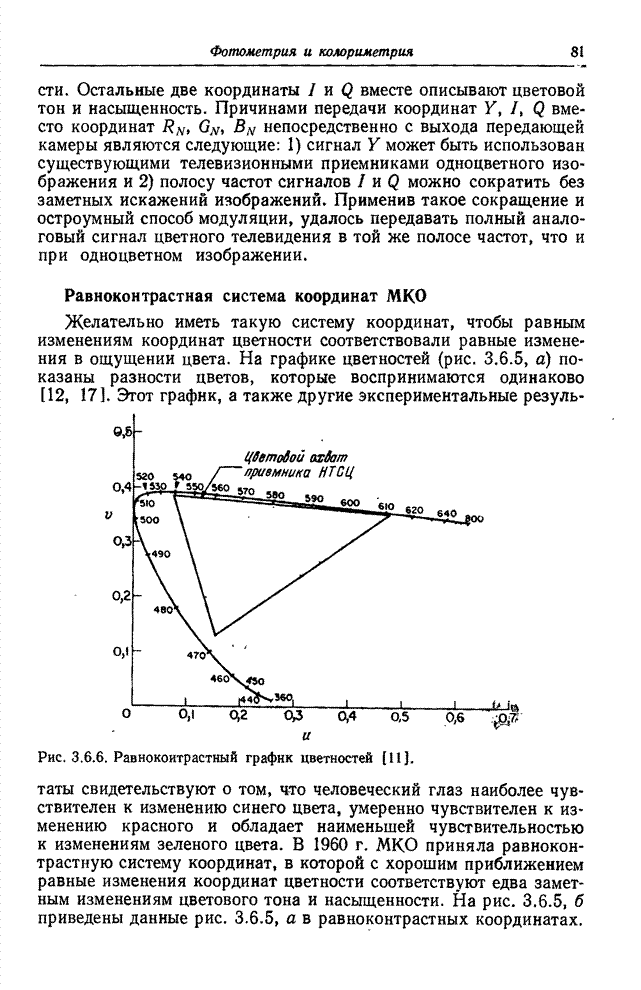
На рис. 4.2.2 приведен график
функции ![]() .
С увеличением
.
С увеличением ![]() и
и
![]() правая
часть формулы (4.2.8) в пределе превращается в набор дельта-функций.
правая
часть формулы (4.2.8) в пределе превращается в набор дельта-функций.
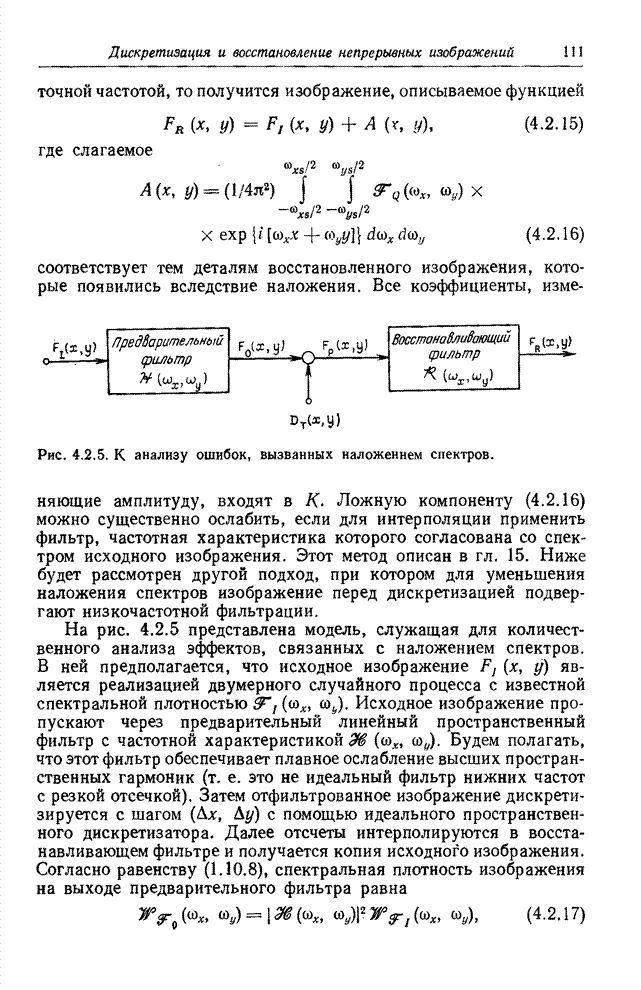
В системе восстановления
изображений непрерывное изображение получается путем интерполяции отсчетов.
Идеальные интерполяционные функции, такие, как ![]() и бесселевы [формулы (4.1.14) и
(4.1.16)], обычно определены на бесконечной плоскости. Если же
дискретизирующая решетка имеет конечные размеры, то на границах отсекаются «хвосты»
интерполяционных функций и вблизи краев восстановленного изображения появляются
ошибки [9, 10]. Однако такие ошибки обычно становятся пренебрежимо малыми при
удалении от границ на 8-10 шагов дискретизации.
и бесселевы [формулы (4.1.14) и
(4.1.16)], обычно определены на бесконечной плоскости. Если же
дискретизирующая решетка имеет конечные размеры, то на границах отсекаются «хвосты»
интерполяционных функций и вблизи краев восстановленного изображения появляются
ошибки [9, 10]. Однако такие ошибки обычно становятся пренебрежимо малыми при
удалении от границ на 8-10 шагов дискретизации.
Числовые значения отсчетов
изображения получаются путем пространственного интегрирования ![]() по некоторой конечной
площадке - элементу изображения. В сканирующей системе
по некоторой конечной
площадке - элементу изображения. В сканирующей системе

Рис. 4.2.2. Усеченная дискретизирующая последовательность и ее спектр.
(рис. 4.2.1) интегрирование фактически
проводится на светочувствительной поверхности фотодетектора. Значение отсчета,
соответствующего ![]() -му
элементу, можно найти по формуле
-му
элементу, можно найти по формуле
 (4.2.9)
(4.2.9)
где ![]() и
и ![]() обозначают наибольшие размеры этого
элемента. Здесь предполагается, что за время интегрирования в системе берется
лишь один отсчет. В противном случае приходится решать сложную проблему
перекрестных искажений. В рассматриваемой системе дискретизации размеры
элемента могут оказаться больше, чем расстояние между отсчетами. Поэтому в
модели допускается, что последовательные (во времени) отсчеты соответствуют
частично перекрывающимся элементам изображения.
обозначают наибольшие размеры этого
элемента. Здесь предполагается, что за время интегрирования в системе берется
лишь один отсчет. В противном случае приходится решать сложную проблему
перекрестных искажений. В рассматриваемой системе дискретизации размеры
элемента могут оказаться больше, чем расстояние между отсчетами. Поэтому в
модели допускается, что последовательные (во времени) отсчеты соответствуют
частично перекрывающимся элементам изображения.
Простой заменой переменных равенство (4.2.9) можно преобразовать к виду
 (4.2.10)
(4.2.10)
Поскольку предполагается, что за
время интегрирования берется только один отсчет, пределы в интеграле (4.2.10)
можно расширить до бесконечности. В такой форме выражение (4.2.10) можно рассматривать
как результат свертки исходного изображения ![]() с импульсным откликом
с импульсным откликом ![]() и последующей
дискретизации этой свертки в конечной области с помощью дельта-функций. Тогда,
пренебрегая эффектами, связанными с конечными размерами дискретизирующей
решетки дельта-функций, получим
и последующей
дискретизации этой свертки в конечной области с помощью дельта-функций. Тогда,
пренебрегая эффектами, связанными с конечными размерами дискретизирующей
решетки дельта-функций, получим
![]() (4.2.11)
(4.2.11)
В большинстве систем
дискретизации дискретизирующий импульс симметричен, поэтому ![]() .
.
Несложное по форме соотношение
(4.2.11) полезно при оценке эффектов, возникающих при дискретизации с
использованием импульсов конечной ширины. Если спектр изображения ограничен по
ширине, а ![]() и
и
![]() удовлетворяют
критерию Найквиста, то конечная ширина импульса приводит к тем же результатам,
как если бы исходное изображение перед идеальной дискретизацией подверглось
линейному искажению (смазыванию). В части 4 будут рассмотрены методы
компенсации подобных искажений. Однако конечность размеров дискретизирующего
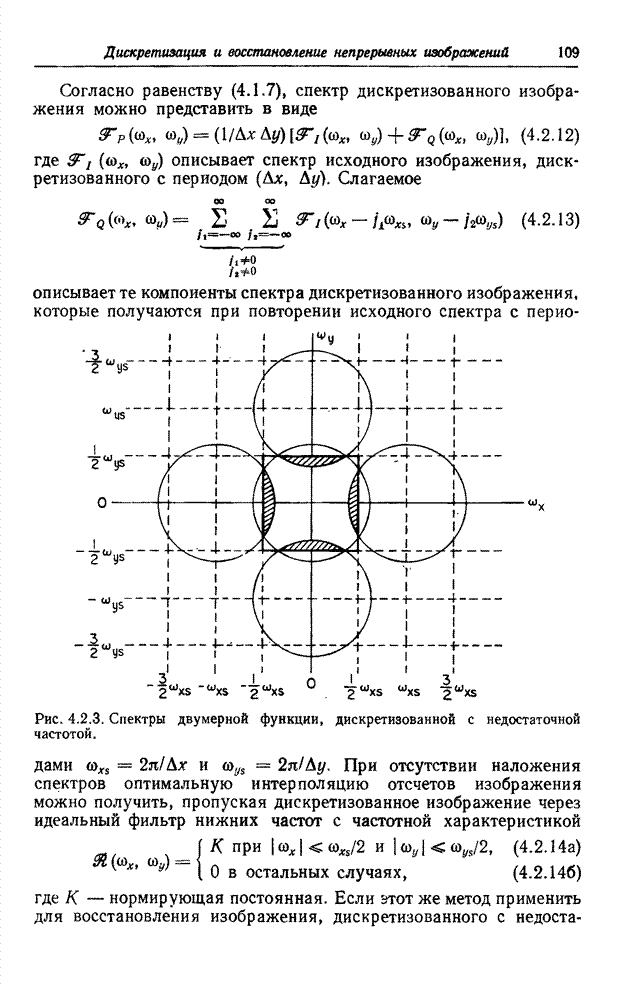
импульса не всегда является недостатком. Рассмотрим случай, когда спектр
исходного изображения очень широкий, и поэтому оно дискретизируется с
недостаточной частотой. Импульс с конечными размерами фактически осуществляет
низкочастотную фильтрацию исходного изображения, что приводит к сужению
спектра и, следовательно, уменьшает ошибки, вызванные наложением спектров.
удовлетворяют
критерию Найквиста, то конечная ширина импульса приводит к тем же результатам,
как если бы исходное изображение перед идеальной дискретизацией подверглось
линейному искажению (смазыванию). В части 4 будут рассмотрены методы
компенсации подобных искажений. Однако конечность размеров дискретизирующего
импульса не всегда является недостатком. Рассмотрим случай, когда спектр
исходного изображения очень широкий, и поэтому оно дискретизируется с
недостаточной частотой. Импульс с конечными размерами фактически осуществляет
низкочастотную фильтрацию исходного изображения, что приводит к сужению
спектра и, следовательно, уменьшает ошибки, вызванные наложением спектров.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
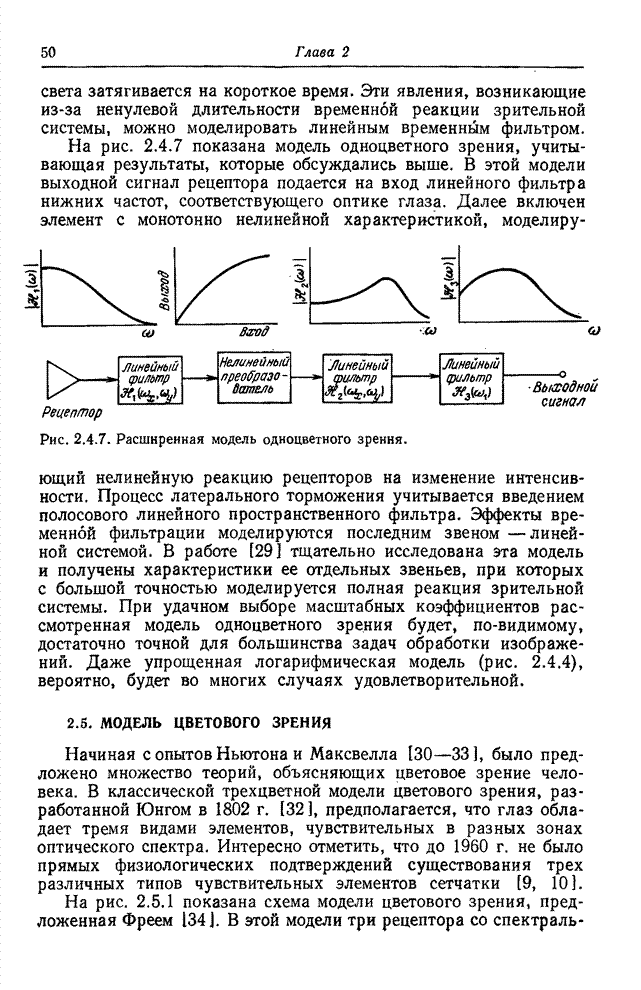
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
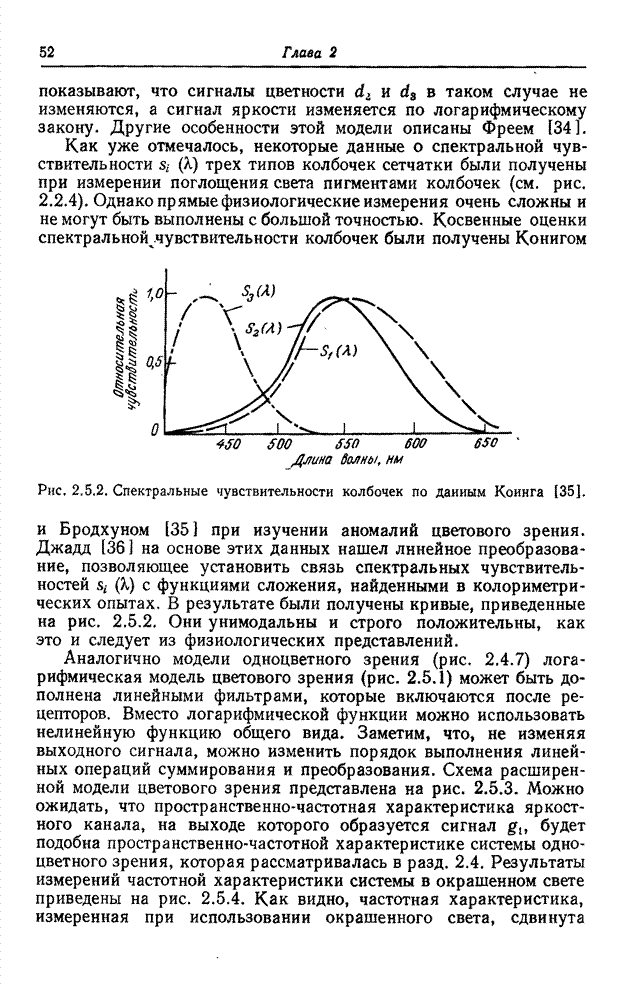
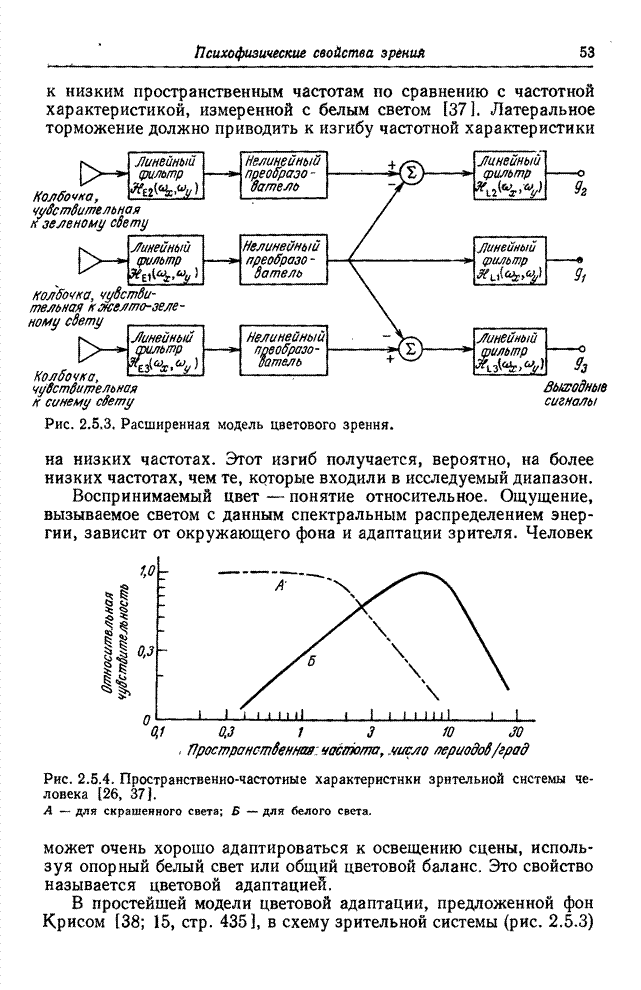
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
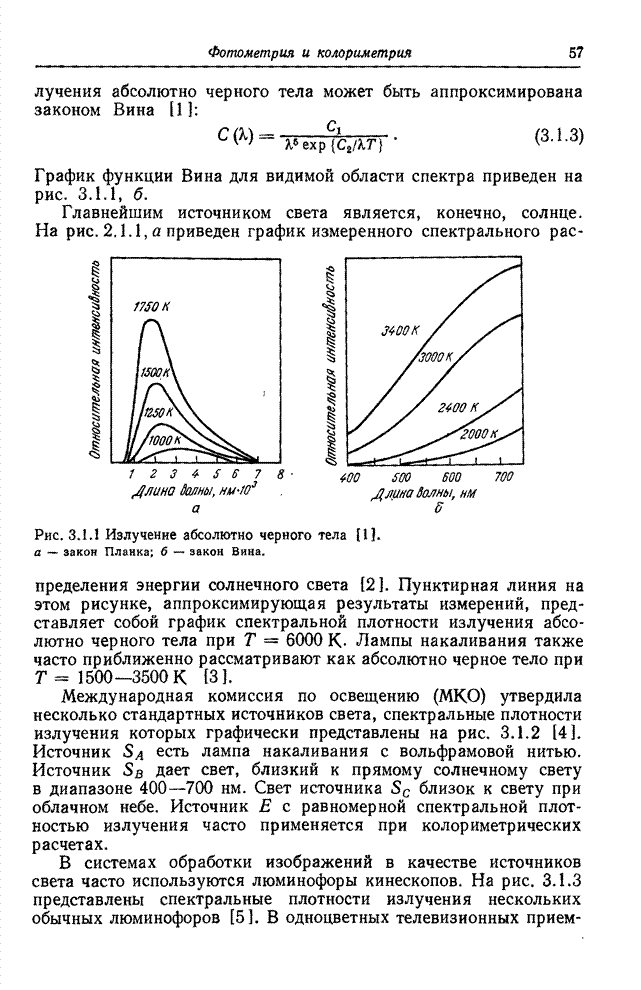
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
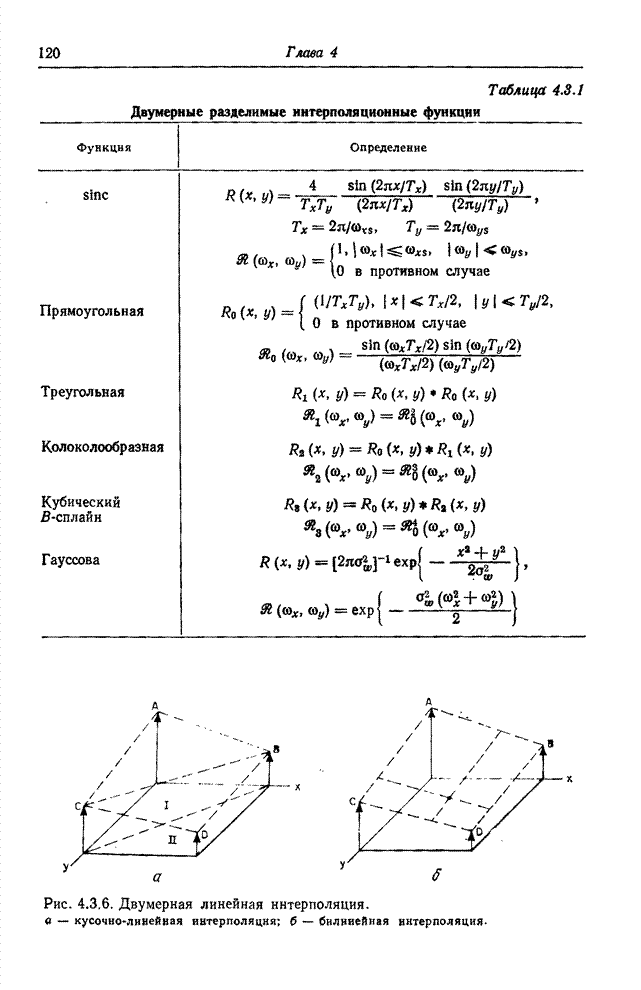
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
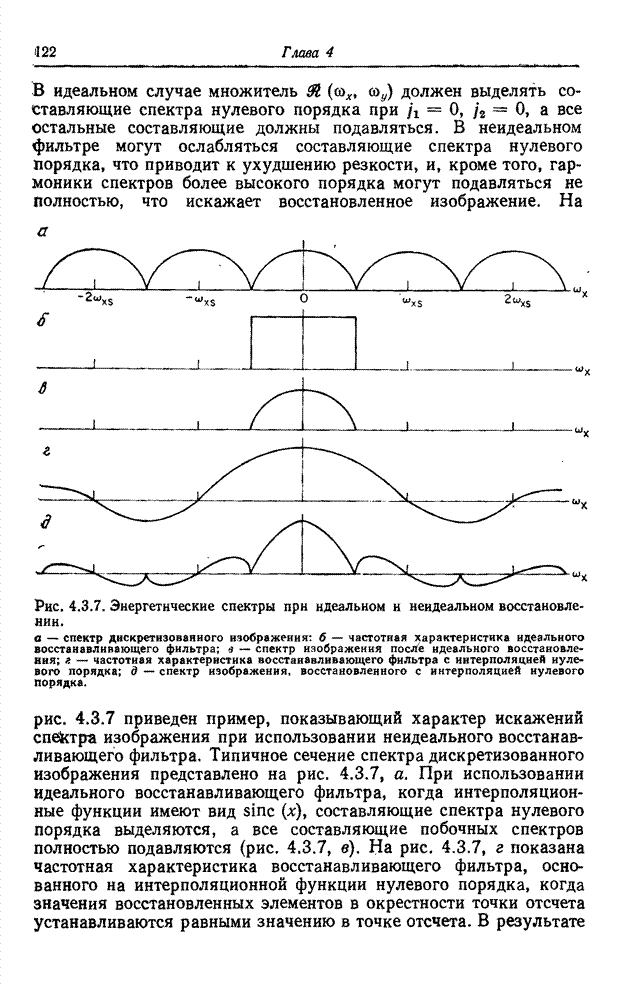
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
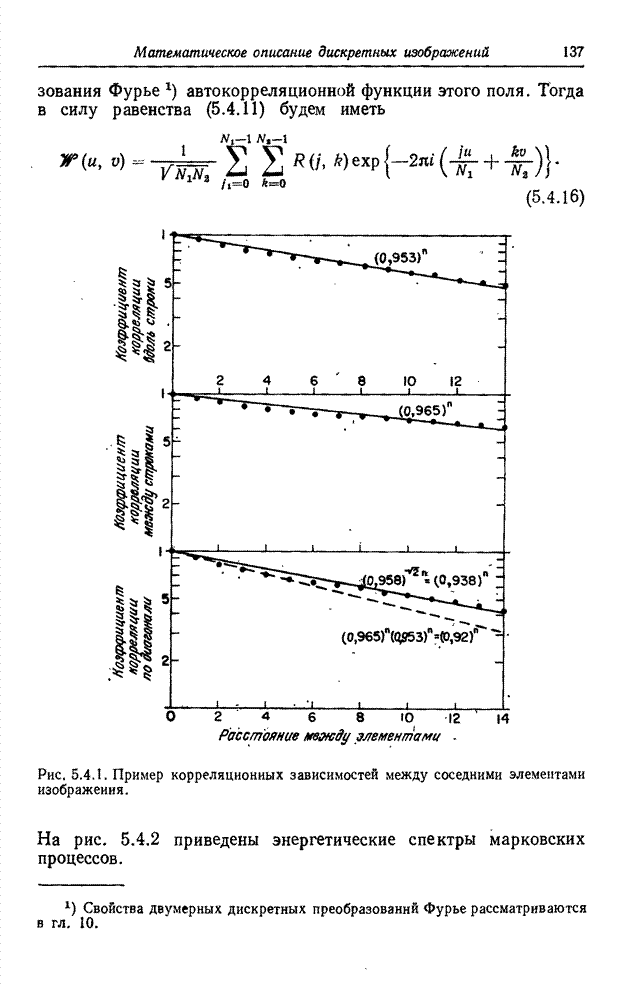
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
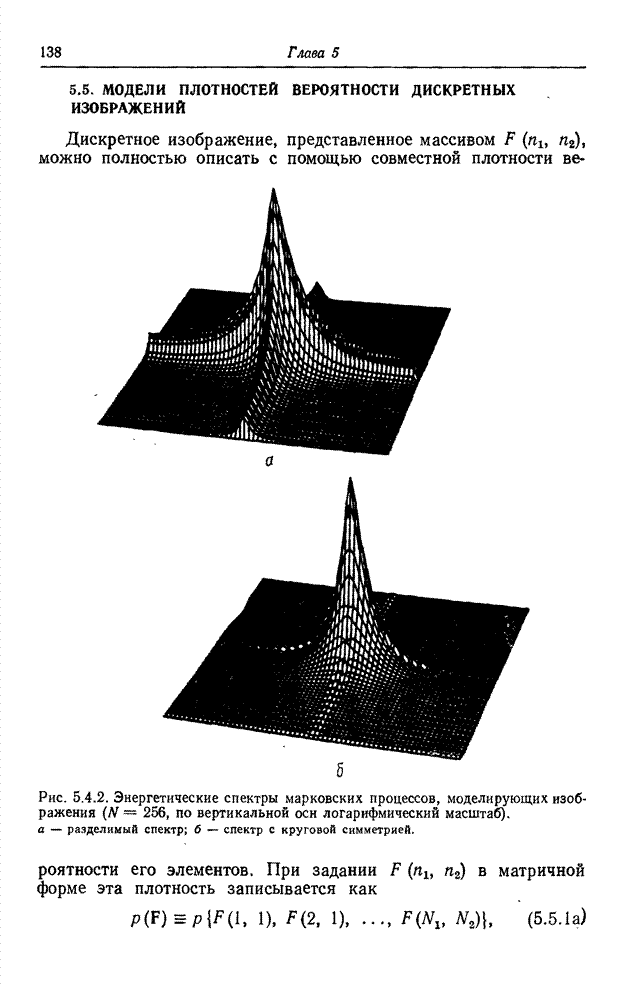
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
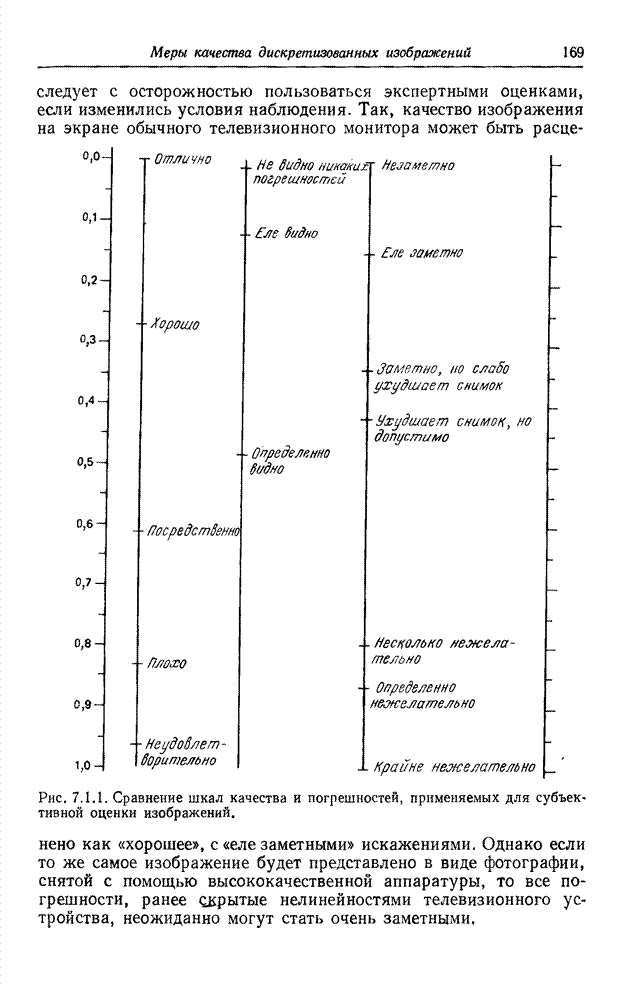
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
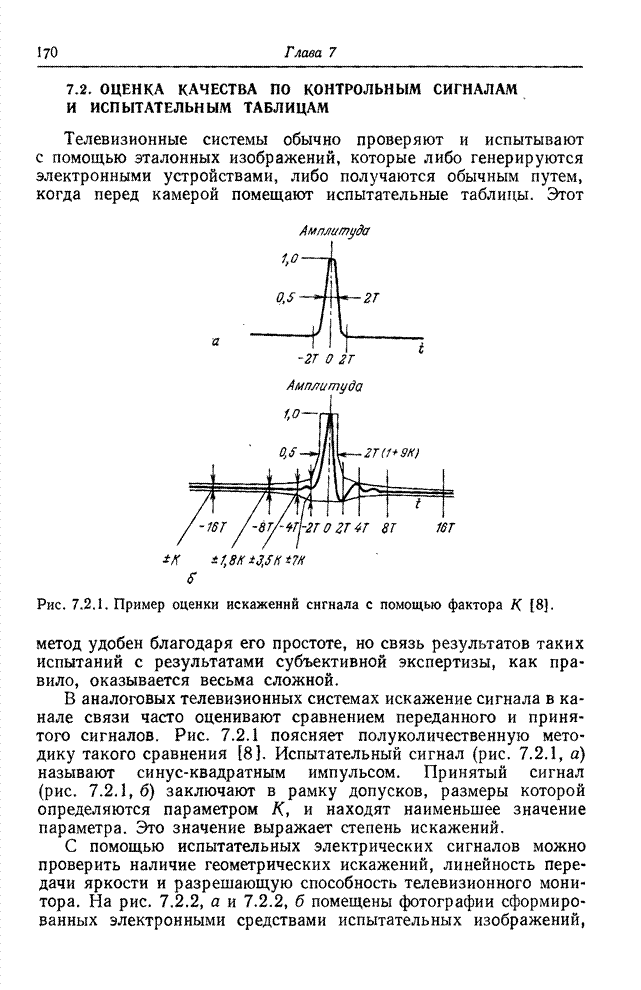
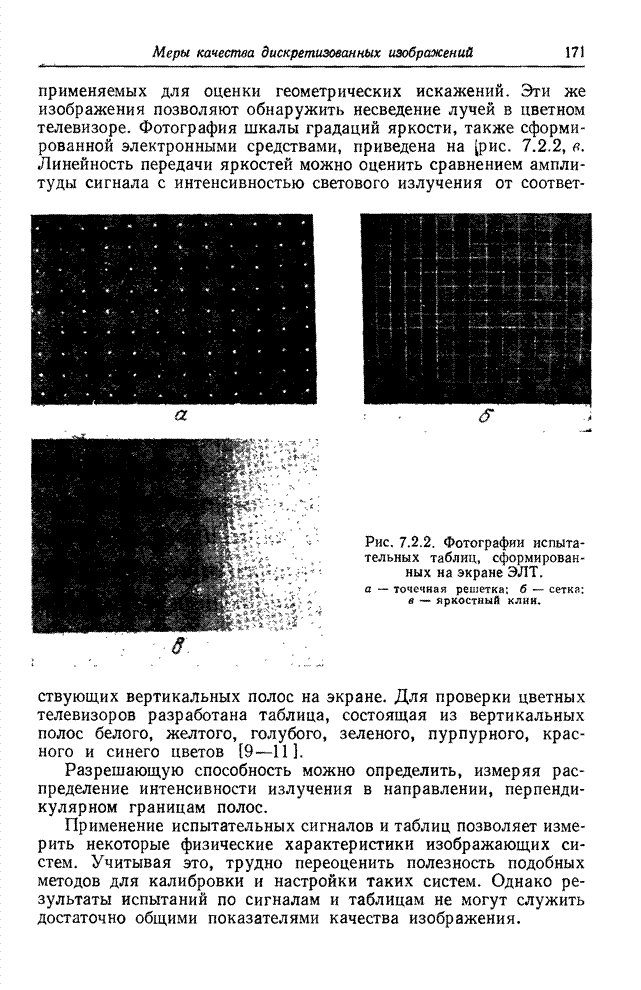
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
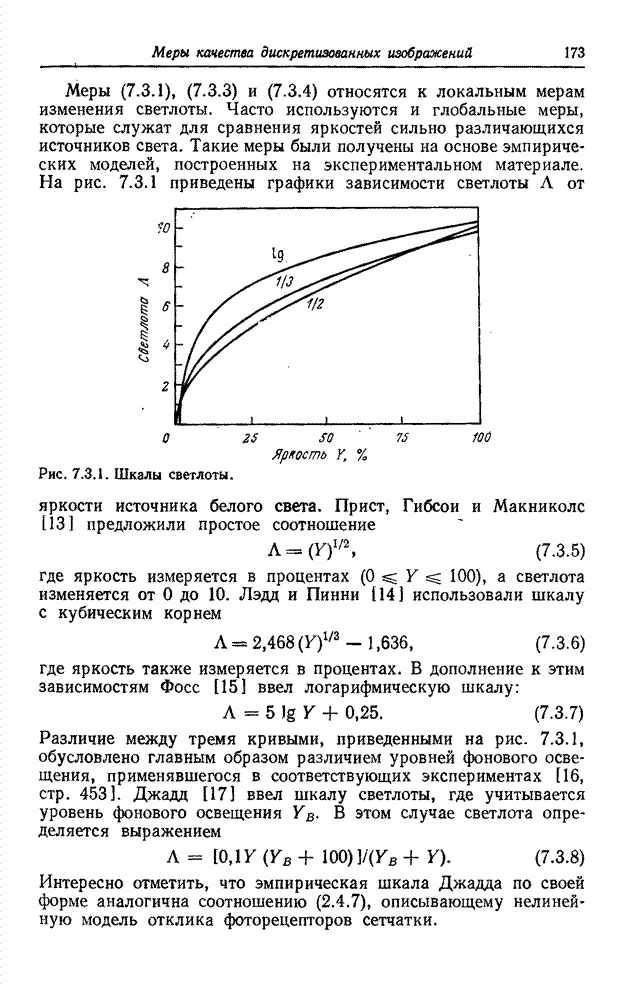
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
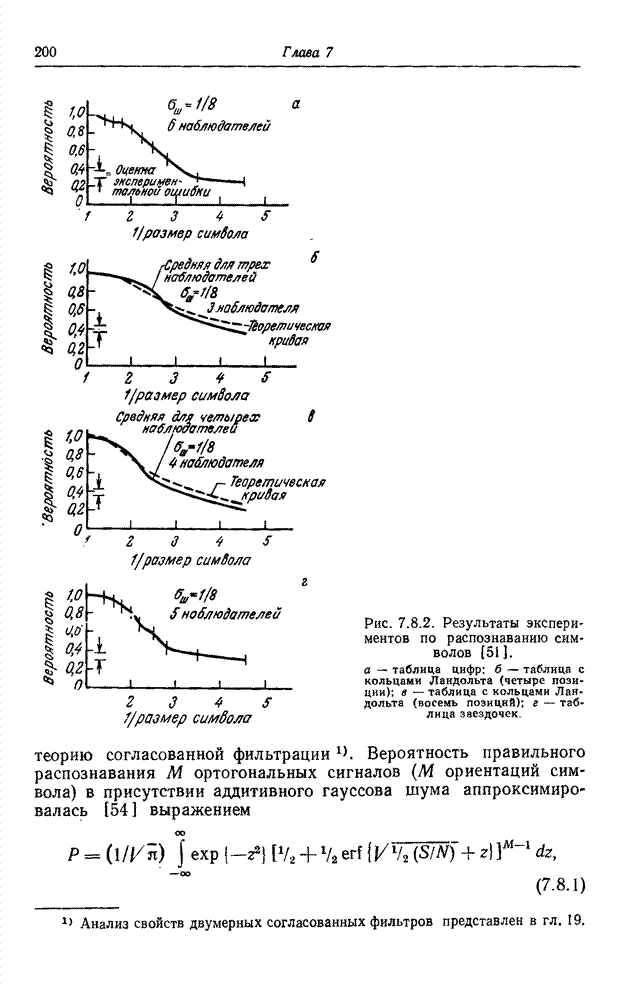
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
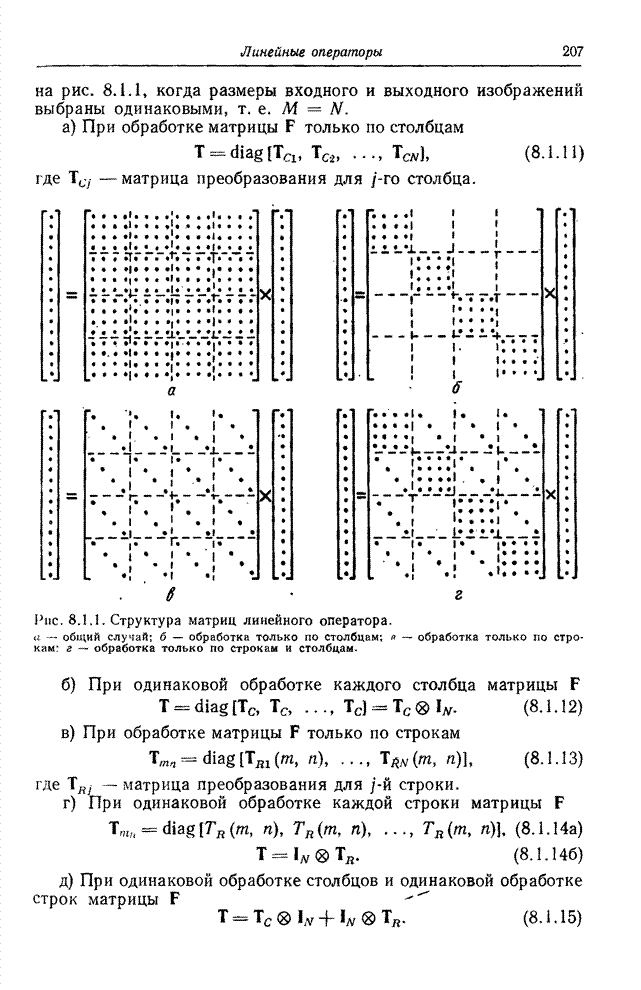
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
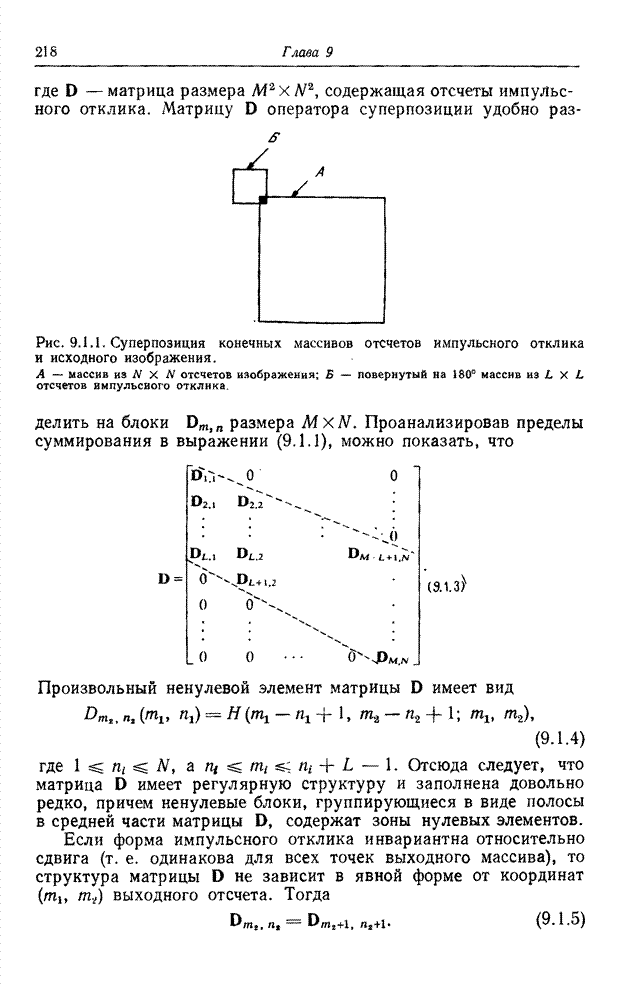
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
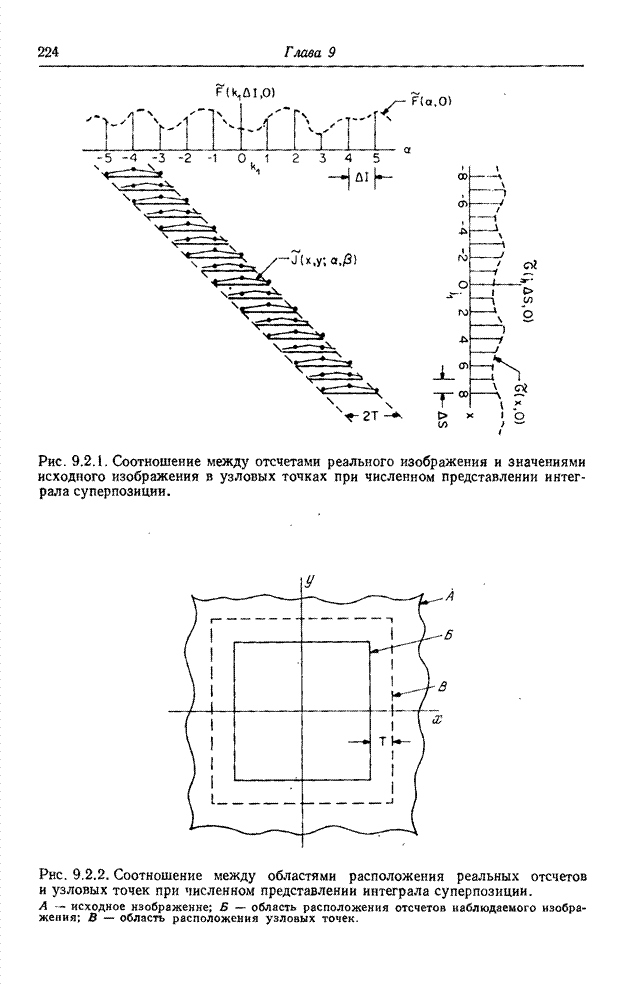
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
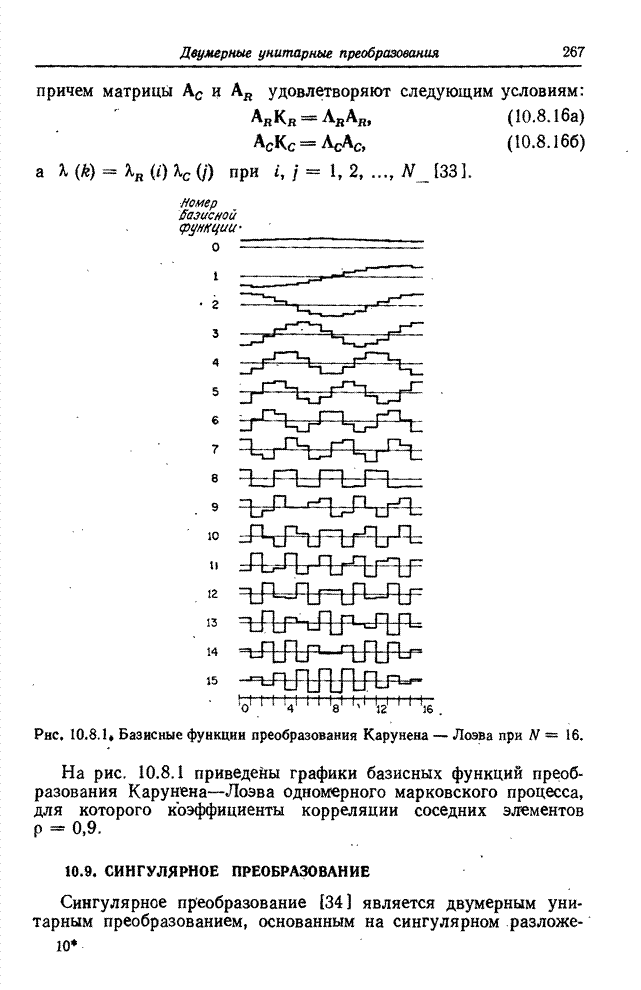
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
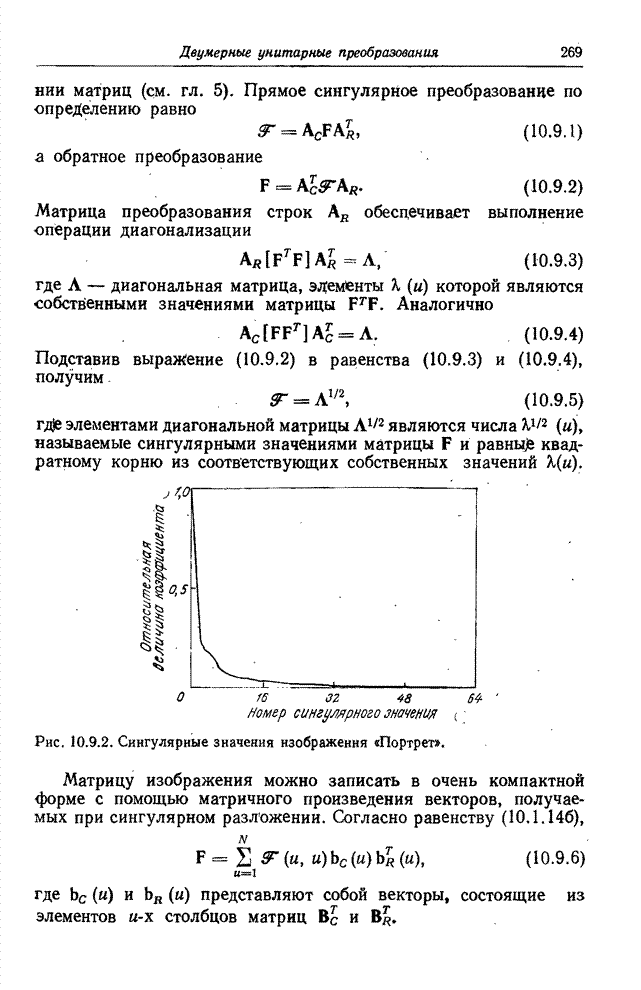
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
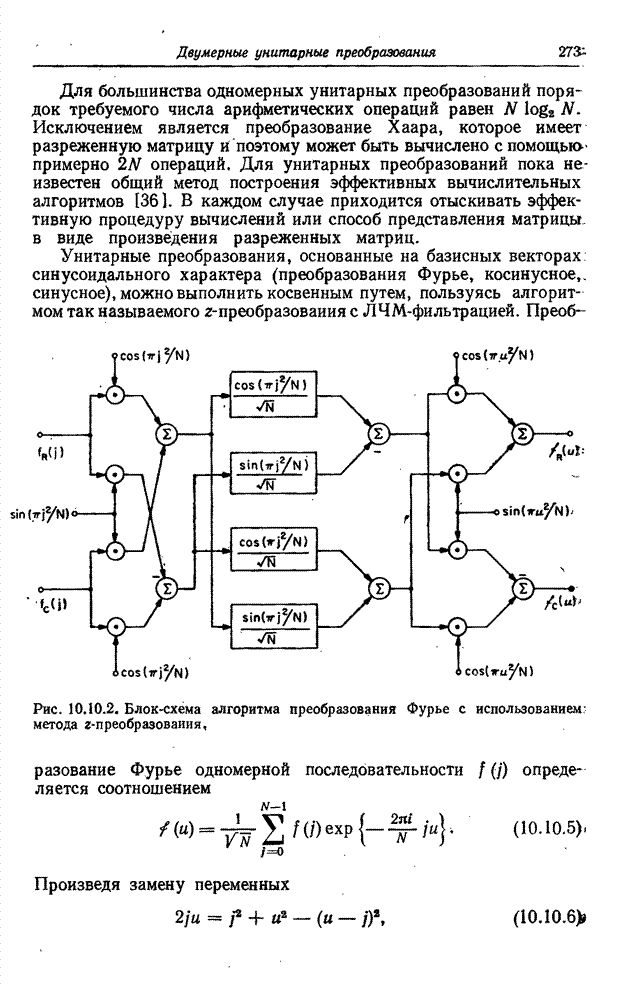
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
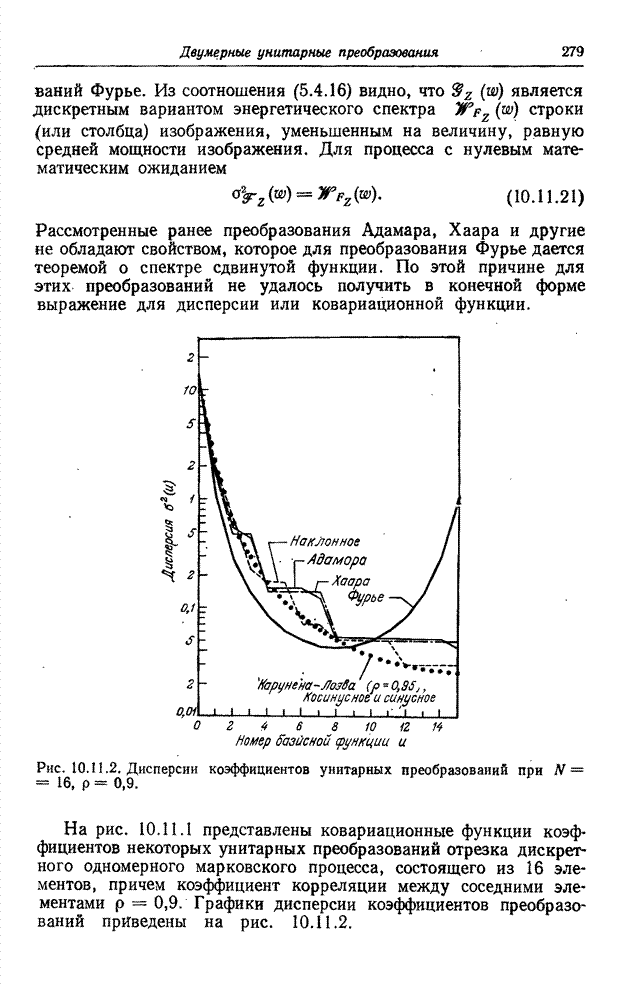
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА