| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
В гл. 2 были рассмотрены вопросы, связанные с математическим описанием непрерывных изображений. В настоящей главе даны способы формального представления дискретных изображений с использованием как детерминированных, так и статистических моделей.
5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
В данном разделе коротко рассмотрены встречающиеся в тексте математические действия, выполняемые с векторами и матрицами. Строгий вывод и доказательства теорем и положений, приведенных ниже, можно найти в литературе [1-5].
Вектор
Вектор-столбец
![]() размера
размера ![]() представляет
собой совокупность элементов
представляет
собой совокупность элементов ![]() , где
, где ![]() , расположенных
в виде вертикального столбца
, расположенных
в виде вертикального столбца
 (5.1.1)
(5.1.1)
Вектор-строка
![]() размера
размера ![]() представляет собой
упорядоченную совокупность элементов
представляет собой
упорядоченную совокупность элементов ![]() , где
, где ![]() , расположенных
в виде горизонтальной строки
, расположенных
в виде горизонтальной строки
![]() (5.1.2)
(5.1.2)
В книге полужирными строчными буквами будут, как правило, обозначаться вектор-столбцы. Вектор-строка будет обозначаться как транспонированный вектор-столбец:
![]() (5.1.3)
(5.1.3)
Матрица
Матрица
![]() размера
размера ![]() представляет собой
совокупность элементов
представляет собой
совокупность элементов ![]() где
где ![]() и
и ![]() , расположенных
в виде строк и столбцов двумерной таблицы
, расположенных
в виде строк и столбцов двумерной таблицы
 (5.1.4)
(5.1.4)
Символ
![]() обозначает
нулевую матрицу, все элементы которой равны нулю. Диагональная матрица – это
квадратная матрица (когда
обозначает
нулевую матрицу, все элементы которой равны нулю. Диагональная матрица – это
квадратная матрица (когда ![]() ), все элементы которой, не лежащие на
главной диагонали, равны нулю, т.е.
), все элементы которой, не лежащие на
главной диагонали, равны нулю, т.е. ![]() , если
, если ![]() . Единичная
матрица, обозначаемая символом
. Единичная
матрица, обозначаемая символом ![]() , есть диагональная матрица, все
диагональные элементы которой равны единице. Индекс при символе единичной
матрицы указывает ее размеры;
, есть диагональная матрица, все
диагональные элементы которой равны единице. Индекс при символе единичной
матрицы указывает ее размеры; ![]() обозначает
единичную матрицу размера
обозначает
единичную матрицу размера ![]() . Матрица
. Матрица ![]() может быть
разделена на блоки (подматрицы)
может быть
разделена на блоки (подматрицы) ![]() :
:
 . (5.1.5)
. (5.1.5)
Сложение матриц
Сумма
двух матриц ![]() определена
только в том случае, когда обе матрицы имеют одинаковые размеры. Матрица
определена
только в том случае, когда обе матрицы имеют одинаковые размеры. Матрица ![]() - сумма матриц
- сумма матриц ![]() и
и ![]() , имеет размеры
, имеет размеры ![]() , а ее элементы
, а ее элементы ![]() .
.
Умножение матриц
Произведение
двух матриц ![]() определено
только тогда, когда число столбцов матрицы
определено
только тогда, когда число столбцов матрицы ![]() равно числу строк матрицы
равно числу строк матрицы ![]() . При умножении
матрицы
. При умножении
матрицы ![]() размера
размера
![]() на
матрицу
на
матрицу ![]() размера
размера
![]() получается
матрица
получается
матрица ![]() размера
размера ![]() , элементы
которой определяются равенством
, элементы
которой определяются равенством
![]() (5.1.6)
(5.1.6)
При
умножении матрицы ![]() на скаляр
на скаляр ![]() получается
матрица
получается
матрица ![]() ,
элементы которой
,
элементы которой ![]() .
.
Обращение матриц
Если
![]() - квадратная
матрица, то матрица, обратная относительно нее и обозначаемая как
- квадратная
матрица, то матрица, обратная относительно нее и обозначаемая как ![]() , обладает
следующими свойствами:
, обладает
следующими свойствами: ![]() и
и ![]() . Если матрица
. Если матрица ![]() существует, то
матрица
существует, то
матрица ![]() называется
неособенной (невырожденной). В противном случае она называется особенной
(вырожденной). Если у некоторой матрицы есть обратная, то эта обратная матрица
единственна. Матрица, обратная относительной обратной, совпадает с исходной
матрицей, т.е.
называется
неособенной (невырожденной). В противном случае она называется особенной
(вырожденной). Если у некоторой матрицы есть обратная, то эта обратная матрица
единственна. Матрица, обратная относительной обратной, совпадает с исходной
матрицей, т.е.
![]() (5.1.7)
(5.1.7)
Если
матрицы ![]() и
и
![]() неособенные,
то
неособенные,
то
![]() (5.1.8)
(5.1.8)
Если
матрица ![]() неособенная,
а скаляр
неособенная,
а скаляр ![]() , то
, то
![]() . (5.1.9)
. (5.1.9)
Обращение особенных квадратных матриц и неквадратных матриц будет рассмотрено в гл. 8. Матрицу, обратную относительно блочной квадратной матрицы
![]() , (5.1.10)
, (5.1.10)
можно представить в виде
 (5.1.11)
(5.1.11)
при
условии, что матрицы ![]() и
и ![]() не являются
особенными.
не являются
особенными.
Транспонирование матриц
При
транспонировании матрицы ![]() размера
размера ![]() образуется матрица размера
образуется матрица размера ![]() , которую
обозначают через
, которую
обозначают через ![]() .
Строки матрицы
.
Строки матрицы ![]() совпадают
со столбцами, а столбцы — со строками матрицы
совпадают
со столбцами, а столбцы — со строками матрицы ![]() . Для любой матрицы
. Для любой матрицы ![]()
![]() . (5.1.12)
. (5.1.12)
Если
![]() , то матрицу
, то матрицу ![]() называют
симметричной. Для любых матриц
называют
симметричной. Для любых матриц ![]() и
и ![]()
![]() (5.1.13)
(5.1.13)
Если
матрица ![]() неособенная,
то матрица
неособенная,
то матрица ![]() также
неособенная и
также
неособенная и
![]() . (5.1.14)
. (5.1.14)
Прямое произведение матриц
Левое
прямое произведение матрицы ![]() размера
размера ![]() на матрицу
на матрицу ![]() размера
размера ![]() представляет собой
матрицу размера
представляет собой
матрицу размера ![]()
 . (5.1.15)
. (5.1.15)
Аналогично
можно определить правое прямое произведение. В этой книге будет использоваться
только левое прямое произведение. Прямые произведения ![]() и
и ![]() могут
различаться между собой. Ниже указаны свойства операций умножения, сложения,
транспонирования и обращения прямого произведения матриц:
могут
различаться между собой. Ниже указаны свойства операций умножения, сложения,
транспонирования и обращения прямого произведения матриц:
![]() , (5.1.16)
, (5.1.16)
![]() , (5.1.17)
, (5.1.17)
![]() , (5.1.18)
, (5.1.18)
![]() , (5.1.18)
, (5.1.18)
След матрицы
След
квадратной матрицы ![]() размера
размера ![]() равен сумме ее
диагональных элементов и обозначается как
равен сумме ее
диагональных элементов и обозначается как
![]() . (5.1.20)
. (5.1.20)
Если
![]() и
и ![]() - квадратные
матрицы, то
- квадратные
матрицы, то
![]() . (5.1.21)
. (5.1.21)
След прямого произведения двух матриц равен
![]() . (5.1.22)
. (5.1.22)
Норма вектора
Евклидовой
нормой вектора ![]() размера
размера
![]() называется
скаляр, определяемый как
называется
скаляр, определяемый как
![]() . (5.1.23)
. (5.1.23)
Норма матрицы
Евклидовой
нормой матрицы ![]() размера
размера
![]() называется
скаляр, определяемый следующим образом:
называется
скаляр, определяемый следующим образом:
![]() . (5.1.24)
. (5.1.24)
Ранг матрицы
Матрица
![]() размера
размера ![]() имеет ранг
имеет ранг ![]() , если наибольший
из всех ее квадратных неособенных блоков имеет размер
, если наибольший
из всех ее квадратных неособенных блоков имеет размер ![]() . Понятие о
ранге используется при обращении матриц. Если матрицы
. Понятие о
ранге используется при обращении матриц. Если матрицы ![]() и
и ![]() неособенные, а
неособенные, а ![]() - произвольная
матрица, то
- произвольная
матрица, то
![]() . (5.1.25)
. (5.1.25)
Ранг
произведения матриц ![]() и
и ![]() удовлетворяет неравенствам
удовлетворяет неравенствам
![]() , (5.1.26а)
, (5.1.26а)
![]() . (5.1.26б)
. (5.1.26б)
Ранг
суммы матриц ![]() и
и
![]() удовлетворяет
неравенству
удовлетворяет
неравенству
![]() . (5.1.27)
. (5.1.27)
Скалярное произведение векторов
Скалярным
произведением векторов ![]() и
и ![]() размера
размера ![]() является скаляр
является скаляр
![]() (5.1.28)
(5.1.28)
или
![]() . (5.1.29)
. (5.1.29)
Матричное произведение векторов
Матричным
произведением вектора ![]() размера
размера ![]() на вектор
на вектор ![]() размера
размера ![]() является матрица
является матрица
![]() , (5.1.30)
, (5.1.30)
где
![]() .
.
Квадратичная форма
Квадратичной
формой вектора ![]() размера
размера
![]() является скаляр
является скаляр
![]() , (5.1.31)
, (5.1.31)
где
![]() -
матрица размера
-
матрица размера ![]() . Часто матрицу
. Часто матрицу ![]() берут
симметричной.
берут
симметричной.
Векторная производная
Производная
от скалярного произведения ![]() по
по ![]() есть
есть
![]() , (5.1.32)
, (5.1.32)
а
производная от скалярного произведения ![]() по вектору
по вектору ![]() равна
равна
![]() . (5.1.33)
. (5.1.33)
Производная
от квадратичной формы ![]() по
по ![]() есть
есть
![]() . (5.1.34)
. (5.1.34)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
- 3.1. ИСТОЧНИКИ СВЕТА
- 3.2. ФОТОМЕТРИЯ
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
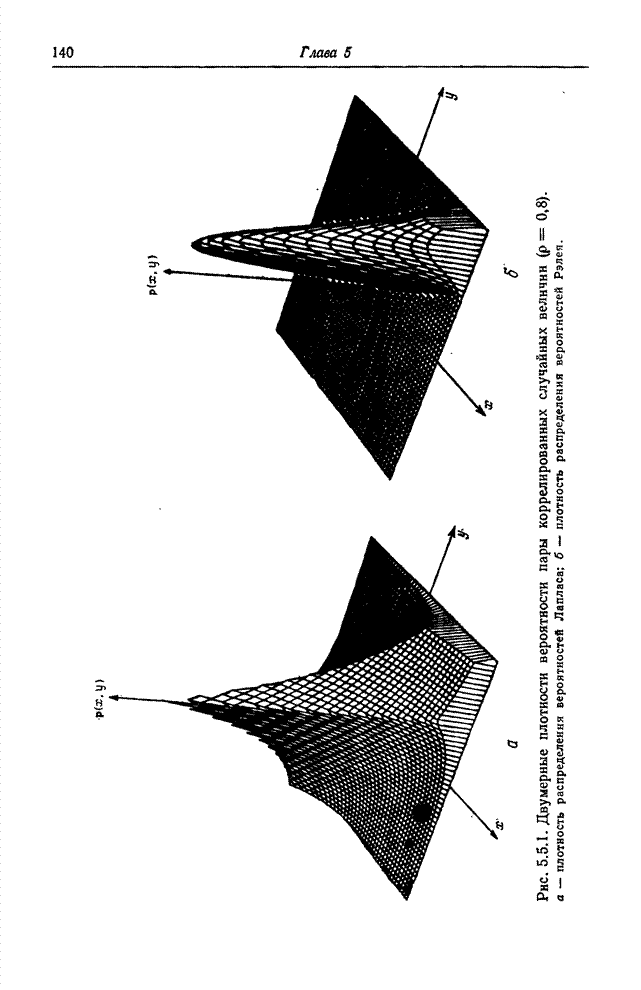
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
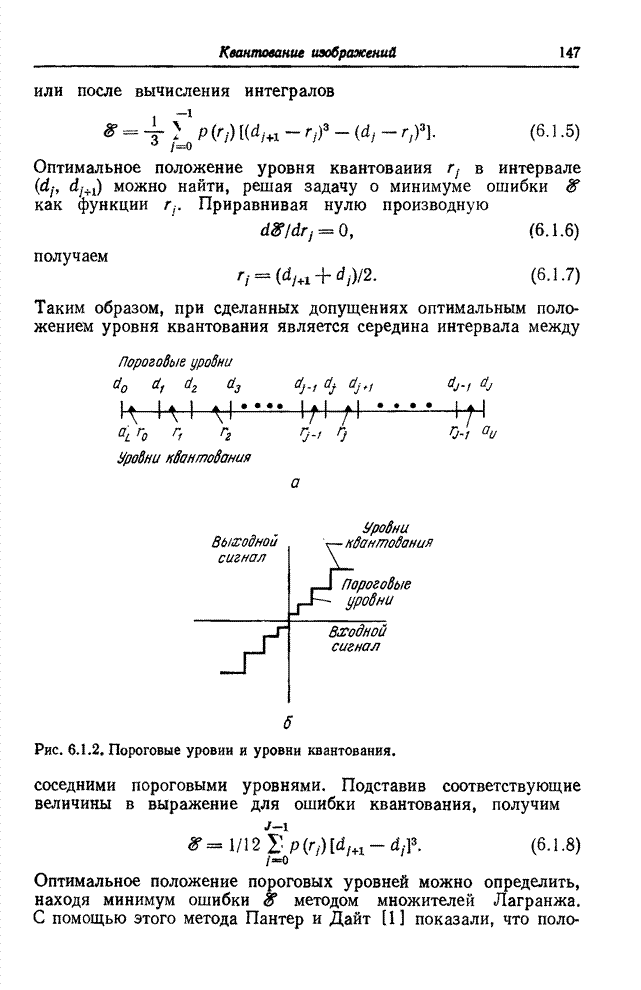
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА