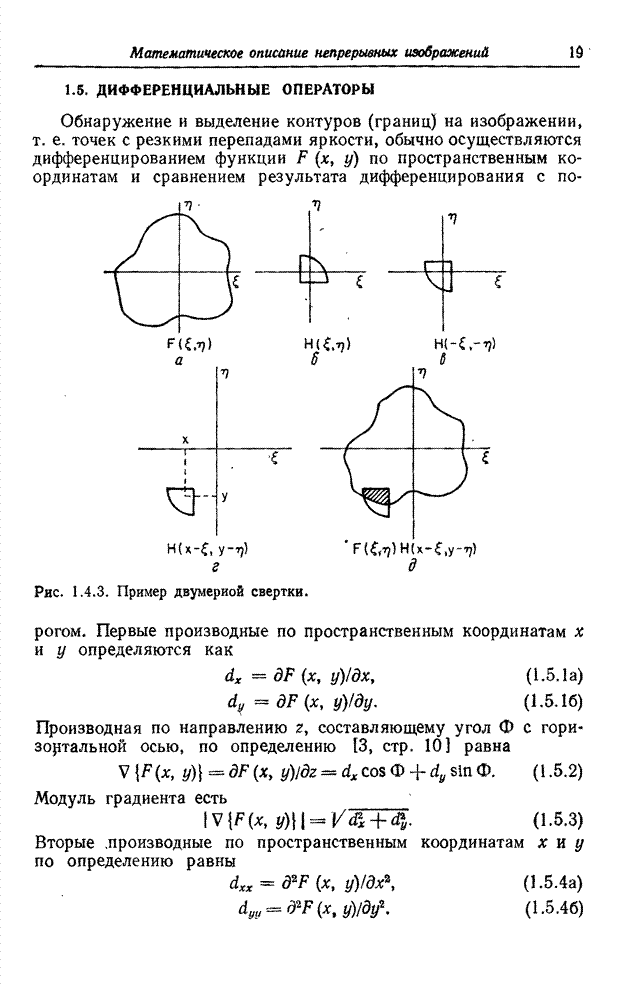
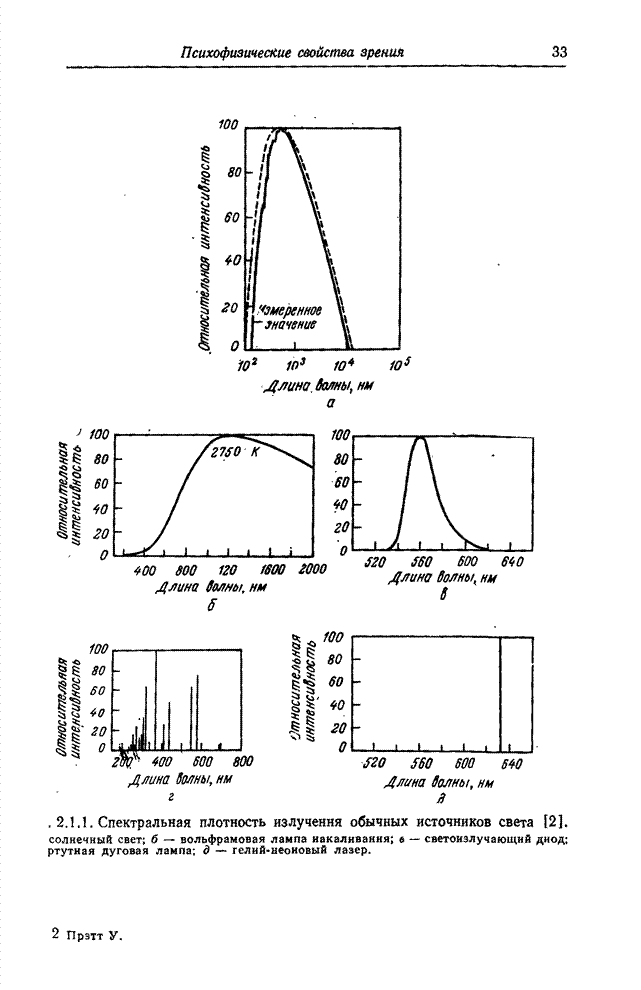
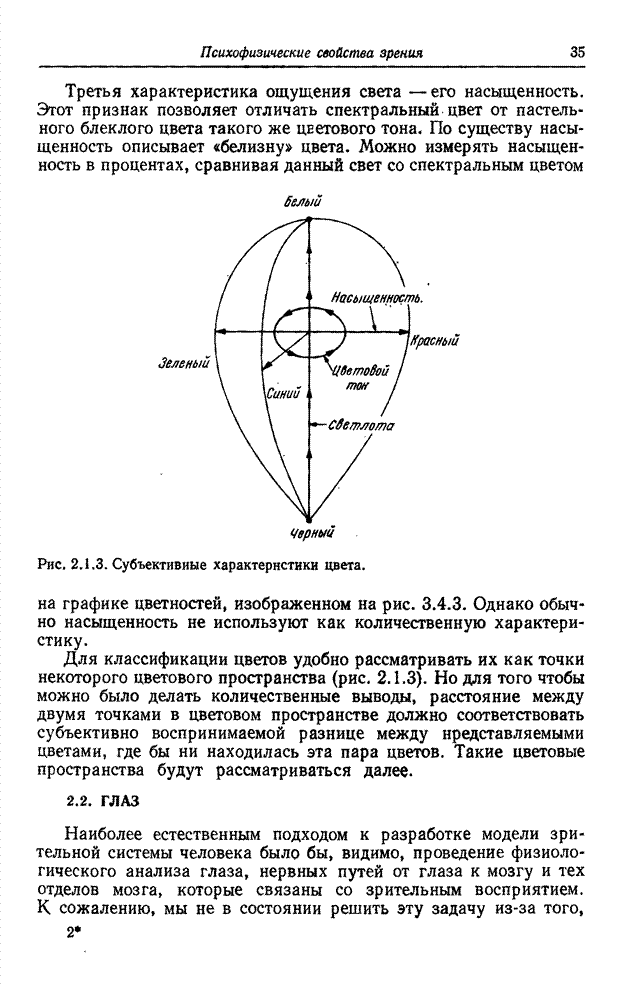
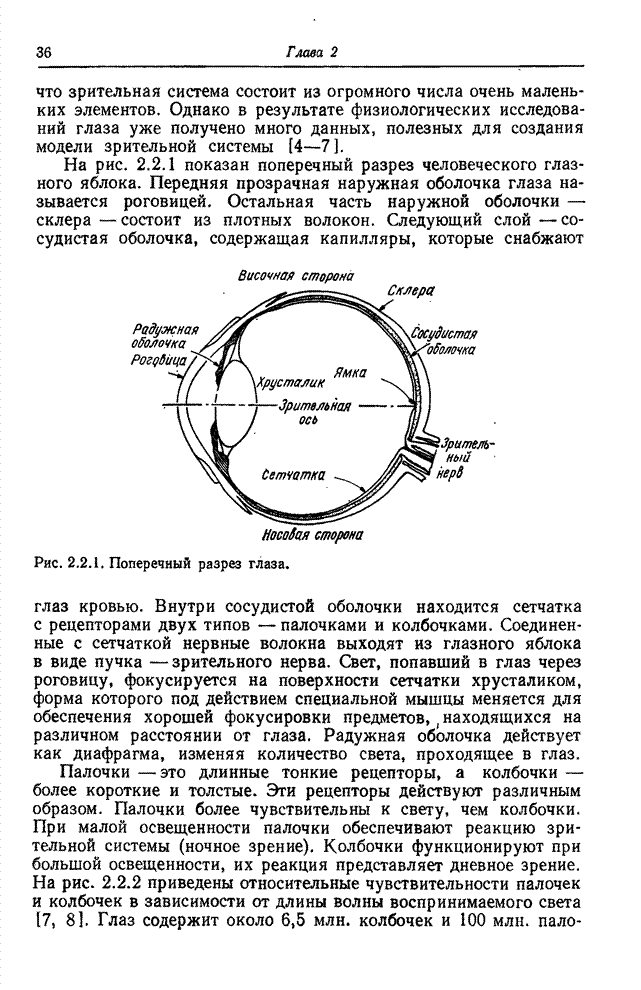
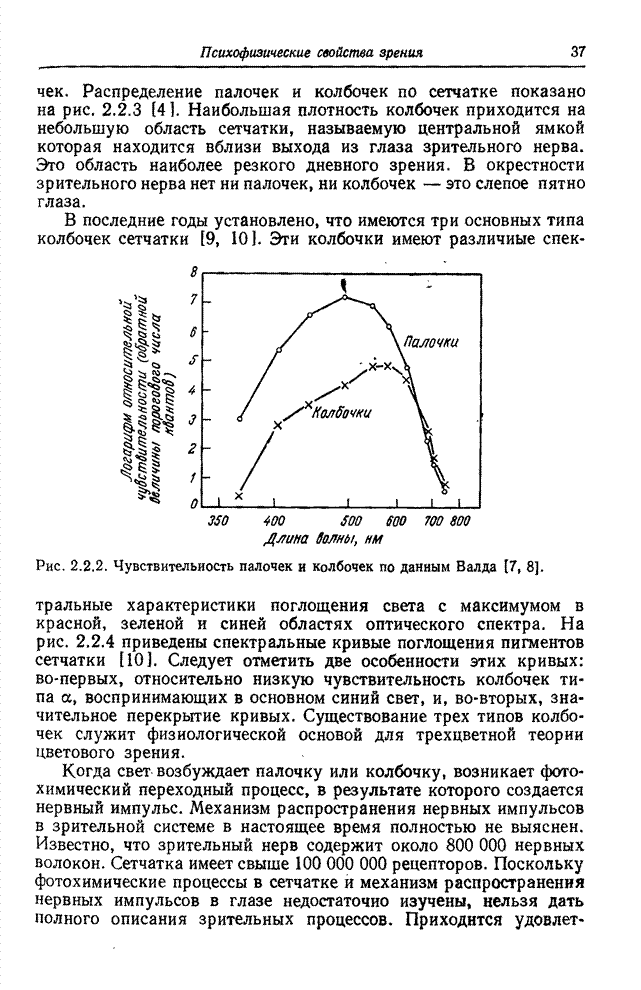
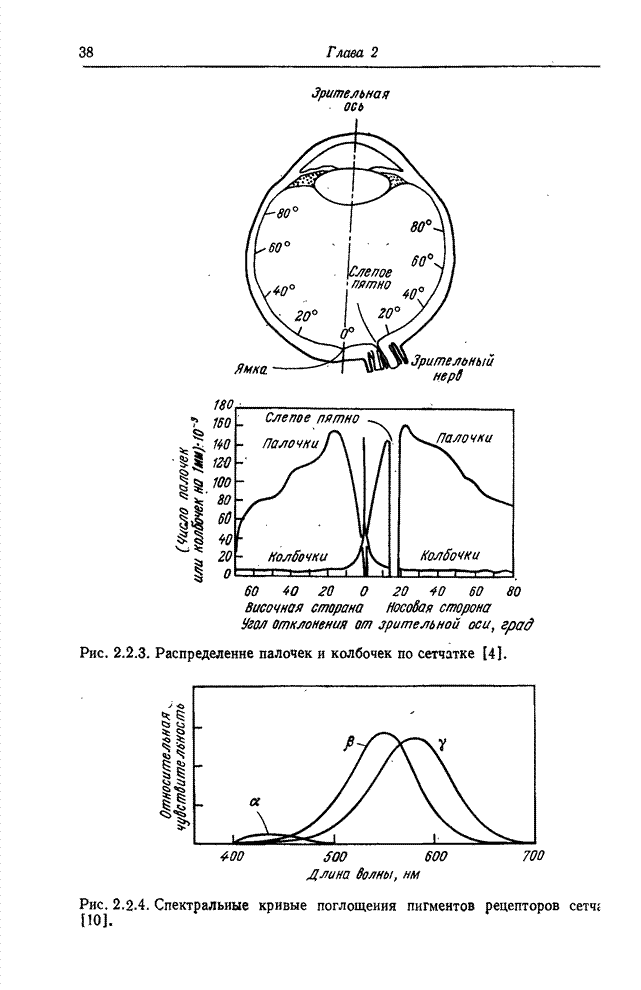
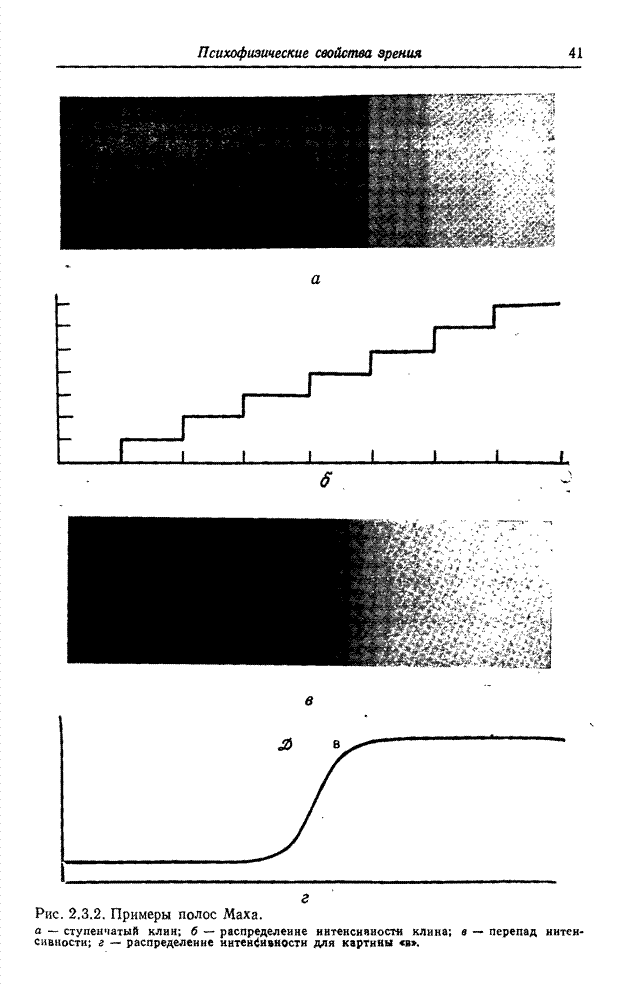
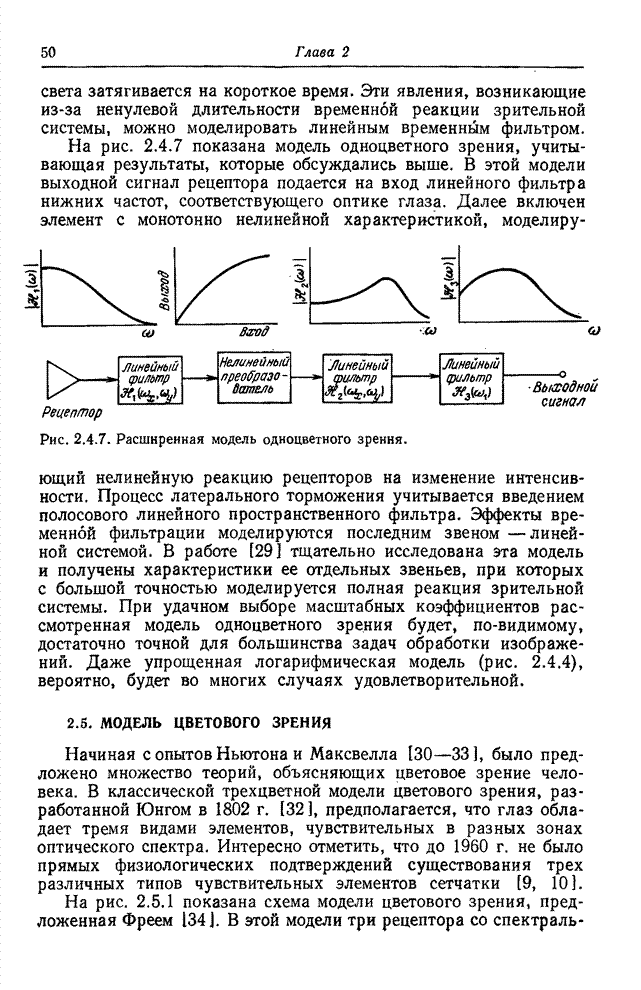
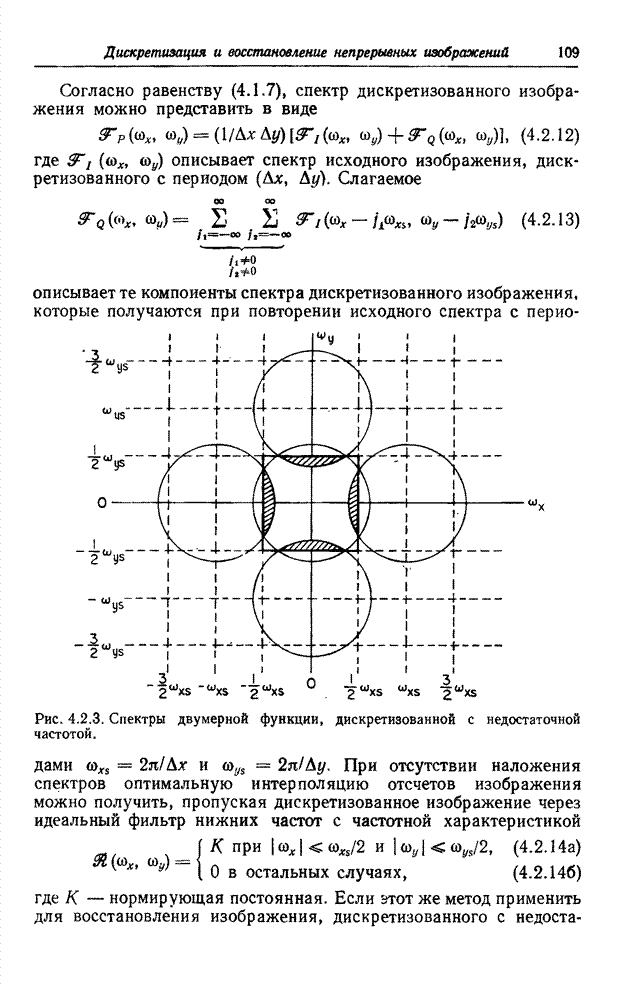
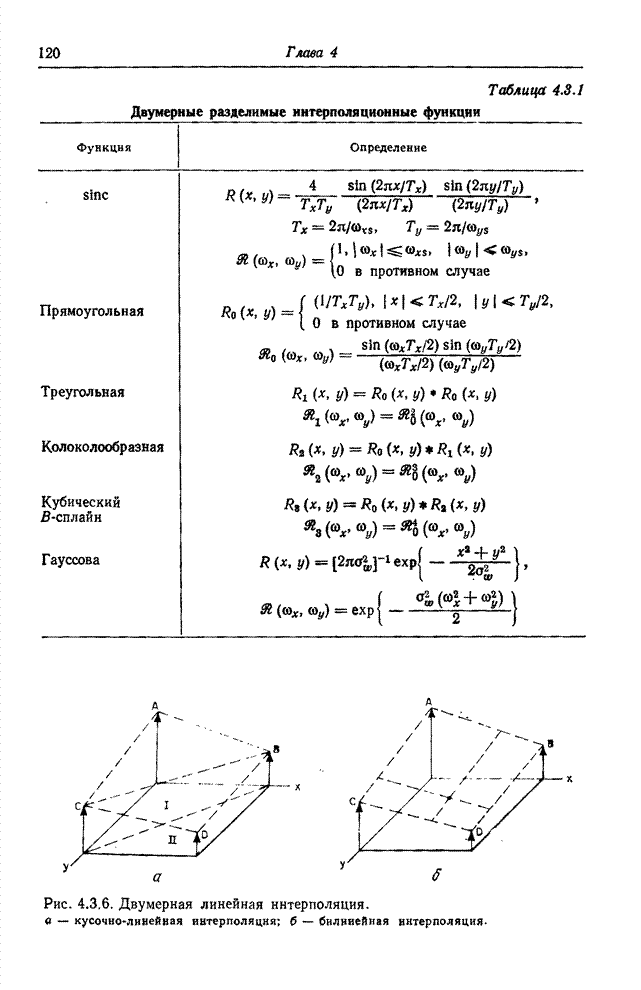
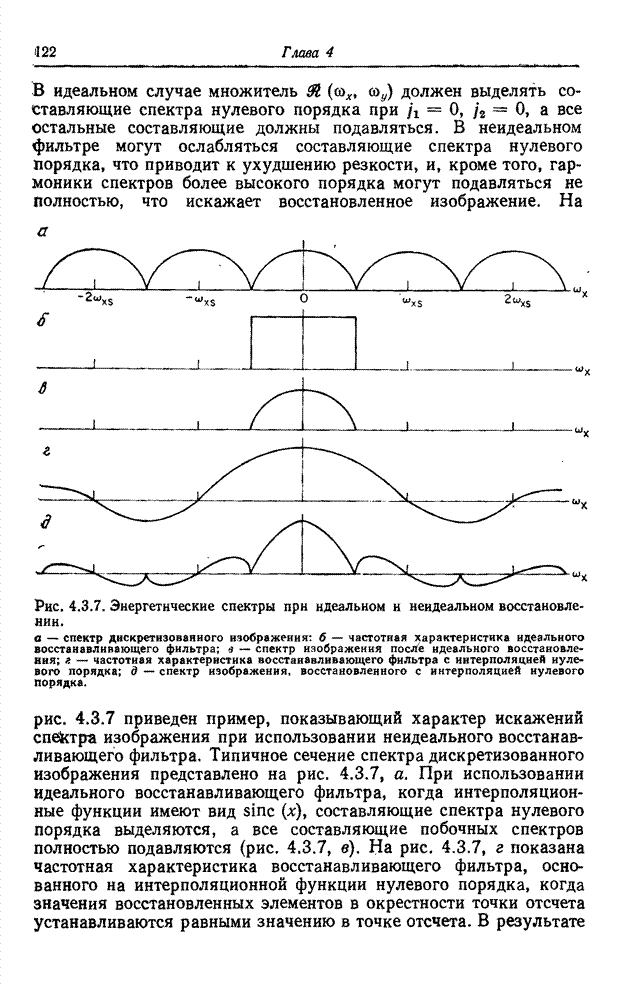
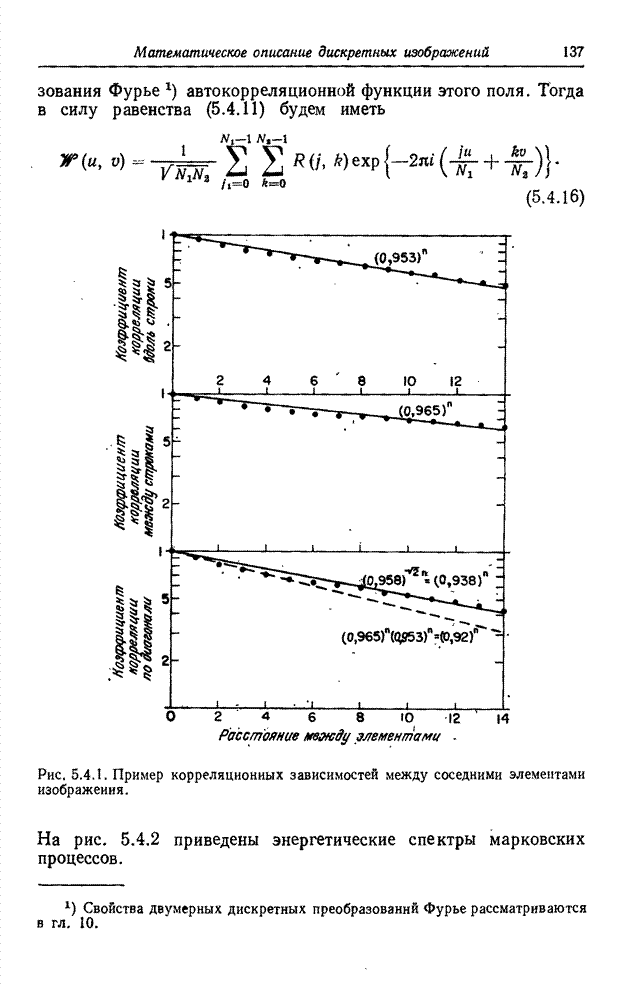
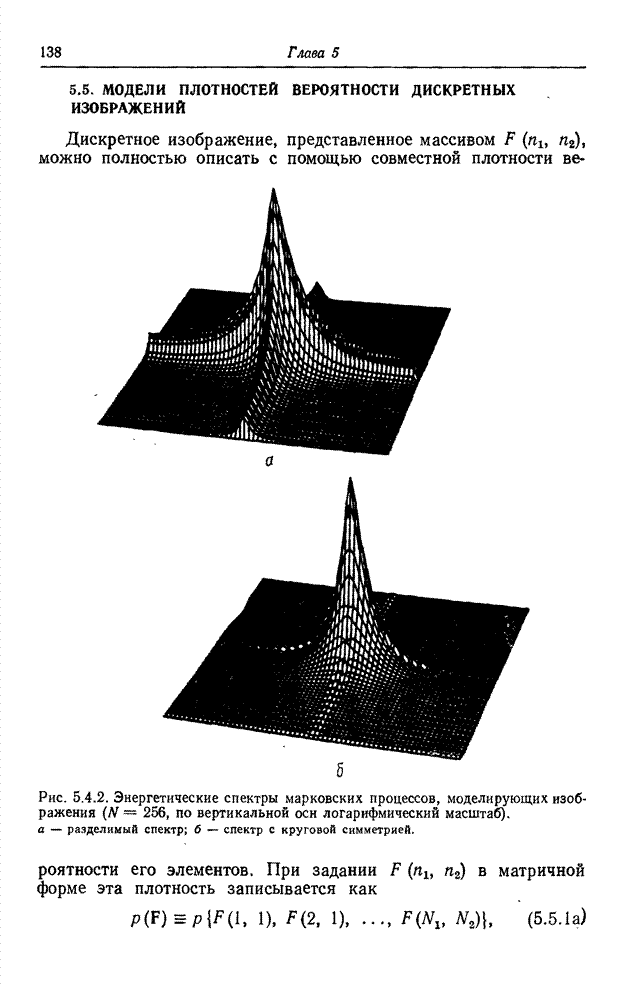
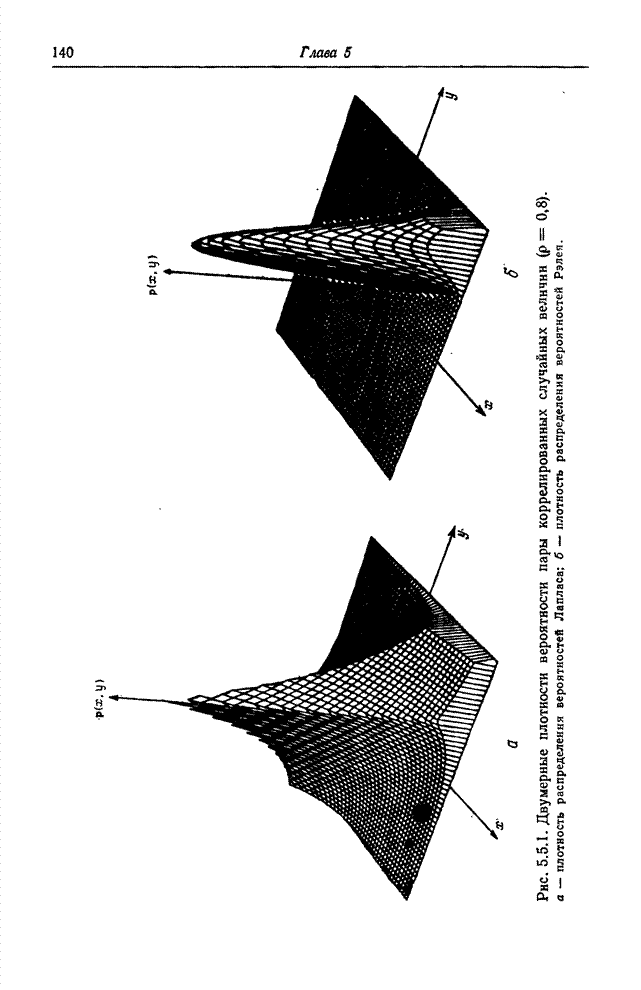
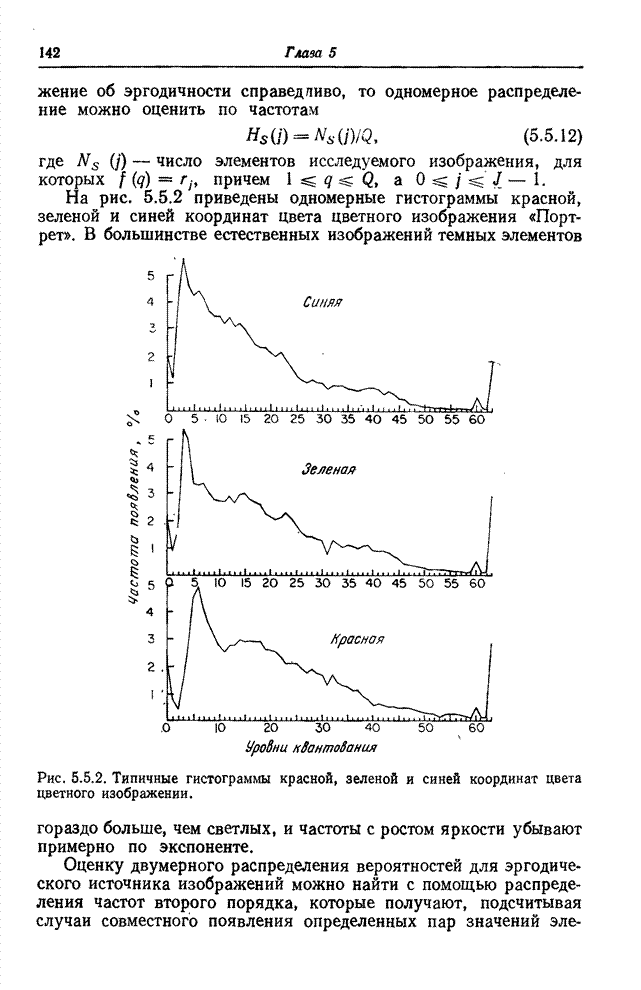
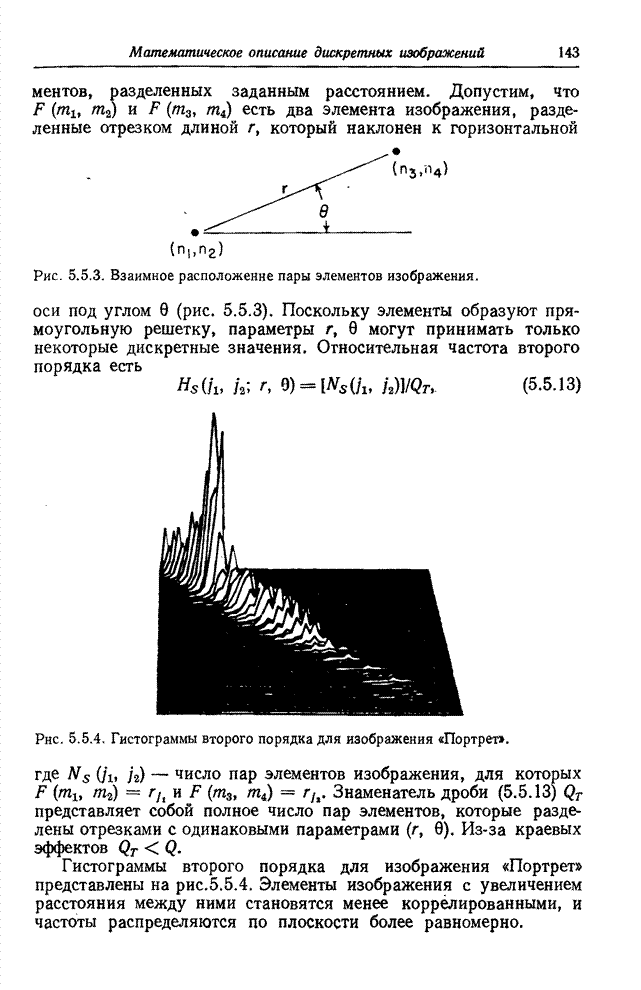
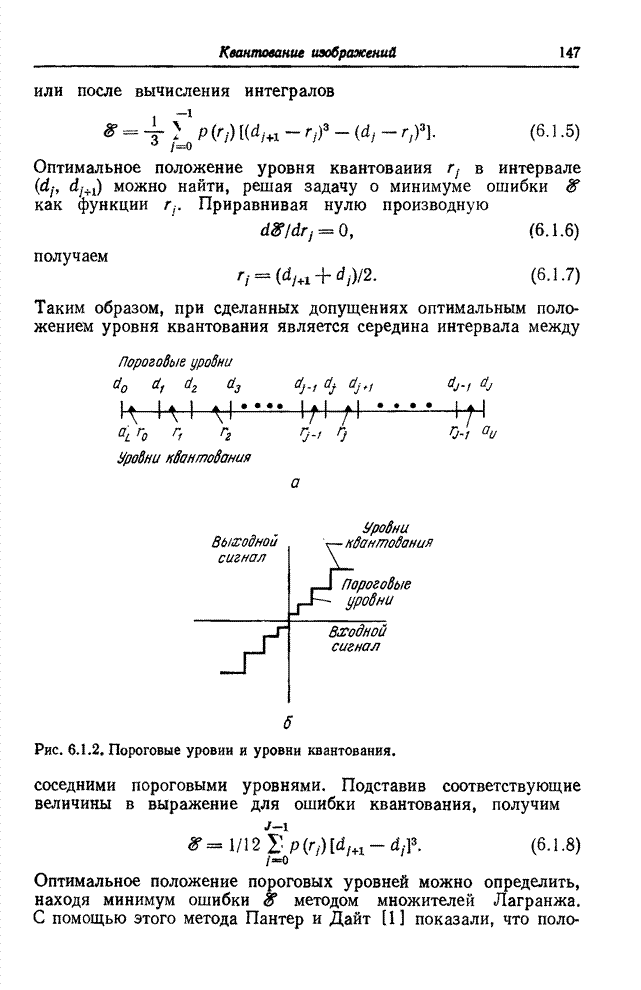
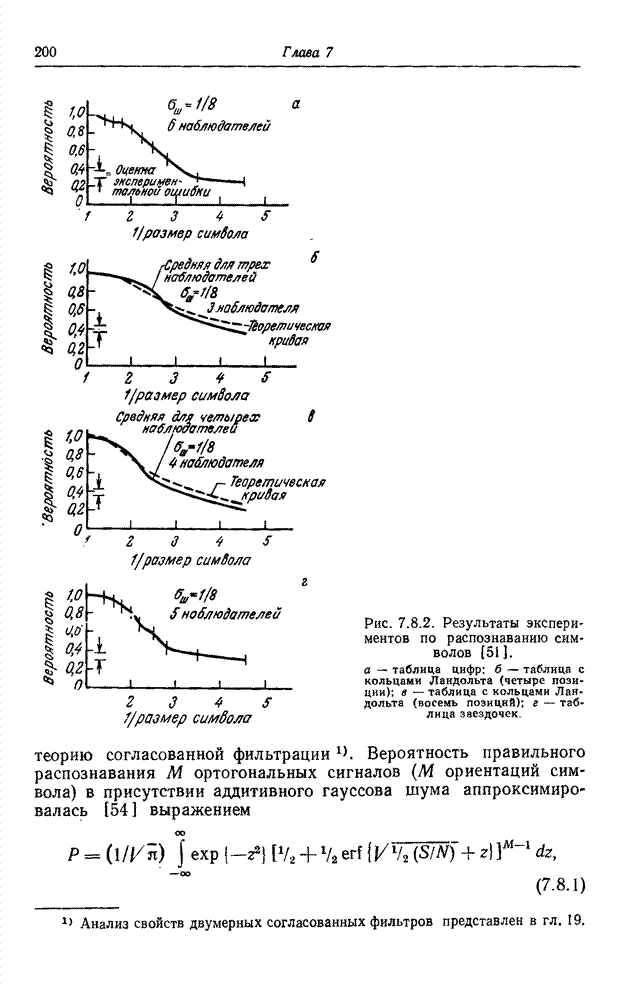
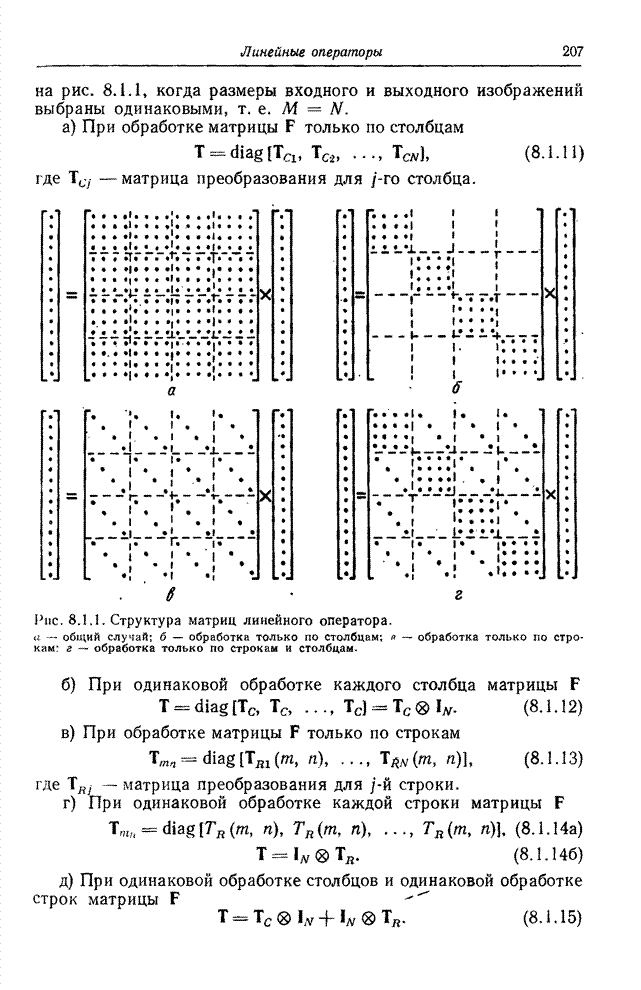
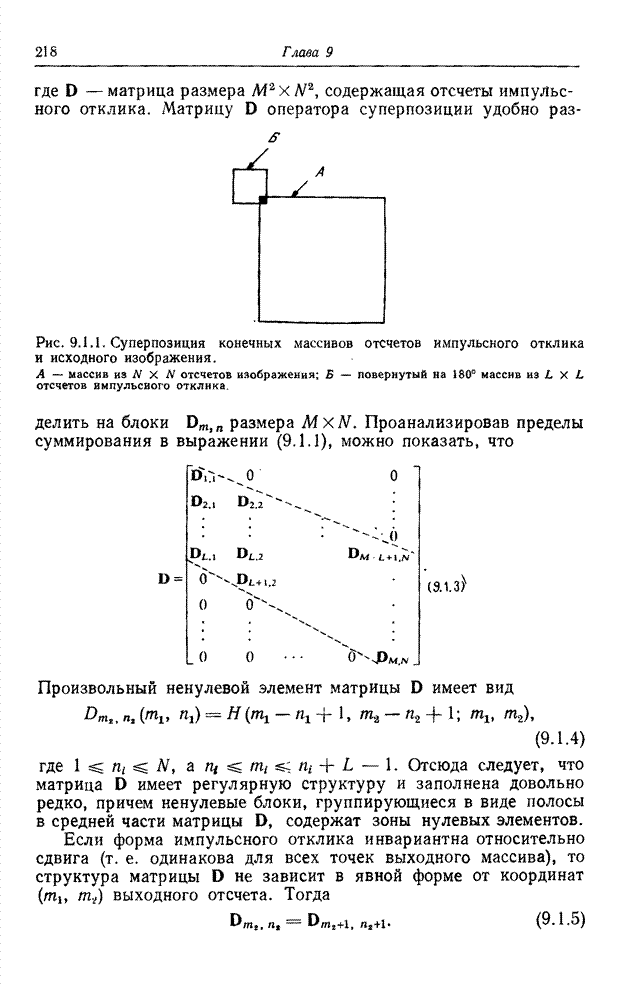
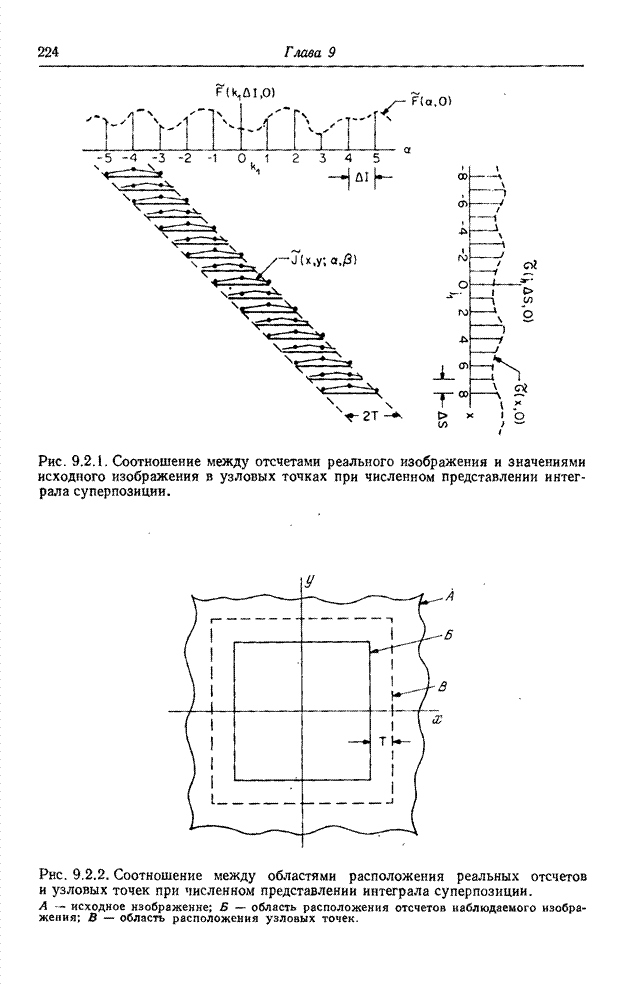
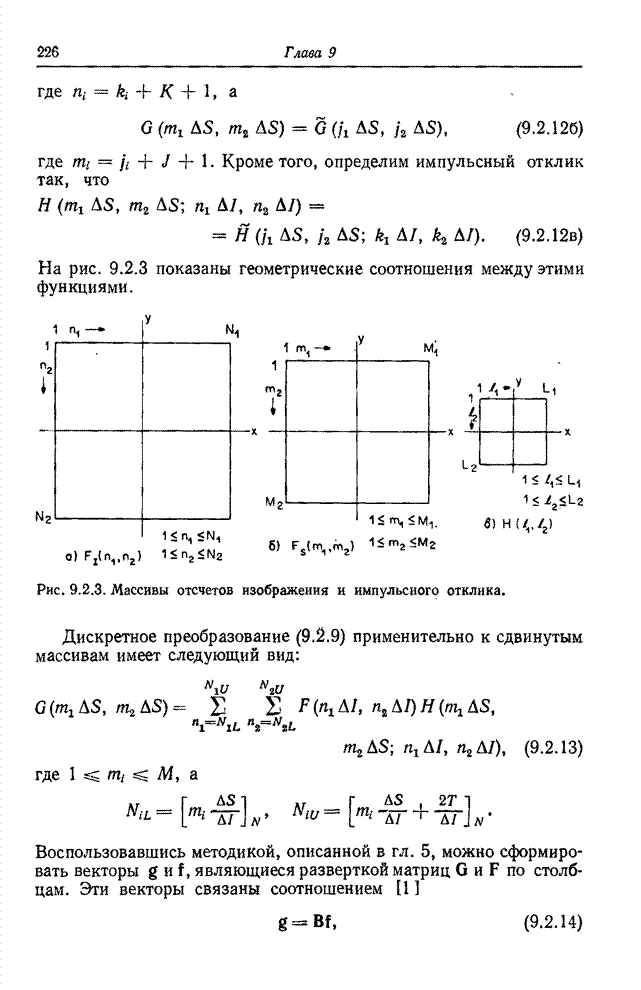
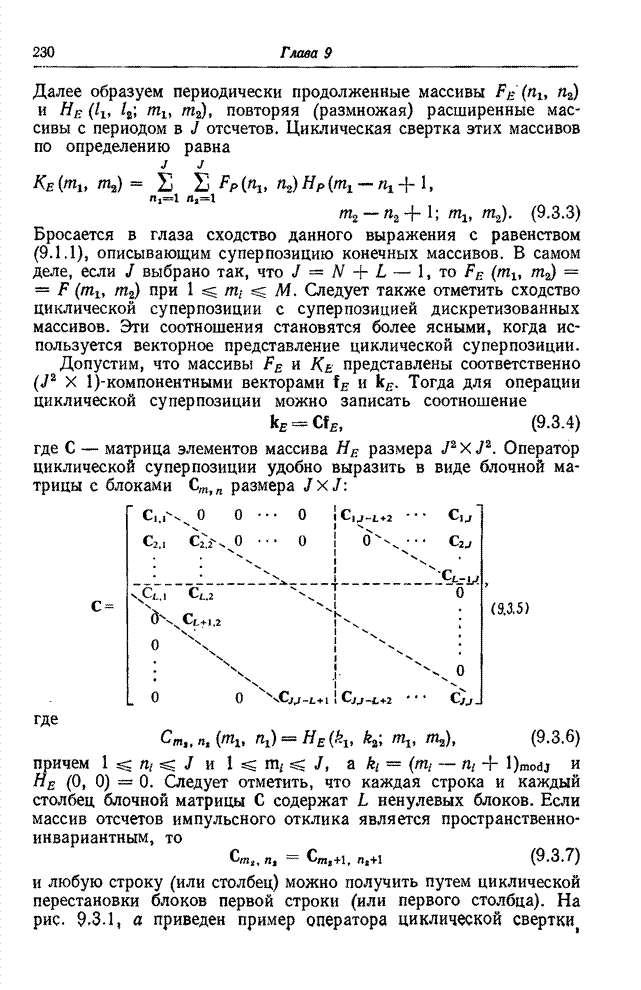
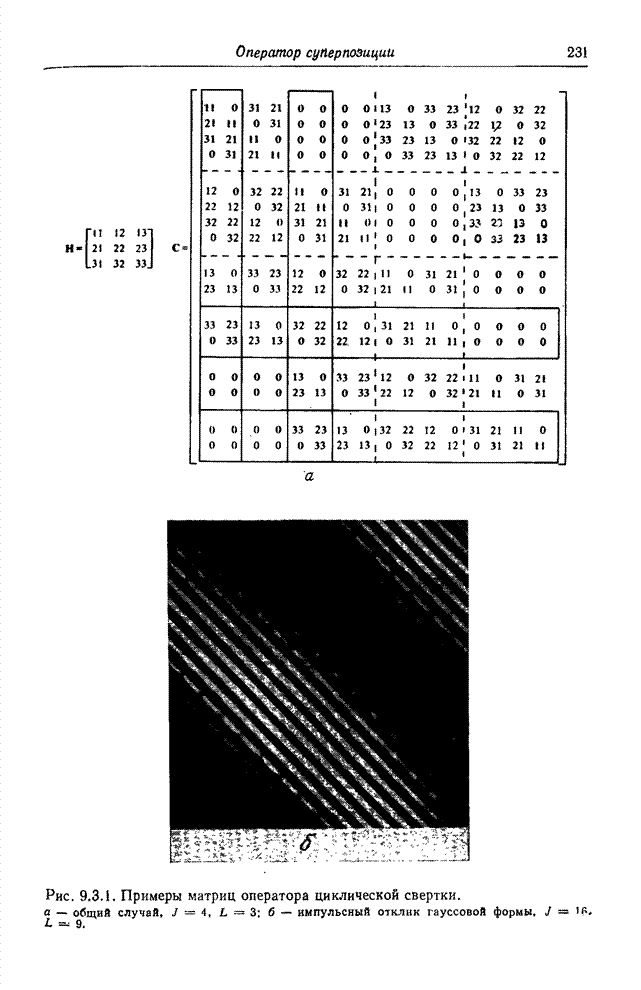
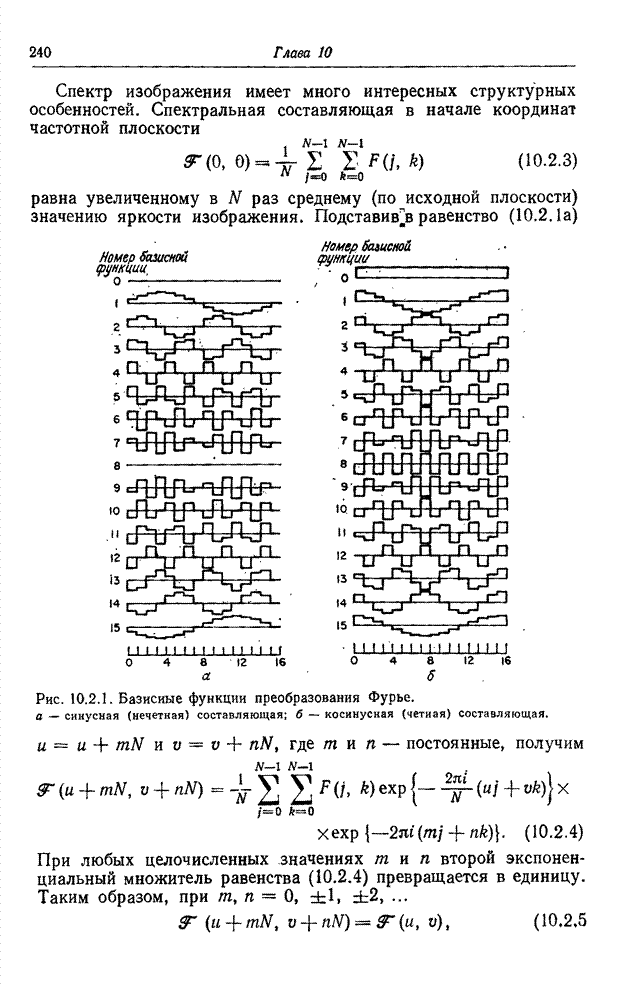
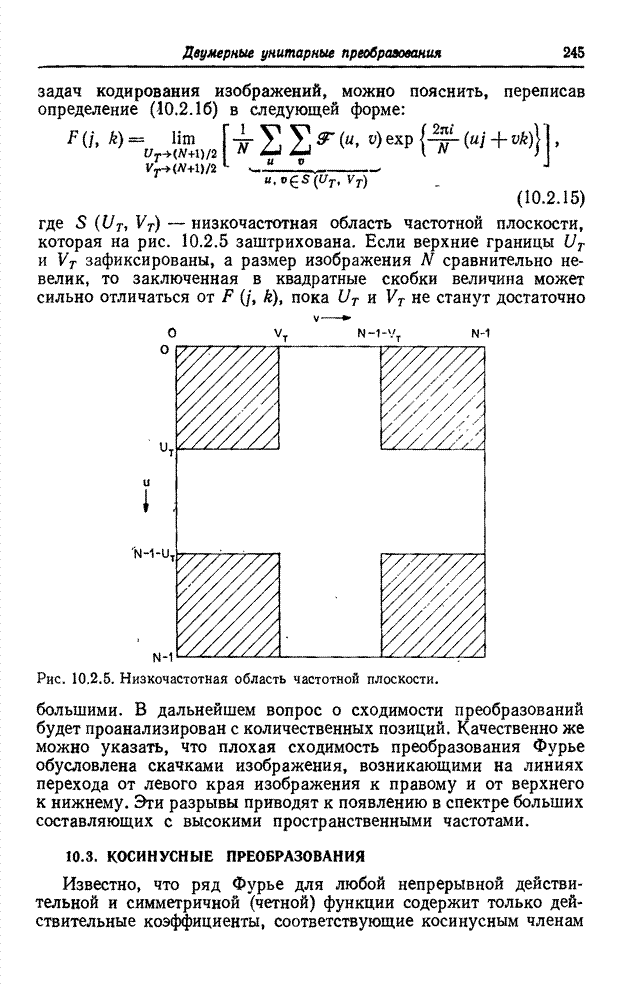
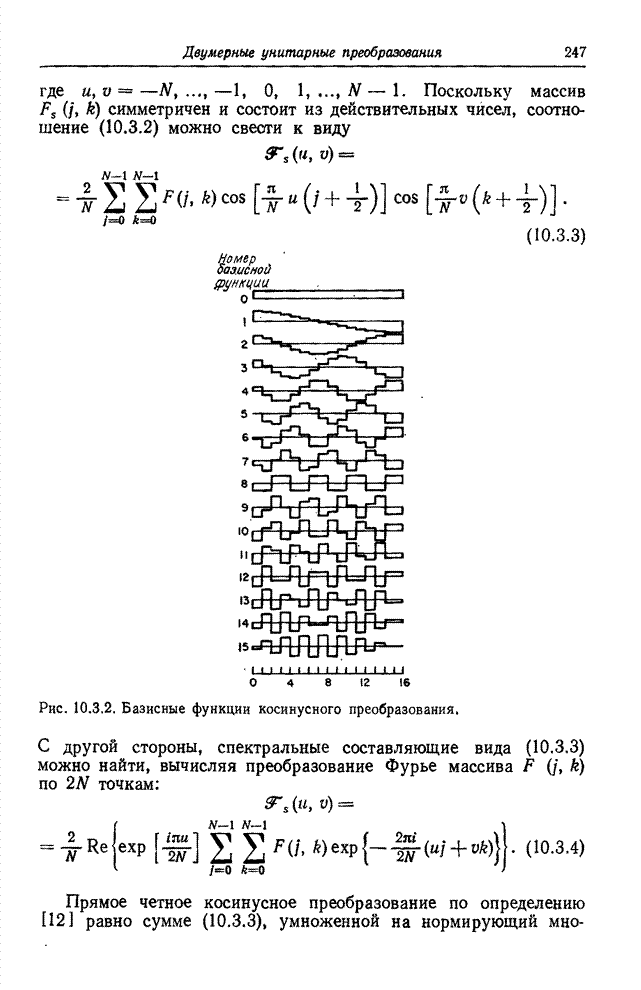
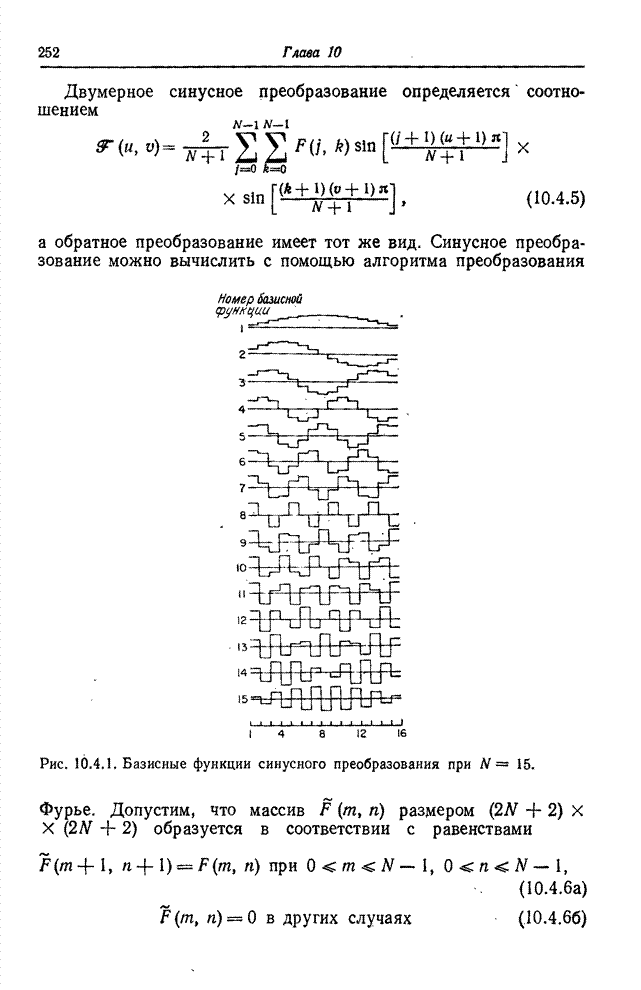
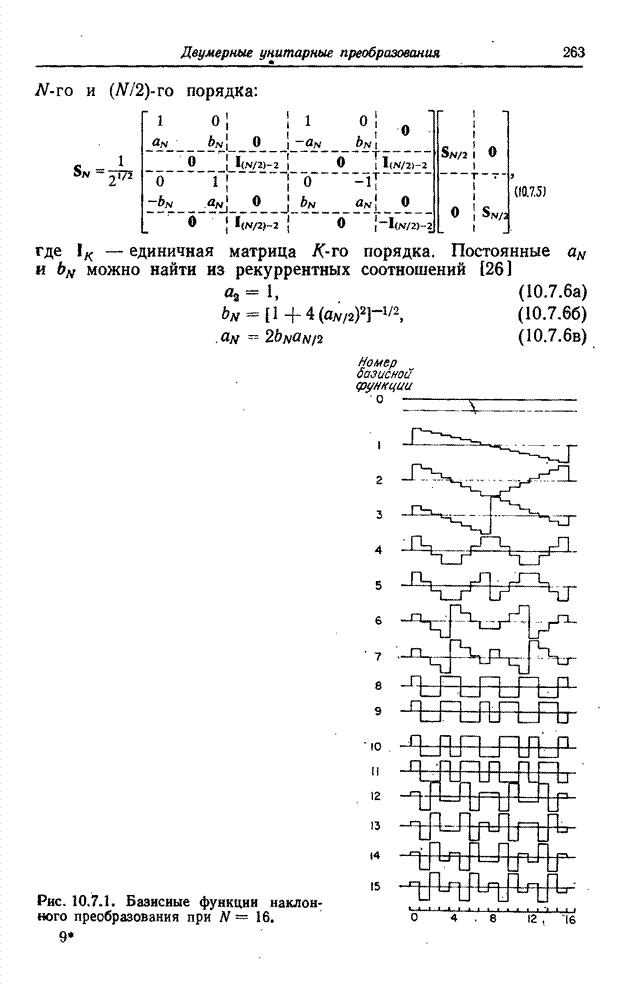
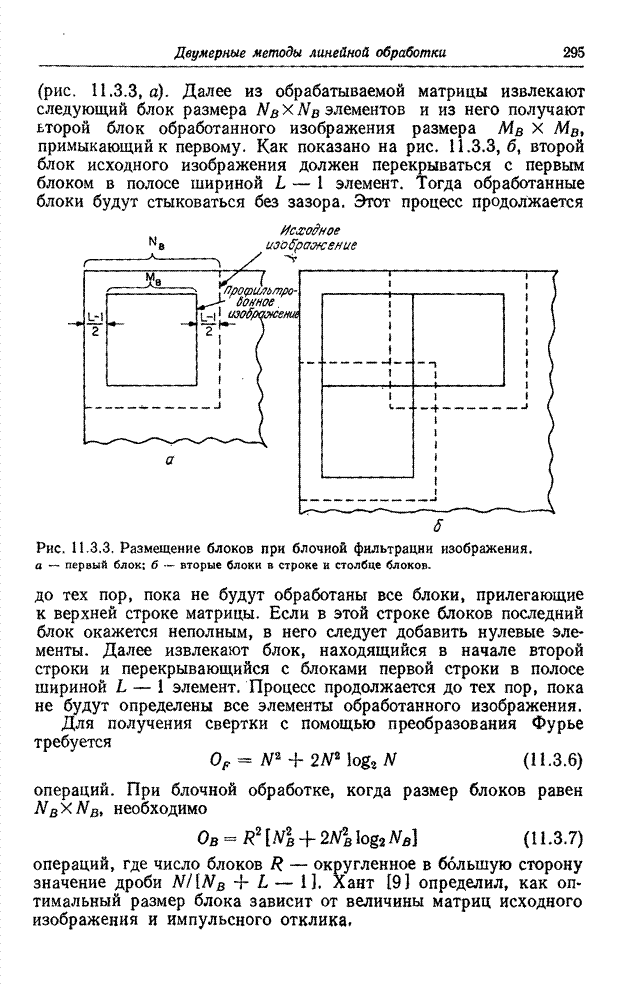
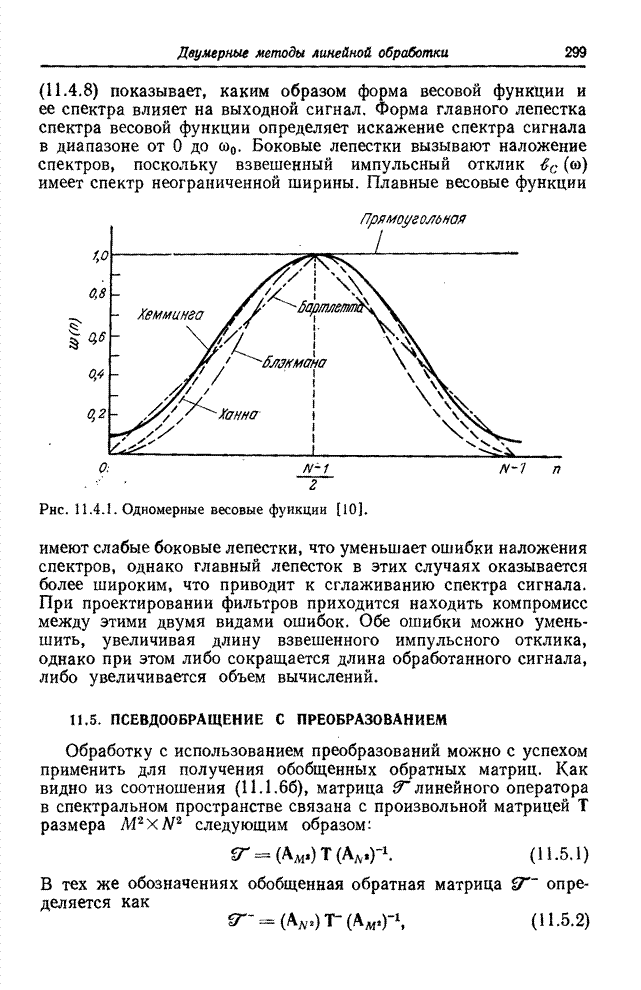
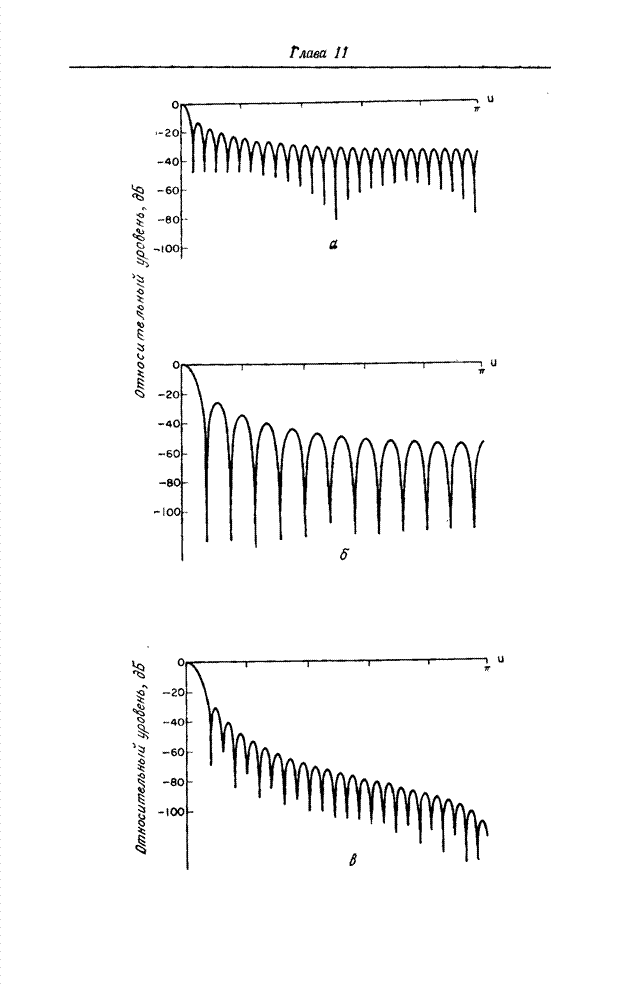
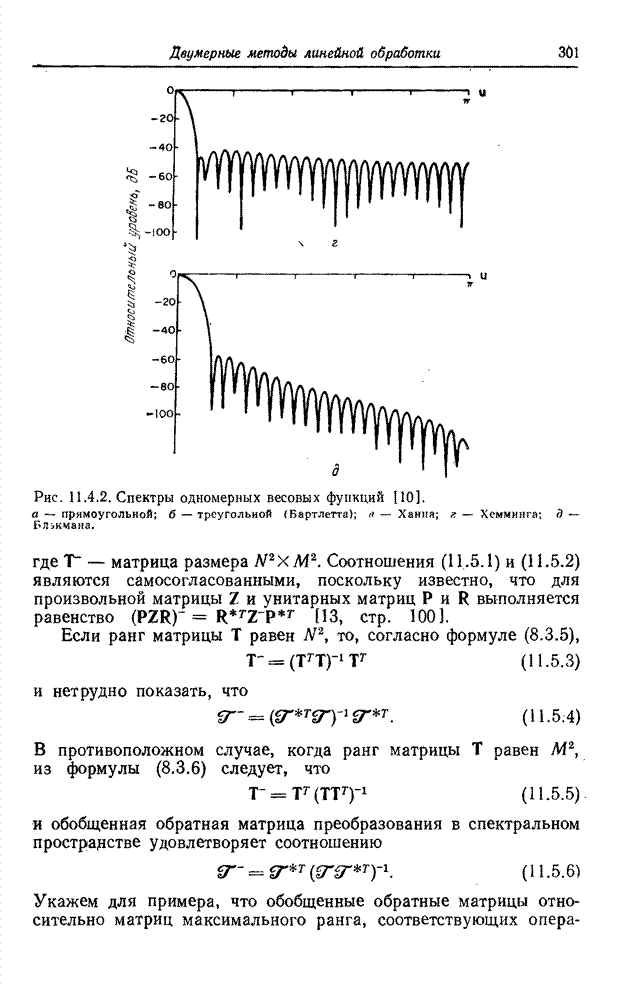
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
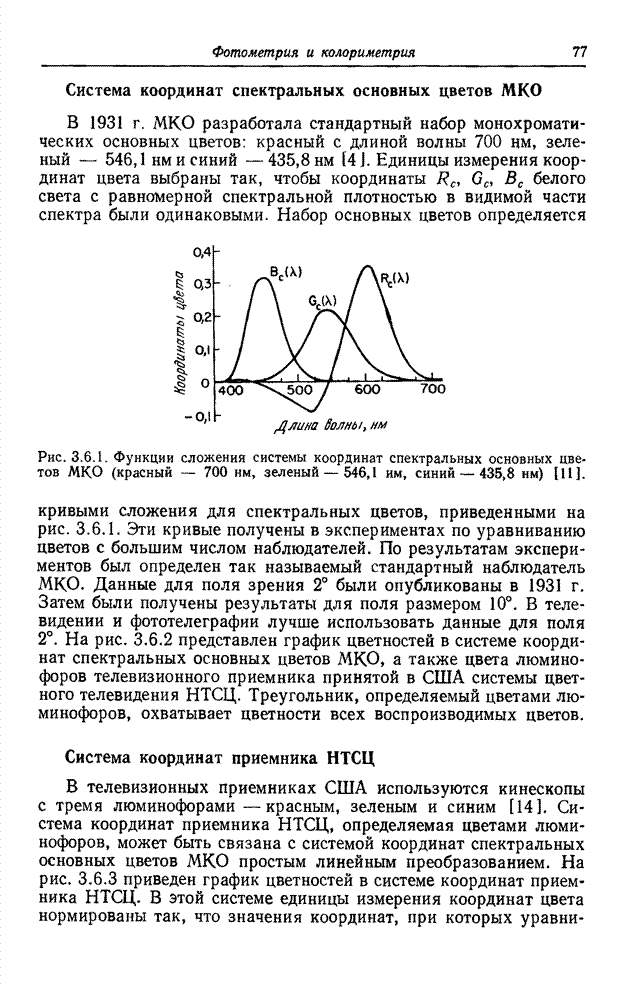
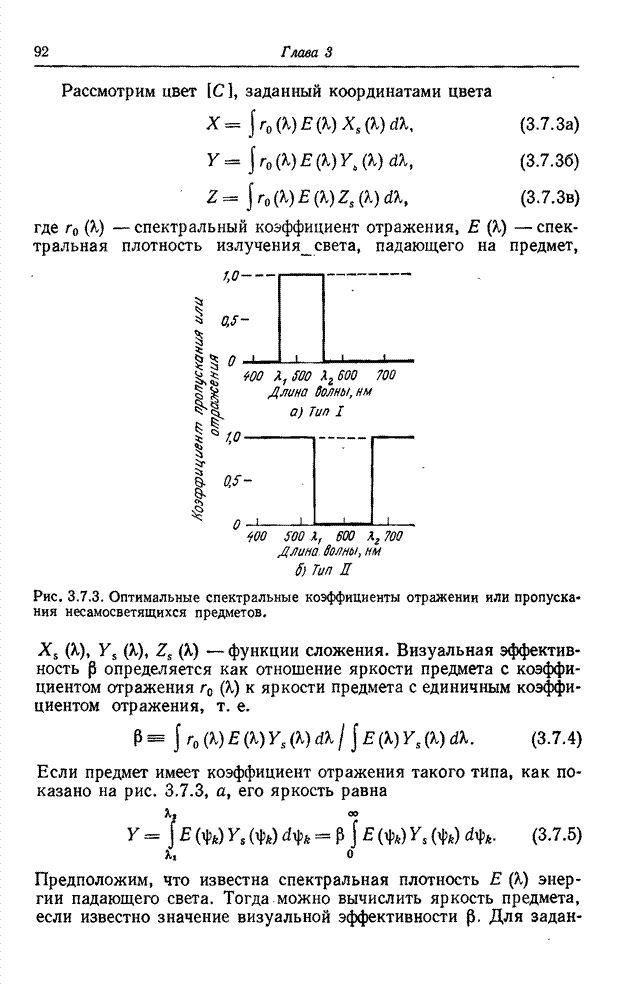
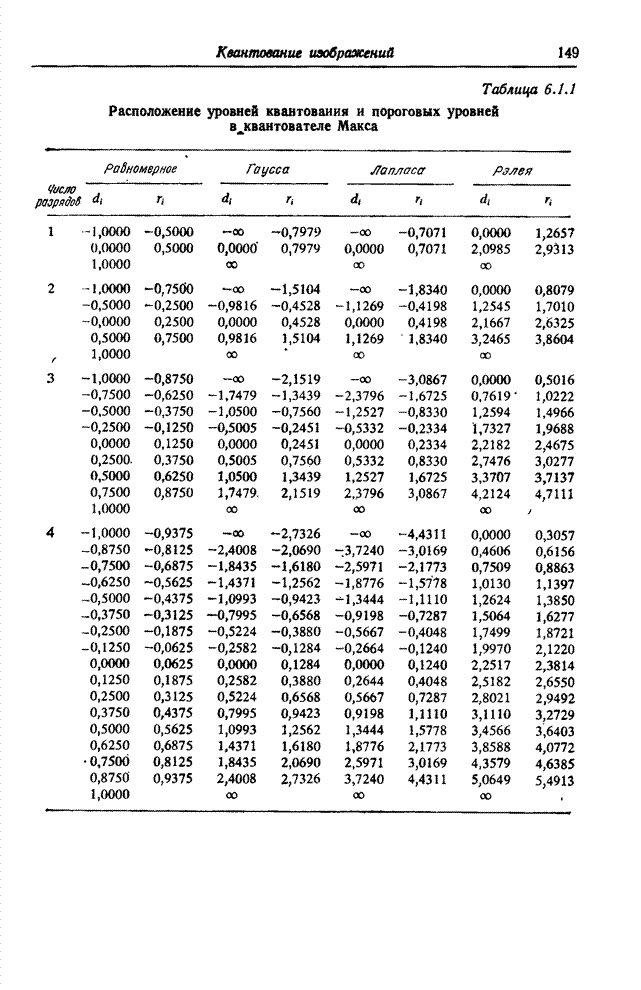
7.3.2. МЕТРИКИ ЦВЕТА
Для
определения цветовых различий можно ввести детерминированную меру, если
рассматривать цветовое пространство, определяемое тремя координатами цвета, как
евклидово пространство. Тогда цвет ![]() , заданный значениями трех координат
, заданный значениями трех координат ![]() , будет отделен от
цвета
, будет отделен от
цвета ![]() с координатами
цвета
с координатами
цвета ![]() расстоянием
расстоянием
![]() , определяемым
соотношением
, определяемым
соотношением
![]() . (7.3.9)
. (7.3.9)
Если
данная мера различия цветов согласуется с субъективными представлениями, то при
всех значениях координат цвета одинаковые приращения ![]() должны
соответствовать одинаковым едва заметным (пороговым) различиям цветов. Другими
словами, уравнение
должны
соответствовать одинаковым едва заметным (пороговым) различиям цветов. Другими
словами, уравнение ![]() должно
описывать сферу радиуса в одну пороговую единицу различия цветов с центром в
точке
должно
описывать сферу радиуса в одну пороговую единицу различия цветов с центром в
точке ![]() . Исключением
являются только те точки, которые соответствуют чистым основным цветам —
красному, зеленому и синему. Эксперименты показали, что человеческое зрение
наиболее чувствительно к единичным изменениям синей координаты цвета, а
наименее чувствительно — к зеленой [18].
. Исключением
являются только те точки, которые соответствуют чистым основным цветам —
красному, зеленому и синему. Эксперименты показали, что человеческое зрение
наиболее чувствительно к единичным изменениям синей координаты цвета, а
наименее чувствительно — к зеленой [18].
Чтобы достигнуть лучшего соответствия меры (7.3.9) результатам субъективных испытаний, можно положить, что цветовое пространство является римановым. По определению расстояние в римановом цветовом пространстве выражается как
 , (7.3.10)
, (7.3.10)
где
коэффициенты ![]() являются
функциями
являются
функциями ![]() .
Приравняв выражение (7.3.10) единице, получим уравнение эллипсоида с центром в
точке
.
Приравняв выражение (7.3.10) единице, получим уравнение эллипсоида с центром в
точке ![]() . Установлено,
что цвета, едва заметно отличающиеся от данного цвета, можно довольно точно
описать эллипсоидами в пространстве основных цветов.
. Установлено,
что цвета, едва заметно отличающиеся от данного цвета, можно довольно точно
описать эллипсоидами в пространстве основных цветов.
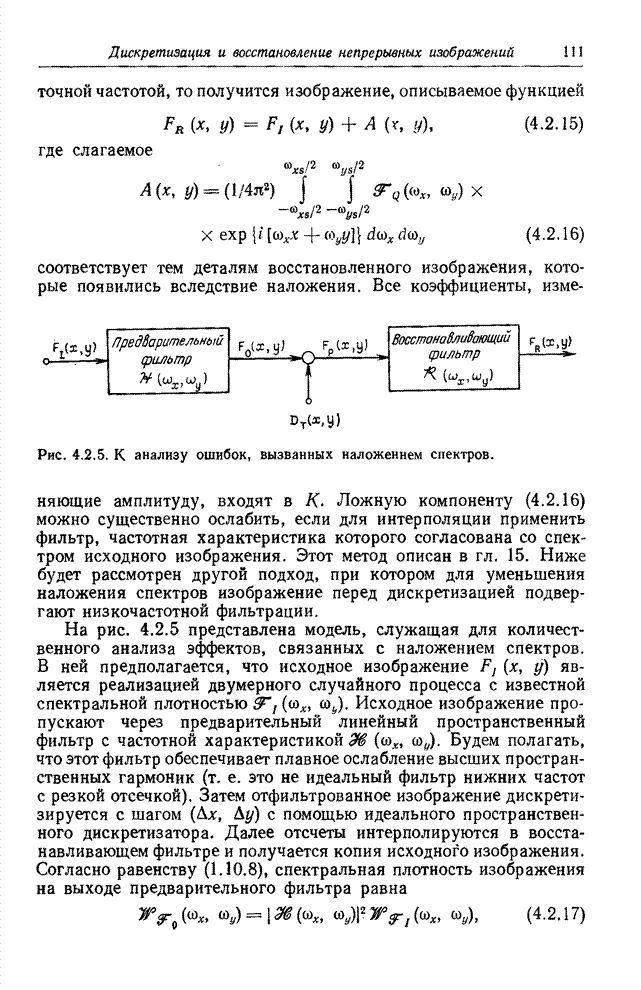
Выражение (7.3.10) применяется в колориметрии в качестве меры различия цветов, если расстояние между ними не превышает нескольких пороговых единиц. Если же цвета различаются сильнее, то следует суммировать элементарные приращения вдоль кратчайшего пути, соединяющего соответствующие точки цветового пространства. Тогда глобальная мера различия цветов будет задана соотношением
 (7.3.11)
(7.3.11)
В евклидовом пространстве таким кратчайшим путем является прямая линия. В римановом пространстве кратчайший путь, называемый геодезической линией, в общем случае проходит вдоль некоторой кривой. Мут и Перселс [19], а также Джейн [20] составили программы для вычисления расстояний между цветами, основанные на построении геодезических линий в пространстве цветов. На основе этих программ удалось создать весьма точную метрику цветового пространства, но для проведения вычислений требуется много времени.
Пользоваться
римановой метрикой (7.3.10) сравнительно сложно, поэтому естественно возникает
вопрос, существует ли такое отображение трехмерного пространства с координатами
![]() на
евклидово трехмерное пространство с координатами
на
евклидово трехмерное пространство с координатами ![]() , при котором метрика различия цветов
сохраняется неизменной. В этом новом пространстве приращения координат цвета
должны удовлетворять соотношению
, при котором метрика различия цветов
сохраняется неизменной. В этом новом пространстве приращения координат цвета
должны удовлетворять соотношению
![]() , (7.3.12)
, (7.3.12)
так,
чтобы поверхность едва различимых цветов представляла собой сферу с центром в
точке ![]() . Было показано
[16, стр. 513], что в общем случае не существует линейного преобразования, в
точности обладающего требуемыми свойствами. Однако было найдено несколько
линейных преобразований со свойствами, близкими к заданным. Международная
комиссия по освещению (МКО) приняла систему координат
. Было показано
[16, стр. 513], что в общем случае не существует линейного преобразования, в
точности обладающего требуемыми свойствами. Однако было найдено несколько
линейных преобразований со свойствами, близкими к заданным. Международная
комиссия по освещению (МКО) приняла систему координат ![]() , основанную на
работах Джадда [21] и Мак-Адама [22]. В этой системе расстояния между цветами
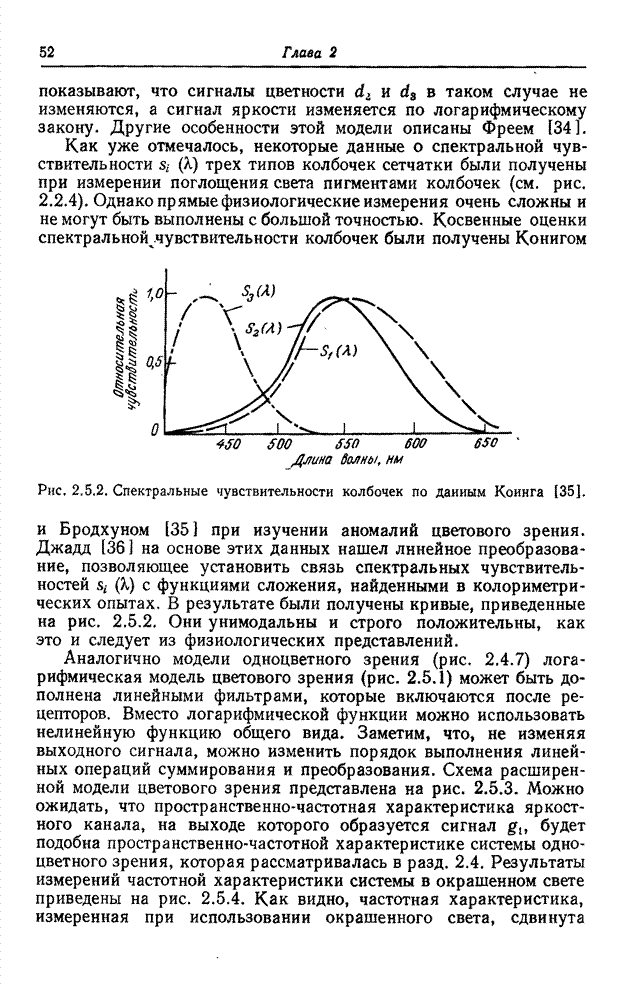
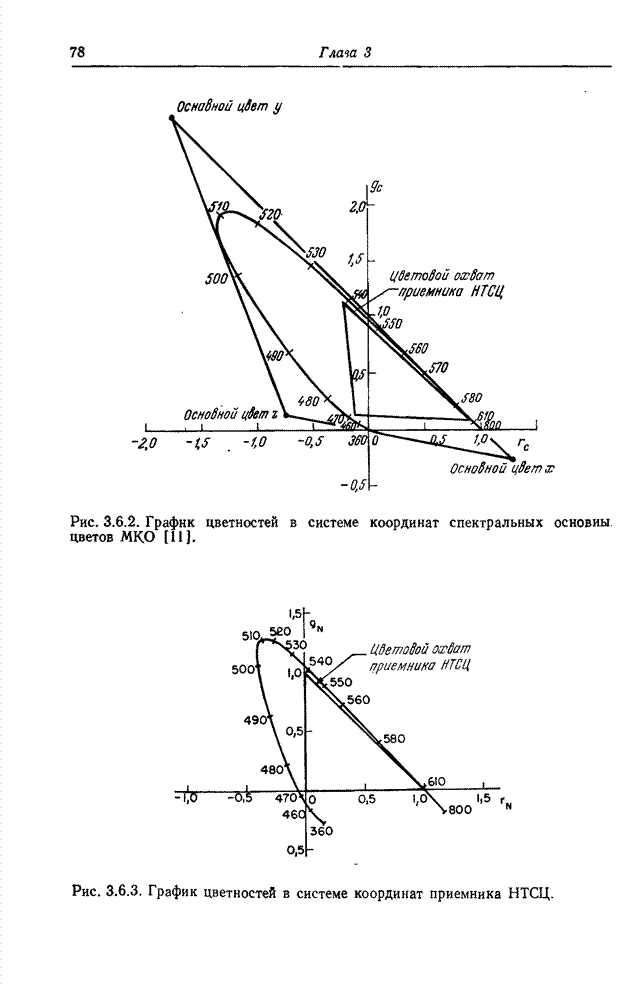
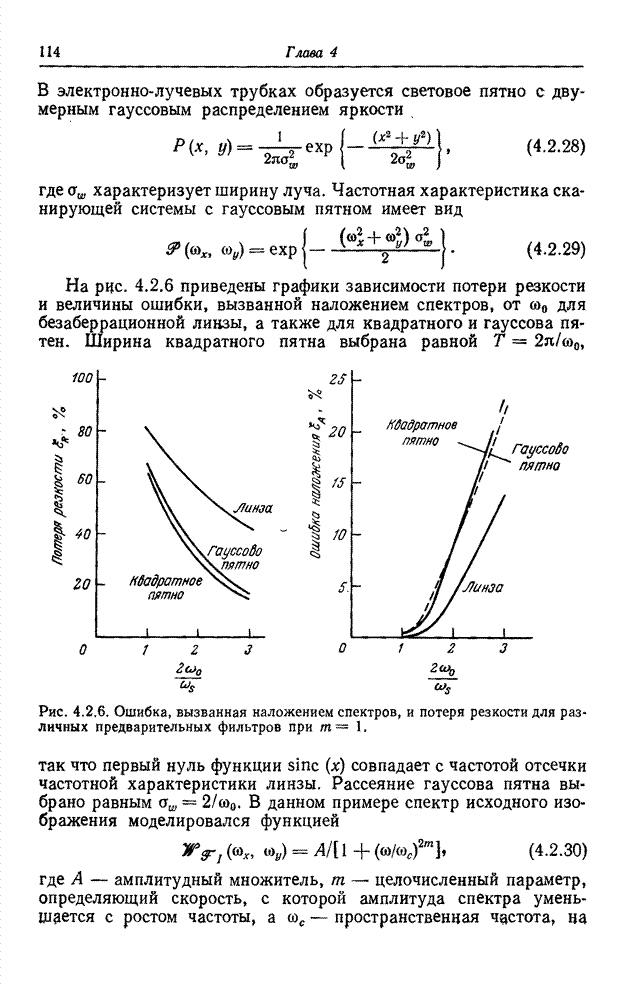
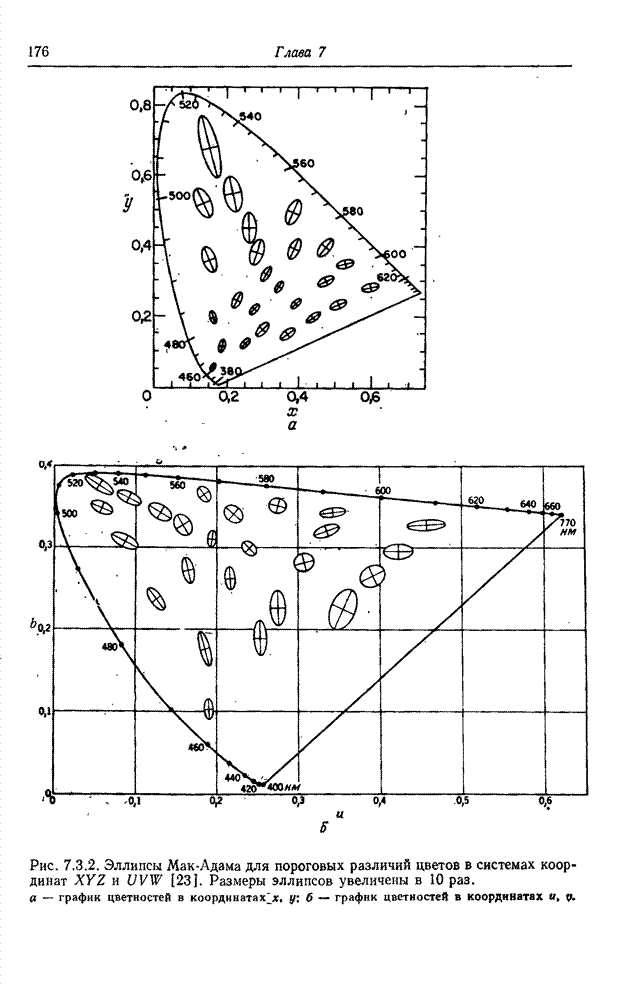
на пороге различения оказываются почти одинаковыми. На рис. 7.3.2, а приведены
результаты измерений едва заметных отличий цветов, выполненных Мак-Адамом [23].
Множества едва отличимых цветов аппроксимированы эллипсами и представлены на
графике цветностей в координатах
, основанную на
работах Джадда [21] и Мак-Адама [22]. В этой системе расстояния между цветами
на пороге различения оказываются почти одинаковыми. На рис. 7.3.2, а приведены
результаты измерений едва заметных отличий цветов, выполненных Мак-Адамом [23].
Множества едва отличимых цветов аппроксимированы эллипсами и представлены на
графике цветностей в координатах ![]() . Если эти же данные представить на
графике цветностей с координатами
. Если эти же данные представить на
графике цветностей с координатами ![]() (рис. 7.3.2, б), то эллипсы
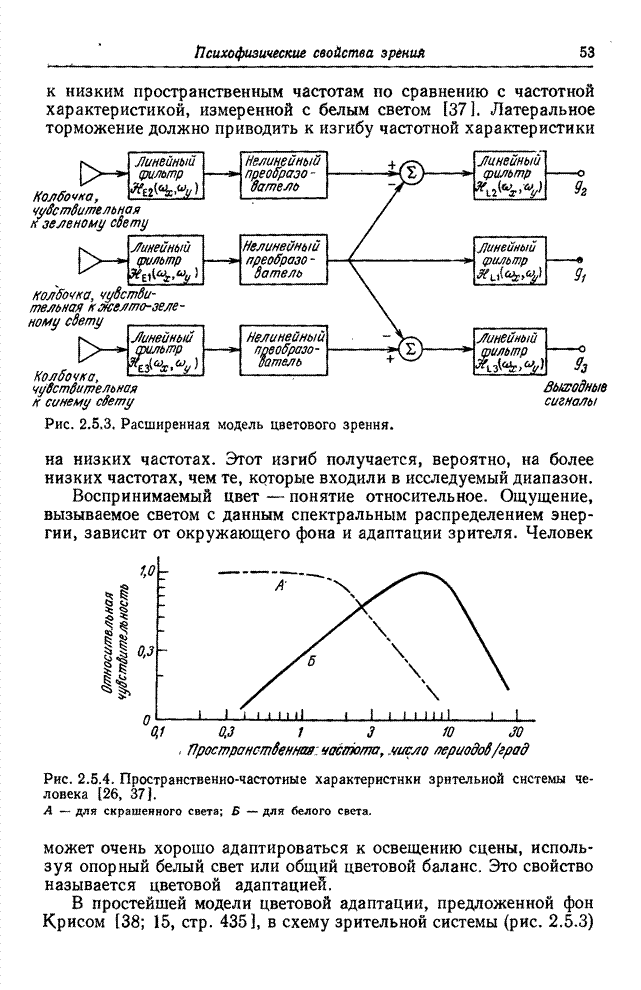
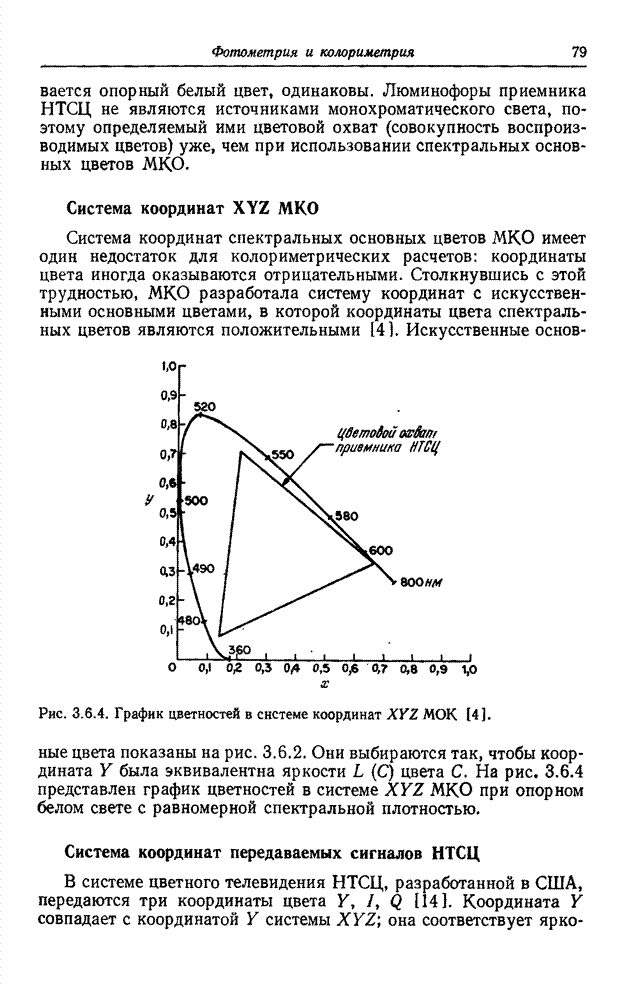
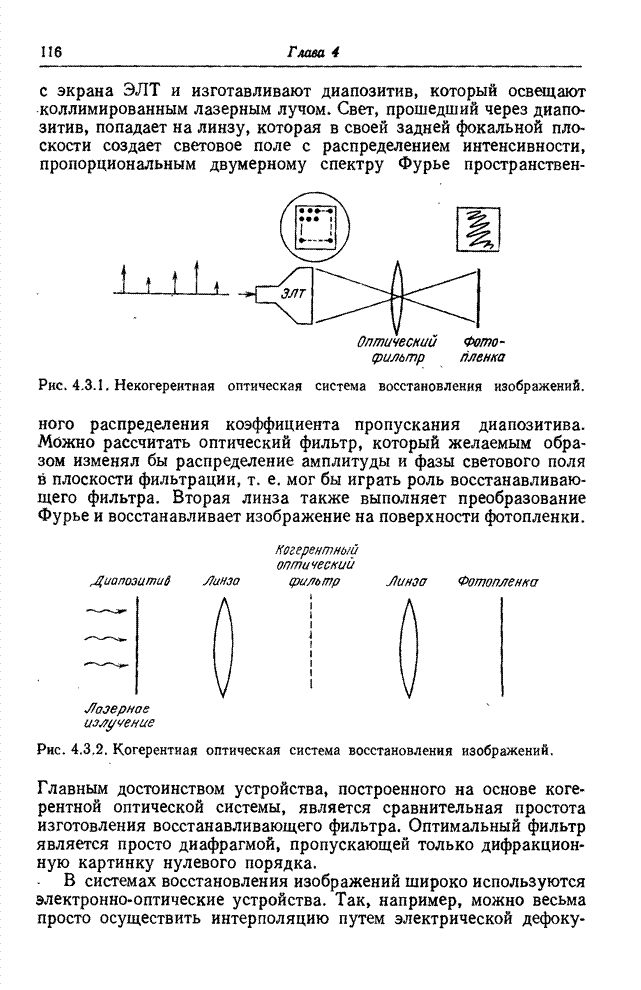
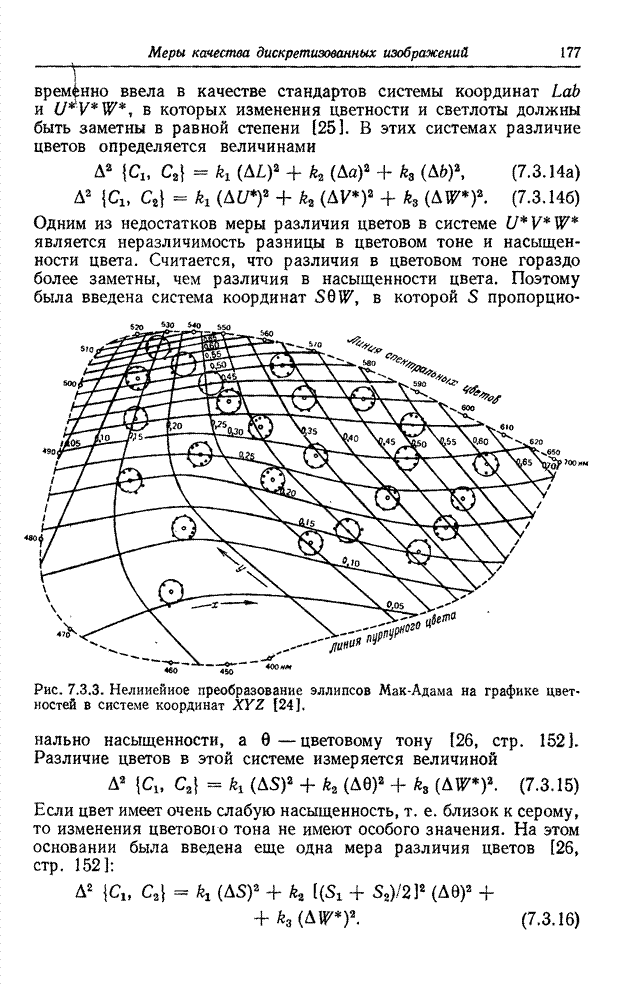
становятся более близкими по размерам и заметно округляются. Фарнсуорт [24]
нашел нелинейное преобразование, в результате которого эллипсы Мак-Адама (в
пределах точности измерений Мак-Адама) превращаются в окружности (рис. 7.3.3).
К. сожалению, это преобразование выражается в виде сложной функции координат
цветности
(рис. 7.3.2, б), то эллипсы
становятся более близкими по размерам и заметно округляются. Фарнсуорт [24]
нашел нелинейное преобразование, в результате которого эллипсы Мак-Адама (в
пределах точности измерений Мак-Адама) превращаются в окружности (рис. 7.3.3).
К. сожалению, это преобразование выражается в виде сложной функции координат
цветности ![]() и
и
![]() и
требует выполнения громоздких вычислений.
и
требует выполнения громоздких вычислений.
В
системе координат ![]() расстояние
между цветами равняется
расстояние
между цветами равняется
![]() , (7.3.13)
, (7.3.13)
где
![]() —
постоянные.
—
постоянные.
Человеческий
глаз более чувствителен к изменению оттенков темных цветов. Стремясь
использовать это обстоятельство, МКО временно ввела в качестве стандартов
системы координат ![]() и
и ![]() , в которых
изменения цветности и светлоты должны быть заметны в равной степени [25]. В
этих системах различие цветов определяется величинами
, в которых
изменения цветности и светлоты должны быть заметны в равной степени [25]. В
этих системах различие цветов определяется величинами
![]() , (7.3.14а)
, (7.3.14а)
![]() . (7.3.14б)
. (7.3.14б)

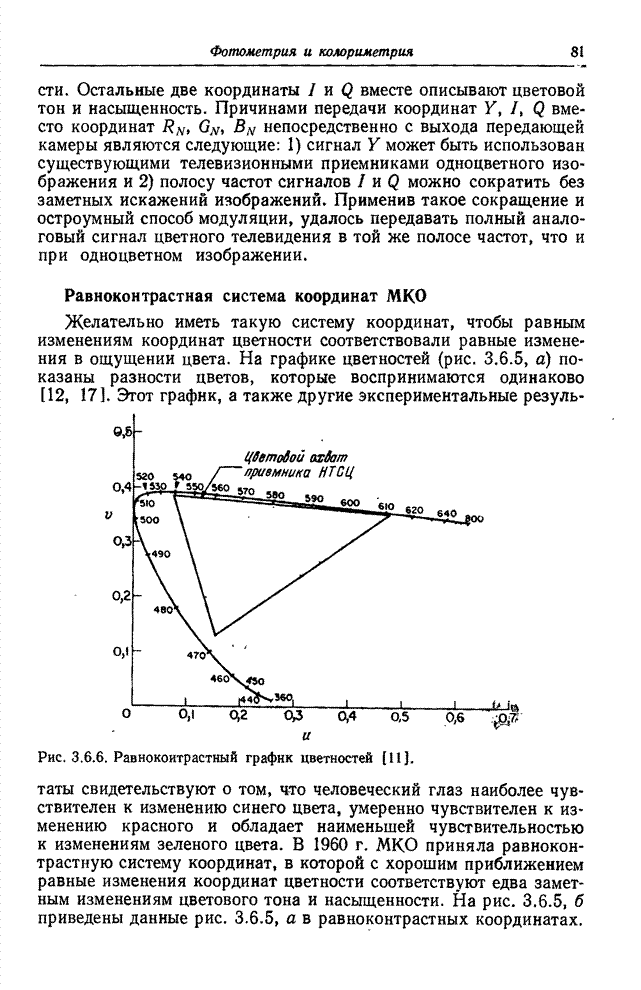
Рис. 7.3.2. Эллипсы Мак-Адама для пороговых различий
цветов в системах координат ![]() и
и ![]() [23]. Размеры эллипсов увеличены в 10
раз: а – график цветностей в координатах
[23]. Размеры эллипсов увеличены в 10
раз: а – график цветностей в координатах ![]() ; б – график цветностей в координатах
; б – график цветностей в координатах ![]() .
.
Одним
из недостатков меры различия цветов в системе ![]() является
неразличимость разницы в цветовом тоне и насыщенности цвета. Считается, что
различия в цветовом тоне гораздо более заметны, чем различия в насыщенности
цвета. Поэтому была введена система координат
является
неразличимость разницы в цветовом тоне и насыщенности цвета. Считается, что
различия в цветовом тоне гораздо более заметны, чем различия в насыщенности
цвета. Поэтому была введена система координат ![]() , в которой
, в которой ![]() пропорционально
насыщенности, а
пропорционально
насыщенности, а ![]() — цветовому
тону [26, стр. 152].
— цветовому
тону [26, стр. 152].

Рис. 7.3.3. Нелинейное преобразование эллипсов
Мак-Адама на графике цветностей в системе координат ![]() [24].
[24].
Различие цветов в этой системе измеряется величиной
![]() . (7.3.15)
. (7.3.15)
Если цвет имеет очень слабую насыщенность, т. е. близок к серому, то изменения цветовою тона не имеют особого значения. На этом основании была введена еще одна мера различия цветов [26, стр. 152]:
![]() . (7.3.16)
. (7.3.16)
Все приведенные выше формулы являются результатами попыток создать субъективно-однородную меру цветовых различий. Экспериментов, которые позволили бы определить ценность каждой из них, проведено мало, так что вопрос о выборе подходящей меры все еще остается открытым.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к переводу
- Предисловие
- БЛАГОДАРНОСТИ
- ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
- Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.2. ДВУМЕРНЫЕ СИСТЕМЫ
- 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
- 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
- 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
- ЛИТЕРАТУРА
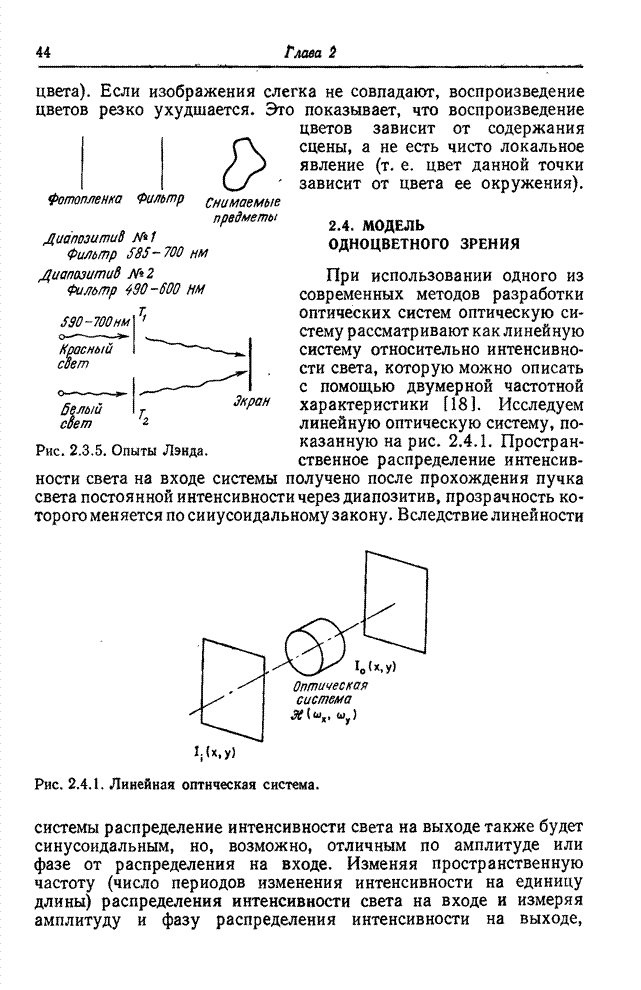
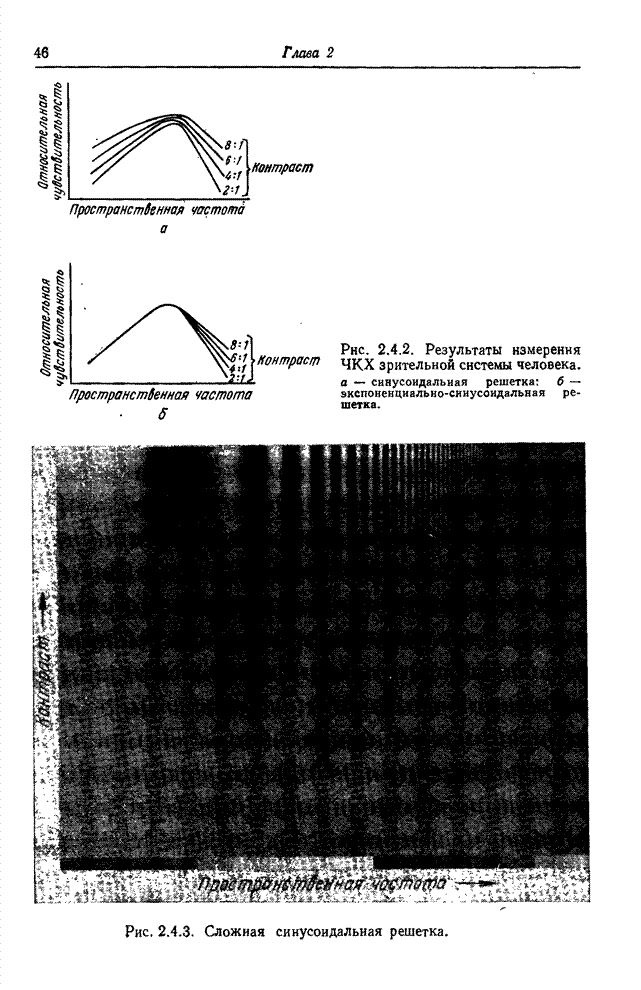
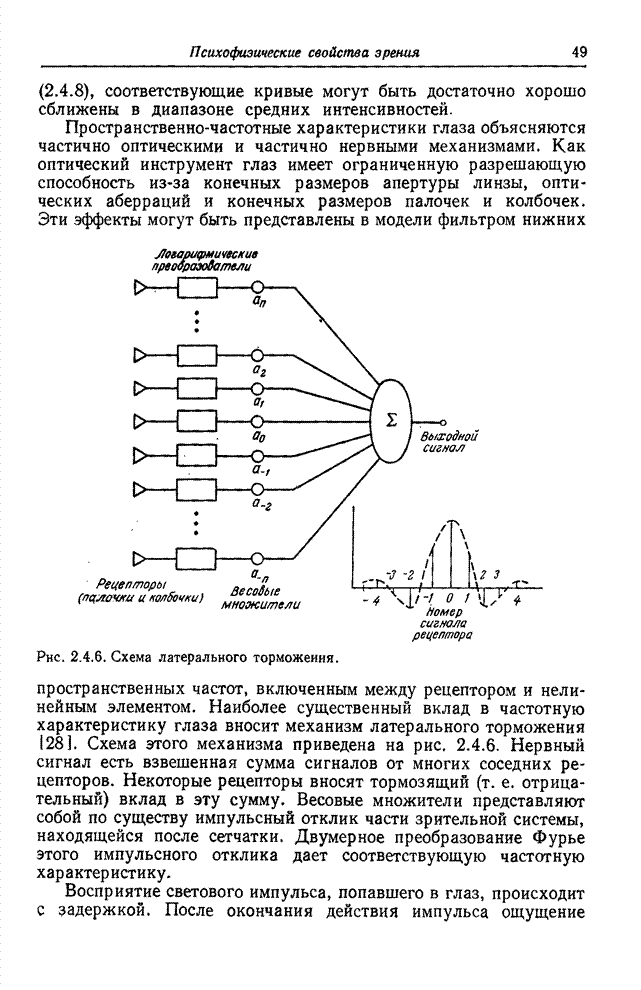
- Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
- 2.1. ВОСПРИЯТИЕ СВЕТА
- 2.2. ГЛАЗ
- 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
- 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ
- 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- ЛИТЕРАТУРА
- Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
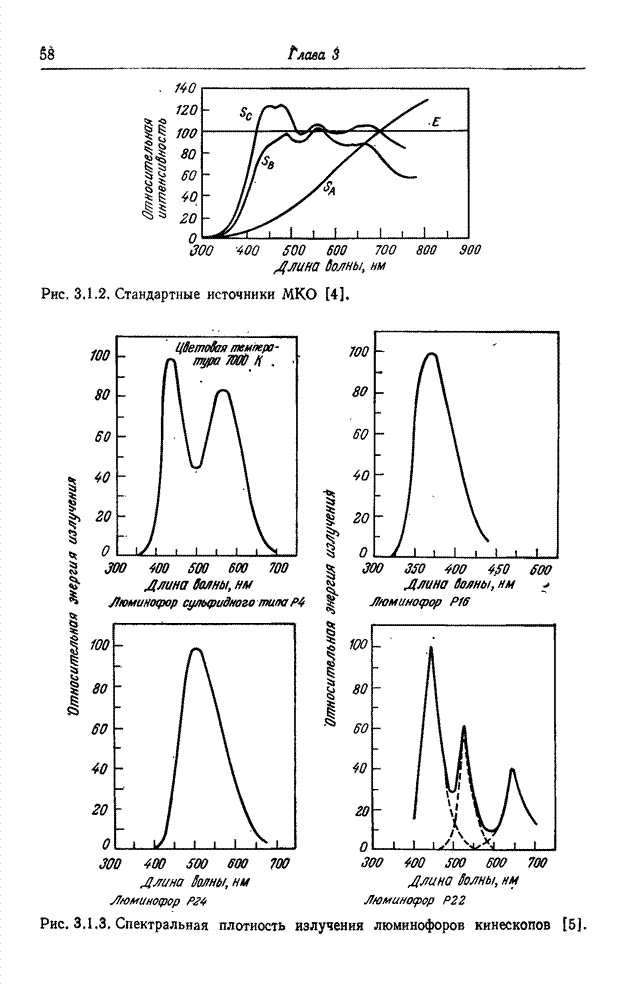
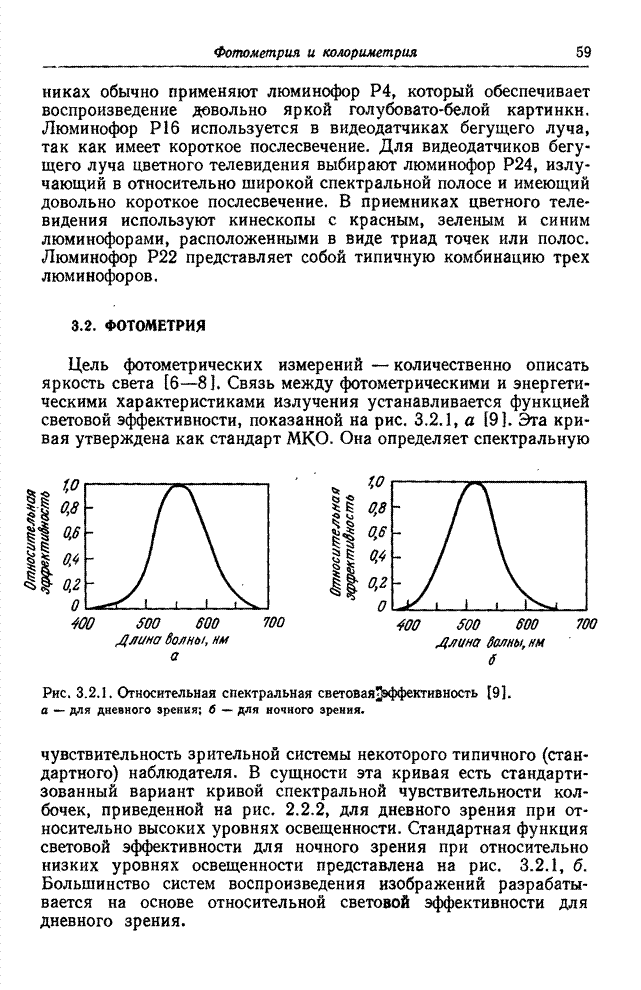
- 3.1. ИСТОЧНИКИ СВЕТА
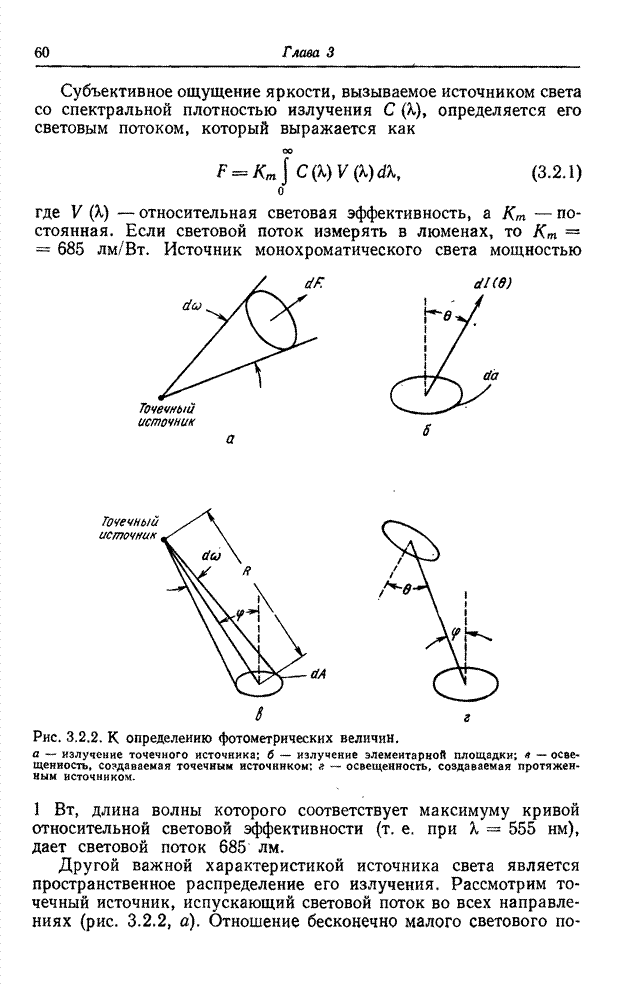
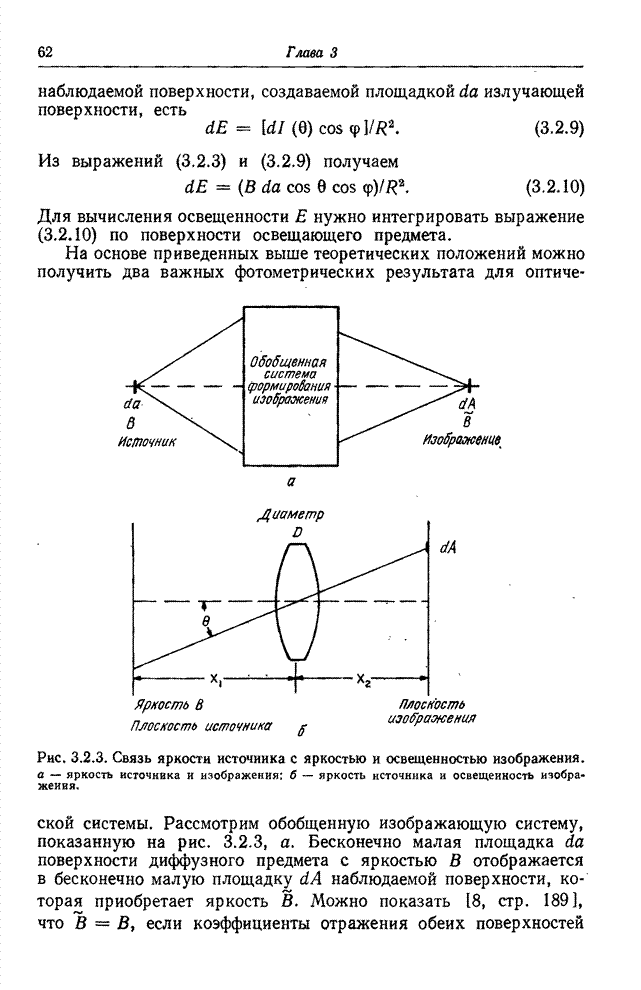
- 3.2. ФОТОМЕТРИЯ
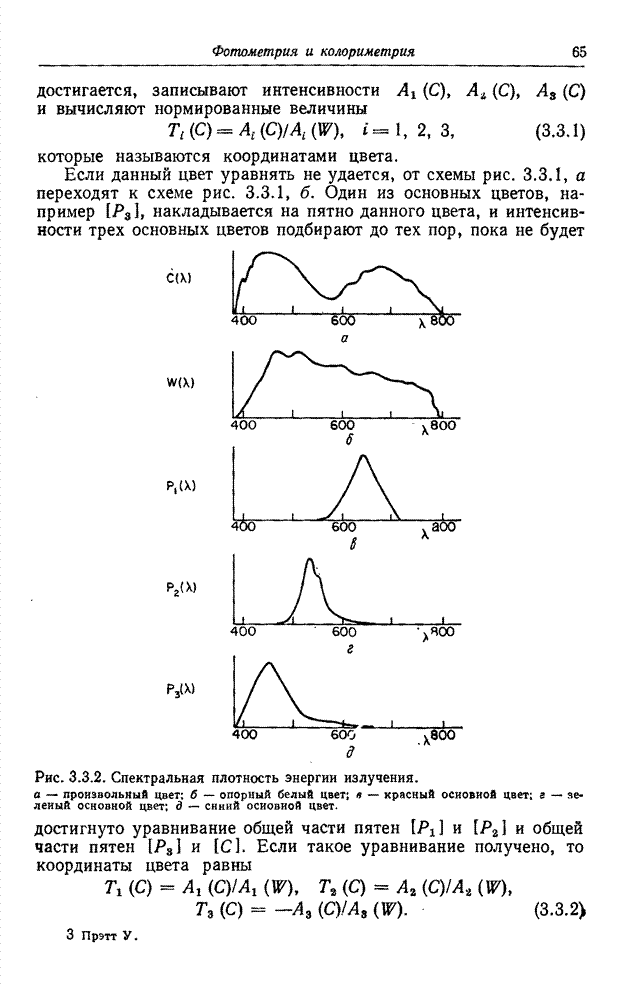
- 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14]
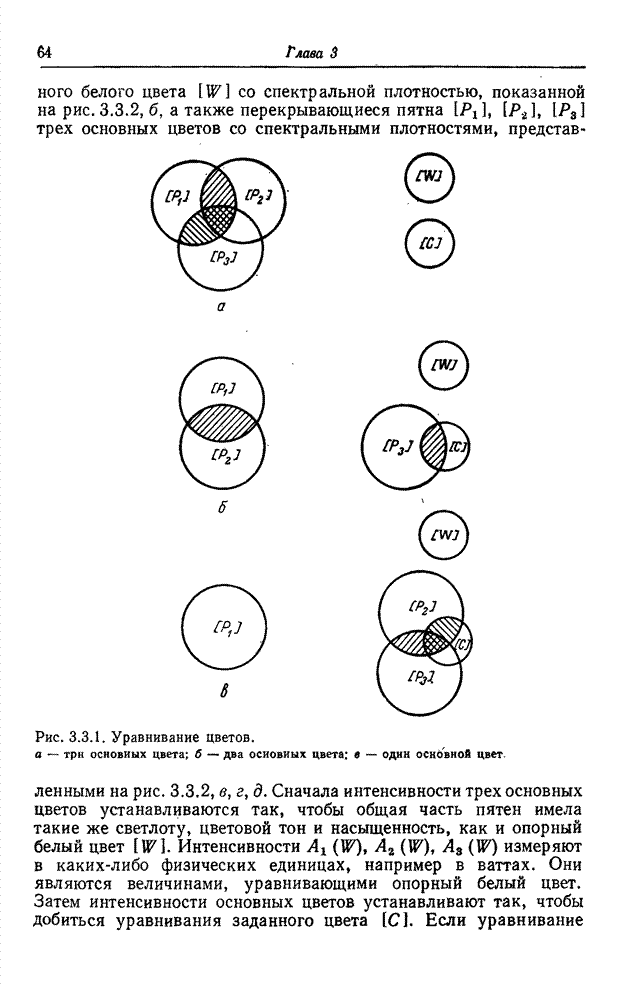
- 3.3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
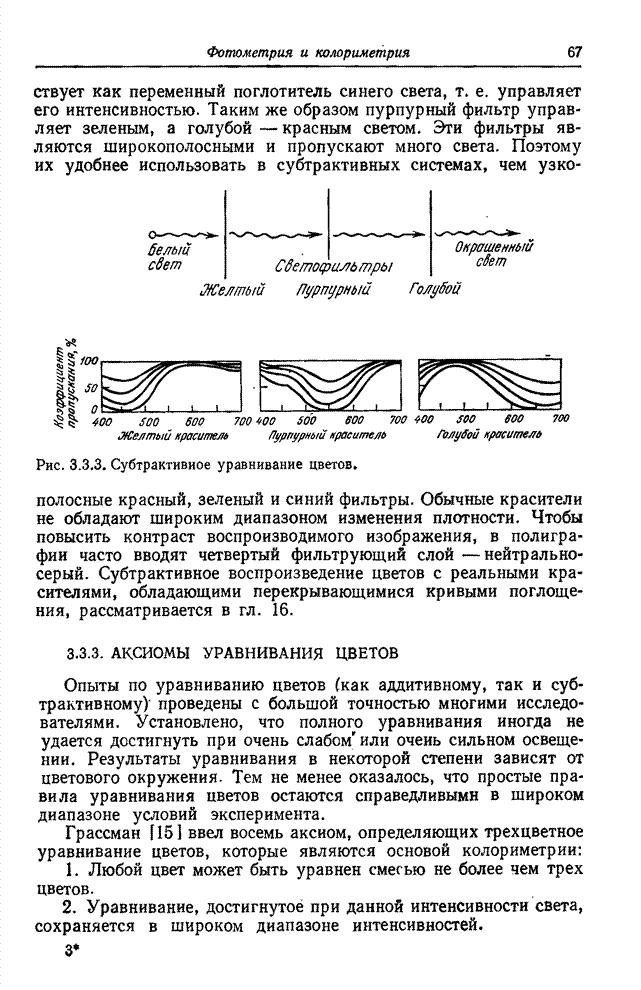
- 3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ
- 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
- 3.4. КОЛОРИМЕТРИЯ
- 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
- 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
- 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
- 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
- 3.7. ЦВЕТОВОЕ ТЕЛО
- 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
- 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
- Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ
- 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
- 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
- 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
- 4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
- 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- 4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
- 4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ
- ЛИТЕРАТУРА
- Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
- 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
- 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
- 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10]
- 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
- 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
- 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
- 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ
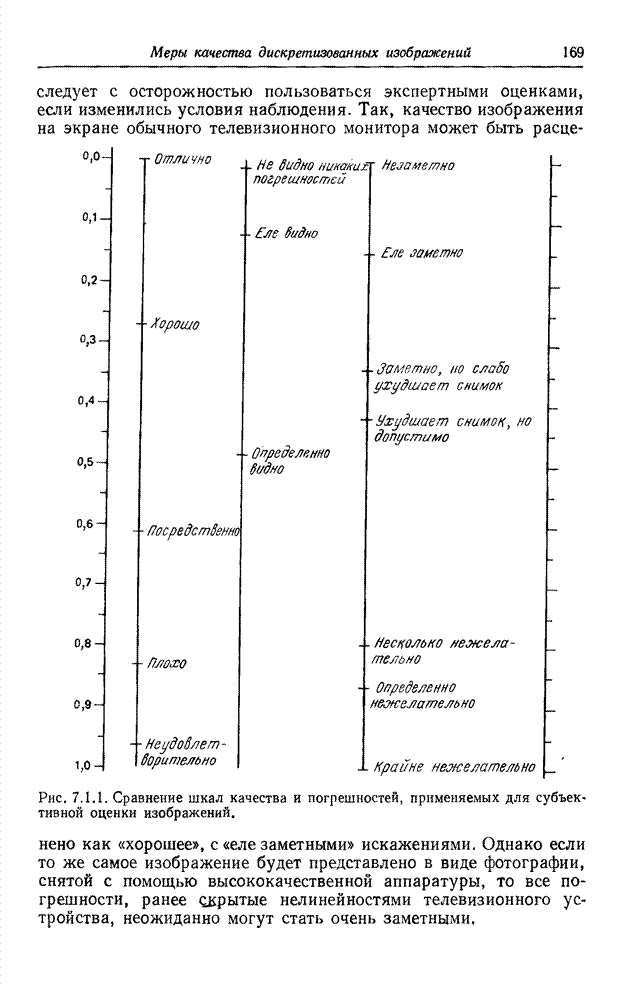
- 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
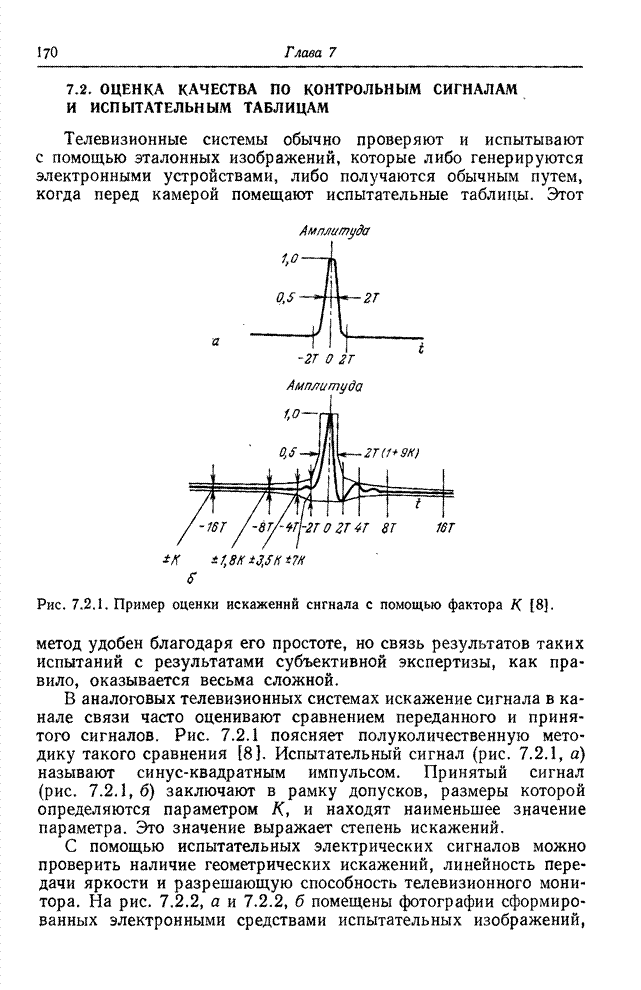
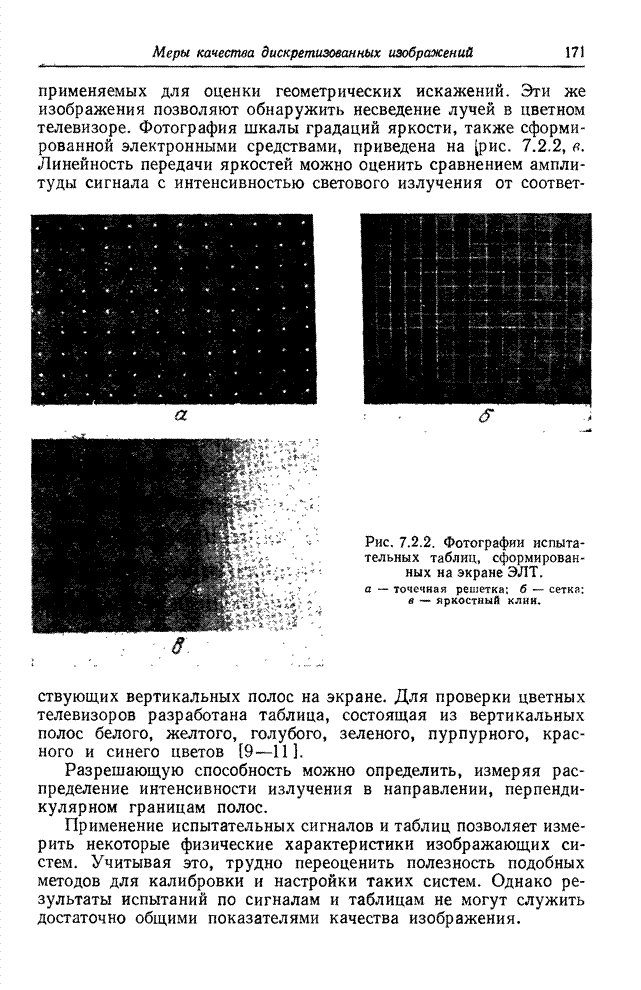
- 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
- 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
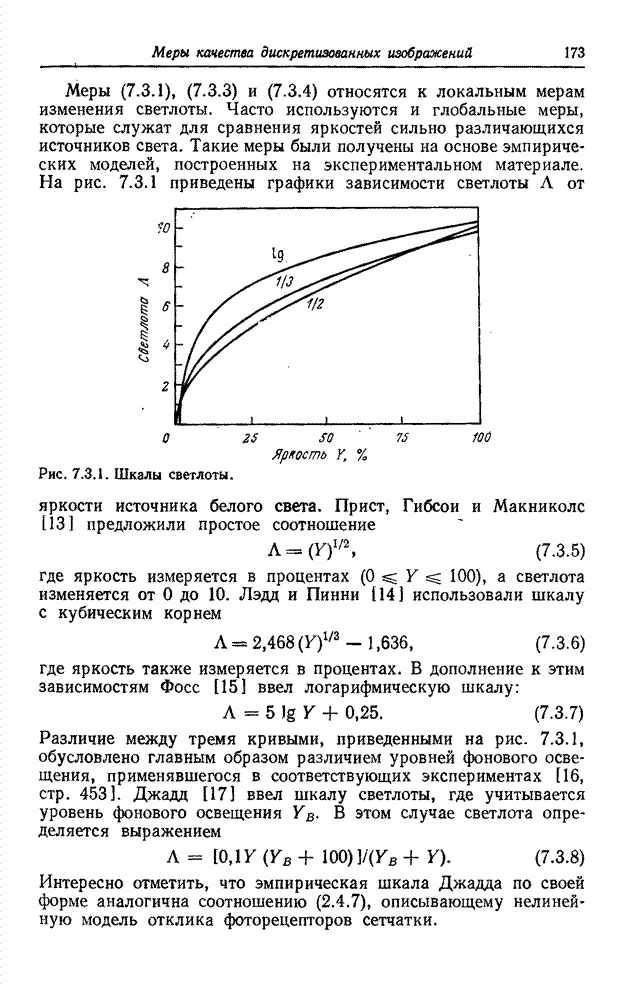
- 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
- 7.3.2. МЕТРИКИ ЦВЕТА
- 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
- 7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
- 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ
- 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
- Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
- 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
- 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
- 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- ЛИТЕРАТУРА
- Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
- 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
- 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
- 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
- ЛИТЕРАТУРА
- Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
- 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
- 10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
- 10.6. ПРЕОБРАЗОВАНИЕ ХААРА
- 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
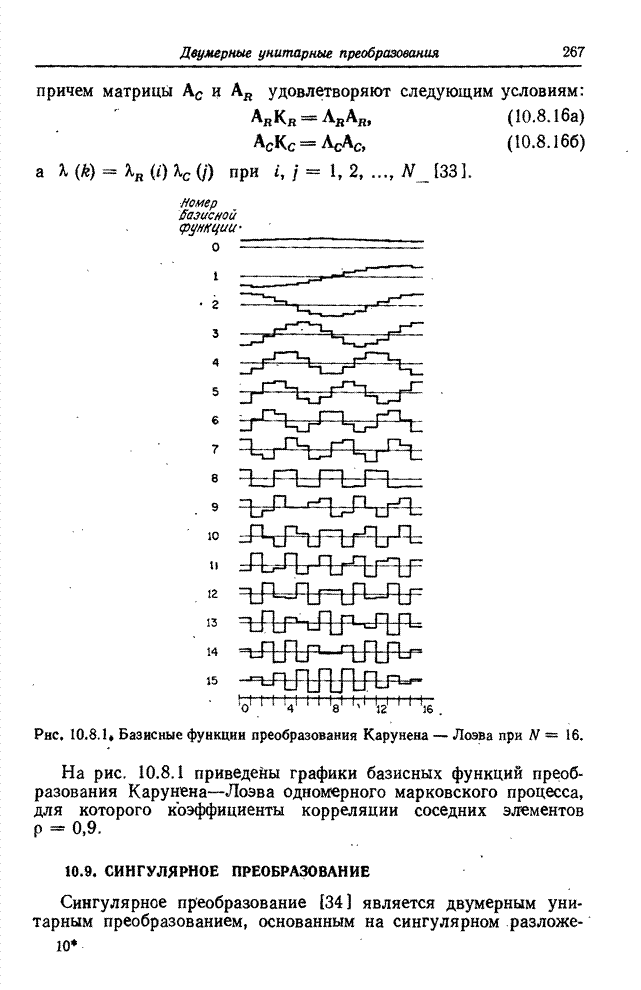
- 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА
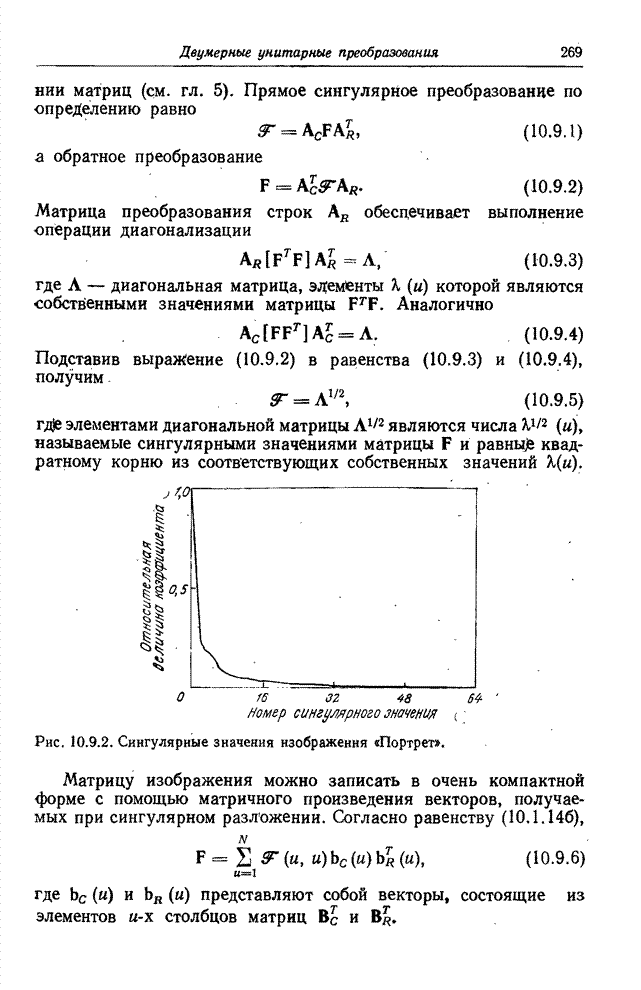
- 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
- 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ
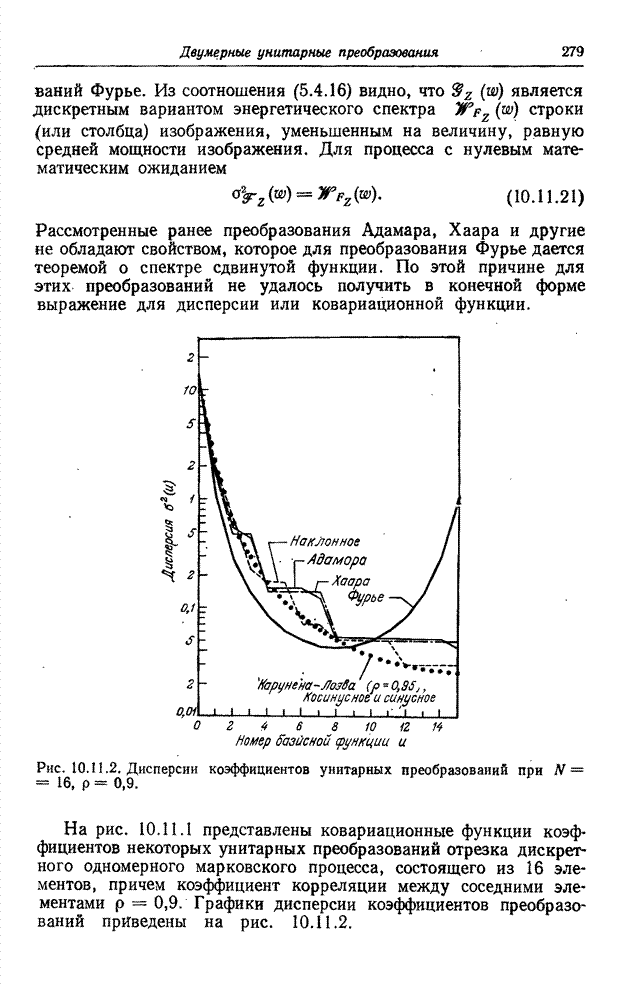
- 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
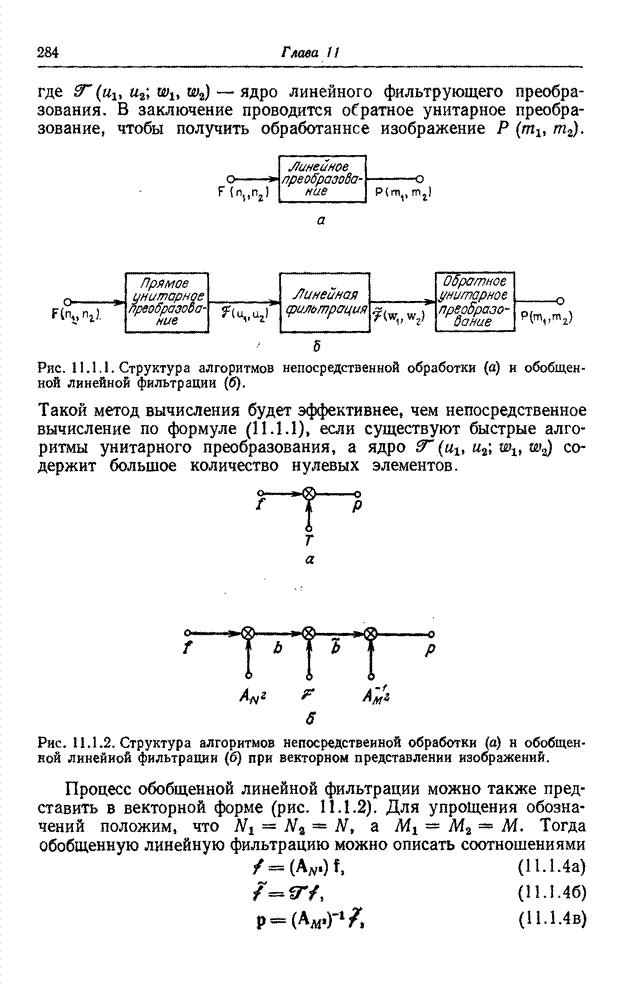
- 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
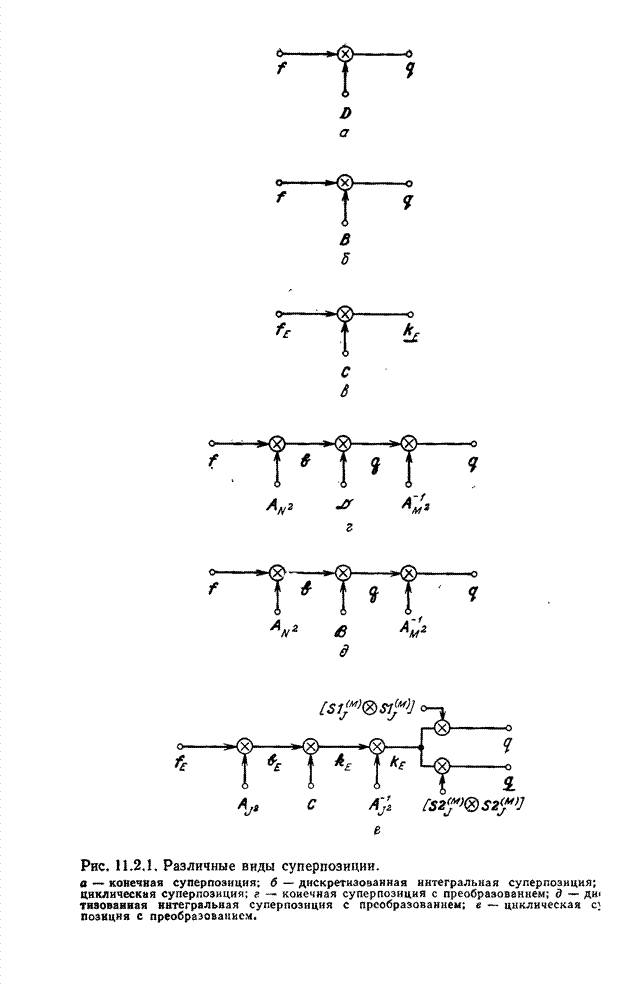
- 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
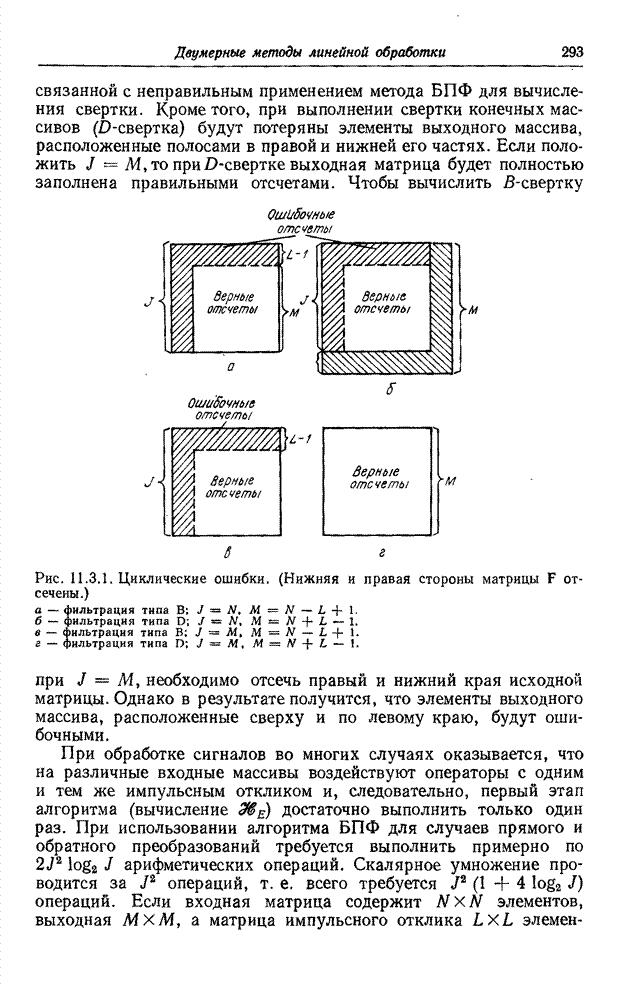
- 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
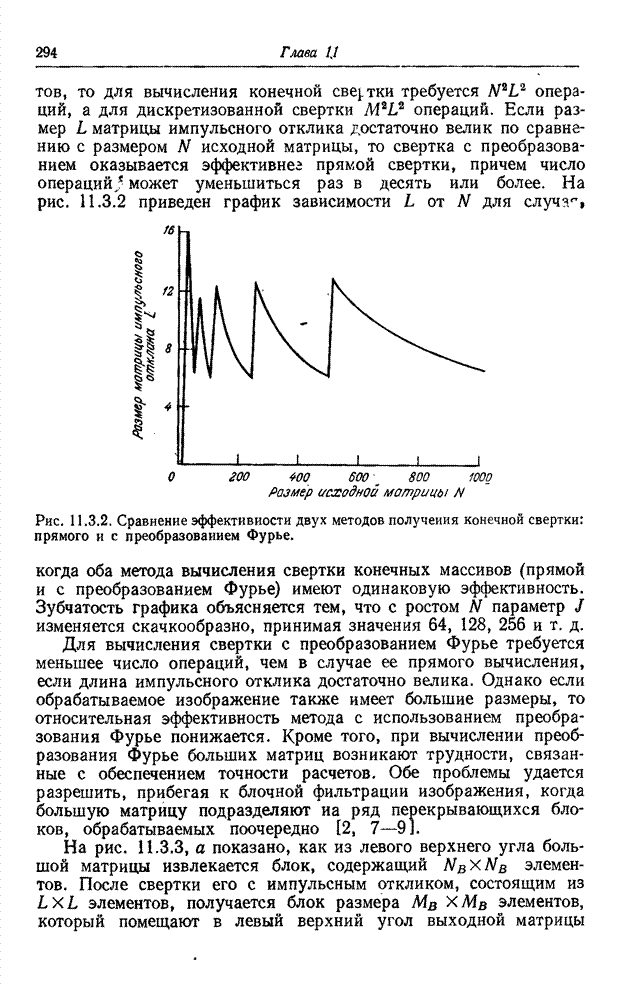
- 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
- 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
- ЛИТЕРАТУРА