| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5. Векторное произведение двух векторов.
Векторным произведением  двух векторов называется вектор
двух векторов называется вектор  (рис. 1.6), направленный перпендикулярно плоскости, в которой, лежат векторы
(рис. 1.6), направленный перпендикулярно плоскости, в которой, лежат векторы  в ту сторону, откуда поворот от первого сомножителя ко второму на меньший угол виден против хода часовой стрелки, и равный по модулю площади параллелограмма, построенного на этих векторах:
в ту сторону, откуда поворот от первого сомножителя ко второму на меньший угол виден против хода часовой стрелки, и равный по модулю площади параллелограмма, построенного на этих векторах:

Если векторы  параллельны, то
параллельны, то  Для векторов ортогонального трехмерного базиса
Для векторов ортогонального трехмерного базиса  в соответствии с определением векторного произведения справедливы соотношения (рис. 1.7)
в соответствии с определением векторного произведения справедливы соотношения (рис. 1.7)

Вектор с можно представить в виде определителя:

Векторное произведение можно записать и в виде

где  символы Леви-Чивита, которые удовлетворяют условиям: 1)
символы Леви-Чивита, которые удовлетворяют условиям: 1)  если в числе индексов
если в числе индексов  имеется хотя бы два одинаковых значения; 2)
имеется хотя бы два одинаковых значения; 2)  если индексы
если индексы  различны и являются циклической перестановкой чисел 1, 2, 3;
различны и являются циклической перестановкой чисел 1, 2, 3;  если индексы различны и не соответствуют циклической перестановке чисел 1, 2, 3.
если индексы различны и не соответствуют циклической перестановке чисел 1, 2, 3.

Рис. 1.6

Рис. 1.7

Рис. 1.8
Так как вектор с можно представить через проекции в виде

то, развернув определитель, получим выражения для проекций вектора с:

В качестве примера векторного произведения рассмотрим момент силы. Если сила  приложена к материальной точке
приложена к материальной точке  (рис. 1.8), то момент
(рис. 1.8), то момент  силы
силы  относительно точки О
относительно точки О

Как следует из рис.  равен удвоенной площади треугольника
равен удвоенной площади треугольника 

Компоненты вектора с можно записать, воспользовавшись символами Леви-Чивита в виде

В прикладных задачах часто один из векторов в векторном произведении неизвестен, например вектор  Для преобразований векторное произведение удобнее представить в виде
Для преобразований векторное произведение удобнее представить в виде

где А — кососимметричная матрица вида

Матрица А является вырожденной матрицей, так как ее определитель равен нулю, что необходимо иметь в виду при преобразованиях.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
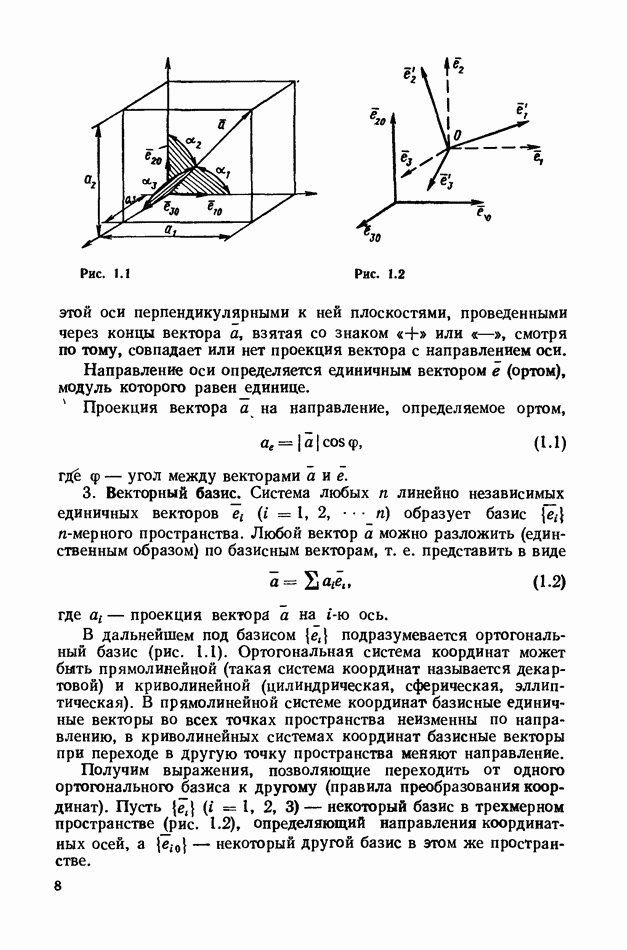
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
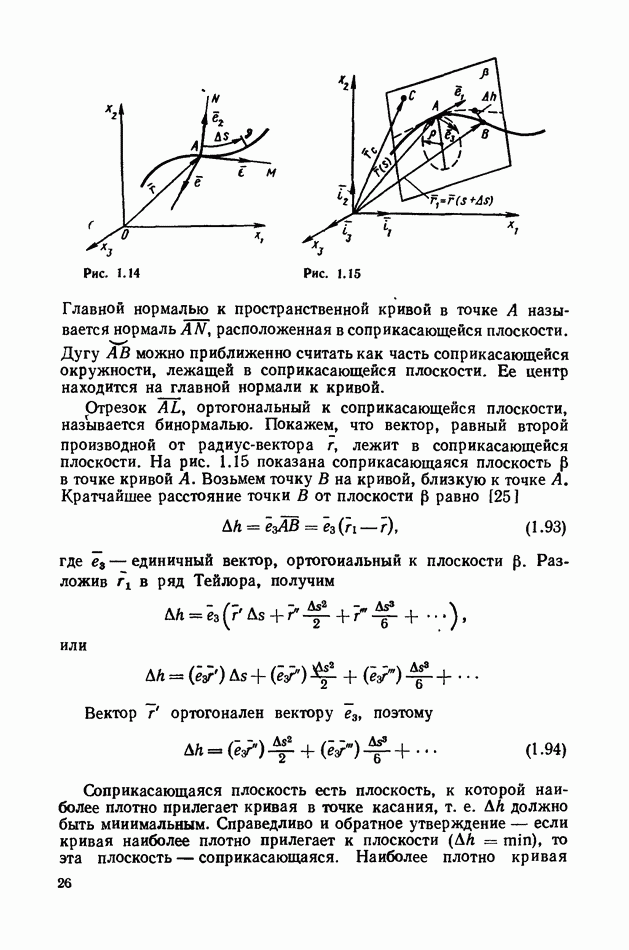
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
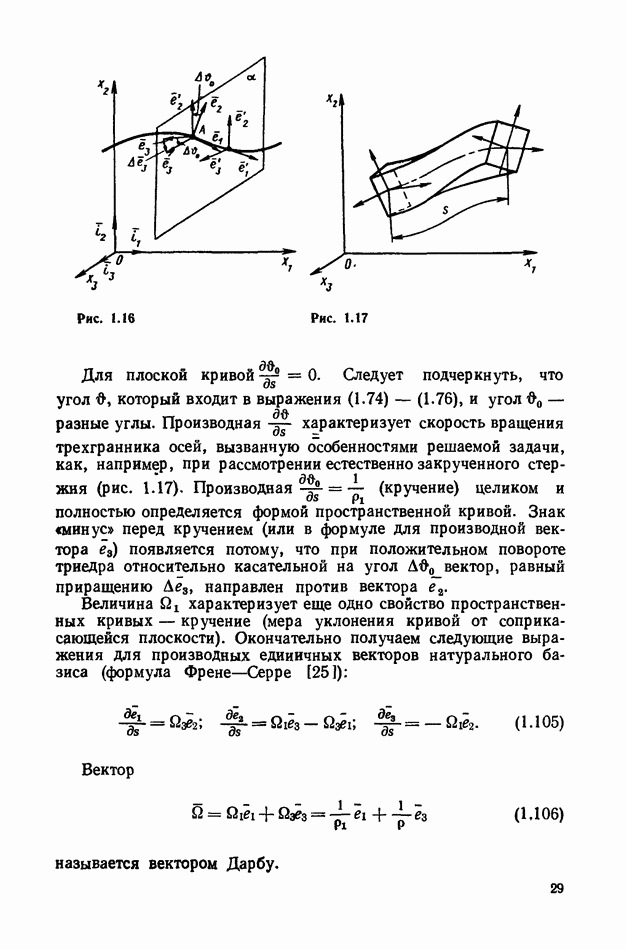
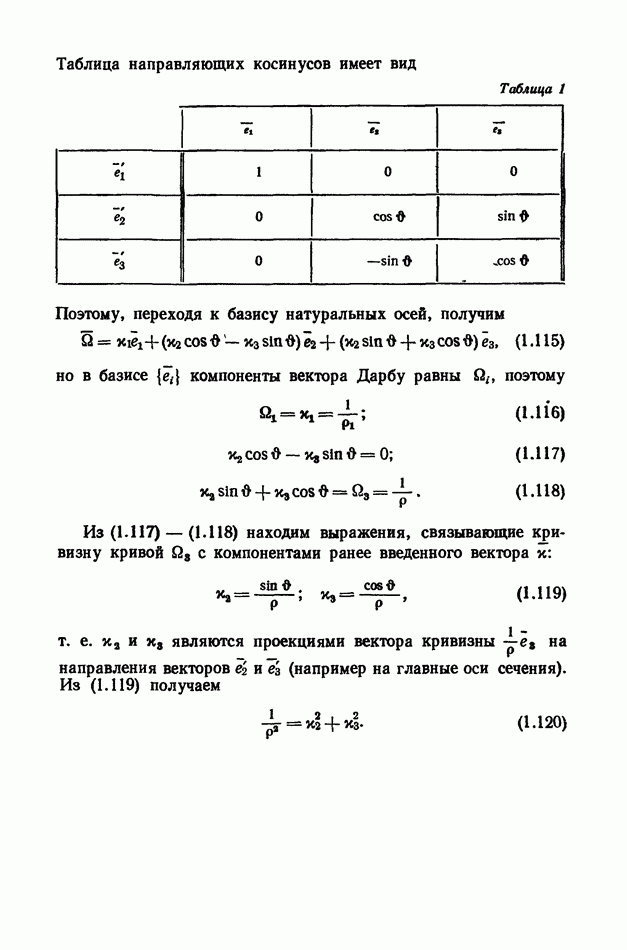
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
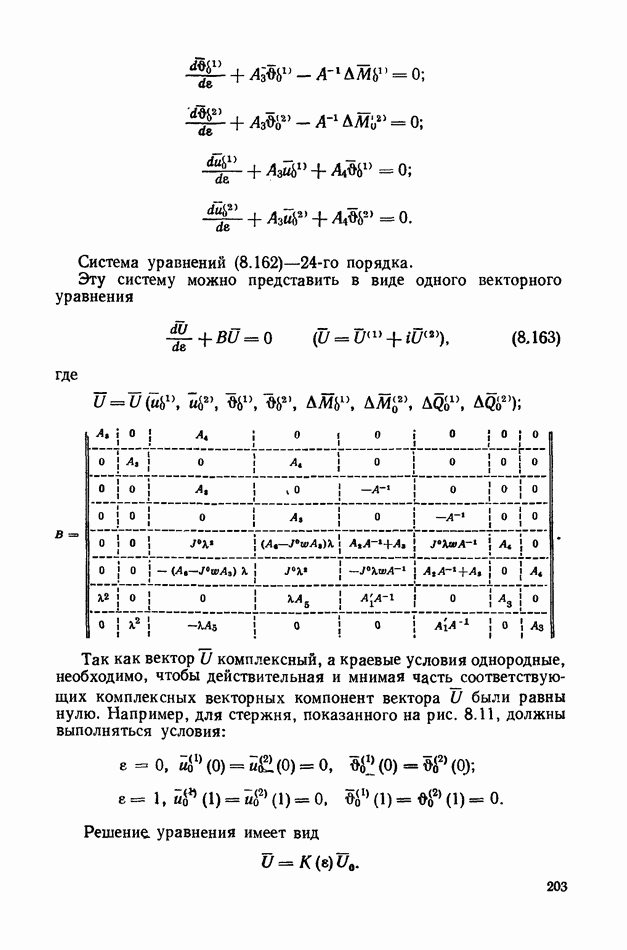
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
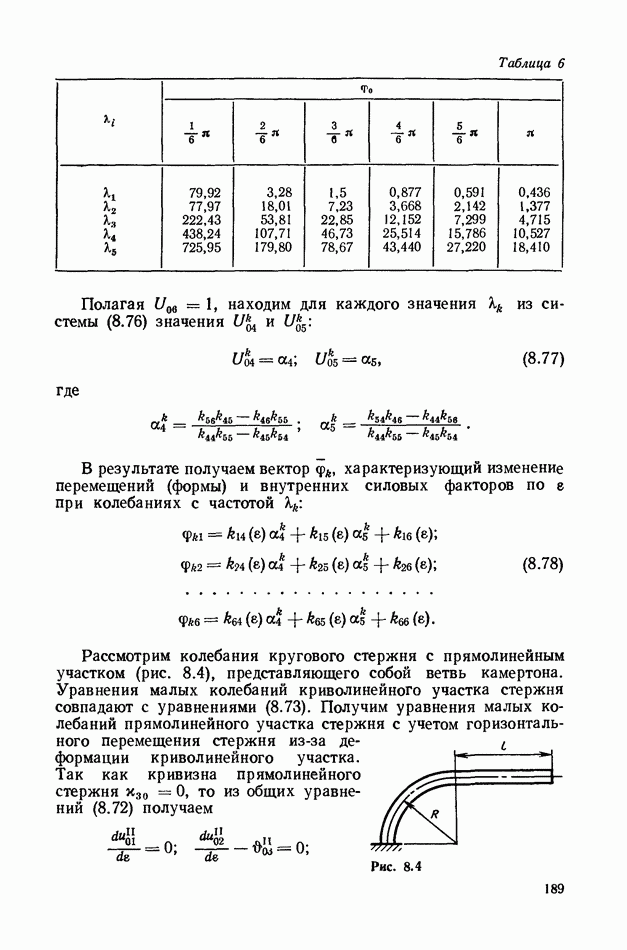
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
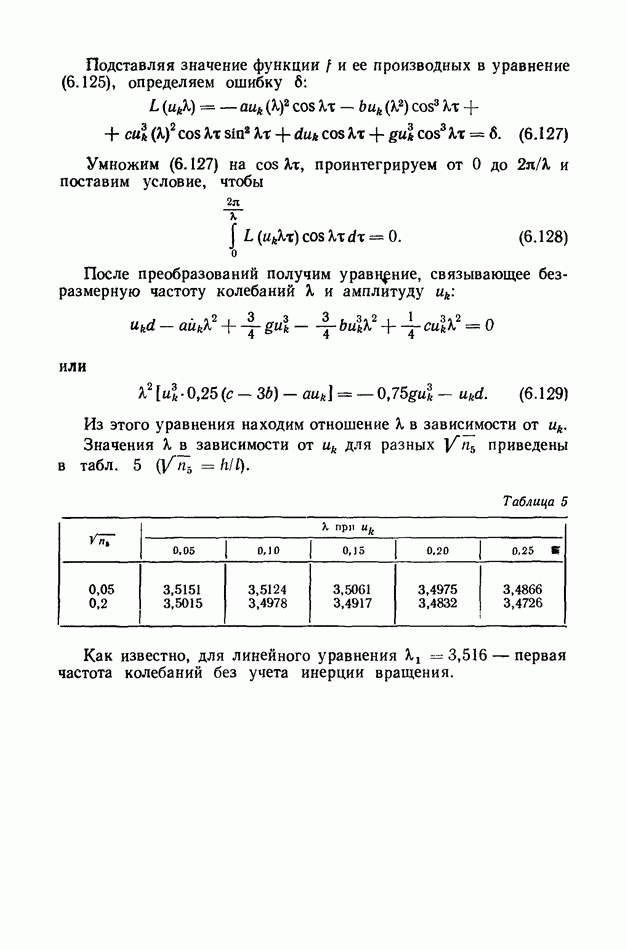
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.