| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
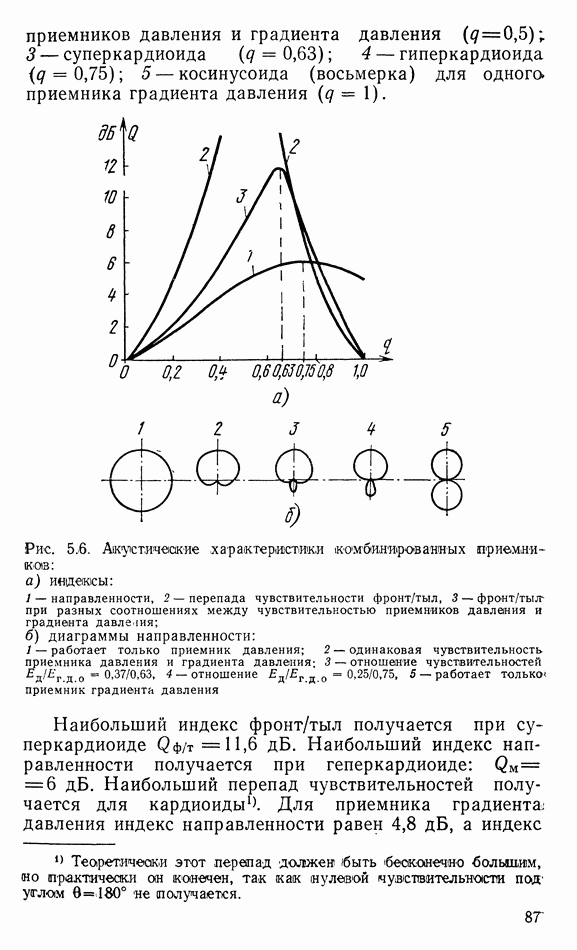
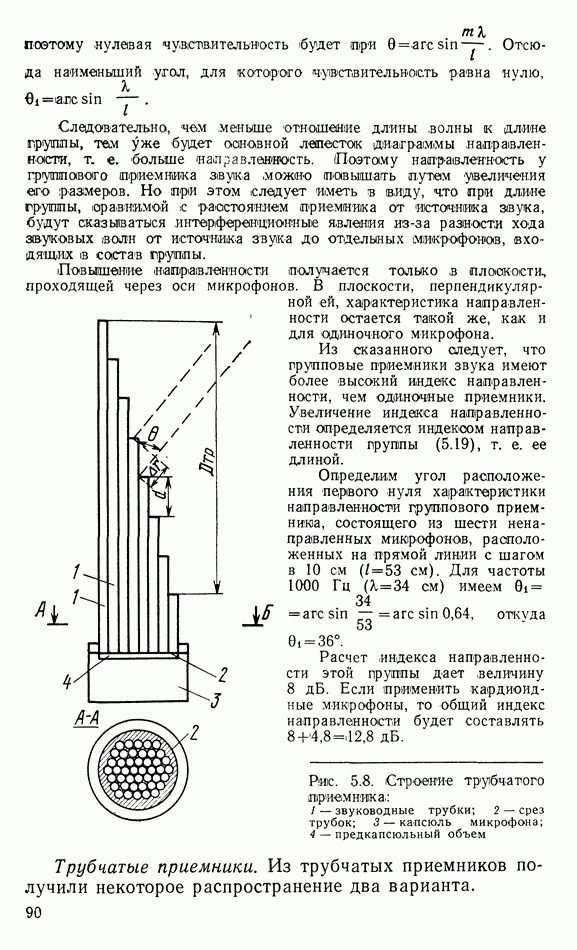
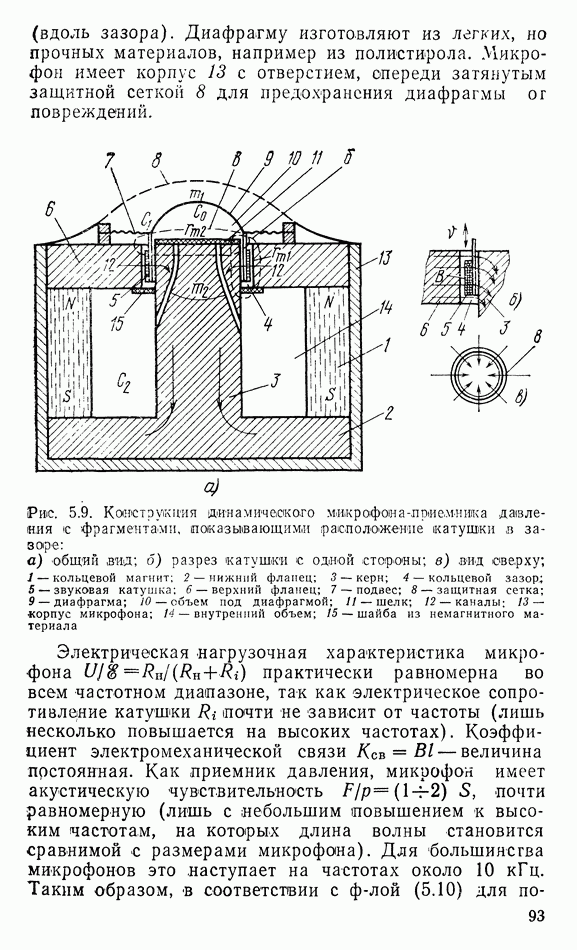
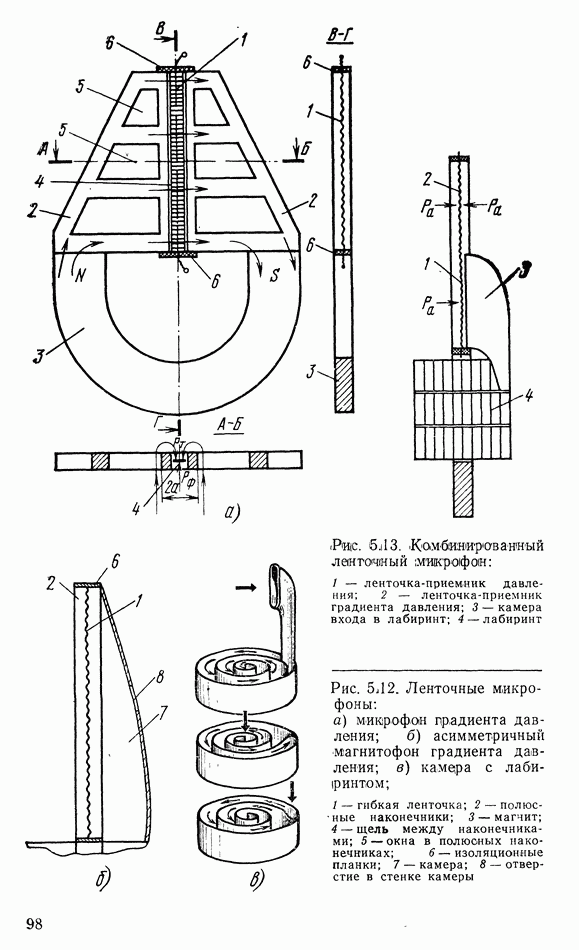
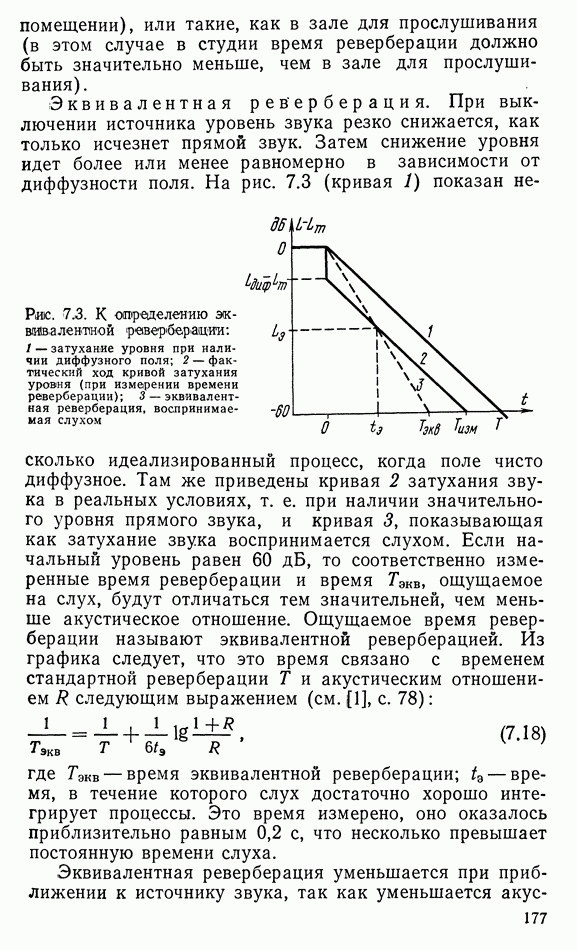
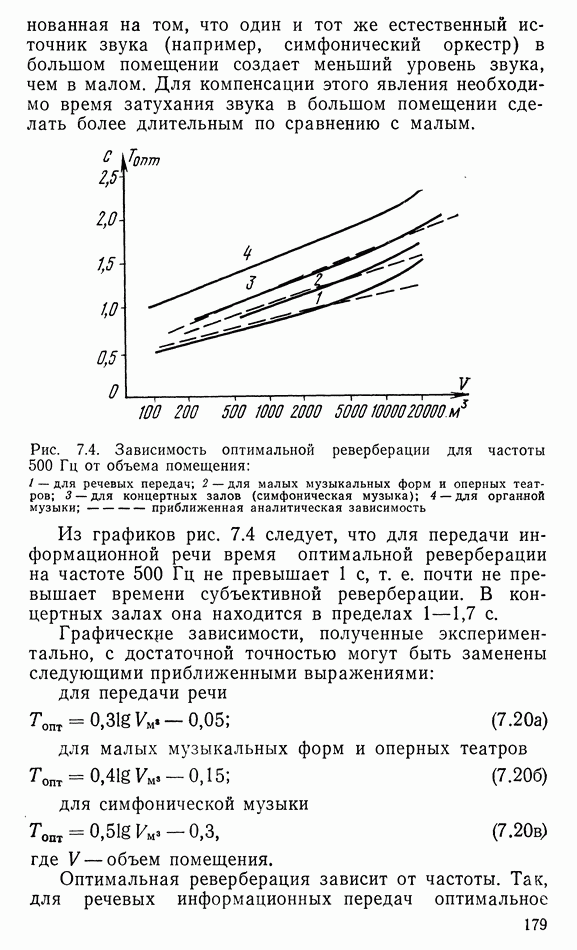
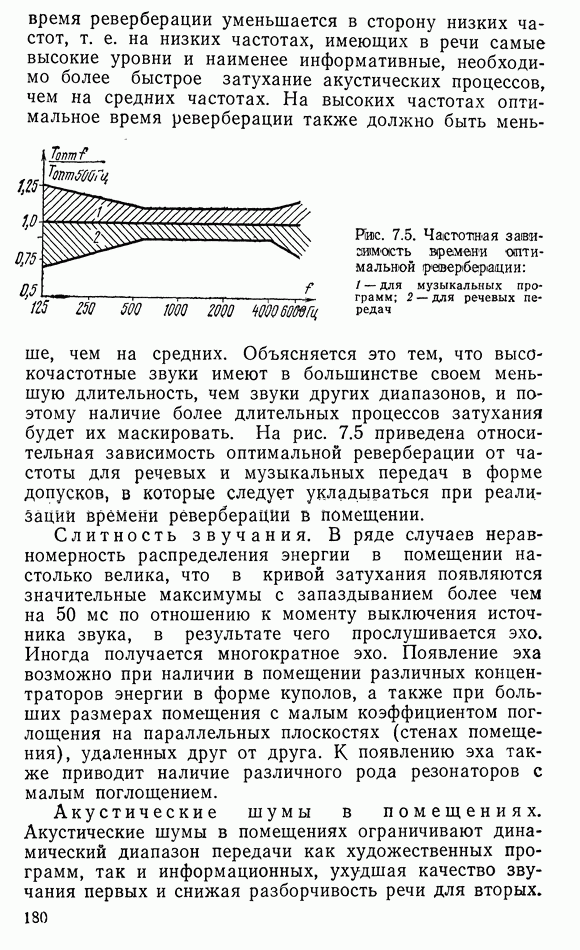
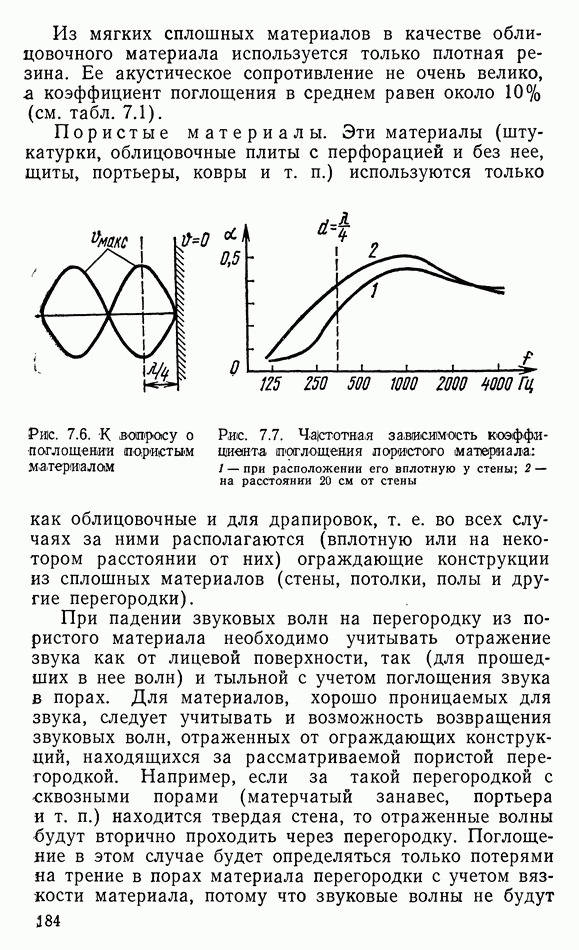
6.2. ДИФФУЗОРНЫЕ ИЗЛУЧАТЕЛИ
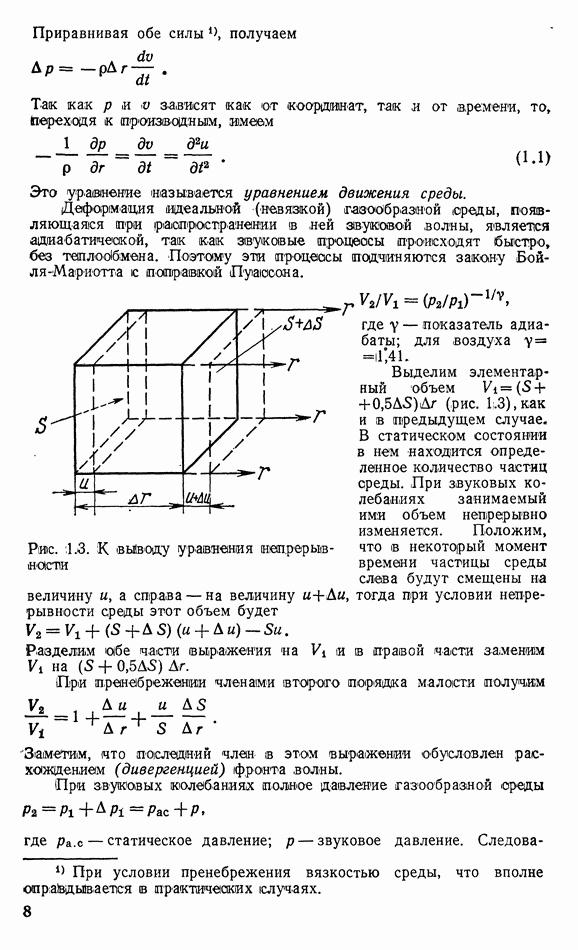
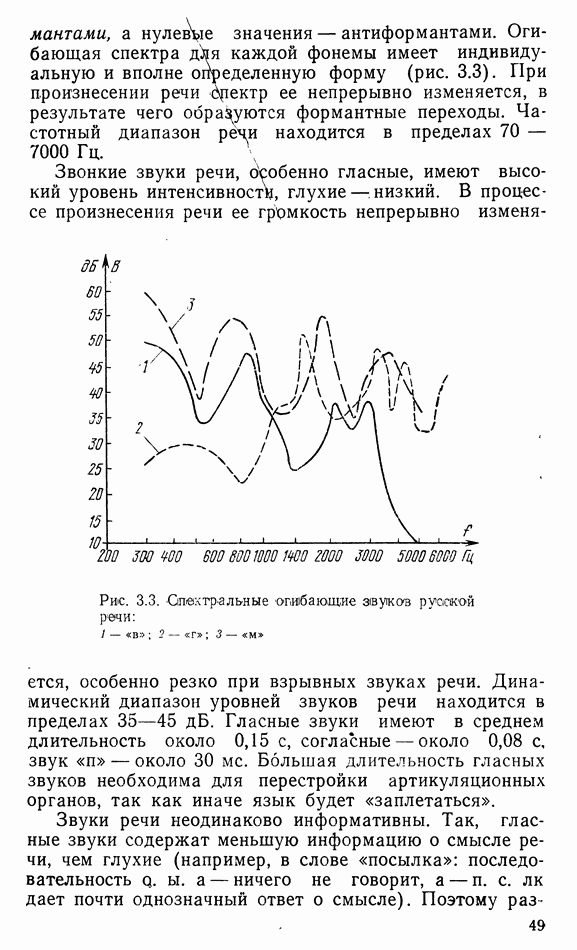
В диффузорных громкоговорителях диафрагма, входящая в его механическую подвижную систему, выполняет как функцию преобразования механических колебаний в акустические, так и функцию излучения звука в окружающую среду. Поэтому эту диафрагму называют диффузором, т. е. рассеивателем, а громкоговоритель ютносят к громкоговорителям с непосредственным излучением. В общем случае диффузор имеет сложную форму, но эксперименты показывают, что все основные выводы об излучении звуковькх волн с помощью диффузора можно получить с достаточной точностью при его замене плоской диафрагмой, колеблющейся как поршень. Это обеспечивается соответствующим креплением диффузора к корпусу громкоговорителя: во-первых, гибким и, во-вторых, не допускающим иных колебаний, кроме осевого.
Процесс излучения звуковых волн довольно прост: при своих колебаниях диафрагма приводит в движение частицы прилегающей к ней среды, создавая попеременно сжатие и разрежение ее. Колебания этих частиц передаются соседним слоям среды и т. д., создаются волны сжатия и разрежения, которые движутся со скоростью звука вдаль. Вследствие принципа неразрывности газообразной (и жидкой) среды скорость колебаний диафрагмы  и прилегающих к ней частиц среды
и прилегающих к ней частиц среды  должна быть одинаковой, т. е.
должна быть одинаковой, т. е.  Иначе пришлось бы допустить появление вакуума около диафрагмы или проникновение частиц среды в твердую диафрагму. При колебаниях диафрагмы среда оказывает сопротивление этим колебаниям. Ясно, что в безвоздушном пространстве диафрагму легче колебать, чем в воздухе, а в воздухе легче, чем в воде. Это сопротивление называют
Иначе пришлось бы допустить появление вакуума около диафрагмы или проникновение частиц среды в твердую диафрагму. При колебаниях диафрагмы среда оказывает сопротивление этим колебаниям. Ясно, что в безвоздушном пространстве диафрагму легче колебать, чем в воздухе, а в воздухе легче, чем в воде. Это сопротивление называют
сопротивлением излучения  Сопротивление излучения добавляется к механическому сопротивлению диафрагмы
Сопротивление излучения добавляется к механическому сопротивлению диафрагмы  , т. е. имеем
, т. е. имеем

Сопротивление излучения по своей сути является акустическим сопротивлением звуковой волны в месте соприкосновения среды с излучающей поверхностью, т. е.

где  площадь излучателя;
площадь излучателя;  среднее удельное акустическое сопротивление среды около излучателя. Полная излучаемая мощность.
среднее удельное акустическое сопротивление среды около излучателя. Полная излучаемая мощность.

В общем случае сопротивление излучения комплексное. Физически это означает, что излучаемая мощность имеет активную составляющую, определяющую поток энергии, уходящей в бесконечность, и реактивную, определяющую запас энергии, создаваемый в звуковом поле. Реактивная составляющая частично возвращается  излучатель обратно после окончания вынужденных колебаний диафрагмы.
излучатель обратно после окончания вынужденных колебаний диафрагмы.
Определим сопротивление излучения для одного из основных излучателей — излучателя нулевого порядка. Это пульсирующий шар, излучающий сферическую волну. Исходя из этого для излучателя с радиусом  удельное сопротивление можно определить из (1.18). Поэтому при подстановке значений радиуса излучателя и величины его излучающей поверхности в (6.10) и (1.18) получим:
удельное сопротивление можно определить из (1.18). Поэтому при подстановке значений радиуса излучателя и величины его излучающей поверхности в (6.10) и (1.18) получим:

где  площадь излучателя;
площадь излучателя;  безразмерные коэффициенты сопротивления излучения.
безразмерные коэффициенты сопротивления излучения.
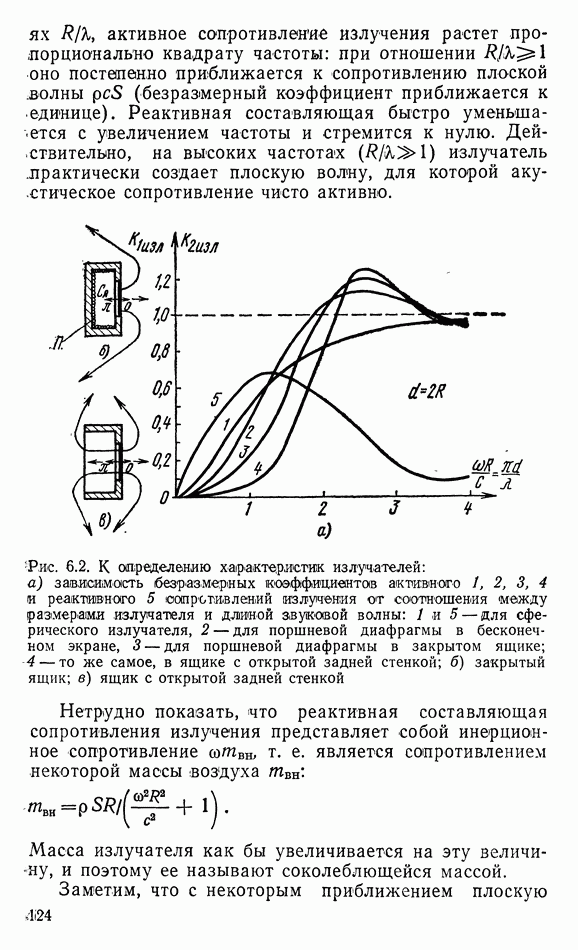
На рис. 6.2а (кривые  и 5) показаны зависимости безразмерных коэффициентов активного и реактивного сопротивлений от частоты, точнее, от соотношения длины волны и размеров излучателя. Как видим из этого графика, на низких частотах, т. е. при малых
и 5) показаны зависимости безразмерных коэффициентов активного и реактивного сопротивлений от частоты, точнее, от соотношения длины волны и размеров излучателя. Как видим из этого графика, на низких частотах, т. е. при малых
отношениях  активное сопротивление излучения растет пропорционально квадрату частоты: при отношении
активное сопротивление излучения растет пропорционально квадрату частоты: при отношении  оно постепенно приближается к сопротивлению плоской волны
оно постепенно приближается к сопротивлению плоской волны  (безразмерный коэффициент приближается к единице). Реактивная составляющая быстро уменьшается с увеличением частоты и стремится к нулю. Действительно, на высоких частотах
(безразмерный коэффициент приближается к единице). Реактивная составляющая быстро уменьшается с увеличением частоты и стремится к нулю. Действительно, на высоких частотах  излучатель практически создает плоскую волну, для которой акустическое сопротивление чисто активно.
излучатель практически создает плоскую волну, для которой акустическое сопротивление чисто активно.

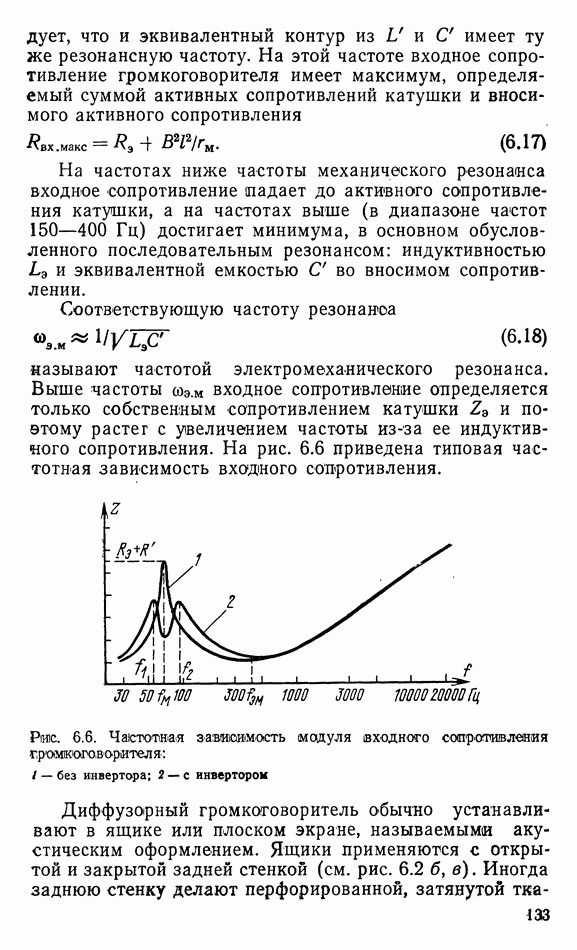
Рис. 6.2. К определению характеристик излучателей: а) зависимость безразмерных коэффициентов активного 1, 2, 3, 4 и реактивного 5 сопротивлений излучения от соотношения «между размерами излучателя и длиной авуковой волны: 1 и 5 — для сферического излучателя, 2 — для поршневой диафрагмы в бесконечном экране, 3 — для поршневой диафрагмы в закрытом ящике; 4 — то же самое, в ящике с открытой задней стенкой; б) закрытый ящик; в) ящик с открытой задней стенкой
Нетрудно показать, что реактивная составляющая сопротивления излучения представляет собой инерционное сопротивление отвн, т. е. является сопротивлением некоторой массы воздуха 

Масса излучателя как бы увеличивается на эту величину, и поэтому ее называют соколеблющейся массой.
Заметим, что с некоторым приближением плоскую
диафрагму, колеблющуюся как поршень в бесконечном акустическом экране, можно приближенно рассматривать как пульсирующий шар, излучающий сферическую волну. Если такую поршневую диафрагму возбуждать на частотах, длины волн которых значительно больше размеров диафрагмы, то излучаемые звуковые волны ничем не будут отличаться от сферических. При длинах волн меньших размеров диафрагмы закон излучения будет несколько сложнее, так как при этом звуковые волны, излучаемые различными участками диафрагмы, будут интерферировать между собой. В результате интерференции в одних точках поля возможно увеличение уровня, а в других — уменьшение по сравнению с уровнями, создаваемыми излучателями нулевого порядка. Причем и то, и другое будет зависеть от частоты колебаний. При длинах волн, значительно меньших размеров излучателя, последний создает плоскую волну.
Поэтому для плоского поршневого излучателя в бесконечном экране безразмерные коэффициенты имеют несколько иной вид (см. рис. 6.2а, кривая 2). Основное отличие в том, что переход от квадратичной зависимости к независимости от частоты совершается не плавно, а волнообразно, что объясняется интерференцией волн, излучаемых отдельными участками плоской диафрагмы.
Поршневая диафрагма, колеблющаяся в экране конечных размеров, также может рассматриваться как излучатель нулевого порядка, если излучаемые колебания будут иметь длину волны значительно меньше размеров экрана. При этом имеют место те же оговорки, что и для случая бесконечного экрана в отношении соизмеримости размеров диафрагмы и длины волны. Если же длина волны будет значительно больше размеров экрана, то имеют дело с излучателем первого порядка — диполем, так как звуковое поле будет образовываться разностным действием излучений лицевой (фронтальной) и
обратной (тыльной) сторон диафрагмы с учетом разности хода звуковьих волн вокруг экрана (рис. 6.2в), поэтому для излучателя без экрана зависимость этих коэффициентов от частоты будет на низких частотах иной, чем с экраном (см. рис. 6.2а, кривая 4). Вследствие дифракции волн, имеющих длину больше размеров диафрагмы, происходит взаимная компенсация излучений, так как тыльная сторона диафрагмы излучает волны в противофазе с фронтальным излучением (наблюдается эффект своего рода короткого замыкания). Поэтому активное сопротивление излучения близко к нулю и начинает увеличиваться только, когда длина волны начинает превосходить размеры излучателя. На высоких частотах, для которых длина волны значительно больше размеров излучателя, такой излучатель по сопротивлению излучения мало отличается от излучателя нулевого порядка.
Определим факторы, влияющие на акустическую характеристику  где
где  звуковое давление на расстоянии
звуковое давление на расстоянии  от рабочего центра по рабочей оси в свободном поле;
от рабочего центра по рабочей оси в свободном поле;  скорость колебаний диафрагмы излучателя.
скорость колебаний диафрагмы излучателя.
Из  следует, что акустическая мощность (поток энергии в звуковом поле)
следует, что акустическая мощность (поток энергии в звуковом поле)

так как по определению  если
если  В то же время излучаемая активная мощность
В то же время излучаемая активная мощность  Поскольку они должны быть равны для пассивной среды, то имеем
Поскольку они должны быть равны для пассивной среды, то имеем

откуда для акустической чувствительности получаем

где  безразмерный коэффициент сопротивления излучения;
безразмерный коэффициент сопротивления излучения;  площадь диафрагмы. Следовательно, акустическая чувствительность зависит от частоты через коэффициенты сопротивления излучения
площадь диафрагмы. Следовательно, акустическая чувствительность зависит от частоты через коэффициенты сопротивления излучения  и осевой концентрации
и осевой концентрации  Первый растет пропорционально квадрату частоты на низких частотах и постоянен на средних и высоких частотах. Второй постоянен на низких и растет на средних и высоких частотах с увеличением частоты. Вследствие этого акустическая
Первый растет пропорционально квадрату частоты на низких частотах и постоянен на средних и высоких частотах. Второй постоянен на низких и растет на средних и высоких частотах с увеличением частоты. Вследствие этого акустическая
тельность растет пропорционально частоте в широком диапазоне частот.
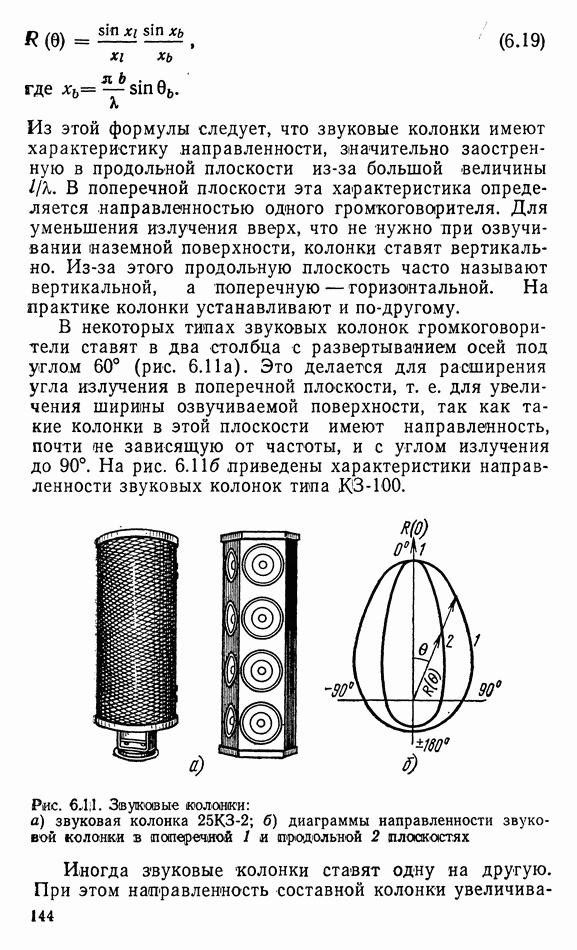
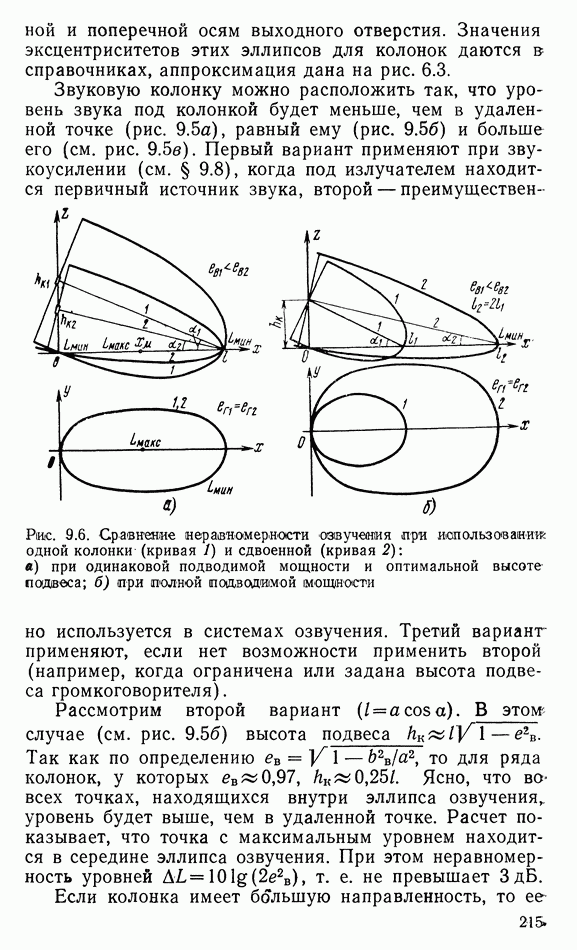
Рассмотрим характеристики направленности излучателей. Возьмем два одинаковых сферических излучателя с расстоянием между ними, равным  Определим звуковое давление, создаваемое этими излучателями в удаленной точке от них под разными углами к оси (за ось примем перпендикуляр к линии, соединяющей центры излучателей; линия и перпендикуляр находятся в рассматриваемой плоскости). На оси звуковое давление удвоится. Под углом 9 к оси разность хода между расстояниями от излучателей до рассматриваемой точки
Определим звуковое давление, создаваемое этими излучателями в удаленной точке от них под разными углами к оси (за ось примем перпендикуляр к линии, соединяющей центры излучателей; линия и перпендикуляр находятся в рассматриваемой плоскости). На оси звуковое давление удвоится. Под углом 9 к оси разность хода между расстояниями от излучателей до рассматриваемой точки  Поэтому звуковые давления будут складываться с учетом разности хода (т. е. разности фаз) между ними. Пока разность хода меньше
Поэтому звуковые давления будут складываться с учетом разности хода (т. е. разности фаз) между ними. Пока разность хода меньше  суммарное звуковое давление меньше, чем на оси, но больше, чем звуковое давление от одного излучателя. При разности хода, равной
суммарное звуковое давление меньше, чем на оси, но больше, чем звуковое давление от одного излучателя. При разности хода, равной  оно будет равно нулю, при
оно будет равно нулю, при  будет равно осевому, а при
будет равно осевому, а при  оно опять будет равно нулю и т. д.
оно опять будет равно нулю и т. д.
Если создаваемое одним излучателем звуковое давление  то создаваемое другим излучателем давление
то создаваемое другим излучателем давление  где
где  разность фаз между этими звуковыми давлениями, а амплитуда суммарного звукового давления
разность фаз между этими звуковыми давлениями, а амплитуда суммарного звукового давления

Следовательно, характеристика направленности такого составного излучателя [см. (6.2)]

где  так как при
так как при  Нетрудно видеть из этого, что при больших расстояниях между излучателями по сравнению с длиной волны получается многолепестковая характеристика направленности. Если же длина волны много больше расстояния между излучателями, то даже под углом 90° к оси излучателя суммарное давление будет лишь
Нетрудно видеть из этого, что при больших расстояниях между излучателями по сравнению с длиной волны получается многолепестковая характеристика направленности. Если же длина волны много больше расстояния между излучателями, то даже под углом 90° к оси излучателя суммарное давление будет лишь
немоного меньше давления на оси. В этом случае диаграмма направленности близка к окружности. Таким образом, из (6.13) следует, что характеристика направленности определяется отношением 
Для круглого поршневого излучателя в бесконечном акустическом экране характеристика направленности имеет вид (см. [3] § 9.1)

где  диаметр излучателя;
диаметр излучателя;  функция Бесселя первого порядка.
функция Бесселя первого порядка.
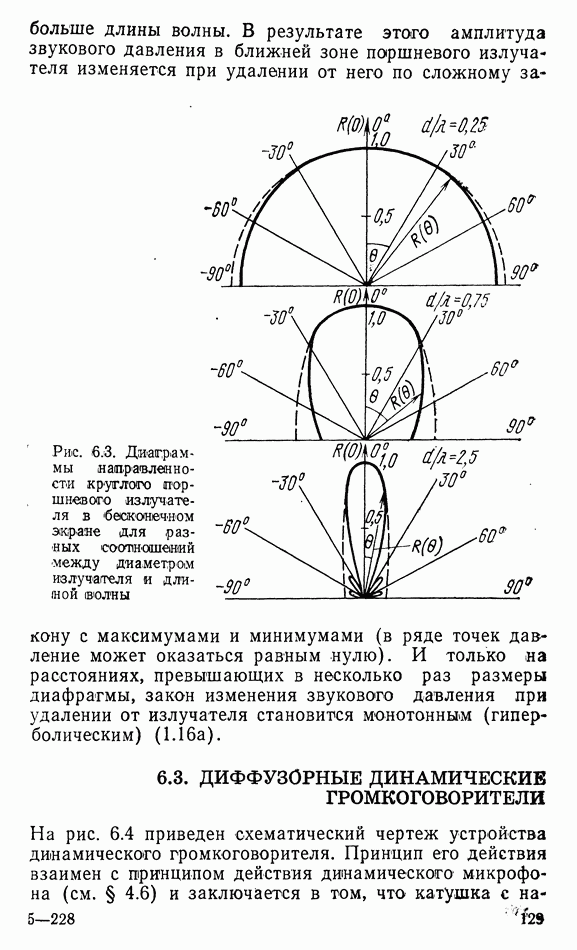
На рис. 6.3 приведены диаграммы направленности для этого излучателя при разных отношениях  Таким образом, во всех случаях направленность определяется отношением размеров излучателя к длине волны: чем оно больше, тем больше коэффициент осевой концентрации. Поэтому для одного и того же излучателя направленность повышается с увеличением частоты, а на одной и той же частоте — с увеличением размеров излучателя.
Таким образом, во всех случаях направленность определяется отношением размеров излучателя к длине волны: чем оно больше, тем больше коэффициент осевой концентрации. Поэтому для одного и того же излучателя направленность повышается с увеличением частоты, а на одной и той же частоте — с увеличением размеров излучателя.
Диаграмма направленности поршневой диафрагмы в экране конечных размеров для низких частот будет иметь форму кривой  так как в плоскости диафрагмы (см. рис. 6.2в) всегда будет полная компенсация излучения от обеих сторон излучателя, поскольку они сдвинуты по фазе на 180°. С увеличением частоты при длинах волн, примерно равных и несколько меньших размеров экрана, характеристика направленности несколько расширяется, а при дальнейшем увеличении частоты она приближается к характеристике направленности поршневой диафрагмы в бесконечном экране, становясь многолепестковой.
так как в плоскости диафрагмы (см. рис. 6.2в) всегда будет полная компенсация излучения от обеих сторон излучателя, поскольку они сдвинуты по фазе на 180°. С увеличением частоты при длинах волн, примерно равных и несколько меньших размеров экрана, характеристика направленности несколько расширяется, а при дальнейшем увеличении частоты она приближается к характеристике направленности поршневой диафрагмы в бесконечном экране, становясь многолепестковой.
Следует еще остановиться на характеристике ближнего поля поршневой диафрагмы, так как оно отличается от поля сферической волны. На небольших расстояниях от поршневого излучателя, находящегося в бесконечном экране, имеет место интерференция звуковых волн, исходящих от разных участков диафрагмы, так как между ними получается разность хода. Если длина волны много больше размеров диафрагмы, эта разность хода невелика и все звуковые волны оказываются почти в одной фазе, если же длина волны значительно меньше размеров диафрагмы, разность хода может оказаться даже
больше длины волны. В результате этого амплитуда звукового давления в ближней зоне поршневого излучателя изменяется при удалении от него по сложному закону с максимумами и минимумами (в ряде точек давление может оказаться равным нулю).

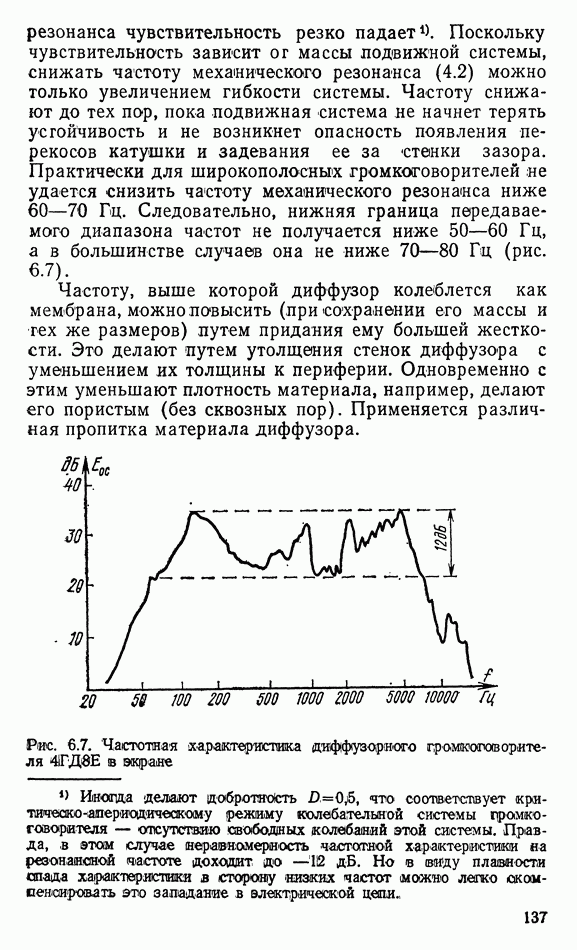
Рис. 6.3. Диаграммы направленности круглого поршневого излучателя в бесконечном экране для разных соотношений между диаметром излучателя и длиной волны
И только на расстояниях, превышающих в несколько раз размеры диафрагмы, закон изменения звукового давления при удалении от излучателя становится монотонным (гиперболическим) (1.16а).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. ЗВУКОВОЕ ПОЛЕ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ
- 1.3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 1.4. ПЛОСКАЯ ВОЛНА
- 1.5. СФЕРИЧЕСКАЯ ВОЛНА
- 1.6. ЦИЛИНДРИЧЕСКАЯ ВОЛНА
- Глава 2. ОСНОВНЫЕ СВОЙСТВА СЛУХА
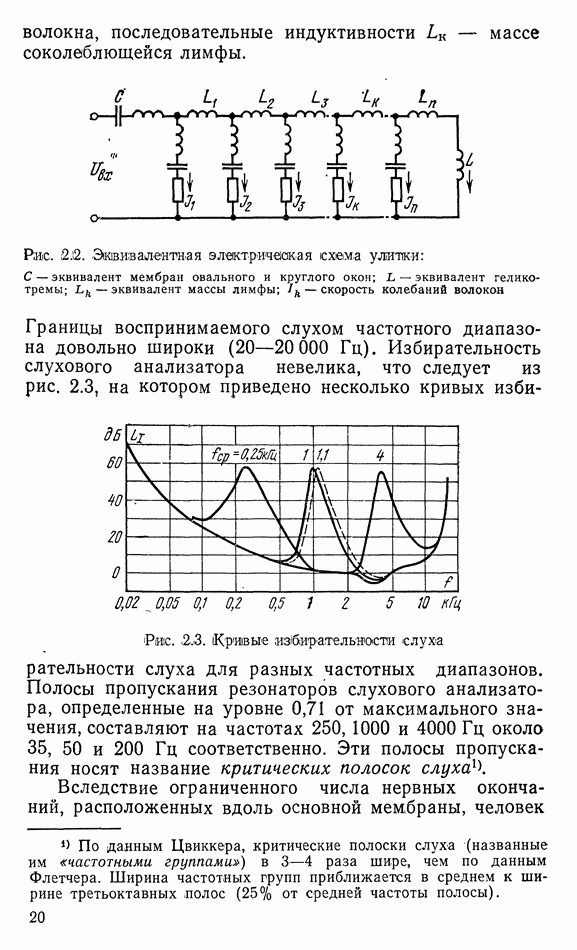
- 2.2. ВОСПРИЯТИЕ ПО ЧАСТОТЕ
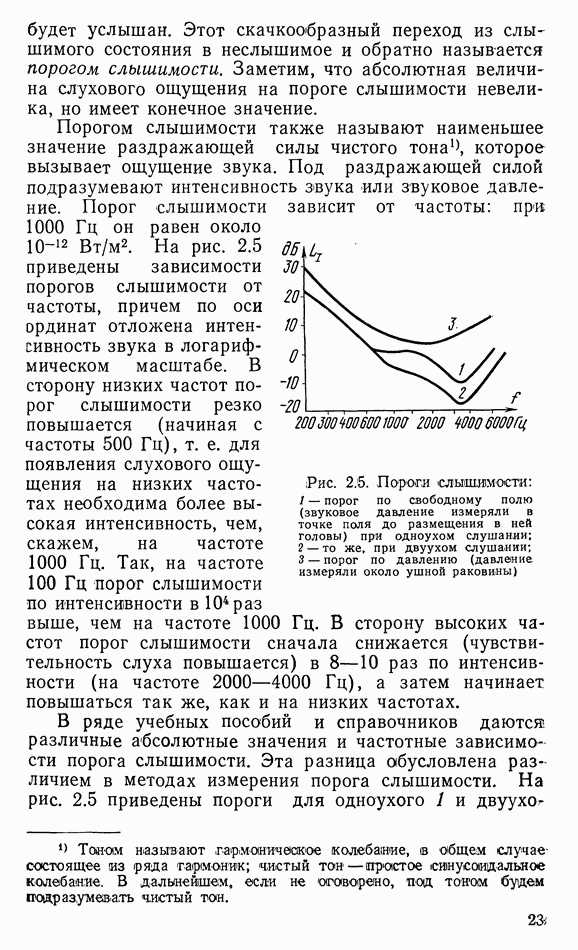
- 2.3. ПОРОГ СЛЫШИМОСТИ
- 2.4. ВОСПРИЯТИЕ ПО АМПЛИТУДЕ
- 2.5. УРОВНИ
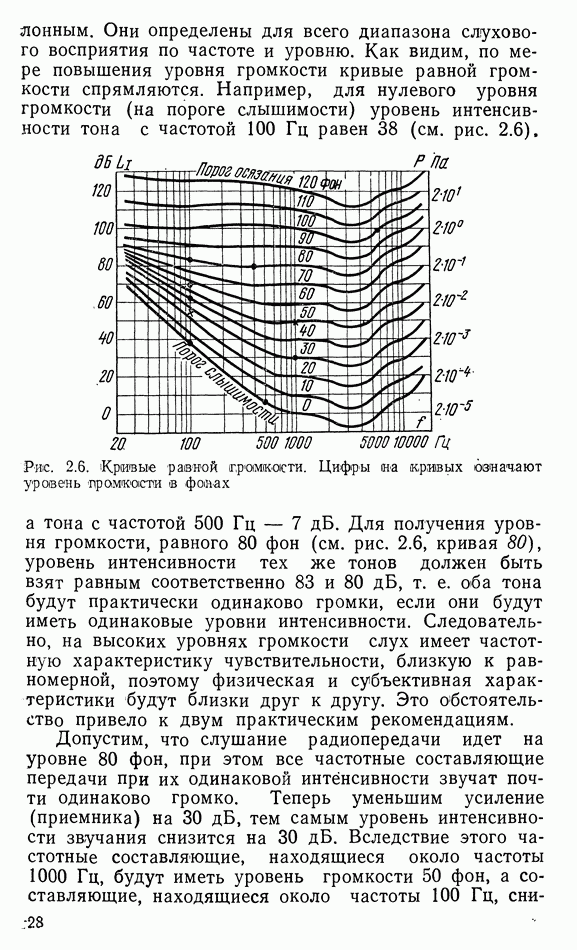
- 2.6. ГРОМКОСТЬ И УРОВЕНЬ ГРОМКОСТИ ЗВУКА
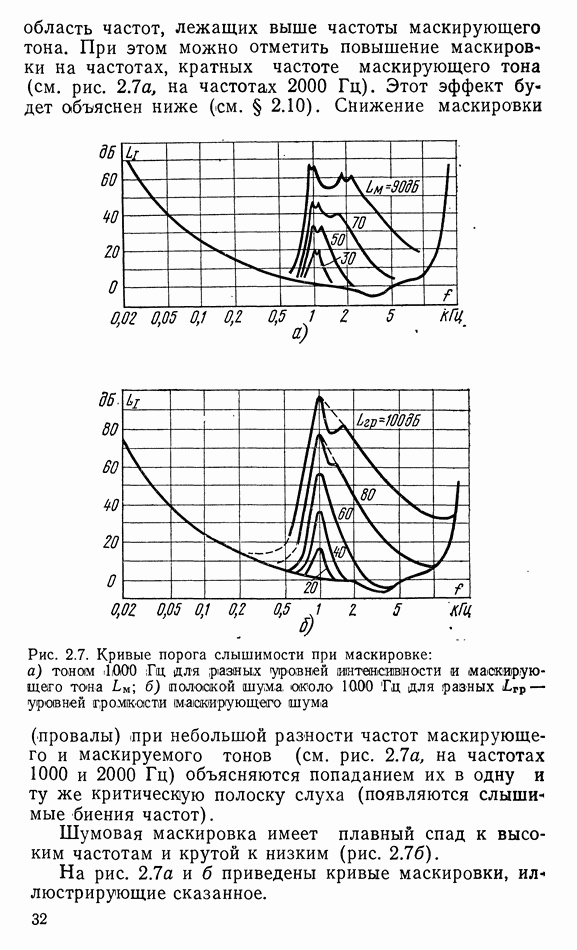
- 2.7. ЭФФЕКТ МАСКИРОВКИ
- 2.8. ГРОМКОСТЬ СЛОЖНЫХ ЗВУКОВ
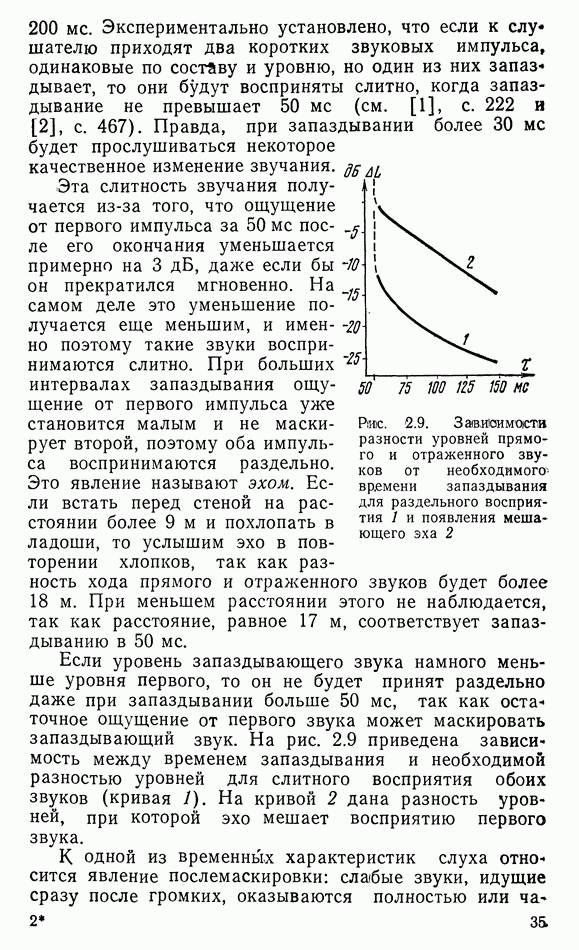
- 2.9. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЛУХОВОГО ВОСПРИЯТИЯ
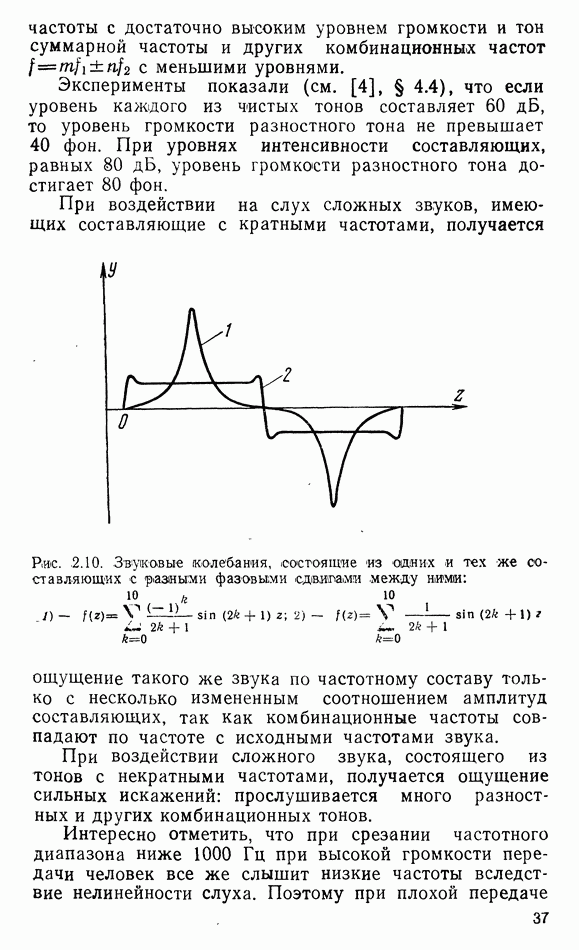
- 2.10 НЕЛИНЕЙНЫЕ СВОЙСТВА СЛУХА
- 2.11. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- Глава 3. АКУСТИЧЕСКИЕ СИГНАЛЫ
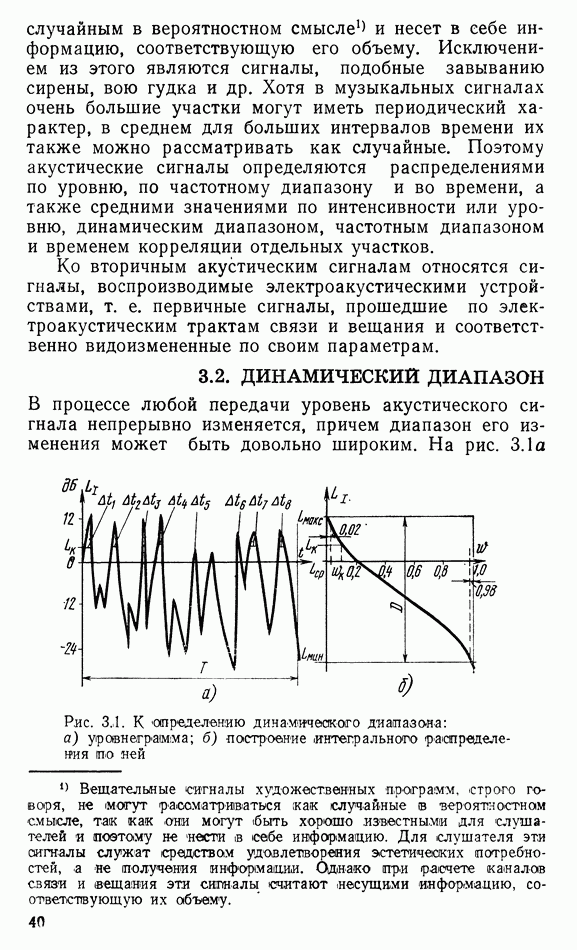
- 3.2. ДИНАМИЧЕСКИЙ ДИАПАЗОН
- 3.3 СРЕДНИЙ УРОВЕНЬ
- 3.4. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
- 3.5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ АКУСТИЧЕСКОГО СИГНАЛА
- 3.6. ПЕРВИЧНЫЙ РЕЧЕВОЙ СИГНАЛ
- 3.7. ВТОРИЧНЫЙ СИГНАЛ
- 3.8. ШУМЫ И ПОМЕХИ
- 3.9. ЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.10. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.11. ПЕРЕХОДНЫЕ ИСКАЖЕНИЯ
- 3.12. ДОПУСТИМЫЕ ВЕЛИЧИНЫ ИСКАЖЕНИЙ
- Глава 4. ЭЛЕКТРОМЕХАНОАКУСТИЧЕСКИЕ СИСТЕМЫ И ИХ ЭЛЕМЕНТЫ
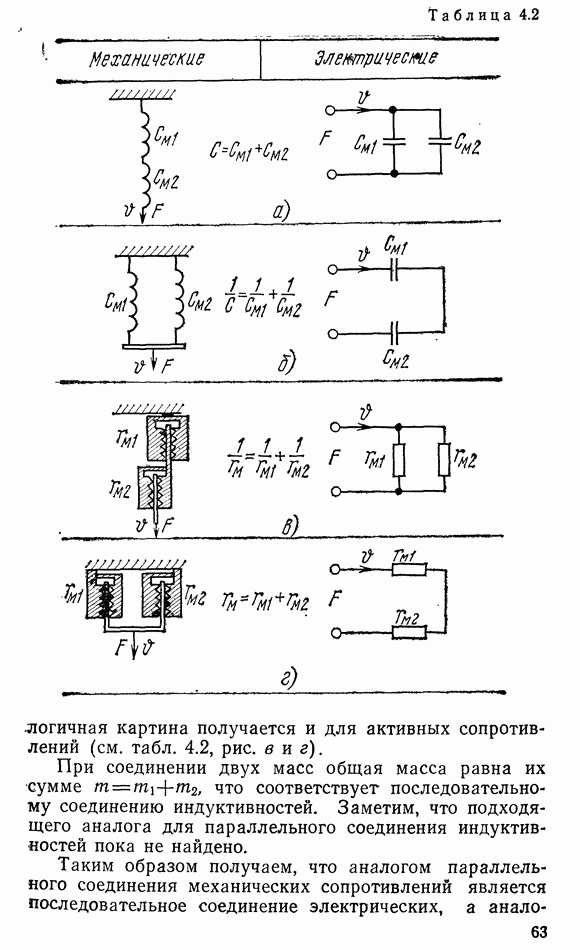
- 4.2. МЕТОД ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
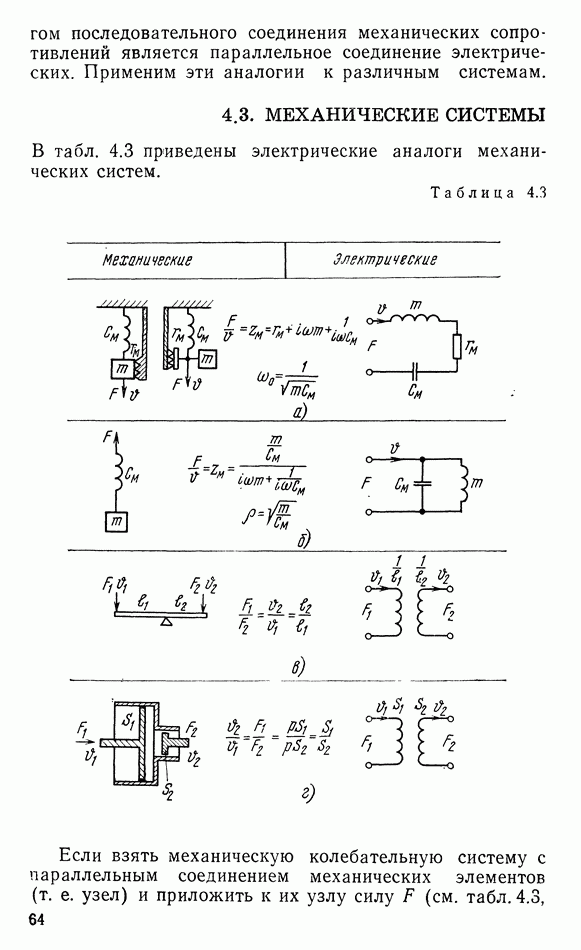
- 4.3. МЕХАНИЧЕСКИЕ СИСТЕМЫ
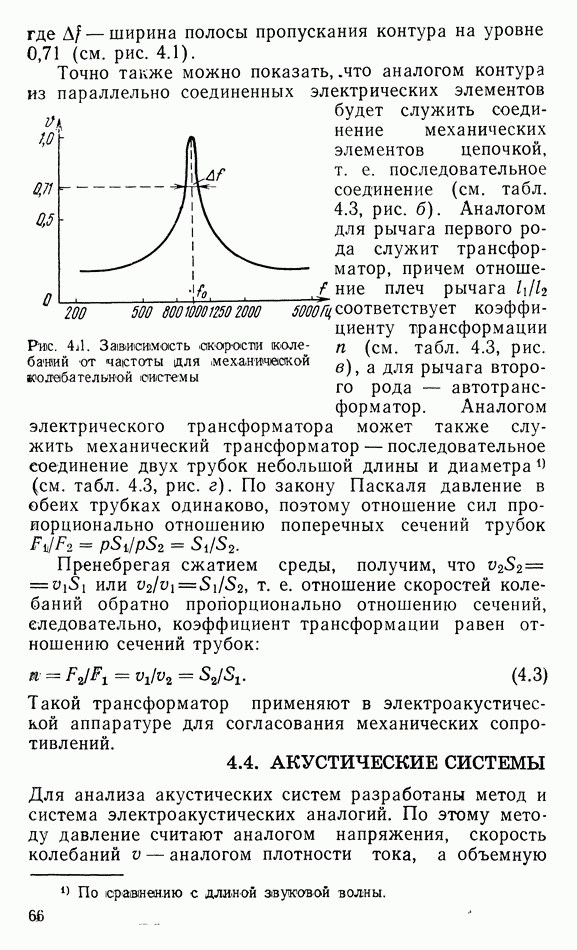
- 4.4. АКУСТИЧЕСКИЕ СИСТЕМЫ
- 4.5. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 5. МИКРОФОНЫ
- 5.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ МИКРОФОНОВ
- 5.3. ДИНАМИЧЕСКИЕ (КАТУШЕЧНЫЕ) МИКРОФОНЫ
- 5.4. ЛЕНТОЧНЫЕ МИКРОФОНЫ
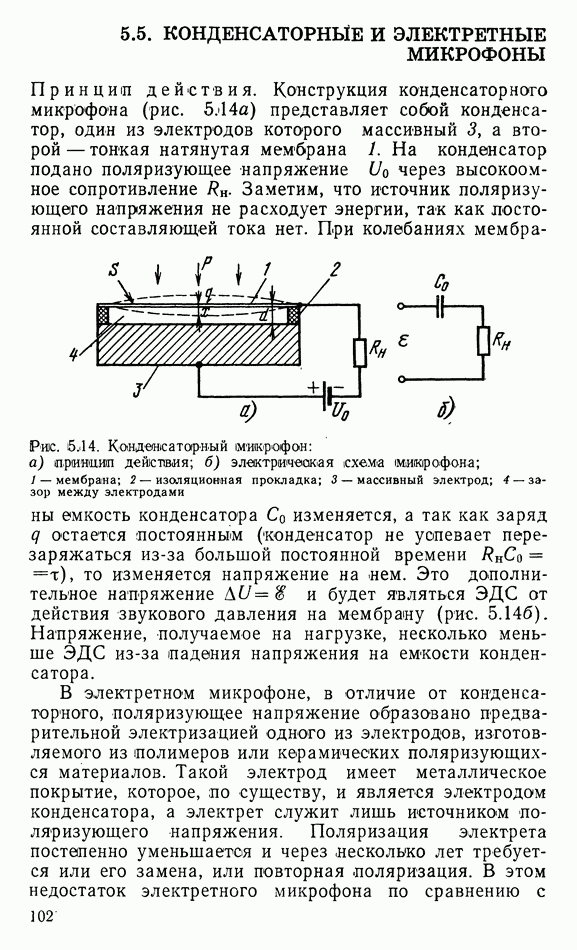
- 5.5. КОНДЕНСАТОРНЫЕ И ЭЛЕКТРЕТНЫЕ МИКРОФОНЫ
- 5.6. ПЬЕЗОМИКРОФОНЫ
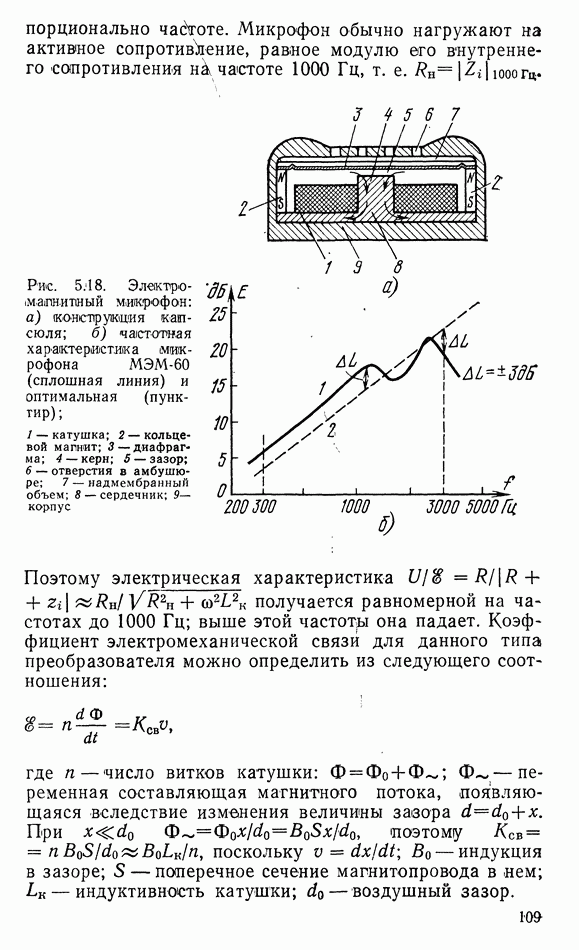
- 5.7. ЭЛЕКТРОМАГНИТНЫЕ МИКРОФОНЫ
- 5.8. УГОЛЬНЫЕ МИКРОФОНЫ
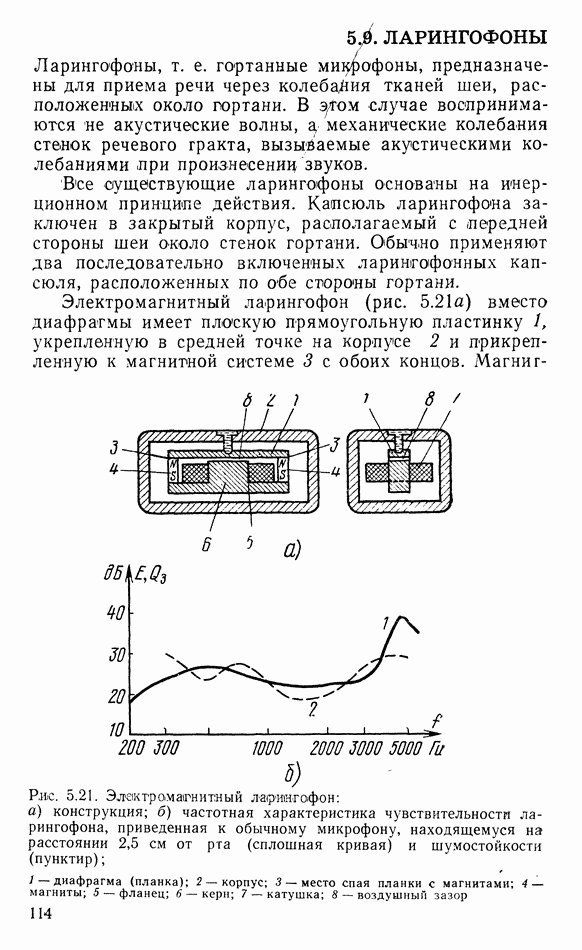
- 5.9. ЛАРИНГОФОНЫ
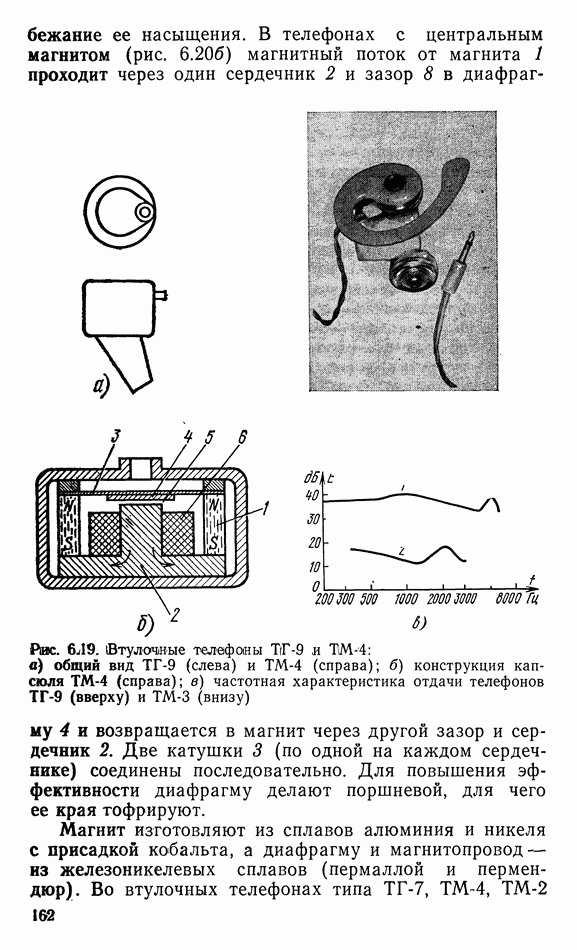
- Глава 6. ГРОМКОГОВОРИТЕЛИ И ТЕЛЕФОНЫ
- 6.2. ДИФФУЗОРНЫЕ ИЗЛУЧАТЕЛИ
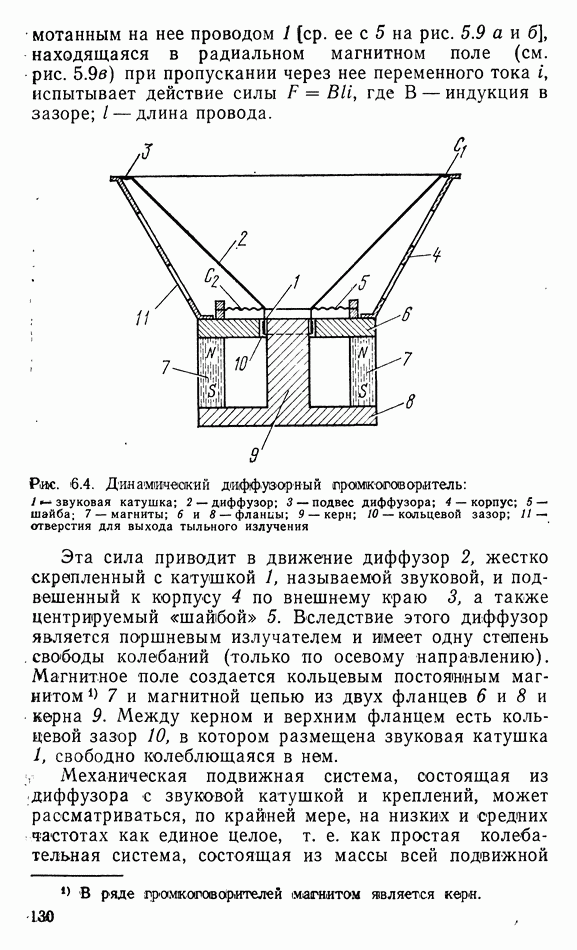
- 6.3. ДИФФУЗОРНЫЕ ДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.4. ГРУППОВЫЕ ИЗЛУЧАТЕЛИ И ГРОМКОГОВОРИТЕЛИ
- 6.5. РУПОРНЫЕ ИЗЛУЧАТЕЛИ
- 6.6. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.7. ЭЛЕКТРОСТАТИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.8. ГРОМКОГОВОРЯЩИЕ АКУСТИЧЕСКИЕ СИСТЕМЫ
- 6.9. ПНЕВМАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
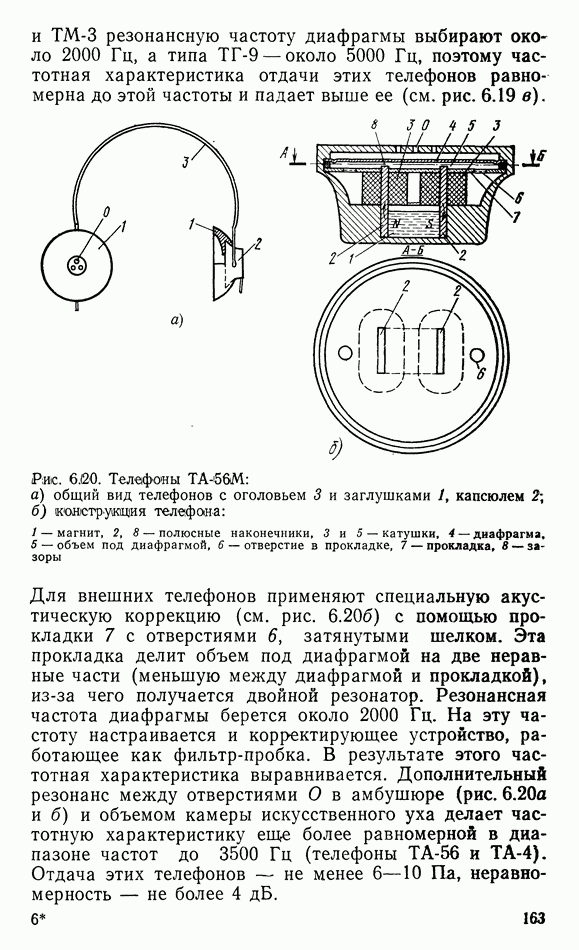
- 6.10. ТЕЛЕФОНЫ
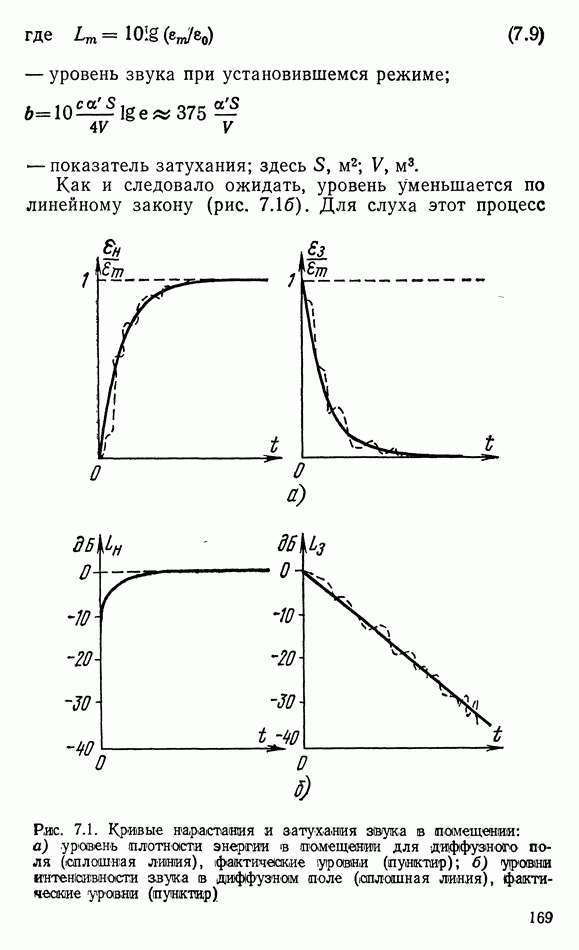
- Глава 7. АКУСТИКА ПОМЕЩЕНИЙ
- 7.1. РАСПРОСТРАНЕНИЕ ЗВУКА В ОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
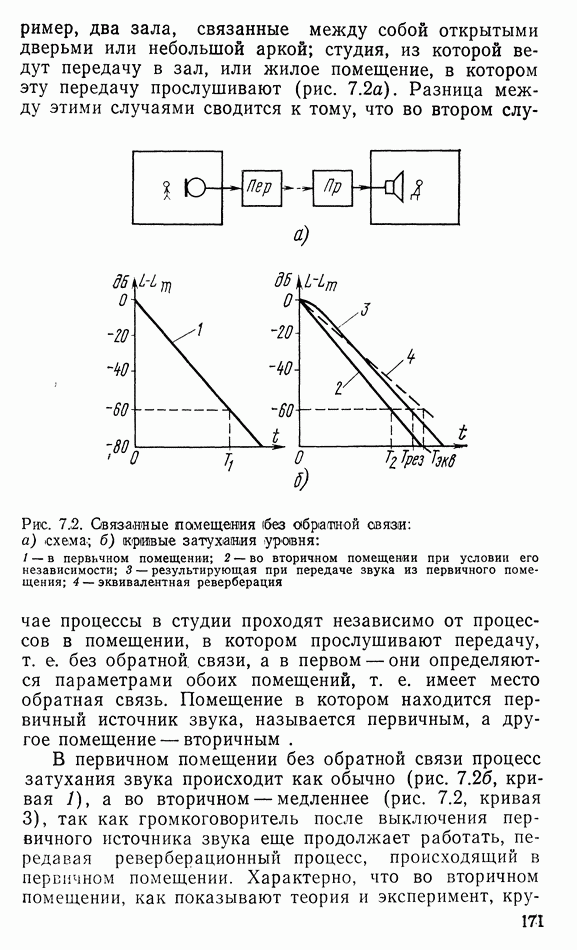
- 7.2. АКУСТИЧЕСКИЕ ПРОЦЕССЫ В ПОМЕЩЕНИЯХ
- 7.3. ХАРАКТЕРИСТИКИ ПОМЕЩЕНИЯ
- 7.4. ЗВУКОПОГЛОЩАЮЩИЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ
- 7.5. ЗВУКОИЗОЛЯЦИЯ ПОМЕЩЕНИЙ
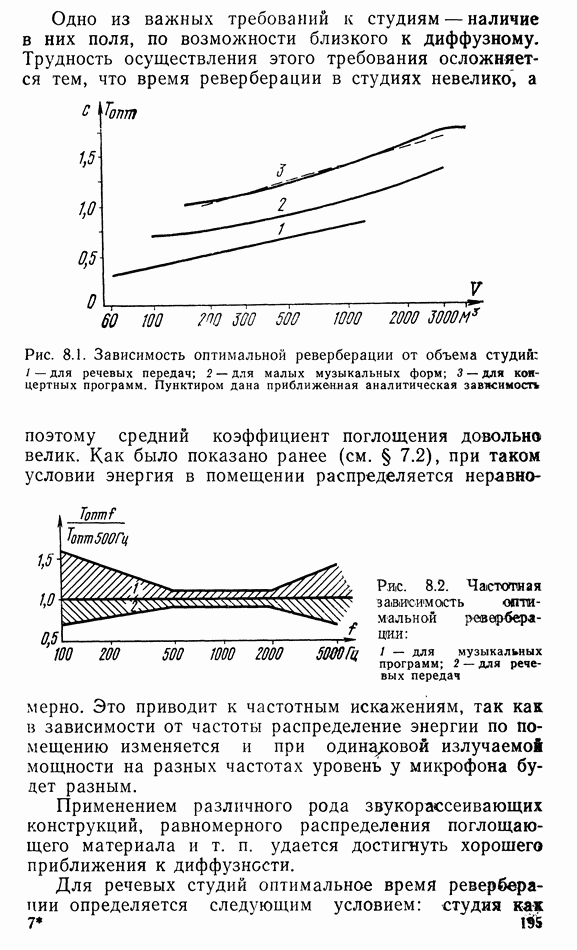
- Глава 8. СТУДИИ ЗВУКОВОГО И ТЕЛЕВИЗИОННОГО ВЕЩАНИЯ
- 8.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СТУДИЙ
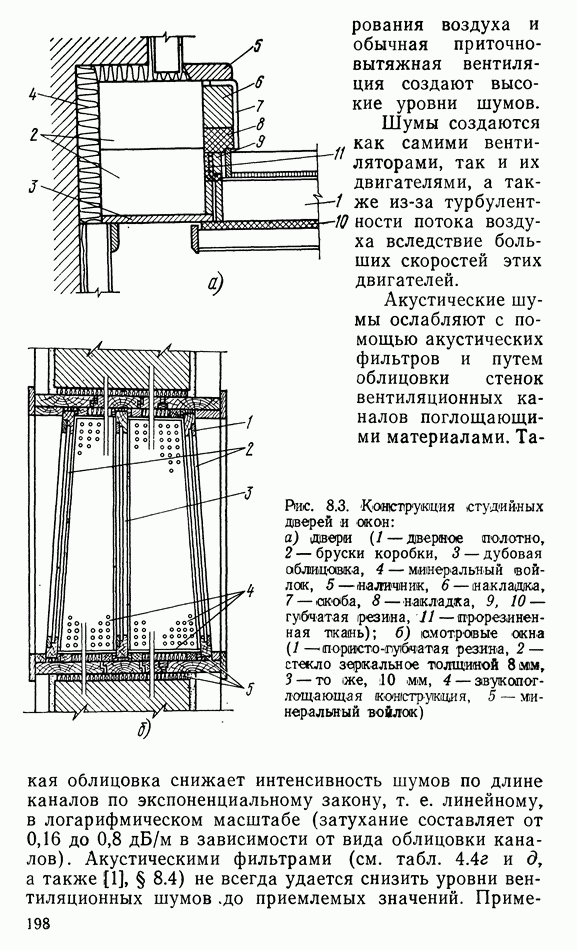
- 8.3. ЗВУКОИЗОЛЯЦИЯ СТУДИЙ
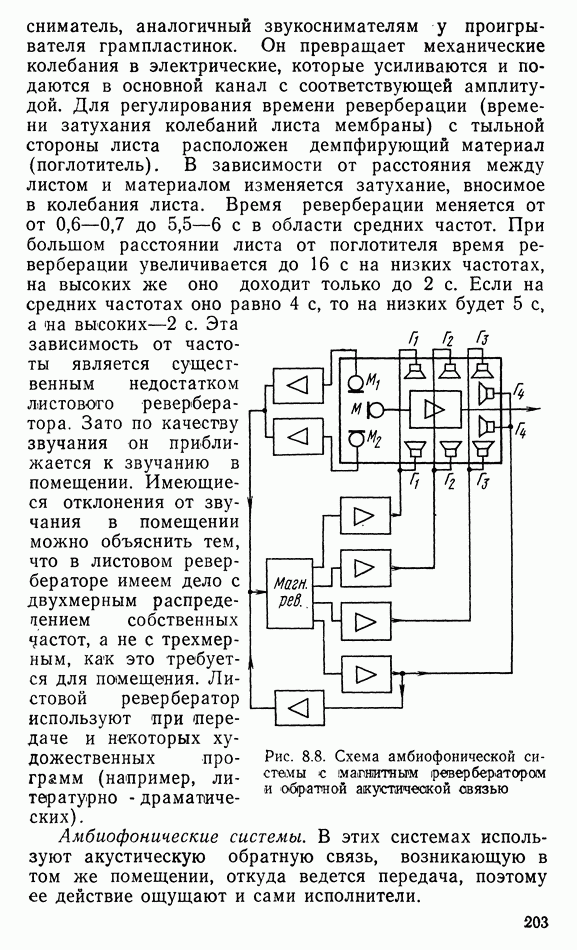
- 8.4. ЭЛЕКТРОАКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ СТУДИЙ И КОМНАТ ПРОСЛУШИВАНИЯ
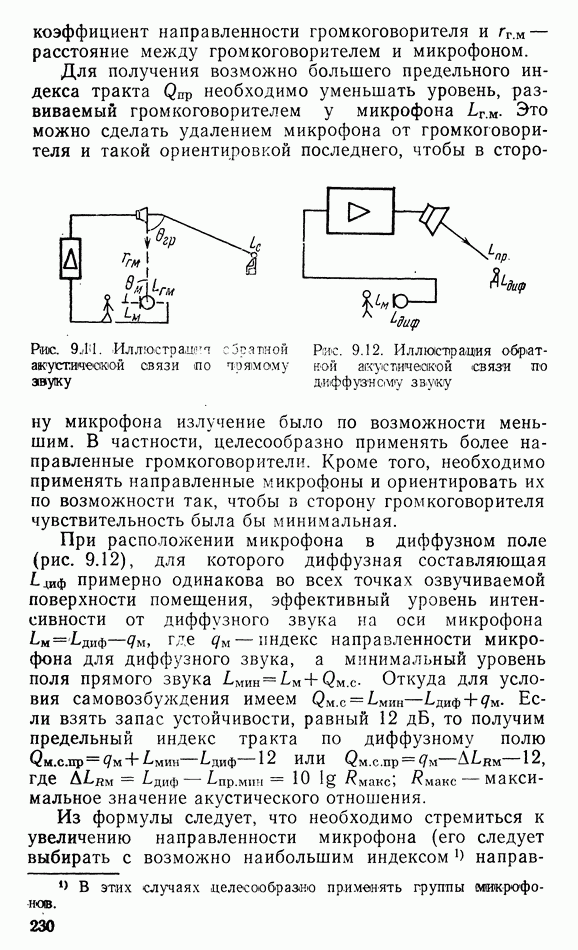
- Глава 9. ОЗВУЧЕНИЕ И ЗВУКОУСИЛЕНИЕ
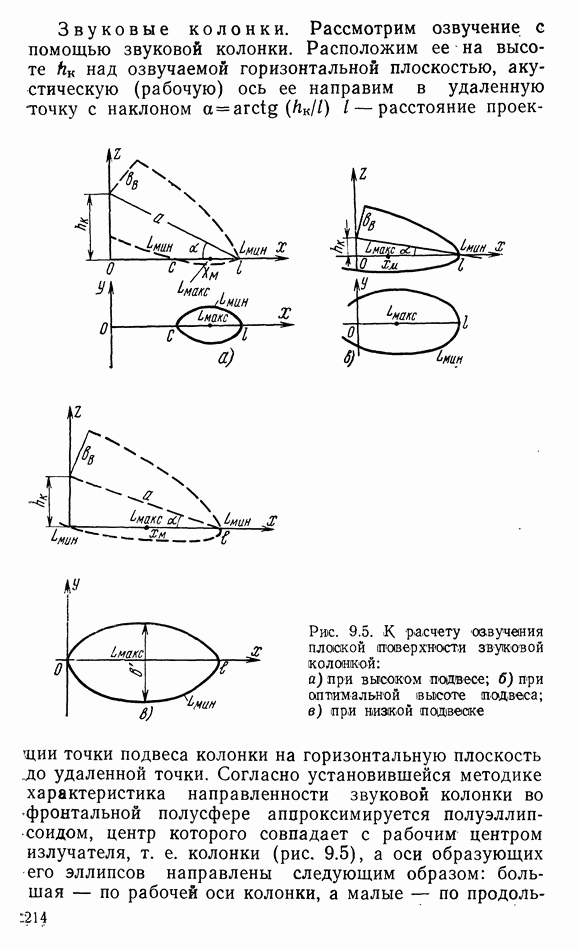
- 9.2. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ОТКРЫТЫХ ПРОСТРАНСТВ
- 9.3. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 9.4. ЗОНАЛЬНЫЕ СИСТЕМЫ
- 9.5. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 9.6. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ДЛЯ ПОМЕЩЕНИЙ
- 9.7. РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ
- 9.8. ЗВУКОУСИЛЕНИЕ
- 9.9. ГРОМКОГОВОРЯЩАЯ СВЯЗЬ
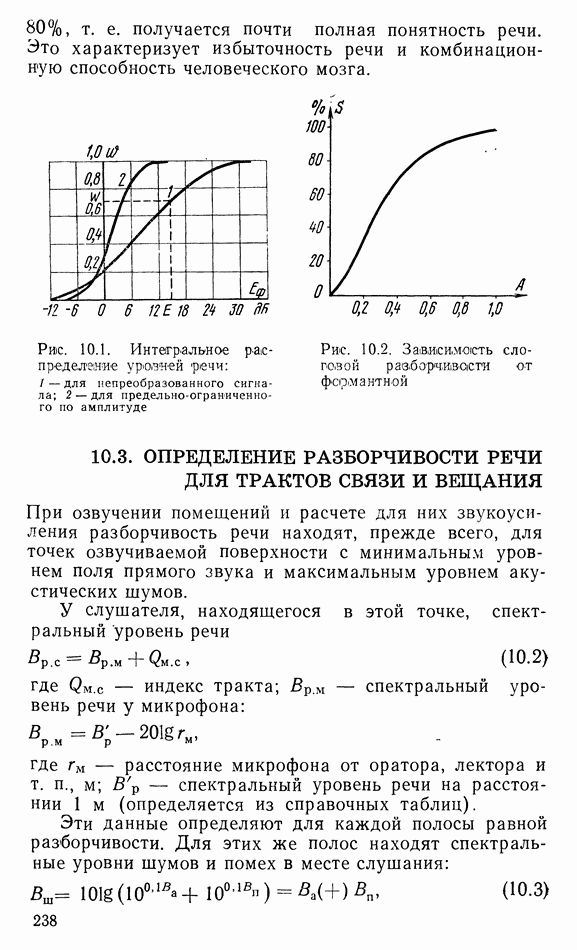
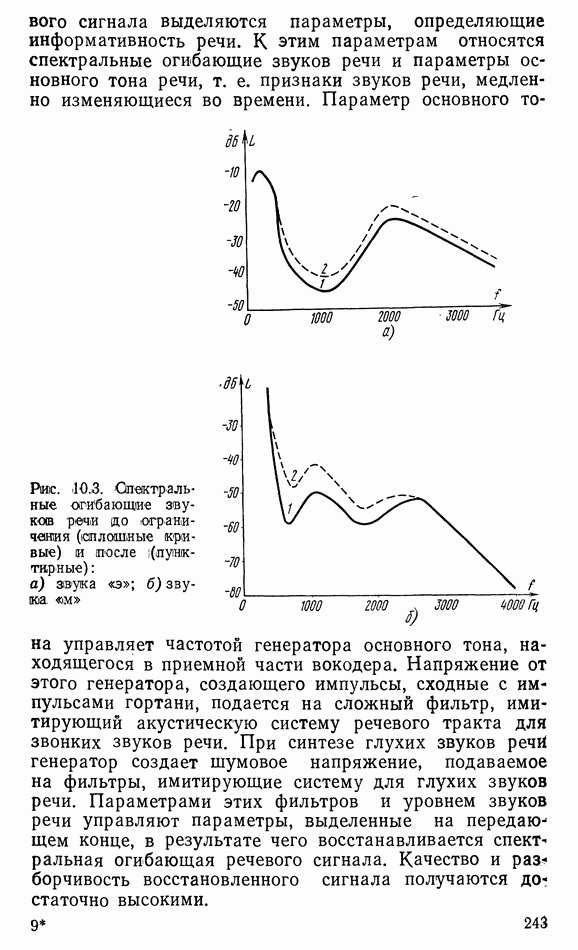
- Глава 10. ПОНЯТНОСТЬ И РАЗБОРЧИВОСТЬ РЕЧИ
- 10.2. ФОРМАНТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- 10.3. ОПРЕДЕЛЕНИЕ РАЗБОРЧИВОСТИ РЕЧИ ДЛЯ ТРАКТОВ СВЯЗИ И ВЕЩАНИЯ
- 10.4. МЕТОДЫ ПОВЫШЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
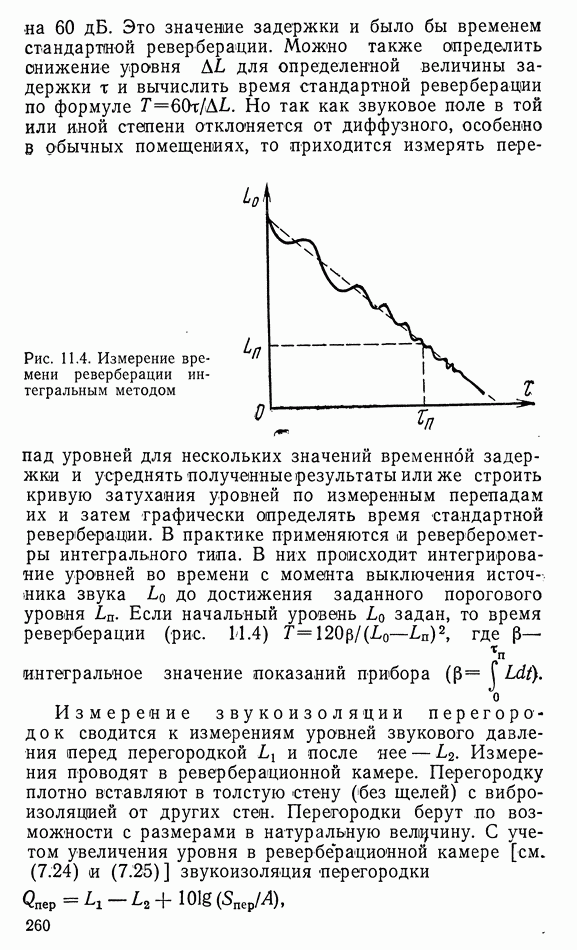
- Глава 11. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ
- 11.2. ЗВУКОМЕРНЫЕ КАМЕРЫ
- 11.3. ИЗМЕРИТЕЛЬНАЯ АППАРАТУРА И АКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ
- 11.4. МЕТОДЫ ИЗМЕРЕНИЙ ОСНОВНЫХ ХАРАКТЕРИСТИК АППАРАТУРЫ И ПОМЕЩЕНИЙ