| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
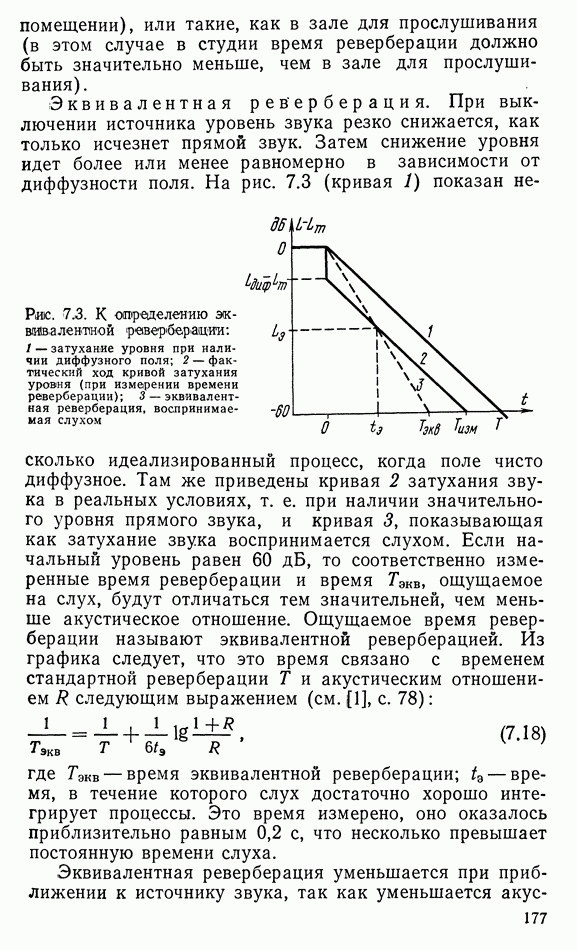
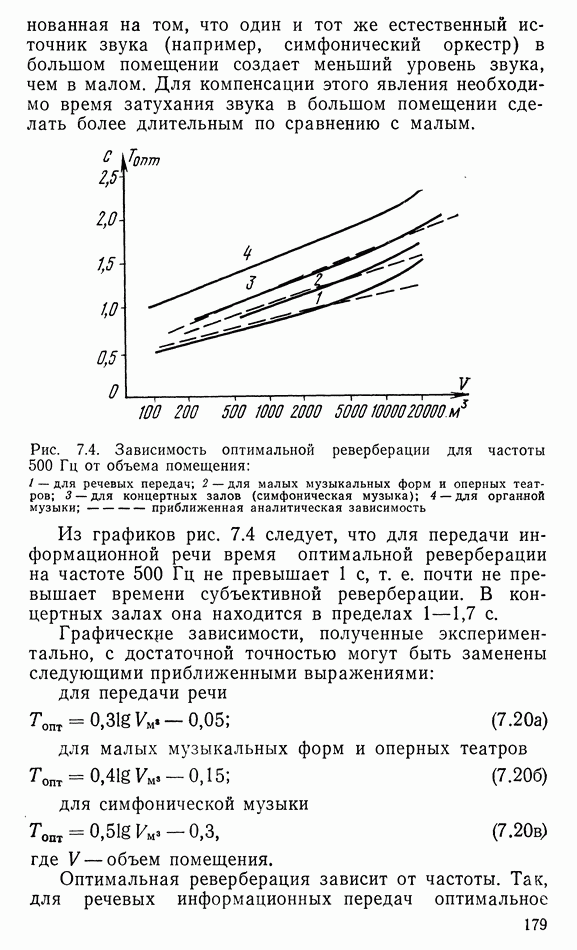
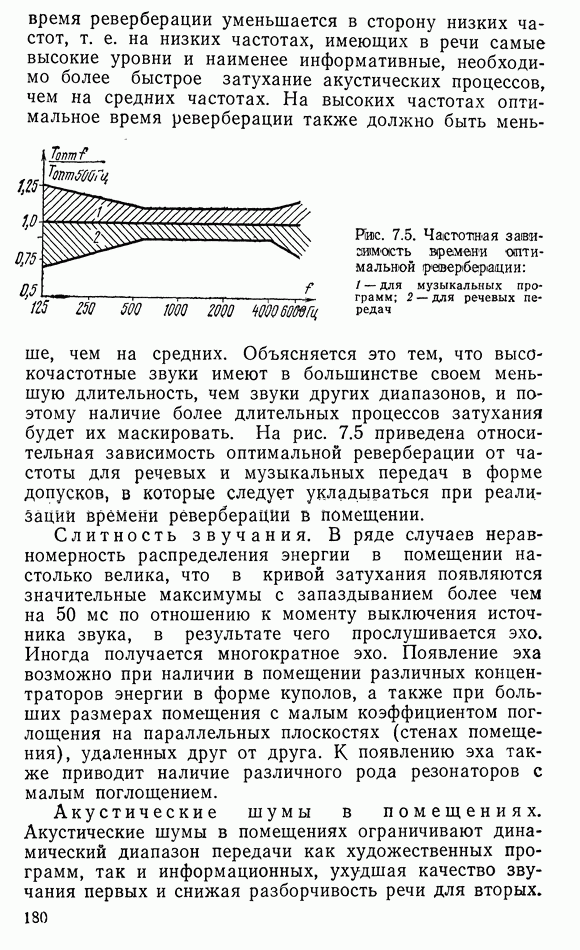
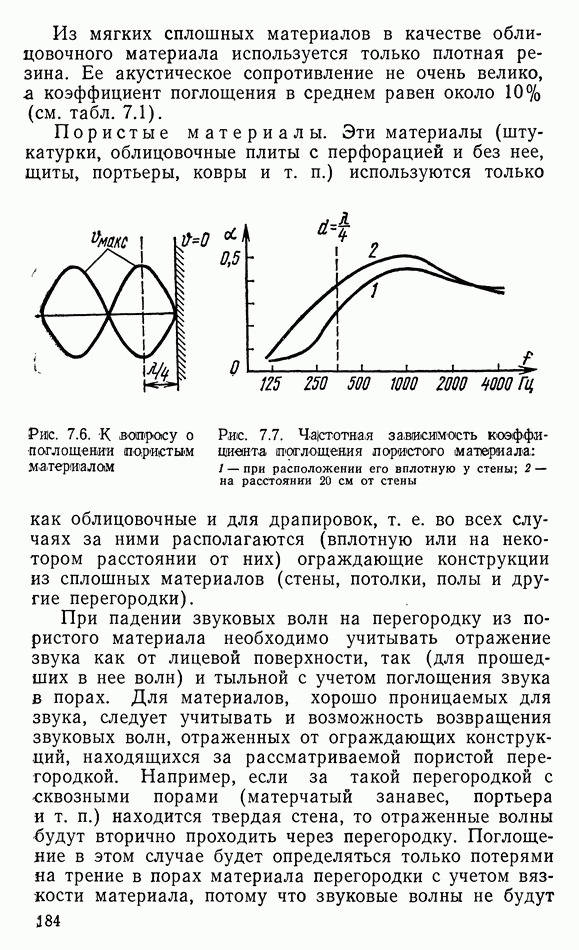
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
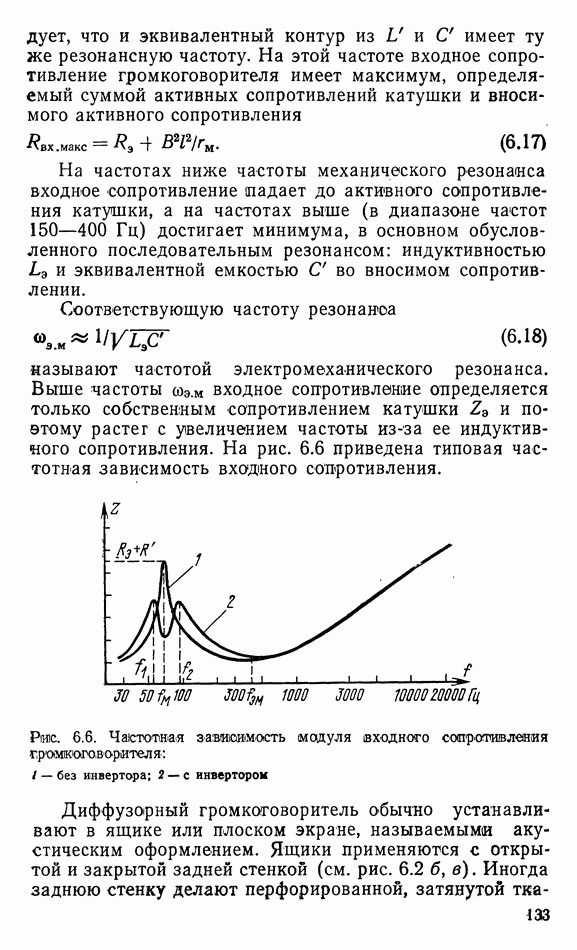
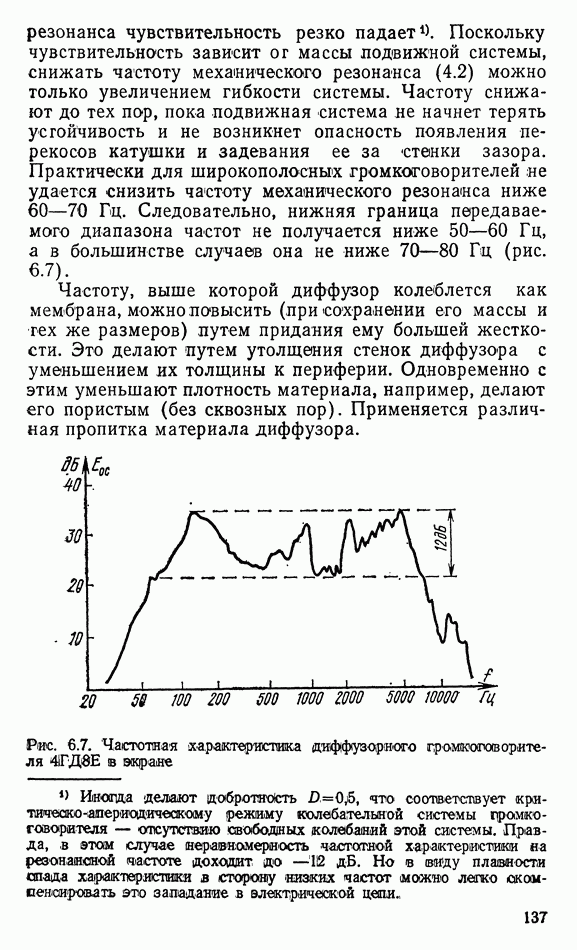
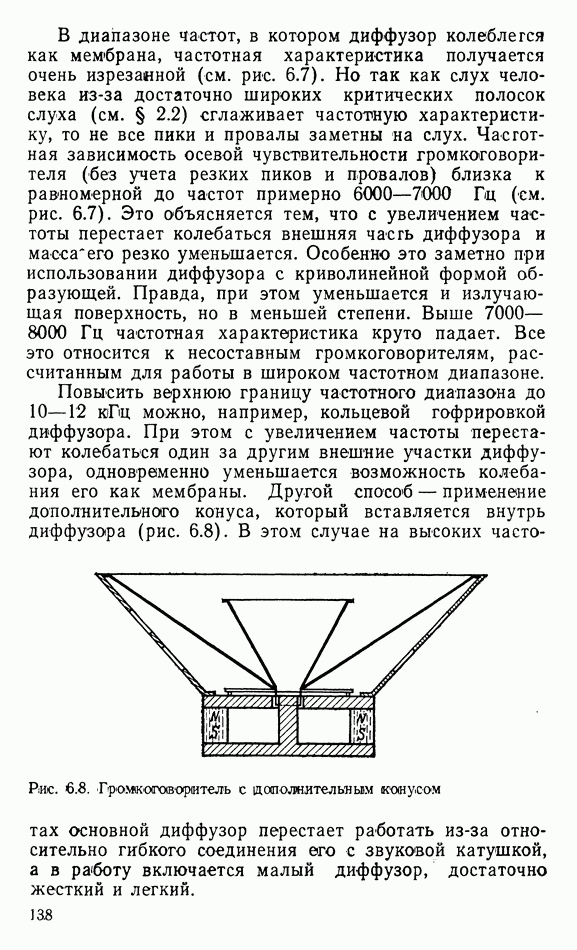
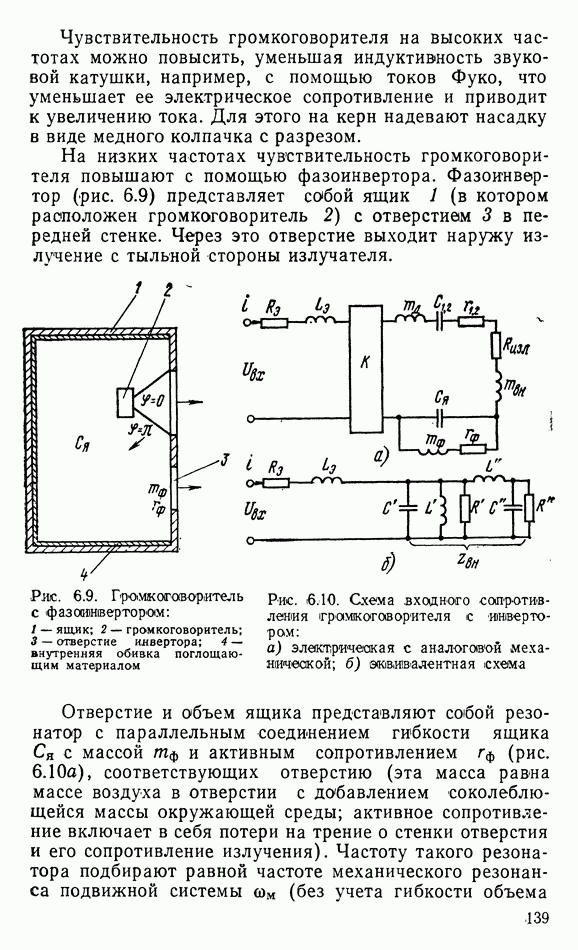
1.4. ПЛОСКАЯ ВОЛНА
Фронт плоской волны представляет собой плоскость. Согласно определению фронта волны звуковые лучи пересекают его под прямым углом, поэтому в плоской волне они параллельны между ссхбой. Так как поток энергии при этом не расходится, интенсивность звука не должна была бы уменьшаться с удалением от источника звука. Тем не менее она уменьшается из-за молекулярного затухания, вязкости среды, запыленности ее, рассеяния и т. п. потерь. Однако эти потери так малы, что с ними можно не считаться при распространении волны на небольшие расстояния. Поэтому обычно полагают, что интенсивность звука в плоской волне не зависит от расстояния до источника звука.
Поскольку  то амплитуды звукового давления и скорости колебаний тоже не зависят от этого расстояния:
то амплитуды звукового давления и скорости колебаний тоже не зависят от этого расстояния: 
Выведем основные уравнения для плоской волны. Уравнение (1.4) имеет вид  так как
так как  Частное решение волнового уравнения для плоской волны, распространяющейся в положительном направлении, имеет вид
Частное решение волнового уравнения для плоской волны, распространяющейся в положительном направлении, имеет вид  где
где  амплитуда звукового давления; со — угловая частота колебаний;
амплитуда звукового давления; со — угловая частота колебаний;  волновое число.
волновое число.
Подставляя звуковое давление в уравнение движения (1.1) и интегрируя во времени, получим скорость колебаний  где
где  амплитуда скорости колебаний.
амплитуда скорости колебаний.
Из этих выражений находим удельное акустическое сопротивление (1.6) для плоской волны:

Для нормального атмосферного давления и температуры 20°С акустическое сопротивление  Акустическое сопротивление для плоской волны определяется только скоростью звука и плотностью среды и является активным, вследствие чего давление и скорость колебаний находятся в одинаковой фазе, т. е.
Акустическое сопротивление для плоской волны определяется только скоростью звука и плотностью среды и является активным, вследствие чего давление и скорость колебаний находятся в одинаковой фазе, т. е.  поэтому интенсивность звука [см. ф-лу (1.10)]
поэтому интенсивность звука [см. ф-лу (1.10)]  где
где  и — действующие значения звукового давления и скорости колебаний. Подставляя в это выражение (1.13), получаем наиболее часто используемое выражение для определения интенсивности звука
и — действующие значения звукового давления и скорости колебаний. Подставляя в это выражение (1.13), получаем наиболее часто используемое выражение для определения интенсивности звука

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. ЗВУКОВОЕ ПОЛЕ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ
- 1.3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 1.4. ПЛОСКАЯ ВОЛНА
- 1.5. СФЕРИЧЕСКАЯ ВОЛНА
- 1.6. ЦИЛИНДРИЧЕСКАЯ ВОЛНА
- Глава 2. ОСНОВНЫЕ СВОЙСТВА СЛУХА
- 2.2. ВОСПРИЯТИЕ ПО ЧАСТОТЕ
- 2.3. ПОРОГ СЛЫШИМОСТИ
- 2.4. ВОСПРИЯТИЕ ПО АМПЛИТУДЕ
- 2.5. УРОВНИ
- 2.6. ГРОМКОСТЬ И УРОВЕНЬ ГРОМКОСТИ ЗВУКА
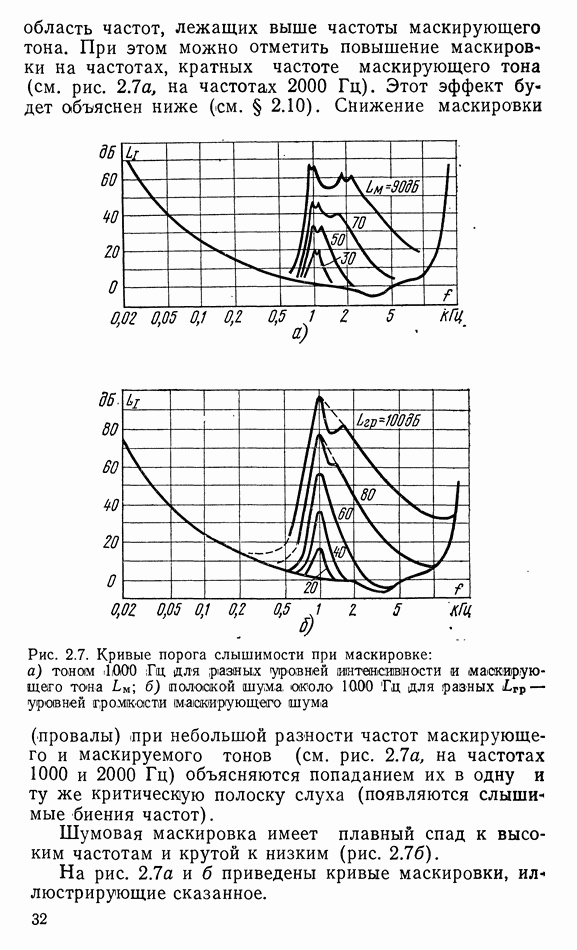
- 2.7. ЭФФЕКТ МАСКИРОВКИ
- 2.8. ГРОМКОСТЬ СЛОЖНЫХ ЗВУКОВ
- 2.9. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЛУХОВОГО ВОСПРИЯТИЯ
- 2.10 НЕЛИНЕЙНЫЕ СВОЙСТВА СЛУХА
- 2.11. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- Глава 3. АКУСТИЧЕСКИЕ СИГНАЛЫ
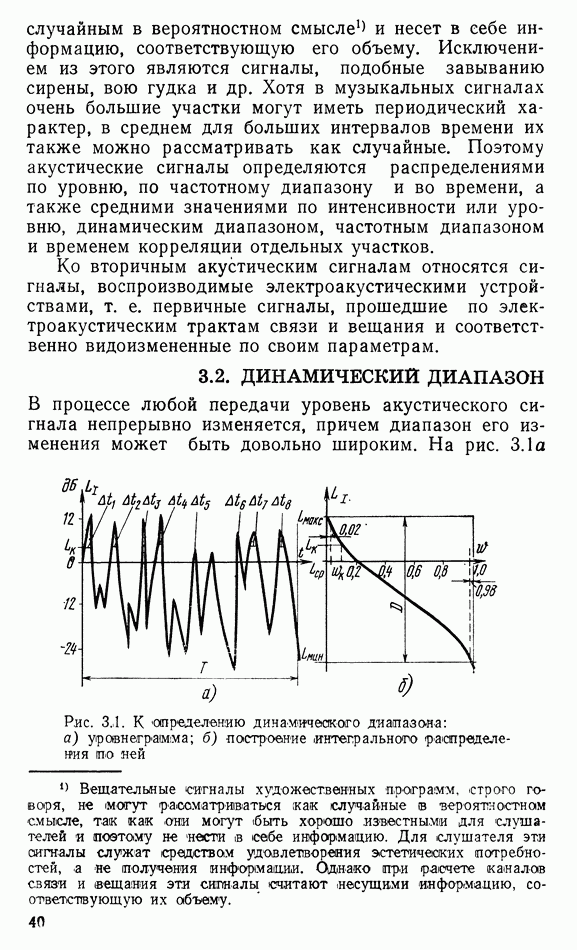
- 3.2. ДИНАМИЧЕСКИЙ ДИАПАЗОН
- 3.3 СРЕДНИЙ УРОВЕНЬ
- 3.4. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
- 3.5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ АКУСТИЧЕСКОГО СИГНАЛА
- 3.6. ПЕРВИЧНЫЙ РЕЧЕВОЙ СИГНАЛ
- 3.7. ВТОРИЧНЫЙ СИГНАЛ
- 3.8. ШУМЫ И ПОМЕХИ
- 3.9. ЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.10. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.11. ПЕРЕХОДНЫЕ ИСКАЖЕНИЯ
- 3.12. ДОПУСТИМЫЕ ВЕЛИЧИНЫ ИСКАЖЕНИЙ
- Глава 4. ЭЛЕКТРОМЕХАНОАКУСТИЧЕСКИЕ СИСТЕМЫ И ИХ ЭЛЕМЕНТЫ
- 4.2. МЕТОД ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 4.3. МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 4.4. АКУСТИЧЕСКИЕ СИСТЕМЫ
- 4.5. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 5. МИКРОФОНЫ
- 5.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ МИКРОФОНОВ
- 5.3. ДИНАМИЧЕСКИЕ (КАТУШЕЧНЫЕ) МИКРОФОНЫ
- 5.4. ЛЕНТОЧНЫЕ МИКРОФОНЫ
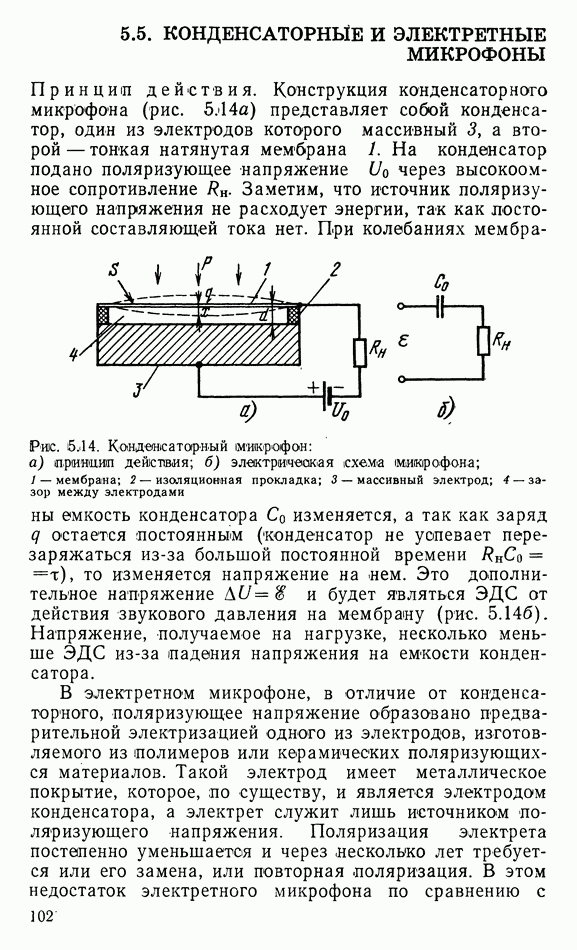
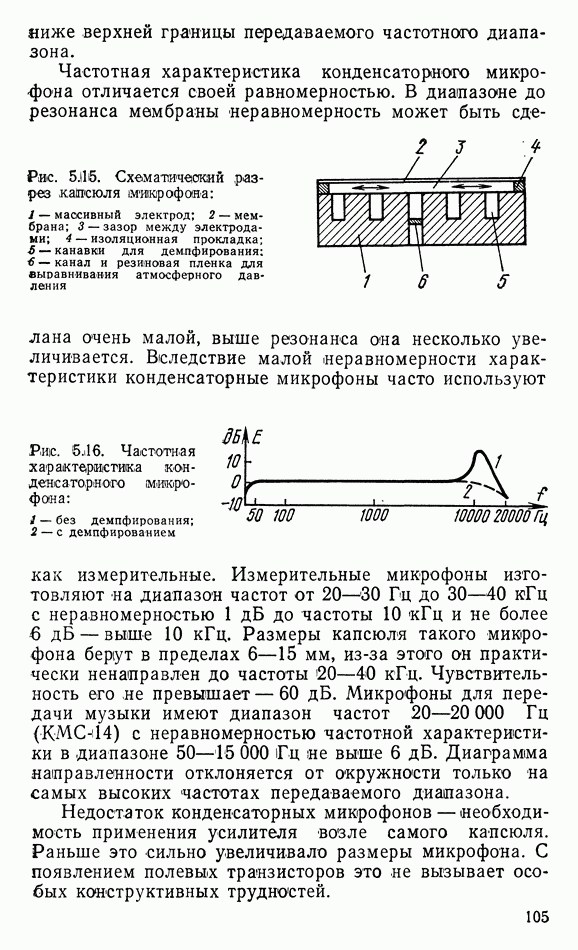
- 5.5. КОНДЕНСАТОРНЫЕ И ЭЛЕКТРЕТНЫЕ МИКРОФОНЫ
- 5.6. ПЬЕЗОМИКРОФОНЫ
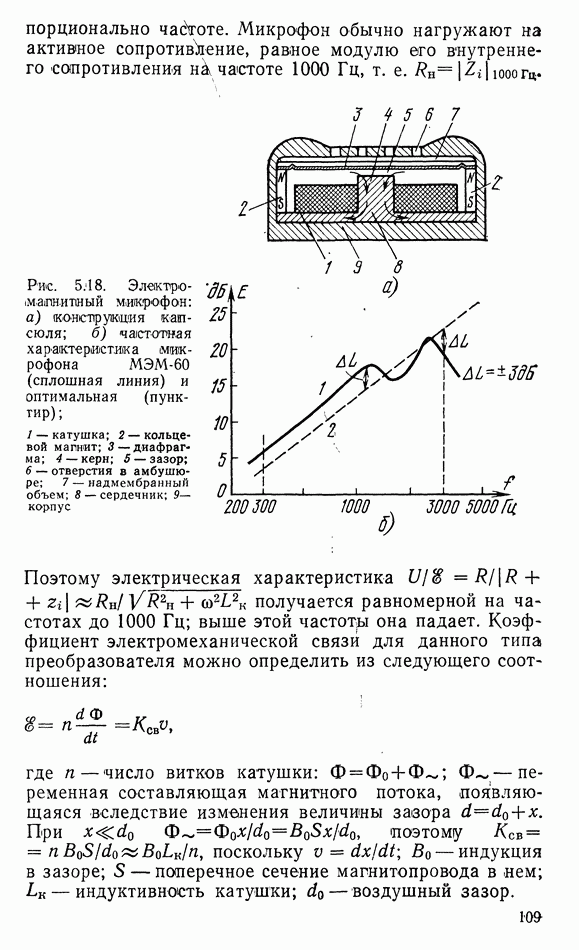
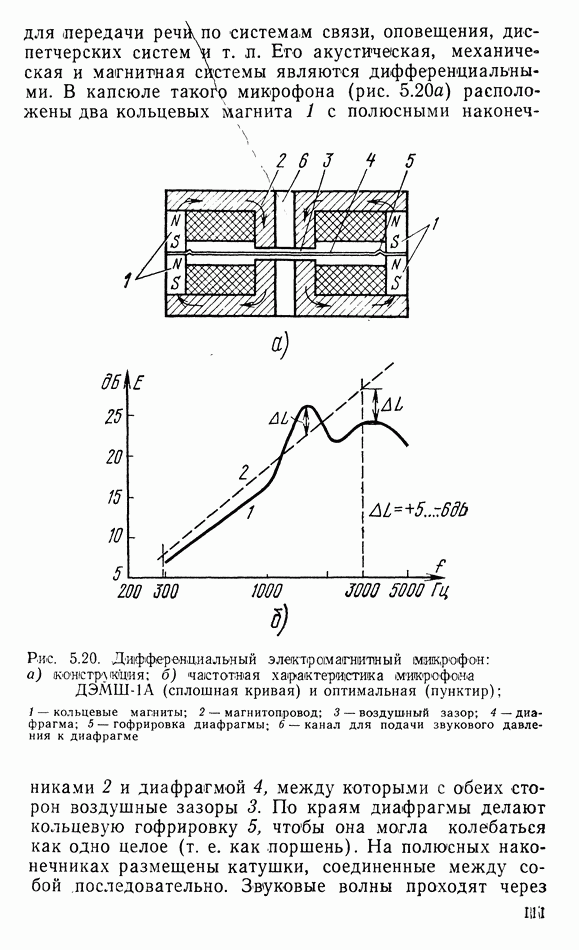
- 5.7. ЭЛЕКТРОМАГНИТНЫЕ МИКРОФОНЫ
- 5.8. УГОЛЬНЫЕ МИКРОФОНЫ
- 5.9. ЛАРИНГОФОНЫ
- Глава 6. ГРОМКОГОВОРИТЕЛИ И ТЕЛЕФОНЫ
- 6.2. ДИФФУЗОРНЫЕ ИЗЛУЧАТЕЛИ
- 6.3. ДИФФУЗОРНЫЕ ДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.4. ГРУППОВЫЕ ИЗЛУЧАТЕЛИ И ГРОМКОГОВОРИТЕЛИ
- 6.5. РУПОРНЫЕ ИЗЛУЧАТЕЛИ
- 6.6. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.7. ЭЛЕКТРОСТАТИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.8. ГРОМКОГОВОРЯЩИЕ АКУСТИЧЕСКИЕ СИСТЕМЫ
- 6.9. ПНЕВМАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
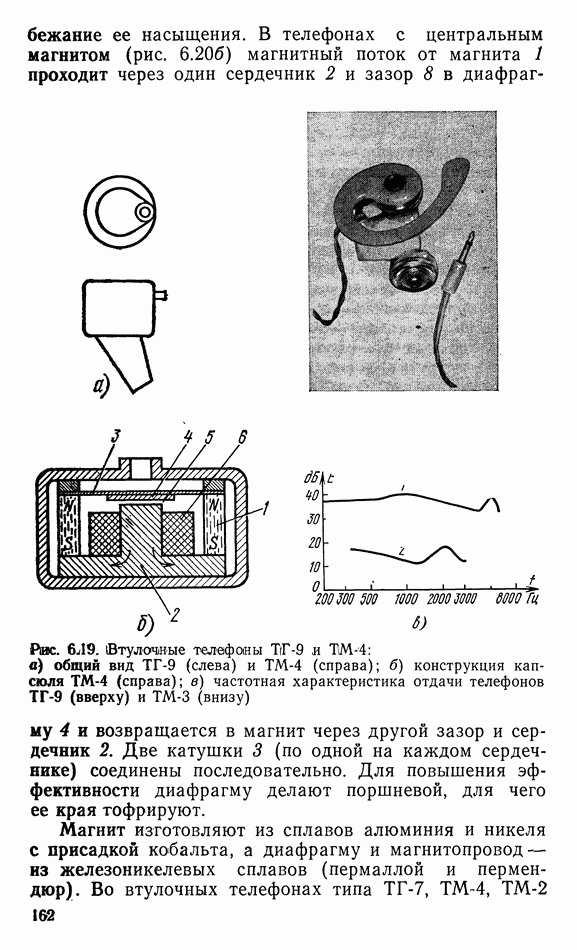
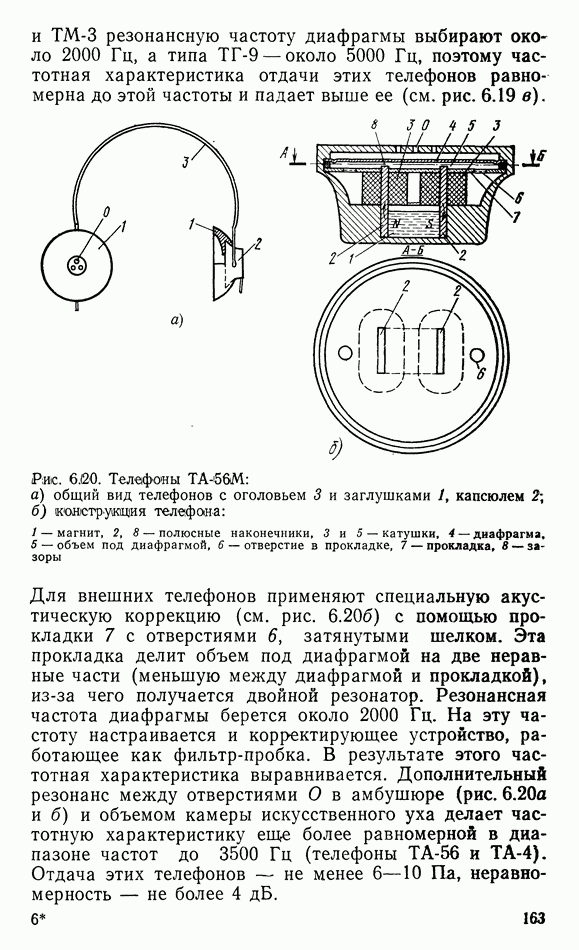
- 6.10. ТЕЛЕФОНЫ
- Глава 7. АКУСТИКА ПОМЕЩЕНИЙ
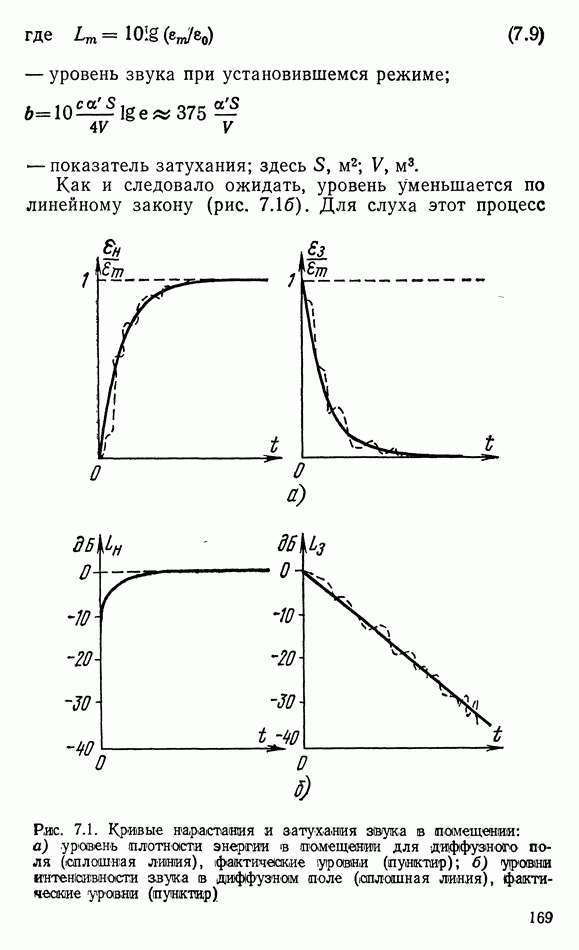
- 7.1. РАСПРОСТРАНЕНИЕ ЗВУКА В ОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
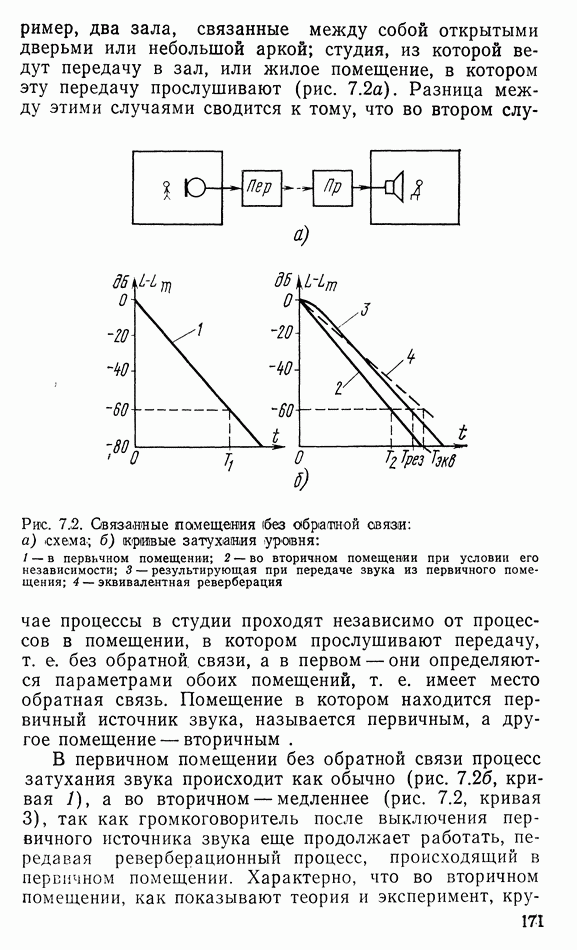
- 7.2. АКУСТИЧЕСКИЕ ПРОЦЕССЫ В ПОМЕЩЕНИЯХ
- 7.3. ХАРАКТЕРИСТИКИ ПОМЕЩЕНИЯ
- 7.4. ЗВУКОПОГЛОЩАЮЩИЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ
- 7.5. ЗВУКОИЗОЛЯЦИЯ ПОМЕЩЕНИЙ
- Глава 8. СТУДИИ ЗВУКОВОГО И ТЕЛЕВИЗИОННОГО ВЕЩАНИЯ
- 8.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СТУДИЙ
- 8.3. ЗВУКОИЗОЛЯЦИЯ СТУДИЙ
- 8.4. ЭЛЕКТРОАКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ СТУДИЙ И КОМНАТ ПРОСЛУШИВАНИЯ
- Глава 9. ОЗВУЧЕНИЕ И ЗВУКОУСИЛЕНИЕ
- 9.2. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ОТКРЫТЫХ ПРОСТРАНСТВ
- 9.3. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 9.4. ЗОНАЛЬНЫЕ СИСТЕМЫ
- 9.5. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 9.6. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ДЛЯ ПОМЕЩЕНИЙ
- 9.7. РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ
- 9.8. ЗВУКОУСИЛЕНИЕ
- 9.9. ГРОМКОГОВОРЯЩАЯ СВЯЗЬ
- Глава 10. ПОНЯТНОСТЬ И РАЗБОРЧИВОСТЬ РЕЧИ
- 10.2. ФОРМАНТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- 10.3. ОПРЕДЕЛЕНИЕ РАЗБОРЧИВОСТИ РЕЧИ ДЛЯ ТРАКТОВ СВЯЗИ И ВЕЩАНИЯ
- 10.4. МЕТОДЫ ПОВЫШЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- Глава 11. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ
- 11.2. ЗВУКОМЕРНЫЕ КАМЕРЫ
- 11.3. ИЗМЕРИТЕЛЬНАЯ АППАРАТУРА И АКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ
- 11.4. МЕТОДЫ ИЗМЕРЕНИЙ ОСНОВНЫХ ХАРАКТЕРИСТИК АППАРАТУРЫ И ПОМЕЩЕНИЙ