| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3.2. Решения, зависящие от времени
Используя решение уравнения Больцмана (21), которое описывает нестационарную плотность частиц в фазовом пространстве, из выражения (30) можно непосредственно получить нестационарные коэффициенты рекомбинации. Однако с помощью уравнения
непрерывности (37), которое для сферически-симметричного потенциала  принимает вид
принимает вид

при условии, что величина  известна, можно получить важный физический результат [27—30]. В уравнении (42а) величина
известна, можно получить важный физический результат [27—30]. В уравнении (42а) величина  отождествляется с радиусом области оттока частиц, а ток, текущий внутрь области [в единицах
отождествляется с радиусом области оттока частиц, а ток, текущий внутрь области [в единицах  равен
равен

В случае когда в газовой или жидкой среде мгновенно образуется диссоциативная пара А и Б, внутри пары  может произойти реакция или за счет диффузионного дрейфа при наличии оттока составляющие пару частицы разлетятся на бесконечно большое расстояние. Определяющей величиной в этом процессе парной рекомбинации являются вероятность рекомбинации
может произойти реакция или за счет диффузионного дрейфа при наличии оттока составляющие пару частицы разлетятся на бесконечно большое расстояние. Определяющей величиной в этом процессе парной рекомбинации являются вероятность рекомбинации  или вероятность выживания
или вероятность выживания  диссоциирующей пары за время
диссоциирующей пары за время  Если реакция протекает между частицей А, находящейся внутри среды (будем называть эти частицы центральными), и частицами другого сорта Б, образующимися в среде на бесконечности под действием непрерывного источника (или же в результате распада пар, участвующих в парной рекомбинации), то такая рекомбинация является гомогенной и характеризуется эффективной двухчастичной константой скорости
Если реакция протекает между частицей А, находящейся внутри среды (будем называть эти частицы центральными), и частицами другого сорта Б, образующимися в среде на бесконечности под действием непрерывного источника (или же в результате распада пар, участвующих в парной рекомбинации), то такая рекомбинация является гомогенной и характеризуется эффективной двухчастичной константой скорости  соответствующей трехмолекулярным реакциям.
соответствующей трехмолекулярным реакциям.
Граничные условия, соответствующие гомогенной рекомбинации, записываются в виде

Эти условия отвечают больцмановскому распределению первоначально образованных по всему пространству ионов, которые непрерывно образуются на бесконечном удалении от положительных ионов. Граничные условия, соответствующие парной рекомбинации, записываются следующим образом:

Эти условия соответствуют образованию  ионов сферически-симметричным источником на расстоянии
ионов сферически-симметричным источником на расстоянии  от центрального положительного иона, т.е. вначале образуются ионные пары с расстоянием между ионами
от центрального положительного иона, т.е. вначале образуются ионные пары с расстоянием между ионами 
Третье граничное условие на сфере  необходимое для решения однородного уравнения, соответствующего (42а), уже содержится в (42а) и получается из него интегрированием по объему сферы радиусом
необходимое для решения однородного уравнения, соответствующего (42а), уже содержится в (42а) и получается из него интегрированием по объему сферы радиусом  В результате получаем следующее квазистационарное условие:
В результате получаем следующее квазистационарное условие:

 условие выполняется в случае, когда
условие выполняется в случае, когда  т.е. на «рекомбинационной» сфере имеется лишь немного ионов. Таким образом, граничное условие (45а) состоит в том, что частота перехода ионов через сферу
т.е. на «рекомбинационной» сфере имеется лишь немного ионов. Таким образом, граничное условие (45а) состоит в том, что частота перехода ионов через сферу  должна быть равна частоте поглощения
должна быть равна частоте поглощения  С помощью уравнений (41) и (42) условие (45а) можйо преобразовать к виду, зависящему от переменной
С помощью уравнений (41) и (42) условие (45а) можйо преобразовать к виду, зависящему от переменной  [см. выражение (33)]. Таким образом, равенство (45а) можно переписать в виде
[см. выражение (33)]. Таким образом, равенство (45а) можно переписать в виде

или

Следовательно, если константа скорости удовлетворяет условию  (что соответствует большим плотностям
(что соответствует большим плотностям  то для самопроизвольной реакции мы имеем
то для самопроизвольной реакции мы имеем  если же
если же  (что соответствует малым плотностям
(что соответствует малым плотностям  то ток
то ток  становится пренебрежимо малым и мы получаем больцмановское распределение. Таким образом, выражения (45), вообще говоря, являются радиационными граничными условиями, поскольку не все ионы, достигающие поверхности сферы
становится пренебрежимо малым и мы получаем больцмановское распределение. Таким образом, выражения (45), вообще говоря, являются радиационными граничными условиями, поскольку не все ионы, достигающие поверхности сферы  поглощаются. Они также имеют аналогию с граничными условиями, которые встречаются в задачах но теплопроводности.
поглощаются. Они также имеют аналогию с граничными условиями, которые встречаются в задачах но теплопроводности.
Гомогенная рекомбинация. Точное решение уравнения (42) для гомогенной рекомбинации при нулевом поле  когда
когда  вписывается в виде [29]
вписывается в виде [29]

где функция ошибок (или интеграл вероятности) дается выражением

Зависимость выражения (46) от времени определяется величинами  . Функция
. Функция  имеет вид
имеет вид

где  — константа скорости реакции, а
— константа скорости реакции, а  — диффузионный коэффициент переноса. Эти величины определяются соответственно выражениями (36) и (35) при условии отсутствия дрейфа
— диффузионный коэффициент переноса. Эти величины определяются соответственно выражениями (36) и (35) при условии отсутствия дрейфа  так что мы имеем
так что мы имеем  Что же касается функции
Что же касается функции

то она обращается в нуль в месте оттока частиц. Таким образом, мы получаем следующее точное выражение для зависящего от времени коэффициента рекомбинации:

При больших плотностях газа  мы имеем
мы имеем  , так что
, так что  обращается в нуль,
обращается в нуль,  Таким образом, мы получаем
Таким образом, мы получаем

Поскольку  обращается в нуль, из (49а) или непосредственно из зависимости
обращается в нуль, из (49а) или непосредственно из зависимости

следует выражение для коэффициента рекомбинации

которое соответствует процессу переноса, определяемому диффузией  и спонтанной
и спонтанной  реакции при начальном хаотическом распределении
реакции при начальном хаотическом распределении  При
При  имеем
имеем  и а стремится к предполагаемой бесконечной скорости реакции. При
и а стремится к предполагаемой бесконечной скорости реакции. При  величина
величина 
становится равной стационарному значению плотности  так что а
так что а  т.е. мы получаем стационарное значение коэффициента рекомбинации.
т.е. мы получаем стационарное значение коэффициента рекомбинации.
Хотя точное решение уравнения (40) для общего вида потенциала  еще не получено, Фланнери [27—30] показал, как можно путем перехода к переменной
еще не получено, Фланнери [27—30] показал, как можно путем перехода к переменной  определяемой выражением (33), найти точные аналитические решения в замкнутой форме. При этом уравнение гомогенной рекомбинации (42а) принимает вид [29, 30]
определяемой выражением (33), найти точные аналитические решения в замкнутой форме. При этом уравнение гомогенной рекомбинации (42а) принимает вид [29, 30]

причем

Здесь величины  даются выражениями (34)-(36). Коэффициент рекомбинации в переходной области равен
даются выражениями (34)-(36). Коэффициент рекомбинации в переходной области равен

Поскольку

величина 

уменьшается от первоначального значения, равного константе скорости реакции, до значения коэффициента рекомбинации, соответствующего большим временам:

Величина  оказывается равной стационарному значению, определяемому выражением (34). Не только зависимость
оказывается равной стационарному значению, определяемому выражением (34). Не только зависимость  при возрастании
при возрастании  демонстрирует [см. выражение (34)] переход от рекомбинации, определяемой скоростью реакции, к рекомбинации, определяемой процессами переноса. Интересные особенности, являющиеся фундаментальными для физики рекомбинации, проявляет также зависимость (53), описывающая поведение
демонстрирует [см. выражение (34)] переход от рекомбинации, определяемой скоростью реакции, к рекомбинации, определяемой процессами переноса. Интересные особенности, являющиеся фундаментальными для физики рекомбинации, проявляет также зависимость (53), описывающая поведение  при фиксированном
при фиксированном  Упомянутая выше зависимость от времени нестационарных коэффициентов рекомбинации наиболее сильно проявляется при высоких плотностях газа, когда
Упомянутая выше зависимость от времени нестационарных коэффициентов рекомбинации наиболее сильно проявляется при высоких плотностях газа, когда  а. В случае чисто кулоновского притяжения между ионами можно написать следующее выражение:
а. В случае чисто кулоновского притяжения между ионами можно написать следующее выражение:

где  — время, измеряемое в единицах
— время, измеряемое в единицах  и приблизительно равное времени, необходимому для того, чтобы ион продиффундировал из граничной в центральную область оттока ионов.
и приблизительно равное времени, необходимому для того, чтобы ион продиффундировал из граничной в центральную область оттока ионов.
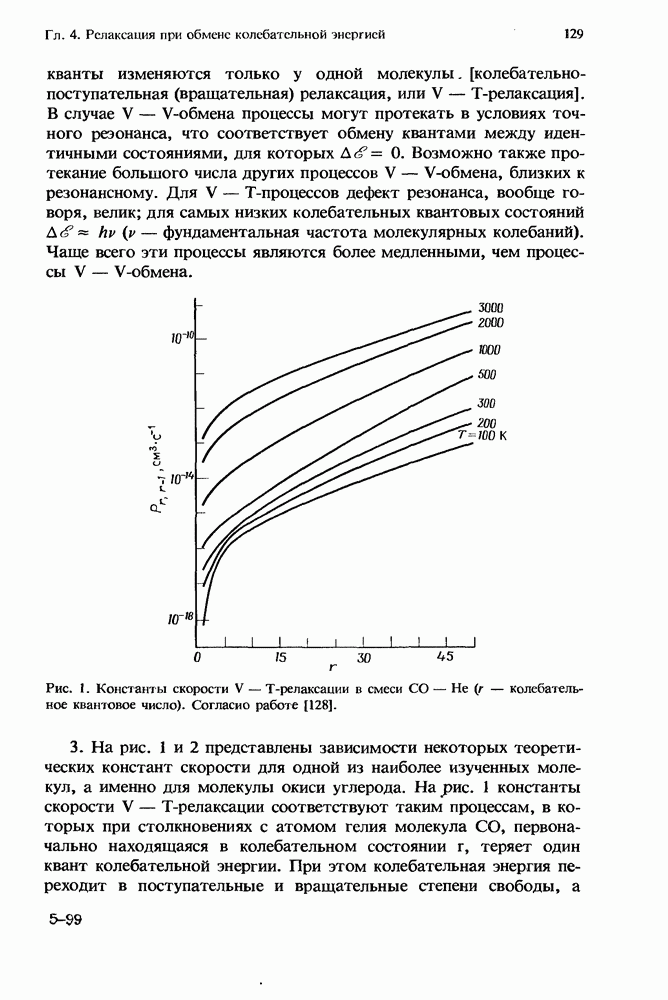
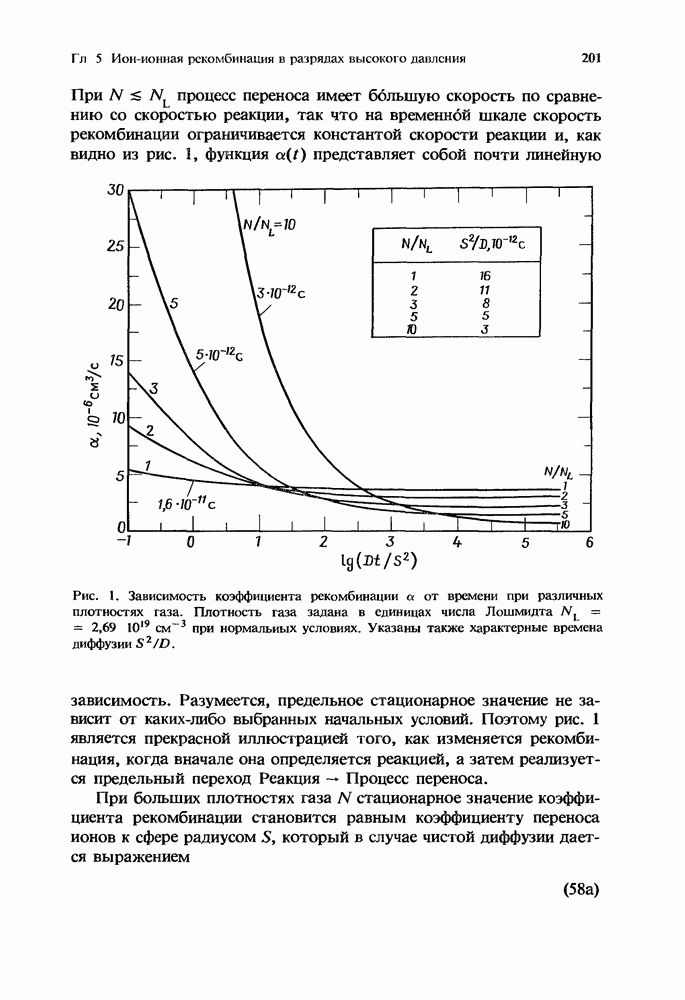
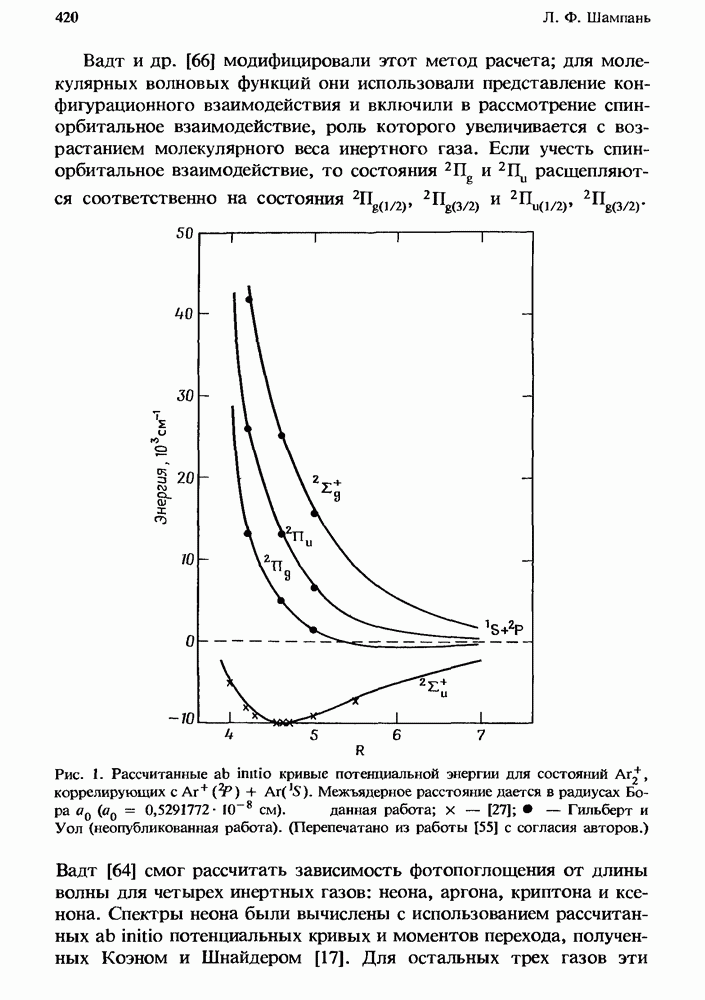
На рис. 1 представлены зависимости  для некоторых значений (1, 2, 3, 5 и 10) плотностей газа
для некоторых значений (1, 2, 3, 5 и 10) плотностей газа  (в единицах числа Лошмидта
(в единицах числа Лошмидта  равного плотности частип
равного плотности частип  при нормальных условиях). Эти коэффициенты рекомбинации [28, 29] соответствуют некоторому фиктивному (но характерному) случаю равных масс
при нормальных условиях). Эти коэффициенты рекомбинации [28, 29] соответствуют некоторому фиктивному (но характерному) случаю равных масс  а.е.) ионных частиц с подвижностью
а.е.) ионных частиц с подвижностью  в буферном газе с такой же молекулярной массой и
в буферном газе с такой же молекулярной массой и  [см. выражение (12)].
[см. выражение (12)].
Поскольку первоначальное распределение ионов предполагается больцмановским, в соответствии с выражением (55) мы имеем  Затем при движении они замещают прореагировавшие ионы за время
Затем при движении они замещают прореагировавшие ионы за время  с. Поскольку скорость рекомбинации определяется предельными переходами к значениям скорости реакции и коэффициенту переноса, то зависимость а от времени наиболее хорошо проявляется при больших плотностях
с. Поскольку скорость рекомбинации определяется предельными переходами к значениям скорости реакции и коэффициенту переноса, то зависимость а от времени наиболее хорошо проявляется при больших плотностях  когда
когда  так что а уменьшается от
так что а уменьшается от  до величины
до величины  соответствующей стационарному состоянию при
соответствующей стационарному состоянию при  Например, зависимость
Например, зависимость  для случая
для случая  отражает тот факт, что а изменяется от значения, определяемого константой скорости реакции, до значения, определяемого коэффициентом переноса. При больших плотностях
отражает тот факт, что а изменяется от значения, определяемого константой скорости реакции, до значения, определяемого коэффициентом переноса. При больших плотностях  скорость реакции велика, поскольку радиус границы оттока частиц
скорость реакции велика, поскольку радиус границы оттока частиц  сжимается до такой степени, что концентрация ионов на границе области оттока значительно увеличивается и компенсирует естественное уменьшение сечения реакции.
сжимается до такой степени, что концентрация ионов на границе области оттока значительно увеличивается и компенсирует естественное уменьшение сечения реакции.
При  процесс переноса имеет большую скорость по сравнению со скоростью реакции, так что на временной шкале скорость рекомбинации ограничивается константой скорости реакции и, как видно из рис. 1, функция
процесс переноса имеет большую скорость по сравнению со скоростью реакции, так что на временной шкале скорость рекомбинации ограничивается константой скорости реакции и, как видно из рис. 1, функция  представляет собой почти линейную зависимость.
представляет собой почти линейную зависимость.

Рис. 1. Зависимость коэффициента рекомбинации а от времени при различных плотностях газа. Плотность газа задана в единицах числа Лошмидта  при нормальных условиях. Указаны также характерные времена диффузии
при нормальных условиях. Указаны также характерные времена диффузии 
Разумеется, предельное стационарное значение не зависит от каких-либо выбранных начальных условий. Поэтому рис. 1 является прекрасной иллюстрацией того, как изменяется рекомбинация, когда вначале она определяется реакцией, а затем реализуется предельный переход Реакция — Процесс переноса.
При больших плотностях газа  стационарное значение коэффициента рекомбинации становится равным коэффициенту переноса ионов к сфере радиусом 5, который в случае чистой диффузии дается выражением
стационарное значение коэффициента рекомбинации становится равным коэффициенту переноса ионов к сфере радиусом 5, который в случае чистой диффузии дается выражением

в случае чистого дрейфа записывается в виде

а в случае диффузионного дрейфа равен

В случае дальнодействующего притяжения имеем следующий закон:  где R — характерный размер, соответствующий данному V, откуда для случая чистого дрейфа коэффициент рекомбинации принимает вид
где R — характерный размер, соответствующий данному V, откуда для случая чистого дрейфа коэффициент рекомбинации принимает вид

расходящийся при  в пределах малых
в пределах малых  в то время как диффузионно-дрейфовый коэффициент рекомбинации, записанный соответственно через неполную и полную гамма-функции у и Г,
в то время как диффузионно-дрейфовый коэффициент рекомбинации, записанный соответственно через неполную и полную гамма-функции у и Г,

при малых R стремится к постоянному пределу. Только для чисто кулоновского притяжения  дрейфовый и диффузионнодрейфовый коэффициенты совпадают в пределе малых
дрейфовый и диффузионнодрейфовый коэффициенты совпадают в пределе малых  Отсюда следует, что метод Ланжевена, основанный на представлениях о дрейфе, верен в силу случайного совпадения в том смысле, что он дает правильное граничное значение только для кулоновского притяжения. Интересно также отметить, что V можно полностью ввести, если в выражении (58а), соответствующем случаю отсутствия поля, заменить 5 на 5 из выражения (58в); кроме того, выражение (58а) само по себе неверно, если для
Отсюда следует, что метод Ланжевена, основанный на представлениях о дрейфе, верен в силу случайного совпадения в том смысле, что он дает правильное граничное значение только для кулоновского притяжения. Интересно также отметить, что V можно полностью ввести, если в выражении (58а), соответствующем случаю отсутствия поля, заменить 5 на 5 из выражения (58в); кроме того, выражение (58а) само по себе неверно, если для  взять реалистическое значение
взять реалистическое значение  вместо произвольного выбора, когда
вместо произвольного выбора, когда  полагают равным
полагают равным  что еще больше делает похожими! выражения для
что еще больше делает похожими! выражения для  и
и  Эти замечания помогают разрешить ранее существовавшую путаницу (см. работу [21], с. 423) между теориями, основанными либо только на представлениях о диффузии [36], либо учитывающих только дрейф [38]. Ни одна из этих теорий не является полностью верной; необходимо одновременно учитывать как диффузию, так и дрейф, хотя ошибки при вычислении величины «к с помощью выражения Ланжевена (586), справедливого только для кулоновского притяжения в пределе высоких плотностей
Эти замечания помогают разрешить ранее существовавшую путаницу (см. работу [21], с. 423) между теориями, основанными либо только на представлениях о диффузии [36], либо учитывающих только дрейф [38]. Ни одна из этих теорий не является полностью верной; необходимо одновременно учитывать как диффузию, так и дрейф, хотя ошибки при вычислении величины «к с помощью выражения Ланжевена (586), справедливого только для кулоновского притяжения в пределе высоких плотностей  когда
когда  становятся пренебрежимо малыми, чего нельзя сказать о выражении (58а). Взаимодействие между диффузией и дрейфом, которое обеспечивает больцмановское распределение плотностей,
становятся пренебрежимо малыми, чего нельзя сказать о выражении (58а). Взаимодействие между диффузией и дрейфом, которое обеспечивает больцмановское распределение плотностей,
является весьма важным, поскольку только с учетом этого взаимодействия мы можем получить общее решение уравнения Больцмана (21) для плотности частиц в фазовом пространстве [29] при промежуточных и больших 
Выражения (58а) и (58в) для рекомбинации в газах получены Харпером [36] и Бейтсом [4]. Аналогичные выражения (в которых  для процесса коагуляции коллоидных суспензий
для процесса коагуляции коллоидных суспензий  в жидкости с диэлектрической проницаемостью
в жидкости с диэлектрической проницаемостью  представили Смолуховский [46] и Дебай [17]. Поэтому уравнение непрерывности (42) для диффузионного дрейфа иногда называют уравнением Дебая — Смолуховского. Это уравнение первоначально было выведено на основе представлений о процессе свободного стохастического блуждания частиц. Однако мы представили его в виде, который автоматически включает граничные условия (45) для излучения. Интересная особенность состоит в том, что уравнение (42) является естественным следствием фундаментальной микроскопической теории [29], кратко рассмотренной в разд. 5.3.1. С помощью этой теории и выражения (28) уравнение (42) можно полностью обобщить на случай ионного оттока произвольного вида на основе рассмотрения детальной столкновительной кинетики, которая в свою очередь зависит от плотности частиц в фазовом пространстве
представили Смолуховский [46] и Дебай [17]. Поэтому уравнение непрерывности (42) для диффузионного дрейфа иногда называют уравнением Дебая — Смолуховского. Это уравнение первоначально было выведено на основе представлений о процессе свободного стохастического блуждания частиц. Однако мы представили его в виде, который автоматически включает граничные условия (45) для излучения. Интересная особенность состоит в том, что уравнение (42) является естественным следствием фундаментальной микроскопической теории [29], кратко рассмотренной в разд. 5.3.1. С помощью этой теории и выражения (28) уравнение (42) можно полностью обобщить на случай ионного оттока произвольного вида на основе рассмотрения детальной столкновительной кинетики, которая в свою очередь зависит от плотности частиц в фазовом пространстве  Однако, если известна плотность
Однако, если известна плотность  можно получить стационарное значение а непосредственно из выражения (30), вместо того чтобы решать уравнение (42) с помощью (28).
можно получить стационарное значение а непосредственно из выражения (30), вместо того чтобы решать уравнение (42) с помощью (28).
Парная рекомбинация. Зависимость  определяемая выражением (53), имеет важное значение не только для анализа лабораторных экспериментов и медицинской радиологии, но также в случаях, когда интенсивная ионизация создается внутри локальной системы под действием пучка высокоэнергетических частиц или излучения, так что большое число ионов за счет диффузии может выйти за пределы этой локальной системы и нанести значительный ущерб, прежде чем произойдет их нейтрализация. Скорость исчезновения ионных пар, рассеянных вдоль направления ионизующих частиц или излучения, зависит от времени, а определение ее представляет серьезную проблему. В случае парной рекомбинации с учетом граничных условий (44) и
определяемая выражением (53), имеет важное значение не только для анализа лабораторных экспериментов и медицинской радиологии, но также в случаях, когда интенсивная ионизация создается внутри локальной системы под действием пучка высокоэнергетических частиц или излучения, так что большое число ионов за счет диффузии может выйти за пределы этой локальной системы и нанести значительный ущерб, прежде чем произойдет их нейтрализация. Скорость исчезновения ионных пар, рассеянных вдоль направления ионизующих частиц или излучения, зависит от времени, а определение ее представляет серьезную проблему. В случае парной рекомбинации с учетом граничных условий (44) и  общего вида можно написать следующее аналитическое решение [29, 30], зависящее от времени:
общего вида можно написать следующее аналитическое решение [29, 30], зависящее от времени:

где R определяется выражением (336), а  выражениями (52) и (57). Зависящие от времени безразмерные величины
выражениями (52) и (57). Зависящие от времени безразмерные величины  имеют вид
имеют вид

Вероятность того, что каждая ионная пара не подвергнется парной рекомбинации, дается выражением

(здесь интегрирование производится по объему У области, внешней по отношению к поверхности Асферической области оттока ионов). Величину  лучше вычислять косвенно из выражения
лучше вычислять косвенно из выражения

где  — число первоначально образованных ионов, равное
— число первоначально образованных ионов, равное  Поскольку при
Поскольку при  величина
величина  в (42а) обращается в нуль, частоту рекомбинации можно записать в виде
в (42а) обращается в нуль, частоту рекомбинации можно записать в виде

Без потери общности можно положить, что источник и отток  ионов совпадают
ионов совпадают  Таким образом,
Таким образом,  в интеграл (606) выражение 1
в интеграл (606) выражение 1

получаем вероятность рекомбинации

которая увеличивается со временем от нуля приблизительно по закону  и стремится к предельному значению
и стремится к предельному значению  Из выражений (62), (53) и (34) мы имеем следующие точные соотношения:
Из выражений (62), (53) и (34) мы имеем следующие точные соотношения:

Эти соотношения связывают нестационарный коэффициент гомогенной рекомбинации  с нестационарной вероятностью
с нестационарной вероятностью 
того, что произойдет рекомбинация ионной пары, и с вероятностью  того, что она избежит рекомбинации в процессе парной рекомбинации
того, что она избежит рекомбинации в процессе парной рекомбинации  с выражениями (40)]. Таким образом, в двух различных задачах, связанных с зависимостью от времени, таких, как гомогенная рекомбинация (процесс определяется непрерывно работающим на бесконечности источником ионов) и внутрипарная (парная) рекомбинация (процесс вначале обусловлен мгновенно действующим источником ионных пар, образующихся в среде, например под действием лазерного импульса, и управляется относительными значениями константы скорости и коэффициента переноса), используются одни и те же основные величины. Эти процессы являются аналогичными в том смысле, что они подчиняются одному и тому же диффузионно-дрейфовому уравнению (42) (уравнению Дебая — Смолуховского), которое решается при различных граничных условиях (43) или (44).
с выражениями (40)]. Таким образом, в двух различных задачах, связанных с зависимостью от времени, таких, как гомогенная рекомбинация (процесс определяется непрерывно работающим на бесконечности источником ионов) и внутрипарная (парная) рекомбинация (процесс вначале обусловлен мгновенно действующим источником ионных пар, образующихся в среде, например под действием лазерного импульса, и управляется относительными значениями константы скорости и коэффициента переноса), используются одни и те же основные величины. Эти процессы являются аналогичными в том смысле, что они подчиняются одному и тому же диффузионно-дрейфовому уравнению (42) (уравнению Дебая — Смолуховского), которое решается при различных граничных условиях (43) или (44).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Введение и общий обзор
- 1.1. Газовые лазеры. Введение
- 1.2. Краткий исторический обзор
- 1.2.2. Лазеры с прямым возбуждением
- 1.2.3. Фотодиссоциативные лазеры
- 1.2.4. Химические лазеры
- 1.2.5. Эксимерные лазеры
- 1.3. Принципы действия лазерных систем
- 1.3.2. Создание возбужденных состояний
- 1.3.3. Кинетика возбужденных состояний
- 1.3.4. Спектроскопия возбужденных состояний и извлечение лазерной энергии
- 1.4. Направления будущей работы
- 2. Образование отрицательных йодов в газовых лазерах
- 2.2. Роль отрицательных ионов в газовых лазерах
- 2.2.2. Образование возбужденных состояний при ион-ионной рекомбинации
- 2.2.3. Образование возбужденных состояний на верхнем лазерном уровне непосредственно в процессе диссоциативного прилипания
- 2.2.4. Опустошение уровней электронами
- 2.2.5. Разрушение молекул, являющихся донорами атомов галогена
- 2.2.6. Неустойчивости разряда
- 2.3. Механизмы образования отрицательных ионов
- 2.4. Методы измерений
- 2.4.2. Масс-спектрометрические измерения
- 2.4.3. Эксперименты с дрейфовой трубкой
- 2.4.4. Разряды с плоской конфигурацией, поддерживаемые электронным пучком
- 2.5. Критический обзор экспериментальных данных
- 2.5.2. Трифторид азота (NF3)
- 2.5.3. Хлористый водород (НСl)
- 2.5.4. Дибромид ртути (HgBr2)
- 2.5.5. Другие газы, представляющие интерес
- 3. Кинетика ионов при высоких давлениях
- 3.2. Скорости ион-молекулярных реакций
- 3.2.2. Трехмолекулярные реакции
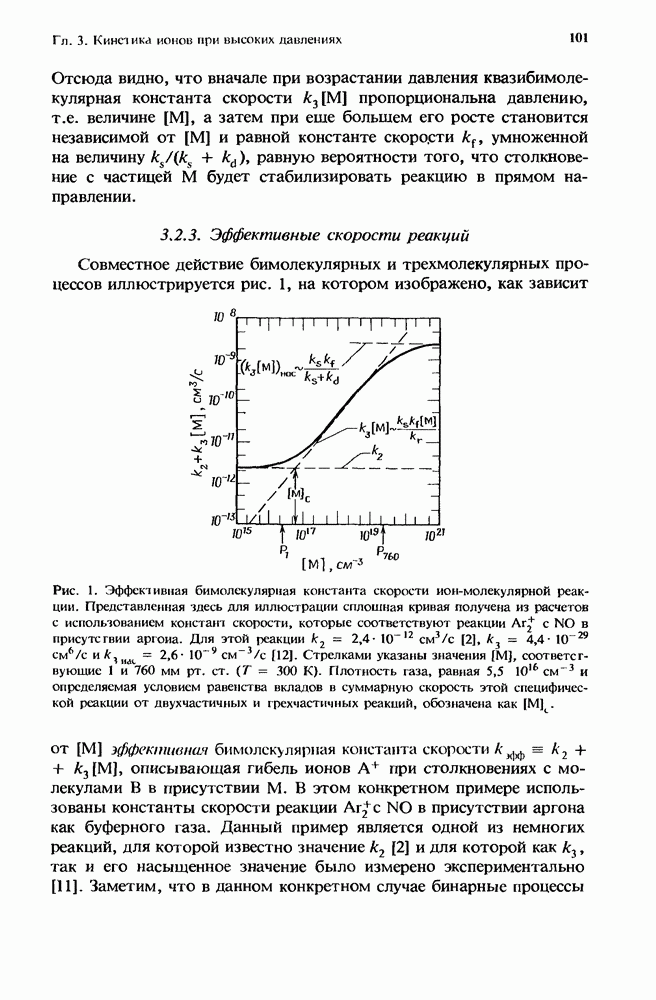
- 3.2.3. Эффективные скорости реакций
- 3.2.4. Зависимость от давления
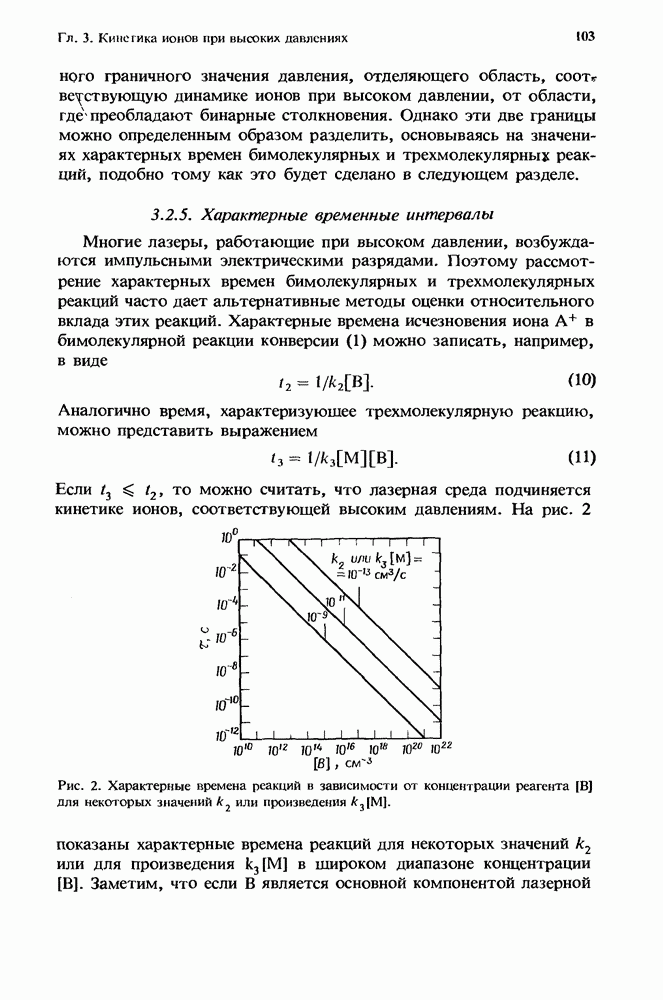
- 3.2.5. Характерные временные интервалы
- 3.3. Энергетический подход к рассмотрению ионных реакций
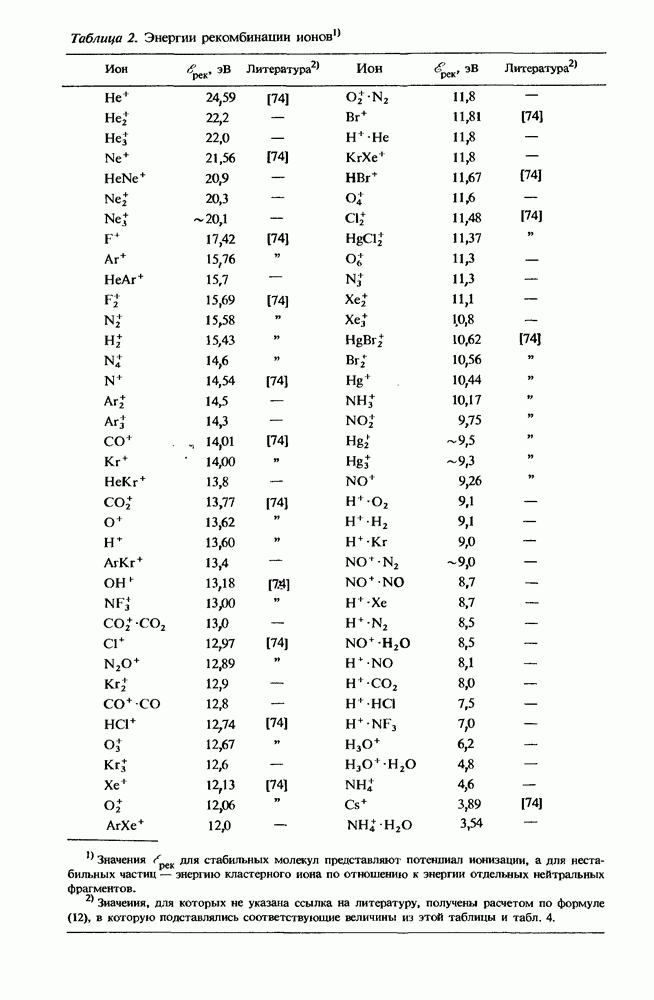
- 3.2.2. Энергетика отрицательных ионов
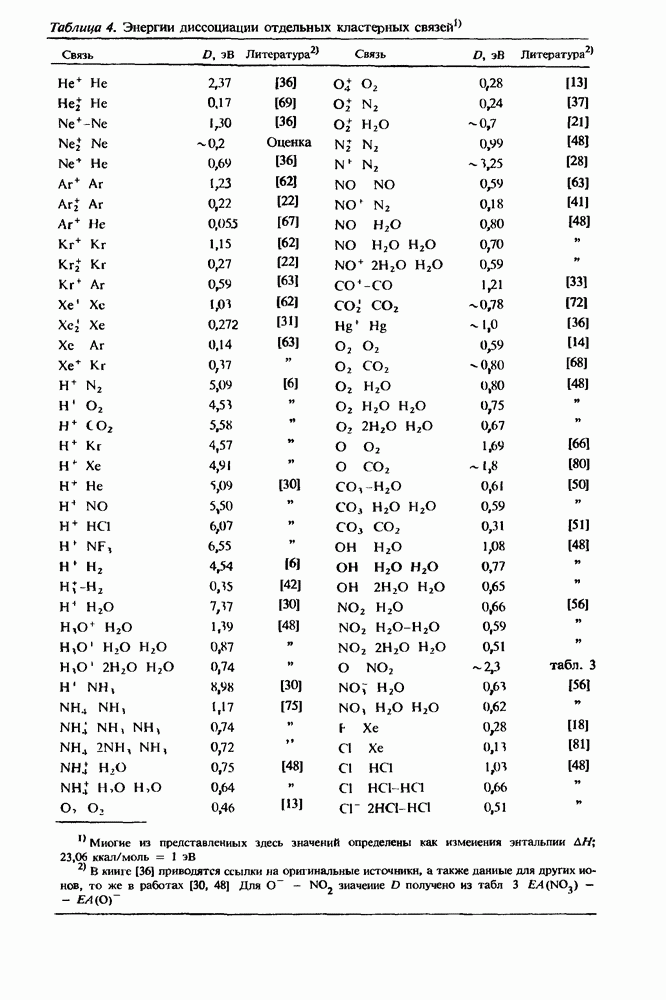
- 3.3.3. Энергия связи в кластерах
- 3.3.4. Равновесие и условие стационарности
- 3.3.5. Продукты диссоциации и примеси
- 3.4. Трехмолекулярная ионная кинетика в тлеющем разряде
- 3.4.2. Конверсия ионов неона в ионы ксенона
- 3.4.3. Рекомбинация кластерных ионов
- 3.4.4. Ион-ионная рекомбинация
- 3.4.5. Трехчастичное прилипание электрона
- 3.5. Способы получения данных по кинетике ионов при высоком давлении
- 3.6. Заключительные замечания
- 4. Релаксация молекул при обмене колебательной энергией
- 4.2. Кинетические уравнения
- 4.2.2. Модели релаксации
- 4.2.2.2. Бинарные смеси газовых молекул
- 4.2.2.3. V — Т-релаксация простого гармонического осциллятора
- 4.2.2.4. V — V-релаксация в простом гармоническом осцилляторе
- 4.2.2.5. Релаксация ангармонического осциллятора
- 4.2.2.6. V — V-накачка в многоатомных молекулах
- 4.2.2.7. Аналитические решения кинетических уравнений
- 4.3. Реализация в экспериментах
- 4.3.2. Лазеры на окиси углерода
- 4.3.2.2. Электроразрядные СО-лазеры
- 4.3.2.3. Измерение скоростей V — Т- и V — V-релаксации для высоколежащих колебательных состояний молекулы СО
- 4.3.2.4. Кинетическая модель СО-лазеров
- 4.3.3. Многоатомные молекулы
- 4.3.4. Химические реакции и разделение изотопов в системах с V — V-накачкой
- 4.3.4.3. Разделение изотопов при V — V-накачке
- 5. Ион-ионная рекомбинация в разрядах высокого давления
- 5.2. Коэффициент рекомбинации как функция плотности газа
- 5.2.2. Промежуточные значения плотности газа
- 5.3. Фундаментальная микроскопическая теория рекомбинации
- 5.3.2. Решения, зависящие от времени
- 5.3.3. Зависимость от плотности ионов
- 5.4. Константы рекомбинации для различных процессов с участием галогенидов инертных газов
- 5.5. Заключение
- 6. Электрон-ионная рекомбинация в газовых лазерах
- 6.2. Основные процессы и определения
- 6.3. Коэффициенты рекомбинации и их зависимость от энергии
- 6.3.2. Трехчастичная рекомбинация
- 6.4. Условия проявления различных процессов рекомбинации
- 6.4.2. Ударно-радиационная рекомбинация
- 6.5. Состояния, образующиеся при рекомбинации
- 6.6. Приложение к лазерным системам
- 7. Столкновительные процессы в химических лазерах
- 7.2. Обмен энергией между колебательными и вращательными степенями свободы
- 7.2.1. Теория обмена энергией между колебательными и поступательными степенями свободы
- 7.2.2. Теория V — R-обмена
- 7.2.3. Экспериментальное подтверждение существования V-R-обмена
- 7.2.3.2. Исследования методом двойного резонанса
- 7.2.3.3. Лазерное моделирование эффектов, связанных с V-К-обменом
- 7.3. Обмен энергией между вращательными уровнями
- 7.3.1.2. Флуоресценция молекул, возбуждаемых в процессе столкновений
- 7.3.1.3. Флуоресценция молекул при лазерной накачке
- 7.3.2. Исследование вращательной релаксации методом двойного ИК резонанса
- 7.4. Частоты столкновительных процессов, полученные из данных по уширению спектральных линий давлением
- 7.5. Заключительные замечания
- 8. Мощные лазерные усилители на СО2
- 8.2. Физические процессы образования инверсии населенностей в СО2-лазере
- 8.2.2. Радиационные времена жизни
- 8.2.3. Кинетическая модель
- 8.2.4. Ввод энергии с помощью электрического разряда
- 8.2.5. Межмолекулярные взаимодействия
- 8.2.6. Кинетические уравнения
- 8.2.7. Выражение для коэффициента усиления слабого сигнала
- 8.2.8. Расчет и измерения усиления слабого сигнала
- 8.3. Кпд CO2-усилителей
- 8.3.2. Эффективность съема энергии с усилителя
- 9. Эксимерные лазеры; спектроскопия и химия возбужденных состояний
- 9.2. Спектроскопия эксимерных систем
- 9.2.2. Электронные состояния и потенциальные кривые
- 9.2.2.2. Галогениды инертных газов
- 9.2.2.3. Молекулы галогенов и галогениды элементов подгруппы IIб
- 9.3. Химические свойства возбужденных состояний
- 10. Лазеры на галогенидах инертных газов
- 10.2. Кинетика образования верхнего лазерного уровня
- 10.2.3. Образование KrF* в разряде
- 10.2.4. Образование XeF* при накачке разрядом
- 10.3. Кинетика тушения галогенидов инертных газов
- 10.4. Накачка
- 10.4.1. Накачка электронным пучком
- 10.4.2. Накачка разрядом
- 10.4.2.2. Устойчивость разряда
- 10.4.2.3. Коэффициент усиления мощности разряда
- 10. 5. Вывод мощности
- 10.5.1. Вывод мощности в KrF*-лазере
- 10.5.2. Вывод мощности в XcF*-лазере
- 11. Свойства разряда, управляемого электронным пучком, в ХеСЦВ — Х)- и HgBr(B — Х)-лазерах
- 11.2. Разряды, управляемые электронным пучком
- 11.2.1. Лазеры на электронных переходах
- 11.3. Лазеры на галогенидах инертных газов и галогенидах ртути
- 11.3.1.1. Возбуждение колебательных уровней и диссоциативное прилипание электрона к молекуле НСl
- 11.3.2. Разряды в диссоциативном лазере
- 11.3.2.2. Ионизация и диссоциативное прилипание для HgBr2
- 11.4. Возбужденные состояния и кинетика ионов
- 11.4.1.2. Концентрации частиц
- 11.4.2. Процессы образования ионных и возбужденных состояний в разряде диссоциативного HgBr-лазера
- 11.4.2.2. Концентрация частиц
- 11.4.3. Диссоциация галогенидов
- 11.4.4. Процессы с участием атомов инертных газов в p-состояниях
- 11.5. Заключение
- 12. Нестационарное поглощение в УФ области спектра
- 12.2. Поглощение в чистых инертных газах
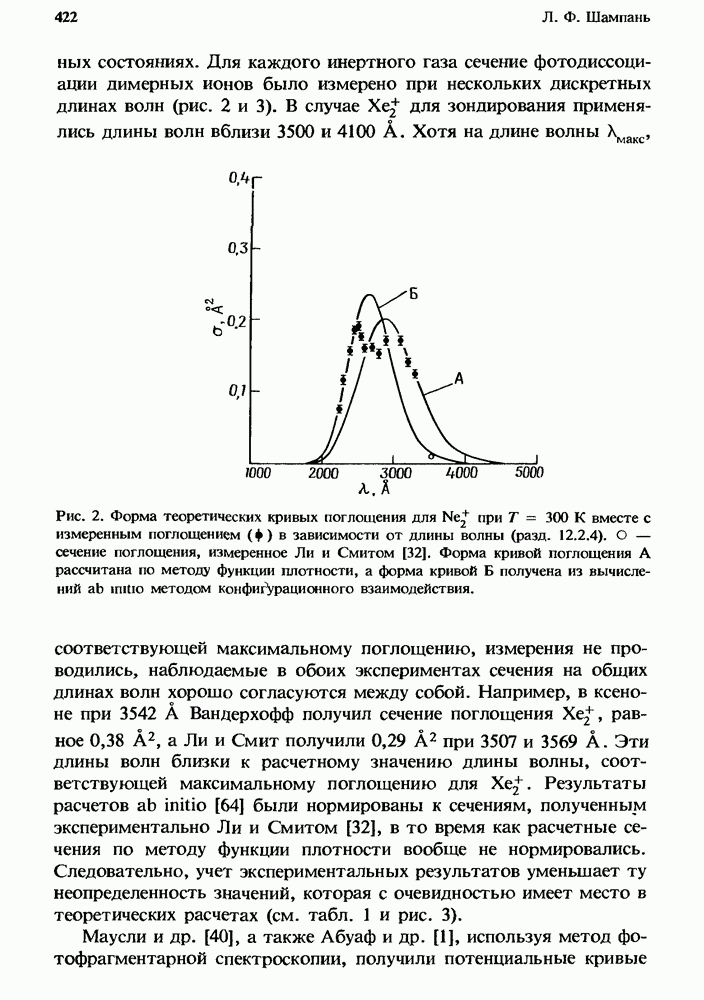
- 12.2.2. Сечение фотопоглощения
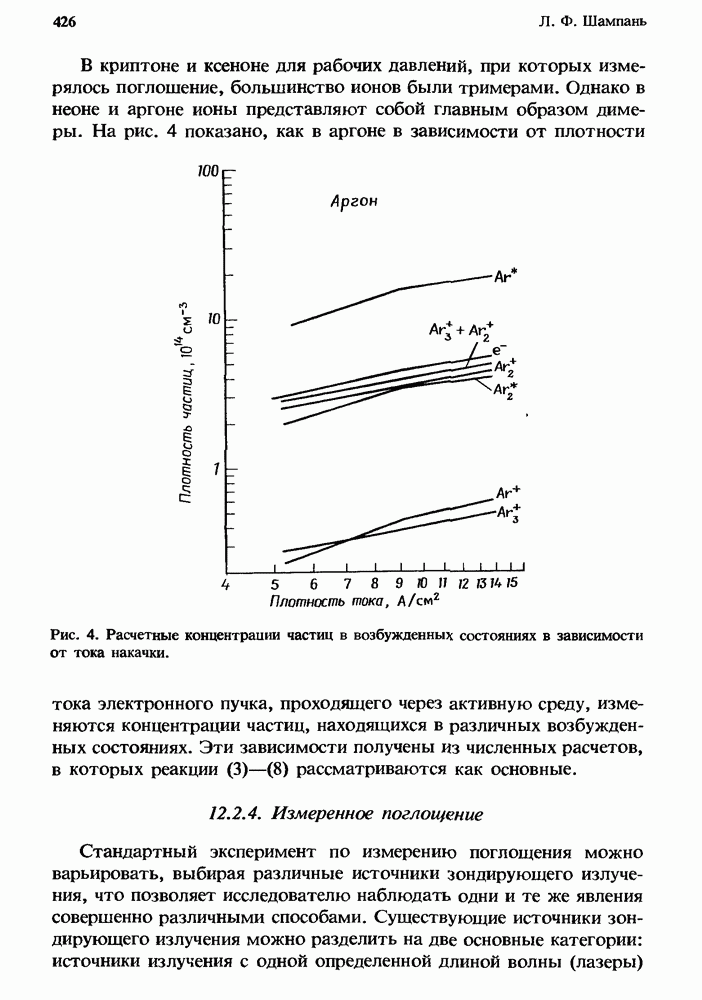
- 12.2.3. Концентрации частиц, находящихся в возбужденных состояниях
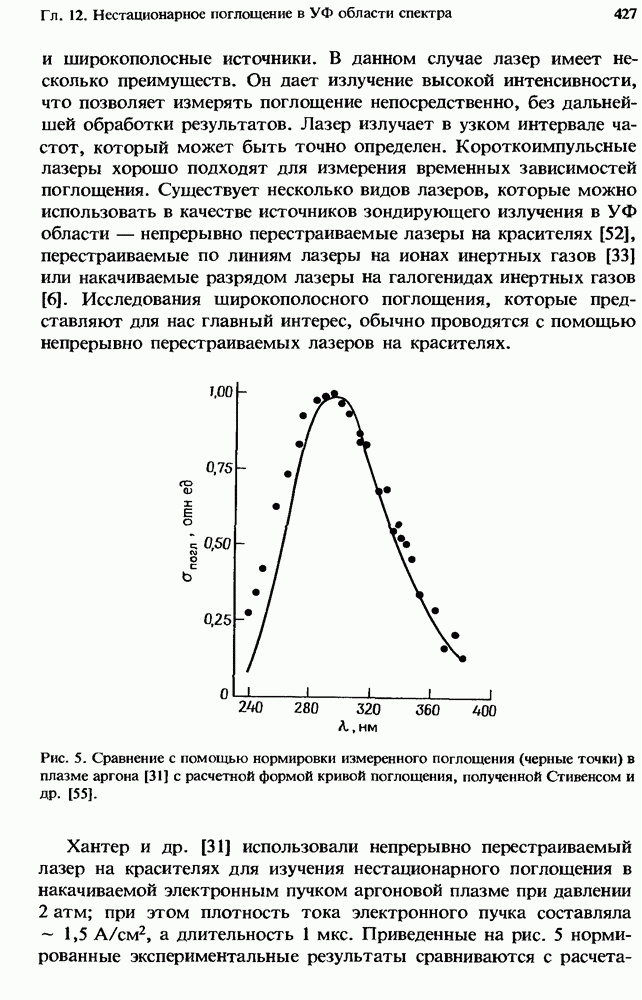
- 12.2.4. Измеренное поглощение
- 12.2.5. Атомные линии поглощения в плазме чистых инертных газов
- 12.3. Двухкомпонентные смеси
- 12.4. Пример
- 12.5. Однородно распределенные потери
- 12.5.2. Распределение поля в приближении цепной линии
- 12.5.3. Метод параметризации
- 13. Самостоятельные разряды с предыонизацией, используемые для накачки лазерных сред
- 13.2. Экспериментальные исследования самостоятельного разряда с предыонизацией
- 13.2.2. Искровая предыонизация
- 13.2.3. Предыонизация излучением высокой энергии
- 13.2.4. Взаимное расположение источника предыонизации и разрядных электродов
- 13.3. Физические механизмы предыонизации УФ излучением
- 13.3.1. Спектр искрового разряда
- 13.3.2. Фотоионизационные спектры
- 13.3.3. Поглощение УФ излучения
- 13.3.4. Измерения плотности предыонизации от отдельной искры
- 13.3.5. Расчет числа фотонов от одиночного искрового разряда
- 13.3.6. Фотоионизация, создаваемая решеткой искровых разрядников
- 13.4. Физика самостоятельного тлеющего разряда
- 13.4.1.2. Взаимодействие разряда и задающей цепи; управление током разряда
- 13.4.1.3. Эффективность накачки лазера
- 13.4.2. Формирование разряда
- 13.4.2.2. Нестационарные разряды
- 13.4.3. Требования к предыонизации
- 13.5. Заключительное обсуждение
- 14. Устойчивость разрядов в эксимерных лазерах
- 14.2. Ионизационная неустойчивость, общая теория
- 14.2.2. Возникновение и характеристики развития ионизационной неустойчивости
- 14.2.2.1. Кинетика одноступенчатой ионизации
- 14.2.2.2. Кинетика двухступенчатой ионизации
- 14.2.2.3. Кинетика трехступенчатой ионизации
- 14.3. Ионизационная неустойчивость в разрядах KrF*-лазеров
- 14.3.2. Методы подавления неустойчивости
- 14.4. Выводы и заключение
- Приложение 1. Теория ионизационной неустойчивости
- Приложение 2. Константы суммарной скорости ионизации