| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ
Звуковое давление. Положим, что давление среды в отсутствие звуковых колебаний равно  это давление называют статическим. При прохождении звуковой волны давление в каждой точке среды будет непрерывно изменяться: в моменты сгущения частиц оно больше статического, а в моменты разрежения — меньше. Разность между мгновенным давлением
это давление называют статическим. При прохождении звуковой волны давление в каждой точке среды будет непрерывно изменяться: в моменты сгущения частиц оно больше статического, а в моменты разрежения — меньше. Разность между мгновенным давлением  и статическим
и статическим  в той же точке среды, т. е. переменная составляющая давления называется звуковым давлением
в той же точке среды, т. е. переменная составляющая давления называется звуковым давлением 
Звуковое давление — величина знакопеременная. Давление  сила, действующая на единицу площади, т. е.
сила, действующая на единицу площади, т. е.  Поэтому за единицу давления в системе
Поэтому за единицу давления в системе  принимают ньютон на квадратный метр, а в абсолютной
принимают ньютон на квадратный метр, а в абсолютной  системе единиц — дину на квадратный сантиметр:
системе единиц — дину на квадратный сантиметр:  Па (паскаль)
Па (паскаль)  В системах связи и вещания имеют дело с звуковыми давлениями, по амплитуде, не превышающими 100 Па, т. е., по крайней мере, в 1000 раз меньше, чем нормальное атмосферное давление.
В системах связи и вещания имеют дело с звуковыми давлениями, по амплитуде, не превышающими 100 Па, т. е., по крайней мере, в 1000 раз меньше, чем нормальное атмосферное давление.
Скорость колебаний. Если давления неодинаковы в соседних точках среды, то ее частицы стремятся сместиться в сторону минимального давления. При знакопеременной разности давлений возникает колебательное движение частиц среды около своего статического положения. Скорость колебаний этих частиц  где
где  смещение частиц. Скорость колебаний обычно измеряют в метрах или сантиметрах в секунду. Не следует путать эту скорость со скоростью звука. Скорость звука — постоянная величина для данной среды и метеорологических условий, а скорость колебаний — переменная, причем если частица среды перемещается по направлению распространения волны, то скорость считают положительной, а при
смещение частиц. Скорость колебаний обычно измеряют в метрах или сантиметрах в секунду. Не следует путать эту скорость со скоростью звука. Скорость звука — постоянная величина для данной среды и метеорологических условий, а скорость колебаний — переменная, причем если частица среды перемещается по направлению распространения волны, то скорость считают положительной, а при  атном перемещении частицы — отрицательной.
атном перемещении частицы — отрицательной.

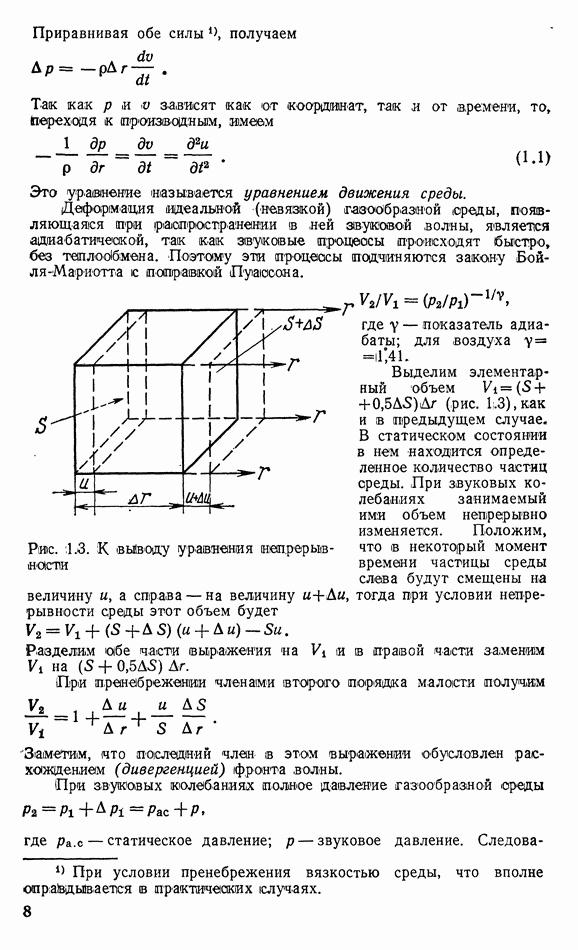
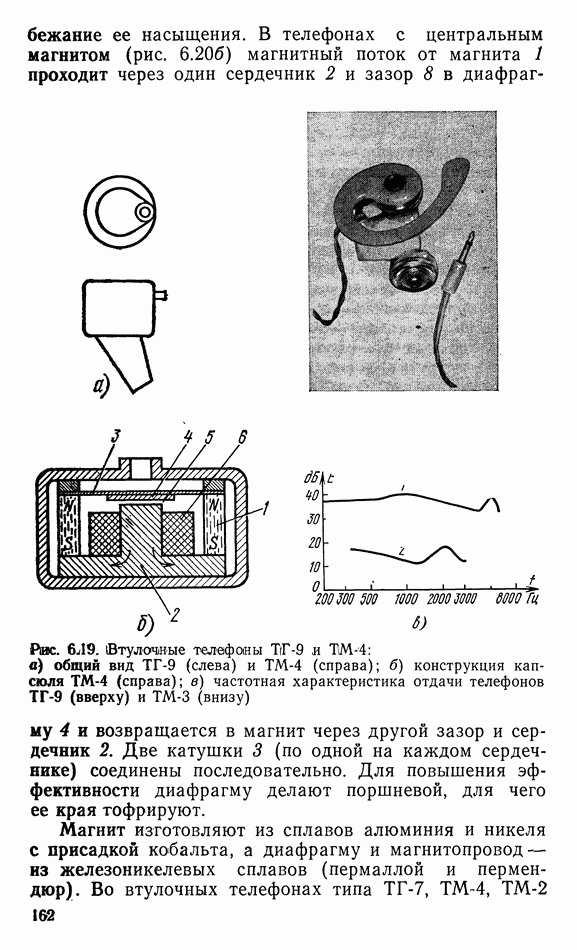
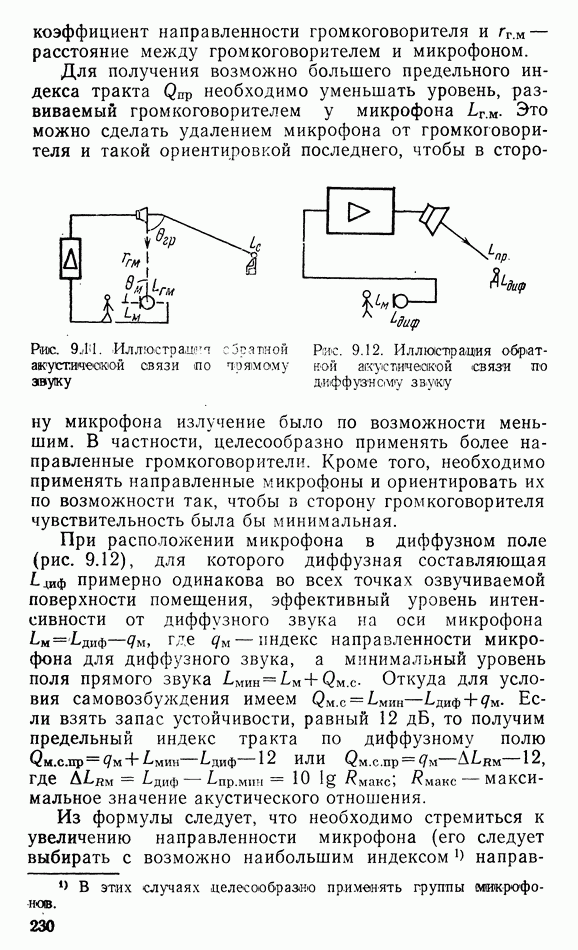
Рис. 1.2. К «выводу уравнения движения
Определим связь между звуковым давлением и скоростью колебаний. Возьмем элементарный объем, заключенный между фронтами волн, находящимися на расстоянии  друг от друга, с боковыми поверхностями, расположенными вдоль звуковых лучей (рис. 1.2). Как видно из рисунка, среда в этом объеме находится под действием разности давлений
друг от друга, с боковыми поверхностями, расположенными вдоль звуковых лучей (рис. 1.2). Как видно из рисунка, среда в этом объеме находится под действием разности давлений  следовательно, испытываемая ею сила
следовательно, испытываемая ею сила

где  площадь, выделенная на поверхности фронта волны. С другой стороны, по второму закону Ньютона сила инерции
площадь, выделенная на поверхности фронта волны. С другой стороны, по второму закону Ньютона сила инерции

где  масса среды, заключенной в этом объеме;
масса среды, заключенной в этом объеме;  средняя плотность среды.
средняя плотность среды.
Приравнивая обе силы получаем 

Так как  зависят как от координат, так
зависят как от координат, так  от времени, то, переходя к производиым, имеем
от времени, то, переходя к производиым, имеем

Это уравнение «взывается уравнением движения среды.
Деформация (идеальной (невязкой) газообразной среды, появляющаяся при (распространении в ней звуковой волны, является адиабатической, так как звуковые процессы (происходят быстро, без теплообмена. Поэтому эти (процессы подчиняются закону Бойля-Мариотта c поправкой Пуассона.

где у — показатель адиабаты; для воздуха 

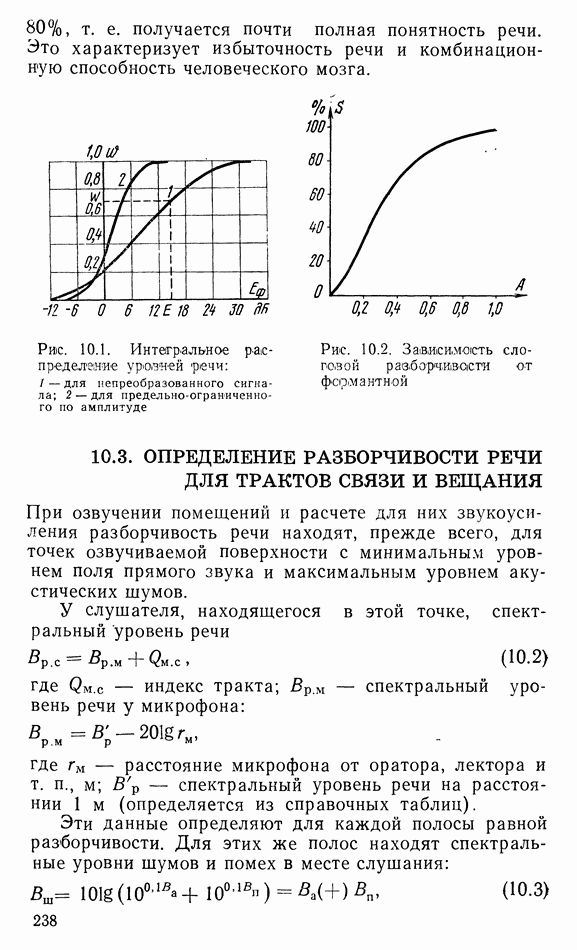
Рис. 1.3. К выводу уравнения непрерывности
Выделим элементарный объем  (рис. 1.3), как и в предыдущем случае, В статическом состоянии в нем находится определенное количество частиц среды. При звуковых колебаниях занимаемый ими объем непрерывно изменяется. Положим, что в некоторый момент времени частицы среды слева будут смещены на величину и, а справа — на величину
(рис. 1.3), как и в предыдущем случае, В статическом состоянии в нем находится определенное количество частиц среды. При звуковых колебаниях занимаемый ими объем непрерывно изменяется. Положим, что в некоторый момент времени частицы среды слева будут смещены на величину и, а справа — на величину  тогда при условии непрерывности среды этот объем будет
тогда при условии непрерывности среды этот объем будет

Разделим обе части выражения на  и в правой части заменим
и в правой части заменим  на
на 
При пренебрежении членами второго порядка малости получим

Заметим, что последний член в этом выражении обусловлен расхождением (дивергенцией) фронта волны.
При звуковых колебаниях полное давление газообразной среды

где  статическое давление;
статическое давление;  звуковое давление.
звуковое давление.
Следовательно,  Подставив
Подставив  в уравнение закона Пуассона, получим
в уравнение закона Пуассона, получим

Как указывалось ранее,  поэтому
поэтому

Переходя к производным, нажодмм

Это уравнение называют уравнением состояния среды. Если это уравнение продифференцировать дважды по  и переставить порядок дафференодирования, то получим
и переставить порядок дафференодирования, то получим

Подставляя в него производную  из уравнения движения
из уравнения движения  получим уравнение для звукового давления
получим уравнение для звукового давления

Заменяя в нем

получим

Это уравнение называют волновым уравнением Вебстера.
Общее решение волнового уравнения имеет вид

Если в первую составляющую решения вместо  подставить
подставить  то для неизменности аргумента следует вместо
то для неизменности аргумента следует вместо  подставить
подставить  Следовательно, первая составляющая представляет собой волну, распространяющуюся в сторону положительных значений
Следовательно, первая составляющая представляет собой волну, распространяющуюся в сторону положительных значений  вторая — в обратном направлении. Из тех же данных следует, что с — скорость распространения волны, так как
вторая — в обратном направлении. Из тех же данных следует, что с — скорость распространения волны, так как  Таким образом, скорость звука
Таким образом, скорость звука  т. е. определяется статическим давлением среды и ее плотностью.
т. е. определяется статическим давлением среды и ее плотностью.
Акустическое сопротивление. Разность давлений является причиной движения частиц среды, а разность потенциалов — причиной движения электрических зарядов. Скорость колебаний частиц среды аналогична скорости движения зарядов — силе тока. Аналогично электрическому сопротивлению введено понятие волнового акустического сопротивления. Удельным волновым акустическим сопротивлением называют отношение звукового давления к скорости колебаний. Удельным оно называется потому, что представляет собой сопротивление для единицы площади фронта волны. Для краткости его часто называют акустическим сопротивлением

Акустическое сопротивление определяется прежде всего свойствами среды. В ряде случаев оно зависит от частоты колебаний и от формы фронта волны. В общем виде оно комплексное:

где  и
и  — активная и реактивная составляющие акустического сопротивления. Наличие реактивной составляющей свидетельствует о том, что между звуковым давлением и скоростью колебаний есть сдвиг фаз. Этот сдвиг определяется из соотношения
— активная и реактивная составляющие акустического сопротивления. Наличие реактивной составляющей свидетельствует о том, что между звуковым давлением и скоростью колебаний есть сдвиг фаз. Этот сдвиг определяется из соотношения

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. ЗВУКОВОЕ ПОЛЕ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ
- 1.3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 1.4. ПЛОСКАЯ ВОЛНА
- 1.5. СФЕРИЧЕСКАЯ ВОЛНА
- 1.6. ЦИЛИНДРИЧЕСКАЯ ВОЛНА
- Глава 2. ОСНОВНЫЕ СВОЙСТВА СЛУХА
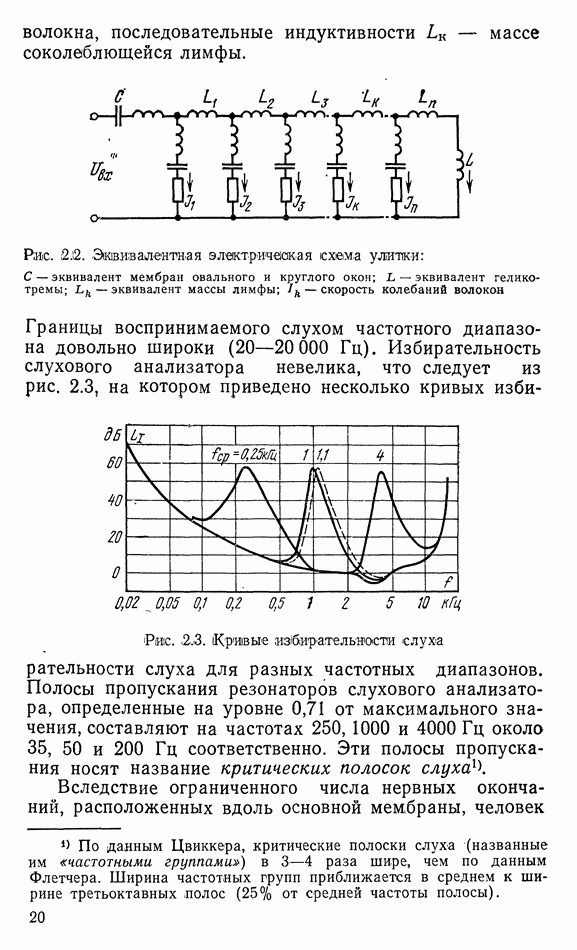
- 2.2. ВОСПРИЯТИЕ ПО ЧАСТОТЕ
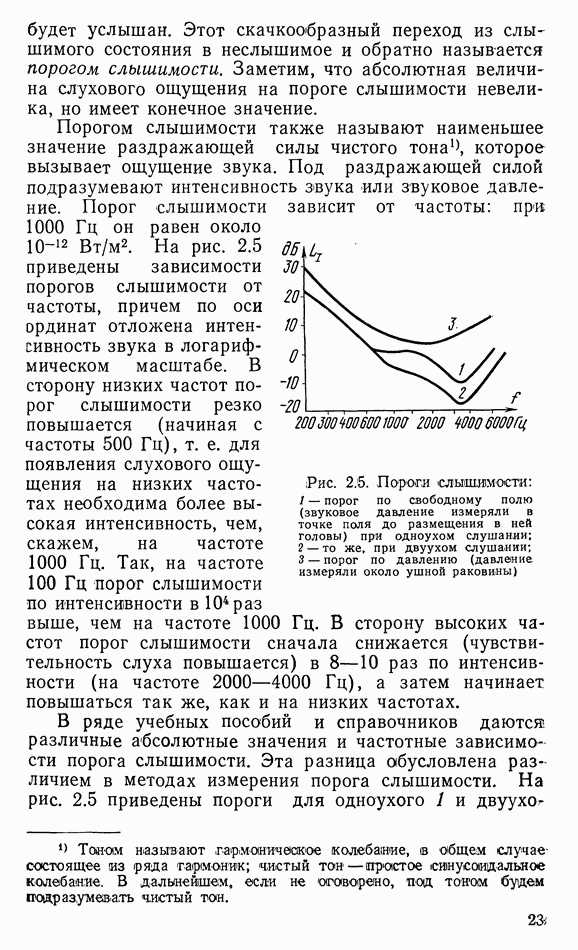
- 2.3. ПОРОГ СЛЫШИМОСТИ
- 2.4. ВОСПРИЯТИЕ ПО АМПЛИТУДЕ
- 2.5. УРОВНИ
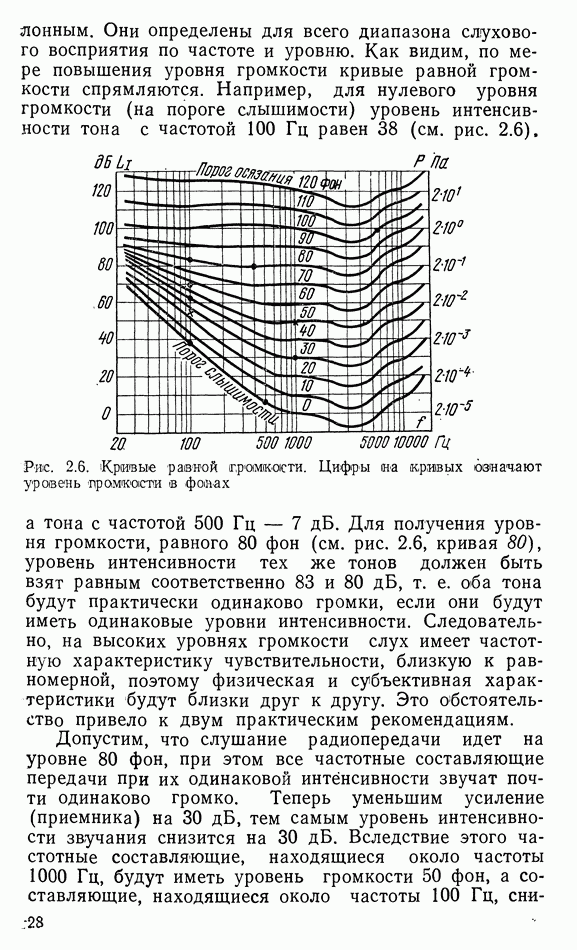
- 2.6. ГРОМКОСТЬ И УРОВЕНЬ ГРОМКОСТИ ЗВУКА
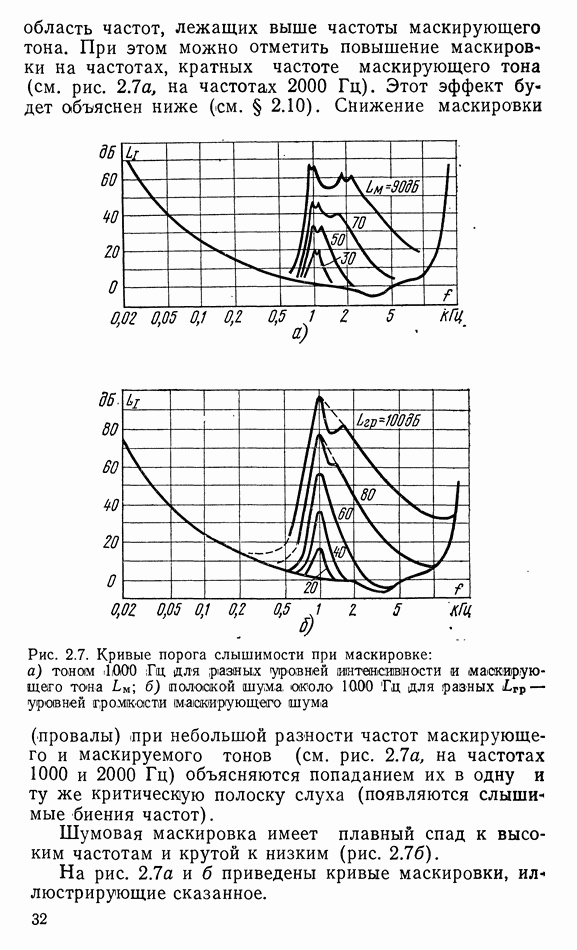
- 2.7. ЭФФЕКТ МАСКИРОВКИ
- 2.8. ГРОМКОСТЬ СЛОЖНЫХ ЗВУКОВ
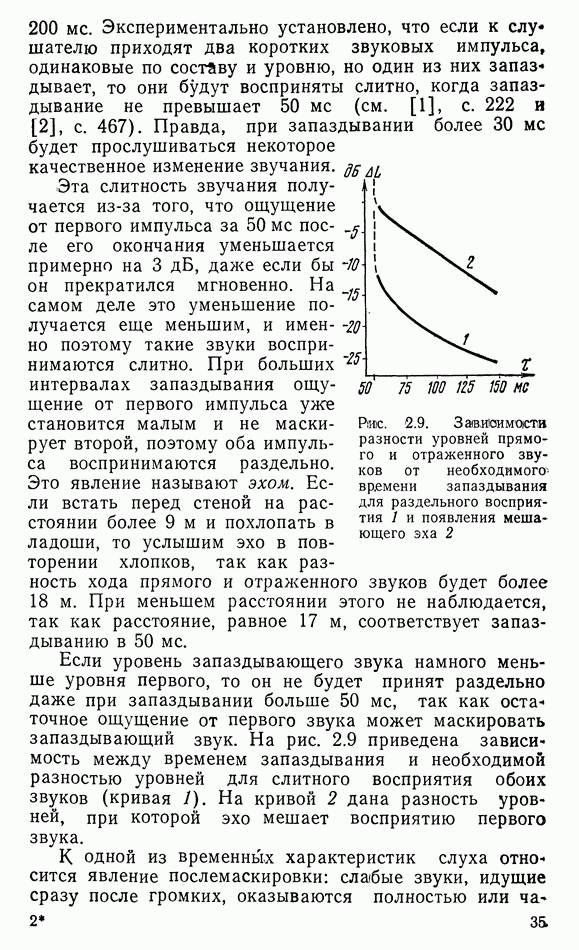
- 2.9. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЛУХОВОГО ВОСПРИЯТИЯ
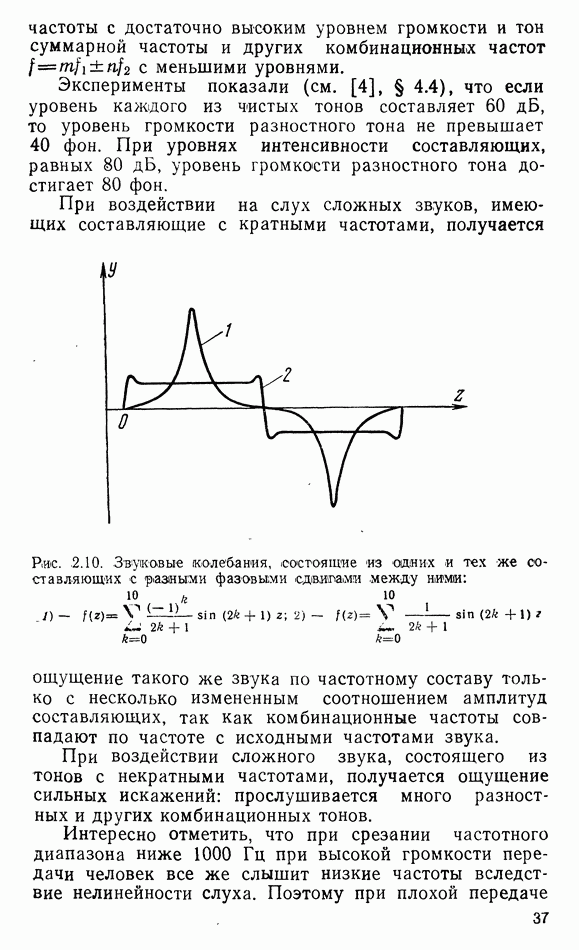
- 2.10 НЕЛИНЕЙНЫЕ СВОЙСТВА СЛУХА
- 2.11. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- Глава 3. АКУСТИЧЕСКИЕ СИГНАЛЫ
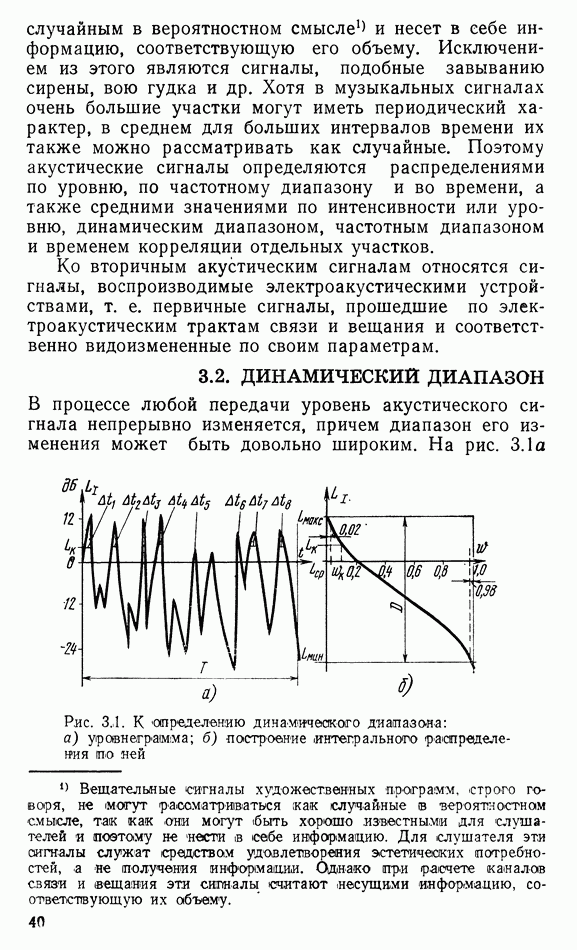
- 3.2. ДИНАМИЧЕСКИЙ ДИАПАЗОН
- 3.3 СРЕДНИЙ УРОВЕНЬ
- 3.4. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
- 3.5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ АКУСТИЧЕСКОГО СИГНАЛА
- 3.6. ПЕРВИЧНЫЙ РЕЧЕВОЙ СИГНАЛ
- 3.7. ВТОРИЧНЫЙ СИГНАЛ
- 3.8. ШУМЫ И ПОМЕХИ
- 3.9. ЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.10. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.11. ПЕРЕХОДНЫЕ ИСКАЖЕНИЯ
- 3.12. ДОПУСТИМЫЕ ВЕЛИЧИНЫ ИСКАЖЕНИЙ
- Глава 4. ЭЛЕКТРОМЕХАНОАКУСТИЧЕСКИЕ СИСТЕМЫ И ИХ ЭЛЕМЕНТЫ
- 4.2. МЕТОД ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 4.3. МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 4.4. АКУСТИЧЕСКИЕ СИСТЕМЫ
- 4.5. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 5. МИКРОФОНЫ
- 5.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ МИКРОФОНОВ
- 5.3. ДИНАМИЧЕСКИЕ (КАТУШЕЧНЫЕ) МИКРОФОНЫ
- 5.4. ЛЕНТОЧНЫЕ МИКРОФОНЫ
- 5.5. КОНДЕНСАТОРНЫЕ И ЭЛЕКТРЕТНЫЕ МИКРОФОНЫ
- 5.6. ПЬЕЗОМИКРОФОНЫ
- 5.7. ЭЛЕКТРОМАГНИТНЫЕ МИКРОФОНЫ
- 5.8. УГОЛЬНЫЕ МИКРОФОНЫ
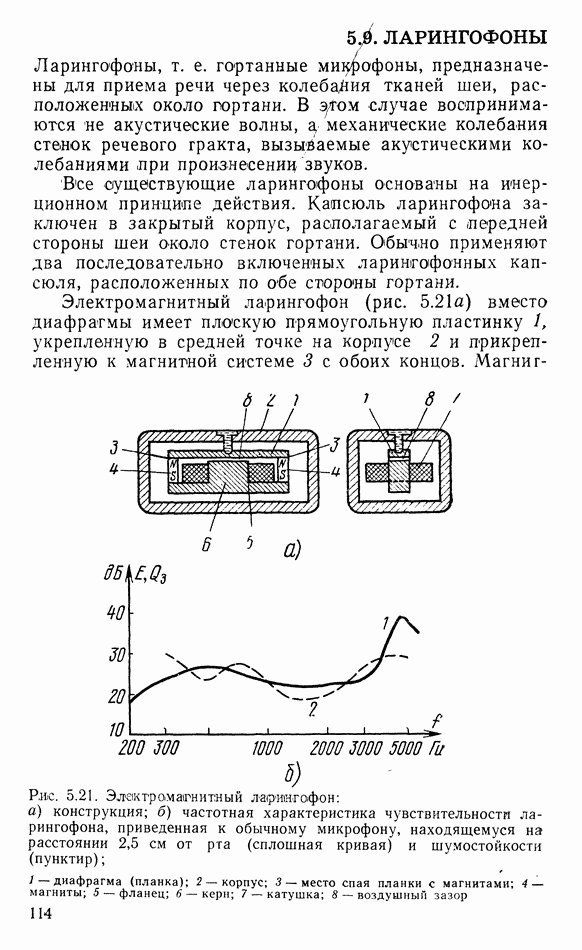
- 5.9. ЛАРИНГОФОНЫ
- Глава 6. ГРОМКОГОВОРИТЕЛИ И ТЕЛЕФОНЫ
- 6.2. ДИФФУЗОРНЫЕ ИЗЛУЧАТЕЛИ
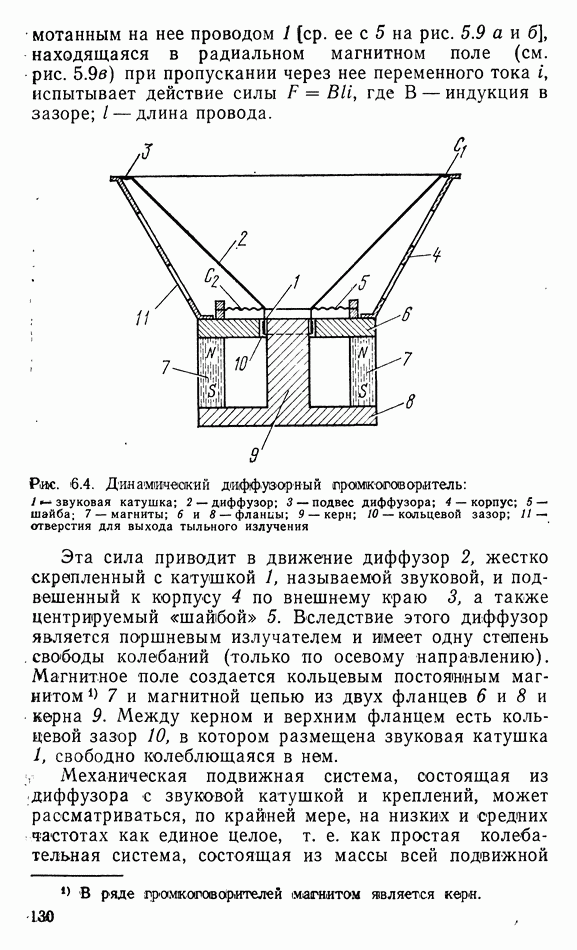
- 6.3. ДИФФУЗОРНЫЕ ДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.4. ГРУППОВЫЕ ИЗЛУЧАТЕЛИ И ГРОМКОГОВОРИТЕЛИ
- 6.5. РУПОРНЫЕ ИЗЛУЧАТЕЛИ
- 6.6. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.7. ЭЛЕКТРОСТАТИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.8. ГРОМКОГОВОРЯЩИЕ АКУСТИЧЕСКИЕ СИСТЕМЫ
- 6.9. ПНЕВМАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 6.10. ТЕЛЕФОНЫ
- Глава 7. АКУСТИКА ПОМЕЩЕНИЙ
- 7.1. РАСПРОСТРАНЕНИЕ ЗВУКА В ОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 7.2. АКУСТИЧЕСКИЕ ПРОЦЕССЫ В ПОМЕЩЕНИЯХ
- 7.3. ХАРАКТЕРИСТИКИ ПОМЕЩЕНИЯ
- 7.4. ЗВУКОПОГЛОЩАЮЩИЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ
- 7.5. ЗВУКОИЗОЛЯЦИЯ ПОМЕЩЕНИЙ
- Глава 8. СТУДИИ ЗВУКОВОГО И ТЕЛЕВИЗИОННОГО ВЕЩАНИЯ
- 8.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СТУДИЙ
- 8.3. ЗВУКОИЗОЛЯЦИЯ СТУДИЙ
- 8.4. ЭЛЕКТРОАКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ СТУДИЙ И КОМНАТ ПРОСЛУШИВАНИЯ
- Глава 9. ОЗВУЧЕНИЕ И ЗВУКОУСИЛЕНИЕ
- 9.2. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ОТКРЫТЫХ ПРОСТРАНСТВ
- 9.3. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 9.4. ЗОНАЛЬНЫЕ СИСТЕМЫ
- 9.5. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 9.6. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ДЛЯ ПОМЕЩЕНИЙ
- 9.7. РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ
- 9.8. ЗВУКОУСИЛЕНИЕ
- 9.9. ГРОМКОГОВОРЯЩАЯ СВЯЗЬ
- Глава 10. ПОНЯТНОСТЬ И РАЗБОРЧИВОСТЬ РЕЧИ
- 10.2. ФОРМАНТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- 10.3. ОПРЕДЕЛЕНИЕ РАЗБОРЧИВОСТИ РЕЧИ ДЛЯ ТРАКТОВ СВЯЗИ И ВЕЩАНИЯ
- 10.4. МЕТОДЫ ПОВЫШЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- Глава 11. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ
- 11.2. ЗВУКОМЕРНЫЕ КАМЕРЫ
- 11.3. ИЗМЕРИТЕЛЬНАЯ АППАРАТУРА И АКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ
- 11.4. МЕТОДЫ ИЗМЕРЕНИЙ ОСНОВНЫХ ХАРАКТЕРИСТИК АППАРАТУРЫ И ПОМЕЩЕНИЙ