| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. СФЕРИЧЕСКАЯ ВОЛНА
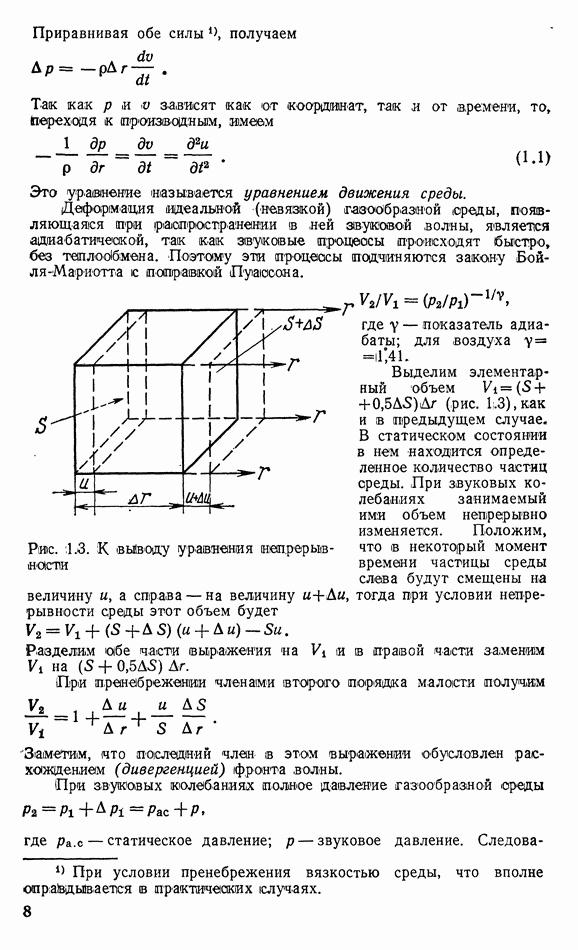
Фронт такой волны представляет собой сферическую поверхность, а звуковые лучи согласно определению фронта волны совпадают с радиусами сферы (рис. 1.4). В результате расхождения волн интенсивность звука убывает с удалением от источника. Так как потери энергии в среде малы, как и в случае плоской волны, то при распространении волны на небольшие расстояния с ними можно не считаться. Поэтому средний поток энергии через сферическую поверхность с радиусом  (рис. 1.4) будет тот же самый, что и через любую другую сферическую поверхность с (большим
(рис. 1.4) будет тот же самый, что и через любую другую сферическую поверхность с (большим
диусом  если в промежутке между ними нет источника или поглотителя энергии. Следовательно, мощность звуковой волны
если в промежутке между ними нет источника или поглотителя энергии. Следовательно, мощность звуковой волны

где  и
и  интенсивность звука для радиусов
интенсивность звука для радиусов  Отсюда получим квадратичный закон убывания интенсивности звука в сферической волне
Отсюда получим квадратичный закон убывания интенсивности звука в сферической волне

где  интенсивность на расстоянии единицы длины (обычно
интенсивность на расстоянии единицы длины (обычно  от центра сферы.
от центра сферы.

Рис. 1.4. Сферическая волна
Волновое уравнение для этого случая сможет быть получено из (1.4) путем подстановки  него выражения для поверхности шарового сектора
него выражения для поверхности шарового сектора  где
где  телесный угол сектора,
телесный угол сектора,  расстояние от центра юферичаокой волны.
расстояние от центра юферичаокой волны.
Так как  то волновое ур-ние (1.4) будет
то волновое ур-ние (1.4) будет

Заменив в нем переменную  на
на  получим волновое уравнение в более наглядной форме:
получим волновое уравнение в более наглядной форме:

Частное решение этого уравнения для расходящейся волны (распространяющейся в положительном направлении) имеет вид

где

 амплитуда звукового давления на расстоянии единицы длины от центра сферы.
амплитуда звукового давления на расстоянии единицы длины от центра сферы.
Как видно из формулы, амплитуда звукового давления уменьшается с увеличением расстояния от центра источника сферической волны по гиперболическому закону.
Подставляя выражение (1.16) в уравнение движения (1.1) и интегрируя его по времени, получаем уравнение для скорости колебаний в сферической волне:

Из этого выражения следует, что скорость колебаний не совпадает по фазе с звуковым давлением (1.16). Из (1.16) и (1.17) получаем акустическое сопротивление для сферической волны

Как видим, акустическое сопротивление содержит активную и реактивную составляющие [см. (1.7)]:

Модуль этого сопротивления

где  сдвиг фаз между звуковым давлением и скоростью колебаний (1.8):
сдвиг фаз между звуковым давлением и скоростью колебаний (1.8):

Из выражения (1.186) следует, что акустическое сопротивление в сферической волне по модулю никогда не превышает сопротивления в плоской волне [см. (1.13)]. А из выражения (1.19) следует, что чем больше отношение длины волны к ее радиусу (т. е. расстоянию от центра источника звука), тем ближе сдвиг фаз к  с уменьшением этого отношения сдвиг фаз стремится к нулю, т. е. сферическая волна приближается к плоской. Например, для частоты 100 Гц (длина волны
с уменьшением этого отношения сдвиг фаз стремится к нулю, т. е. сферическая волна приближается к плоской. Например, для частоты 100 Гц (длина волны  при расстоянии от центра источника звука
при расстоянии от центра источника звука  сдвиг фаз получается равным 65°, а для частоты 5000 Гц
сдвиг фаз получается равным 65°, а для частоты 5000 Гц  см) при расстоянии
см) при расстоянии  сдвиг фаз получается около 0,5°.
сдвиг фаз получается около 0,5°.
Интенсивность звука для синусоидальных колебаний в сферической волне определяется выражением (1.10) с учетом (1.186): 2

Если в это выражение подставить значение  из (1.186), получим, что интенсивность колебаний
из (1.186), получим, что интенсивность колебаний

Подставляя в (1.20) амплитуду звукового давления из (1.16а) и учитывая (1.15а), получаем

где 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. ЗВУКОВОЕ ПОЛЕ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ
- 1.3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 1.4. ПЛОСКАЯ ВОЛНА
- 1.5. СФЕРИЧЕСКАЯ ВОЛНА
- 1.6. ЦИЛИНДРИЧЕСКАЯ ВОЛНА
- Глава 2. ОСНОВНЫЕ СВОЙСТВА СЛУХА
- 2.2. ВОСПРИЯТИЕ ПО ЧАСТОТЕ
- 2.3. ПОРОГ СЛЫШИМОСТИ
- 2.4. ВОСПРИЯТИЕ ПО АМПЛИТУДЕ
- 2.5. УРОВНИ
- 2.6. ГРОМКОСТЬ И УРОВЕНЬ ГРОМКОСТИ ЗВУКА
- 2.7. ЭФФЕКТ МАСКИРОВКИ
- 2.8. ГРОМКОСТЬ СЛОЖНЫХ ЗВУКОВ
- 2.9. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЛУХОВОГО ВОСПРИЯТИЯ
- 2.10 НЕЛИНЕЙНЫЕ СВОЙСТВА СЛУХА
- 2.11. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- Глава 3. АКУСТИЧЕСКИЕ СИГНАЛЫ
- 3.2. ДИНАМИЧЕСКИЙ ДИАПАЗОН
- 3.3 СРЕДНИЙ УРОВЕНЬ
- 3.4. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
- 3.5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ АКУСТИЧЕСКОГО СИГНАЛА
- 3.6. ПЕРВИЧНЫЙ РЕЧЕВОЙ СИГНАЛ
- 3.7. ВТОРИЧНЫЙ СИГНАЛ
- 3.8. ШУМЫ И ПОМЕХИ
- 3.9. ЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.10. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 3.11. ПЕРЕХОДНЫЕ ИСКАЖЕНИЯ
- 3.12. ДОПУСТИМЫЕ ВЕЛИЧИНЫ ИСКАЖЕНИЙ
- Глава 4. ЭЛЕКТРОМЕХАНОАКУСТИЧЕСКИЕ СИСТЕМЫ И ИХ ЭЛЕМЕНТЫ
- 4.2. МЕТОД ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 4.3. МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 4.4. АКУСТИЧЕСКИЕ СИСТЕМЫ
- 4.5. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 5. МИКРОФОНЫ
- 5.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ МИКРОФОНОВ
- 5.3. ДИНАМИЧЕСКИЕ (КАТУШЕЧНЫЕ) МИКРОФОНЫ
- 5.4. ЛЕНТОЧНЫЕ МИКРОФОНЫ
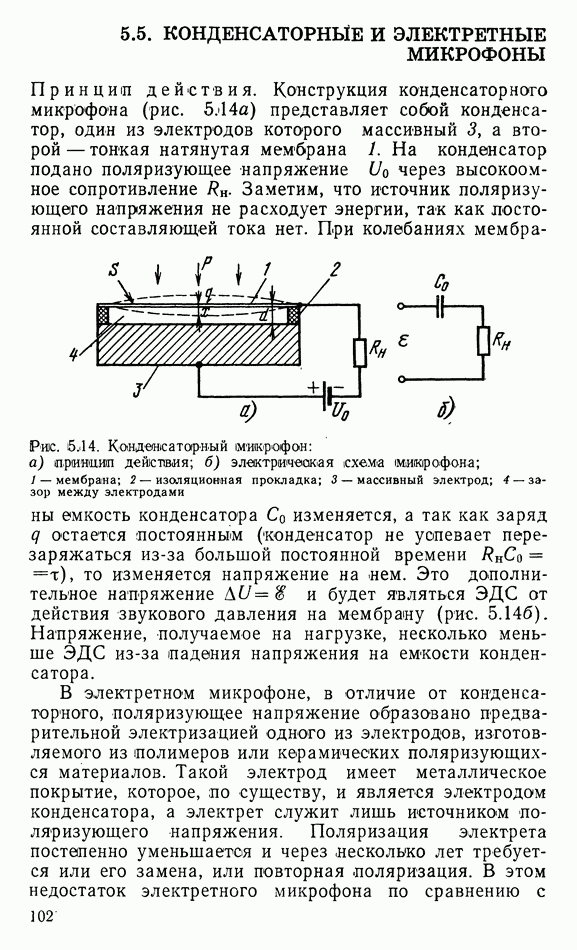
- 5.5. КОНДЕНСАТОРНЫЕ И ЭЛЕКТРЕТНЫЕ МИКРОФОНЫ
- 5.6. ПЬЕЗОМИКРОФОНЫ
- 5.7. ЭЛЕКТРОМАГНИТНЫЕ МИКРОФОНЫ
- 5.8. УГОЛЬНЫЕ МИКРОФОНЫ
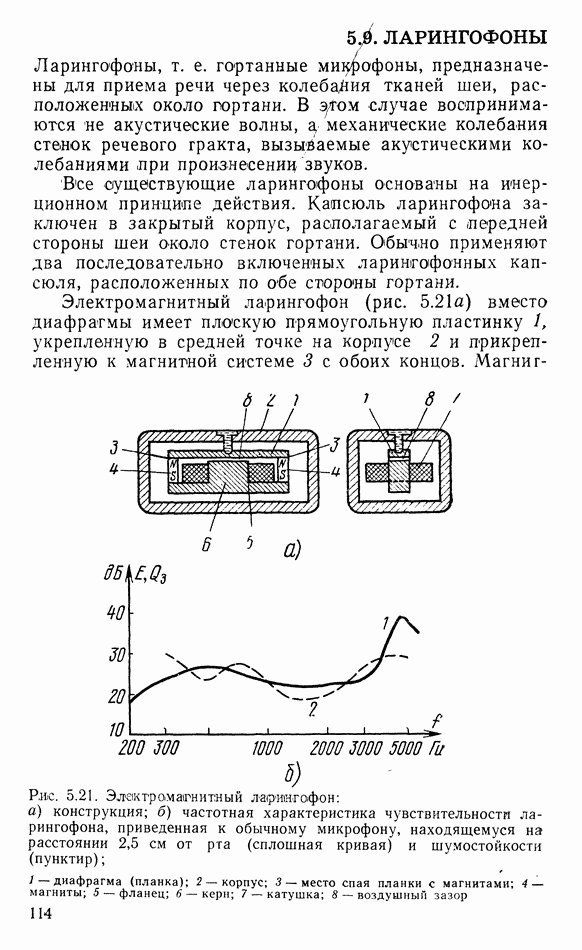
- 5.9. ЛАРИНГОФОНЫ
- Глава 6. ГРОМКОГОВОРИТЕЛИ И ТЕЛЕФОНЫ
- 6.2. ДИФФУЗОРНЫЕ ИЗЛУЧАТЕЛИ
- 6.3. ДИФФУЗОРНЫЕ ДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.4. ГРУППОВЫЕ ИЗЛУЧАТЕЛИ И ГРОМКОГОВОРИТЕЛИ
- 6.5. РУПОРНЫЕ ИЗЛУЧАТЕЛИ
- 6.6. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.7. ЭЛЕКТРОСТАТИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- 6.8. ГРОМКОГОВОРЯЩИЕ АКУСТИЧЕСКИЕ СИСТЕМЫ
- 6.9. ПНЕВМАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 6.10. ТЕЛЕФОНЫ
- Глава 7. АКУСТИКА ПОМЕЩЕНИЙ
- 7.1. РАСПРОСТРАНЕНИЕ ЗВУКА В ОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 7.2. АКУСТИЧЕСКИЕ ПРОЦЕССЫ В ПОМЕЩЕНИЯХ
- 7.3. ХАРАКТЕРИСТИКИ ПОМЕЩЕНИЯ
- 7.4. ЗВУКОПОГЛОЩАЮЩИЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ
- 7.5. ЗВУКОИЗОЛЯЦИЯ ПОМЕЩЕНИЙ
- Глава 8. СТУДИИ ЗВУКОВОГО И ТЕЛЕВИЗИОННОГО ВЕЩАНИЯ
- 8.2. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СТУДИЙ
- 8.3. ЗВУКОИЗОЛЯЦИЯ СТУДИЙ
- 8.4. ЭЛЕКТРОАКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ СТУДИЙ И КОМНАТ ПРОСЛУШИВАНИЯ
- Глава 9. ОЗВУЧЕНИЕ И ЗВУКОУСИЛЕНИЕ
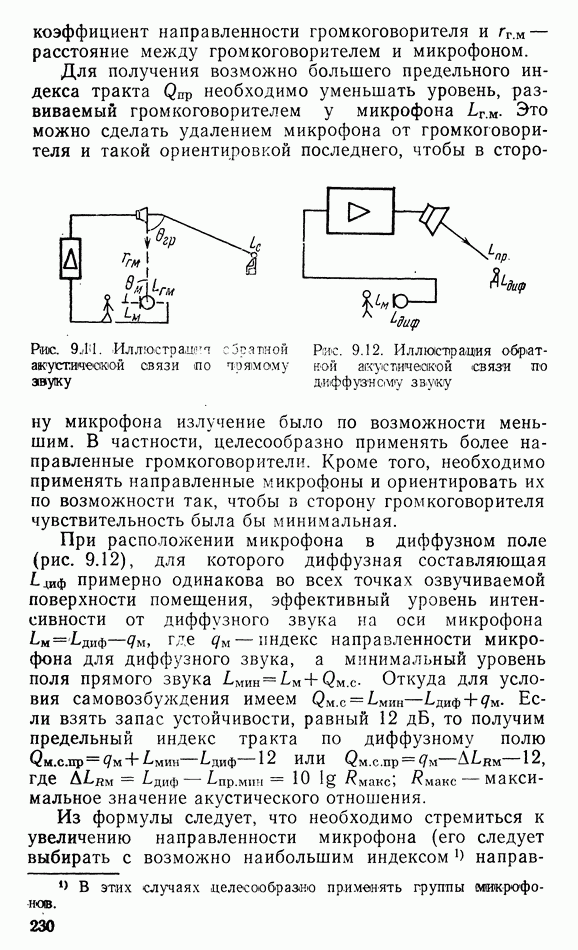
- 9.2. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ОТКРЫТЫХ ПРОСТРАНСТВ
- 9.3. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 9.4. ЗОНАЛЬНЫЕ СИСТЕМЫ
- 9.5. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 9.6. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ДЛЯ ПОМЕЩЕНИЙ
- 9.7. РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ
- 9.8. ЗВУКОУСИЛЕНИЕ
- 9.9. ГРОМКОГОВОРЯЩАЯ СВЯЗЬ
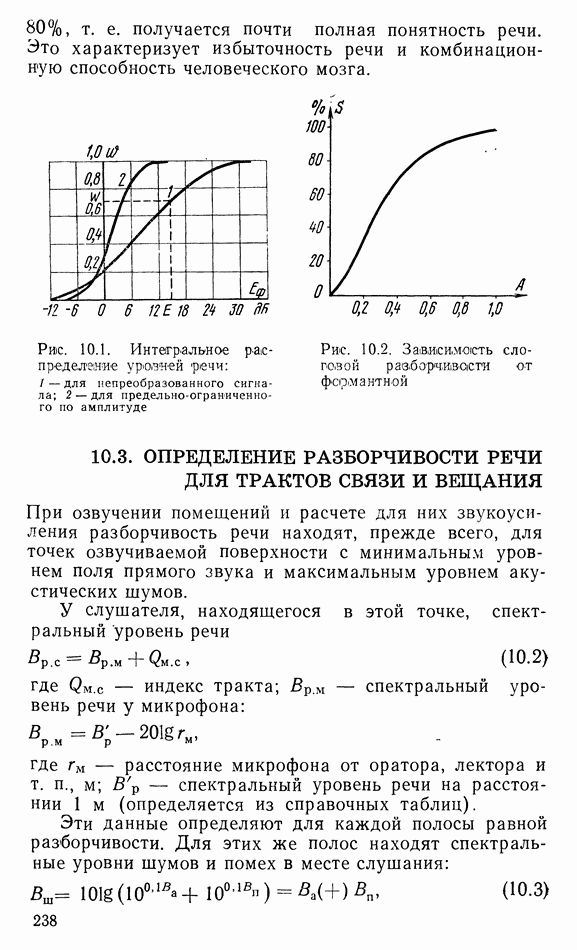
- Глава 10. ПОНЯТНОСТЬ И РАЗБОРЧИВОСТЬ РЕЧИ
- 10.2. ФОРМАНТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- 10.3. ОПРЕДЕЛЕНИЕ РАЗБОРЧИВОСТИ РЕЧИ ДЛЯ ТРАКТОВ СВЯЗИ И ВЕЩАНИЯ
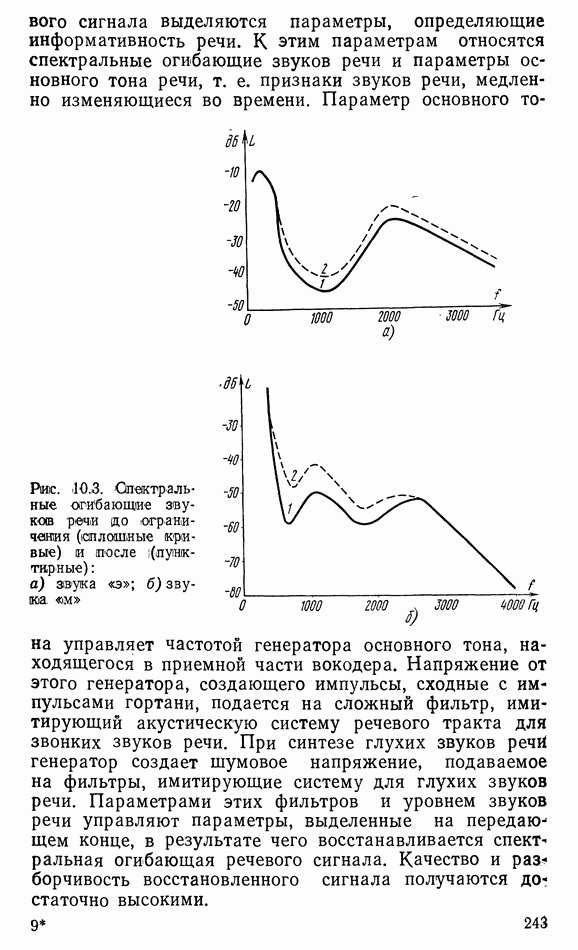
- 10.4. МЕТОДЫ ПОВЫШЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- Глава 11. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ
- 11.2. ЗВУКОМЕРНЫЕ КАМЕРЫ
- 11.3. ИЗМЕРИТЕЛЬНАЯ АППАРАТУРА И АКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ
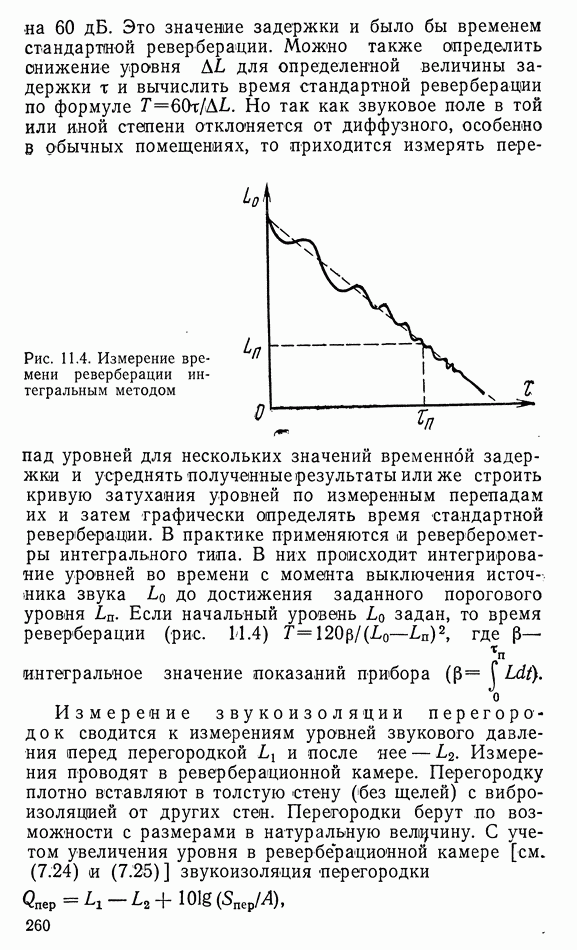
- 11.4. МЕТОДЫ ИЗМЕРЕНИЙ ОСНОВНЫХ ХАРАКТЕРИСТИК АППАРАТУРЫ И ПОМЕЩЕНИЙ