| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Часть III. Физика квантового мира
В этой части книги мы попробуем рассказать о том, какие законы управляют движением мельчайших частиц материи и в каких необычных «сверхявлениях» они непосредственно проявляются при очень низких температурах. Рассказать об этом совсем не просто, так как серьезный разговор на эту тему можно вести только на языке математики. Уж больно необычен, удивителен для нас этот квантовый мир.
Глава 21. Соотношение неопределенностей
Координата и импульс подобны фигуркам мужнины и женщины в старинном барометре. Если появляется одна фигурка, вторая исчезает.
В. Гейзенберг
Немецкий физик Вернер Гейзенберг открыл в  соотношение неопределенностей, которое заключается в следующем: если, исследуя какое-то тело, нам удается определить проекцию его импульса с неопределенностью
соотношение неопределенностей, которое заключается в следующем: если, исследуя какое-то тело, нам удается определить проекцию его импульса с неопределенностью  то мы не сможем одновременно определить соответствующую координату тела с точностью большей, чем
то мы не сможем одновременно определить соответствующую координату тела с точностью большей, чем  где
где  — постоянная Планка.
— постоянная Планка.
Поначалу это соотношение может вызвать чувство недоумения. Ведь законы Ньютона, которые изучают в школе, позволяют найти закон движения тела, то есть рассчитать зависимость координат от времени. Зная закон движения, можно найти проекции скорости тела  (производные от координат по времени) и проекции его импульса
(производные от координат по времени) и проекции его импульса  Получается, что можно одновременно определять координату и импульс, и никакого соотношения неопределенностей нет. Действительно, в классической физике все происходит именно так, а вот в микромире дело обстоит иначе (рис. 21.1).
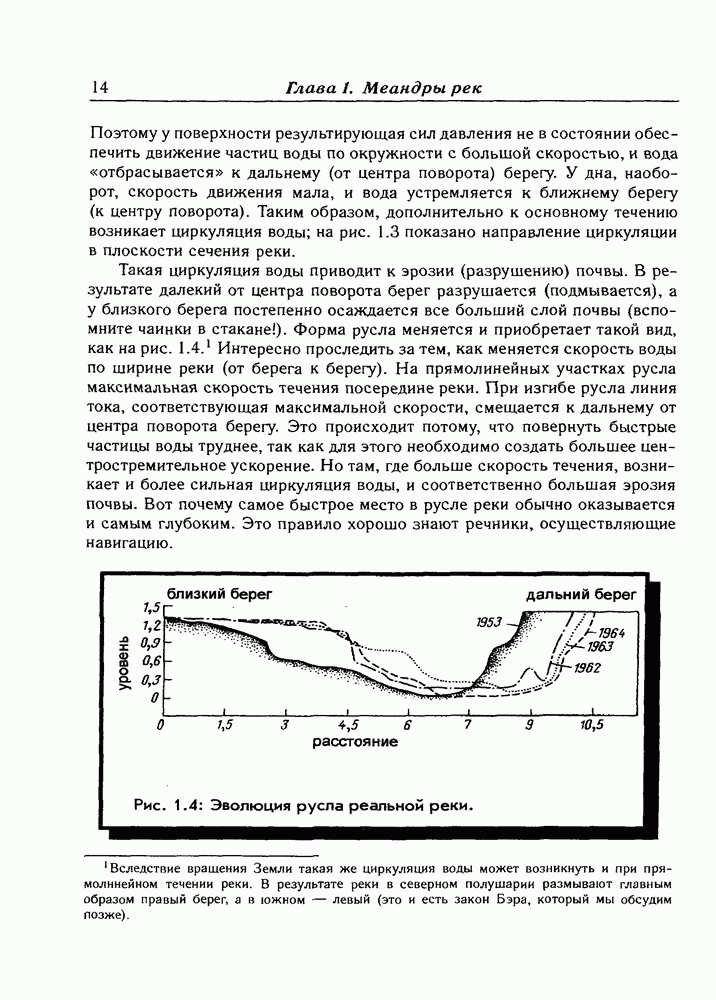
Получается, что можно одновременно определять координату и импульс, и никакого соотношения неопределенностей нет. Действительно, в классической физике все происходит именно так, а вот в микромире дело обстоит иначе (рис. 21.1).

Рис. 21.1: Измерение координаты частицы с точностью  определяемой шириной щели, через которую частица пролетает, приводит к неопределенности соответствующей проекции импульса частицы
определяемой шириной щели, через которую частица пролетает, приводит к неопределенности соответствующей проекции импульса частицы 
Импульс и координата
Представим себе, что нам надо следить за движением электрона. Как это сделать? Глаз — инструмент для этих целей неподходящий. Его разрешающей способности недостаточно, чтобы разглядеть электрон. Ну что  посмотрим на электрон в микроскоп. Разрешающая способность микроскопа определяется длиной волны света, в котором ведется наблюдение. Для обычного видимого света эта величина порядка 100 нм ( т. е.
посмотрим на электрон в микроскоп. Разрешающая способность микроскопа определяется длиной волны света, в котором ведется наблюдение. Для обычного видимого света эта величина порядка 100 нм ( т. е.  и частицы меньших размеров в микроскоп не разглядишь. Атомы имеют размеры порядка
и частицы меньших размеров в микроскоп не разглядишь. Атомы имеют размеры порядка  так что надеяться различить их, а тем более отдельные электроны, не приходится. Но давайте пофантазируем.
так что надеяться различить их, а тем более отдельные электроны, не приходится. Но давайте пофантазируем.
Предположим, что нам удалось сконструировать микроскоп, использующий не видимый свет, а электромагнитные волны с меньшей длиной волны: например, рентгеновское или даже  -излучение. Чем более жесткое
-излучение. Чем более жесткое  -излучение мы будем применять, то есть чем короче соответствующая длина волны, тем меньшие объекты можно наблюдать. Казалось бы, такой воображаемый
-излучение мы будем применять, то есть чем короче соответствующая длина волны, тем меньшие объекты можно наблюдать. Казалось бы, такой воображаемый  -микроскоп был бы идеальным инструментом. С его помощью можно было бы измерить координату электрона сколь угодно точно. При чем же тут соотношение неопределенностей?
-микроскоп был бы идеальным инструментом. С его помощью можно было бы измерить координату электрона сколь угодно точно. При чем же тут соотношение неопределенностей?
Вдумаемся глубже в этот мысленный эксперимент. Для того чтобы мы получили информацию о положении электрона, от него должен отразиться хотя бы один  -квант — носитель минимальной порции энергии Ни (энергия кванта
-квант — носитель минимальной порции энергии Ни (энергия кванта  , где
, где  — угловая частота. Физики используют два определения постоянной Планка,
— угловая частота. Физики используют два определения постоянной Планка,  Чем меньше длина волны, тем больше порция энергии, которой обладает квант. А импульс кванта пропорционален его энергии. Сталкиваясь с электроном,
Чем меньше длина волны, тем больше порция энергии, которой обладает квант. А импульс кванта пропорционален его энергии. Сталкиваясь с электроном,
 -квант обязательно передает ему часть своего импульса. Таким образом, измеряя координату, мы всегда вносим неопределенность в импульс электрона, и чем точнее мы хотим провести измерение, тем большей будет неопределенность. Подробный анализ этого процесса показывает, что произведение неопределенностей нельзя сделать меньшим, чем постоянная Планка.
-квант обязательно передает ему часть своего импульса. Таким образом, измеряя координату, мы всегда вносим неопределенность в импульс электрона, и чем точнее мы хотим провести измерение, тем большей будет неопределенность. Подробный анализ этого процесса показывает, что произведение неопределенностей нельзя сделать меньшим, чем постоянная Планка.
Может создаться впечатление, что мы рассмотрели только частный случай, придумали «плохой» прибор для измерения координаты и можно провести измерения гораздо тоньше, не «толкая» электрон, не изменяя его состояния. Но, увы, это не так.
Лучшие умы (среди них и А. Эйнштейн) пытались придумать такой прибор, который смог бы измерить координату тела и его импульс одновременно, с точностью большей, чем позволяет соотношение неопределенностей. Но никому не удалось это сделать. Сделать это просто нельзя, Таков закон природы.
Все это может показаться несколько туманным, и трудно сразу построить какую-то четкую мысленную модель. Настоящее понимание приходит только в результате серьезного изучения квантовой механики. Для первого знакомства этого достаточно.
Чтобы понять, где лежит граница между макро - и микромиром, сделаем небольшую оценку. Например, в опытах по броуновскому движению используются очень маленькие частички — размером около 1 мкм и массой всего  Но все-таки это кусочки вещества, содержащие огромное количество атомов. Из соотношения неопределенностей в этом случае имеем
Но все-таки это кусочки вещества, содержащие огромное количество атомов. Из соотношения неопределенностей в этом случае имеем  Если, скажем, определять положение частички с точностью до одной сотой ее размера
Если, скажем, определять положение частички с точностью до одной сотой ее размера  см), то
см), то  см/с. Получилась очень маленькая величина, и причина этого — маленькое значение постоянной Планка.
см/с. Получилась очень маленькая величина, и причина этого — маленькое значение постоянной Планка.
Скорость броуновского движения такой частички примерно равна  см/с. Как видно, погрешность в скорости, связанная с соотношением неопределенностей, пренебрежимо мала (одна десятимиллионная доля!) даже у такого небольшого тела. Тем более она не играет роли для больших тел (ведь в правой части соотношения стоит
см/с. Как видно, погрешность в скорости, связанная с соотношением неопределенностей, пренебрежимо мала (одна десятимиллионная доля!) даже у такого небольшого тела. Тем более она не играет роли для больших тел (ведь в правой части соотношения стоит  А вот если мы будем уменьшать массу частицы (возьмем, например, электрон) и увеличивать точность определения координаты
А вот если мы будем уменьшать массу частицы (возьмем, например, электрон) и увеличивать точность определения координаты  см — атомные размеры), то неопределенность в скорости становится сравнимой с самой скоростью частицы. При описании электронов в атоме соотношение
см — атомные размеры), то неопределенность в скорости становится сравнимой с самой скоростью частицы. При описании электронов в атоме соотношение
неопределенностей уже работает в полной мере, с ним не считаться нельзя. И это приводит к удивительным следствиям.
Волны вероятности
В простейшей модели атома — модели Резерфорда — электроны кружатся по орбитам вокруг ядра подобно тому, как планеты движутся вокруг Солнца. Но электроны — заряженные частицы, и при их вращении обязательно создаются переменные электрические и магнитные поля — возникает излучение, приводящее к потере энергии. Вот почему в планетарной модели электроны ждет незавидная судьба — они обязательно упадут на ядра, и атом разрушится. Но ведь стабильность атомов — это твердо установленный экспериментальный факт.
Нужно было «подправить» модель Резерфорда, и сделал это Нильс Бор в 1913 г. Электронам в модели Бора разрешается вращаться только по определенным орбитам, где они обладают строго заданными энергиями. Изменять эту энергию электроны могут только скачком, излучая и поглощая кванты при переходе с одной орбиты на другую. Такое «квантовое» поведение электронов в атоме позволяет объяснить многое — в частности, устойчивость атома и атомные спектры. Эту модель порой и сейчас используют для упрощенного объяснения квантовых явлений. Но она противоречит соотношению неопределенностей! Ведь при движении даже по квантовой орбите импульс и координата могут быть определены одновременно, а в микромире, как мы теперь знаем, такого быть не может.
Пришлось исправить и эту, как ее называют, квазиклассическую модель атома. Действительная картина, описывающая поведение электрона в атоме, оказалась еще более сложной.
Представьте себе, что нам удалось определить положение электрона в атоме в какой-то момент времени. Сможем ли мы точно сказать, где он будет в следующий момент (для определенности, скажем, через одну секунду)? Нет, измерение координаты, как мы знаем, всегда вносит неопределенность в импульс электрона, и, пользуясь даже самыми лучшими
устройствами, нельзя точно предсказать, куда попадет электрон. Что же нам остается в таком случае делать?
Давайте отметим точкой то место в пространстве, где мы обнаружили электрон. Результат еще одного измерения координат электрона в точно таком же атоме снова изобразим точкой в пространстве. Еще измерение — опять точка и т. д. Оказывается, что, хотя и нельзя сказать заранее, где точно будет находиться следующая точка, в характере расположения точек в пространстве имеется определенная закономерность. В некоторых областях точки располагаются гуще, в других — реже, указывая на то, где с большей, а где с меньшей вероятностью может встретиться электрон.

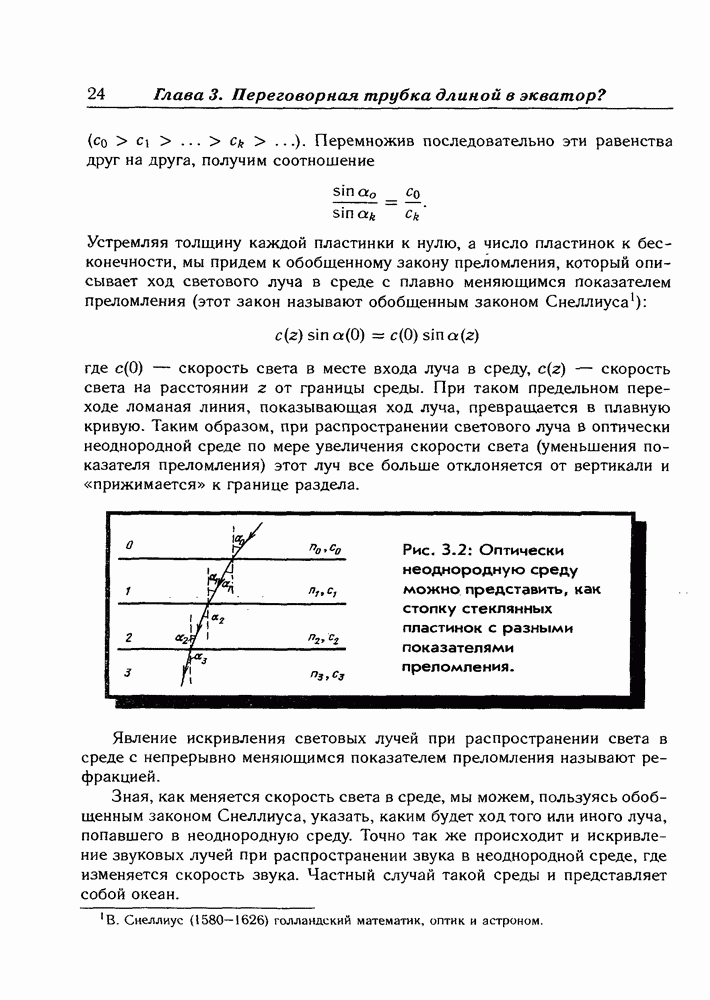
Рис. 21.2: Такая картина возникает в опыте по диффракции электронов: 1 — электронная пушка; 2 — препятствие; 3 — область тени; 4 — флуоресцентный экран.
Нам пришлось отказаться от точного описания движения электрона, но мы в состоянии предсказывать шансы обнаружить его в различных точках пространства. Поведение электрона в микромире описывается вероятностно! Такая картина поведения частиц в микромире читателю может не
понравиться — уж больно она непривычна, уж больно противоречит нашей интуиции, нашему опыту. Но ничего не поделаешь — так устроена природа. В микромире действуют совсем другие законы, нежели те, к которым мы привыкли в обычной жизни. По образному выражению А. Эйнштейна, приходится «играть в кости» для того, чтобы предсказывать поведение электронов. Без этого, увы, обойтись нельзя.
Итак, в микромире состояние электрона определяется заданием вероятности его обнаружения в разных точках пространства. В нашей наглядной модели мерой вероятности будет плотность меток, и можно представить себе, что эти метки образуют некоторое подобие облака, определяющего образ жизни электрона.
Как устроены облака вероятности? Аналогично тому, как в классической механике законы Ньютона определяют движение тел, в квантовой механике имеется свое уравнение, из которого можно найти «размазку» электрона в пространстве. Такое уравнение придумал в 1925 г. австрийский физик Эрвин Шредингер (заметьте, это случилось раньше, чем было открыто соотношение неопределенностей, то есть раньше, чем прояснилась причина размазки микрочастиц, — такое в физике бывает). Уравнение Шредингера количественно, точно и подробно описывает атомные явления. Но рассказать об этом без сложной математики нельзя. Мы приведем здесь просто ответы — покажем точные портреты размазки электрона в некоторых случаях.
На рис. 21.2 показана схема опыта по дифракции электронов и фотография системы полос, возникающей на экране. Картина совершенно аналогична той, которая возникает при дифракции света. Если считать, что электроны движутся по прямолинейным траекториям, как им положено в данном случае по законам классической физики, объяснить этот опыт нельзя. А вот если они размазаны в пространстве, то результат опыта можно понять. Более того, из опыта следует, что облако вероятности обладает волновыми свойствами. С волнами вероятности мы встречаемся и в обычной жизни — например, волны эпидемии, рождаемости, преступности и т. п. В том месте, где амплитуда волны максимальна, — наибольшая вероятность чему-то произойти. В нашем случае в этих местах с наибольшей вероятностью можно обнаружить электрон, и такие области на фотографии получаются более светлыми.
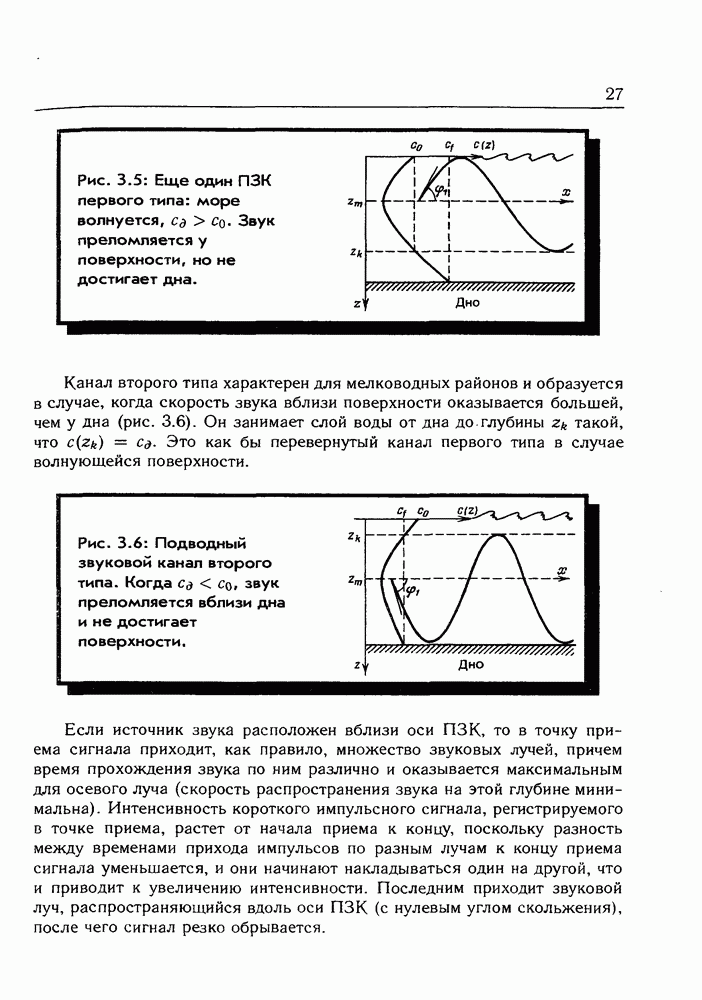
На рис. 21.3 представлена размазка электрона в различных состояниях атома водорода, найденная на основе точных математических расчетов.

Рис. 21.3: Это, конечно, не фотографии реальных электронов, а результаты расчетов, показывающих, как «размазаны» электроны в атоме. Симметрия этих картин во многом определяет симметрию молекул и кристаллов. Можно даже сказать, что здесь находится ключ к пониманию красоты упорядоченных форм живой природы.
Это аналог квантовых орбит, по которым движется электрон в модели атома Бора. Чем светлее область, тем вероятнее встретить в ней электрон, Рисунки напоминают картины стоячих волн, возникающих, когда волновой процесс происходит в ограниченной области пространства. Какие удивительные формы могут принимать облака вероятности! И эти красивые абстрактные картинки действительно определяют поведение электронов в атоме и объясняют, например, уровни энергии и все, что касается химической связи.
Не вдаваясь в детали устройства облаков вероятности, можно с помощью соотношения неопределенностей оценить их характерный размер. Если облако вероятности имеет размер порядка  то бессмысленно
то бессмысленно
говорить о большей, чем  неопределенности в координате частицы. Следовательно, неопределенность импульса частицы
неопределенности в координате частицы. Следовательно, неопределенность импульса частицы  не может быть меньшей, чем
не может быть меньшей, чем  По порядку величины это же выражение определяет и минимальное значение импульса частицы.
По порядку величины это же выражение определяет и минимальное значение импульса частицы.
Чем меньше размер облака вероятности, тем большим становится импульс, и следовательно, тем быстрее движется частица внутри области локализации. Оказывается, что уже этих общих рассуждений достаточно, чтобы правильно оцепить размер атома.
Электрон в атоме обладает кинетической и потенциальной энергиями. Кинетическая энергия электрона — это энергия его движения. Она связана с импульсом по известной формуле  р2/2т. Потенциальная энергия электрона — это энергия кулоновского взаимодействия с ядром. Для нее также имеется формула:
р2/2т. Потенциальная энергия электрона — это энергия кулоновского взаимодействия с ядром. Для нее также имеется формула:  где знак «минус» соответствует притяжению,
где знак «минус» соответствует притяжению,  — заряд электрона,
— заряд электрона,  — расстояние от электрона до ядра,
— расстояние от электрона до ядра,  — коэффициент, зависящий от выбора единиц измерения.
— коэффициент, зависящий от выбора единиц измерения.
В каждом состоянии у электрона имеется определенное значение полной энергии Е. Состояние с минимальной энергией называется основным (невозбужденным) состоянием. Оценим размер атома в основном состоянии.
Пусть электрон размазан в некоторой области размером  Притяжение электрона к ядру стремится уменьшить
Притяжение электрона к ядру стремится уменьшить  «схлопнуть» облако вероятности. Этому соответствует уменьшение потенциальной энергии электрона, которая по порядку величины равна
«схлопнуть» облако вероятности. Этому соответствует уменьшение потенциальной энергии электрона, которая по порядку величины равна  (при уменьшении
(при уменьшении  растет модуль отрицательной величины). Если бы электрон не обладал кинетической энергией, то он упал бы на ядро. Но, как вы уже знаете, кинетическая энергия у локализованной частицы всегда имеется вследствие соотношения неопределенностей. Оно и «мешает» электрону упасть на ядро! При уменьшении
растет модуль отрицательной величины). Если бы электрон не обладал кинетической энергией, то он упал бы на ядро. Но, как вы уже знаете, кинетическая энергия у локализованной частицы всегда имеется вследствие соотношения неопределенностей. Оно и «мешает» электрону упасть на ядро! При уменьшении  увеличивается минимальный импульс частицы
увеличивается минимальный импульс частицы  а следовательно, растет кинетическая энергия
а следовательно, растет кинетическая энергия  Из условия равенства нулю производной от полной энергии частицы получаем, что ее минимуму соответствует значение
Из условия равенства нулю производной от полной энергии частицы получаем, что ее минимуму соответствует значение

которое определяет характерный размер области локализации электрона в основном состоянии, то есть размер атома. Величина  равна 0,05 нм, а мы знаем, что таковы по порядку величины размеры атомов в действительности. Ясно, что соотношение неопределенностей, позволяющее правильно оценить размер атомов, — один из самых глубоких законов микромира.
равна 0,05 нм, а мы знаем, что таковы по порядку величины размеры атомов в действительности. Ясно, что соотношение неопределенностей, позволяющее правильно оценить размер атомов, — один из самых глубоких законов микромира.
Для сложных атомов существует определенная закономерность, также непосредственно вытекающая из соотношения неопределенностей.
Экспериментально довольно точно определяется работа, которую надо совершить, чтобы вырвать электрон из атома (она равна энергии ионизации  Так вот, для самых разных атомов произведение
Так вот, для самых разных атомов произведение  на размер атома
на размер атома  с точностью до 10 — 20% одинаково. Читатель, наверное, догадался, в чем тут дело: импульс электрона
с точностью до 10 — 20% одинаково. Читатель, наверное, догадался, в чем тут дело: импульс электрона  а постоянство произведения следует из соотношения неопределенностей.
а постоянство произведения следует из соотношения неопределенностей.
Нулевые колебания
Весьма впечатляющие результаты получаются при исследовании с помощью соотношения неопределенностей колебаний атомов в твердых телах. Атомы (или ионы) совершают колебания в узлах кристаллической решетки. Обычно такие колебания связаны с тепловым движением атомов — чем выше температура, тем сильнее колебания. А что будет, если температуру понизить? С классической точки зрения амплитуда колебаний будет уменьшаться, и при абсолютном нуле атомы вовсе остановятся. Но возможно ли это с точки зрения квантовых законов?
Уменьшение амплитуды колебаний на квантовом языке означает уменьшение размера облака вероятности (область локализации частицы). А за это, как мы уже знаем, приходится, в силу соотношения неопределенностей, расплачиваться увеличением импульса частицы — попытка остановить микрочастицу не приводит к успеху. Оказывается, что даже при абсолютном нуле температур атомы в твердом теле совершают колебания. Их называют нулевыми колебаниями, и проявляются они в целом ряде красивых физических эффектов.
Попробуем прежде всего оценить энергию нулевых колебаний. В колебательной системе при отклонении тела на малую величину  от положения равновесия на него действует возвращающая сила
от положения равновесия на него действует возвращающая сила  (в случае пружины
(в случае пружины  — ее жесткость; у атома в твердом теле величина
— ее жесткость; у атома в твердом теле величина  определяется силами межатомного взаимодействия). Соответственно у тела появляется потенциальная энергия
определяется силами межатомного взаимодействия). Соответственно у тела появляется потенциальная энергия

где  — частота колебаний.
— частота колебаний.
Отсюда следует, что амплитуда колебания  связана с запасом энергии тела Е формулой
связана с запасом энергии тела Е формулой

Но амплитуда колебаний на квантовом языке как раз определяет характерный размер области локализации частицы, который в силу соотношения неопределенностей связан с минимальным импульсом частицы. Получается, с одной стороны, чем меньше энергия колебаний, тем меньше должна быть амплитуда; с другой стороны, уменьшение амплитуды приводит к увеличению импульса, а следовательно, и энергии частицы. Минимальная энергия, которой может обладать частица, определяется из оценки

Сравнивая здесь первое и последнее выражения, находим  Точный расчет дает вдвое меньшее значение. Энергия нулевых колебаний равна
Точный расчет дает вдвое меньшее значение. Энергия нулевых колебаний равна  Она максимальна у легких атомов, которые колеблются с большей частотой.
Она максимальна у легких атомов, которые колеблются с большей частотой.
Пожалуй, самое яркое проявление нулевых колебаний — это существование жидкости, которая вообще не замерзает, даже при абсолютном нуле температур. Ясно, что жидкость не замерзает, если кинетической энергии колебаний атомов достаточно для того, чтобы разрушить кристаллическую решетку. При этом совершенно неважно происхождение кинетической энергии — связана ли она с тепловым движением атомов или с нулевыми квантовыми колебаниями. Наиболее вероятные кандидаты в незамерзающие жидкости — водород и гелий. В этих легчайших веществах энергия нулевых колебаний максимальна. Но гелий к тому же — инертный газ. Его атомы взаимодействуют друг с другом очень слабо, и расплавить кристаллическую решетку гелия сравнительно легко. Оказывается, что энергии нулевых колебаний в гелии для этого достаточно, и он не замерзает даже при абсолютном нуле. А вот водород, хотя его атомы и обладают большей, чем у гелия, энергией нулевых колебаний, все-таки замерзает, так как взаимодействие атомов водорода между собой гораздо более сильное.
Все остальные вещества также замерзают при абсолютном нуле температур. Так что гелий — единственное вещество, которое при нормальном давлении всегда остается жидким. Можно даже сказать, что именно соотношение неопределенностей не позволяет ему замерзнуть. Физики называют жидкий гелий квантовой жидкостью. Она обладает таким удивительным макроскопическим квантовым свойством, как сверхтекучесть.
При давлении около 25 атмосфер жидкий гелий все-таки затвердевает. Твердый гелий, правда, тоже не совсем кристалл. В нем нулевые колебания определяют, например, кинетическую энергию атомов на границе между твердым и жидким гелием, и вследствие этого поверхность
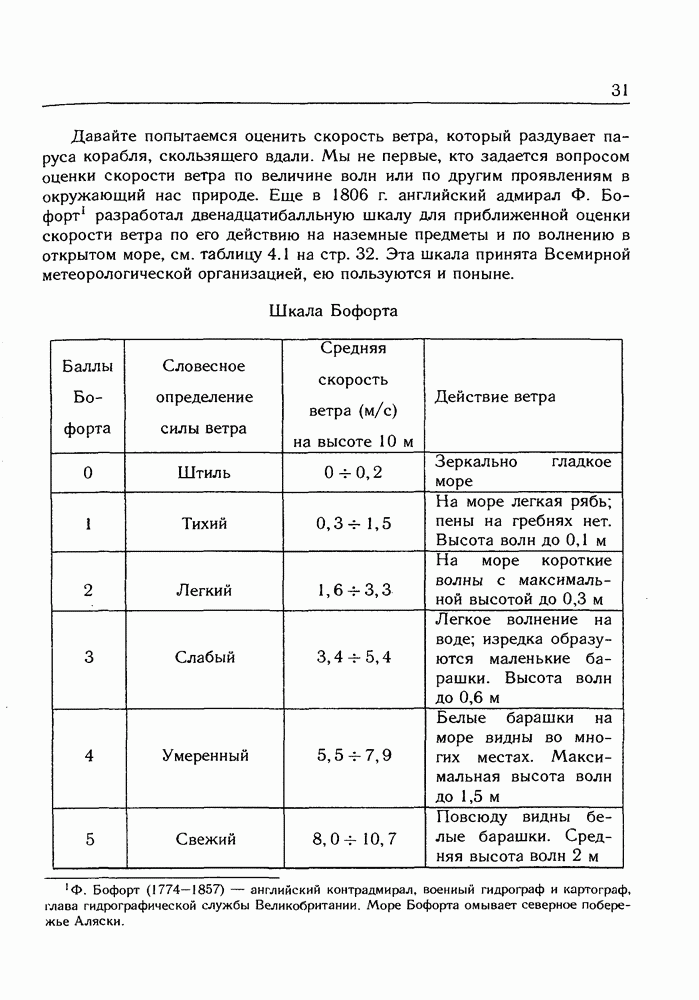
кристалла может совершать гигантские колебания, словно граница между двумя неперемешивающимися жидкостями (рис. 21.4). Твердый гелий физики назвали квантовым кристаллом, и его свойства сейчас интенсивно исследуются.

Рис. 21.4: Волны на границе между твердым (светлая область) и жидким гелием.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Часть I. Физика природных явлений
- Как движутся чаинки в стакане
- Как меняются русла рек
- Как образуются меандры рек
- Глава 2. О реках и озерах
- Глава 3. Переговорная трубка длиной в экватор?
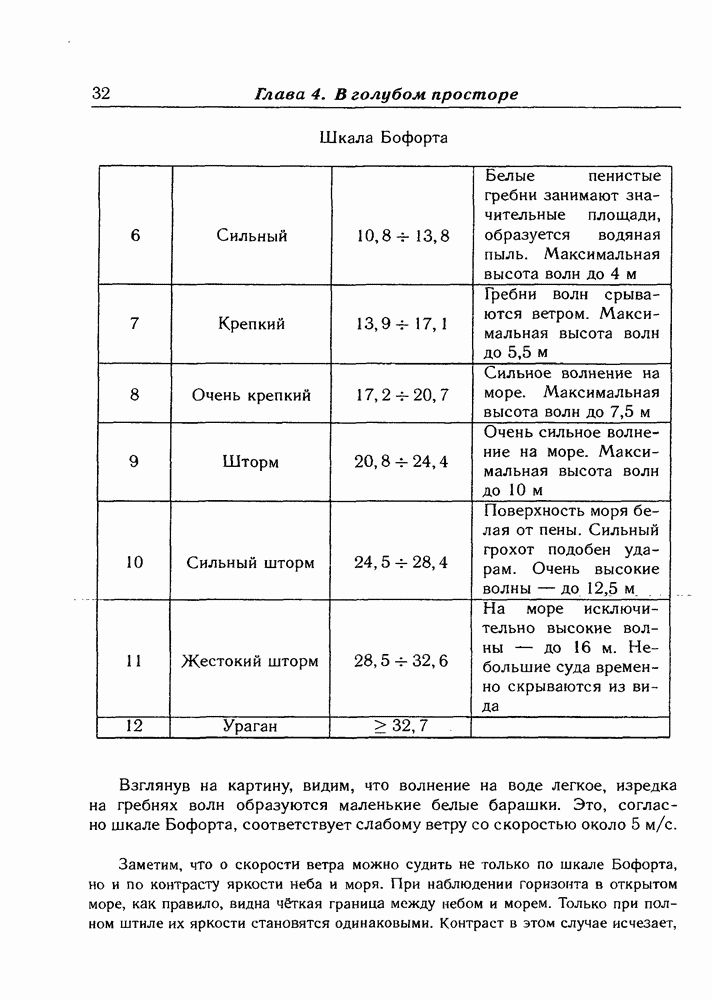
- Глава 4. В голубом просторе
- Глава 5. Лунные дорожки
- Глава 6. Маятник Фуко и закон Бэра
- Глава 7. Лунный тормоз
- Часть II. Простая физика сложных явлений
- Глава 9. Поющие и безмолвствующие бокалы
- Глава 10. Пузырь и капля
- Глава 11. Тайны волшебной лампы
- Глава 12. Пока чайник не закипел…
- Глава 13. Можно ли зажарить мамонта в микроволновой печи?
- Глава 14. Физика приготовления кофе
- Глава 15. Водяной микрофон
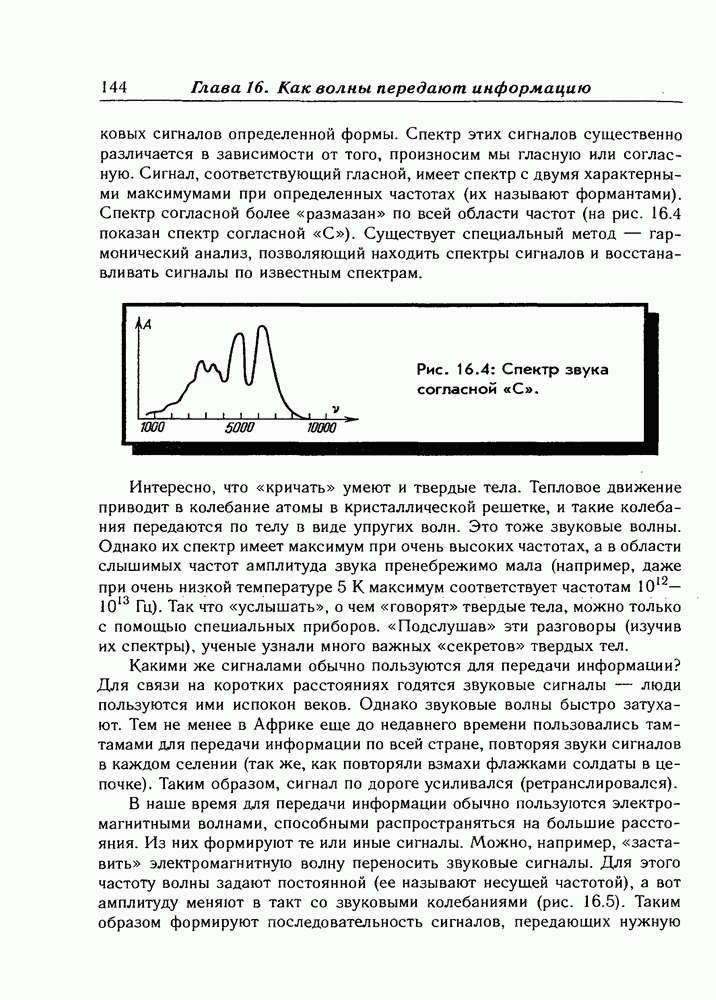
- Глава 16. Как волны передают информацию
- Глава 17. Почему гудят провода
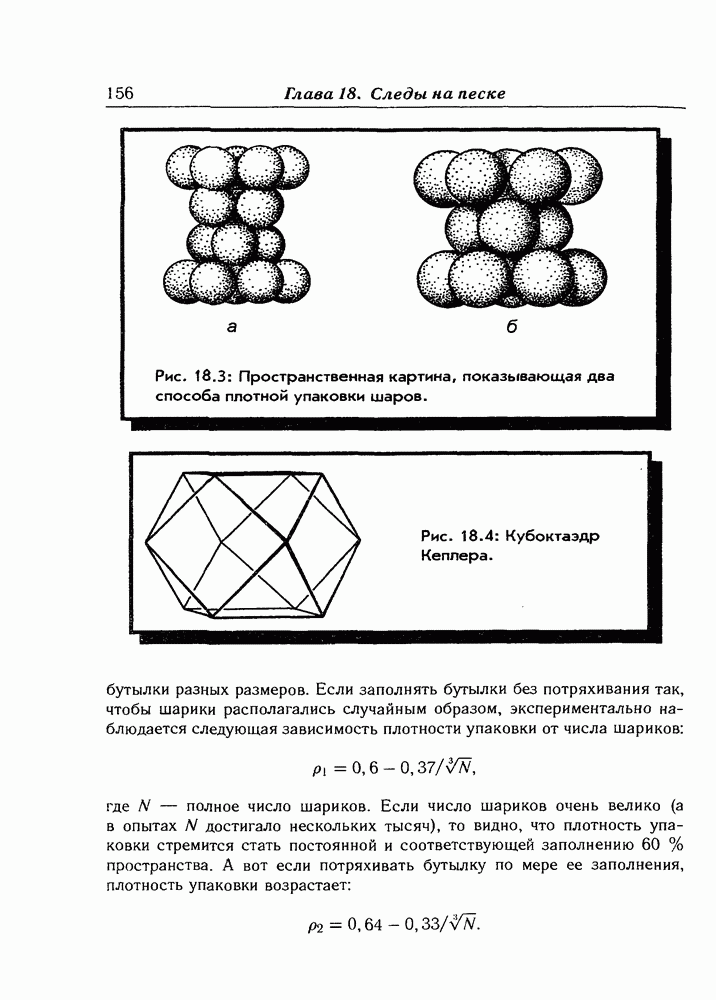
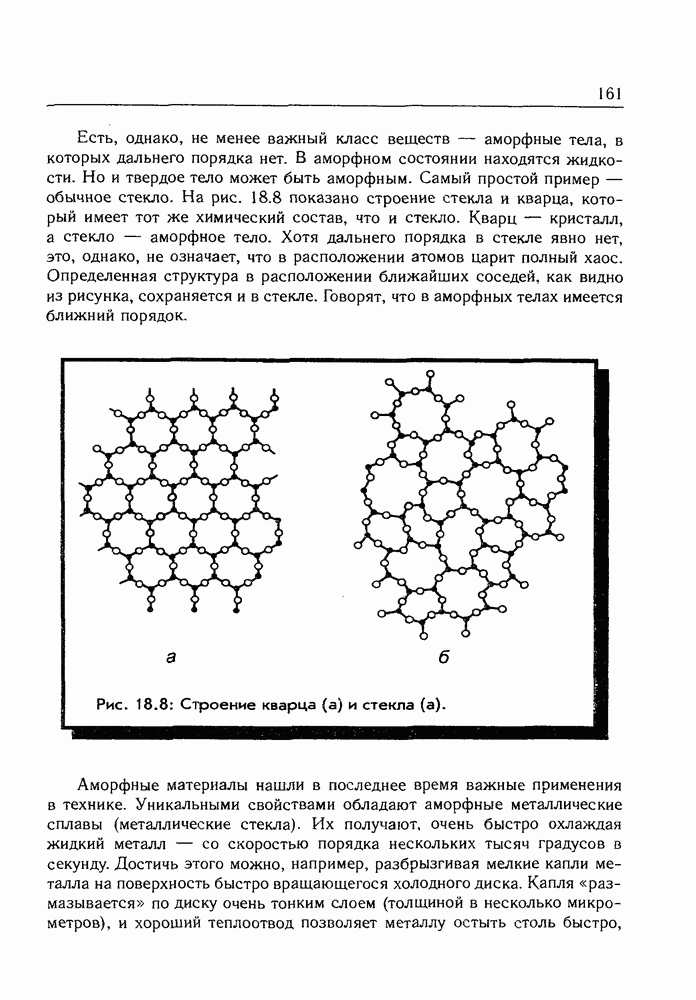
- Глава 18. Следы на песке
- Глава 19. Как устраняют заносы
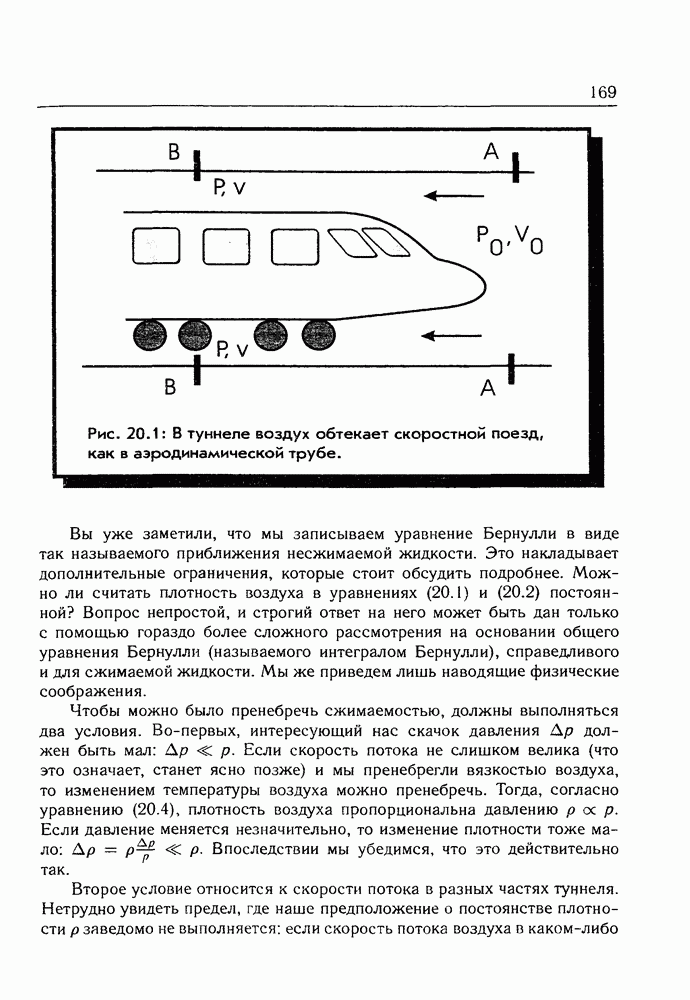
- Глава 20. Случай в поезде
- Часть III. Физика квантового мира
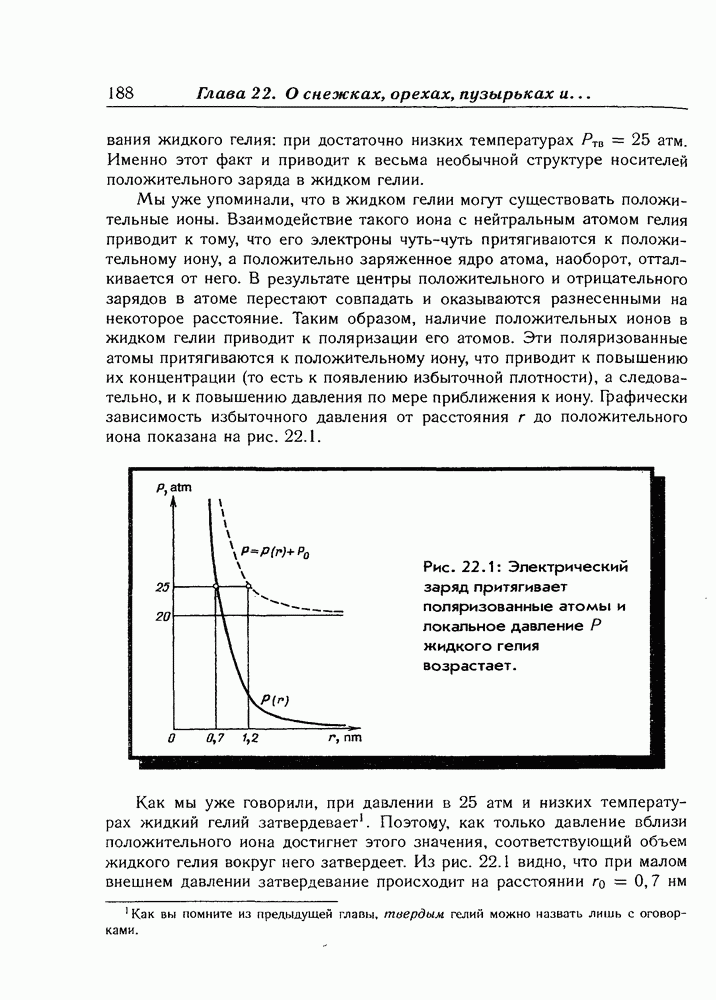
- Глава 22. О снежках, орехах, пузырьках и… жидком гелии
- Глава 23. Страсти по сверхпроводимости в конце тысячелетия
- Глава 24. Что такое сквид?
- Глава 25. Сверхпроводящие магниты
- Заключение