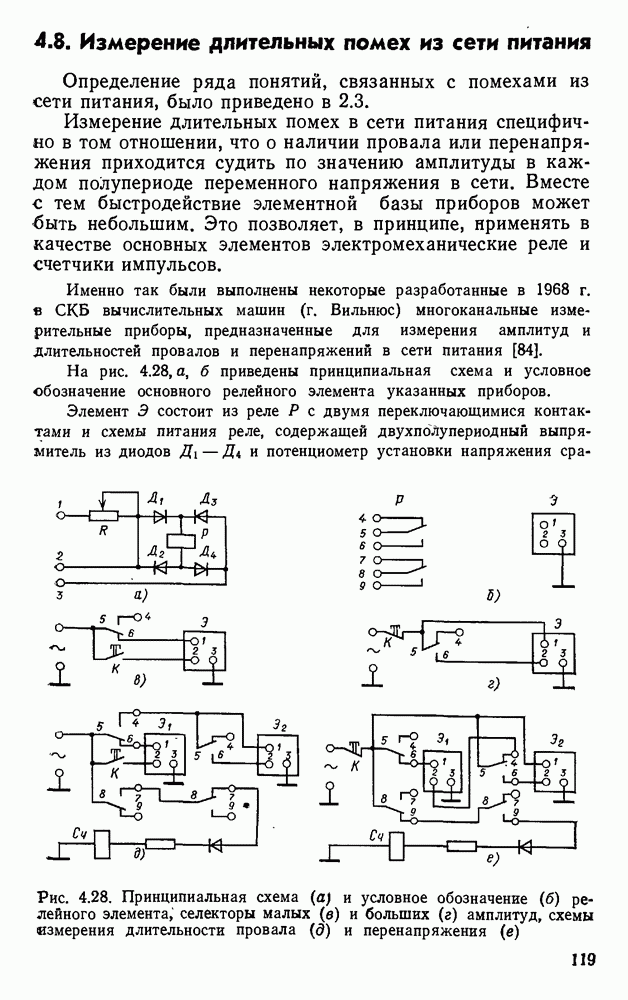
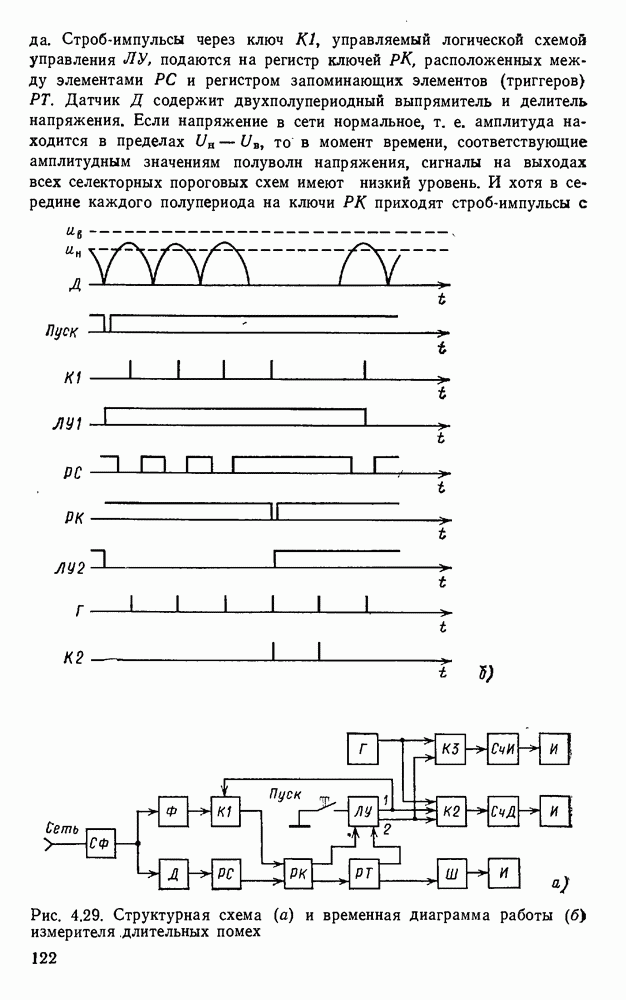
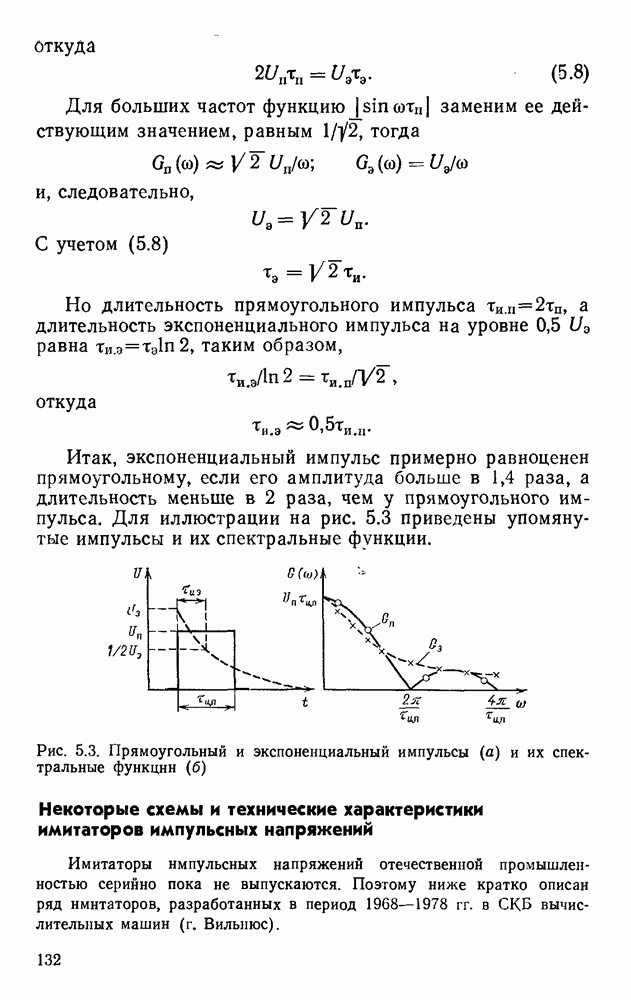
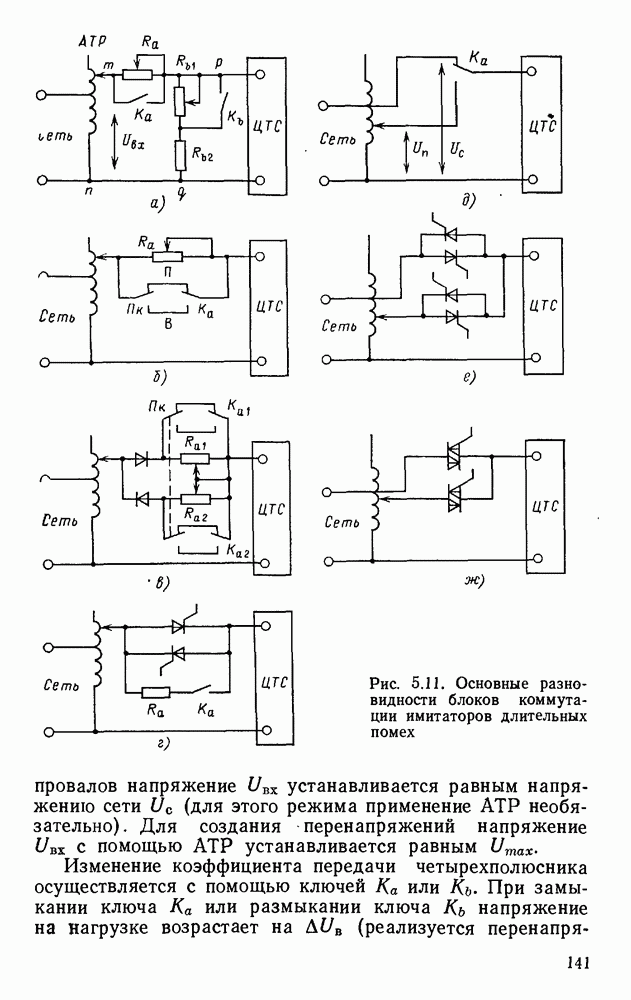
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
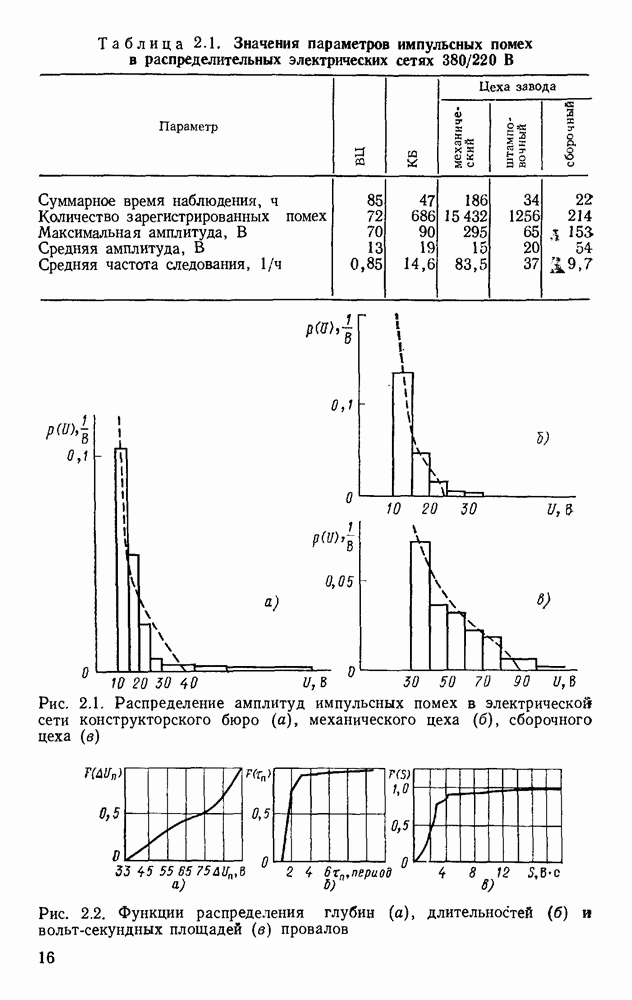
2.7. Теоретическое распределение амплитуд импульсных помех
Логарифмический нормальный и экспоненциальный законы, применяемые для аппроксимации эмпирических функций распределения амплитуд импульсных помех в распределительной электрической сети, не имеют удовлетворительного физического обоснования. Ниже произведена попытка отыскания физически обоснованного теоретического закона.
Распределительная электрическая сеть представляет собой совокупность линий с рассредоточенными параметрами, активных и реактивных нагрузок с сосредоточенными параметрами. При коммутациях нагрузок в сети возникают кратковременные переходные процессы (возмущения), обусловленные главным образом волновыми свойствами длинных линий. Полагая, что для высоких частот параметры сети и «агрузок являются линейными, можно сделать вывод, что амплитуда переходного процесса, возникшего от коммутации нагрузки, в момент t пропорциональна мгновенному значению невозмущенного напряжения сети в момент  , где
, где  зависит от реактивности нагрузки. При этом максимальная амплитуда переходного процесса при включении какой-либо нагрузки в общем случае не может превысить амплитудного значения напряжения промышленной частоты. При выключении же амплитуда может достигать величины
зависит от реактивности нагрузки. При этом максимальная амплитуда переходного процесса при включении какой-либо нагрузки в общем случае не может превысить амплитудного значения напряжения промышленной частоты. При выключении же амплитуда может достигать величины  где
где  — ток нагрузки
— ток нагрузки
в момент выключения, а  волновое сопротивление линии (в идеальной линии, в предположении отсутствия дуги на контактах) [58].
волновое сопротивление линии (в идеальной линии, в предположении отсутствия дуги на контактах) [58].
Длительность возмущений, как правило, несоизмеримо меньше времени между коммутациями. Поэтому плотность распределения амплитуд возмущений  можно выразить в виде полусуммы распределений амплитуд возмущений от включений нагрузок
можно выразить в виде полусуммы распределений амплитуд возмущений от включений нагрузок  и выключений
и выключений  поскольку одному включению обычно соответствует и одно выключение:
поскольку одному включению обычно соответствует и одно выключение:

В предположении, что вид функций  одинаков и они ограничены справа максимальными значениями аргументов
одинаков и они ограничены справа максимальными значениями аргументов  выражение (2.2) можно преобразовать к виду
выражение (2.2) можно преобразовать к виду

где

Эмпирические распределения обычно усечены также и слева на уровне пороговой чувствительности измерительного прибора. Поэтому теоретическое распределение тоже должно быть усеченным:

где y — коэффициент, обеспечивающий тождество

При 

Функция распределения

Здесь F если 
Из (2.5) легко найти у:

откуда

Математическое ожидание амплитуды возмущений

причем

Здесь

Второй начальный момент

причем

Здесь  если
если 
Таким образом, для построения теоретического распределения и определения его основных числовых характеристик достаточно знать выражение для функции 
Отыскание вида функции  для некоторых частных случаев выполнено ниже.
для некоторых частных случаев выполнено ниже.
Чтобы определить параметры  эмпирических распределений, можно прибегнуть к следующему способу.
эмпирических распределений, можно прибегнуть к следующему способу.
В соответствии о (2.4) и (2.8) строятся два семейства вспомогательных графиков

где  выбирается в качестве аргумента, a
выбирается в качестве аргумента, a  — в качестве параметра. Затем из графиков определяются корни
— в качестве параметра. Затем из графиков определяются корни  уравнений (2.12), в левые части которых подставляются известные из эксперимента величины.
уравнений (2.12), в левые части которых подставляются известные из эксперимента величины.
В первом приближении за величину  можно принять
можно принять  -ный квантиль эмпирического распределения
-ный квантиль эмпирического распределения 
Одна нагрузка в сети переменного тока
Амплитуда импульсной помехи U в момент включения устройства при условии, что параметры сети линейны, прямо пропорциональна напряжению в сети  в данный момент (или в момент, предшествующий ему на время
в данный момент (или в момент, предшествующий ему на время  .
.
Коэффициент k в общем случае зависит от параметров сети и устройства, скорости включения и взаимного расположения устройства и измерителя.
Фаза момента включения случайна и распределена равномерно, поэтому величина  также случайна и распределена с плотностью 159]
также случайна и распределена с плотностью 159]

Здесь  — амплитуда напряжения в сети.
— амплитуда напряжения в сети.
Следовательно, амплитуда помехи U также случайна и распределена с плотностью

Обозначим  тогда
тогда

я, наконец,

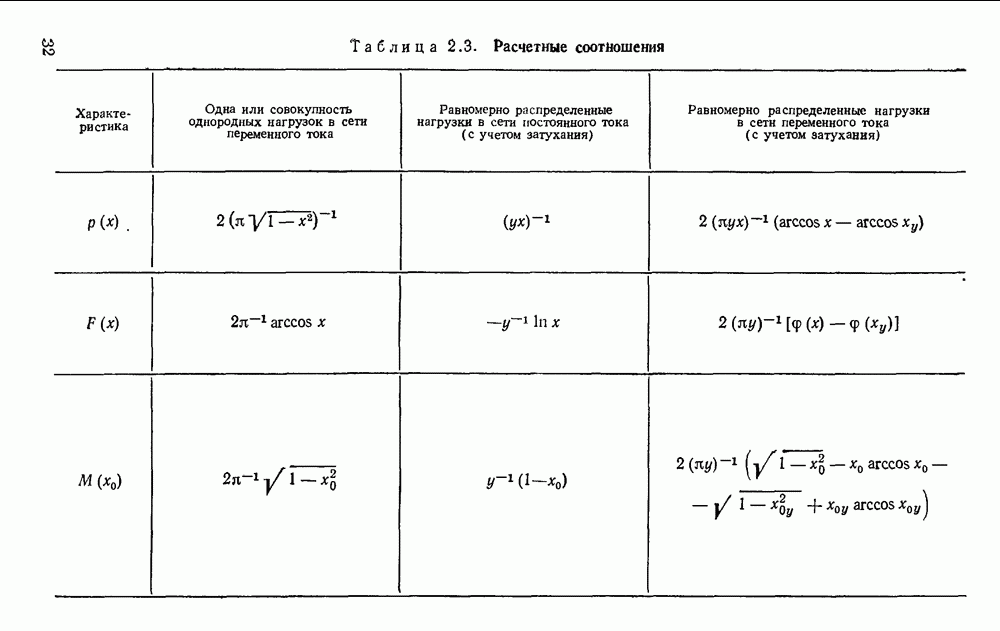
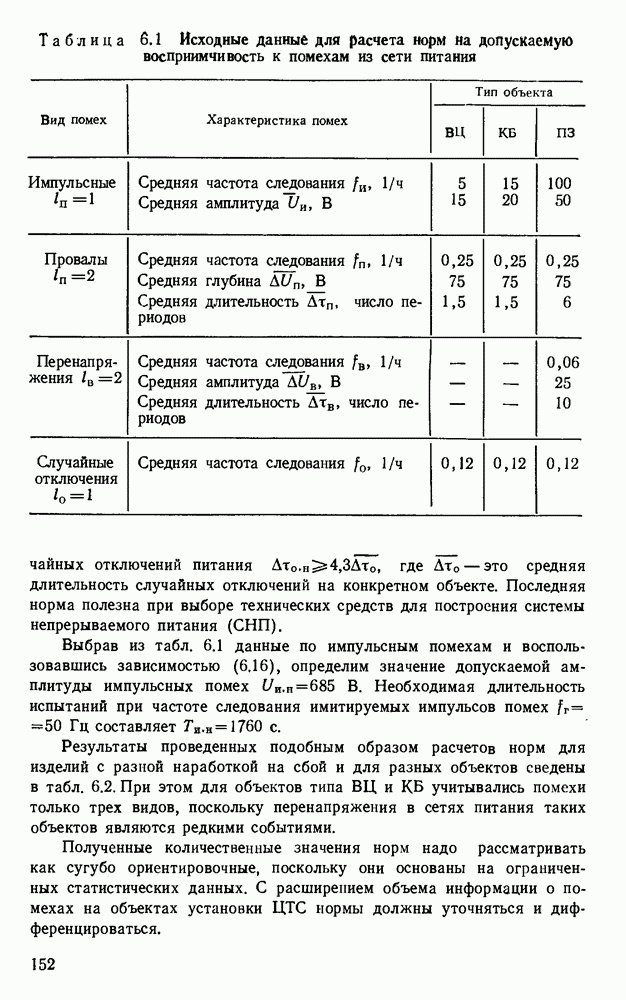
Вид функции (2.13) приведен на рис.  (кривая 1). Остальные зависимости, полученные по (2.3) — (2.10), сведены в табл. 2.3, где приняты следующие обозначения:
(кривая 1). Остальные зависимости, полученные по (2.3) — (2.10), сведены в табл. 2.3, где приняты следующие обозначения: 
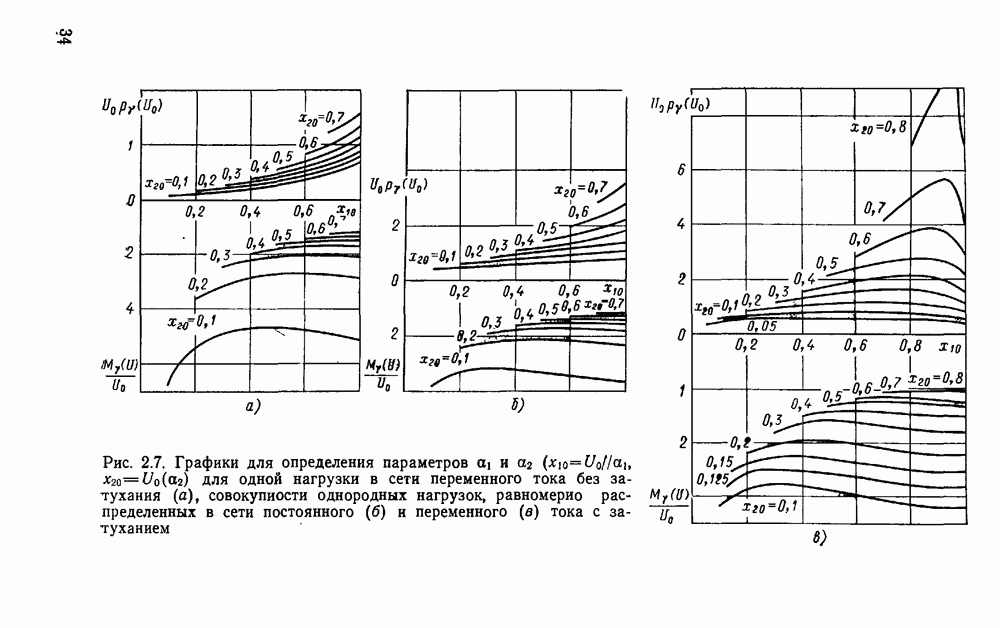
Графики для определения параметров  по формулам (2.12) приведены на рис. 2.7, а.
по формулам (2.12) приведены на рис. 2.7, а.
Совокупность нагрузок
В совокупности нагрузок  нагрузка коммутируется в случайные моменты времени с некоторой средней частотой
нагрузка коммутируется в случайные моменты времени с некоторой средней частотой  Параметр распределения амплитуд возмущений от коммутаций в месте расположения
Параметр распределения амплитуд возмущений от коммутаций в месте расположения

Рис. 2.6. Функция плотности распределения  относительных значений амплитуд
относительных значений амплитуд  импульсных помех при одной нагрузке в сети переменного тока без учета затухания (кривая 1) и функция произведения плотности распределения
импульсных помех при одной нагрузке в сети переменного тока без учета затухания (кривая 1) и функция произведения плотности распределения  на коэффициент затухания у для совокупности однородных нагрузок, распределенных равномерно в сети постоянного (кривая 2) и переменного (кривая 3) тока с учетом затухания
на коэффициент затухания у для совокупности однородных нагрузок, распределенных равномерно в сети постоянного (кривая 2) и переменного (кривая 3) тока с учетом затухания
нагрузки равен  а в месте расположения измерителя —
а в месте расположения измерителя —  . Если сеть мала и затуханием в ней можно пренебречь, то
. Если сеть мала и затуханием в ней можно пренебречь, то  . В общем случае
. В общем случае 
Длительность импульсного возмущения несоизмеримо меньше интервала между коммутациями, поэтому вероятностью совпадения моментов коммутации можно пренебречь даже при большой совокупности нагрузок. С учетом данного допущения средняя частота следования возмущений

где  — число нагрузок.
— число нагрузок.
Если плотность распределения амплитуд возмущений  нагрузки обозначить
нагрузки обозначить  то общая плотность распределения амплитуд
то общая плотность распределения амплитуд

где  — относительная средняя частота коммутаций
— относительная средняя частота коммутаций  устройства. Если все нагрузки однородны, т. е. все
устройства. Если все нагрузки однородны, т. е. все  , то
, то

Таким образом, распределение для совокупности нагрузок не отличается от распределения для одной нагрузки и не зависит от средней частоты коммутации каждой нагрузки.
Если все нагрузки имеют одинаковую среднюю частоту коммутации, то из (2.14) следует

Таблица 2.3. Расчетные соотношения
(см. скан)
Продолжение табл. 2.3
(см. скан)
(см. скан)
Рис. 2.7. Графики для определения параметров  для одной нагрузки в сети переменного тока без затухания (а), совокупности однородных нагрузок, равномерно распределенных в сети постоянного (б) и переменного (в) тока с затуханием
для одной нагрузки в сети переменного тока без затухания (а), совокупности однородных нагрузок, равномерно распределенных в сети постоянного (б) и переменного (в) тока с затуханием
т. е. распределение ДЛЯ Совокупности является усредненной по U функцией плотности распределений для отдельных нагрузок.
Для случая, когда нагрузок весьма много и вид функции  для них одинаков (отличны только значения
для них одинаков (отличны только значения  ), выражение (2.14) можно преобразовать. Перенумеруем нагрузки так, чтобы
), выражение (2.14) можно преобразовать. Перенумеруем нагрузки так, чтобы  с изменением
с изменением  менялось монотонно, и вместо номера будем характеризовать нагрузки величиной
менялось монотонно, и вместо номера будем характеризовать нагрузки величиной  Тогда вместо относительной средней частоты
Тогда вместо относительной средней частоты  можно иерейти к плотности распределения
можно иерейти к плотности распределения  параметра р, а вместо операции суммирования применять интегрирование по Р:
параметра р, а вместо операции суммирования применять интегрирование по Р:

где

Совокупность однородных нагрузок в сети переменного тока (без учета затухания)
Данный случай описывается такими же зависимостями [см. (2.13) и табл. 2.3], как и случай одной нагрузки в сети переменного тока. Такое распределение можно ожидать в производственных помещениях, где установлено однородное оборудование.
Совокупность однородных нагрузок, распределенных равномерно в сети постоянного тока (с учетом затухания)
Предполагается, что одинаковые нагрузки распределены равномерно по сети на длине L. Измерительный прибор расположен у крайней нагрузки. Декремент затухания в сети равен б. Амплитуда напряжения помехи от коммутации одной нагрузки в месте ее расположения равна  для включения и
для включения и  для выключения). Из-за затухания в сети амплитуда напряжения помехи от нагрузки, расположенной на расстоянии s от измерителя, равна:
для выключения). Из-за затухания в сети амплитуда напряжения помехи от нагрузки, расположенной на расстоянии s от измерителя, равна:

Плотность распределения нагрузок по s равна:

Найдем распределение 
Функция (2.16) монотонная, поэтому согласно [59]

где  — функция, обратная
— функция, обратная 
Найдем эту функцию и ее производную из (2.16):

Обозначим  тогда
тогда

В рассматриваемом частном случае поэтому

И, наконец,

Вид произведения функции (2.18) на коэффициент затухания у приведен на рис. 2.6 (кривая 2).
Другие необходимые для расчетов зависимости, полученные по формулам (2.3) — (2.10), сведены в табл. 2.3.
Графики для определения параметров  приведены на рис. 2.7, б.
приведены на рис. 2.7, б.
Для случая, когда измерительный прибор расположен посередине между нагрузками, все зависимости сохраняются с учетом 
Совокупность однородных нагрузок, распределенных равномерно в сети переменного тока (с учетом затухания)
В этом случае плотность распределения амплитуд возмущений от каждой нагрузки у измерителя - согласно (2.13) равна:

Плотность распределения максимальных амплитуд согласно (2.17) равна:

Плотность распределения амплитуд от совокупности согласно (2.15) имеет вид

И, наконец,
 (2.19)
(2.19)
Б (2.19) следует принимать  когда
когда 
Вид произведения функции (2.19) на коэффициент затухания у приведен на рис. 2.6 (кривая 3). Другие необходимые для расчетов зависимости, полученные по  сведены в табл. 2.3.
сведены в табл. 2.3.

Рис. 2.8. Распределения амплитуд для частного случая, когда 
Графики для определения параметров  (при условии
(при условии  ) приведены на рис. 2.7, в.
) приведены на рис. 2.7, в.
В расчетные зависимости (табл.
2.3) для рассмотренного случая входит функция вида

Интеграл такого вида можно разложить в ряд [60]:

Ограничившись первыми двумя членами, получим

Форма распределения существенно зависит от параметров у и  (рис. 2.8).
(рис. 2.8).
При больших значениях у и  функция монотонно убывает. При малых значениях у и
функция монотонно убывает. При малых значениях у и  — это кривая с двумя максимумами.
— это кривая с двумя максимумами.
Теоретические плотности распределения, рассчитанные по выведенным выше формулам, нанесены на эмпирические гистограммы рис. 2.1 (пунктирные кривые), а расчетные параметры распределений сведены в табл. 2.4.
Таблица 2.4. Параметры функций распределения

Из рисунков, следует, что форма эмпирических гистограмм удовлетворительно объясняется найденным теоретическим распределением. Некоторое расхождение теоретических и эмпирических распределений, особенно для больших значений амплитуд, объясняется тем, что предложенное теоретическое распределение не учитывает неоднородность реальных нагрузок и неравномерность их распределения в сети.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава первая. ЭЛЕКТРОМАГНИТНАЯ СОВМЕСТИМОСТЬ
- 1.1. Электромагнитная совместимость ЦТС с внешней средой
- 1.2. Основные понятия, относящиеся к проблеме ЭМС ЦТС
- 1.3. Краткий обзор литературы
- Глава вторая. КОЛИЧЕСТВЕННЫЕ ЗНАЧЕНИЯ ВНЕШНИХ ПОМЕХ
- 2.1. Опасные виды внешних помех
- 2.2. Кратковременные импульсные помехи в сети питания
- 2.3. Длительные помехи в сети питания
- 2.4. Результаты узкополосных измерений помех в сети питания
- 2.5. Импульсные помехи в линиях связи
- 2.6. Электрическое и магнитное поле
- 2.7. Теоретическое распределение амплитуд импульсных помех
- Глава третья. ВОСПРИИМЧИВОСТЬ ЦТС К ВНЕШНИМ ПОМЕХАМ
- 3.1. Воздействие кратковременных импульсных помех
- 3.2. Воздействие длительных импульсных помех из сети питания
- 3.3. Воздействие разрядов электростатических зарядов на корпус ЦТС
- 3.4. Воздействие импульсных электрических полей
- 3.5. Воздействие импульсных магнитных полей
- 3.6. Критерии оценки помехозащищенности
- 3.7. Количественные значения параметров помехозащищенности ЦТС
- Глава четвертая. ТЕХНИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЯ ВНЕШНИХ ПОМЕХ
- 4.2. Основные разновидности измерителей импульсных помех
- 4.3. О проектировании измерителей импульсных помех
- 4.4. Особенности измерения импульсных помех в сети питания
- 4.5. Измерение импульсных помех в линиях связи
- 4.6. Особенности измерения помех от импульсных электрических полей
- 4.7. Измерение гармонических помех
- 4.8. Измерение длительных помех из сети питания
- 4.9. Обработка результатов измерений
- Глава пятая. ТЕХНИЧЕСКИЕ СРЕДСТВА ИМИТАЦИИ ВНЕШНИХ ПОМЕХ
- 5.2. Имитаторы импульсных напряжений
- 5.3. Имитаторы импульсных электрических полей
- 5.4. Имитаторы разрядов электростатических зарядов
- 5.5. Имитаторы длительных помех из сети питания
- 5.6. Имитаторы узкополосных помех
- Глава шестая. НОРМИРОВАНИЕ ДОПУСКАЕМОЙ ВОСПРИИМЧИВОСТИ К ВНЕШНИМ ПОМЕХАМ И ДОПУСКАЕМОГО ПОМЕХОИЗЛУЧЕНИЯ
- 6.2. Обзор существующих технических требований
- 6.3. Нормы на допускаемую восприимчивость изделий к внешним помехам, распространяющимся по проводам
- 6.4. Нормы на допускаемую восприимчивость изделий к внешним помехам, распространяющимся в пространстве
- 6.5. Нормы на допускаемое излучение изделиями помех
- 6.6. Определение необходимого ослабления помех проводящими корпусами и сетевыми фильтрами изделий
- Глава седьмая. МЕТОДЫ ИСПЫТАНИЙ НА ДОПУСКАЕМУЮ ВОСПРИИМЧИВОСТЬ К ВНЕШНИМ ПОМЕХАМ И ДОПУСКАЕМОЕ ПОМЕХОИЗЛУЧЕНИЕ
- 7.2. Методы испытаний на восприимчивость изделий к внешним помехам, распространяющимся по проводам
- 7.3. Методы испытаний на восприимчивость изделий к внешним помехам, распространяющимся в пространстве
- 7.4. Методы испытаний изделий на допускаемое излучение помех
- Глава восьмая. НЕКОТОРЫЕ РЕКОМЕНДАЦИИ ПО ОБЕСПЕЧЕНИЮ ЭМС ЦТС
- 8.2. Системы земель
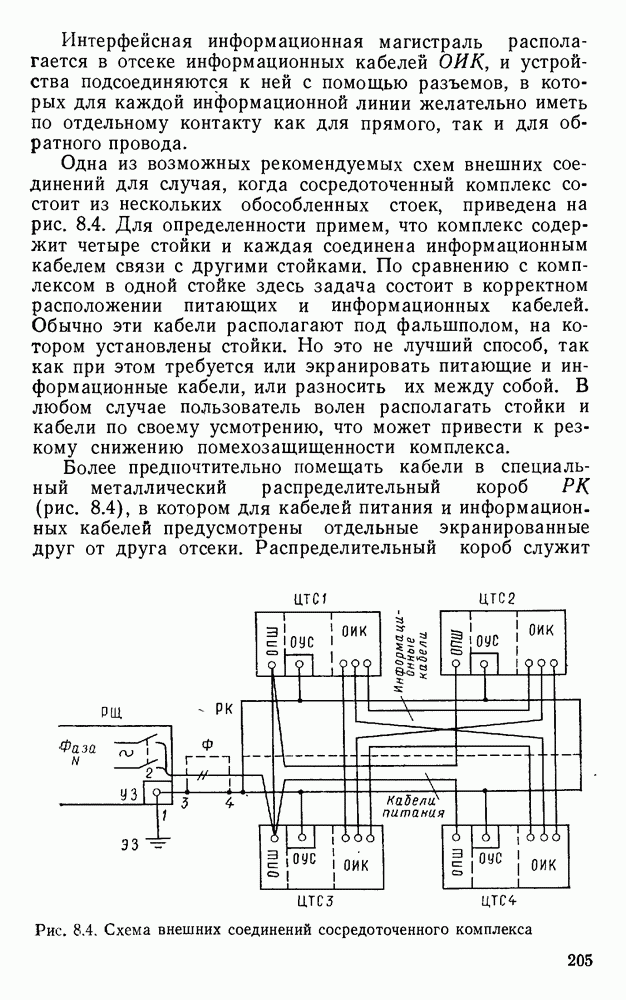
- 8.3. Рекомендации по выполнению внешних соединений
- 8.4. Экранирование и фильтрация
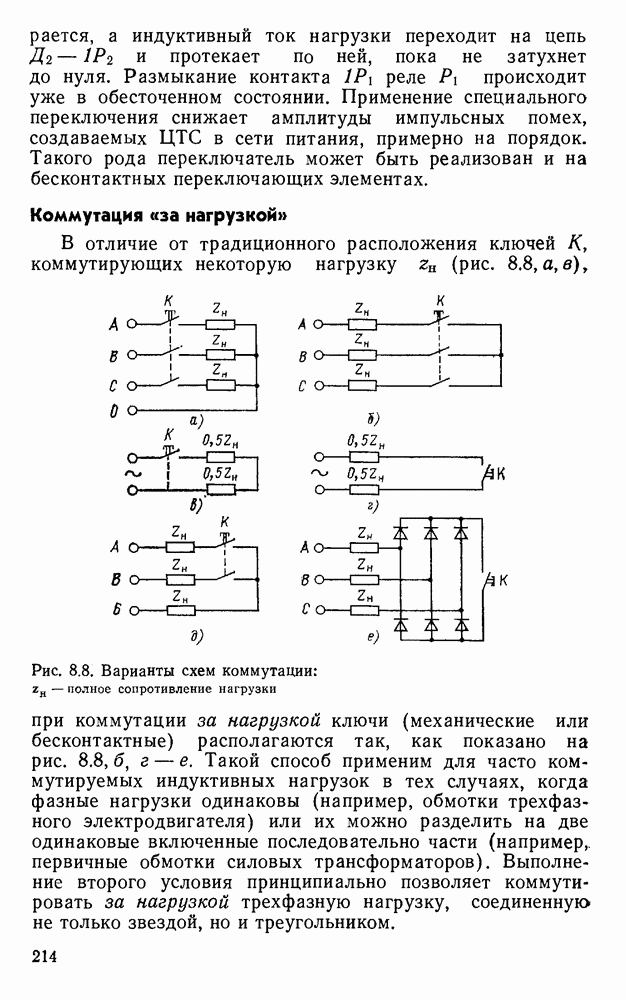
- 8.5. Снижение уровня импульсных помех, создаваемых ЦТС в сети питания переменного тока
- 8.6. Резервирование питания ЦТС
- Список литературы