| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5. Воздействие импульсных магнитных полей
Иногда ЦТС могут быть установлены близко от источников импульсных магнитных полей. Такими источниками, например, могут стать провода сети питания при быстрой коммутации больших токов нагрузки. Полагая, как и в § 3.4, что ЦТС находится в ближней зоне излучения источника, магнитное поле в этой зоне будем считать квазистатическим и для анализа применим модель связей между источником и приемником, показанную на рис. 3.10.
На схеме изображены два индуктивно связанных контура. Первый — контур источника, содержит генератор  с внутренним
с внутренним

Рис. 3.10. Схема индуктивной связи между источником и приемником помех
сопротивлением  . Второй — контур приемника с входным сопротивлением
. Второй — контур приемника с входным сопротивлением  . Из схемы после несложных преобразований следует (в изображениях по Карсону)
. Из схемы после несложных преобразований следует (в изображениях по Карсону)

Как правило, связь между контурами является весьма слабой, т. е.  поэтому членом
поэтому членом  в знаменателе можно пренебречь. Если сигнал на источнике представляет собой скачок напряжения, то
в знаменателе можно пренебречь. Если сигнал на источнике представляет собой скачок напряжения, то  и (3.61) преобразуется к виду
и (3.61) преобразуется к виду

где
Соответствующий оригинал

Из (3.63) следует, что в общем случае переходная функция представляет собой импульс, сформированный из двух экспонент с постоянными времени 
Вольт-секундная площадь импульса

Амплитуда импульса

где 
Эквивалентная длительность импульса

Длительность переднего фронта импульса в первом приближении можно принять равной:

Если внутреннее сопротивление источника мало, а вход, ное сопротивление приемника велико и выполняется условие  ТО
ТО  а
а

Если, наоборот,  то
то  и
и

Из (3.64) — (3.69) следует, что для оценки влияния источника на приемник необходимо знать значения собственных индуктивностей  и взаимной индуктивности М.
и взаимной индуктивности М.
Расчетные соотношения для собственных и взаимных индуктивностей далеко не во всех случаях можно получить в конечном виде как функции топологических параметров контуров. Однако для некоторых простых случаев такие соотношения известны. Так, например, индуктивность прямолинейного провода кругового сечения [66]

где  — магнитная постоянная;
— магнитная постоянная;  — длина и радиус провода.
— длина и радиус провода.
Индуктивность однофазной (двухпроводной) линии с проводами кругового сечения [66]

где d — расстояние между осями проводов.
Индуктивность выпуклого плоского контура площадью s из провода кругового сечения [66]

где  — длина периметра контура.
— длина периметра контура.
Что касается взаимной индуктивности между контурами источника и приемника, то практический интерес представляют случаи, когда контур источника — одиночный провод или двухпроводная линия, а контур приемника — одиночный провод, двухпроводная линия или выпуклый плоский контур.
Взаимная индуктивность двух параллельных одиночных проводов равна [66]:

где L — расстояние между осями проводов.
Выражение (3.73) верно, если выполняется условие
Взаимная индуктивность параллельных одиночных провода и двухпроводной линии при условии, что все провода лежат в одной плоскости и равна:

Если к тому же  то
то

Взаимную индуктивность между одиночным проводом и удаленным от него выпуклым плоским контуром площади s, лежащим в одной плоскости с проводом, определим из следующих соображений. Пусть расстояние от провода до центра контура равно L, а наибольший размер контура Тогда можно считать, что напряженность магнитного поля Н во всех точках, ограниченных контуром, одинакова и по закону полного тока  где I — ток в одиночном проводе. Искомая взаимная индуктивность
где I — ток в одиночном проводе. Искомая взаимная индуктивность 
Соответственно взаимная индуктивность между двухпроводной линией и выпуклым плоским контуром площади s, лежащим в одной плоскости с проводами линии, при условии, что  — расстояние между проводами линии, L — расстояние между осью симметрии линии и центром контура), равна:
— расстояние между проводами линии, L — расстояние между осью симметрии линии и центром контура), равна:

Взаимная индуктивность между двумя параллельными двухпроводными линиями [66]

где  — расстояние между осями
— расстояние между осями  проводов, причем в индексе цифры 1 и 2 относятся к проводам одной линии, а цифры 3 и 4 — к проводам другой линии.
проводов, причем в индексе цифры 1 и 2 относятся к проводам одной линии, а цифры 3 и 4 — к проводам другой линии.
Если все провода лежат в одной плоскости, расстояние между осями проводов линий равно d, а расстояние между осями симметрии линий равно L, то из (3.77) легко получить

Из (3.64) и (3.65) следует, что воздействие источника на приемник в решающей степени определяется значением взаимной индуктивности М.
Количественно оценим М для случаев, когда контуры представляют собой одиночный провод длиной  однофазную линию такой же длины с расстоянием между проводами
однофазную линию такой же длины с расстоянием между проводами  замкнутый контур площадью
замкнутый контур площадью  и периметром
и периметром  Расстояние между контурами
Расстояние между контурами 
После подстановки указанных данных в (3.73) — (3.77) взаимная индуктивность оказывается равной: между двумя одиночными проводами  между одиночным проводом и двухпроводной линией
между одиночным проводом и двухпроводной линией  между двумя двухпроводными линиями
между двумя двухпроводными линиями  между однопроводной линией и замкнутым контуром
между однопроводной линией и замкнутым контуром  между двухпроводной линией и замкнутым контуром
между двухпроводной линией и замкнутым контуром 
Из (3.64), (3.65) и (3.73) — (3.77) следует, что наиболее эффективными способами снижения  вольт-секундной площади и амплитуды помех, наводимых от импульсных магнитных полей, являются уменьшение площади контуров аппаратуры ЦТС и удаление этих контуров от источников полей.
вольт-секундной площади и амплитуды помех, наводимых от импульсных магнитных полей, являются уменьшение площади контуров аппаратуры ЦТС и удаление этих контуров от источников полей.
Уменьшение площади контуров может быть достигнуто путем применения симметричных линий связи: бифиляров, коаксиальных кабелей, многослойного печатного монтажа, в котором отдельные проводящие слои отводятся для образования плоскостей «земли» системы вторичного питания.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава первая. ЭЛЕКТРОМАГНИТНАЯ СОВМЕСТИМОСТЬ
- 1.1. Электромагнитная совместимость ЦТС с внешней средой
- 1.2. Основные понятия, относящиеся к проблеме ЭМС ЦТС
- 1.3. Краткий обзор литературы
- Глава вторая. КОЛИЧЕСТВЕННЫЕ ЗНАЧЕНИЯ ВНЕШНИХ ПОМЕХ
- 2.1. Опасные виды внешних помех
- 2.2. Кратковременные импульсные помехи в сети питания
- 2.3. Длительные помехи в сети питания
- 2.4. Результаты узкополосных измерений помех в сети питания
- 2.5. Импульсные помехи в линиях связи
- 2.6. Электрическое и магнитное поле
- 2.7. Теоретическое распределение амплитуд импульсных помех
- Глава третья. ВОСПРИИМЧИВОСТЬ ЦТС К ВНЕШНИМ ПОМЕХАМ
- 3.1. Воздействие кратковременных импульсных помех
- 3.2. Воздействие длительных импульсных помех из сети питания
- 3.3. Воздействие разрядов электростатических зарядов на корпус ЦТС
- 3.4. Воздействие импульсных электрических полей
- 3.5. Воздействие импульсных магнитных полей
- 3.6. Критерии оценки помехозащищенности
- 3.7. Количественные значения параметров помехозащищенности ЦТС
- Глава четвертая. ТЕХНИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЯ ВНЕШНИХ ПОМЕХ
- 4.2. Основные разновидности измерителей импульсных помех
- 4.3. О проектировании измерителей импульсных помех
- 4.4. Особенности измерения импульсных помех в сети питания
- 4.5. Измерение импульсных помех в линиях связи
- 4.6. Особенности измерения помех от импульсных электрических полей
- 4.7. Измерение гармонических помех
- 4.8. Измерение длительных помех из сети питания
- 4.9. Обработка результатов измерений
- Глава пятая. ТЕХНИЧЕСКИЕ СРЕДСТВА ИМИТАЦИИ ВНЕШНИХ ПОМЕХ
- 5.2. Имитаторы импульсных напряжений
- 5.3. Имитаторы импульсных электрических полей
- 5.4. Имитаторы разрядов электростатических зарядов
- 5.5. Имитаторы длительных помех из сети питания
- 5.6. Имитаторы узкополосных помех
- Глава шестая. НОРМИРОВАНИЕ ДОПУСКАЕМОЙ ВОСПРИИМЧИВОСТИ К ВНЕШНИМ ПОМЕХАМ И ДОПУСКАЕМОГО ПОМЕХОИЗЛУЧЕНИЯ
- 6.2. Обзор существующих технических требований
- 6.3. Нормы на допускаемую восприимчивость изделий к внешним помехам, распространяющимся по проводам
- 6.4. Нормы на допускаемую восприимчивость изделий к внешним помехам, распространяющимся в пространстве
- 6.5. Нормы на допускаемое излучение изделиями помех
- 6.6. Определение необходимого ослабления помех проводящими корпусами и сетевыми фильтрами изделий
- Глава седьмая. МЕТОДЫ ИСПЫТАНИЙ НА ДОПУСКАЕМУЮ ВОСПРИИМЧИВОСТЬ К ВНЕШНИМ ПОМЕХАМ И ДОПУСКАЕМОЕ ПОМЕХОИЗЛУЧЕНИЕ
- 7.2. Методы испытаний на восприимчивость изделий к внешним помехам, распространяющимся по проводам
- 7.3. Методы испытаний на восприимчивость изделий к внешним помехам, распространяющимся в пространстве
- 7.4. Методы испытаний изделий на допускаемое излучение помех
- Глава восьмая. НЕКОТОРЫЕ РЕКОМЕНДАЦИИ ПО ОБЕСПЕЧЕНИЮ ЭМС ЦТС
- 8.2. Системы земель
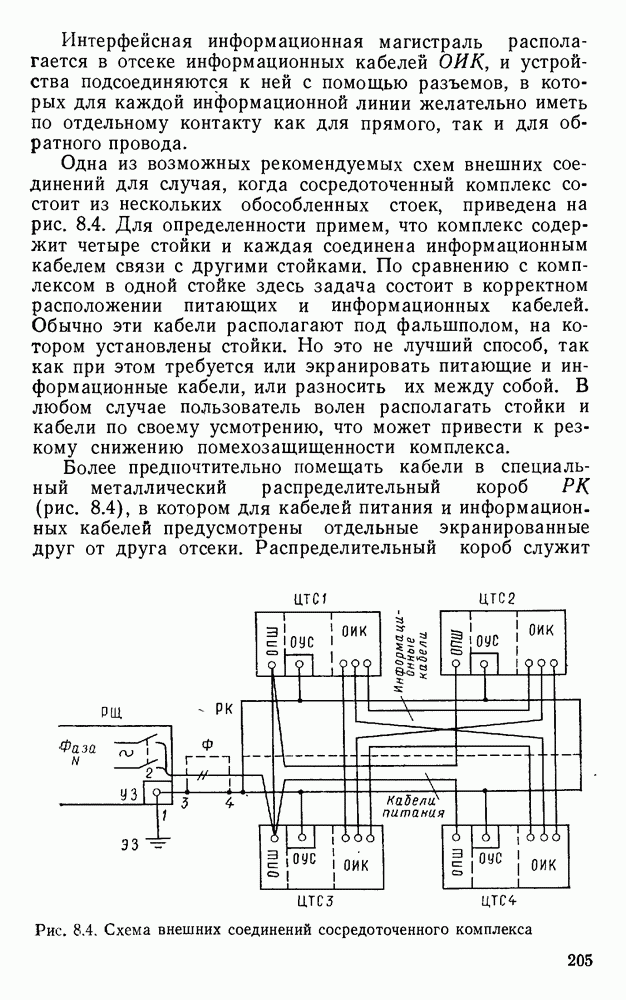
- 8.3. Рекомендации по выполнению внешних соединений
- 8.4. Экранирование и фильтрация
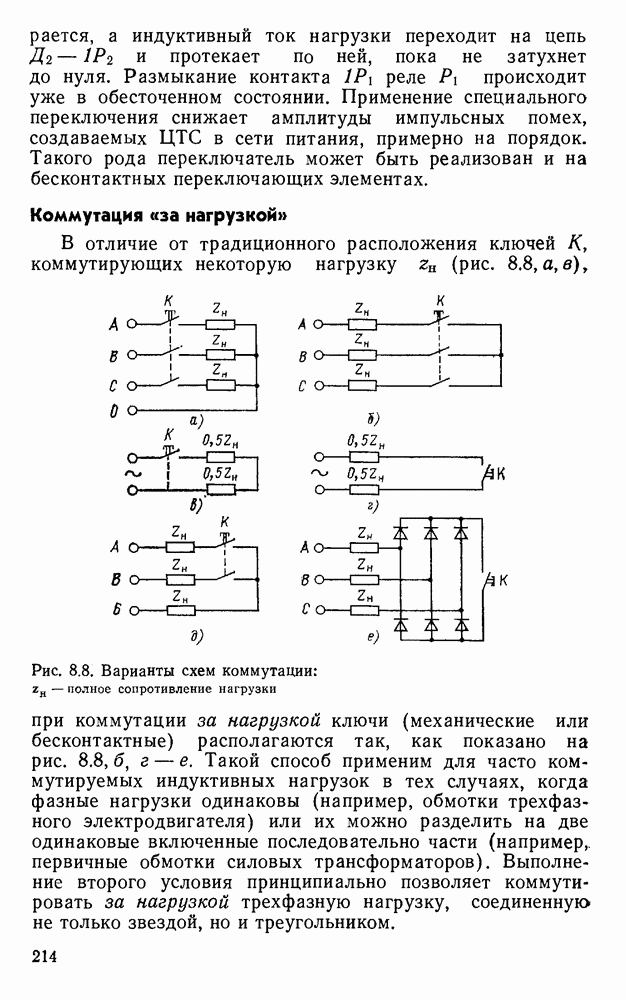
- 8.5. Снижение уровня импульсных помех, создаваемых ЦТС в сети питания переменного тока
- 8.6. Резервирование питания ЦТС
- Список литературы