| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Главное значение несобственного интеграла
Определение. Пусть функция  определена на прямой
определена на прямой  и интегрируема на каждом сегменте, принадлежащем этой прямой. Будем говорить, что функция
и интегрируема на каждом сегменте, принадлежащем этой прямой. Будем говорить, что функция  интегрируема по Коши, если существует предел
интегрируема по Коши, если существует предел 
Этот предел мы будем называть главным значением несобственного интеграла от функции  (в смысле Коши) и обозначать символом
(в смысле Коши) и обозначать символом

Пример 1. Найдем главное значение интеграла от функции? х. Поскольку в силу нечетности х,

Точно так же заключаем, что 
Справедливо следующее
Утверждение. Пусть функция  интегрируема на каждом сегменте прямой
интегрируема на каждом сегменте прямой  Если эта функция
Если эта функция  нечетна, то она интегрируема по Коши и главное значение интеграла от нее равняется нулю.
нечетна, то она интегрируема по Коши и главное значение интеграла от нее равняется нулю.
Если функция  четна, то она интегрируема по Коши тогда и только тогда, когда сходится несобственный интеграл
четна, то она интегрируема по Коши тогда и только тогда, когда сходится несобственный интеграл

Первая часть этого утверждения является очевидной. Для доказательства второй части достаточно воспользоваться равенством  справедливым для любой четной функции, и определением сходимости несобственного интеграла (9.1.17).
справедливым для любой четной функции, и определением сходимости несобственного интеграла (9.1.17).
Понятие интегрируемости по Коши можно ввести и для несобственных интегралов второго рода в случае, когда особая точка, является внутренней точкой сегмента, по которому производится: интегрирование.
Определение. Пусть функция  определена на сегменте
определена на сегменте  кроме, быть может, точки
кроме, быть может, точки  и интегрируема на любом сегменте, принадлежащем либо
и интегрируема на любом сегменте, принадлежащем либо  , либо
, либо  . Будем говорить, что функция
. Будем говорить, что функция  интегрируема по Коши, если существует предел
интегрируема по Коши, если существует предел

называемый главным значением интеграла в смысле Коши.
Пример 2. Функция  не интегрируема на сегменте
не интегрируема на сегменте  в несобственном смысле, однако она интегрируема по Коши. При этом
в несобственном смысле, однако она интегрируема по Коши. При этом

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРА
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- Глава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Недостаточность рациональных чисел для измерения отрезков числовой оси.
- 3. Упорядочение множества бесконечных десятичных дробей.
- § 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
- 2. Существование точных граней.
- § 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
- § 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Существование и единственность суммы и произведения вещественных чисел.
- § 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Некоторые часто употребляемые соотношения.
- 3. Некоторые конкретные множества вещественных чисел.
- § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Аксиоматическое введение множества вещественных чисел.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
- 2. Операции над множествами.
- 3. Счетные и несчетные множества. Несчетность сегмента [0, 1]. Мощность множества.
- 4. Свойства операций над множествами. Отображение множеств.
- Глава 3. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
- 2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- 3. Основные свойства бесконечно малых последовательностей.
- 4. Сходящиеся последовательности и их свойства.
- § 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Теорема о сходимости монотонной ограниченной последовательности.
- 4. Примеры сходящихся монотонных последовательностей.
- § 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Расширение понятий предельной точки и верхнего и нижнего пределов.
- 3. Критерий Коши сходимости последовательности.
- § 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ
- 2. Предел функции по Гейне и по Коши.
- 3. Критерий Коши существования предела функции.
- 4. Арифметические операции над функциями, имеющими предел.
- 5. Бесконечно малые и бесконечно большие функции.
- § 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ
- Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
- 2. Арифметические операции над непрерывными функциями.
- 3. Сложная функция и ее непрерывность.
- § 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ
- 2. Понятие обратной функции.
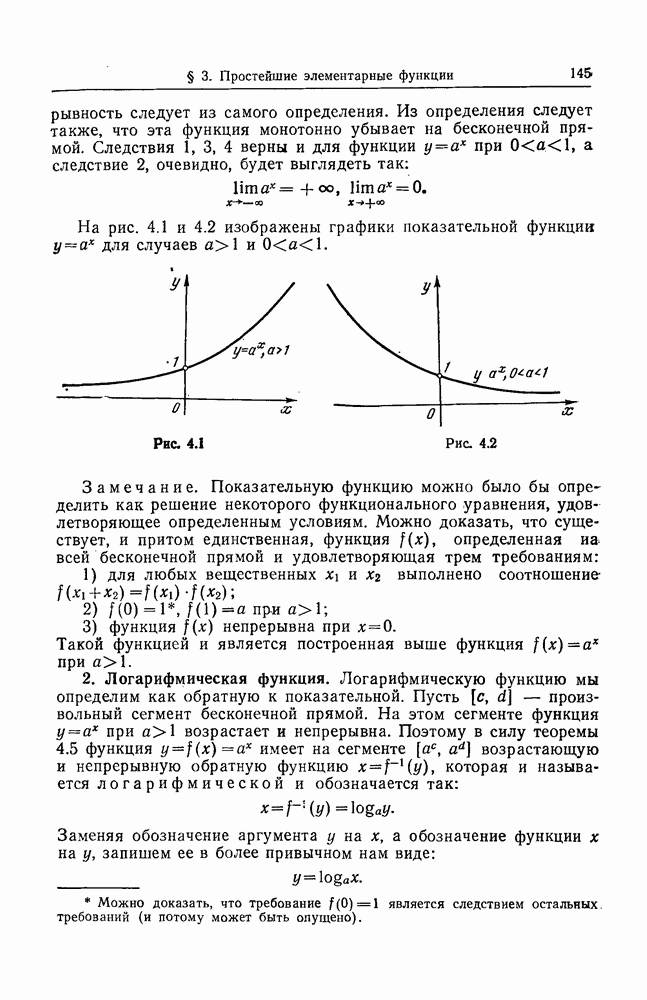
- § 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
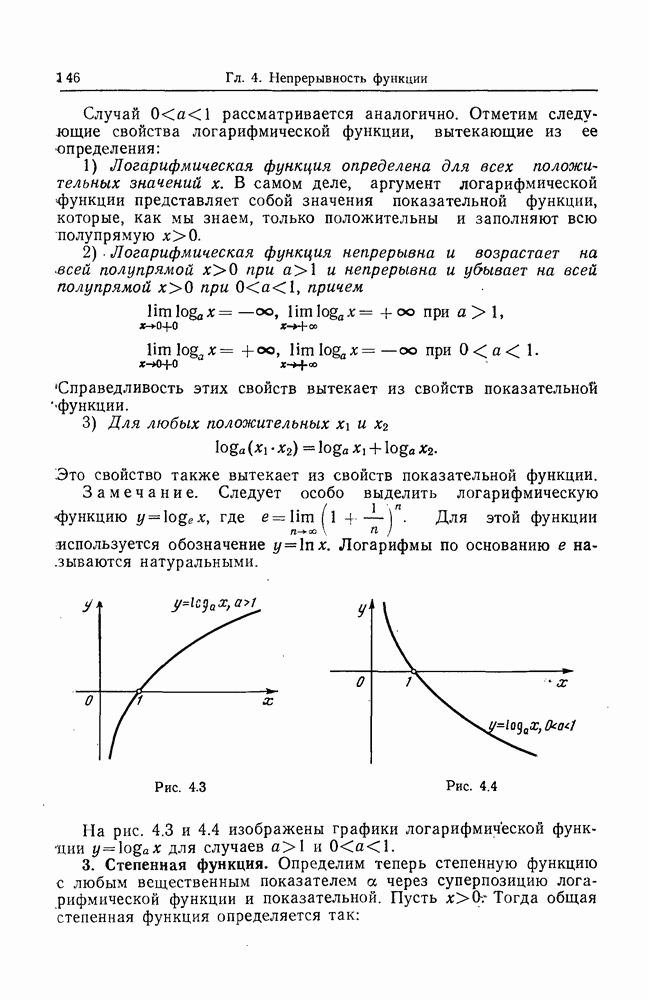
- 2. Логарифмическая функция.
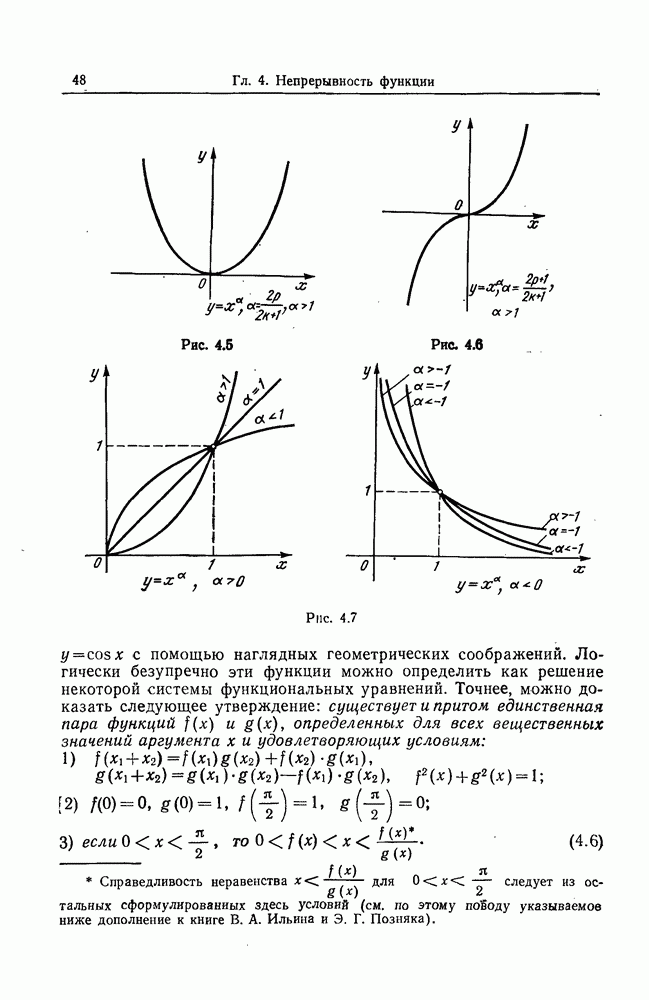
- 3. Степенная функция.
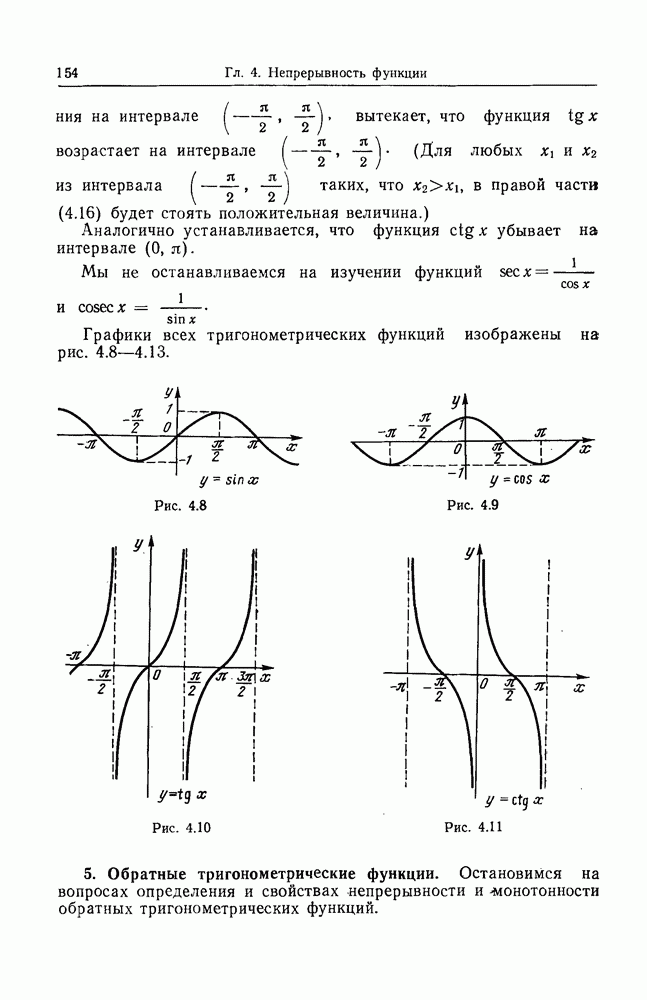
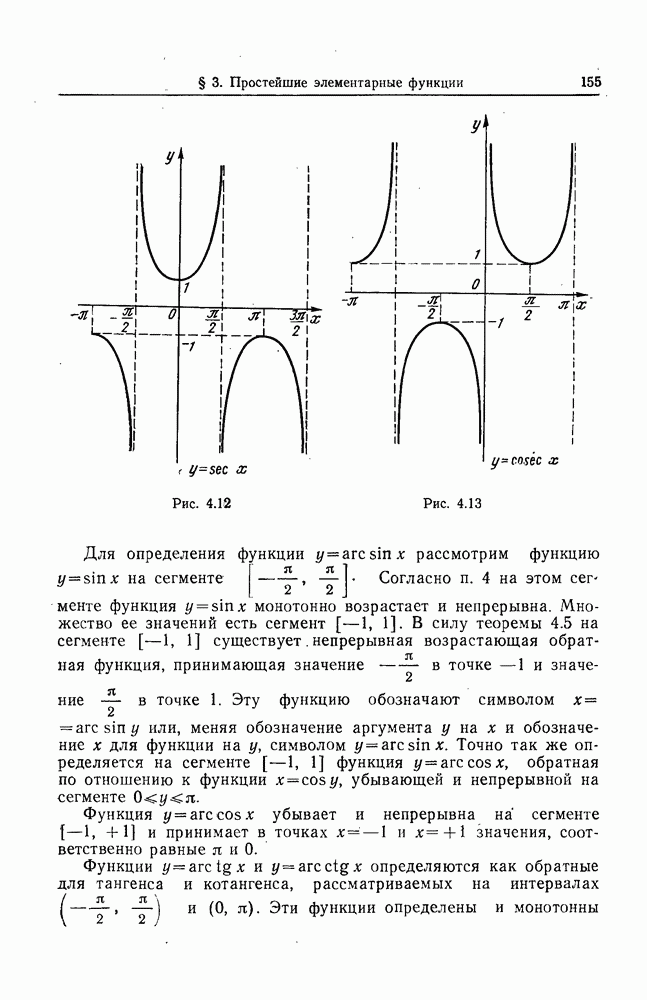
- 4. Тригонометрические функции.
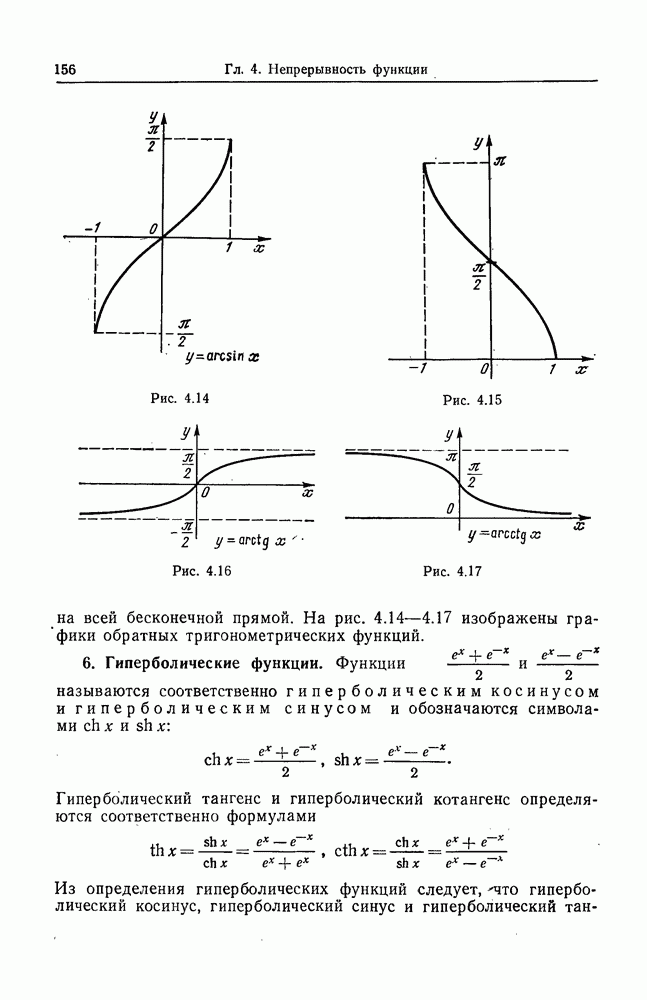
- 5. Обратные тригонометрические функции.
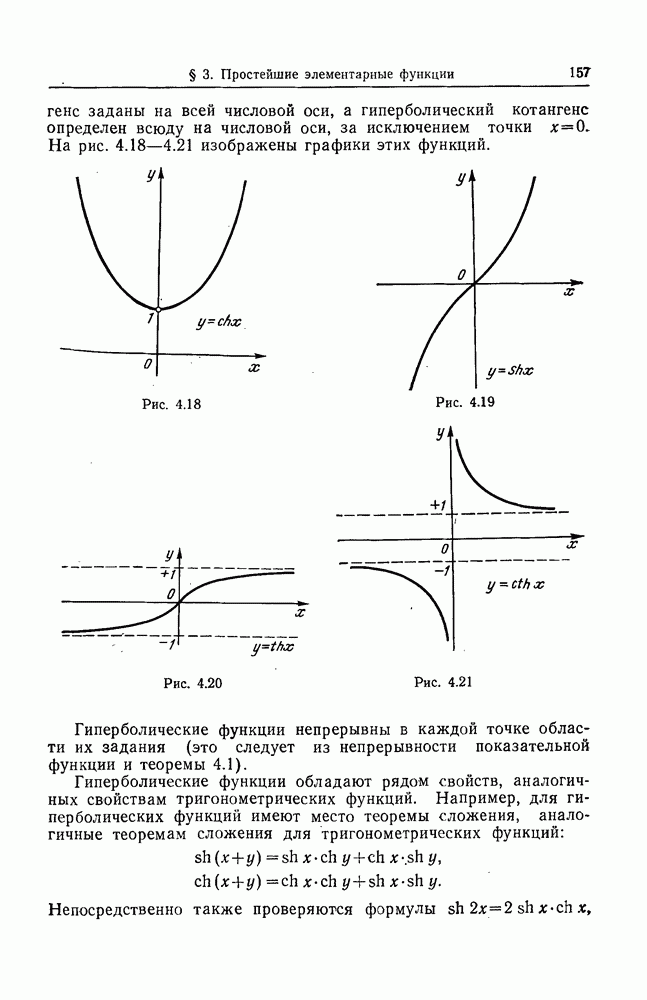
- 6. Гиперболические функции.
- § 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА
- 2. Второй замечательный предел.
- § 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ
- 2. О точках разрыва монотонной функции.
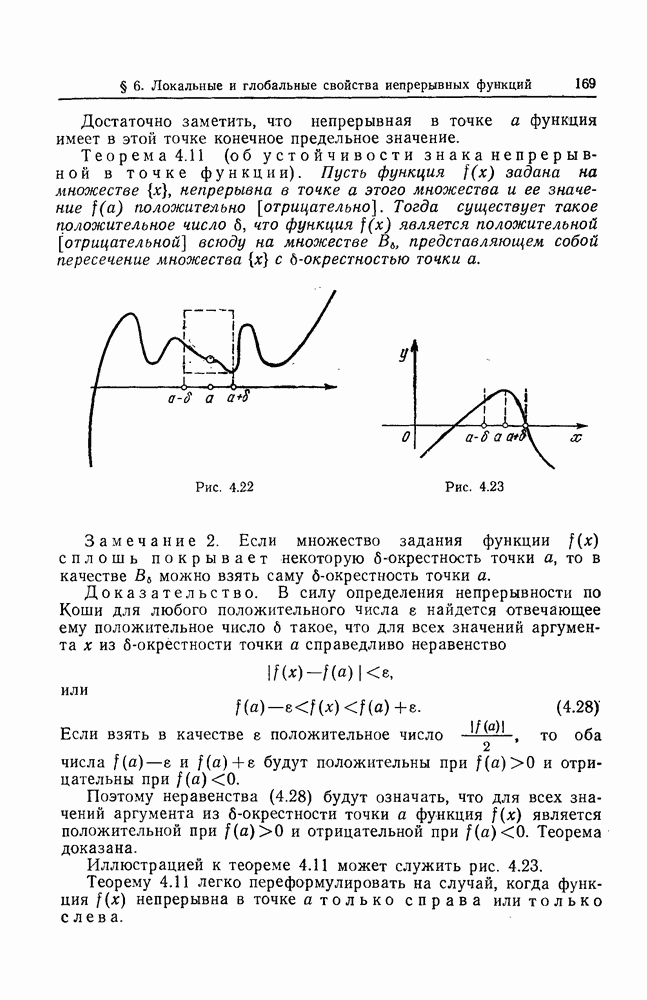
- § 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
- 2. Глобальные свойства непрерывных функций.
- 3. Понятие равномерной непрерывности функции.
- 4. Понятие модуля непрерывности функции.
- § 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА
- 2. О покрытиях множества системой открытых множеств.
- 3. Понятие компактности множества.
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. ПОНЯТИЕ ПРОИЗВОДНОЙ
- 2. Определение производной.
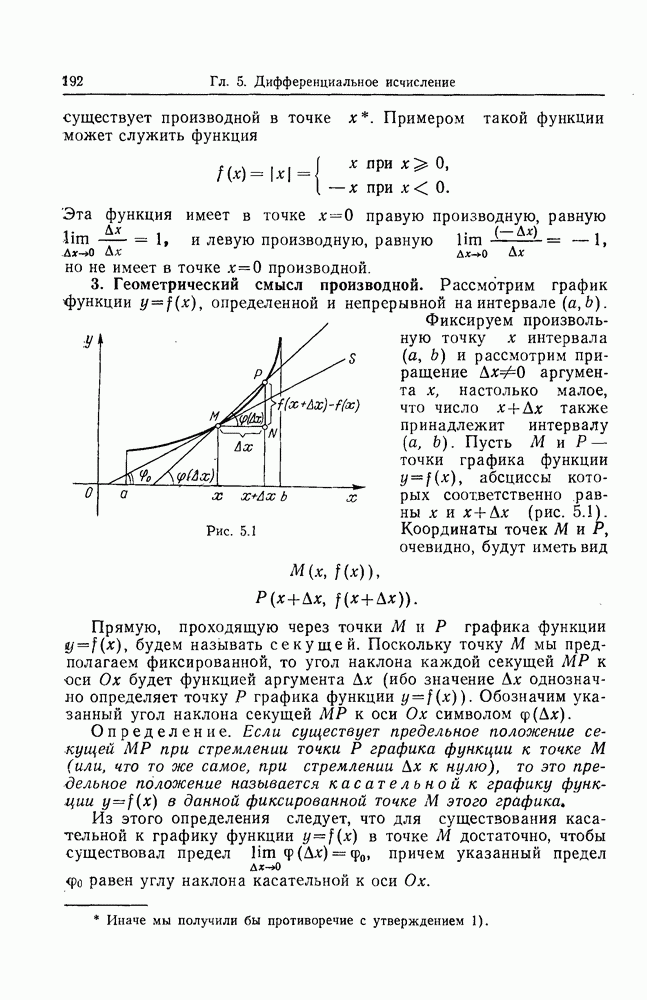
- 3. Геометрический смысл производной.
- § 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
- 2. Дифференцируемость и непрерывность.
- 3. Понятие дифференциала функции.
- § 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ
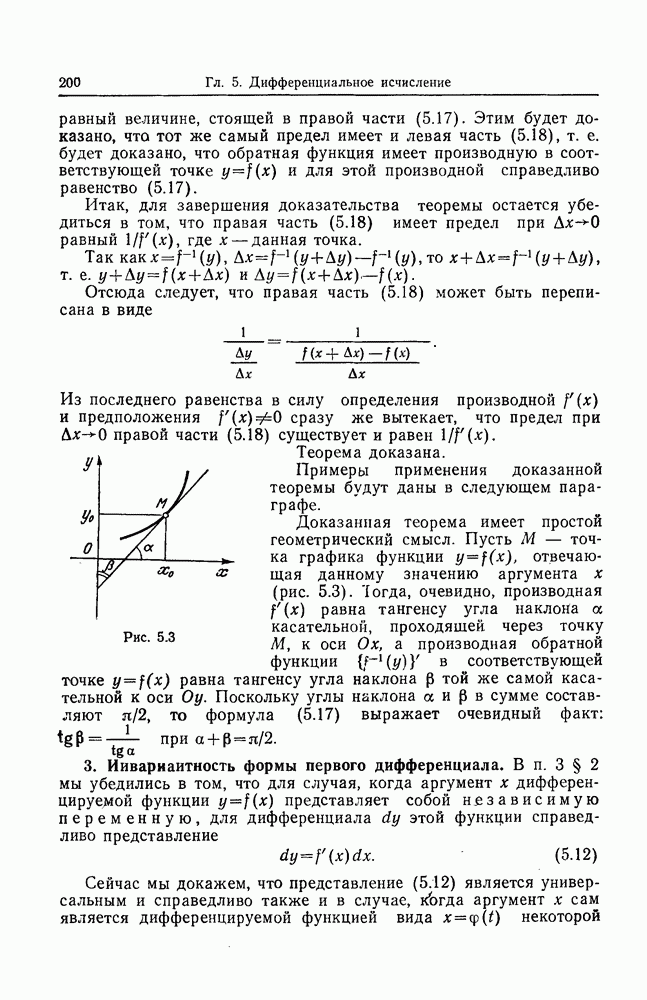
- 2. Дифференцирование обратной функции.
- 3. Инвариантность формы первого дифференциала.
- 4. Применение дифференциала для установления приближенных формул.
- § 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ
- § 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Производная логарифмической функции.
- 3. Производные показательной и обратных тригонометрических функций.
- 4. Производная степенной функции.
- 5. Таблица производных простейших элементарных функций.
- 6. Таблица дифференциалов простейших элементарных функций.
- 7. Логарифмическая производная. Производная степенно-показательной функции.
- § 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. n-ые производные некоторых функций.
- 3. Формула Лейбница для n-й производной произведения двух функций.
- 4. Дифференциалы высших порядков.
- § 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
- § 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ
- Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
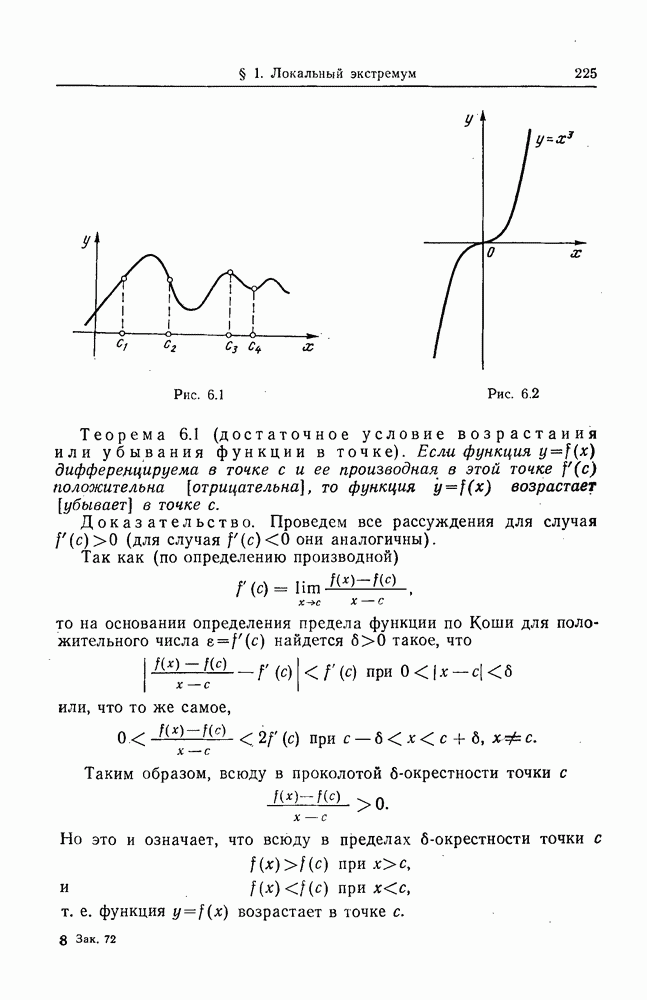
- § 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
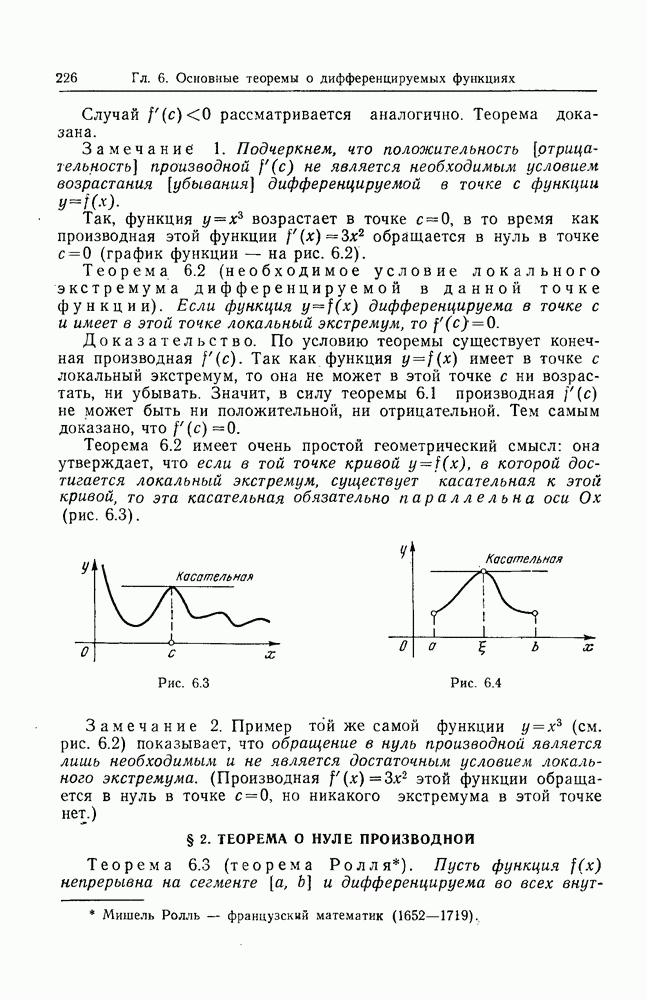
- § 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ
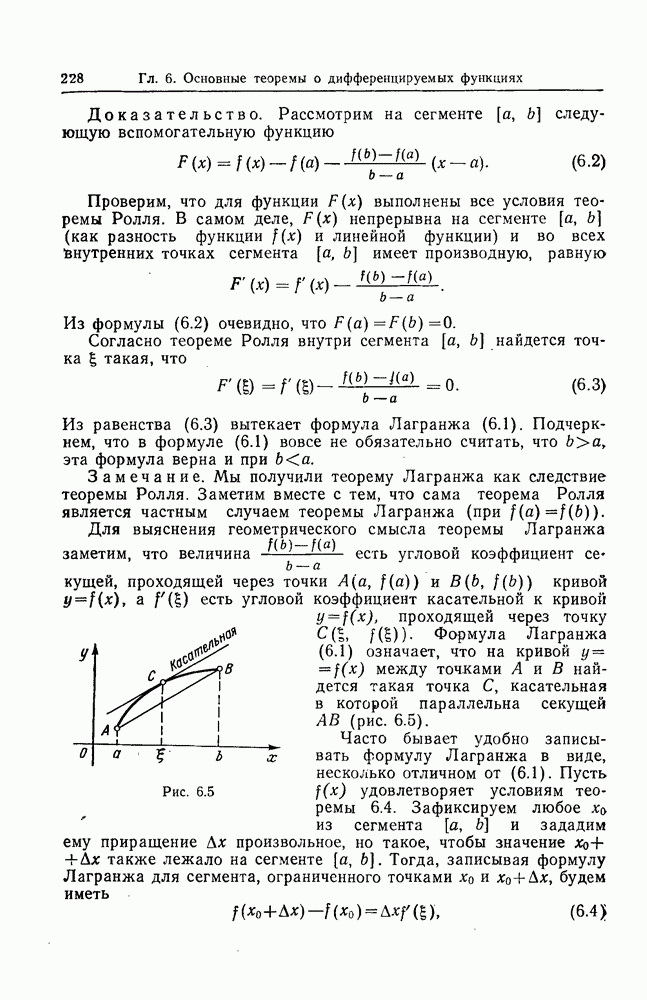
- § 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА)
- § 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА
- 2. Условия монотонности функции на интервале.
- 3. Отсутствие разрывов первого рода и устранимых разрывов у производной.
- 4. Вывод некоторых неравенств.
- § 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ)
- § 6. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ)
- 2. Раскрытие неопределенности вида oo/oo
- 3. Раскрытие неопределенностей других видов.
- § 7. ФОРМУЛА ТЕЙЛОРА
- § 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА
- 2. Другая запись формулы Тейлора.
- 3. Формула Маклорена.
- § 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Разложение по формуле Маклорена некоторых элементарных функций.
- § 10. ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА
- 2. Доказательство иррациональности числа е.
- 3. Вычисление значений тригонометрических функций.
- 4. Асимптотическая оценка элементарных функций и вычисление пределов.
- Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ
- § 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК
- 2. Отыскание стационарных точек.
- 3. Первое достаточное условие экстремума.
- 4. Второе достаточное условие экстремума.
- 5. Третье достаточное условие, экстремума.
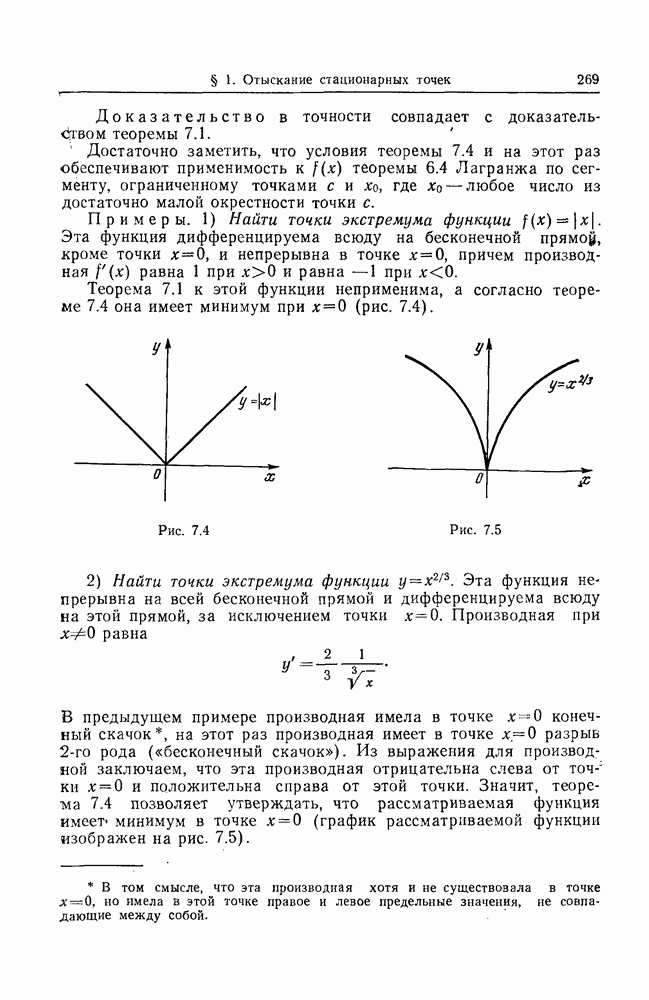
- 6. Экстремум функции, недифференцируемой в данной точке.
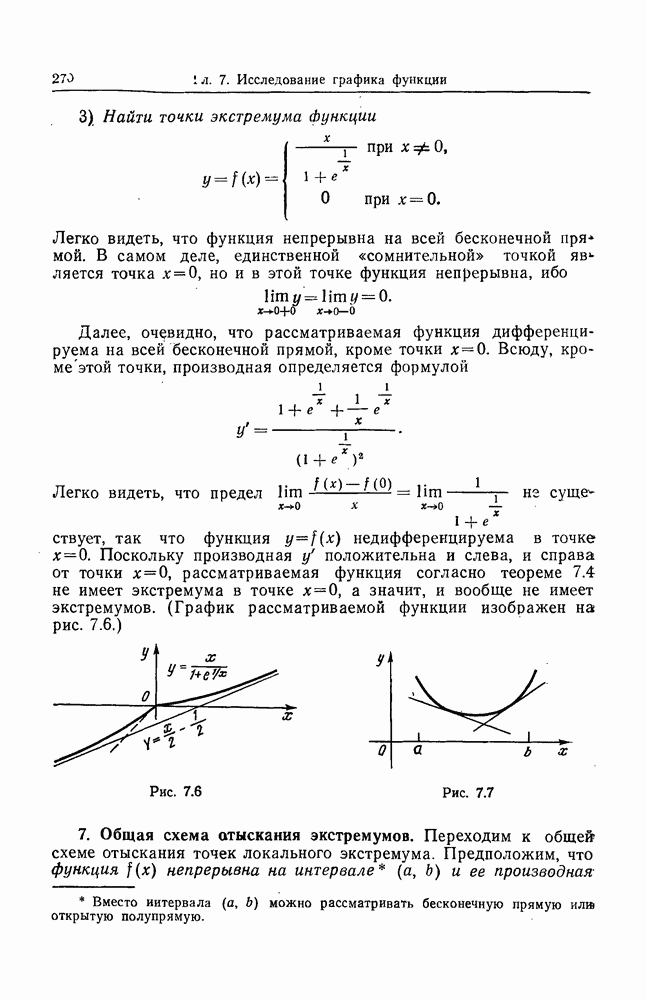
- 7. Общая схема отыскания экстремумов.
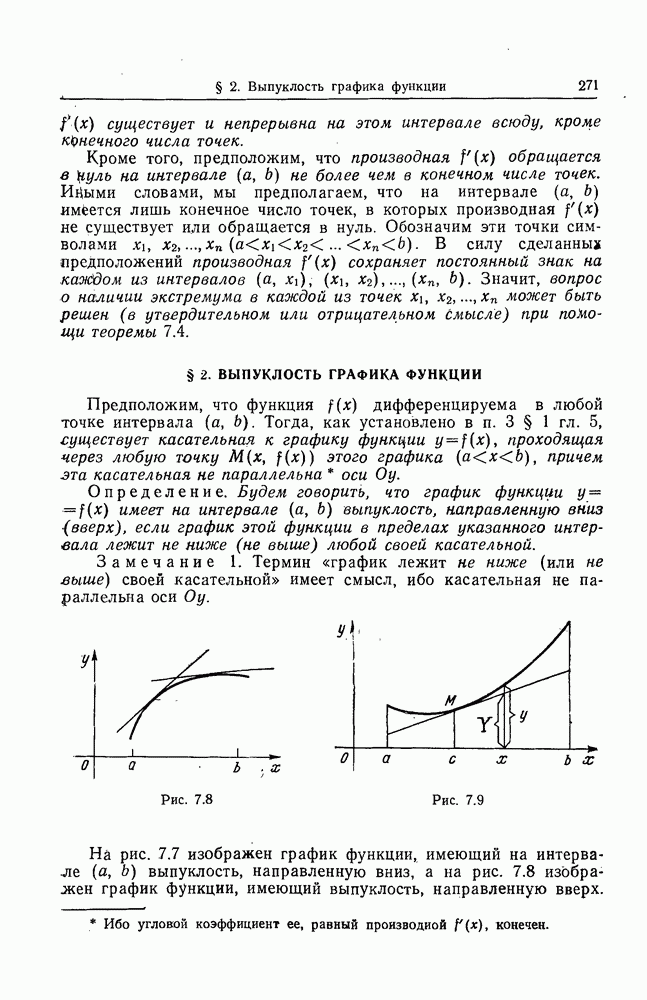
- § 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ
- § 3. ТОЧКИ ПЕРЕГИБА
- 2. Первое достаточное условие перегиба.
- 3. Некоторые обобщения первого достаточного условия перегиба.
- 4. Второе достаточное условие перегиба.
- 5. Третье достаточное условие перегиба.
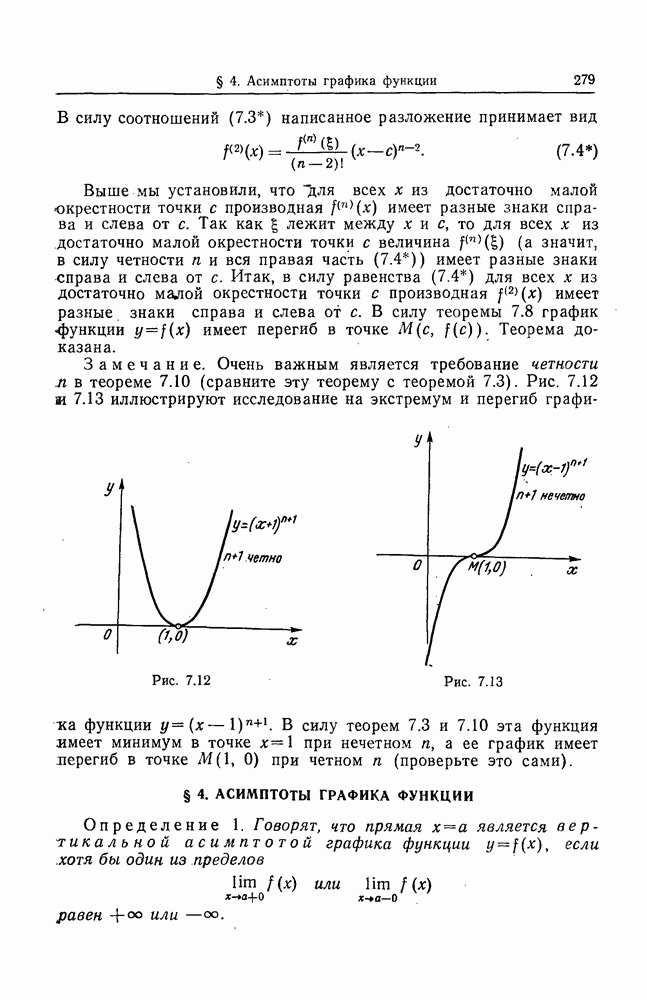
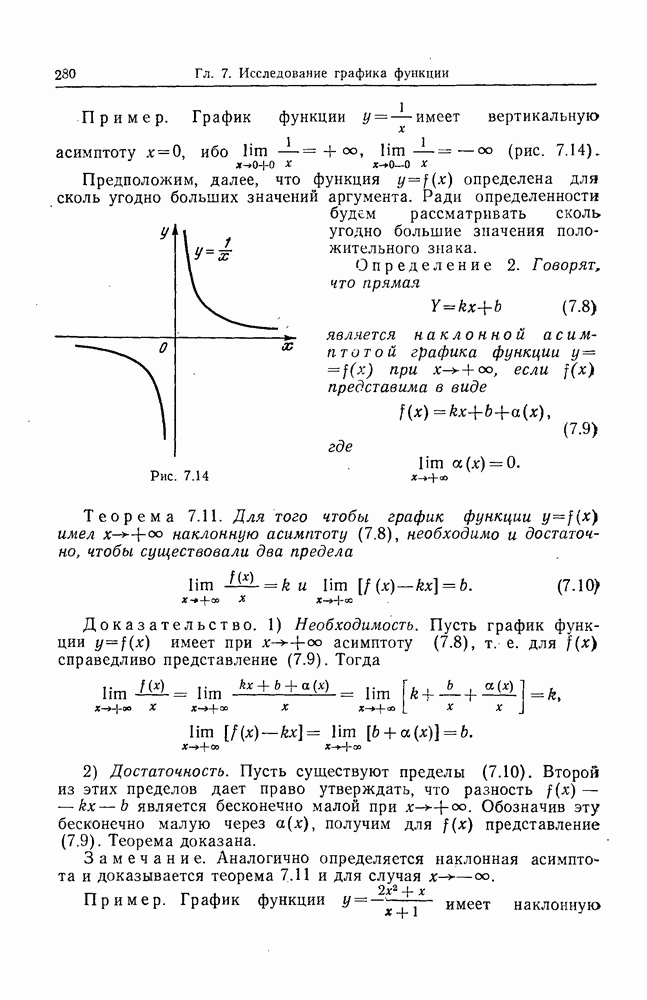
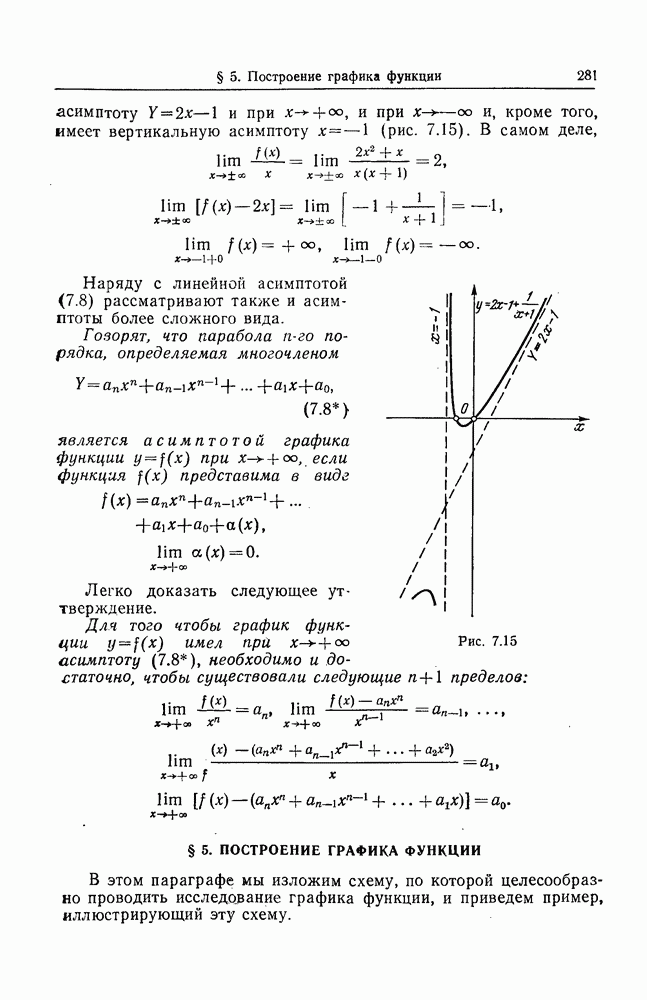
- § 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
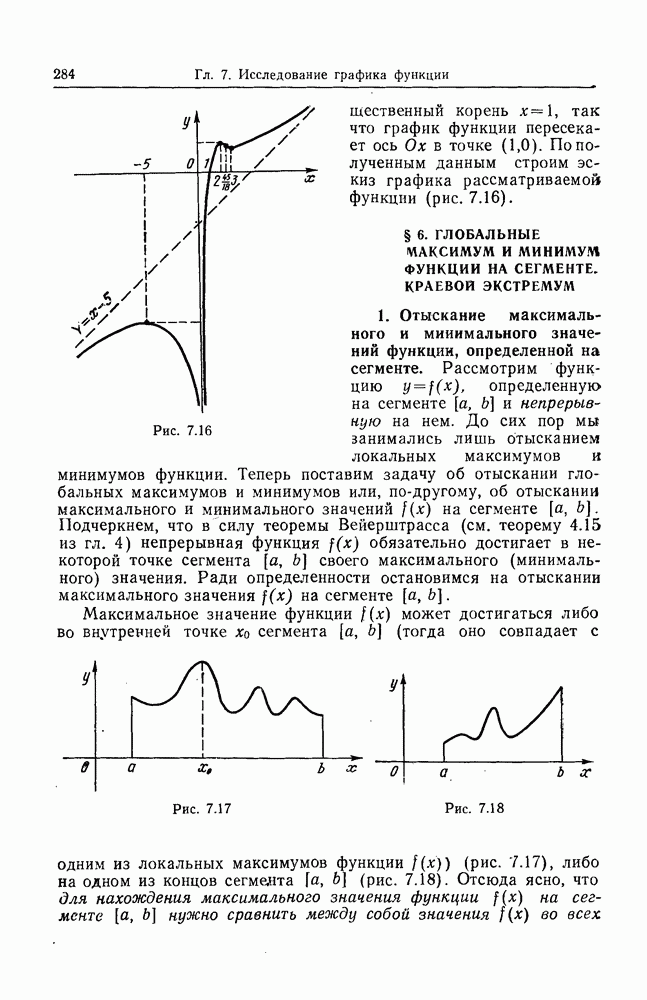
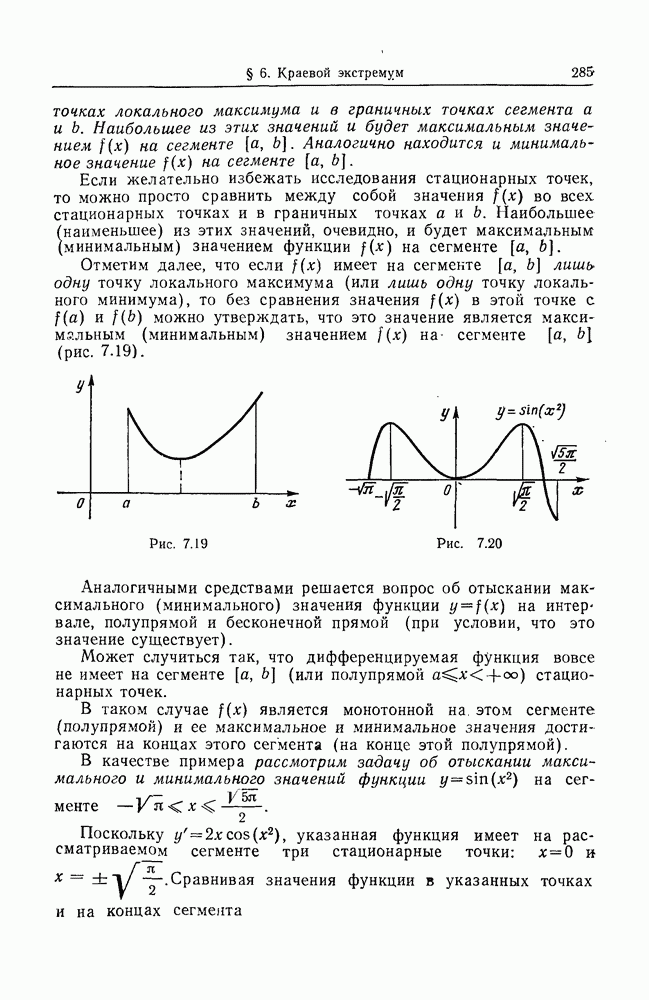
- § 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ
- 2. Краевой экстремум.
- 3. Теорема Дарбу.
- ДОПОЛНЕНИЕ
- Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции
- Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Неопределенный интеграл.
- 3. Основные свойства неопределенного интеграла.
- 4. Таблица основных неопределенных интегралов.
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование по частям.
- § 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Краткие сведения о корнях алгебраических многочленов.
- 3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей.
- 4. Разложение правильной рациональной дроби на сумму простейших дробей.
- 5. Интегрируемость рациональной дроби в элементарных функциях.
- 6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
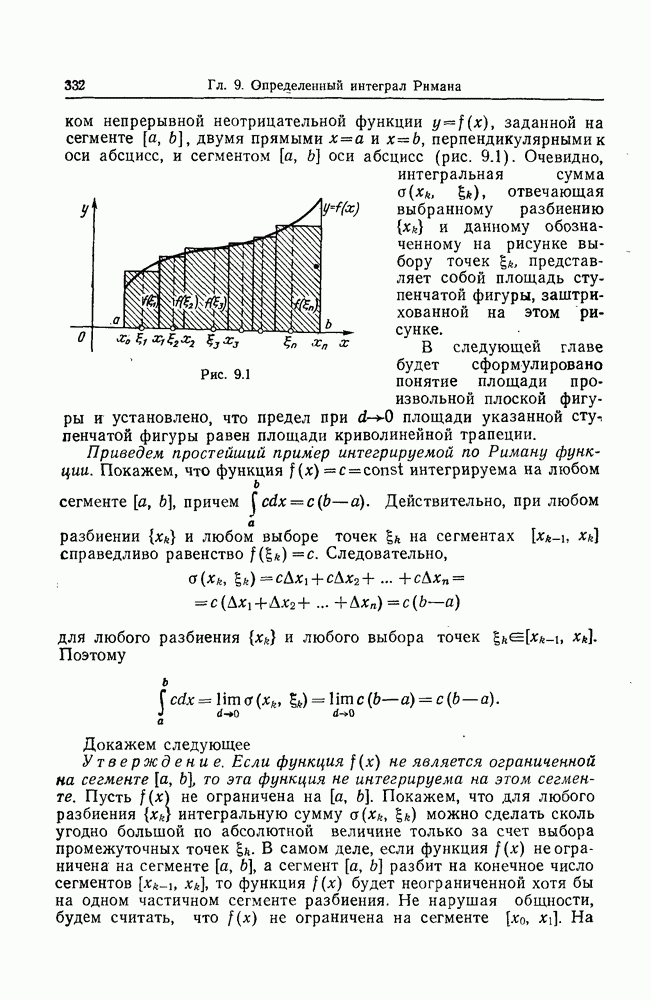
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
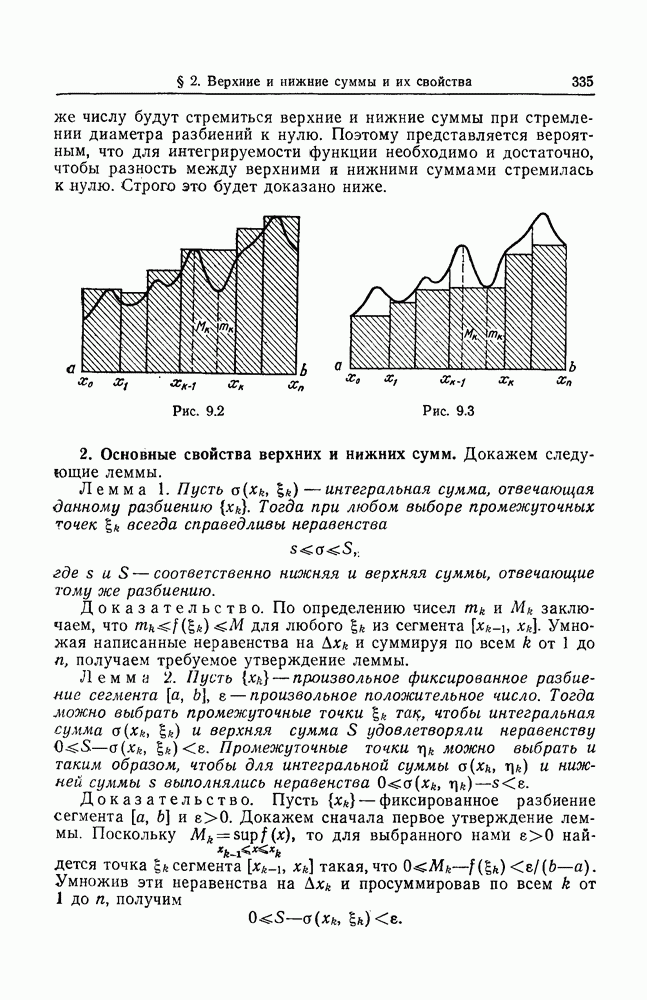
- ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА
- 2. Основные свойства верхних и нижних сумм.
- § 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- 2. Классы интегрируемых функций.
- § 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ
- 2. Оценки интегралов.
- § 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ
- 2. Основная формула интегрального исчисления.
- 3. Важные правила, позволяющие вычислять определенные интегралы.
- 4. Остаточный член формулы Тейлора в интегральной форме.
- § 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ
- 2. Неравенство Гёльдера для сумм.
- 3. Неравенство Минковского для сумм.
- 4. Неравенство Гёльдера для интегралов.
- 5. Неравенство Минковского для интегралов.
- § 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА
- 2. Критерий интегрируемости Лебега.
- ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Критерий Коши сходимости несобственного интеграла первого рода.
- 3. Абсолютная и условная сходимость несобственных интегралов.
- 4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям.
- § 2. Несобственные интегралы второго рода
- § 3. Главное значение несобственного интеграла
- ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса
- 2. Свойства интеграла Стилтьеса.
- Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. ДЛИНА ДУГИ КРИВОЙ
- 2. Понятие параметризуемой кривой.
- 3. Длина дуги кривой. Понятие спрямляемой кривой.
- 4. Критерий спрямляемости кривой. Вычисление длины дуги кривой.
- 5. Дифференциал дуги.
- 6. Примеры.
- § 2. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
- 2. Площадь плоской фигуры.
- 3. Площадь криволинейной трапеции и криволинейного сектора.
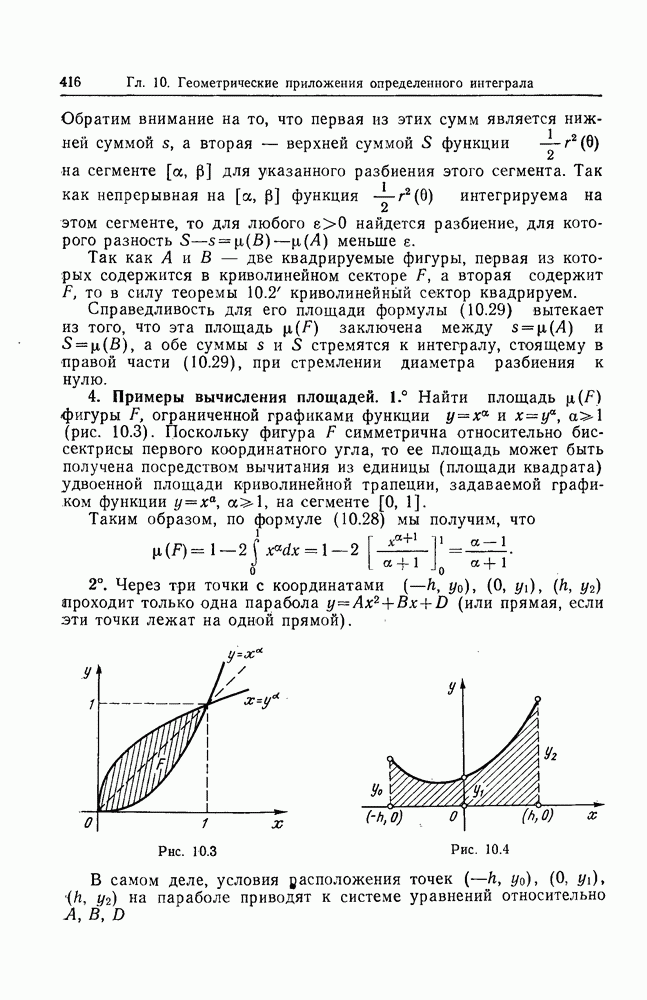
- 4. Примеры вычисления площадей.
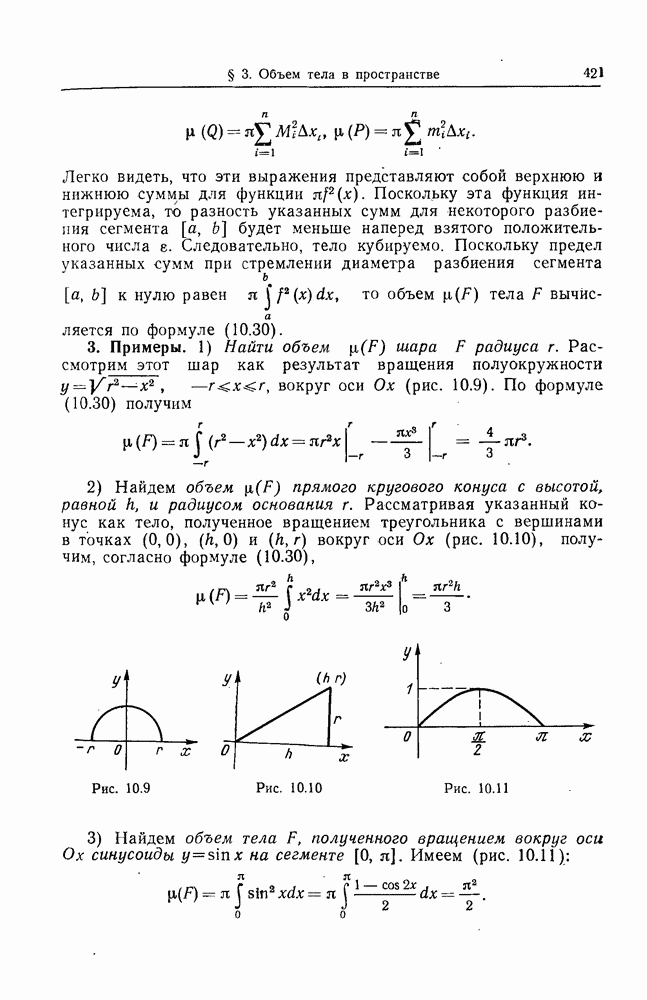
- § 3. ОБЪЕМ ТЕЛА В ПРОСТРАНСТВЕ
- 2. Некоторые классы кубируемых тел.
- 3. Примеры.
- Глава 11. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- § 1. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ
- 2. Метод итераций.
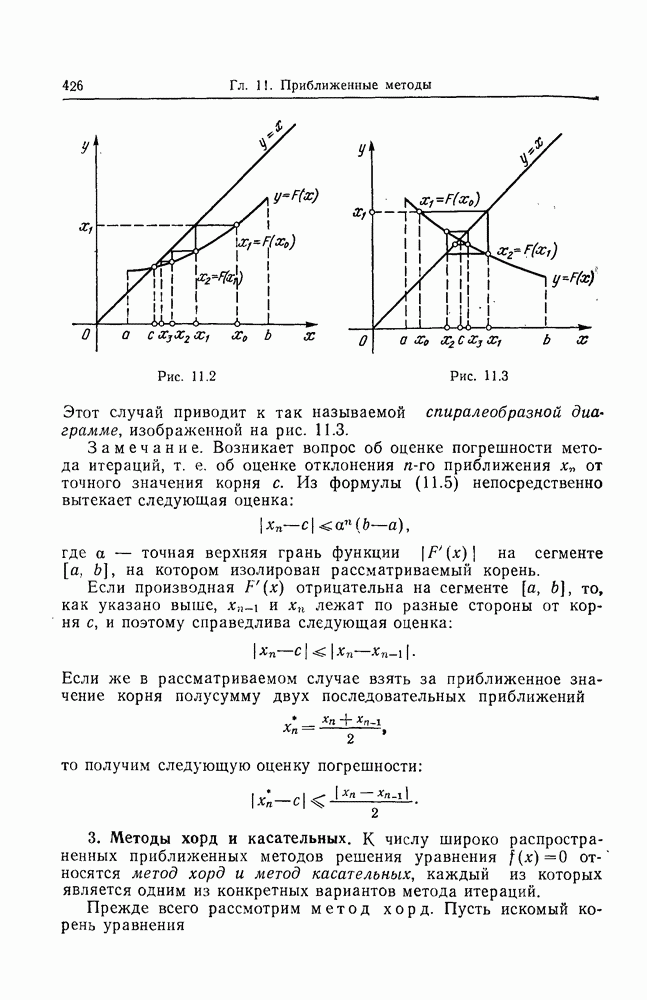
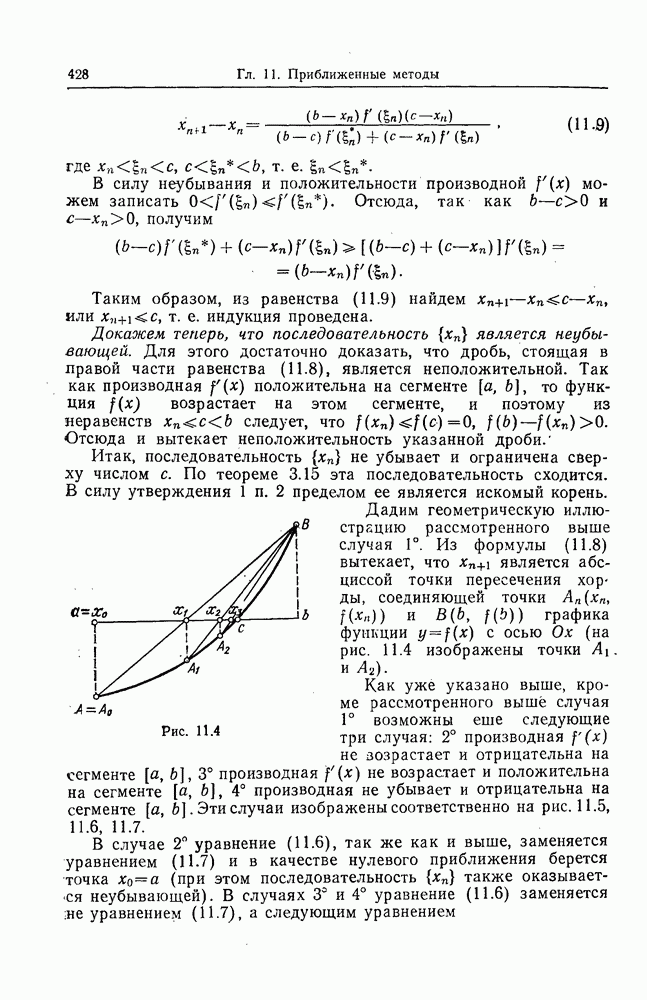
- 3. Методы хорд и касательных.
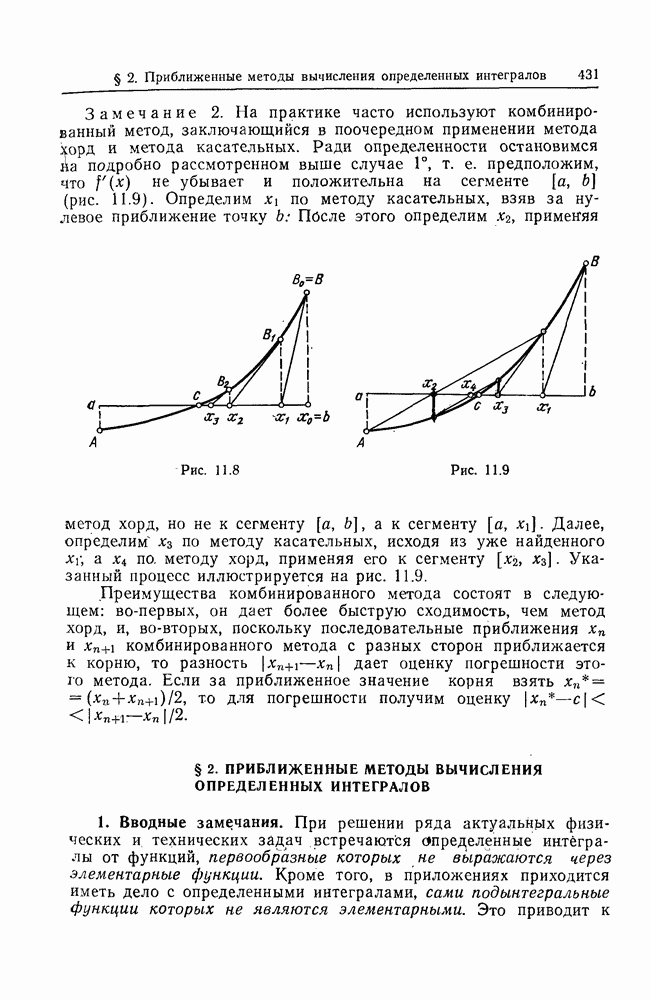
- § 2. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- 2. Метод прямоугольников.
- 3. Метод трапеций.
- 4. Метод парабол.
- Глава 12. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ПОНЯТИЕ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Множества точек m-мерного евклидова пространства.
- 3. Понятие функции m переменных.
- § 2. ПРЕДЕЛ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Свойство ограниченной последовательности точек E^m.
- 3. Предел функции m переменных.
- 4. Бесконечно малые функции m переменных.
- 5. Повторные пределы.
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Непрерывность функции m переменных по одной переменной.
- 3. Основные свойства непрерывных функций нескольких переменных.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Дифференцируемость функции нескольких переменных.
- 3. Геометрический смысл условия дифференцируемости функции двух переменных.
- 4. Достаточные условия дифференцируемости.
- 5. Дифференциал функции нескольких переменных.
- 6. Дифференцирование сложной функции.
- 7. Инвариантность формы первого дифференциала.
- 8. Производная по направлению. Градиент.
- § 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. Дифференциалы высших порядков.
- 3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме.
- 4. Формула Тейлора с остаточным членом в форме Пеано.
- § 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Достаточные условия локального экстремума функции m переменных.
- 3. Случай функции двух переменных.
- ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции
- 1. Выпуклые множества и выпуклые функции.
- 2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции.
- 3. Поиск минимума сильно выпуклой функции.
- ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства
- 2. Открытые и замкнутые множества.
- 3. Прямое произведение метрических пространств.
- 4. Всюду плотные и совершенные множества.
- 5. Сходимость. Непрерывные отображения.
- 6. Компактность.
- 7. Базис пространства.
- Топологические пространства
- Линейные нормированные пространства, линейные операторы
- ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах
- 2. Формула Лагранжа конечных приращений.
- 3. Связь между слабой и сильной дифференцируемостью.
- 4. Дифференцируемость функционалов.
- 5. Интеграл от абстрактных функций.
- 6. Формула Ньютона — Лейбница для абстрактных функций.
- 7. Производные второго порядка.
- 8. Отображение m-мерного евклидова пространства в n-мерное.
- 9. Производные и дифференциалы высших порядков.
- 10. Формула Тейлора для отображений одного нормированного пространства в другое.
- Исследование на экстремум функционалов в нормированных пространствах
- 2. Достаточные условия экстремума.
- Глава 13. НЕЯВНЫЕ ФУНКЦИИ
- § 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ
- 2. Вычисление частных производных неявно заданной функции.
- 3. Особые точки поверхности и плоской кривой.
- 4. Условия, обеспечивающие существование для функции y=f(x) обратной функции.
- § 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
- 2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений.
- 3. Взаимно однозначное отображение двух множеств m-мерного пространства.
- § 3. ЗАВИСИМОСТЬ ФУНКЦИЙ
- 2. Функциональные матрицы и их приложения.
- § 4. УСЛОВНЫЙ ЭКСТРЕМУМ
- 2. Метод неопределенных множителей Лагранжа.
- 3. Достаточные условия.
- 4. Пример.
- ДОПОЛНЕНИЕ
- Отображения банаховых пространств. Аналог теоремы о неявной функции
- 2. Случай конечномерных пространств.
- 3. Особые точки поверхности в пространстве n измерений. Обратное отображение.
- 4. Условный экстремум в случае отображений нормированных пространств.