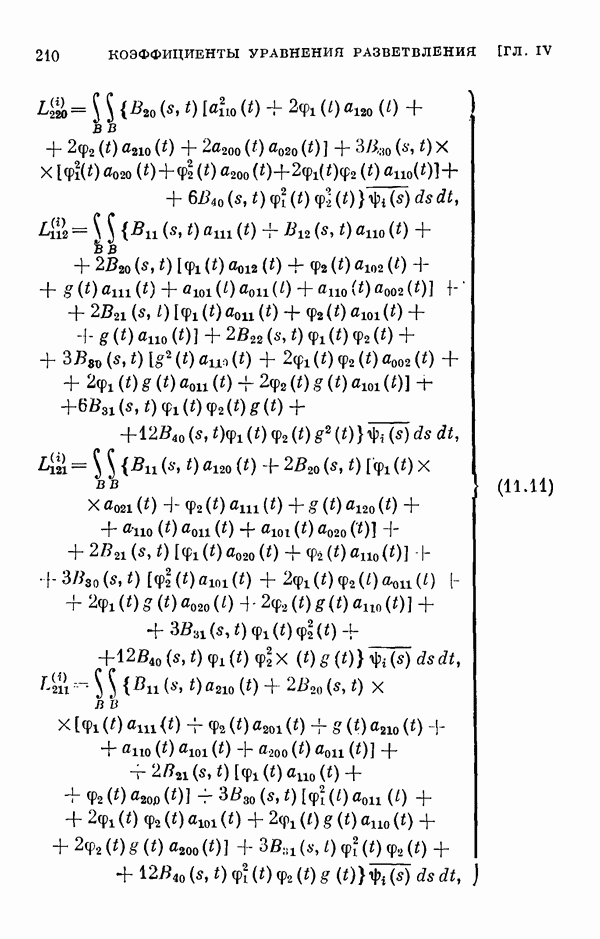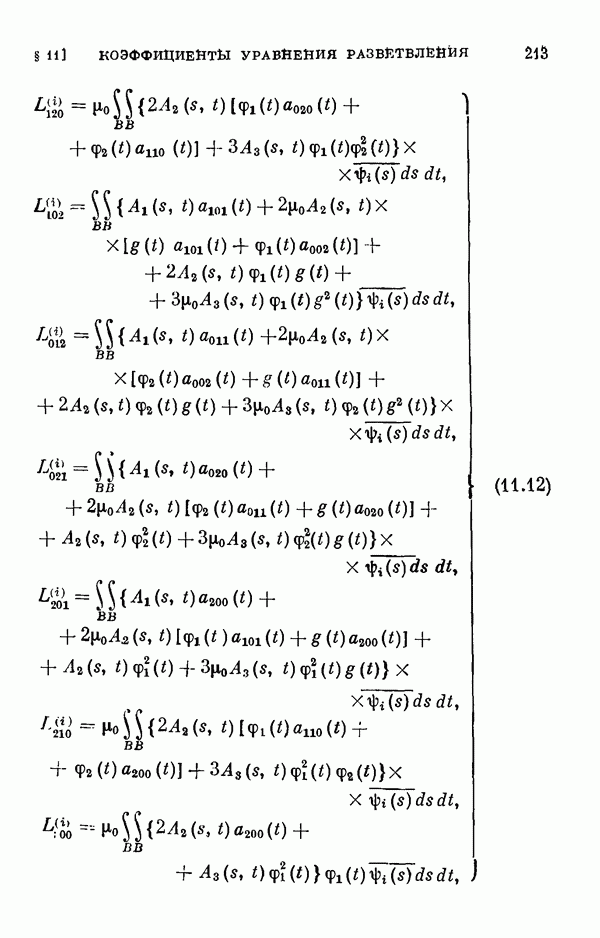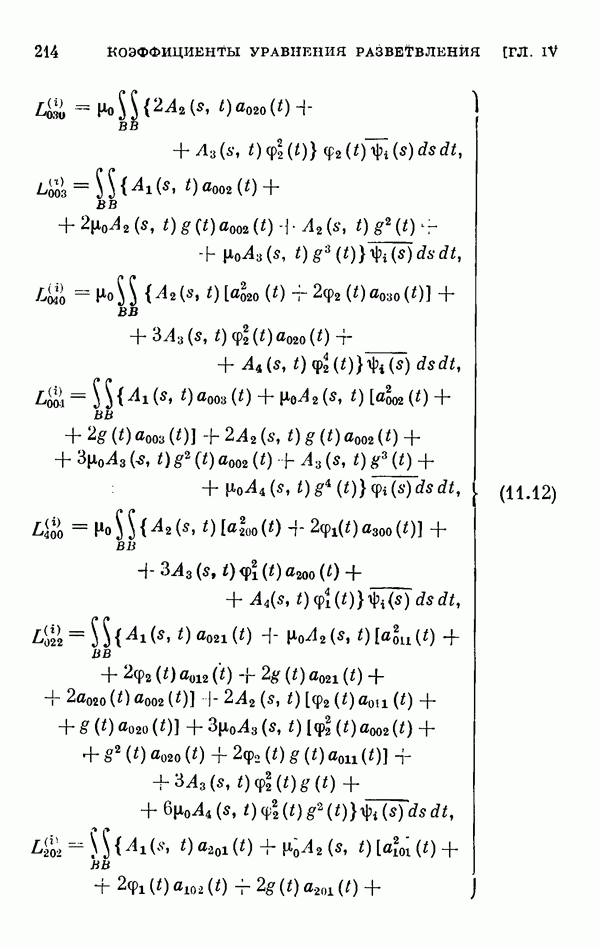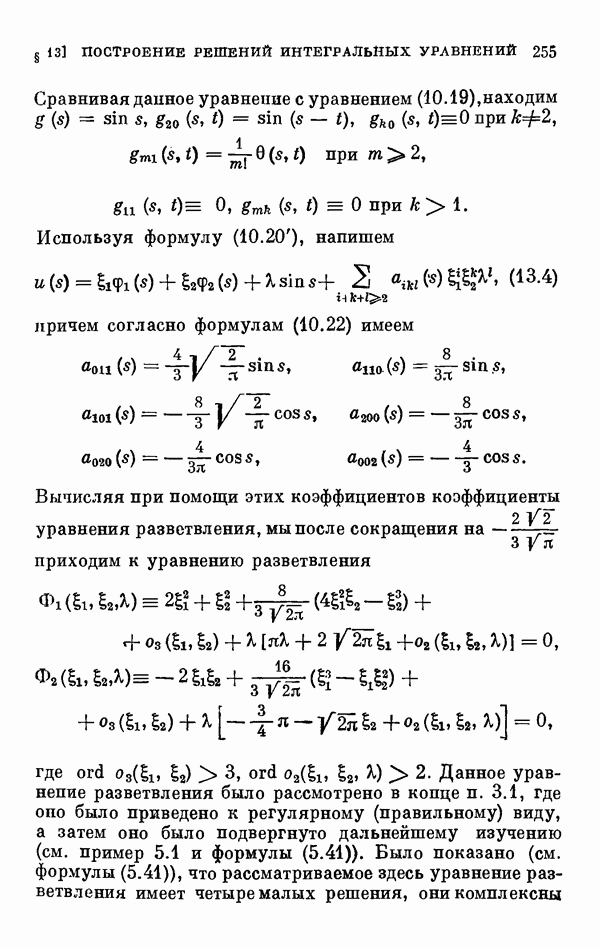| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
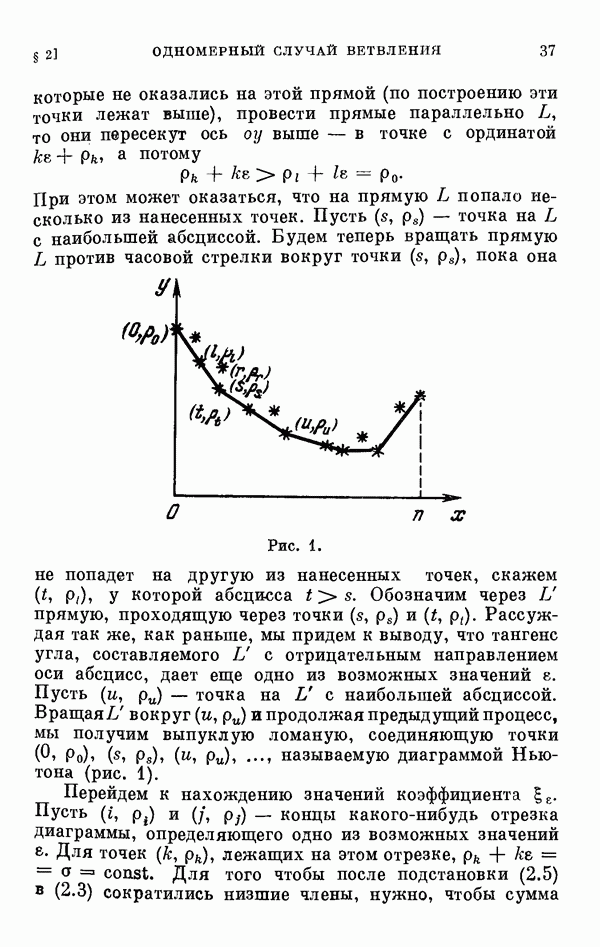
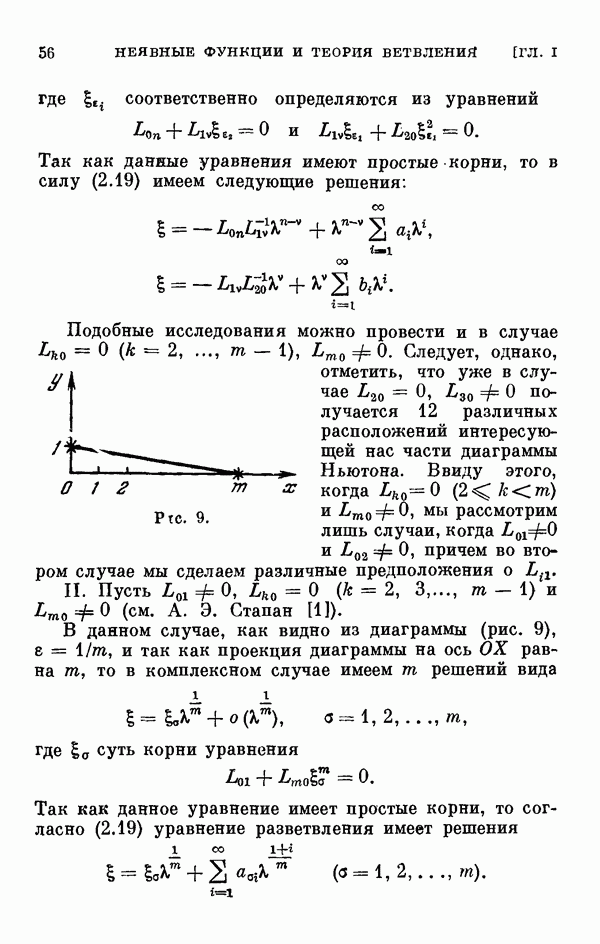
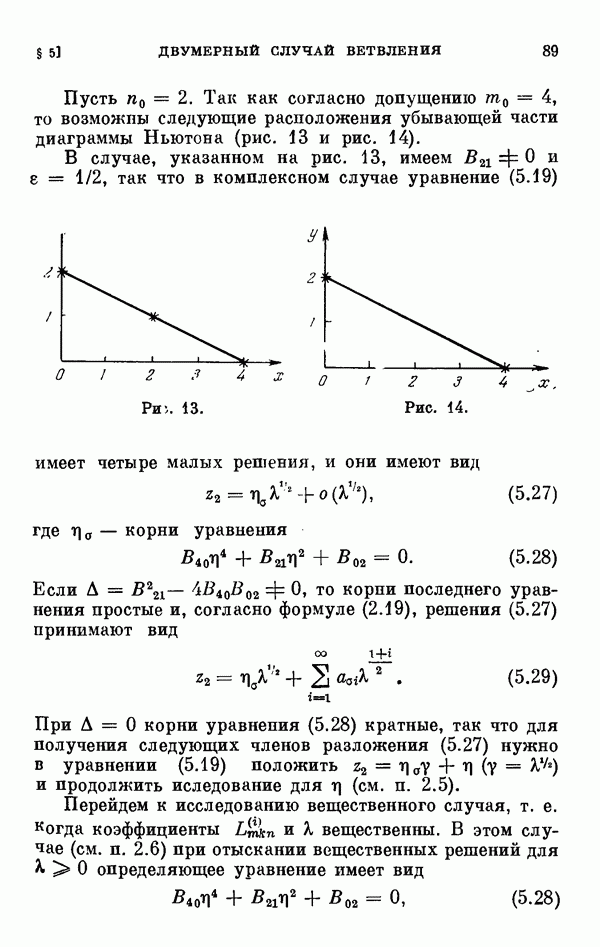
§ 36. О колебаниях спутника в плоскости эллиптической орбиты
Колебания спутника в плоскости его эллиптической орбиты около направления радиуса-вектора описываются следующим уравнением:

Здесь  — удвоенный угол между одной из главных осей эллипсоида инерции спутника, лежащей в плоскости орбиты, и радиусом-вектором орбиты,
— удвоенный угол между одной из главных осей эллипсоида инерции спутника, лежащей в плоскости орбиты, и радиусом-вектором орбиты,  — истинная аномален,
— истинная аномален,  где А, В, С — главные центральные моменты инерции, причем
где А, В, С — главные центральные моменты инерции, причем  — эксцентриситет:
— эксцентриситет: 
Представляет интерес изучение периодических решений уравнения (36.1) с периодом, равным периоду обращения центра масс спутника по орбите, т. е.  -периодических решений уравнения (36.1).
-периодических решений уравнения (36.1).
Ограничимся отысканием нечетных  -периодических решений, что эквивалентно решению для уравнения (36.1) краевой задачи с граничными условиями
-периодических решений, что эквивалентно решению для уравнения (36.1) краевой задачи с граничными условиями

Введем (ср. § 34) вещественные банаховы пространства  Пусть
Пусть  — пространство непрерывных на
— пространство непрерывных на  функций, а
функций, а  — пространство дважды непрерывно дифференцируемых на
— пространство дважды непрерывно дифференцируемых на  функций, удовлетворяющих граничным условиям (36.2). Нормы в
функций, удовлетворяющих граничным условиям (36.2). Нормы в  вводятся, как в § 34. Краевую задачу (36.1) — (36.2) в пространстве
вводятся, как в § 34. Краевую задачу (36.1) — (36.2) в пространстве
 можно теперь рассматривать как одно нелинейное уравнение вида
можно теперь рассматривать как одно нелинейное уравнение вида

с двумя вещественными параметрами  и
и  и с нелинейным оператором
и с нелинейным оператором  задаваемым на функциях
задаваемым на функциях  из
из  дифференциальным выражением, стоящим в левой части уравнения (36.1). Значения
дифференциальным выражением, стоящим в левой части уравнения (36.1). Значения  — аналитический оператор.
— аналитический оператор.
Рассмотрим случай малого эксцентриситета  . При
. При  уравнение (36.1) превращается в уравнение математического маятника
уравнение (36.1) превращается в уравнение математического маятника

При  задача (36.4) — (36.2) имеет лишь тривиальное решение, а при
задача (36.4) — (36.2) имеет лишь тривиальное решение, а при  эта задача имеет три решения:
эта задача имеет три решения:

причем параметр к  эллиптической функции должен быть определен из уравнения
эллиптической функции должен быть определен из уравнения

Таким образом, точка  является точкой ветвления уравнения (36.4): от тривиального решения при
является точкой ветвления уравнения (36.4): от тривиального решения при  ответвляется два малых нетривиальных решения. Итак,
ответвляется два малых нетривиальных решения. Итак, 
Рассмотрим задачу продолжения по параметрам  и решения
и решения  уравнения (36.3). а Положим
уравнения (36.3). а Положим

где  — новый малый параметр. Уравнение (36.3) теперь можно записать в виде
— новый малый параметр. Уравнение (36.3) теперь можно записать в виде

где

где 
Оператор В фредгольмовский с числом нулей  причем его нуль
причем его нуль  и дефектный функционал
и дефектный функционал  можно выбрать так:
можно выбрать так:

Для построения приближенного уравнения разветвления Ляпунова — Шмидта мы поступим следующим образом (см. п. 23.2). Для того чтобы уравнение (36.8) имело решение  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы

Учитывая вторую из формул (36.9), после интегрирования по частям последнее уравнение можно записать так:

Далее, непосредственно из уравнения (36.8) и формул (36.9) заключаем, что

где  содержит члены второго и высших порядков относительно
содержит члены второго и высших порядков относительно  и
и  .
.
Подставляя (36.12) в (36.11), после простых выкладок приходим к уравнению разветвления

где  содержат лишь члены третьего и высших порядков,
содержат лишь члены третьего и высших порядков,  — лишь члены выше третьего порядка по
— лишь члены выше третьего порядка по 
Приближенно имеем следующее уравнение разветвления: 


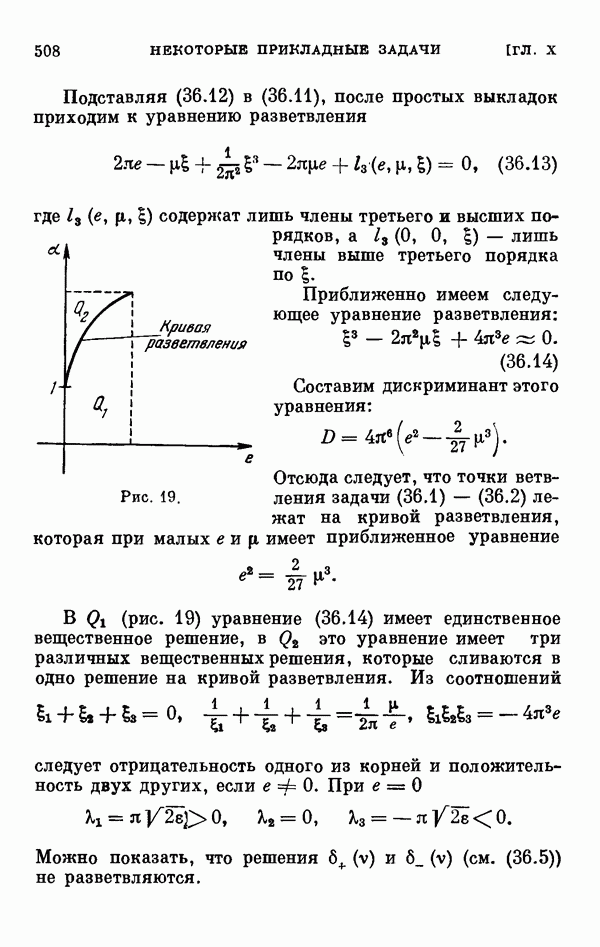
Рис. 19.
Составим дискриминант этого уравнения:

Отсюда следует, что точки ветвления задачи (36.1) — (36.2) лежат на кривой разветвления, которая при малых  имеет приближенное уравнение
имеет приближенное уравнение

В  (рис. 19) уравнение (36.14) имеет единственное вещественное решение, в
(рис. 19) уравнение (36.14) имеет единственное вещественное решение, в  это уравнение имеет три различных вещественных решения, которые сливаются в одно решение на кривой разветвления. Из соотношений
это уравнение имеет три различных вещественных решения, которые сливаются в одно решение на кривой разветвления. Из соотношений

следует отрицательность одного из корней и положительность двух других, если  При
При 

Можно показать, что решения  (см. (36.5)) не разветвляются.
(см. (36.5)) не разветвляются.
Окончательно имеем приближенную формулу

где  определяется из уравнения (36.14). Используя формулу (36.13), можно получить
определяется из уравнения (36.14). Используя формулу (36.13), можно получить  с любой степенью точности. Приведем без доказательства такую формулу с точностью до
с любой степенью точности. Приведем без доказательства такую формулу с точностью до 

( определяется из уравнения (36.14)).
определяется из уравнения (36.14)).
На кривой разветвления

В области, лежащей ниже кривой разветвления, решение может быть эффективно построено в виде ряда по целым степеням е.
В заключение заметим, что, используя рассуждения п. 35, можно дать асимптотику решений задачи как вблизи кривой разветвления, так и вне этой кривой.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА I. Системы неявных функций и классическая теория ветвления
- § 1. Задача о неявных функциях
- 1.2. Общее исследование задачи о неявных функциях.
- 1.3. Аналитический случай.
- § 2. Одномерный сличай ветвления и диаграмма Ньютона
- 2.2. О свойствах решений.
- 2.3. Примеры.
- 2.4. Исследование уравнения разветвления. Случай простых корней определяющего уравнения.
- 2.5. Случай кратных корней определяющего уравнения.
- 2.6. О вещественных решениях.
- 2.7. Некоторые частные случаи расположения диаграммы Ньютона.
- ГЛАВА II. Исследование уравнения разветвления в многомерном случае
- 3.2. Приведение к нормальному виду.
- § 4. Некоторые вопросы теории делимости
- 4.2. Общий делитель и аналог алгоритма Евклида.
- 4.3. Примитивный ОНД.
- 4.4. Применение к отмеченным многочленам.
- § 5. Двумерный случай ветвления
- 5.2. Указатели двумерного случая ветвления.
- 5.3. Частные случаи.
- § 6. Многомерный случай ветвления
- 6.2. Малые решения уравнения разветвления и метод исключения неизвестных.
- 6.3. Квазирегулярный случай ветвления.
- 6.4. Вырожденный случай ветвления.
- 6.5. Об изолированности нулевого решения.
- ГЛАВА III. Уравнение разветвления для нелинейных интегральных и интегро-дифференциальных уравнений
- § 7. Интегральные уравнения Ляпунова — Шмидта
- 7.2. Интегро-степенные ряды от многих функциональных аргументов.
- 7.3. Интегро-степенные ряды от интегро-степенных рядов.
- 7.4. Сжатость оператора Ляпунова—Шмидта.
- 7.5. Простейшее уравнение.
- 7.6. Последовательные приближения Лихтенштейна.
- 7.7. Применение метода мажорант.
- 7.8. Простейшее уравнение в случае равномерной сходимости.
- § 8. Общее интегральное уравнение Ляпунова—Шмидта
- 8.2. Регулярный случай при наличии многих аргументов.
- 8.3. Лемма Шмидта.
- 8.4. Одномерный случай ветвления.
- 8.5. Многомерный случай ветвления.
- 8.6. Возможные обобщения.
- § 9. Системы уравнений Ляпунова—Шмидта и некоторые интегро-дифференциальные уравнения
- 9.2. Регулярный случай.
- 9.3. Случай ветвления.
- 9.4. Некоторые нелинейные интегро-дифференциальные уравнения первого порядка.
- 9.5. Другие виды интегро-дифференциальных уравнений.
- 9.6. Другой способ построения уравнения разветвления
- ГЛАВА IV. Общее интегральное уравнение и коэффициенты уравнения разветвления
- 10.2. Регулярный случай.
- 10.3. Одномерный случай ветвления.
- 10.4. Многомерный случай ветвления.
- 10.5 Частный случай.
- 10.6. Уравнение Гаммерштейна.
- § 11. Коэффициенты уравнения разветвления
- 11.2. Коэффициенты одиомерного уравнения разветвления нелинейного интегрального уравнения Гаммерштейна.
- 11.3. Коэффициенты двумерного уравнения разветвления общего нелинейного интегрального уравнения.
- 11.4. Коэффициенты двумерного уравнения разветвления для частных случаев.
- 11.5. Некоторые свойства коэффициентов уравнения разветвления.
- ГЛАВА V. Описание и построение решений нелинейных интегральных уравнений
- § 12. Описание решений нелинейных интегральных уравнений
- 12.2. Описание решении в одномерном случае ветвления.
- 12.3. О точках бифуркации в одномерном случае ветвления.
- 12.4. Описание решений в двумерном случае ветвления.
- 12.5. Описание решений в многомерном случае ветвления.
- 12.6. О ветвлении изолированного решения.
- 12.7. Точки бифуркации в многомерном случае ветвления.
- § 13. Построение решений нелинейных интегральных уравнений
- 13.3. Двумерный случай ветвления.
- 13.4. Уравнение Некрасова.
- 13.5. Уравнение разветвления для уравнения Некрасова.
- § 14. Особые решения нелинейных интегральных уравнений
- 14.2. Сведение к малым решениям.
- 14.3. Особые решения в регулярном случае.
- 14.4. Исследование вспомогательного уравнения.
- 14.5. Ветвление решений основного уравнения.
- 14.6 Особые решения в пространствах Лебега.
- ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
- § 15. Периодические решения неавтономных систем
- 15.2. Метод Пуанкаре.
- 15.3. Условия периодичности и уравненне разветвления.
- 15.4. Описание решений в регулярном случае.
- 15.5. Описание решений в одномерном случае ветвления.
- 15.6. Описание решений в многомерном случае ветвления.
- § 16. Периодические решения квазилинейных систем
- 16.2. Условия периодичности.
- 16.3. Вывод уравнения разветвления.
- 16.4. Описание решений и дополнительные замечания.
- § 17. Периодические решения автономных систем
- 17.2. Уравнение разветвления.
- 17.3. Основные выводы.
- 17.4. Метод неопределенных коэффициентов.
- 17.5. Автономные системы с одной степенью свободы.
- § 18. Примеры
- 18.1. Неавтономные системы с одной степенью свободы.
- 18.2 Автономные системы с одной степенью свободы.
- § 19. Другие задачи о периодических решениях
- 19.1. Особые периодические решения неавтономных систем.
- 19.2. Ветвление периодических решений в банаховых пространствах
- § 20. Об устойчивости периодических решений, зависящих от малого параметра
- 20.2. Устойчивость решений задачи Пуанкаре.
- ГЛАВА VII. Нелинейные уравнения в банаховых пространствах
- § 21. Некоторые вопросы теории линейных операторов в банаховых пространствах
- 21.2. Специальные разложения пространств в прямые суммы подпространств.
- 21.3. Сужение оператора и обобщенная лемма Шмидта.
- 21.4 Связь с сопряженным оператором.
- 21.5. Неограниченные фредгольмовские операторы.
- § 22. Степенные операторы, ряды Тейлора, теоремы о неявных операторах
- 22.2 Степенные ряды. Ряды Тейлора.
- 22.3 Теоремы о неявных операторах.
- § 23. Уравнение разветвления Ляпунова — Шмидта
- 23.2. Вывод уравнения разветвления с помощью сужения оператора B.
- 23.3. Вывод уравнения разветвления с помощью леммы Шмидта.
- 23.4. Основная теорема об уравнении разветвления.
- 23.5. Уравление разветвления в аналитическом случае.
- 23.6. Уравнение разветвления для неограниченных операторов.
- § 24. Исследование одномерного случая ветвления
- 24.2. Вырожденный случай.
- 24.3. Квазирегулярный случай (задача А).
- 24.4. Задача Б (невырожденный случай).
- 24.5 Вещественный случай.
- 24.6. О ветвлении решений уравнений о достаточно гладкими операторами.
- 24.7 Случай функционального параметра. Ряды по однородным операторам.
- 24.8. Случай двух числовых параметров.
- § 25. Многомерный случай ветвления
- 25.2. Коэффициенты двумерного уравнения разветвления.
- 25.3. Двумерный случай ветвления.
- 25.4 Общий случай.
- 25.5. О ветвлении изолированного решения.
- 25.6. О точках бифуркации.
- ГЛАВА VIII. Ветвление решений нелинейных уравнений в сингулярном случае
- 26.2. Разложение пространств в прямые суммы подпространств.
- 26.3. Теорема Аткинсона.
- 23.4. О нетеровских неограниченных операторах.
- § 27. Теоремы о ветвлении решений
- 27.2. Случай n > 0, m = 0.
- 27.3. Случай n = 0, m > 0.
- 27.4. Основной случай. Уравнение разветвления.
- 27.5. О ветвлении решений уравнения с неограниченным оператором.
- § 28. Ветвление решений нелинейных сингулярных интегральных уравнений.
- 28.2. Нелинейные сингулярные интегральные уравнения с ядром типа Коши в пространствах Гёльдера.
- 28.3. Аналитический случай.
- 28.4. Нелинейные сингулярные интегральные уравнения с ядром Гильберта в пространствах Лебега.
- § 29. Ветвление решений краевых задач для нелинейных эллиптических уравнений
- 29.2. Краевые задачи на плоскости для эллиптических систем k-го порядка в пространстве Гёльдера.
- 29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
- ГЛАВА IX. Некоторые задачи теории вовмущений
- § 30. Жордановы цепочки и наборы фредгольмовских операторов
- 30.2. А-жордановы цепочки и наборы при n > 1.
- 30.3. Условия полноты А-жорданова набора.
- 30.4. Пример.
- § 31. Возмущение линейного уравнения малым линейным слагаемым
- 31.2. Случай n > 1.
- 31.3. Метод неопределенных коэффициентов.
- § 32. Ветвление собственных значений и собственных элементов фредгольмовских операторов
- 32.2. Уравнение разветвления в аналитическом случае.
- 32.3. Вырожденный и невырожденный случаи.
- 32.4. Одномерный случай.
- 32.5. Метод неопределенных коэффициентов.
- 32.6. Многомерный случай.
- 32.7. Некоторые обобщения.
- § 33. Особые решения нелинейных уравнений
- 33.2. Задача о возмущении линейного уравнения малым нелинейным слагаемым.
- 33.3. Понятие обобщенной жордановой цепочки.
- 33.4. Свойства некоторых многочленов.
- 33.5 Основной случай задачи о возмущении.
- 33.6. Случаи возмущения второго порядка.
- 33.7. Решения порядка …
- ГЛАВА X. Некоторые прикладные задачи
- § 34. О малых изгибах прямолинейного стержня под действием постоянной нагрузки
- § 35. К теории малых прогибов гибких пластин
- 35.2. Случай круглой пластины.
- 35.3. Исследование уравнения разветвления.
- 35.4. Круглая пластина с нулевой внешней нагрузкой.
- § 36. О колебаниях спутника в плоскости эллиптической орбиты
- § 37. Об одном виде установившихся волн
- 37.2. Сведение к системе.
- 37.3. Регулярный случай.
- 37.4. Случай ветвления.
- Литература