Аналогия с вычислительными машинами: клетка как конечный автомат

Рассмотрение взаимодействия эпигенетических цепей управления, основанное на представлении о процессах генетического контроля как о логических переключающих цепях, на первый взгляд представляется подходом, полностью противоположным использованному выше для анализа поведения клеток. Предположение, что активность генов можно рассматривать в терминах таких бинарных элементов типа «да-нет», высказывалось в нескольких работах (например, Monod, Jacob, 1961; Sugita, 1963; Apter, 1966). Однако систематический анализ свойств больших ансамблей таких единиц был впервые проведен Кауфманом (Kauffman, 1969), получившим ряд очень интересных результатов. Предположения, сделанные Кауфманом при конструировании модели эпигенетического поведения в виде сети функционально взаимодействующих генов, состояли в следующем:

1. Ген или включен, или выключен, и поэтому ему может быть приписано число 1 или 0 соответственно.

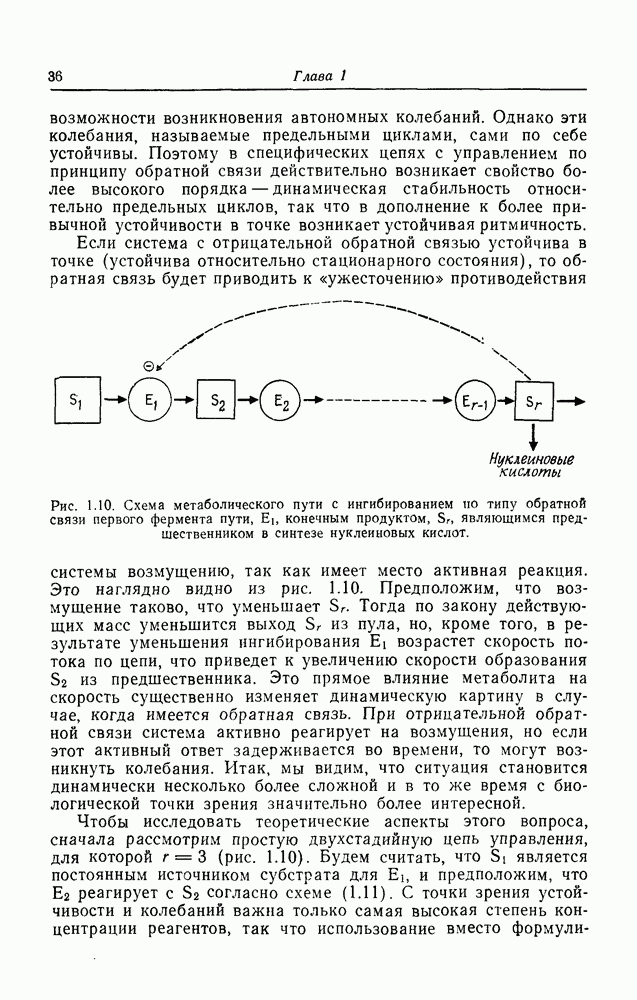
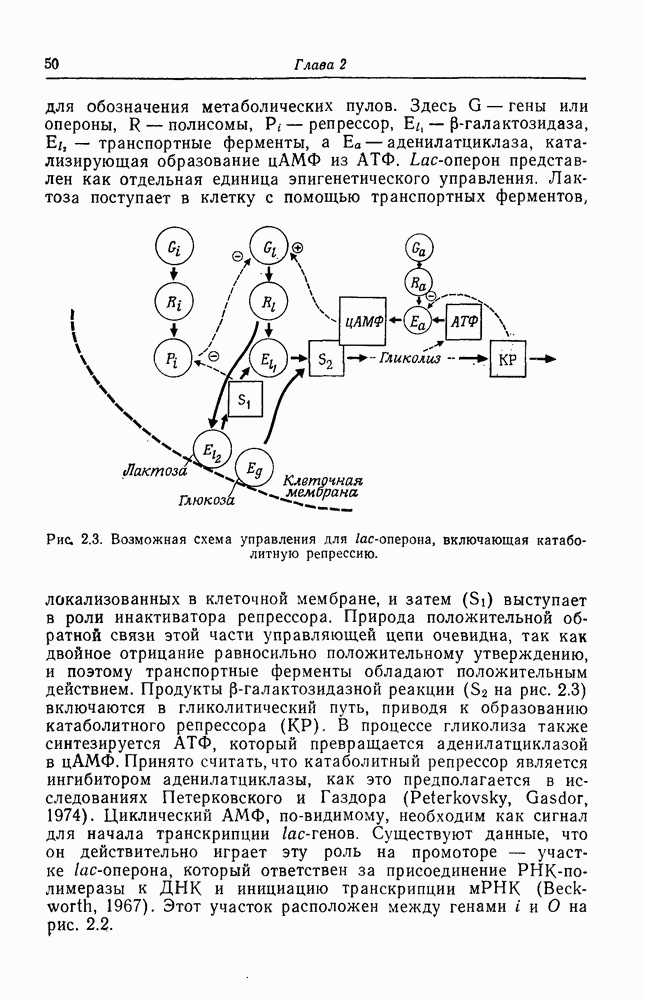
2. Каждый ген имеет только два «входа», т. е. управляется только двумя метаболическими сигналами (например, lac-оперон реагирует на репрессор и на цАМФ, как показано на рис. 2.3). Это требование можно сделать менее жестким, т. е. допустить, что число входов мало, практически не повлияв на результат.

3. Входы могут быть положительными и отрицательными (опять по аналогии с lac-опероном, где репрессор обладает ингибирующим, а цАМФ стимулирующим действием), а расположение входов и соединений относительно генов случайно. Поэтому исследуемые сети сконструированы случайным образом и имеют примерно одинаковое количество из всех возможных комбинаций входов и соединений.

Используя эти основные положения, можно представить поведение гена с помощью таблицы переходов между состояниями следующим образом. Предположим, мы рассматриваем ген X с входами из генов У и Z. Эти входы, конечно, связаны не прямо с генами, а через их продукты (репрессор является продуктом гена , а цАМФ — продуктом гена, кодирующего аденилатциклазу)

Время квантуется единичными шагами такой логической машины или автомата, поэтому мы можем представить переход между состояниями гена X так, как сделано на рис. 2.9. Пары возможных значений входных сигналов в момент Т приведены в колонках под переменными У и Z, а значения для X, соответствующие этим входным сигналам в момент времени под переменной X. Таблица построена для lac-оперона с У, соответствующим гену i, и Z — гену, кодирующему аденилатциклазу. Lac-оперон активен только в том случае, если репрессор инактивирован и присутствует цАМФ (Z = 1). Эта таблица определяет функцию, известную под названием булевой функции бинарных переменных У и

Для изображения логических функций такого рода вместо графиков используются таблицы.

Рис. 2.9. Булевая функция, использующаяся для описания переключения структурных генов lac-оперона в ответ на входные сигналы, полученные в результате активности гена и гена, управляющего образованием аденилатциклазы (Z); X представляет собой активность структурных генов.

Очевидно, по-разному размещая нули и единицы в колонке под X, можно получить множество булевых функций двух переменных. Поскольку число возможных мест в колонке равно 4 и для каждого из них существует выбор из двух переменных, полное число булевых функций двух переменных равно

Сеть взаимодействующих генов конструируется путем выбора некоторого числа генов, скажем и присвоения каждому гену случайным образом одной из 16 возможных булевых функций. Затем генам приписываются входы с помощью случайного выбора из общего числа генов, причем если данный ген выбирается несколько раз, то считается, что он выступает в качестве входа для нескольких других генов. В случае N генов состояние сети в любой момент времени будет задаваться вектором, состоящим из ряда N нулей и единиц в порядке нумерации генов. Число возможных состояний сети равно, очевидно, Начиная с некоторого начального момента, скажем, когда все гены выключены (0), сеть последовательно пройдет через ряд определенных состояний, согласно правилам перехода (булевым функциям), приписанным каждому гену. Таково поведение множества подобных сетей, исследованных Кауфманом с помощью ЭВМ.

Может показаться, что такое исследование не имеет никакого явного смысла. Для очень большое число; такие сети имеют множество возможных состояний и, как предполагают, переходят из одного состояния в другое случайным образом. Поскольку сети являются конечными автоматами, совершаемые ими циклы должны иметь конечный период, который может быть, однако, очень большим — до 2100 шагов. В действительности это и есть тот результат, который получается, когда число входов на ген равно N, числу генов. Как отмечает Кауфман, если для перехода между состояниями необходима 1 мкс, то время, в течение которого сеть проходит полный цикл, равно примерно 107, умноженному на возраст Вселенной, оцененный Хабблом. Никакая биологическая система не имеет в своем распоряжении такого большого времени.

Было показано, что сети с одним входом на элемент имеют только несколько меньшие времена цикла. Поэтому, когда Кауфман обнаружил, что при числе связей на элемент, равном получаются малые продолжительности цикла, причем среднее значение было порядка этот результат показался удивительным. Так, для среднее время цикла равно десяти единицам. Если каждая единица равна 1 мин, то среднее время цикла — 10 мин.

Здесь нам необходимо снова рассмотреть биологическую систему и попытаться сделать некоторые оценки величины N и времени перехода. N — число генов в клетке, а время перехода — время, необходимое для активации гена и получения заметного метаболического ответа. Мы уже оценили, что время перехода варьирует от нескольких минут до одного часа. Для единичных ответов типа рассматриваемых мы можем принять, что это время равно примерно 10 мин.

Оценка числа генов в клетке значительно менее надежна. Для бактерий эта величина равна , а для высших — .

Возьмем . Тогда для временного шага, равного 10 мин (по оценкам Кауфмана, эта величина равна 1 мин, что скорее всего слишком мало для клеток многоклеточных), средние времена циклов равны мин, или 16,6 ч. Эта величина лежит в том же временном интервале, что и оценки для периодов колебаний в эпигенетической системе, и попадает в диапазон длительностей клеточных циклов многоклеточных. Кауфман применил свои рассуждения к длительности клеточных циклов в клетках различных типов, связывая их с общим содержанием ДНК. Ясно, что основания для этого весьма шатки, и мне кажется, что вдаваться в детали его подхода не следует. Что же на самом деле интересно, так это замечательное

сближение двух подходов к явлению ритмической активности в эпигенетической системе и ожидаемому диапазону значений периода, По-видимому, внутриклеточная динамика процессов управления генами включает колебательную активность, и следствием этого является ритмическое поведение клеток, такое, как клеточный цикл и биологические часы. Интересная особенность подхода Кауфмана состоит в том, что система не нуждается ни в какой специальной конструкции, большинство случайных сетей будут обладать устойчивым циклическим поведением с разумными длительностями цикла. Этот момент очень важен для понимания того, как возникает порядок из неупорядоченности. Это имеет большое эволюционное значение и вводит, таким образом, соображения, касающиеся статистического построения, которые очень интересным образом дополняют статистические динамические подходы, рассмотренные ранее.

Подход Кауфмана к эпигенетическим процессам представляется разумным в аспекте универсальности конструкции, но в плане возможностей применения математического анализа он очень слаб. Это в точности противоположно вышерассмотренному статистическому динамическому приближению, где анализ возможен, но только за счет всеобщности характера взаимодействий. Более поздние исследования Гласса и Кауфмана (Glass, Kauffman, 1973) показали, однако, как можно подойти к анализу рассматриваемой модели. Помимо того, Кауфман (Kauffman, 1973) очень интересно развил свои собственные первоначальные идеи. При применении идеи о переключающихся цепях к изменениям эпигенетического состояния, связанного с явлениями детерминации и трансдетерминации у Drosophila (Hadorn, 1966), из рассмотрений вероятностей перехода между состояниями в имагинальных дисках Drosophila был сделан ряд интересных выводов, касающихся пространственных границ в развивающемся эмбрионе насекомого. То, что такие выводы удалось получить из модели эпигенетических управляющих процессов, основанной на простом фундаменте булевой логики, указывает на скрытую мощь этого подхода, а также на творческую фантазию Кауфмана и четкость его работы.