Коллективные моды в ритмических процессах

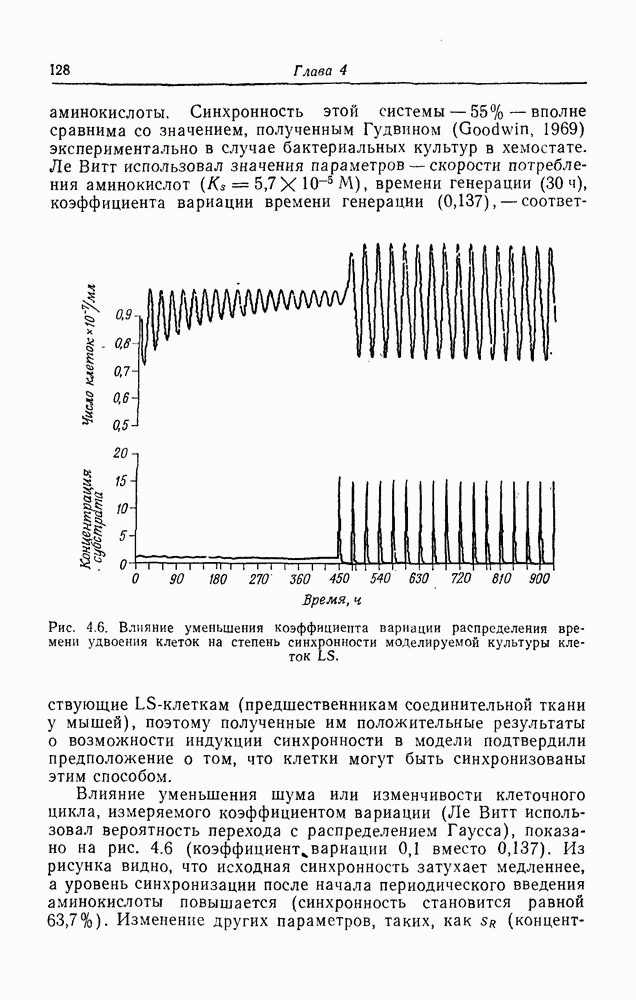
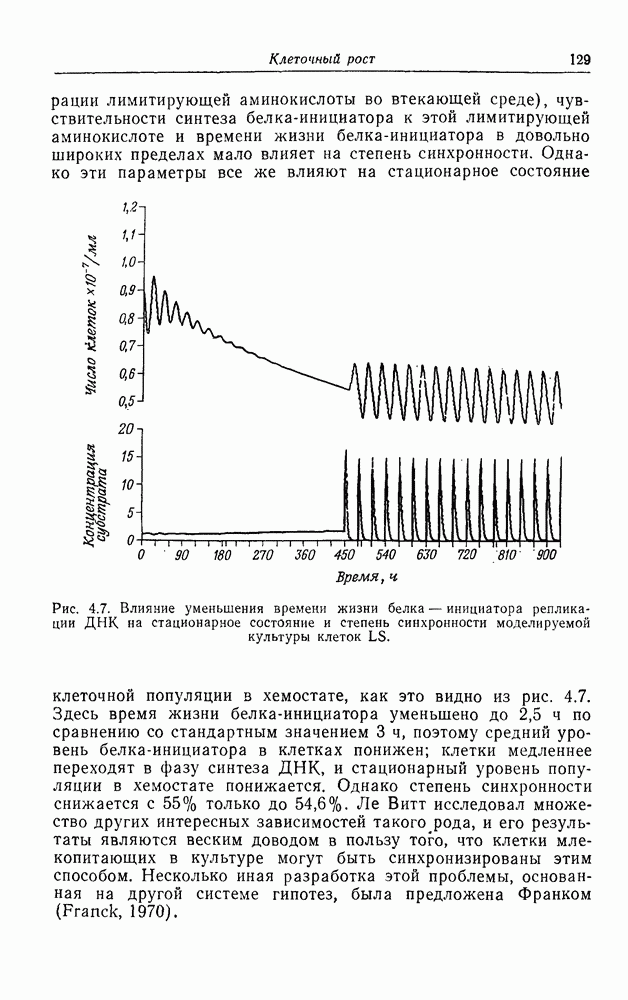
Рассмотрим способы описания некоторых видов временной упорядоченности, которые уже анализировались в предыдущих главах с помощью потенциальных функций, относящихся к семействам элементарных катастроф. Пусть мы имеем непрерывную культуру бактерий, растущую в хемостате и синхронизированную с помощью периодического добавления фосфата (гл. 4). Синхронность в такай культуре (Goodwin, 1969 с) контролируется интенсивностью периодического стимула, которую можно охарактеризовать параметром К. Суть этого процесса состоит в том, что при некотором значении параметра клеточные деления в системе начинают происходить синхронно, и эта синхронность растет с увеличением Я. Частота синхронных изменений числа клеток определяется условиями роста в хемостате, генетическими характеристиками клеток и частотой периодической вынуждающей функции. Для описания появления периодичности в популяции воспользуемся потенциальной функцией одной переменной, которая задает амплитуду коллективных мод колебаний в культуре, т. е. среднюю амплитуду вынужденных колебаний. Такая функция имеет вид

где — амплитуда моды, — критическое значение вынуждающего параметра, а a и b — положительные константы. Эта потенциальная функция была использована для описания появления коллективной моды в лазере в ответ на воздействие внешнего источника энергии — лампы накачки (Graham, 1973)), - процесс, совершенно аналогичный рассматриваемому. Из уравнения

потенциальной функции (7.12) мы можем получить динамику г, амплитуды синхронных колебаний, обычным методом получения дифференциальных уравнений с помощью потенциальных функций, а именно

Очевидно, если устойчивым стационарным решением будет в этом случае никакой макроскопической, характерной для всей популяции амплитуды не существует. Но если устойчивое решение есть

Для описания колебаний нам нужны две переменные; в качестве второй можно взять частоту . Поскольку она не входит в потенциальную функцию, мы имеем

откуда со есть константа, определяемая факторами, описанными выше. Уравнение (7.12) относится к тому же семейству, что и уравнение, используемое для описания конденсации газа (7.11), и характеризуется катастрофой сборки, или Римана — Гюгонио, с той лишь разницей, что из соображений симметрии в отношении колебаний один из параметров деформации, необходимо принять равным 0. В результате потенциальная функция описывает не ударную волну, а только бифуркацию, определяемую параметром и интерпретируемую как фазовый переход.

Динамическое описание системы можно сделать более общим, что позволит включить в процесс случайные флуктуации, если просто ввести в уравнение потенциальной функции (7.12) член , в котором с — параметр, определяющий размеры флуктуаций. Можно также вывести функцию распределения вероятности для этой системы, которая является решением уравнения Фоккера — Планка, при условии, что процесс удовлетворяет некоторым требованиям. Этот метод описан Грэхэмом (Graham, 1973), я же хочу только отметить, что равновесная функция распределения, аналогичная используемой в статистической механике, имеет хорошо знакомый вид

где N — нормировочная константа. С помощью этой функции можно получить любые необходимые статистические характеристики процесса синхронизации. Сходство между этим методом и подходом, принятым в статистической механике, теперь

очевидно, хотя мы имеем дело с системой, далекой от термодинамического равновесия. В этой трактовке обобщенная функция , очевидно, играет роль гамильтониана. Заметим, что макроскопическая переменная, аналогичная температуре, которая входит в уравнение (7.8) в виде здесь отсутствует вследствие предположения, что переход мембраны из невозбужденного состояния в возбужденное является равновесным процессом. При выводе уравнения (7.13) для системы, которая далека от термодинамического равновесия, можно обойтись без этого ограничения, хотя другие требования, связанные с марковской природой флуктуаций и стационарностью значений параметров, должны быть удовлетворены. Мне кажется, что возможность использования потенциальных функций теории катастроф в рамках этого обобщенного динамического подхода имеет большое значение, поскольку позволяет построить макроскопическое описание биологических процессов, обладающее многими свойствами равновесной термодинамики, но при этом строго применимое к поведению открытых систем. Основной слабостью трактовки неравновесных процессов Глансдорфа — Пригожина является, на мой взгляд, именно отсутствие наглядных потенциальных функций, что превращает ее по существу в применение теории устойчивости для описания сложных биологических процессов.

Способ описания, использующий уравнение потенциальной функции (7.12) или его стохастический вариант, применим и к другим популяционным ритмам, таким, как суточный ритм митотической активности в эпидермисе млекопитающих, где в качестве синхронизирующего периодического сигнала выступает концентрация адреналина (Bullough, Laurence, 1964), или появление циркадного ритма в популяции в результате захвата периодической внешней силой, т. е. пейсмекером (водителем ритма). Во всех таких ситуациях имеется внешний параметр, управляющий возникновением коллективного ритма, частота которого определяется целым рядом факторов, включая и частоту вынуждающей функции. Интересно выяснить, как следует модифицировать это описание при рассмотрении цикла клеточного роста и деления отдельных клеток. В этом случае рост также управляется внешним параметром, например концентрацией скорость-лимитирующего компонента питания в среде культивирования, но при этом частота клеточного цикла не определяется только периодической вынуждающей функцией, а задается динамикой всей системы. Попытаемся описать это феноменологически.

Допустим, что переход отдельной клетки от нерастущего состояния к растущему вызывает появление коллективной или кооперативной периодичности среди различных функциональных

цепей управления или познающих единиц растущей клетки, причем этот переход происходит в тот момент, когда концентрация скорость-лимитирующего компонента питания поднимается выше некоторого порогового значения. При этом мы не будем рассматривать никаких деталей микроскопической или молекулярной динамики взаимодействующих процессов, которые лежат в основе появления этой макроскопической периодичности, проявляемой как рост и деление клетки и ее потомства. Как и прежде, для описания динамического фазового перехода будет использоваться потенциальная функция, которая зависит от двух переменных — амплитуды моды и частоты а. Амплитуда характеризует когерентность коллективных колебаний, в то время как — их частоту, причем в этом случае нужны обе переменные. Это заставляет нас рассматривать потенциальные функции Тома с двумя переменными, названными омбилическими. Первая из этих функций — гиперболическая омбилическая точка с потенциальной функцией

что дает следующие уравнения, описывающие динамику системы:

Эти уравнения можно использовать для описания предельного цикла с амплитудой и частотой причем и амплитуда, и частота устойчивы к возмущению. Удобно принять и считать А управляющим параметром, который является функцией концентрации лимитирующего компонента питания. Соображения, высказанные в гл. 4, относящиеся к росту клеток в управляемых условиях, приводят к выражению

где первый член — хорошо знакомое выражение Моно для роста клеток на лимитирующем субстрате s, а константа k определяет критическое значение s (назовем его ), при котором начинается рост. Это значение является корнем уравнения откуда

Стационарные значения определяются из системы

Очевидно, если , то это означает, что в системе не существует коллективных или когерентных колебаний, так как нет роста. Для действительных решений не существует, поэтому справедлива та же самая интерпретация. Колебания в отдельных цепях управления в нерастущей клетке могут при этом продолжаться, но характер взаимодействий будет таков, что никаких коллективных колебаний во всей клетке не будет. Интересное следствие, вытекающее из этой точки зрения на переход от покоя к росту, заключается в том, что у некоторых эпигенетических или метаболических переменных могут существовать характерные частоты, не совместимые с коллективным периодическим поведением целой клетки, так что, воздействуя на внутриклеточные переменные с определенными частотами (скажем, периодически изменяя pH в культуре), можно рассогласовать динамику процессов и остановить рост.

Ясно, что скорость роста клетки будет прямо пропорциональна частоте коллективных колебаний в цепях управления; поэтому мы примем

где — скорость роста, константа. Точно так же, как это было сделано выше, можно получить стохастическое описание феноменологических процессов, введя в потенциальную функцию члены , где — постоянные, и получить распределение вероятности, которое позволяет определить статистические свойства системы. Тогда можно вычислить средние и дисперсии переменных системы, а также, если потребуется, и более высокие моменты. Средние значения будут равны их стационарным значениям; поэтому из уравнения (7.18) мы находим, что

Теперь, если положить мы найдем, что так что

Эмпирическое соотношение, которое используется для описания роста клеток в хемостате, есть

где Y — константа выхода, определенная в гл. 4, Q — скорость потребления лимитирующего компонента питания, постоянная поддержания, т. е. количество этого компонента питания, необходимое в единицу времени для поддержания клетки в жизнеспособном состоянии без роста. Эта величина в гл. 4 не рассматривалась, поскольку она дает лишь малую поправку,

но она необходима для точного описания процесса роста. Члены уравнения (7.19) легко идентифицировать с помощью (7.20), так что используемая модель приводит к известному выражению. Это обусловлено определением как параметра деформации потенциальной функции, а также характером зависимости этого параметра от концентрации лимитирующего компонента питания.

Если рассматривать клеточную синхронизацию, с одной стороны, и процесс роста — с другой, как фазовые переходы, описываемые феноменологическими потенциальными функциями, то важной особенностью последнего процесса окажется трактовка амплитуды и частоты как переменных с устойчивой динамикой, которая определяется уравнениями (7.15). Эти уравнения обладают свойствами, необходимыми для описания системы с предельным циклом, так как возмущение, которое увеличивает амплитуду по сравнению со стационарным значением, приводит к появлению отрицательной скорости изменения амплитуды и положительной скорости изменения частоты и наоборот. Именно этот тип устойчивости следует из экспериментов Кауфмана и Вилле (Kauffman, Wille, 1975) по анализу митотического цикла у Physarum и подобных им исследований. Переменные , использованные выше, при этом оказываются средними для полного цикла значениями радиальной координаты и угловой скорости dQ/dt.

Чтобы распространить анализ на случай, когда взаимодействия между растущими клетками приводят к спонтанной синхронизации, необходимо ввести члены, описывающие это взаимодействие. Предположим, что динамика каждой клетки описывается такой же потенциальной функцией как в уравнении (7.14), где индекс относится к клетке популяции. Кроме того, между клетками существуют взаимодействия, которые приводят к следующей потенциальной функции для популяции:

Это дает динамические уравнения

Взаимодействие стремится привести клетки в состояние синхронности, когда . Обобщая динамику системы обычным способом, т. е. включая в рассмотрение флуктуации, можно описать синхронные колебания популяции при наличии шумов.

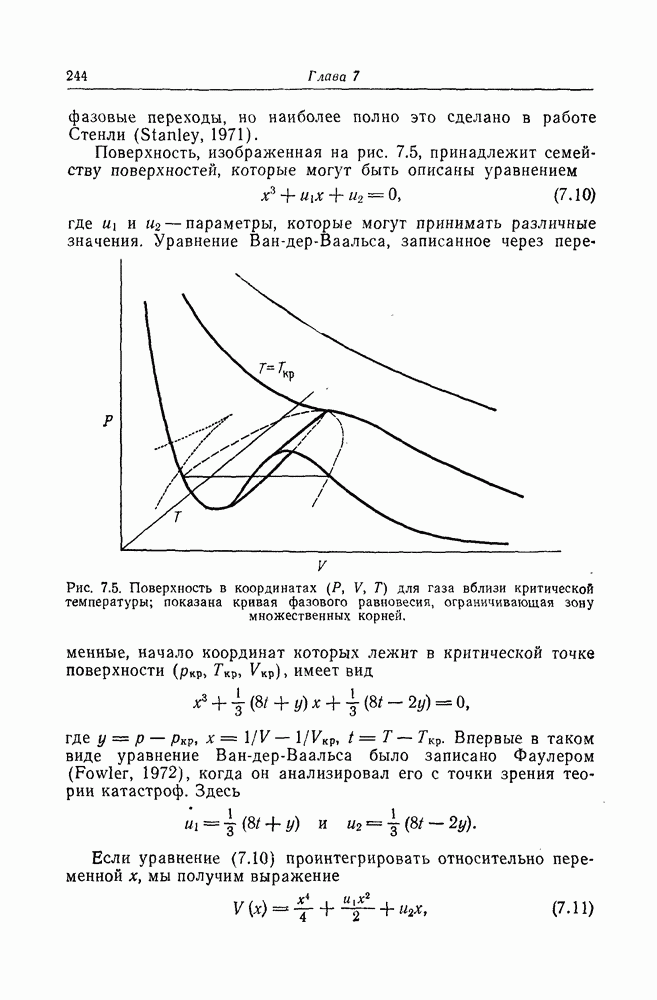
Эти примеры иллюстрируют ценность феноменологических потенциальных функций при описании нелинейных сложных процессов в биологических системах, проявляющих коллективные или кооперативные свойства. В описанных выше примерах временной организации никаких скачкообразных изменений состояния, аналогичных процессу конденсации газа или переходу из невозбудимого состояния в возбудимое, не рассматривалось, так что зоны появления «ударных волн» в соответствующих потенциальных функциях отсутствуют. Однако эти функции, вообще говоря, пригодны для описания скачкообразных переходов из одного стационарного состояния в другое в соответствии с некоторыми правилами, скажем, правилом Максвелла. Пример поведения такого типа дает развитие Dictyostelium discoideum, где частота пейсмекера изменяется довольно резко примерно от мин до мин (Durston, 1974). Такой разрыв частоты можно описать, воспользовавшись понятием области деформации типа складки в уравнении потенциальной функции (7.14), приводящей к скачку с одного участка поверхности на другой при движении вдоль оси частоты, как это происходит в случае конденсации газа при движении вдоль оси V. Временные разрывы такого типа для процесса развития до сих пор не известны, но они, конечно, представляют важное свойство системы, аналогичное внезапному изменению частоты, связанному с изменениями режима работы, например при переходе от ходьбы к бегу. Некоторые данные о связи между процессами, лежащими в основе эмбриогенеза и поведения, будут рассмотрены ниже.

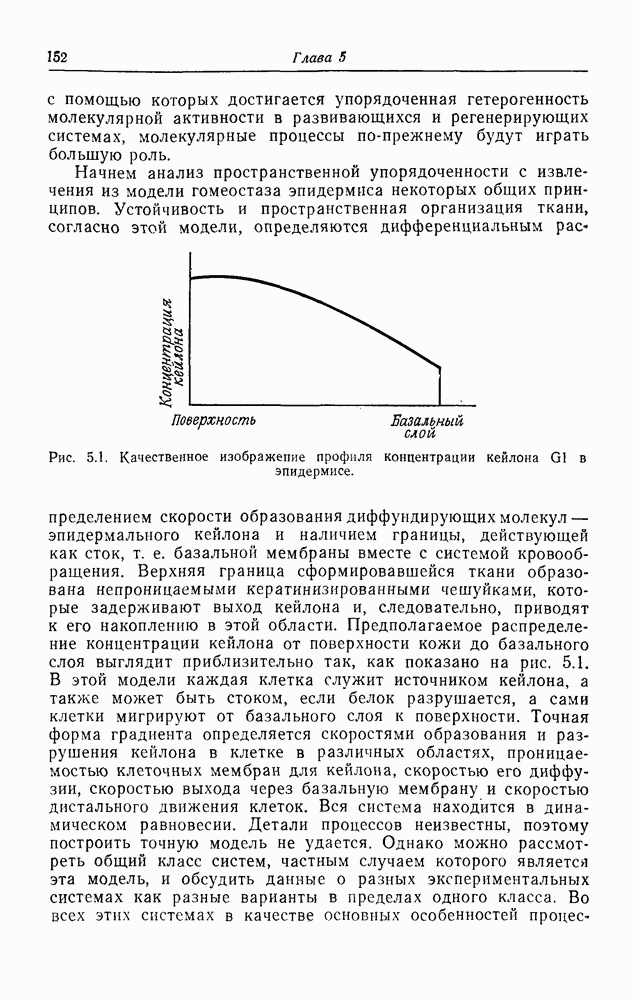
Разрывы состояния вдоль пространственной оси возникают таким же образом, как и разрывы во времени, но в этом случае один из параметров деформации потенциальной функции представляет пространство. Зиман (Zeeman, 1974) дал исчерпывающее описание этого метода применительно к гаструляции амфибий и к кульминации у миксомицетов, использовав катастрофу сборки. Вдоль пространственной оси состояние клеток изменяется монотонно в соответствии с градиентом морфогена, так что аналогом критической температуры в этом случае является критическое значение концентрации морфогена в какой-то точке пространства, за которой может произойти скачкообразное изменение состояния клетки. Тогда между этими двумя областями возникает граница, по разные стороны которой клетки находятся в разных состояниях, и образуются пространственно организованные дифференцированные зоны; эта граница аналогична

той, которая отделяет презумптивную мезодерму от эктодермы или хрящ от мышцы. Особенно интересным моментом в подходе Зимана является его вывод о том, каким образом волны изменения состояния перемещаются по развивающейся ткани в области, где возникает разрыв, останавливаясь на границах, которые определяются градиентом морфогена. Функции, используемые для описания этих разрывов, могут дать некоторую информацию о геометрии разрывов, но ничего не говорят об общих свойствах ткани, где возникает такая управляемая разрывность, поэтому ограничения метода очевидны. Для полного описания процессов нужна подлинно общая теория генерации формы в живых системах, которая требует, на мой взгляд, совершенно иного подхода к биологической упорядоченности, в корне отличающегося от современного, где основное внимание уделяется локальным взаимодействиям и межмолекулярным силам, с которыми мы и имели дело в этой книге. Однако математическое описание сложных переходов между состояниями и включение этого описания в теорию неравновесных динамических процессов с макроскопическими функциями распределения вероятностей очень полезно — оно помогает нам правильно трактовать основные качественные особенности эпигенетических и морфогенетических процессов. Кроме того, можно обобщить эти методы путем включения в описание распространения волн активности, рассматриваемого как процесс перемещения разрывов, в результате чего общую картину эмбриогенеза, представленную в гл. 5 и 6, удастся описать и проанализировать математически. Тогда этот подход можно будет встроить в общую структуру обратных предельных систем, описанных в начале главы, что позволит выявить познавательный смысл всего процесса развития. Заканчивая главу, я хотел бы рассмотреть некоторые наиболее общие выводы из этого подхода.