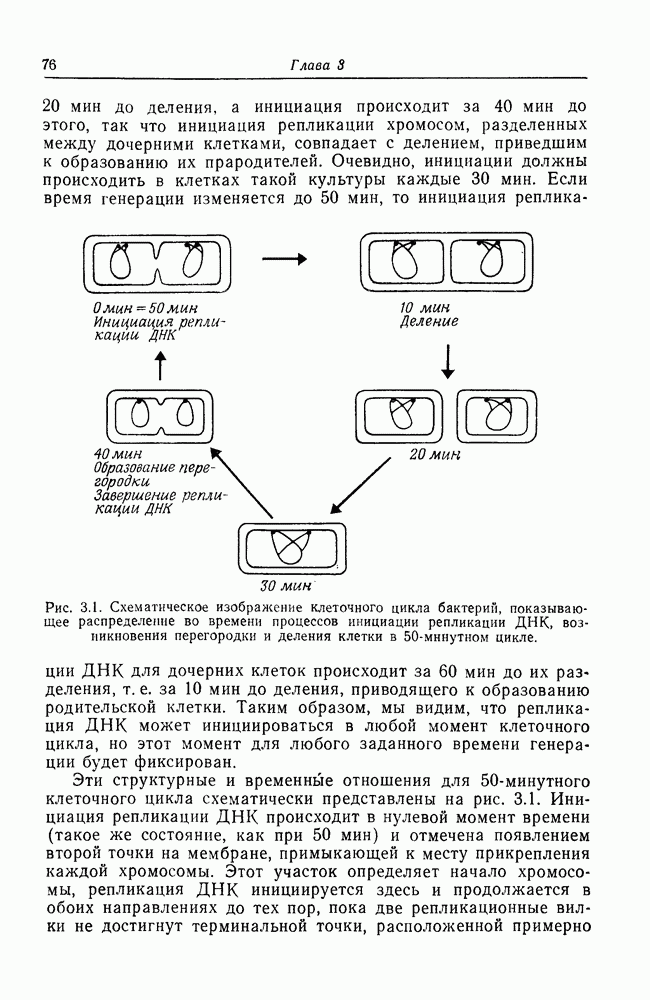
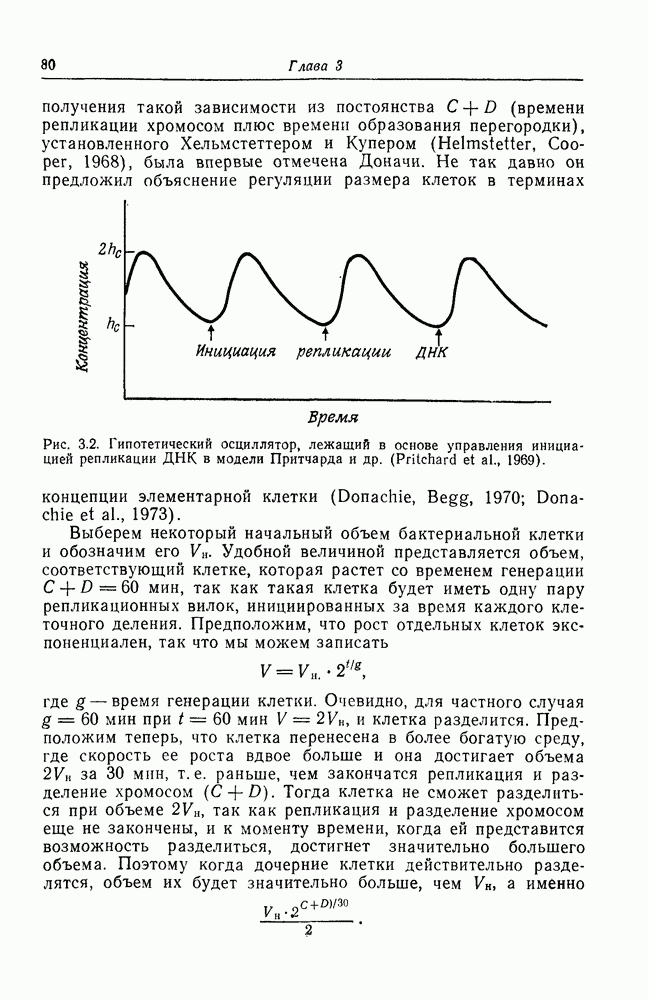
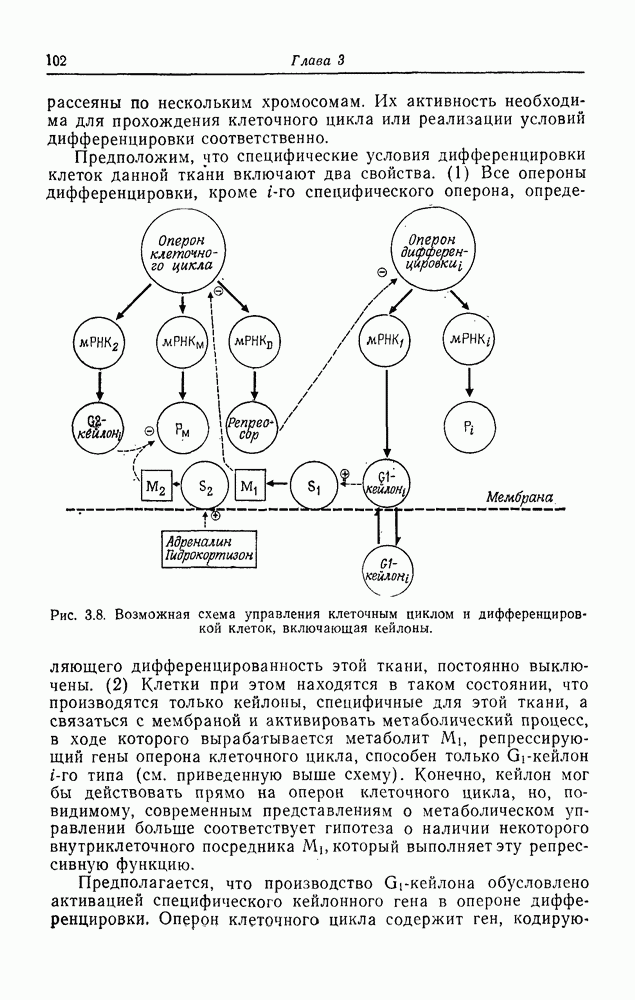
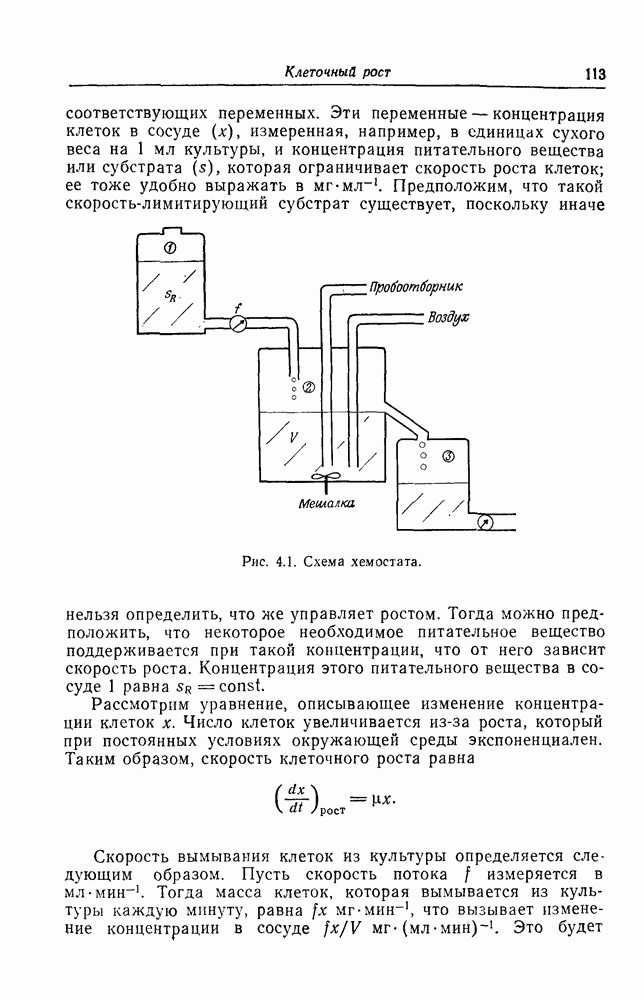
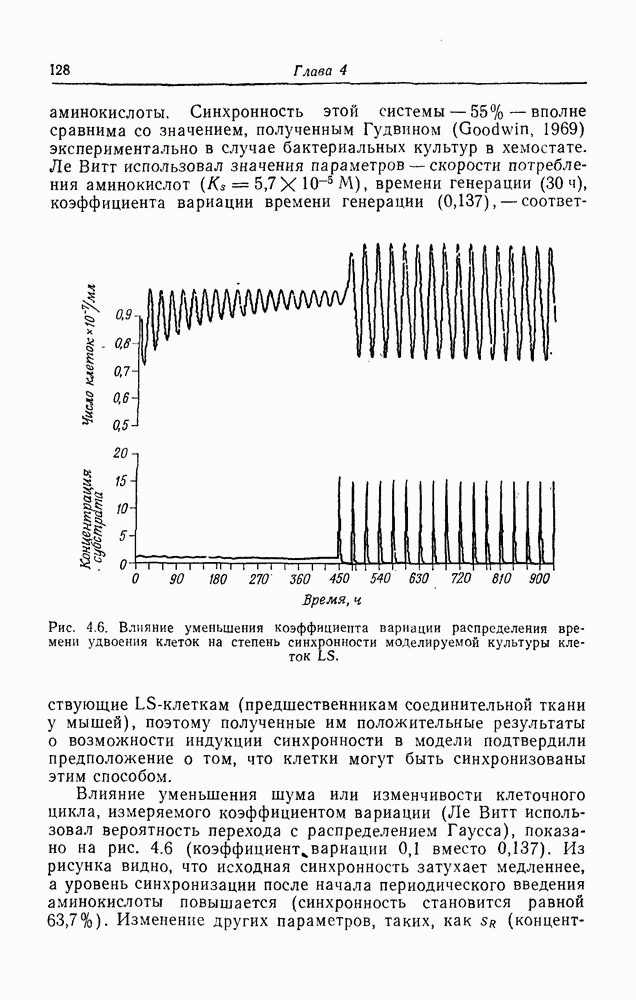
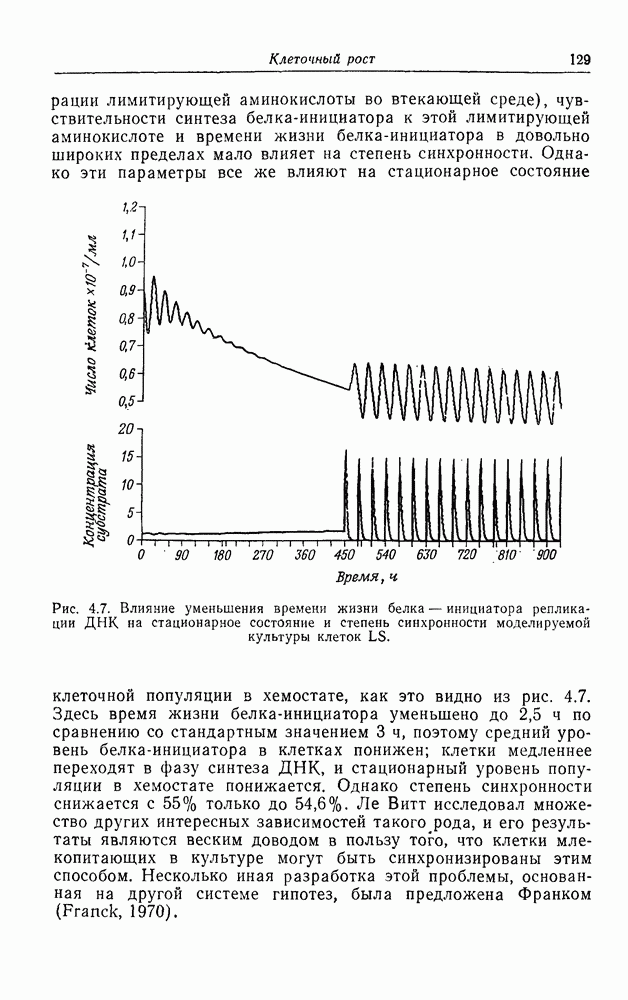
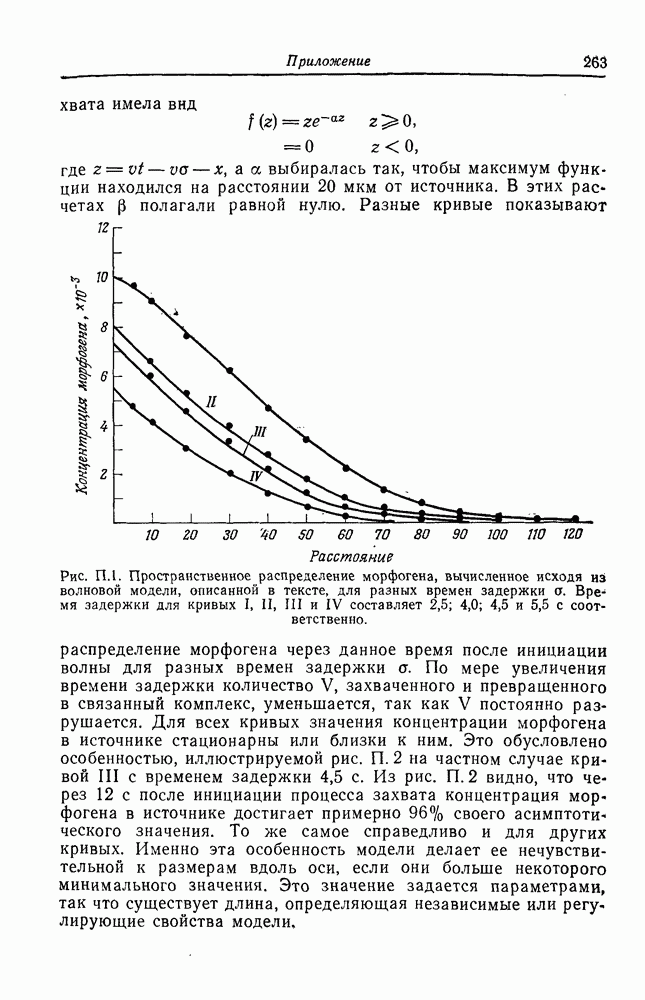
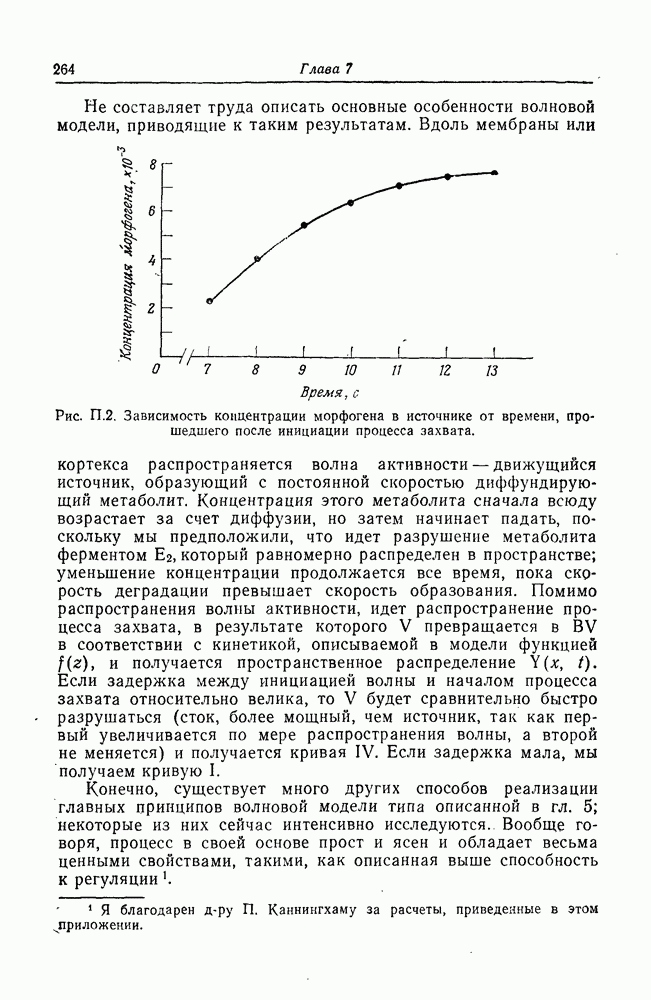
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Кооперативная ферментативная кинетика
Рассмотрим сначала, как объясняется сигмоидный характер кинетики АКТ. Мы знаем, что нативный фермент имеет шесть центров связывания аспарагиновой кислоты, поэтому разумно продолжить видоизменения классической ферментативной схемы, просто увеличивая стехиометрию реакции фермента с субстратом. В общем случае для стехиометрии порядка  мы можем записать
мы можем записать

Это приводит к дифференциальному уравнению

В стационарных условиях

где

Используя условие

получаем

откуда

Тогда из уравнения (1.11) получим, что

Очевидно, что при  мы будем иметь уравнение Михаэлиса — Ментен, которое получается из соотношения (1.9), если положить
мы будем иметь уравнение Михаэлиса — Ментен, которое получается из соотношения (1.9), если положить  . Какова форма кривой при
. Какова форма кривой при  Простейший способ выявить качественные особенности V как функции
Простейший способ выявить качественные особенности V как функции  — это найти точки максимумов и минимумов и все точки перегиба. Для этого найдем первую и вторую производные. Положим
— это найти точки максимумов и минимумов и все точки перегиба. Для этого найдем первую и вторую производные. Положим  , где а — константа, и опустим квадратные скобки в обозначениях концентраций. Тогда
, где а — константа, и опустим квадратные скобки в обозначениях концентраций. Тогда

Значения S, которые обращают это выражение в 0 и определяют минимум и максимум функции, равны соответственно 0 и  при остальных S в этом интервале первая производная положительна. Этим выражение (1.12) отличается от уравнения Михаэлиса—Ментен, для которого, как это видно из рис. 1.5, при
при остальных S в этом интервале первая производная положительна. Этим выражение (1.12) отличается от уравнения Михаэлиса—Ментен, для которого, как это видно из рис. 1.5, при  наклон максимален. Наличие у функции единственного максимума и минимума означает, что между ними обязательно имеется точка перегиба. Чтобы найти ее, продифференцируем (1.13):
наклон максимален. Наличие у функции единственного максимума и минимума означает, что между ними обязательно имеется точка перегиба. Чтобы найти ее, продифференцируем (1.13):

Это выражение обращается в 0 при значениях S, равных корням уравнения

или

откуда

Ясно, что у этого уравнения имеется только один положительный корень, а следовательно, и одна точка перегиба у функции (1.12) для  Из (1.12) видно, что скорость, равная половине максимальной, достигается при
Из (1.12) видно, что скорость, равная половине максимальной, достигается при  в то время как из (1.14) следует, что точка перегиба всегда достигается при меньшем значении концентрации субстрата, приближаясь к
в то время как из (1.14) следует, что точка перегиба всегда достигается при меньшем значении концентрации субстрата, приближаясь к  только в пределе, когда
только в пределе, когда  Для
Для  (значение
(значение  для АКТ) точка перегиба имеет место при
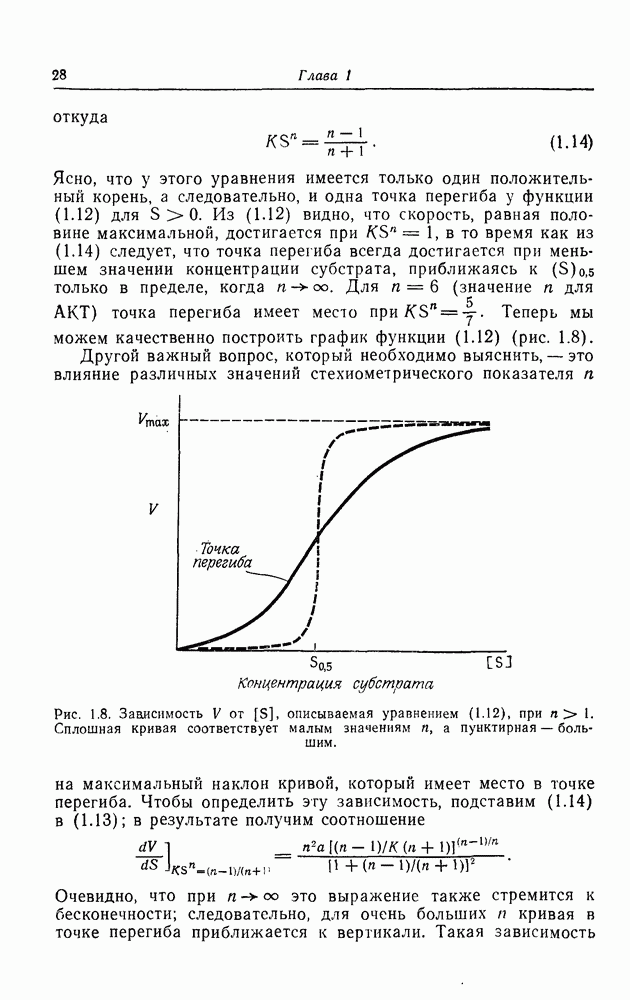
для АКТ) точка перегиба имеет место при  . Теперь мы можем качественно построить график функции (1.12) (рис. 1.8).
. Теперь мы можем качественно построить график функции (1.12) (рис. 1.8).
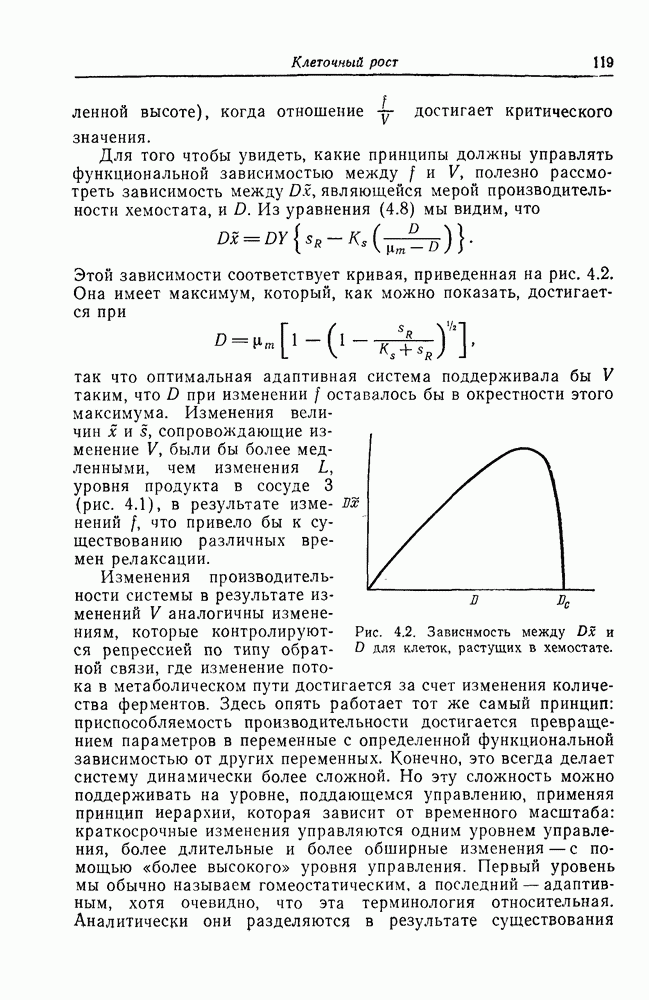
Другой важный вопрос, который необходимо выяснить, — это влияние различных значений стехиометрического показателя  на максимальный наклон кривой, который имеет место в точке перегиба.
на максимальный наклон кривой, который имеет место в точке перегиба.

Рис. 1.8. Зависимость V от  описываемая уравнением (1.12), при
описываемая уравнением (1.12), при  Сплошная кривая соответствует малым значениям
Сплошная кривая соответствует малым значениям  , а пунктирная — большим.
, а пунктирная — большим.
Чтобы определить эту зависимость, подставим (1.14) в (1.13); в результате получим соотношение

Очевидно, что при  это выражение также стремится к бесконечности; следовательно, для очень больших
это выражение также стремится к бесконечности; следовательно, для очень больших  кривая в точке перегиба приближается к вертикали. Такая зависимость
кривая в точке перегиба приближается к вертикали. Такая зависимость
изображена на рис. 1.8 (пунктирная кривая). Фермент, характеризующийся поведением такого типа, действовал бы как своего рода метаболический выключатель; до тех пор пока концентрация субстрата не приблизится к  его активность была бы практически равна нулю, а затем быстро возрастала бы до максимального значения в очень узкой области концентраций субстрата. На первый взгляд существование таких ферментов кажется невероятным, но уже сейчас показано, что ряд ферментов имеет стехиометрию, равную 8, что дает значение
его активность была бы практически равна нулю, а затем быстро возрастала бы до максимального значения в очень узкой области концентраций субстрата. На первый взгляд существование таких ферментов кажется невероятным, но уже сейчас показано, что ряд ферментов имеет стехиометрию, равную 8, что дает значение  это близко к значению, характерному для переключения.
это близко к значению, характерному для переключения.
Вернемся теперь к допущениям нашей модели и посмотрим, можем ли мы узнать, во-первых, почему простое изменение стехиометрии в модели Михаэлиса — Ментен приводит к таким значительным последствиям, и во-вторых, применима ли эта модель для многомерных ферментов (ферментов, состоящих из субъединиц). При описании сигмоидной кинетики также используется понятие кооперативности. Связано это с тем, что вплоть до точки перегиба малые последовательные приращения концентрации субстрата все больше и больше влияют на скорость реакции, т. е. связь между переменными нелинейна, с положительной второй производной. Кажется, что эти последовательные приращения вызывают такое кооперативное взаимодействие в ферменте, что дальнейшее образование комплекса облегчается, и поэтому скорость реакции возрастает. На первый взгляд мы просто взяли в этом случае  не делая никаких предположений относительно взаимодействия между субъединицами. Однако в действительности, записывая реакцию в виде (1.11), мы сделали очень сильное допущение, а именно: мы предположили, что образование комплекса
не делая никаких предположений относительно взаимодействия между субъединицами. Однако в действительности, записывая реакцию в виде (1.11), мы сделали очень сильное допущение, а именно: мы предположили, что образование комплекса  может произойти только в случае, если одновременно столкнутся
может произойти только в случае, если одновременно столкнутся  молекул субстрата с
молекул субстрата с  каталитическими центрами молекулы. С ростом концентрации такая
каталитическими центрами молекулы. С ростом концентрации такая  -молекулярная реакция постепенно становится все более вероятной, и это происходит до тех пор, пока не начнет сказываться насыщение и вторая производная не станет отрицательной. Такое поведение названо случаем бесконечной кооперативности, так как в этой модели субъединицы либо реагируют с субстратом все одновременно, либо не реагируют вовсе.
-молекулярная реакция постепенно становится все более вероятной, и это происходит до тех пор, пока не начнет сказываться насыщение и вторая производная не станет отрицательной. Такое поведение названо случаем бесконечной кооперативности, так как в этой модели субъединицы либо реагируют с субстратом все одновременно, либо не реагируют вовсе.
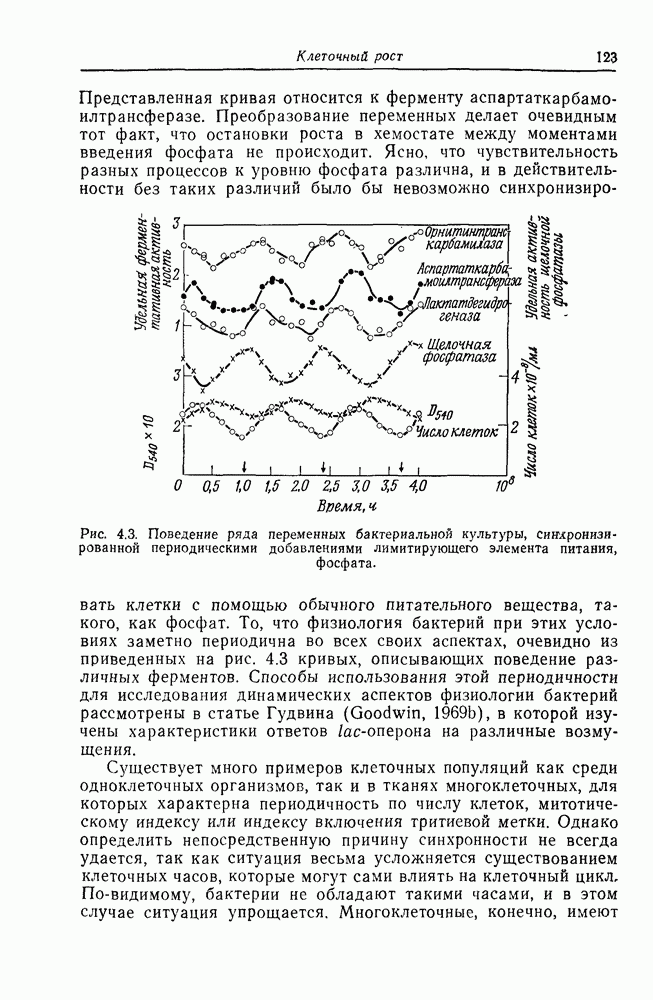
Прежде чем a priori решать вопрос о возможной применимости модели, давайте посмотрим, какие результаты были получены при сопоставлении этой модели с экспериментальными Данными. Хотя исследования сигмоидной кинетики ферментов начались сравнительно недавно, основные черты модели, описываемой уравнением (1.11), были использованы Э. Хиллом еще в 1913 г. в его классических исследованиях оксигенации
гемоглобина. Запишем уравнение (1.11) в применении к гемоглобину. Е заменим на  будем рассматривать как концентрацию молекулярного кислорода и положим
будем рассматривать как концентрацию молекулярного кислорода и положим  О (потому что при обратимом связывании и высвобождении кислорода гемоглобином не происходит химической реакции); тогда мы получим соотношение
О (потому что при обратимом связывании и высвобождении кислорода гемоглобином не происходит химической реакции); тогда мы получим соотношение

В этой системе величиной, удобной для наблюдения, является та часть общего гемоглобина, которая оксигенирована:

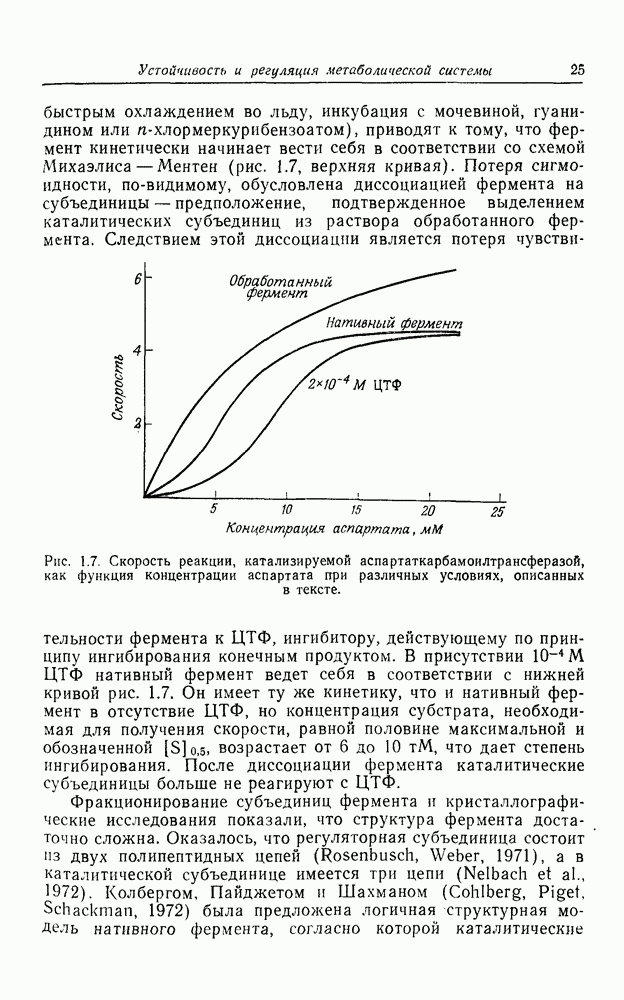
Это уравнение, конечно, графически представляется такой же кривой, как и приведенная на рис. 1.8. Хилл показал, что для соответствия кривой экспериментальным данным необходимо взять  . С точки зрения схемы реакции (1.11) это число не имеет смысла, так как оно означает, что с молекулой гемоглобина реагирует 2,7 молекул кислорода. Ясно, что его необходимо рассматривать как среднее, т. е. считать, что одни молекулы гемоглобина несут только одну молекулу кислорода, другие — четыре (максимум, поскольку в гемоглобине четыре гема на молекулу), но большинство — две или три. Этот факт отвергает модель, основанную на предположении, что
. С точки зрения схемы реакции (1.11) это число не имеет смысла, так как оно означает, что с молекулой гемоглобина реагирует 2,7 молекул кислорода. Ясно, что его необходимо рассматривать как среднее, т. е. считать, что одни молекулы гемоглобина несут только одну молекулу кислорода, другие — четыре (максимум, поскольку в гемоглобине четыре гема на молекулу), но большинство — две или три. Этот факт отвергает модель, основанную на предположении, что  молекул (обязательно целое число) реагируют одновременно, образуя комплекс. На самом деле число занятых центров у разных молекул может быть различно, и это необходимо учесть в нашей модели. Но если субъединицы могут реагировать с лигандами независимо, то чем обусловлен сигмоидный характер кинетики, который указывает на то, что между субъединицами существует взаимодействие? Очевидно, для выхода из создавшегося положения необходимо построить модель, которая лежит где-то между схемой Михаэлиса, считающей, что единицы независимы (один центр, реагирующий за один раз, без какого-либо взаимодействия с другими), и схемой Хилла с бесконечной кооперативностью.
молекул (обязательно целое число) реагируют одновременно, образуя комплекс. На самом деле число занятых центров у разных молекул может быть различно, и это необходимо учесть в нашей модели. Но если субъединицы могут реагировать с лигандами независимо, то чем обусловлен сигмоидный характер кинетики, который указывает на то, что между субъединицами существует взаимодействие? Очевидно, для выхода из создавшегося положения необходимо построить модель, которая лежит где-то между схемой Михаэлиса, считающей, что единицы независимы (один центр, реагирующий за один раз, без какого-либо взаимодействия с другими), и схемой Хилла с бесконечной кооперативностью.
На этом этапе ферментативная кинетика несколько усложняется. Я опишу простейшую из моделей, предложенных для объяснения кооперативности и аллостерических эффектов, модель Моно, Уаймена и Шанжё (Monod, Wyman, Changeux, 1965), да и в этом случае ограничусь лишь основами. Идею модели иллюстрирует схема рис. 1.9, изображающая частный случай фермента с четырьмя субъединицами, каждая из которых имеет один активный центр. Предполагается, что существует два конформационно различных состояния фермента: Р и Е, и фермент спонтанно переходит из одного состояния в другое с константами
скоростей  в соответствии со схемой рис. 1.9. С субстратом способен реагировать только фермент, находящийся в состоянии Е, и в этом случае каждая субъединица может реагировать независимо, причем константы скоростей для этих реакций одинаковы. Моно и др. (Monod et al., 1965) допускали, что с субстратом реагируют обе формы фермента, Р и Е, но они обладают разным сродством. Здесь для простоты принято, что сродство для одной из форм равно нулю. В этом случае с точки зрения молекулы субстрата активные центры неразличимы, поэтому нельзя дискриминировать возможные комбинации занятости центров. Я показал только одну из возможных комбинаций для каждого комплекса
в соответствии со схемой рис. 1.9. С субстратом способен реагировать только фермент, находящийся в состоянии Е, и в этом случае каждая субъединица может реагировать независимо, причем константы скоростей для этих реакций одинаковы. Моно и др. (Monod et al., 1965) допускали, что с субстратом реагируют обе формы фермента, Р и Е, но они обладают разным сродством. Здесь для простоты принято, что сродство для одной из форм равно нулю. В этом случае с точки зрения молекулы субстрата активные центры неразличимы, поэтому нельзя дискриминировать возможные комбинации занятости центров. Я показал только одну из возможных комбинаций для каждого комплекса 

Рис. 1.9. Простейший вариант модели Моно — Уаймена — Шанжё, описывающий кооперативную кинетику фермента.
Для получения кинетики этой системы будем действовать постадийно следующим образом. В рамках предположения о стационарности связь между концентрациями Е и Р есть просто

Зависимость между Е и  должна учитывать концентрацию активных центров, доступных для реакции с S, которая равна
должна учитывать концентрацию активных центров, доступных для реакции с S, которая равна  . Поэтому мы имеем
. Поэтому мы имеем

откуда

где

На следующей стадии концентрация активных центров равна  , так как один центр уже занят, в то время как для обратной реакции, от
, так как один центр уже занят, в то время как для обратной реакции, от  концентрация занятых центров равна
концентрация занятых центров равна  . Поэтому
. Поэтому

откуда

Подставляя сюда выражение для  получаем
получаем

Аналогичным образом для связи между  имеем соотношение
имеем соотношение

откуда

а подстановка  из уравнения (1.17) дает
из уравнения (1.17) дает

Наконец, последняя пара комплексов дает нам

откуда

Используя уравнение (1.18), получаем

Теперь для описания состояния этой системы наиболее полезной функцией является отношение концентрации связанного субстрата к полной концентрации фермента. Это то же самое, что среднее число занятых центров на молекулу фермента; обозначим его через  . Полная концентрация связанного субстрата, согласно уравнениям
. Полная концентрация связанного субстрата, согласно уравнениям  равна, очевидно,
равна, очевидно,

Выражение в скобках — это  , поэтому правая часть равенства есть
, поэтому правая часть равенства есть

Полная концентрация фермента равна

Функция, которую мы хотим получить, есть отношение уравнений (1.20) и (1.21), что дает

В общем случае  центров функции имеет вид
центров функции имеет вид

Сравнивая его с уравнением Хилла (1.15), мы видим, что главное отличие состоит в появлении всех степеней концентрации субстрата между 0 и п, что соответствует одновременному наличию всех возможных комплексов фермента с субстратом.
Кроме того, в уравнении (1.23) имеется члену. Если  или Р на рис. 1.9 отсутствует), то уравнение (1.22) сводится к
или Р на рис. 1.9 отсутствует), то уравнение (1.22) сводится к  являющемуся просто уравнением Михаэлиса, в котором значение
являющемуся просто уравнением Михаэлиса, в котором значение  на насыщении (при
на насыщении (при  ) равно 4. Таким образом, сигмоидность кинетики обусловлена присутствием члена
) равно 4. Таким образом, сигмоидность кинетики обусловлена присутствием члена  Наличие у
Наличие у  точки перегиба можно показать тем же способом, что и использованный для анализа кинетики схемы, описываемой уравнением (1.12). Поскольку каждый активный центр реагирует с субстратом независимо, в чем же заключается кооперативность в этой схеме? Мы уже обращали внимание на член
точки перегиба можно показать тем же способом, что и использованный для анализа кинетики схемы, описываемой уравнением (1.12). Поскольку каждый активный центр реагирует с субстратом независимо, в чем же заключается кооперативность в этой схеме? Мы уже обращали внимание на член  в (1.22), обусловливающий сигмоидную природу кривой, поэтому можно предположить, что к кооперативности приводят конформационные взаимодействия между Р и Е. Основное предположение этой модели состоит в том, что все субъединицы изменяют свое конформационное состояние одновременно. Если молекула субстрата прореагировала с каким-либо центром, образовав
в (1.22), обусловливающий сигмоидную природу кривой, поэтому можно предположить, что к кооперативности приводят конформационные взаимодействия между Р и Е. Основное предположение этой модели состоит в том, что все субъединицы изменяют свое конформационное состояние одновременно. Если молекула субстрата прореагировала с каким-либо центром, образовав  то этот комплекс не может вернуться к Р кроме как через Е. Поэтому на первой стадии реакции субстрата с Е образуется молекула с тремя реакционными центрами, которые будут существовать до тех пор, пока S связан с одним из ее центров. Следующая стадия дает аналогичный, но меньший эффект, так как у
то этот комплекс не может вернуться к Р кроме как через Е. Поэтому на первой стадии реакции субстрата с Е образуется молекула с тремя реакционными центрами, которые будут существовать до тех пор, пока S связан с одним из ее центров. Следующая стадия дает аналогичный, но меньший эффект, так как у  имеется только два центра. После этого начинает преобладать насыщение и кривая асимптотически приближается к своему верхнему пределу. Таким образом, мы видим, что источником кооперативности в этой модели является существование альтернативных конформационных конфигураций Р и Е вместе со стабилизирующим действием S на каталитически активную форму молекулы.
имеется только два центра. После этого начинает преобладать насыщение и кривая асимптотически приближается к своему верхнему пределу. Таким образом, мы видим, что источником кооперативности в этой модели является существование альтернативных конформационных конфигураций Р и Е вместе со стабилизирующим действием S на каталитически активную форму молекулы.
Этим исчерпывается все, что имеет отношение к сигмоидной кинетике в этой модели. Как же быть с аллостерическими эффектами? Предполагается, что они возникают за счет изменения константы равновесия L. Если она уменьшается (например, уменьшается  ), то функциональная зависимость (1.22) при увеличении S будет расти медленнее. Это аналогично ингибированию по типу обратной связи, представленному на рис. 1.7. Тогда механизм действия ингибитора может быть основан на
), то функциональная зависимость (1.22) при увеличении S будет расти медленнее. Это аналогично ингибированию по типу обратной связи, представленному на рис. 1.7. Тогда механизм действия ингибитора может быть основан на
стабилизации состояния Р, происходящей при связывании ингибитора аллостерическими центрами, которые имеются в данной конформации. Такие центры нужно было бы включить в модель и тогда рассматривать ингибиторы с тех же позиций, что и субстраты, как это и сделано в статье Моно и др. (Monod et al., 1965). Аналогичным образом можно представить себе лиганды, стабилизирующие Е и увеличивающие таким образом L. В этом случае они являлись бы активаторами фермента, как АТФ по отношению к АКТ. Другим хорошо изученным примером такого типа является изоцитратдегидрогеназа, которая активируется АМФ (Atkinson et al., 1965).
В еще более общей модели аллостерического поведения белков субъединицы должны были бы изменять свою конформацию индивидуально, но все-таки взаимодействуя друг с другом так, чтобы вероятность конформационного перехода зависела от состояния других субъединиц в мультимере. Такое обобщение включает целый класс возможных моделей; ряд из них исследован Кошландом (Koshland, 1970). Соответствующие этим моделям алгебраические выражения более сложны, чем относительно простое уравнение (1.22), а при современном состоянии вопроса трудно экспериментально различить разные возможности. Несмотря на кажущуюся сложность, из простой геометрической схемы рис. 1.9 видно, что идейные основы наших представлений о поведении макромолекул относительно примитивны. Представленная теория ни в каком смысле не может считаться физической, так как она не располагает выражениями для энергий различных конформационных состояний. Это отражает трудность разработки сколько-нибудь удовлетворительной теории макромолекулярной упорядоченности, чему вряд ли стоит удивляться, если иметь в виду разнообразие и тонко сбалансированный характер поведения, на которое способны белки. Белки составляют молекулярные узнающие системы огромного разнообразия и совершенства, что дает им возможность играть роль тонких дискриминаторов, необходимых для регулирования течения метаболизма.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ЛИТЕРАТУРА
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ МЕТАБОЛИЧЕСКОЙ СИСТЕМЫ
- Устойчивость и закон действующих масс в метаболической системе
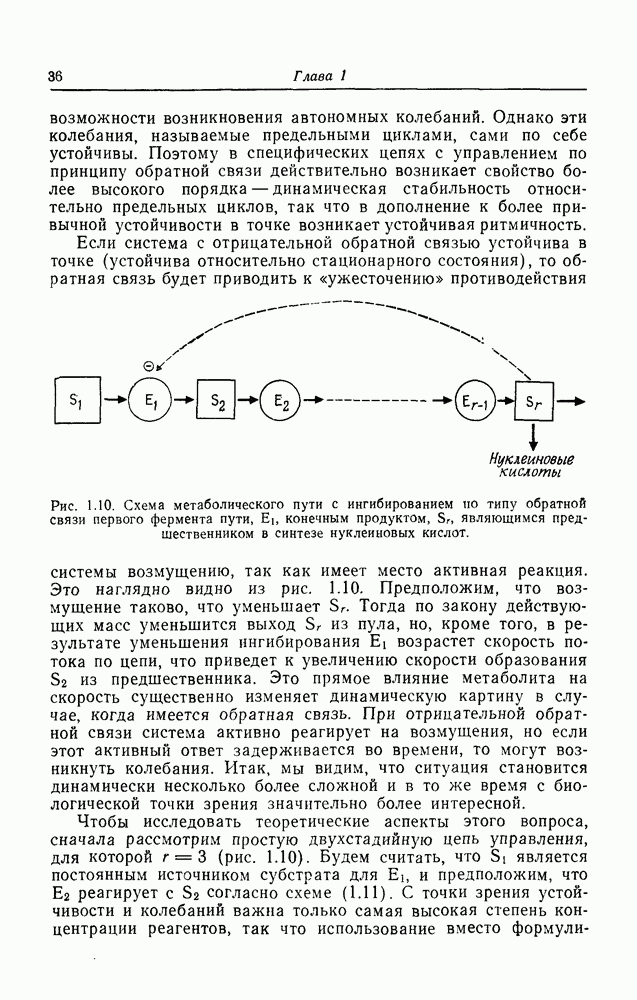
- Ингибирование по типу обратной связи в метаболических системах
- Аллостерические свойства ферментов
- Кооперативная ферментативная кинетика
- Цепи управления метаболизмом и их динамика
- Заключение
- Глава 2. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ ЭПИГЕНЕТИЧЕСКОЙ СИСТЕМЫ
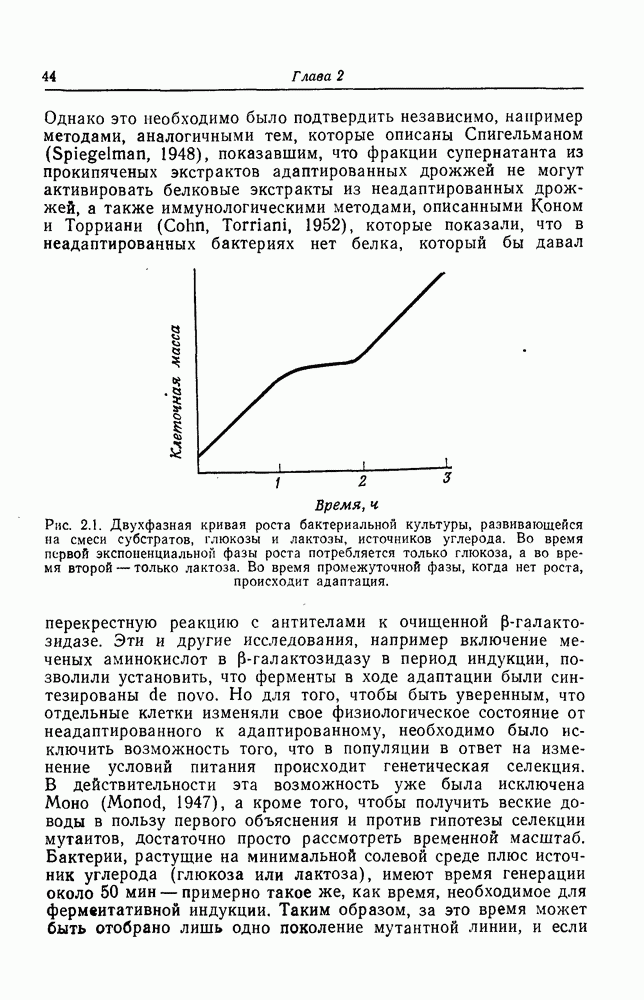
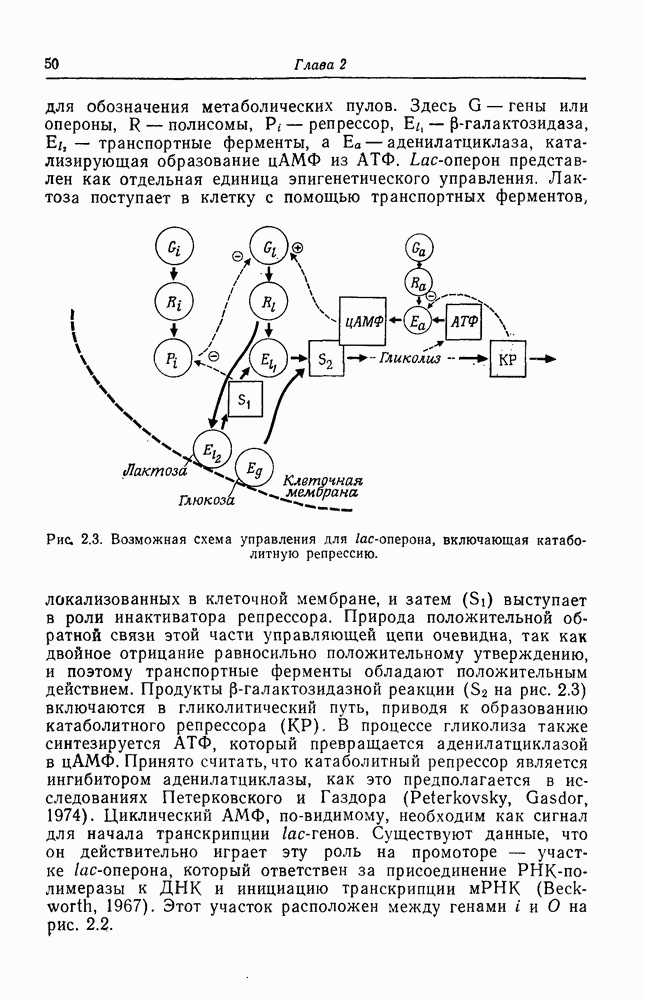
- Индукция и репрессия генов
- Репрессия путей биосинтеза по типу обратной связи
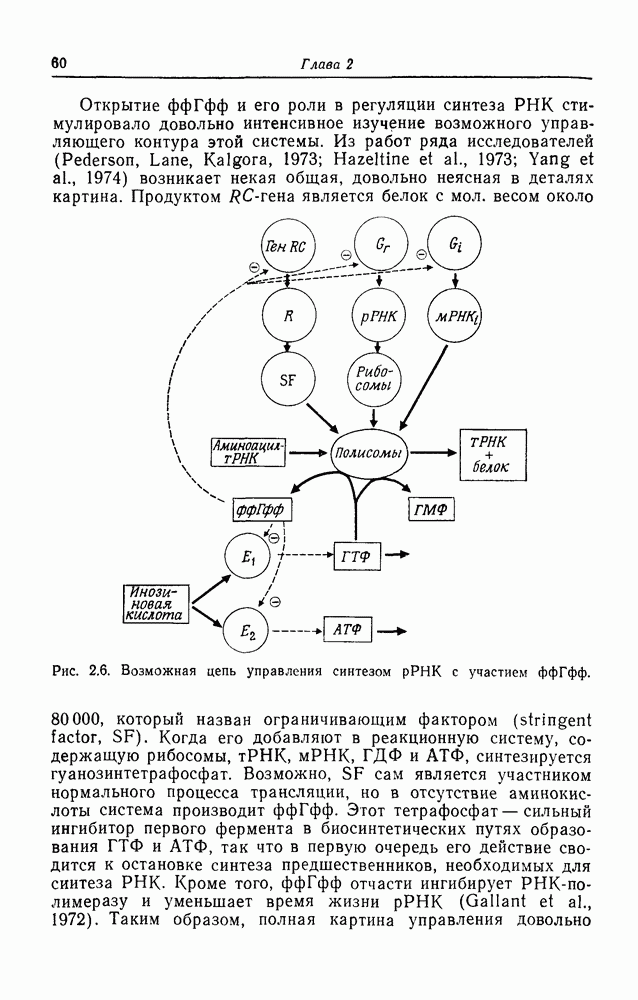
- Контроль синтеза рибосомной РНК
- Динамика эпигенетических сетей
- Аналогия со статистической термодинамикой
- Аналогия с вычислительными машинами: клетка как конечный автомат
- Глава 3. МИТОТИЧЕСКИЙ И КЛЕТОЧНЫЙ ЦИКЛЫ
- Репликон и гипотеза инициатора
- Гипотеза репрессора инициации
- Эукариоты
- Представление клеточного цикла в виде последовательности стадий
- Клеточный цикл млекопитающих
- Управление скоростью цикла и клеточная дифференцировка
- Эпидермис млекопитающих и кейлонная теория
- Вероятностные модели клеточного цикла и его управления
- Глава 4. КЛЕТОЧНЫЙ РОСТ, СИНХРОННОСТЬ КЛЕТОЧНЫХ ЦИКЛОВ И БИОЛОГИЧЕСКИЕ ЧАСЫ
- Хемостат
- Адаптивное поведение хемостата
- Системы восстановления клеток
- Синхронизация клеток
- Суточные ритмы деления клеток в тканях млекопитающих
- Контактное торможение
- Клеточные часы
- Физиология клеточных часов
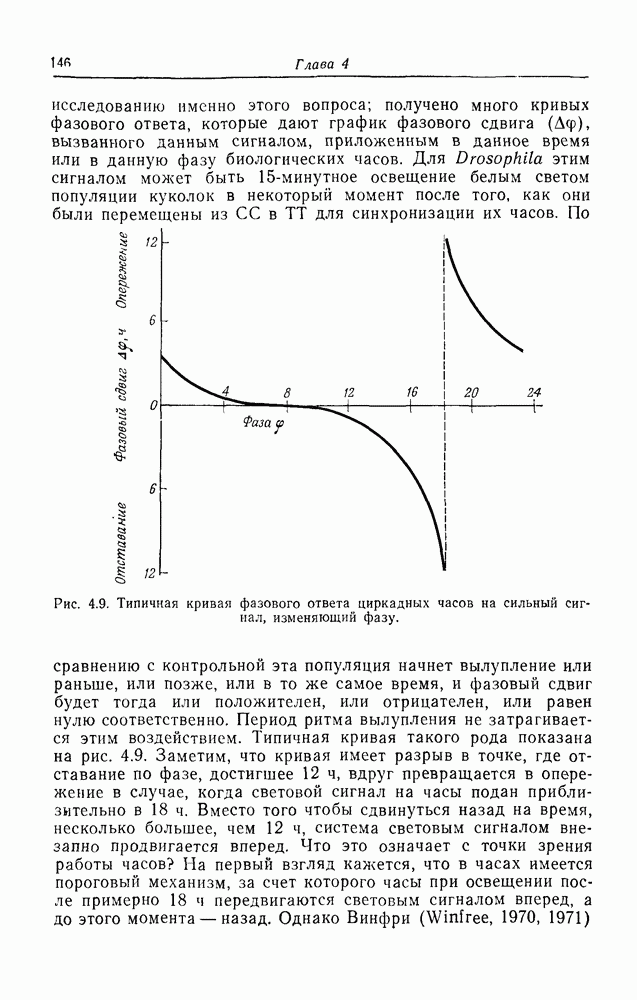
- Динамика часов, контролирующих вылупление личинок у Drosophila
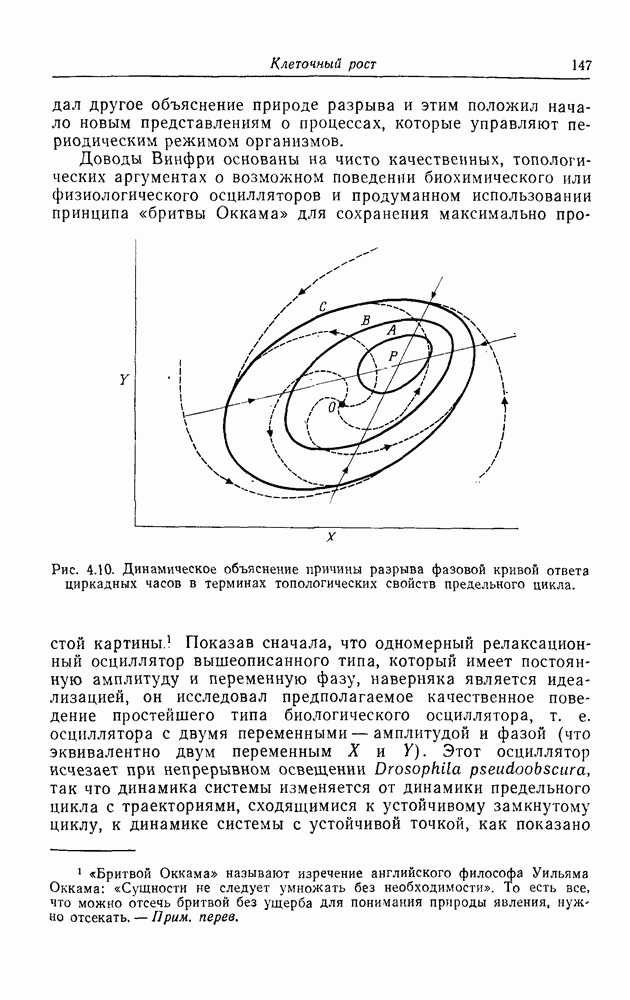
- Глава 5. МОРФОГЕНЕЗ: ОДНОМЕРНАЯ АПЕРИОДИЧЕСКАЯ УПОРЯДОЧЕННОСТЬ
- Полярность и осевые градиенты
- Пейсмекеры и волны активности
- Морфогенез одноклеточных
- Мембраны и морфогенез
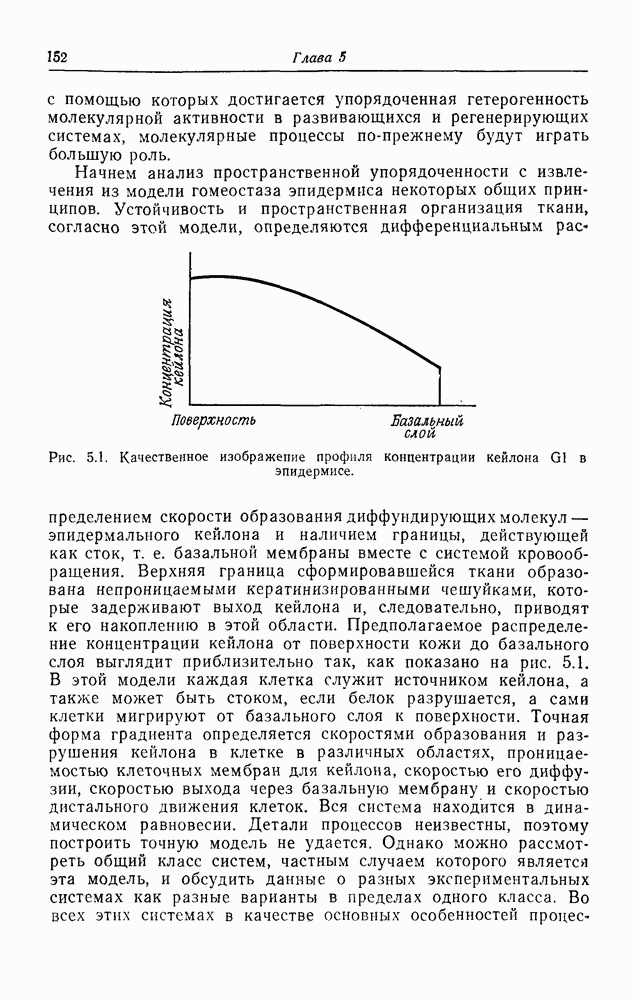
- Регуляция и устойчивость
- Периодические режимы у гидроидов
- Глава 6. МОРФОГЕНЕЗ: ПРОСТРАНСТВЕННЫЕ ПЕРИОДИЧНОСТИ И МНОГОМЕРНАЯ УПОРЯДОЧЕННОСТЬ
- Распространение волн и пространственные периодичности
- Эпидермис насекомых
- Мембрана и эпидермис насекомых
- Эпиморфоз: крыло цыпленка
- Волновая модель и эпиморфоз
- Локальная и глобальная упорядоченность: имагинальный диск и конечность таракана
- Ретино-тектальная проекция в зрительной системе амфибий
- Механизм образования двумерной проекции
- Глава 7. ОРГАНИЗМ КАК ПОЗНАЮЩАЯ И КООПЕРАТИВНАЯ СИСТЕМА
- Функциональная иерархия
- Обратные предельные системы
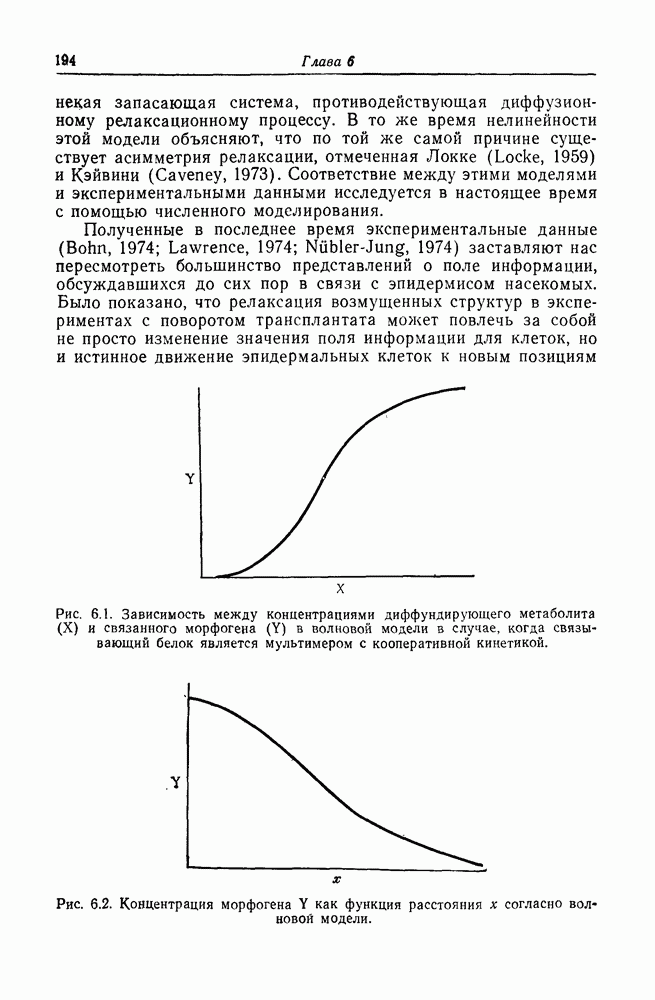
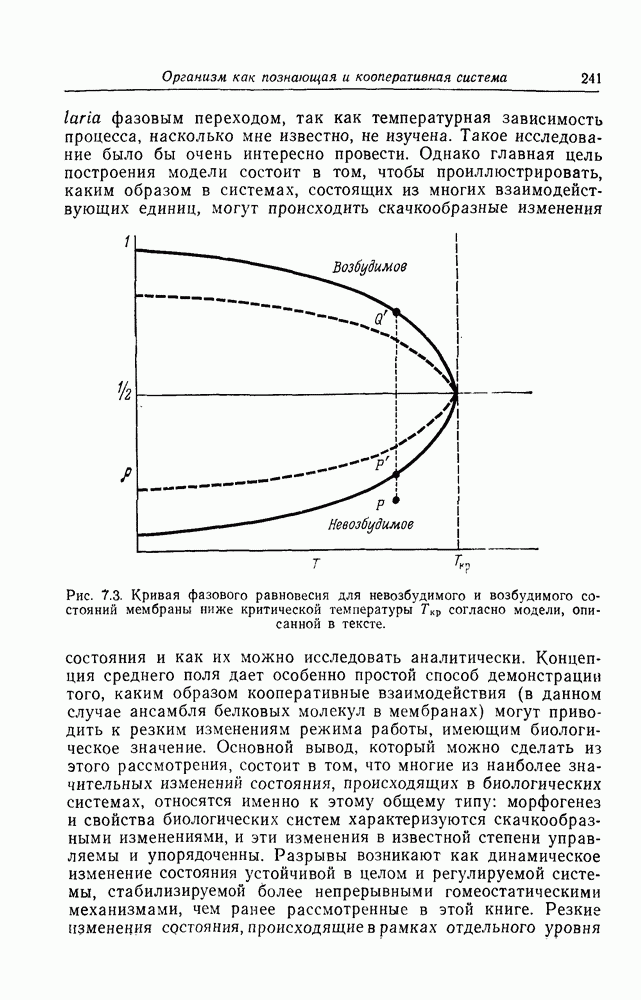
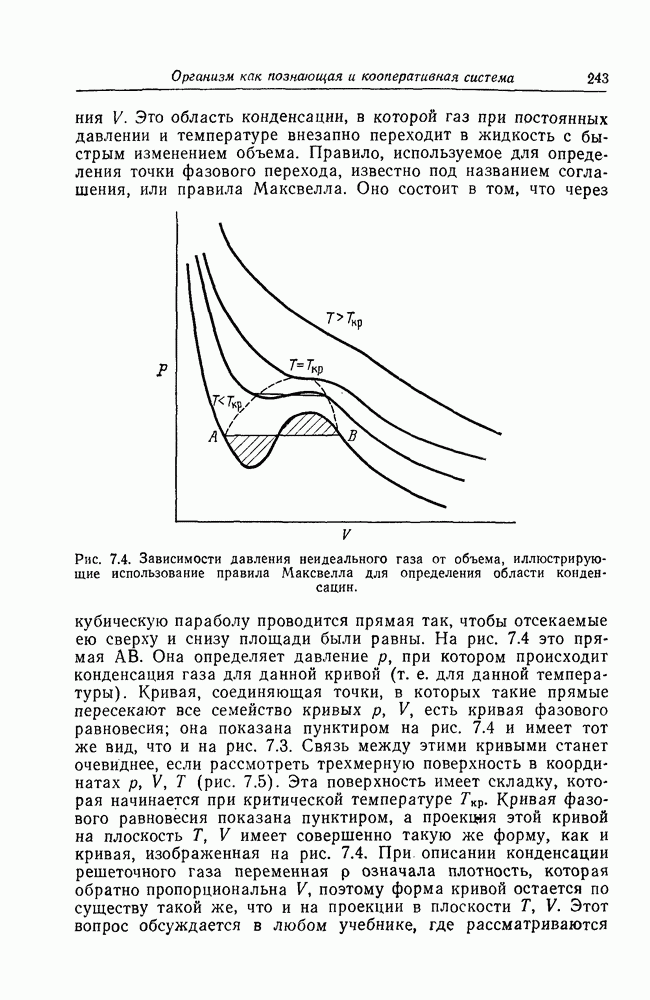
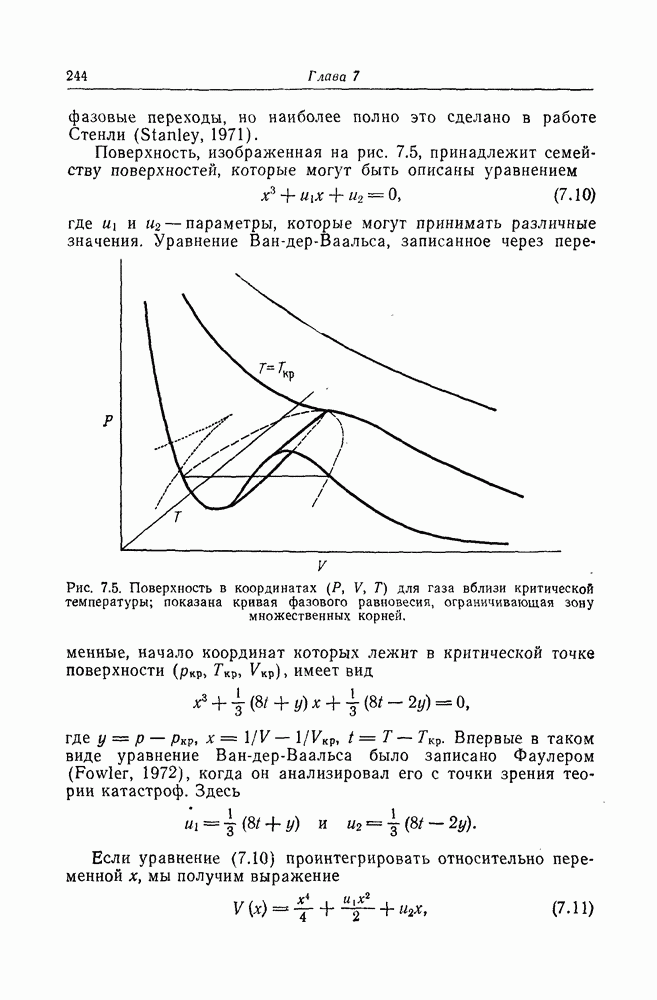
- Кооперативные взаимодействия и фазовые переходы в познающих системах
- Фазовые переходы и теория катастроф
- Коллективные моды в ритмических процессах
- Процессы генерации в познающих системах
- ПРИЛОЖЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ