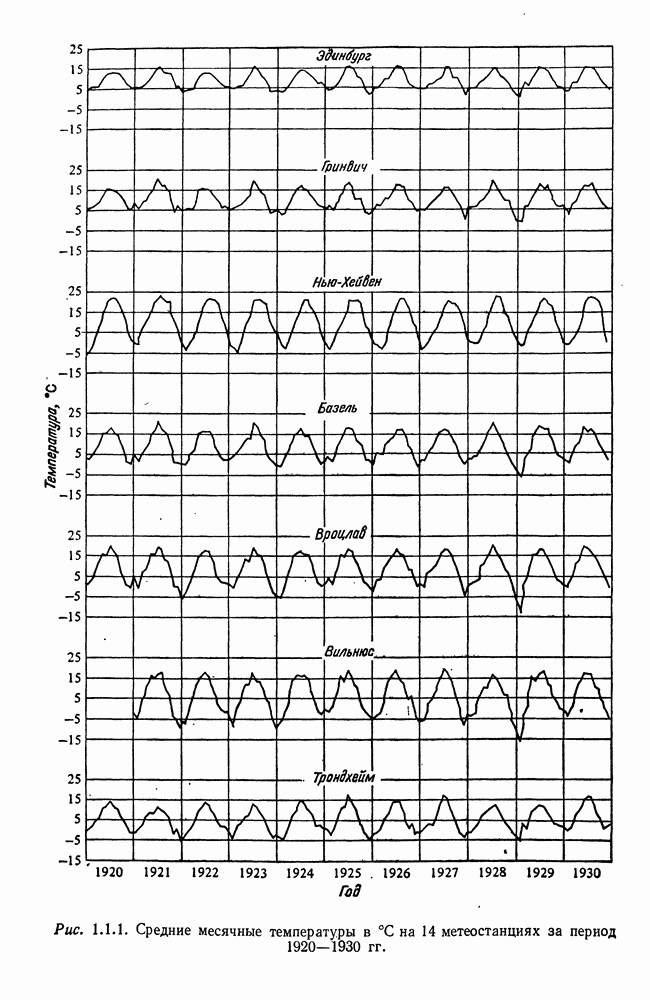
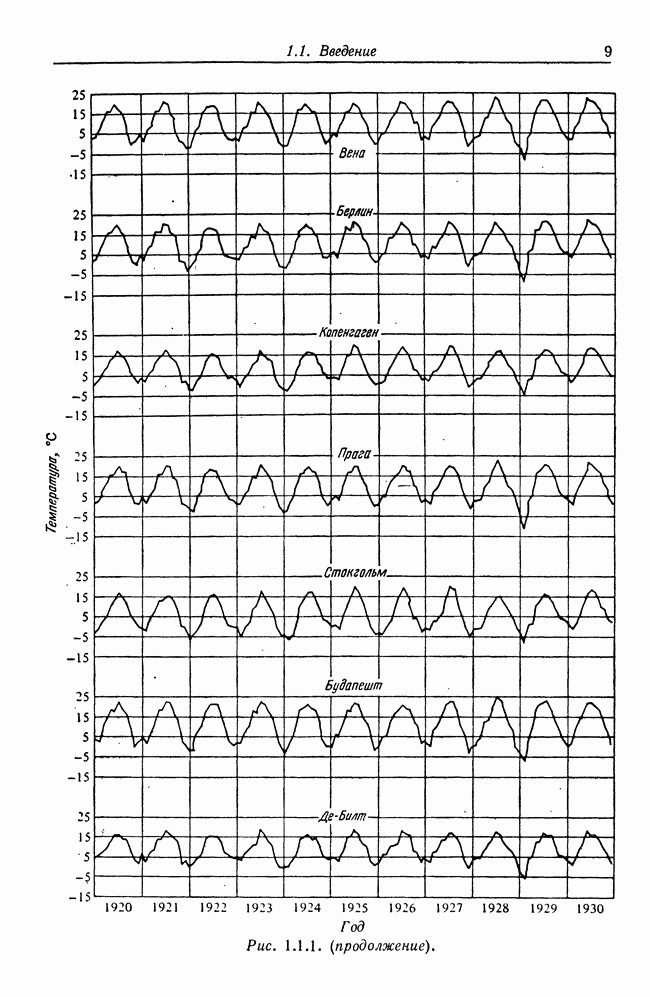
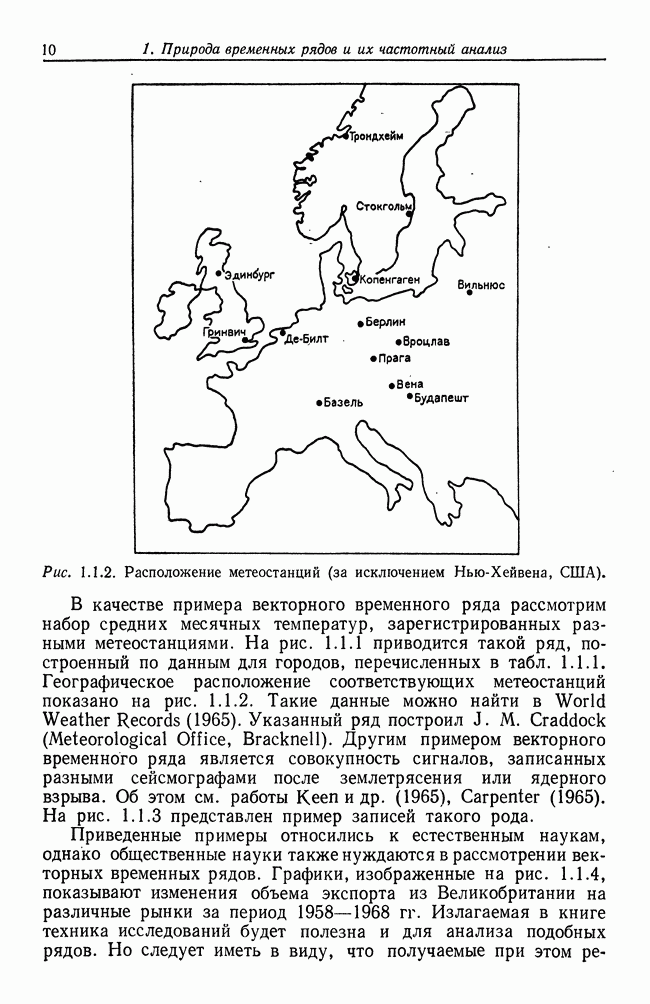
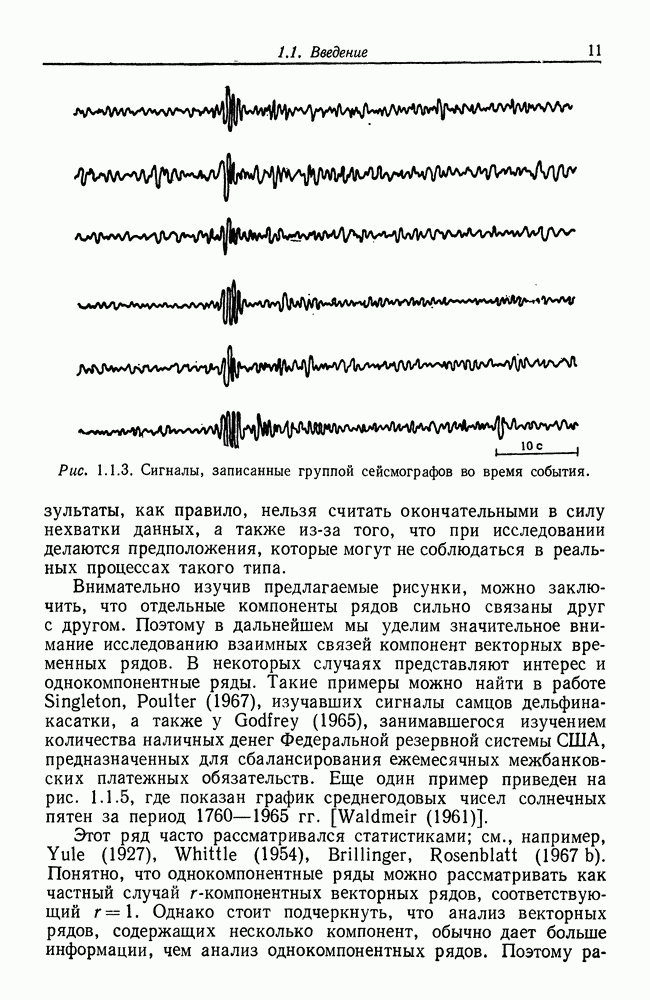
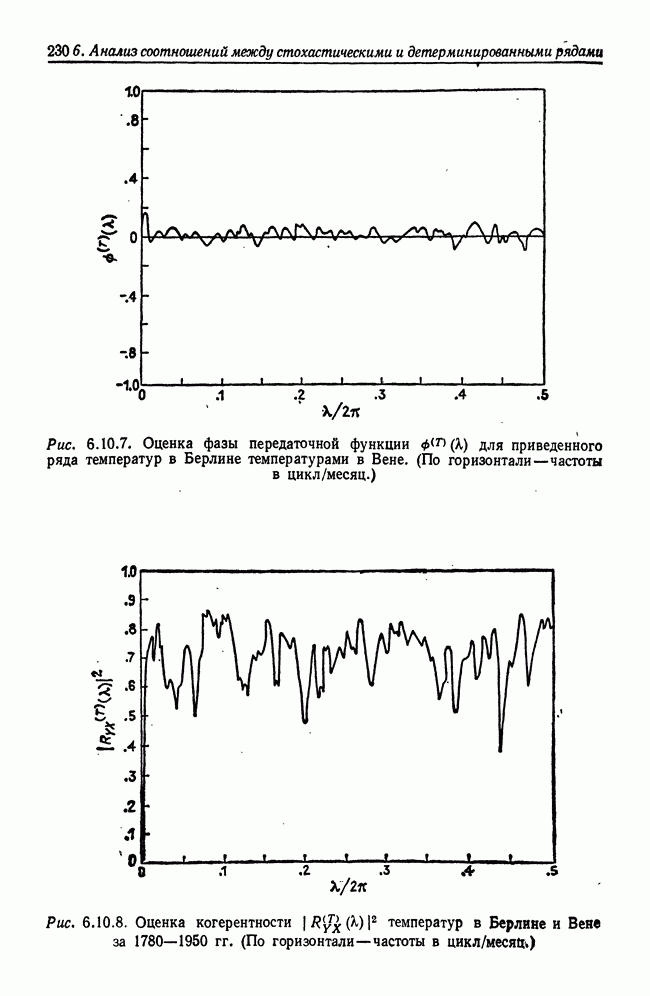
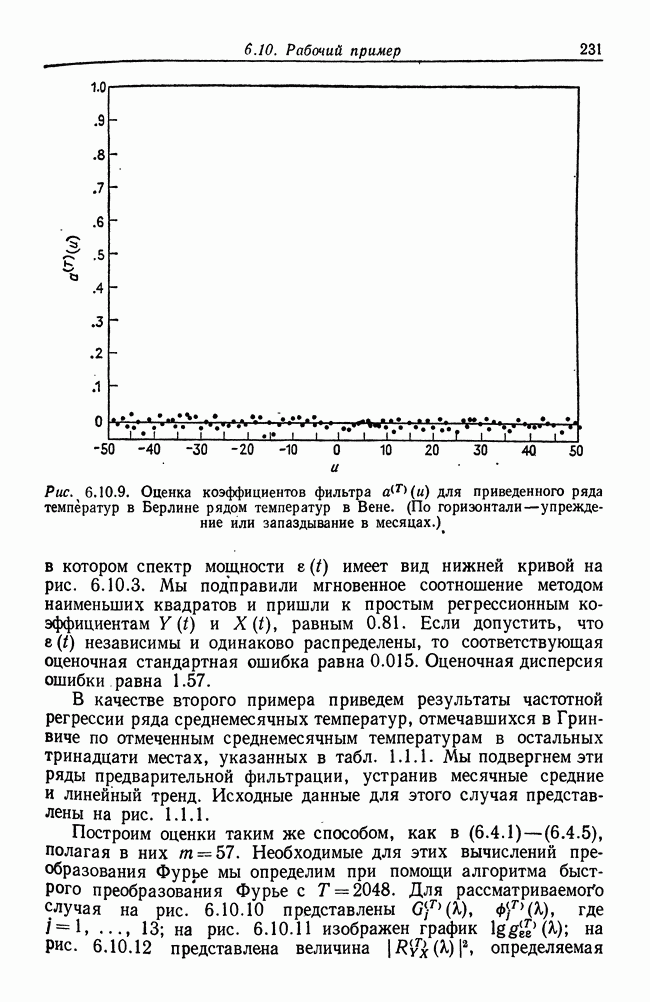
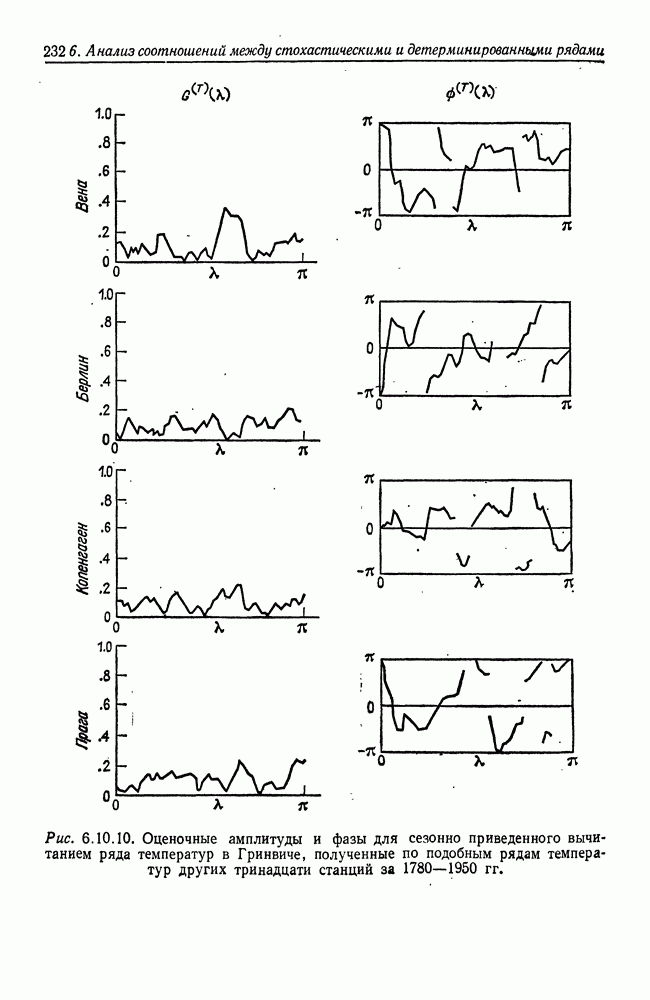
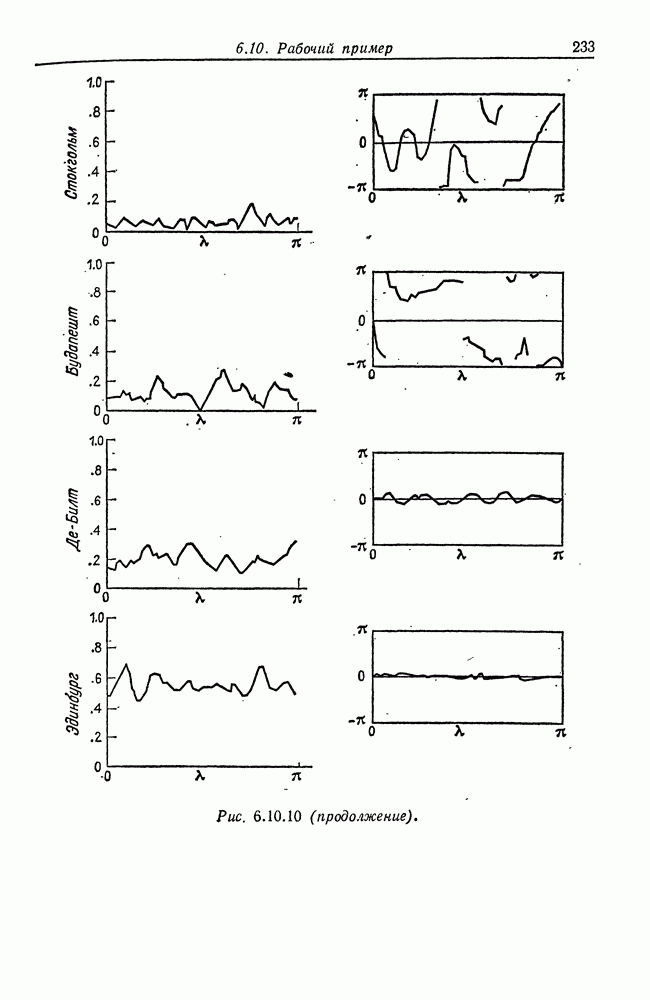
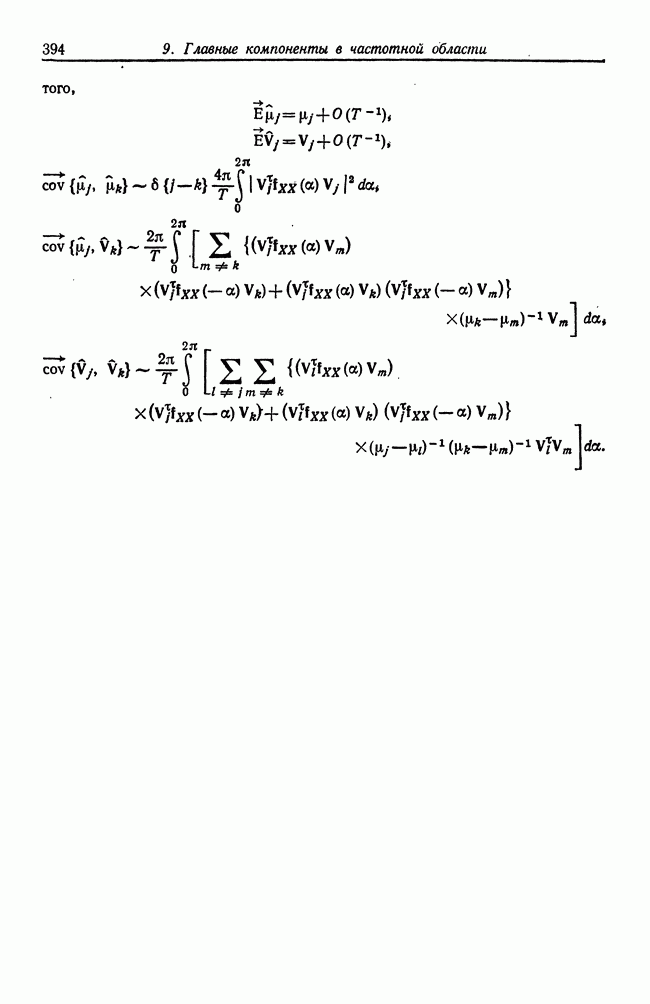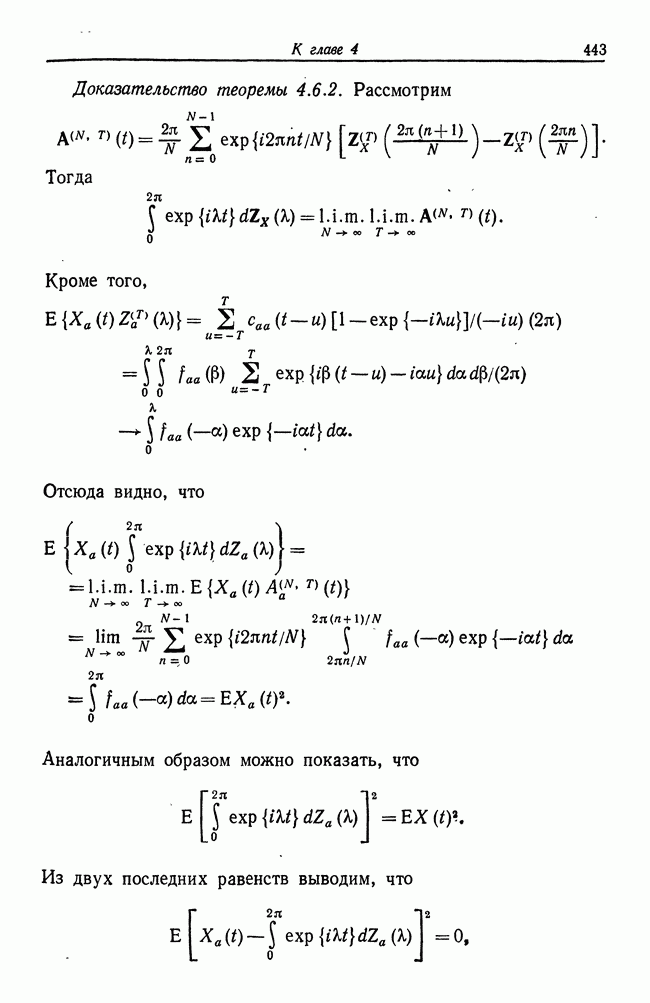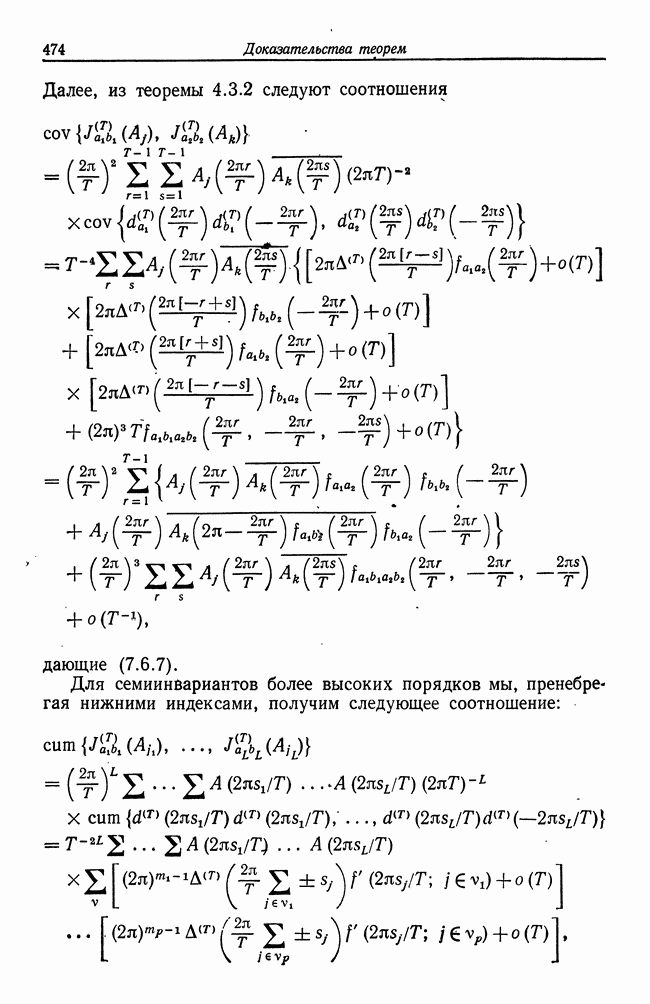| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДОКАЗАТЕЛЬСТВА ТЕОРЕМ
К главе 2
Доказательство теоремы 2.3.1. Следует непосредственно рассмотреть соответствующие коэффициенты ряда Тейлора и сравнить их с выражением (2.3.1).
Доказательство леммы 2.3.1. Начнем с необходимости условия. Если разбиение не будет неразложимым, то, согласно 2.3.5), разности  будут порождать только величины
будут порождать только величины  и не существует способа получить
и не существует способа получить  при
при 
Теперь о. достаточности условия. Предположим, что  порождают
порождают 
Но тогда любая пара  множеств разбиения окажется сообщающейся, иначе не порождалась бы разность
множеств разбиения окажется сообщающейся, иначе не порождалась бы разность  Тем самым показана неразложимость.
Тем самым показана неразложимость.
Продемонстрируем справедливость другой формулировки леммы. Если не выполнено свойство неразложимости разбиения, то, в силу (2.3.5),  порождают лишь разности —
порождают лишь разности —  и величины
и величины  , получить нельзя.
, получить нельзя.
С другой стороны, если  порождают все величины
порождают все величины  то должна существовать некоторая последовательность множеств
то должна существовать некоторая последовательность множеств  начинающаяся с i и кончающаяся Г; поэтому все множества сообщаются.
начинающаяся с i и кончающаяся Г; поэтому все множества сообщаются.
Доказательство теоремы 2.3.2. Проведем индукцию по  Согласно теореме 2.3.1, имеем при каждом
Согласно теореме 2.3.1, имеем при каждом 

где  и суммирование ведется по всем разбиениям
и суммирование ведется по всем разбиениям  множества
множества  Кроме того,
Кроме того,

где  обозначают пары целых чисел и суммирование распространяется на все разбиения множества
обозначают пары целых чисел и суммирование распространяется на все разбиения множества 
Из  видим, что
видим, что

Здесь  берется по всем разбиениям с
берется по всем разбиениям с  . Тем самым в этом выражении члены, соответствующие разложимым разбиениям, будут вычитаться, откуда и вытекает утверждение.
. Тем самым в этом выражении члены, соответствующие разложимым разбиениям, будут вычитаться, откуда и вытекает утверждение.
Доказательство теоремы 2.5.1. Будем писать  , подразумевая, что матрица А неотрицательно определенная. То обстоятельство, что
, подразумевая, что матрица А неотрицательно определенная. То обстоятельство, что  - эрмитова матрица, следует из (2.5.7) и равенства
- эрмитова матрица, следует из (2.5.7) и равенства  .
.
Далее можно предположить, что  Рассмотрим
Рассмотрим

По построению  и тем самым
и тем самым  . Математическое ожидание
. Математическое ожидание

представляет собой среднее Чезаро для ряда  Из условий теоремы вытекает, что этот ряд сходится, поэтому из упр. 1.7.10 получаем, что
Из условий теоремы вытекает, что этот ряд сходится, поэтому из упр. 1.7.10 получаем, что

и, следовательно, 
Доказательство теоремы 2.5.2. Пусть  Рассмотрим
Рассмотрим 

при  По построению Далее введем
По построению Далее введем

Заметим, что и  Из
Из  получаем
получаем

при  Последовательность
Последовательность

матричных мер заключена между  Обобщение теоремы Хелли о выборе показывает, что эта последовательность содержит подпоследовательность, слабо сходящуюся к некоторой матричной мере. Обозначим через
Обобщение теоремы Хелли о выборе показывает, что эта последовательность содержит подпоследовательность, слабо сходящуюся к некоторой матричной мере. Обозначим через  предел такой сходящейся подпоследовательности
предел такой сходящейся подпоследовательности  . Аппроксимируя интегралы конечными суммами, убеждаемся, что
. Аппроксимируя интегралы конечными суммами, убеждаемся, что

Помимо этого, из  следует, что предел семейства интегралов равен
следует, что предел семейства интегралов равен  Отсюда получается (2.5.8).
Отсюда получается (2.5.8).
Выражение (2.5.9) вытекает из обычной формулы обращения преобразования Фурье—Стилтьеса. Приращения  по построению 0.
по построению 0.
Доказательство леммы 2.7.1. Исйользуя свойства линейности и временной инвариантности, получаем

Полагая  имеем
имеем

т. е. (2.7.6), где 
Доказательство леммы 2.7.2. Указанные свойства — это стандартные результаты, относящиеся к преобразованию Фурье абсолютно суммируемых последовательностей; см., например, Zygmund (1968).
Доказательство леммы 2.7.3. Отметим, что

следовательно,

так что сумма  конечна с вероятностью 1. Стационарность ряда
конечна с вероятностью 1. Стационарность ряда  вытекает из временной инвариантности операции.
вытекает из временной инвариантности операции.
Далее мы получим неравенства

завершающие доказательство.
Доказательство теоремы 2.7.1. Введем

для  Суммирование слагаемых с
Суммирование слагаемых с  обозначим символом
обозначим символом  . Тогда при
. Тогда при  найдется некоторая константа К, такая, что
найдется некоторая константа К, такая, что

Выражение справа стремится к 0 при  согласно (2.7.23). Значит, последовательность
согласно (2.7.23). Значит, последовательность  является последовательностью Коши, и предел (2.7.25) существует в силу полноты.
является последовательностью Коши, и предел (2.7.25) существует в силу полноты.
Доказательство леммы 2.7.4. Обозначив

видим, что операции действительно линейны и инвариантны во времени. Полагая

убеждаемся в справедливости (2.7.34) и (2.7.35).
Доказательство теоремы 2.8.1. Векторный ряд  с
с  компонентами строго стационарен и имеет кумулянтные спектры
компонентами строго стационарен и имеет кумулянтные спектры  , где
, где  - коэффициенты
- коэффициенты
 -фильтра, такого, что
-фильтра, такого, что  По лемме 2.7.3 ряд
По лемме 2.7.3 ряд  тоже строго стационарен и существуют его кумулянтные функции
тоже строго стационарен и существуют его кумулянтные функции  Тогда
Тогда

где

Поскольку  абсолютно суммируемы, из теоремы Фубини вытекает абсолютная суммируемость ряда
абсолютно суммируемы, из теоремы Фубини вытекает абсолютная суммируемость ряда  Следовательно,
Следовательно,

Оправдано будет и изменение порядка усреднения и суммирования, позволяющее перейти от  Теперь функция
Теперь функция  представима как сумма сверток абсолютно суммируемых функций, а потому сама абсолютно суммируема. Значит, ряд
представима как сумма сверток абсолютно суммируемых функций, а потому сама абсолютно суммируема. Значит, ряд  удовлетворяет условию 2.6.1. Выражение (2.8.1) мы получим, применив преобразование Фурье к кумулянтной функции ряда
удовлетворяет условию 2.6.1. Выражение (2.8.1) мы получим, применив преобразование Фурье к кумулянтной функции ряда  и воспользовавшись при этом тем, что рассматривается сумма сверток.
и воспользовавшись при этом тем, что рассматривается сумма сверток.
Доказательство леммы 2.9.1. Если  - марковский гауссовский ряд, то
- марковский гауссовский ряд, то  не зависит
не зависит  Поэтому
Поэтому  а так как
а так как  где К — константа, то
где К — константа, то

Это показывает, что

Для завершения доказательства остается заметить, что 
Доказательство теоремы 2.9.1. Начнем с того, что при сделанных предположениях  существует с вероятностью 1, так как
существует с вероятностью 1, так как

Рассмотрим далее

Кумулянты, зависящие от значений X, согласно теореме 2.3.2, являются суммами произведений совместных кумулянтов величин  . Суммы эти берутся по неразложимым разбиениям и имеют вид
. Суммы эти берутся по неразложимым разбиениям и имеют вид

Поскольку ряд стационарен, кумулянты зависят только от разностей  . В силу леммы 2.3.1, среди разностей
. В силу леммы 2.3.1, среди разностей  будет
будет  независимых. Пусть для определенности это
независимых. Пусть для определенности это  Полагая
Полагая  мы видим теперь, что
мы видим теперь, что

где g — абсолютно суммируемая функция своих аргументов. Сделав замену переменных

убеждаемся, что кумулянты ряда  абсолютно суммируемы.
абсолютно суммируемы.
Доказательство теоремы 2.10.1. Мы несколько предвосхитим дальнейшее изложение материала. В § 4.6 будет показано, что можно представить ряды в виде

где

Подстановка этих выражений в (2.9.15) показывает, что

Теперь, применив теорему 2.3.2 и воспользовавшись выписанными выражениями, получаем нужную нам формулу (2.10.10).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ПРИРОДА ВРЕМЕННЫХ РЯДОВ И ИХ ЧАСТОТНЫЙ АНАЛИЗ
- 1.2. Основания для применения гармонического анализа
- 1.3. Перемешивание
- 1.4. Исторический обзор
- 1.5. Применение частотного анализа
- 1.6. Заключительные замечания
- 1.7. Упражнения
- 2. ОСНОВНЫЕ ПОНЯТИЯ
- 2.2. Стохастические процессы
- 2.3. Кумулянты
- 2.4. Стационарность
- 2.5. Спектр второго порядка
- 2.6. Кумулянтные спектры порядка k
- 2.7. Фильтры
- 2.8. Инвариантные свойства кумулянтного спектра
- 2.9. Примеры стационарных временных рядов
- 2.10. Примеры кумулянтного спектра
- 2.11. Функциональный и стохастический подходы к анализу временных рядов
- 2.12. Тренды
- 2.13. Упражнения
- 3. АНАЛИТИЧЕСКИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ И КОМПЛЕКСНЫЕ МАТРИЦЫ
- 3.2. Ряд Фурье
- 3.3. Множители, улучшающие сходимость
- 3.4. Конечные преобразования Фурье и их свойства
- 3.5. Быстрое преобразование Фурье
- 3.6. Применения дискретного преобразования Фурье
- 3.7. Комплексные матрицы и их экстремальные значения
- 3.8. Функции от преобразования Фурье
- 3.9. Спектральные представления при функциональном подходе к анализу временных рядов
- 3.10. Упражнения
- 4. СТОХАСТИЧЕСКИЕ СВОЙСТВА КОНЕЧНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 4.2. Комплексное нормальное распределение
- 4.3. Стохастические свойства конечного преобразования Фурье
- 4.4. Асимптотическое распределение конечного преобразования Фурье
- 4.5. Оценки, имеющие место с вероятностью 1
- 4.6. Представление Крамера
- 4.7. Анализ главных компонент и его связь с представлением Крамера
- 4.8. Упражнения
- 5. ОЦЕНКА СПЕКТРА МОЩНОСТИ
- 5.2. Периодограмма
- 5.3. Дальнейшее изучение периодограммы
- 5.4. Сглаженная периодограмма
- 5.5. Общий класс спектральных оценок
- 5.6. Состоятельные оценки
- 5.7. Доверительные интервалы
- 5.8. Смещения и предварительная фильтрация
- 5.9. Другие оценки спектра мощности
- 5.10. Оценки спектральной меры и ковариационной функции
- 5.11. Отступление от принятых предположений
- 5.12. Использование анализа спектров мощности
- 5.13. Упражнения
- 6. АНАЛИЗ ИНВАРИАНТНЫХ ВО ВРЕМЕНИ ЛИНЕЙНЫХ СООТНОШЕНИЙ МЕЖДУ СТОХАСТИЧЕСКИМИ И НЕКОТОРЫМИ ДЕТЕРМИНИРОВАННЫМИ РЯДАМИ
- 6.2. Метод наименьших квадратов и регрессионная теория
- 6.3. Эвристическое построение оценок
- 6.4. Вид асимптотического распределения
- 6.5. Математические ожидания оценок передаточной функции и спектра ошибок
- 6.6. Асимптотические ковариации предложенных оценок
- 6.7. Асимптотическая нормальность оценок
- 6.8. Оценивание импульсной характеристики
- 6.9. Доверительные области
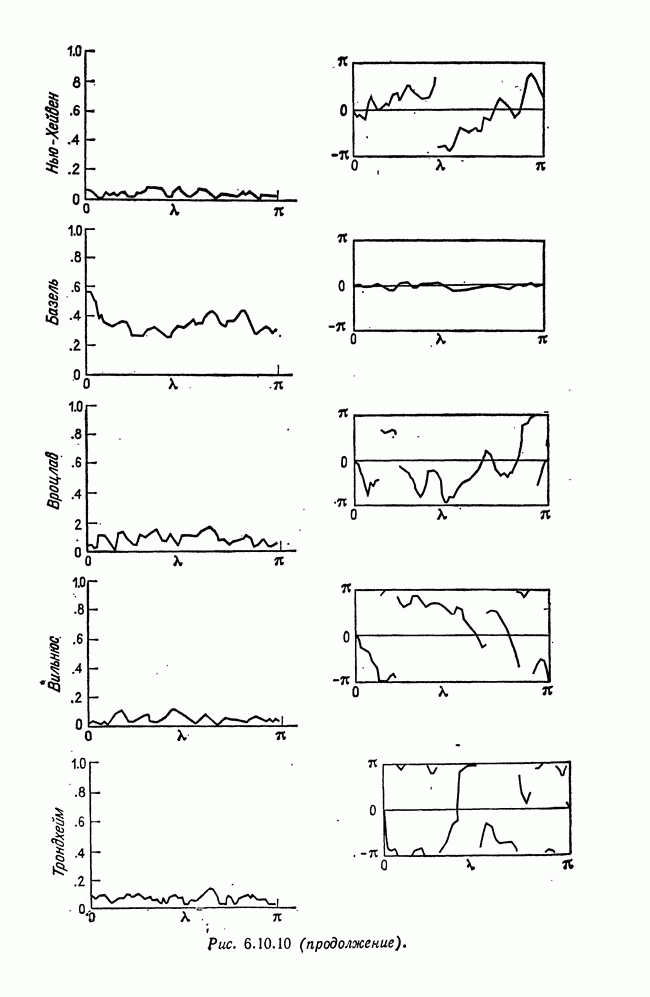
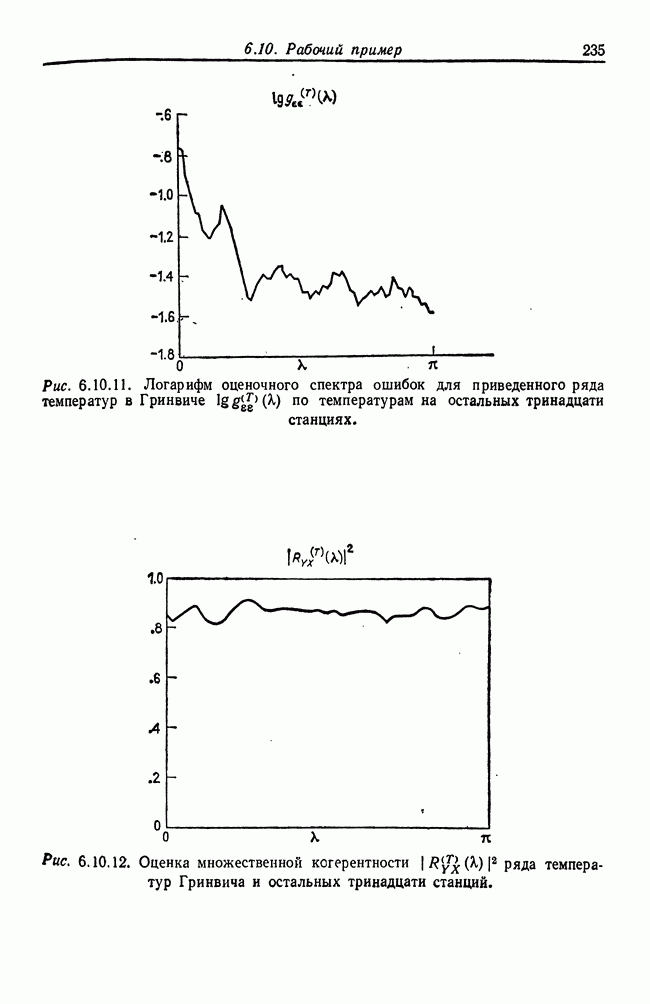
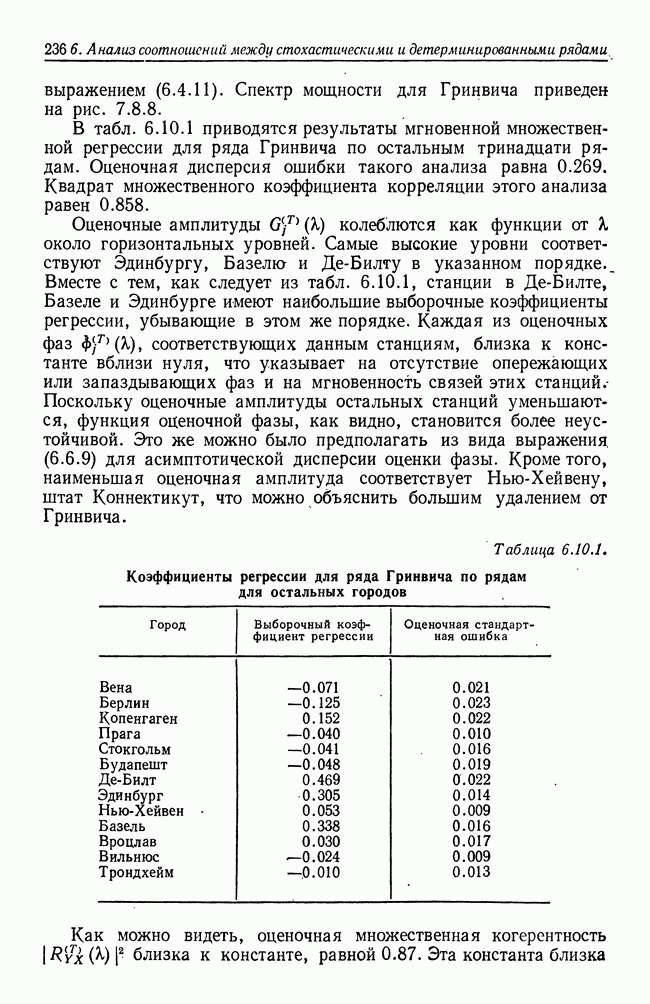
- 6.10. Рабочий пример
- 6.11. Дальнейшие исследования
- 6.12. Сравнение трех оценок импульсной характеристики
- 6.13. Использование предложенных методов
- 6.14. Упражнения
- 7. ОЦЕНКИ СПЕКТРА ВТОРОГО ПОРЯДКА МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
- 7.2. Периодограммы второго порядка
- 7.3. Оценка матрицы спектральной плотности путем осреднения периодограммы
- 7.4. Состоятельные оценки матрицы спектральной плотности
- 7.5. Построение доверительных границ
- 7.6. Оценки родственных величин
- 7.7. Дальнейшее развитие оценок спектра второго порядка
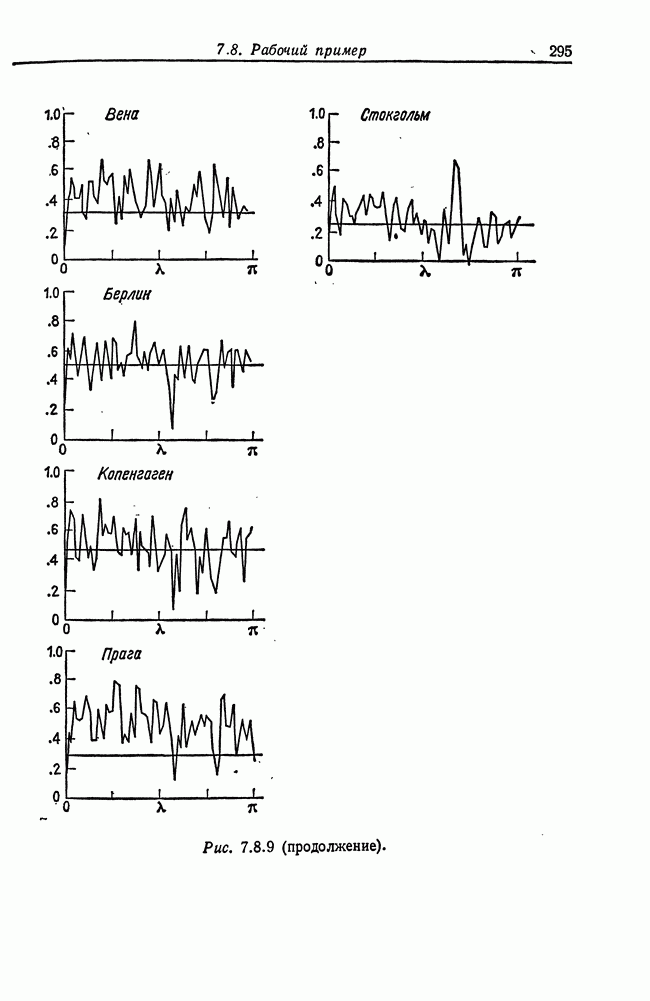
- 7.8. Рабочий пример
- 7.9. Изучение рядов, встречающихся в планировании эксперимента
- 7.10. Упражнения
- 8. АНАЛИЗ ЛИНЕЙНЫХ ИНВАРИАНТНЫХ ВО ВРЕМЕНИ СООТНОШЕНИЙ МЕЖДУ ДВУМЯ МНОГОМЕРНЫМИ СТОХАСТИЧЕСКИМИ РЯДАМИ
- 8.2. Результаты для многомерных случайных величин
- 8.3. Определение оптимального линейного фильтра
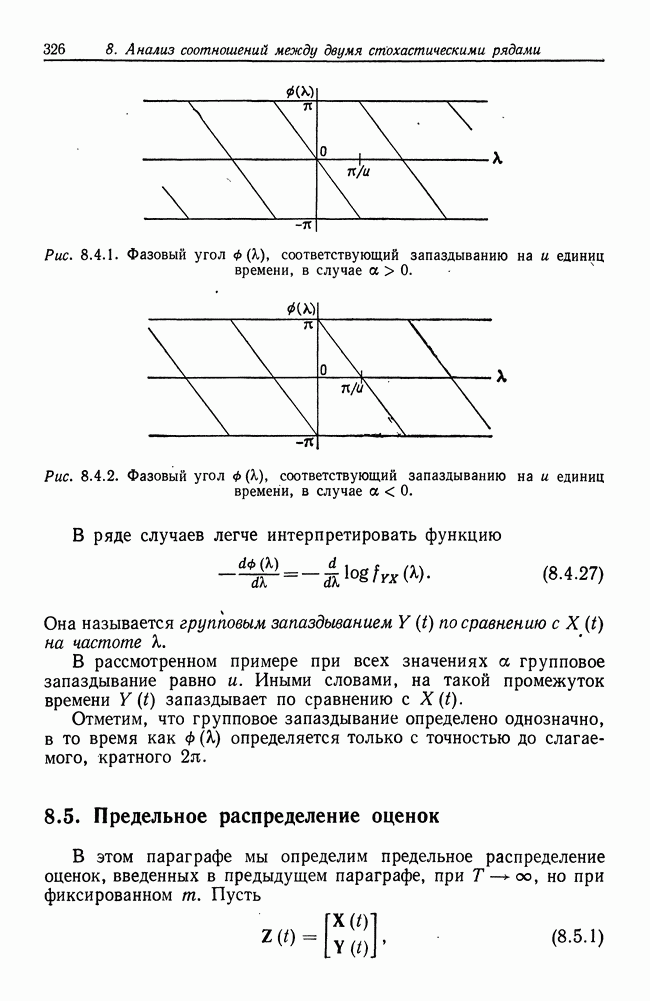
- 8.4. Эвристическая интерпретация параметров и построение оценок
- 8.5. Предельное распределение оценок
- 8.6. Класс состоятельных оценок
- 8.7. Асимптотические моменты второго порядка рассмотренных оценок
- 8.8. Асимптотическое распределение оценок
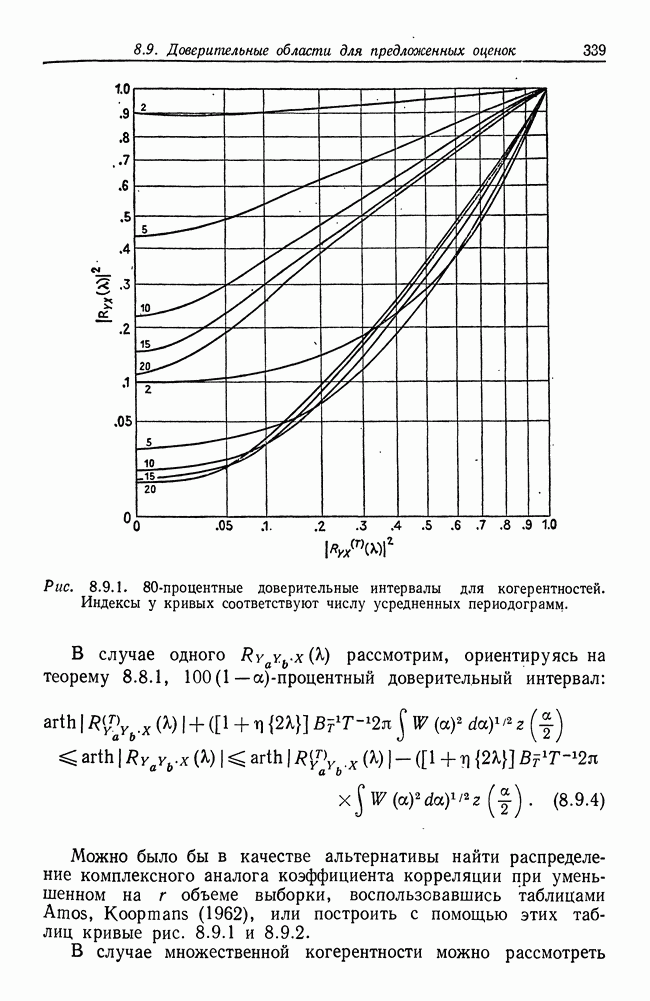
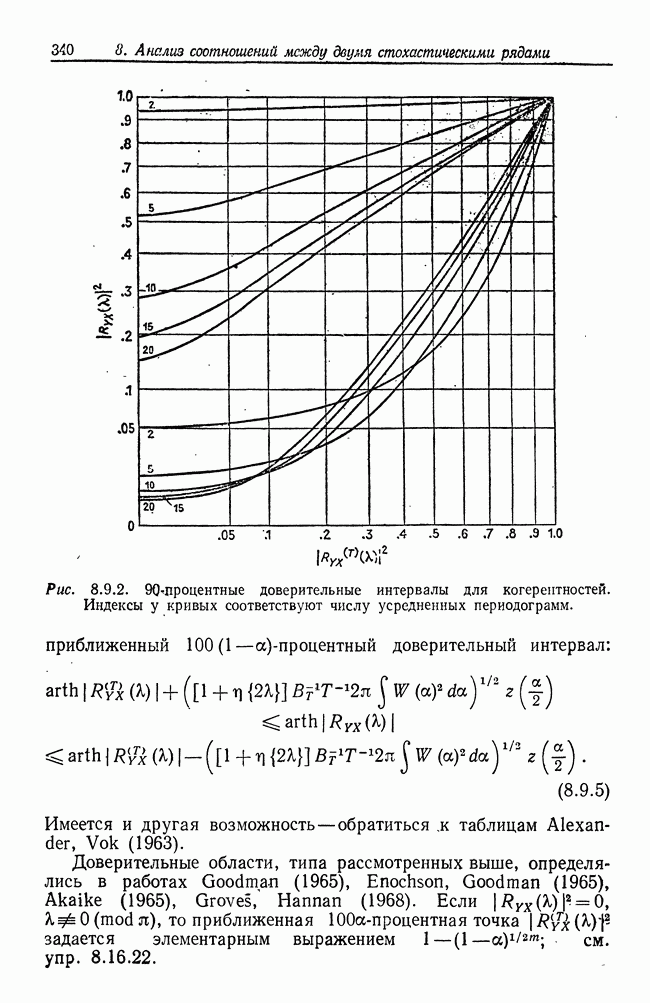
- 8.9. Доверительные области для предложенных оценок
- 8.10. Оценки коэффициентов фильтра
- 8.11. Оценки отклонений, имеющие место с вероятностью 1
- 8.12. Дальнейшее обсуждение
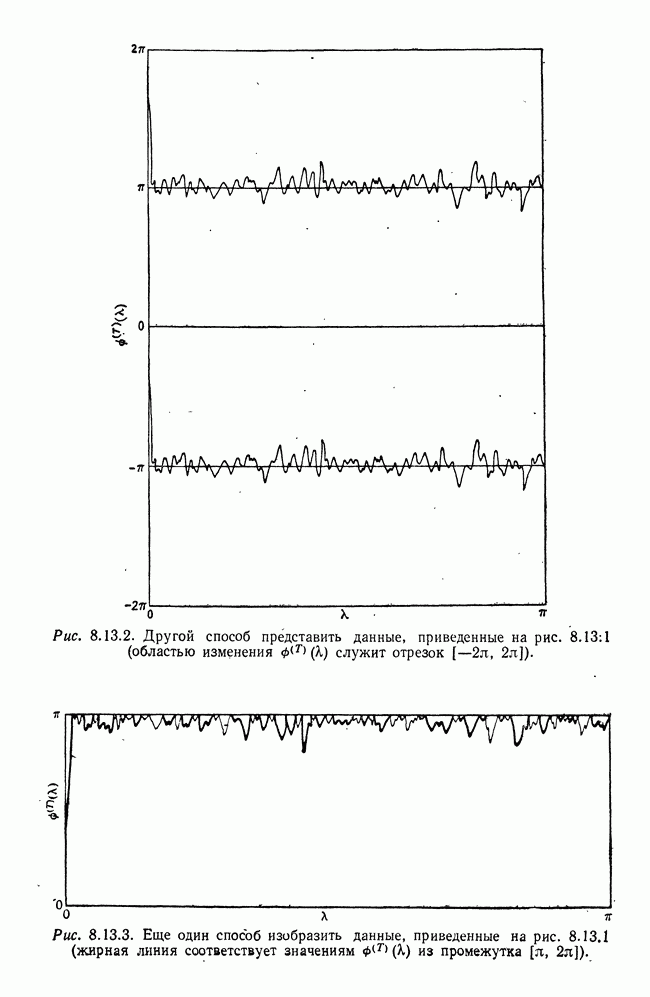
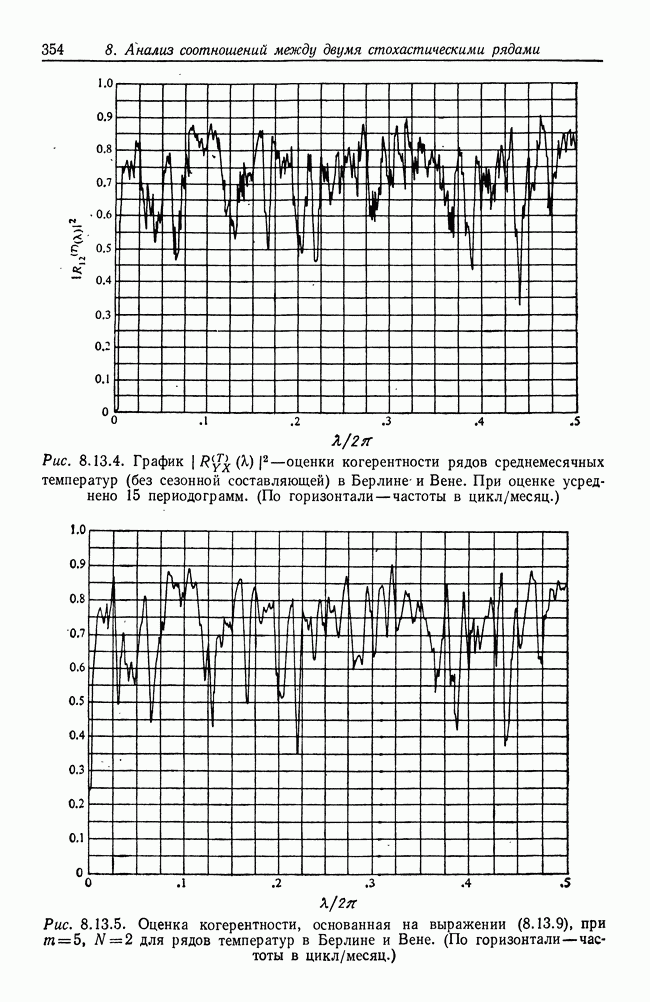
- 8.13. Другие типы оценок
- 8.14. Рабочий пример
- 8.15. Применения материала настоящей главы
- 8.16. Упражнения
- 9. ГЛАВНЫЕ КОМПОНЕНТЫ В ЧАСТОТНОЙ ОБЛАСТИ
- 9.2. Анализ главных компонент векторных величин
- 9.3. Ряды главных компонент
- 9.4. Построение оценок и их асимптотические свойства
- 9.5. Дальнейшие свойства главных компонент
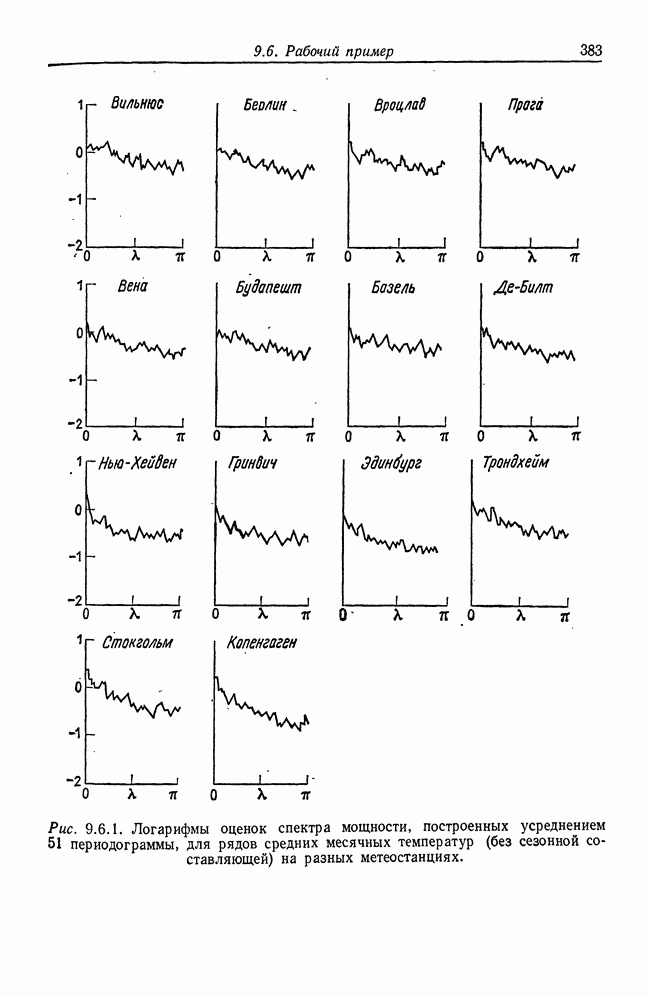
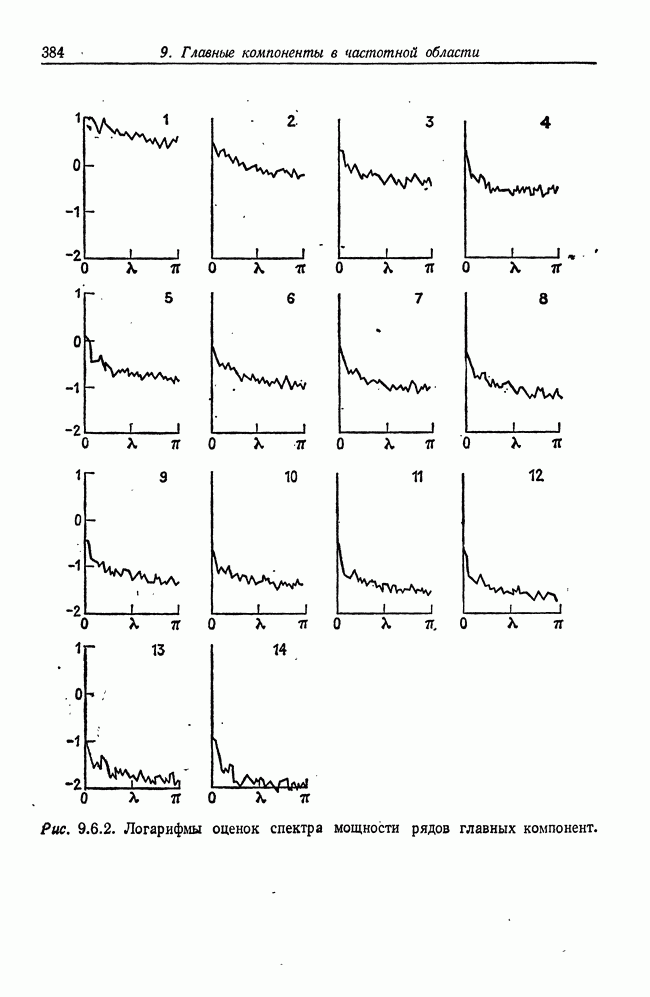
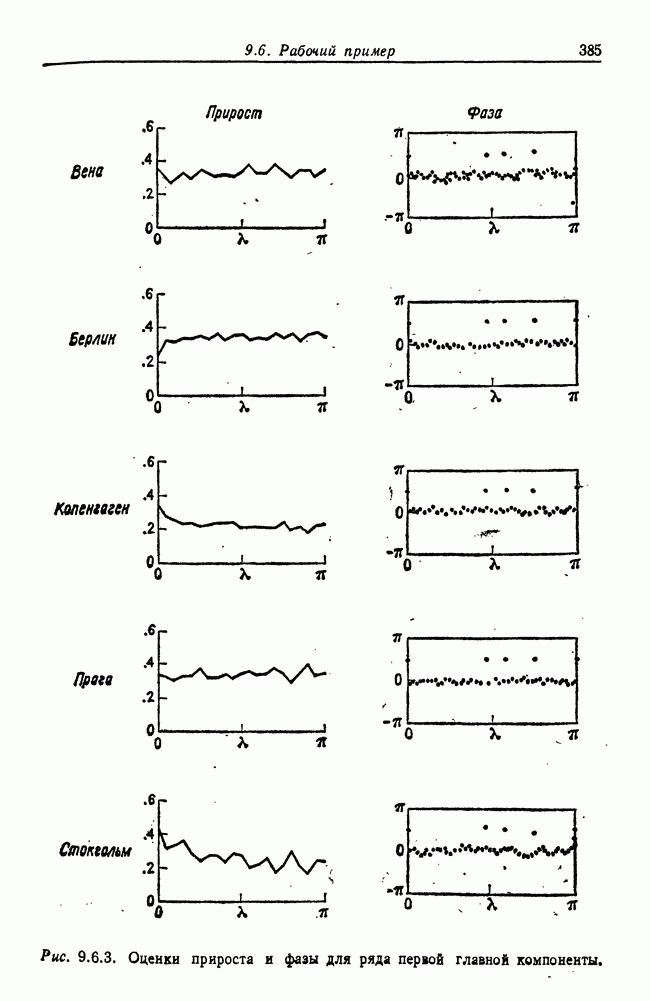
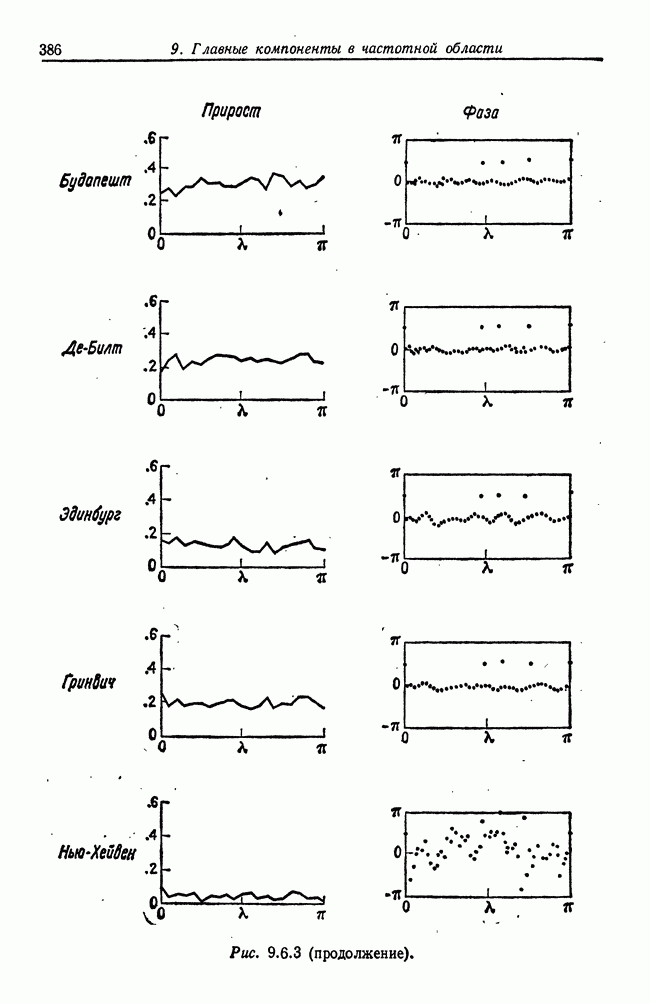
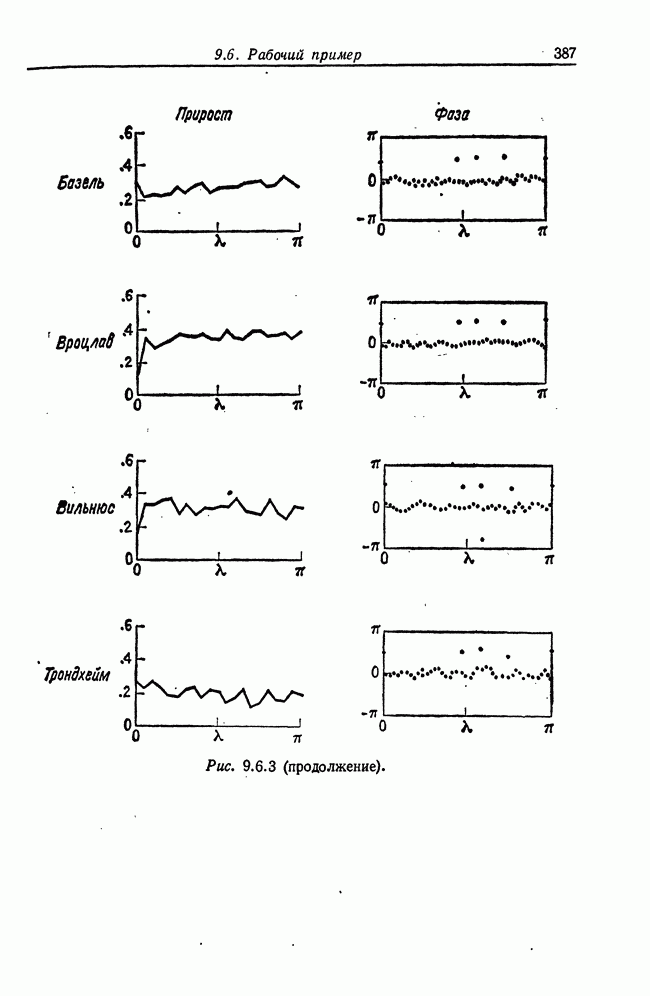
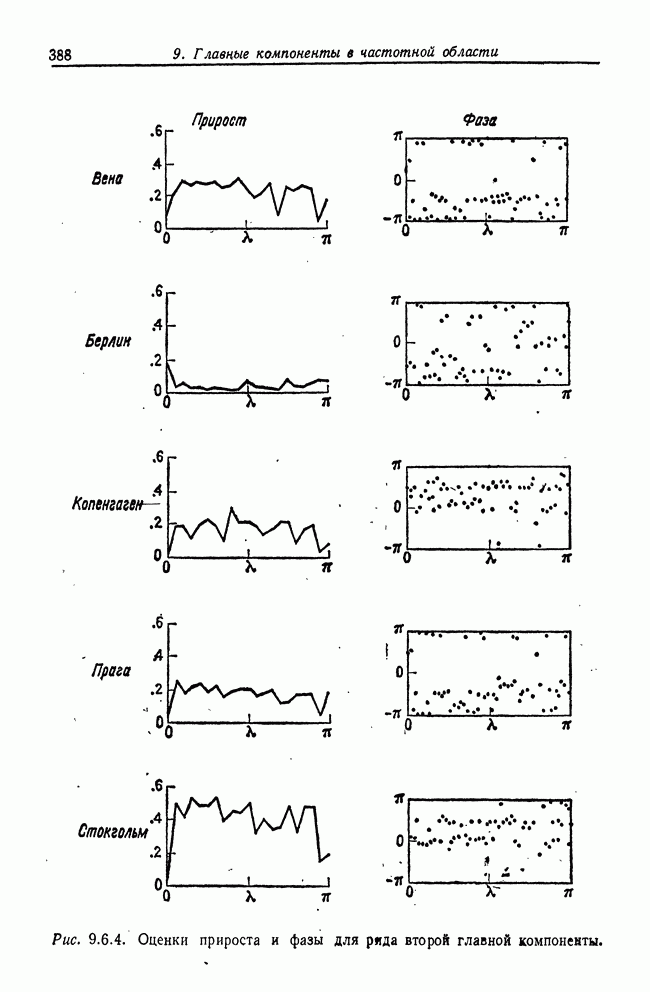
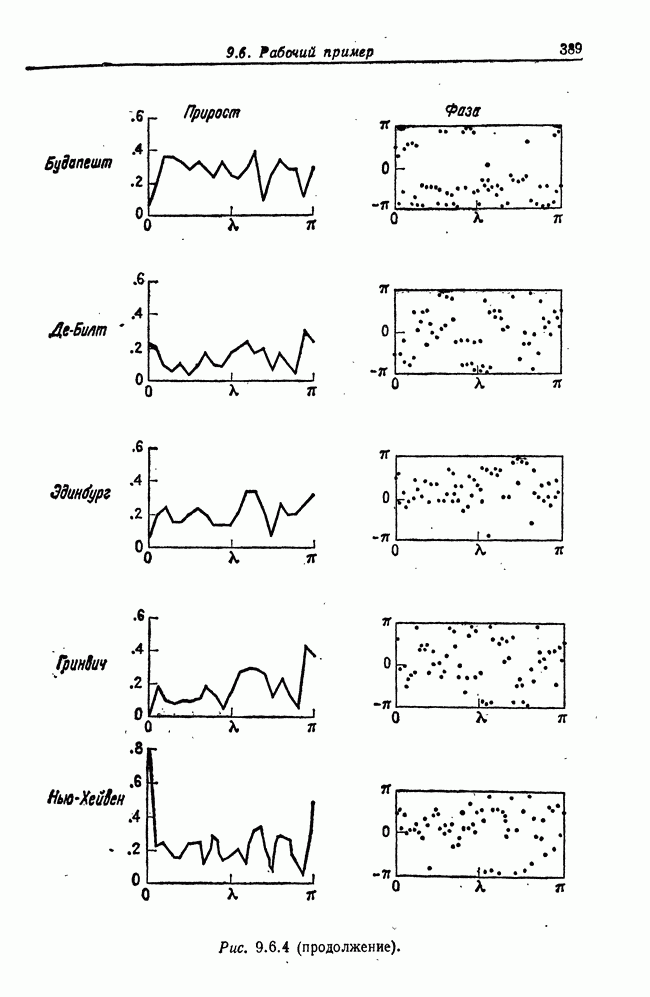
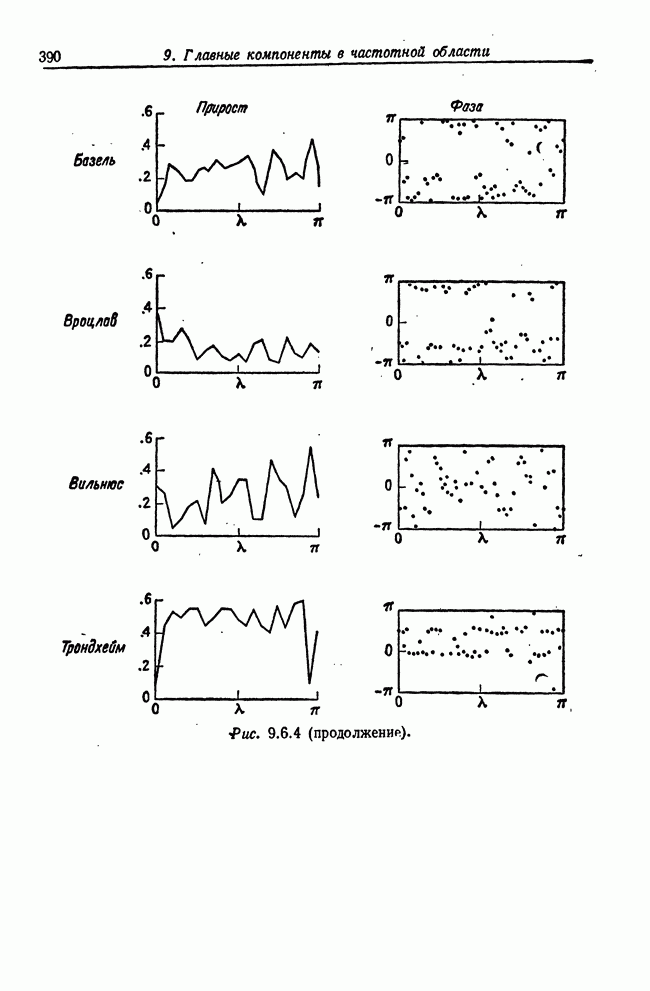
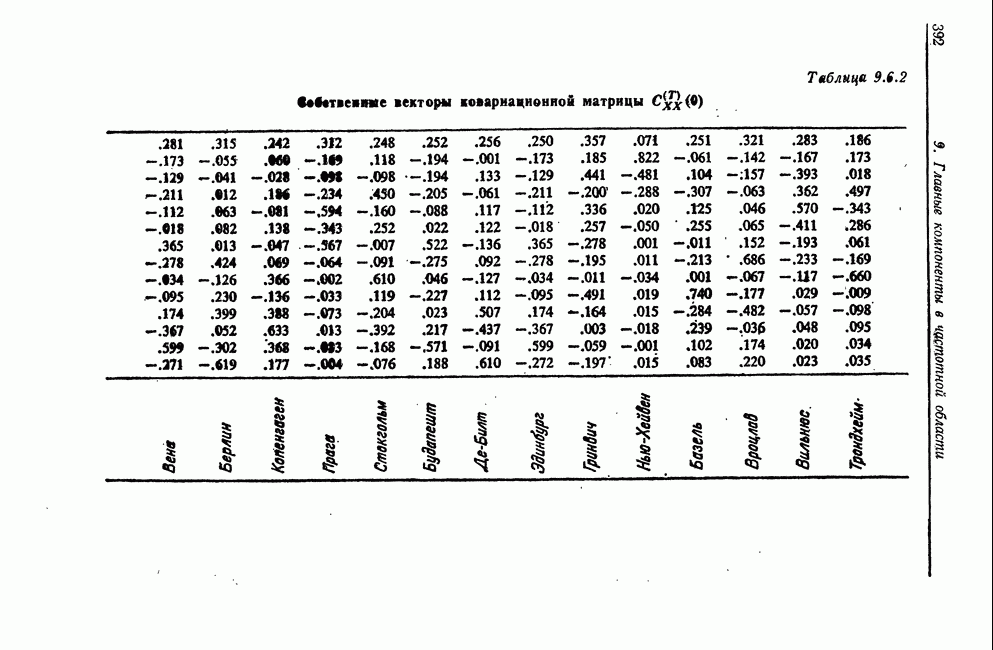
- 9.6. Рабочий пример
- 9.7. Упражнения
- 10. КАНОНИЧЕСКИЙ АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
- 10.2. Канонический анализ векторных случайных величин
- 10.3 Ряды канонических переменных
- 10.4. Построение оценок и их асимптотические свойства
- 10.5. Дальнейшие свойства канонических переменных
- 10.6. Упражнения
- ДОКАЗАТЕЛЬСТВА ТЕОРЕМ
- К главе 3
- К главе 4
- К главе 5
- К главе 6
- К главе 7
- К главе 8
- К главе 9
- К главе 10
- Список литературы