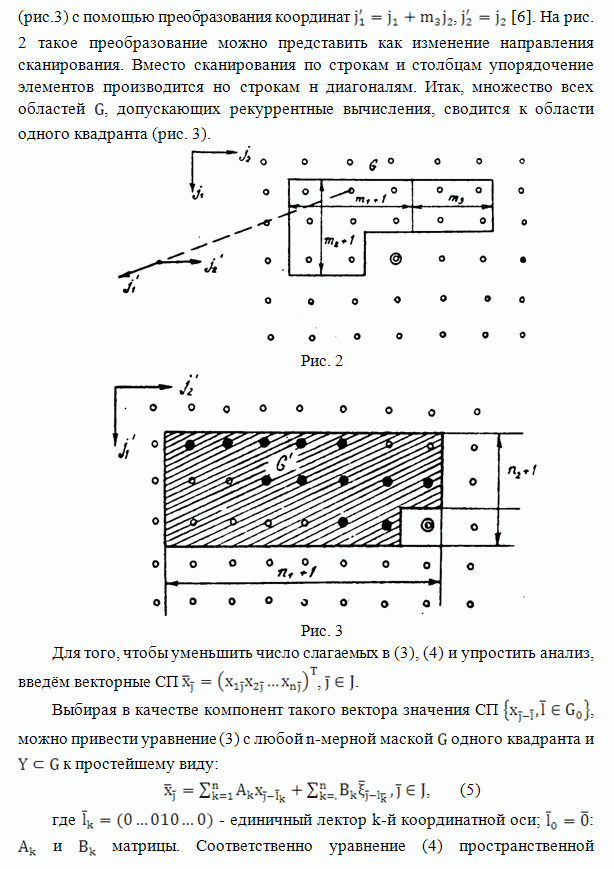
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
УДК
621.391
М.А.Райфельд
РАНГОВАЯ СЕГМЕНТАЦИЯ БИНАРНЫХ ИЗОБРАЖЕНИЙ
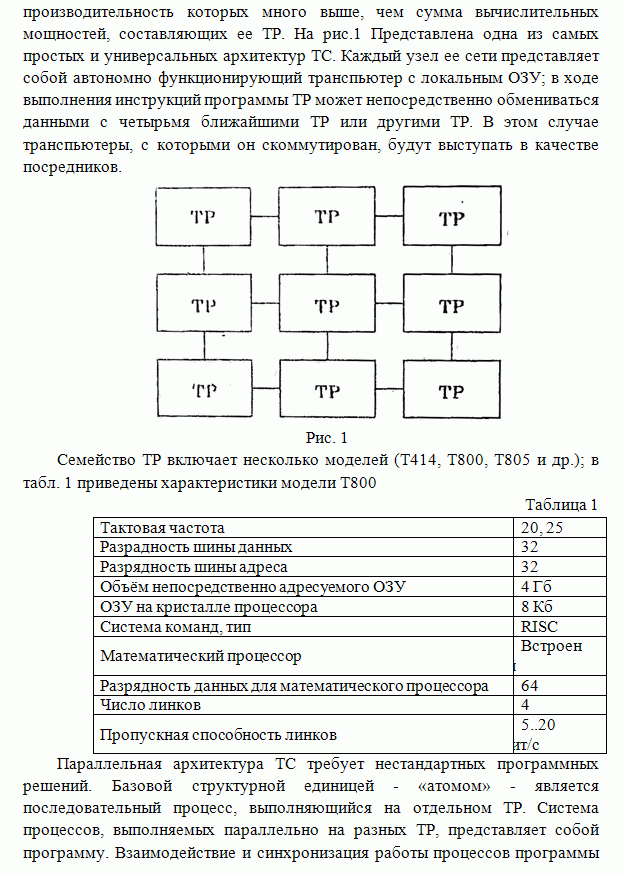
При решении задач, связанных с обработкой изображений, часто используются алгоритмы сегментации отсчётов по яркостному признаку. Это может быть необходимым, например, для компактного представления данных, для локализации на изображениях объектов произвольной формы и размеров и т.д. [3]. В ряде случаев результатом сегментации многоуровневого (полутонового) изображения является изображение, представленное двумя уровнями. Такая бинарная сегментация используется, когда, например, исходным является изображение однородного по яркости объекта, наблюдаемого на однородном фоне при наличии шума. Для большинства реальных приложений алгоритмов сегментации характерна априорная неопределенность относительно вида функции распределения (ФР) яркости наблюдений. При этом известно, что распределения яркости объекта и фона имеют различные средние значения. В этих условиях сегментация осуществляется с помощью гистограммных методов (например, метода квантования мод [4]). Эти методы применимы если моды гистограммы, соответствующие разным яркостным классам хорошо различимы, Это условие вместе с требованием унимодальности распределений классов, а также с проблемами формализации задачи выделения глобального минимума гистограммы (особенно при малых объемах выборок) зачастую делают задачу сегментации даже для бинарного случая трудноразрешимой.
В данной статье предлагается ранговый метод сегментации полутоновых изображений, использование которого позволяет снять ряд проблем, имеющих место при использовании гистограммных методов. Этот алгоритм применим для пространственно-неоднородных изображений, адекватно описываемых моделью сдвига ФР наблюдений различных классов (имеется в виду случай двух классов) при априорной неопределенности относительно вида ФР. Предполагается также, что с каждым яркостным классом на изображении связана некоторая пространственно - компактная область (или группа областей), наблюдения различных классов пространственно не перемешиваются ( рис. 1а, б). Изображения такого типа также называются фасеточными или лоскутнымих [4]. В контексте решаемой бинарной задачи без ограничения общности рассуждений положим, что на изображении имеется область (условно называемая объектом), средняя яркость которой выше, чем средняя яркость другой области, на фоне которой она наблюдается.

а б
Рис. 1
Если наблюдения областей характеризуются ФР одного вида, то можно записать:
![]() . (1)
. (1)
Здесь ![]() ,
, ![]() - ФР
объекта и фона, соответственно. Такая модель адекватно описывает изображения,
получаемые, например, в результате аддитивного взаимодействия двумерного двухуровнего
эталона
- ФР
объекта и фона, соответственно. Такая модель адекватно описывает изображения,
получаемые, например, в результате аддитивного взаимодействия двумерного двухуровнего
эталона ![]() и
белого шума
и
белого шума ![]() (рис.1a,б).
При этом
(рис.1a,б).
При этом
![]() , (2)
, (2)
где ![]() –
отсчёт изображения. Упомянутый выше алгоритм квантования мод для
бинарного случая представляется в виде
–
отсчёт изображения. Упомянутый выше алгоритм квантования мод для
бинарного случая представляется в виде
 (3)
(3)
где ![]() - метка
яркостного класса отсчета;
- метка
яркостного класса отсчета; ![]() - порог
сегментации. Для метода квантования мод он выбирается по межмодовому минимуму
гистограммы. Представим правило ранговой бинарной сегментации в форме, подобной
(3):
- порог
сегментации. Для метода квантования мод он выбирается по межмодовому минимуму
гистограммы. Представим правило ранговой бинарной сегментации в форме, подобной
(3):
 (4)
(4)
где ![]() ранг
ранг ![]() отсчета
изображения;
отсчета
изображения; ![]() -
порог сегментации. Можно показать, что выбор порога
-
порог сегментации. Можно показать, что выбор порога ![]() , где 1
– количество элементов фона изображения, обеспечивает минимум безусловной
ошибки классификации
, где 1
– количество элементов фона изображения, обеспечивает минимум безусловной
ошибки классификации ![]() отсчета
изображения с помощью правила (4):
отсчета
изображения с помощью правила (4):
![]() (5)
(5)
Здесь ![]() ,
, ![]() условные
вероятности ошибки классификации фонового отсчета, как отсчета объекта, и
отсчета объекта, как фонового, соответственно;
условные
вероятности ошибки классификации фонового отсчета, как отсчета объекта, и
отсчета объекта, как фонового, соответственно; ![]() -
общее количество элементов изображения. При неперекрывающихся распределениях
яркости объекта и фона правило (4) обеспечивает нулевую вероятность ошибки
классификации. Очевидно, что в большинстве реальных приложений информации о
количестве элементов фона изображения, которое является параметром алгоритма
сегментации, заранее не существует. Поэтому в (4) предлагается использовать
оценку количества элементов фона, построенную по имеющейся выборке наблюдений.
В книге [2] показано, как получить упомянутую оценку для случая двух классов нормально
распределенных наблюдений, отличающихся средними значениями при известных
дисперсиях. Указанную оценку можно получить также с помощью гистограммных
методов, однако, при этом возникают те же трудности, которые имеют место и при
сегментации изображений с помощью этих методов.
-
общее количество элементов изображения. При неперекрывающихся распределениях
яркости объекта и фона правило (4) обеспечивает нулевую вероятность ошибки
классификации. Очевидно, что в большинстве реальных приложений информации о
количестве элементов фона изображения, которое является параметром алгоритма
сегментации, заранее не существует. Поэтому в (4) предлагается использовать
оценку количества элементов фона, построенную по имеющейся выборке наблюдений.
В книге [2] показано, как получить упомянутую оценку для случая двух классов нормально
распределенных наблюдений, отличающихся средними значениями при известных
дисперсиях. Указанную оценку можно получить также с помощью гистограммных
методов, однако, при этом возникают те же трудности, которые имеют место и при
сегментации изображений с помощью этих методов.
Покажем,
как построить упомянутую оценку количества , фоновых элементов с помощью
выборки рангов отсчетов сегментируемого изображения. Предположим, что на
изображении, состоящем из ![]() точек,
имеются области фона, содержащие 1 элементов. Количество элементов объекта в
этом случае -
точек,
имеются области фона, содержащие 1 элементов. Количество элементов объекта в
этом случае - ![]() .
Предположим также, что каждому отсчету
.
Предположим также, что каждому отсчету ![]() поставлен
в соответствие его ранг
поставлен
в соответствие его ранг ![]() в вариационном
ряду, составленном из всех элементов изображение. Сформируем рабочую выборку из
рангов
в вариационном
ряду, составленном из всех элементов изображение. Сформируем рабочую выборку из
рангов ![]() элементов
изображения
элементов
изображения ![]() локализующихся
в компактную (пространственно) область на изображении. Форма упомянутой
области, из которой извлекаются отсчеты рабочей выборки, роли не играет. Так
рабочая выборка может быть, например, сформирована из отсчетов, попадающих в
квадратное "окно". Ранги наблюдений, не попавших в рабочую выборку,
составляют опорную выборку. В общем случае, вследствие произвольного способа
формирования рабочей выборки, последняя является неоднородной, т.е. содержит
ранги элементов как объекта, так и фона. Распределение рангов неоднородной
рабочей выборки зависит от количества фоновых элементов
локализующихся
в компактную (пространственно) область на изображении. Форма упомянутой
области, из которой извлекаются отсчеты рабочей выборки, роли не играет. Так
рабочая выборка может быть, например, сформирована из отсчетов, попадающих в
квадратное "окно". Ранги наблюдений, не попавших в рабочую выборку,
составляют опорную выборку. В общем случае, вследствие произвольного способа
формирования рабочей выборки, последняя является неоднородной, т.е. содержит
ранги элементов как объекта, так и фона. Распределение рангов неоднородной
рабочей выборки зависит от количества фоновых элементов ![]() имеющихся на данном
изображении (
имеющихся на данном
изображении (![]() параметр, который нам
необходимо оценить), и от количества элементов фона, содержащихся в рабочей
выборке
параметр, который нам
необходимо оценить), и от количества элементов фона, содержащихся в рабочей
выборке ![]() . При
неперекрывающихся распределениях яркости объекта и фона можно показать [1. 2] ,
что достаточной статистикой для параметра
. При
неперекрывающихся распределениях яркости объекта и фона можно показать [1. 2] ,
что достаточной статистикой для параметра ![]() является вектор
является вектор ![]() . C
учетом
этого максимально правдоподобная (МП) оценка
. C
учетом
этого максимально правдоподобная (МП) оценка ![]() вычисляется следующим
образом:
вычисляется следующим
образом:
![]() . (6)
. (6)
Положим
сначала, что количество фоновых отсчетов изображения, попавших к рабочую
выборку, известно и равно ![]() .
Подставляя выражения для соответствующих распределении и (6) получаем следующий
алгоритм вычисления МП оценки
.
Подставляя выражения для соответствующих распределении и (6) получаем следующий
алгоритм вычисления МП оценки ![]() :
:
 (7)
(7)
Здесь ![]() -
функция, определенная на множестве натуральных чисел следующим образом:
-
функция, определенная на множестве натуральных чисел следующим образом:
![]() . (8)
. (8)
В
реальной ситуации параметр ![]() заранее
неизвестен. Построим МП оценку
заранее
неизвестен. Построим МП оценку ![]() помощью
наблюдений рабочей выборки. Можно показать, что для неперекрывающихся
распределений эта оценка может быть найдена следующим образом:
помощью
наблюдений рабочей выборки. Можно показать, что для неперекрывающихся
распределений эта оценка может быть найдена следующим образом:
![]() . (9)
. (9)
С учётом этого:
![]() , (10)
, (10)
где ![]() - МП
оценка количества фонопых элементов рабочей выборки, а
- МП
оценка количества фонопых элементов рабочей выборки, а ![]() -
функция (7). Необходимо отметить, что МП оценка
-
функция (7). Необходимо отметить, что МП оценка ![]() , вычисляемая согласно
(7), является смещенной. Можно показать, что несмещенная оценка
, вычисляемая согласно
(7), является смещенной. Можно показать, что несмещенная оценка ![]() вычисляется следующим
образом
вычисляется следующим
образом
 (11)
(11)
Все
приведенные выше рассуждения справедливы в предположении о том, что
распределения яркости элементов объекта и фона не перекрываются. Рассмотрим
теперь случай перекрытия распределений объекта и фона. Для изображения,
описываемого моделью аддитивного взаимодействия двухуровневого эталона S и шума
![]() ,
приведенное условие означает, что среднеквадратическое отклонение шума
,
приведенное условие означает, что среднеквадратическое отклонение шума ![]() оказывается
соизмеримым с расстоянием между уровнями эталона
оказывается
соизмеримым с расстоянием между уровнями эталона ![]() .
Перекрытие распределений яркости объекта и фона приводит к смещенности оценки
.
Перекрытие распределений яркости объекта и фона приводит к смещенности оценки ![]() , построенной на
основании статистик
, построенной на
основании статистик ![]() ,
, ![]() тем
большей, чем меньше контраст яркости областей объекта и фона
тем
большей, чем меньше контраст яркости областей объекта и фона ![]() :
:
![]() . (12)
. (12)
Исследования
показали, что большей устойчивостью к шуму обладает оценка ![]() ,
построенная на основе статистик
,
построенная на основе статистик ![]() ,
, ![]() . Указанные
статистике получают в результате отбрасывания
. Указанные
статистике получают в результате отбрасывания ![]() элемента
верхней части вариационного ряда из отсчётов рабочей выборки
элемента
верхней части вариационного ряда из отсчётов рабочей выборки ![]() (q – кратное
цензурирование) и
(q – кратное
цензурирование) и ![]() элементов
нижней части вариационного ряда из отсчётов
элементов
нижней части вариационного ряда из отсчётов ![]() (
(![]() – кратное
цензурирование). Опуская громоздкие выкладки, выполненные по аналогии с
приведенными выше, запишем сразу выражение для вычисления несмещенной МП оценки
– кратное
цензурирование). Опуская громоздкие выкладки, выполненные по аналогии с
приведенными выше, запишем сразу выражение для вычисления несмещенной МП оценки
![]() с учётом цензурирования
рабочей выборки
с учётом цензурирования
рабочей выборки
 (13)
(13)
Здесь:

![]() -
операция взятия целой части числа. По определению
-
операция взятия целой части числа. По определению ![]() . В том
случае, если при вычислении по формулам (13),(14) получается величина большая
. В том
случае, если при вычислении по формулам (13),(14) получается величина большая ![]() , либо
меньшая нуля, то в качестве оценки
, либо
меньшая нуля, то в качестве оценки ![]() принимается
принимается ![]() , либо
нуль, соответственно.
, либо
нуль, соответственно.
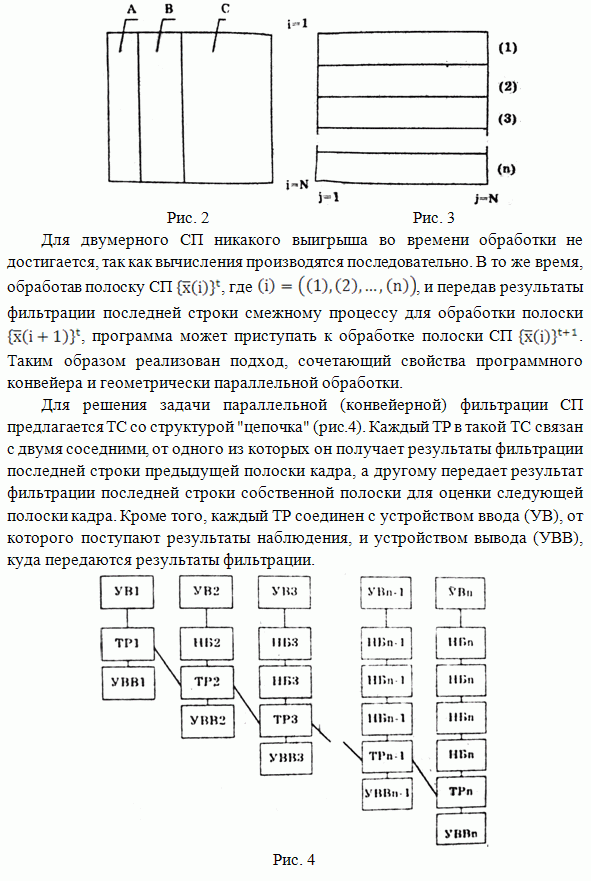
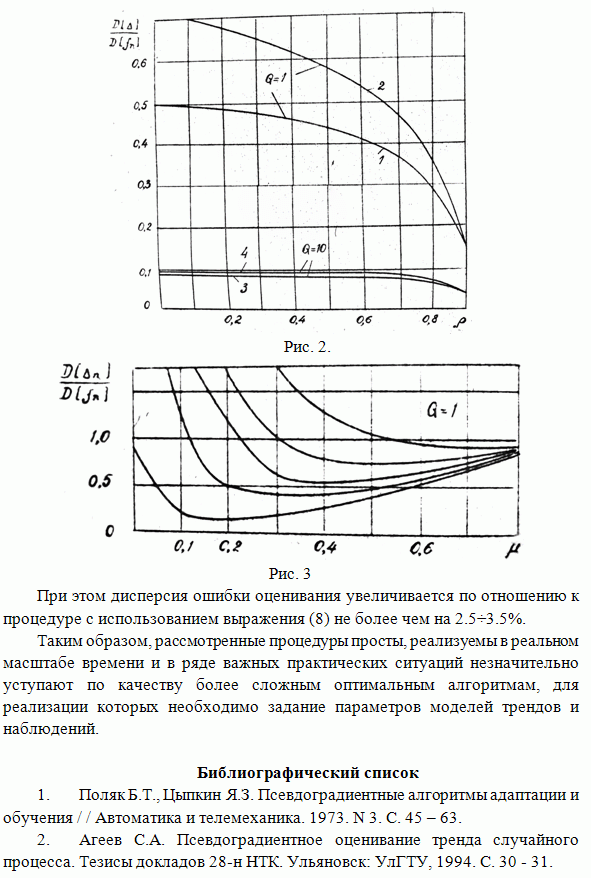
Качественные
характеристики ранговой МП оценки количества элементов фона на изображении при
наличии аддитивного шума (зависимость дисперсии оценок (11).(13) от яркостного
контраста объекта и фона ![]() ),
полученные методом статистического моделирования для гауссовского распределения
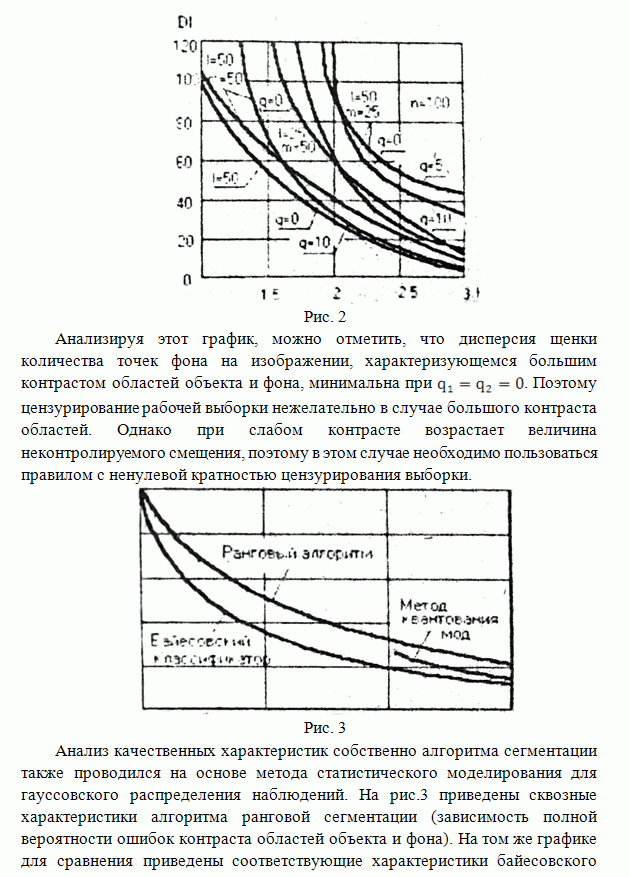
наблюдении, приведены в виде графика на рис.2.
),
полученные методом статистического моделирования для гауссовского распределения
наблюдении, приведены в виде графика на рис.2.

Рис. 2
Анализируя
этот график, можно отметить, что дисперсия щенки количества точек фона на
изображении, характеризующемся большим контрастом областей объекта и фона,
минимальна при ![]() . Поэтому
цензурирование рабочей выборки нежелательно в случае большого контраста
областей. Однако при слабом контрасте возрастает величина неконтролируемого
смещения, поэтому в этом случае необходимо пользоваться правилом с ненулевой
кратностью цензурирования выборки.
. Поэтому
цензурирование рабочей выборки нежелательно в случае большого контраста
областей. Однако при слабом контрасте возрастает величина неконтролируемого
смещения, поэтому в этом случае необходимо пользоваться правилом с ненулевой
кратностью цензурирования выборки.

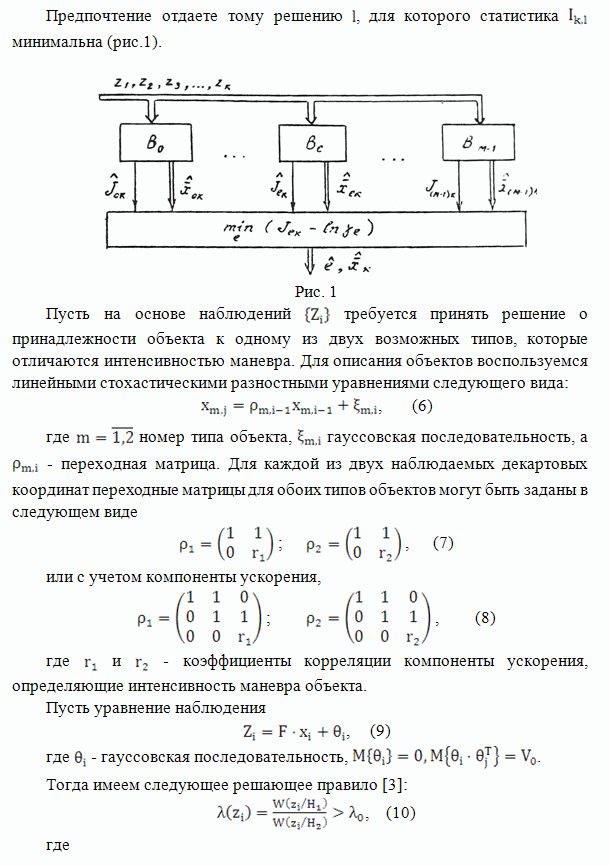
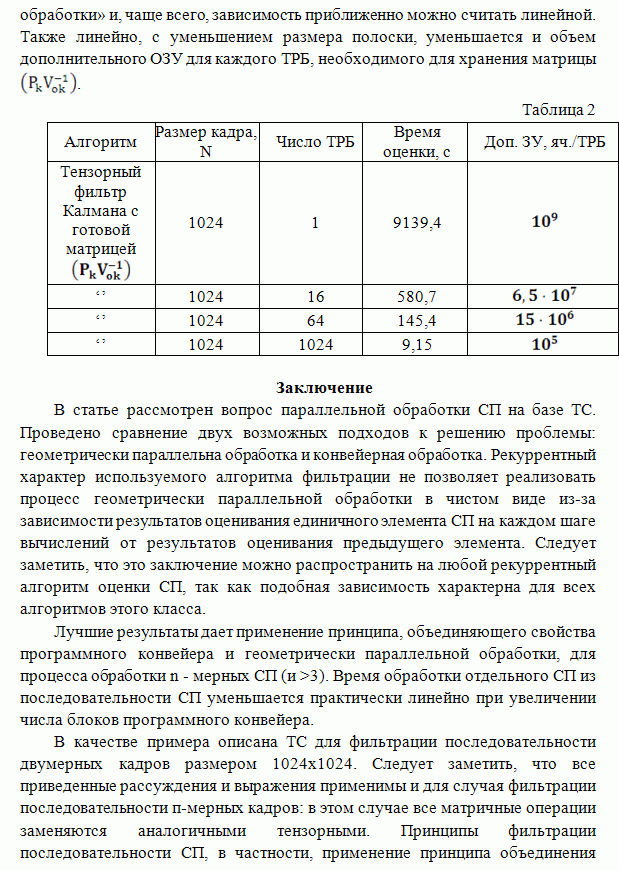
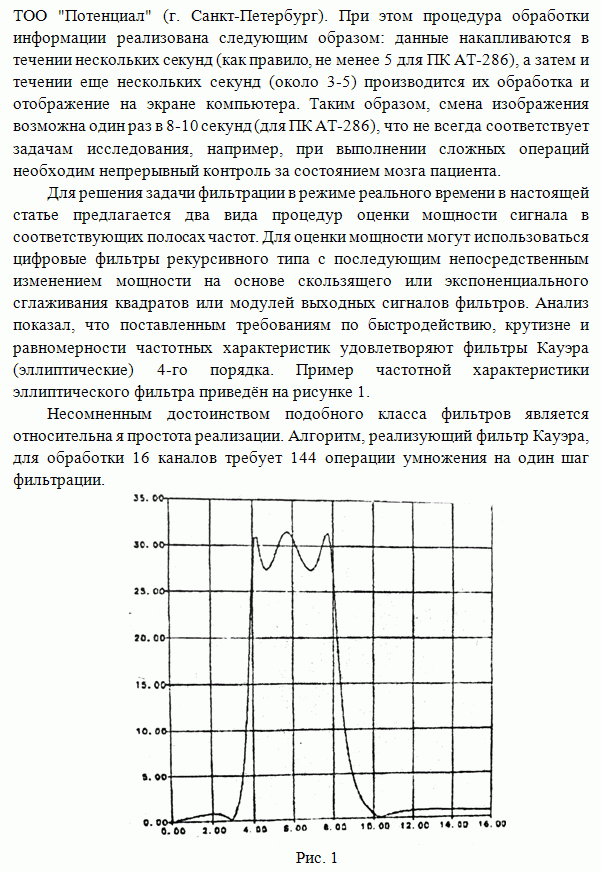
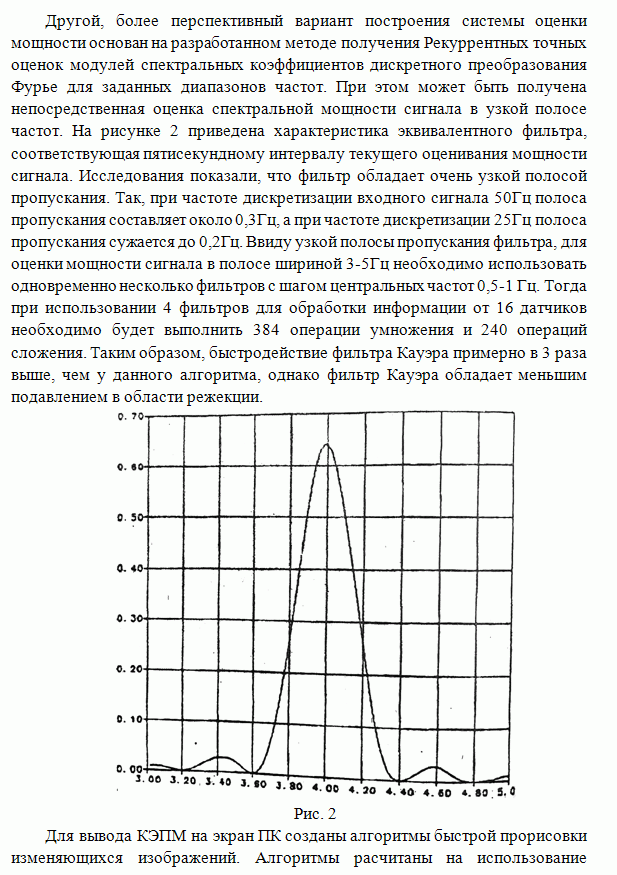
Рис. 3
Анализ качественных характеристик собственно алгоритма сегментации также проводился на основе метода статистического моделирования для гауссовского распределения наблюдений. На рис.3 приведены сквозные характеристики алгоритма ранговой сегментации (зависимость полной вероятности ошибок контраста областей объекта и фона). На том же графике для сравнения приведены соответствующие характеристики байесовского классификатора и алгоритма квантования мод. Отметим, что предлагаемое ранговое правило сегментации работоспособно при более низких значениях контраста областей, чем гистограммный метод (исследования показали, что это Правило остается работоспособным, пока выполняется условие (1)). При этом характеристики рангового алгоритма сегментации достаточно близки потенциально достижимым характеристикам байесовского классификатора.
Библиографический список
1. Дэйвид Г. Порядковые статистики. М.: Наука, 1979. 320 С.
2. Леман Э. Теория точечного оценивания. М.: Наука, 1991. 360 С.
3. Прэтт У. Цифровая обработка изображений. М.: Мир, 1982. Кн.2. 480 С.
4. Ярославский Л.П. Ведение в цифровую обработку изображений. М.: Сов. радио, 1979. 312 С
| << Предыдущий параграф |
- МЕТОДЫ ПРЕДСТАВЛЕНИЯ И ОБРАБОТКИ СЛУЧАЙНЫХ ПОЛЕЙ (предисловие редколлегии)
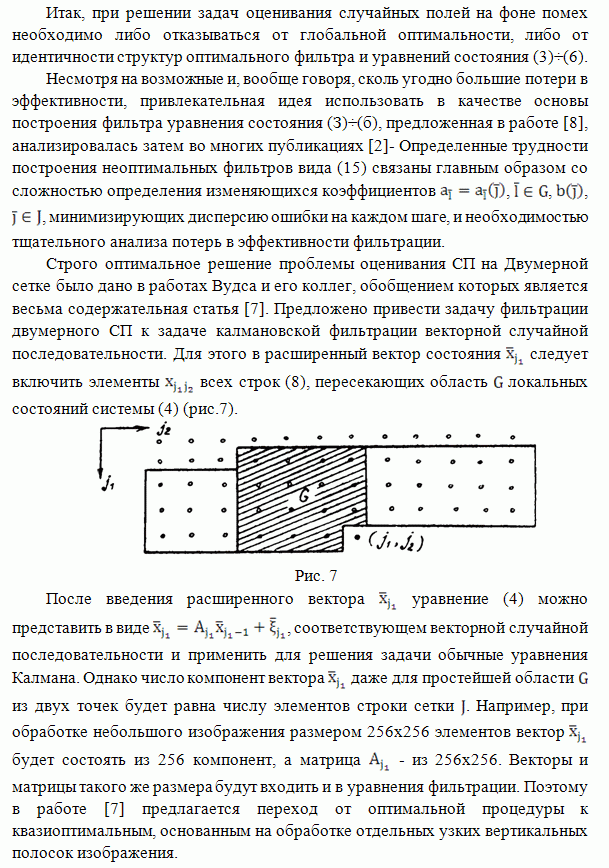
- КАУЗАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ ПОЛЕЙ НА МНОГОМЕРНЫХ СЕТКАХ
- ГИББСОВСКИЕ СЛУЧАЙНЫЕ ПОЛЯ КАК ВЕРОЯТНОСТНЫЕ МОДЕЛИ ИЗОБРАЖЕНИЙ НА НИЖНЕМ УРОВНЕ ВЫЧИСЛИТЕЛЬНОГО ЗРЕНИЯ
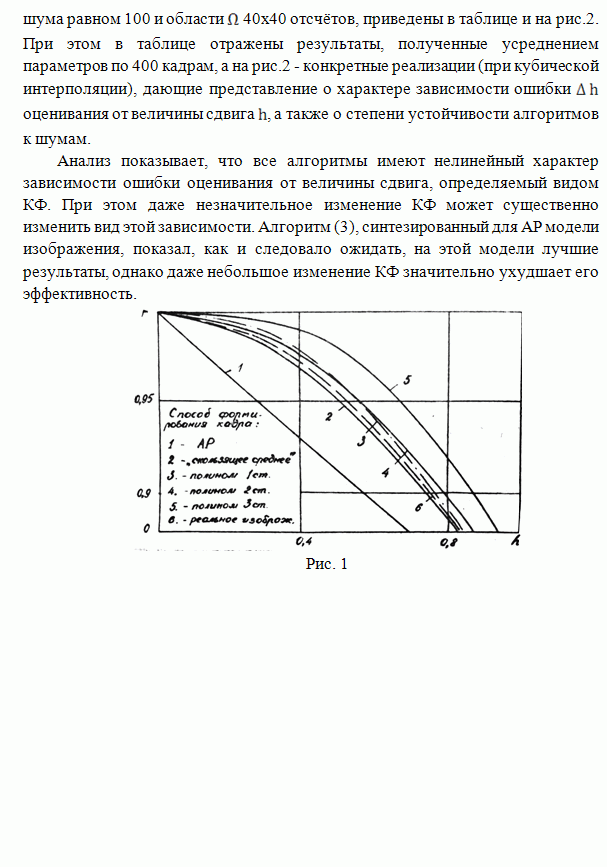
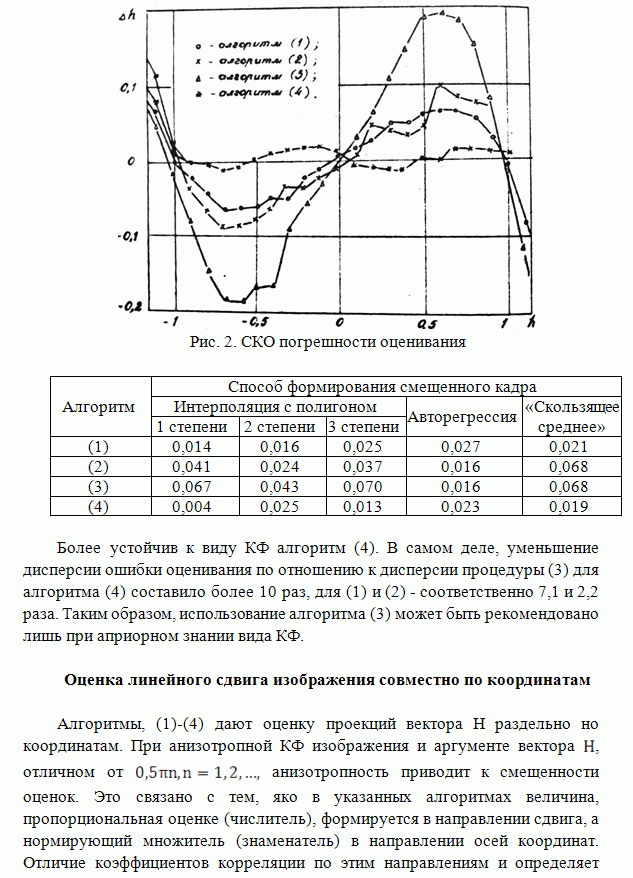
- ОЦЕНКА МЕЖКАДРОВОГО СДВИГА ИЗОБРАЖЕНИЙ
- КЛАССИФИКАЦИЯ АЭРОКОСМИЧЕСКИХ ИЗОБРАЖЕНИЙ ПРИ РАЗЛИЧНОМ УРОВНЕ АПРИОРНОЙ ИНФОРМАЦИИ
- РАНГОВАЯ СЕГМЕНТАЦИЯ БИНАРНЫХ ИЗОБРАЖЕНИЙ
- ДВУХЭТАППЫЙ АЛГОРИТМ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ С ПРОИЗВОЛЬНЫМИ ОДНОМЕРНЫМИ СПЕКТРАЛЬНО-КОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ
- СПЕКТР ДВУМЕРНОЙ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ, НАБЛЮДАЕМОЙ В ОБЛАСТИ ОГРАНИЧЕННОЙ ПРОТЯЖЕННОСТИ
- ПСЕВДОГРАДИЕНТНЫЕ АЛГОРИТМЫ СТАБИЛИЗАЦИИ ПОРОГА ОБНАРУЖЕНИЯ
- ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ ПРИ ТРАЕКТОРНОЙ ОБРАБОТКЕ
- ПАРАЛЛЕЛЬНАЯ РЕАЛИЗАЦИЯ АЛГОРИТМОВ ОЦЕНИВАНИЯ МНОГОМЕРНЫХ ИЗОБРАЖЕНИЙ НА БАЗЕ ТРАНСПЬЮТЕРНЫХ СИСТЕМ
- ПСЕВДОГРАДИЕНТНАЯ ФИЛЬТРАЦИЯ СТОХАСТИЧЕСКОГО ТРЕНДА
- ПРИМЕНЕНИЕ СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ С МАЛЫМИ ВЫЧИСЛИТЕЛЬНЫМИ ЗАТРАТАМИ
- КОМПЬЮТЕРНЫЙ ЭЛЕКТРОЭНЦЕФАЛОГРАФ