| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
УДК
621.391
С. А.
АГЕЕВ
ПСЕВДОГРАДИЕНТНАЯ ФИЛЬТРАЦИЯ СТОХАСТИЧЕСКОГО ТРЕНДА
При обработке сигналов и изображений возникает задача оценки тренда наблюдений в порядке регистрации исследуемого сигнала или изображения. Как показано в работах [1,2], перспективными для решения этой задачи являются псевдоградиентные процедуры. Рассмотрим случайный тренд, описываемый авторегрессионной моделью первого порядка
![]() , (1)
, (1)
где ![]() - коэффициент
корреляции;
- коэффициент
корреляции; ![]() -
независимы, имеют нулевые средние и дисперсии
-
независимы, имеют нулевые средние и дисперсии ![]() . Пусть
наблюдения имеют вид
. Пусть
наблюдения имеют вид
![]() , (2)
, (2)
где ![]() -
независимые шумы с нулевыми средними и дисперсиями. Ограничений на вид
распределений не накладывается.
-
независимые шумы с нулевыми средними и дисперсиями. Ограничений на вид
распределений не накладывается.
Будем искать оценку тренда на n-ом шаге с помощью псевдоградиентной процедуры
![]() ,
,
где ![]() следующая
за
следующая
за ![]() оценка
и
оценка
и ![]() .
Критерием качества оценивания пусть будет функционал
.
Критерием качества оценивания пусть будет функционал
![]() . (4)
. (4)
Можно
показать, что разность ![]() является
псевдоградиентом по отношению к функционалу (4) , поэтому шаги в (3) делаются,
в среднем, в сторону уменьшения (4).
является
псевдоградиентом по отношению к функционалу (4) , поэтому шаги в (3) делаются,
в среднем, в сторону уменьшения (4).
Значение
параметра ![]() существенно
влияет на качество решения задачи. Найдем его оптимальное значение. Для этого
исследуем среднее значение и дисперсию ошибки оценивания
существенно
влияет на качество решения задачи. Найдем его оптимальное значение. Для этого
исследуем среднее значение и дисперсию ошибки оценивания ![]() .Используя
(3), можно получить рекуррентное соотношение
.Используя
(3), можно получить рекуррентное соотношение
![]() . (5)
. (5)
Или,
учитывая, что ![]() , для достаточно
больших n можно записать приближенное
равенство
, для достаточно
больших n можно записать приближенное
равенство
![]() . (6)
. (6)
Дисперсия ошибки удовлетворяет отношению
![]() . (7)
. (7)
Находя
минимум (7) по ![]() ,
получаем значение
,
получаем значение ![]() для n-го
шага, при котором достигается минимум дисперсии ошибки оценивания
для n-го
шага, при котором достигается минимум дисперсии ошибки оценивания
![]() . (8)
. (8)
Полученные
выражения можно обобщить для авторегрессионной модели более высокого порядка.
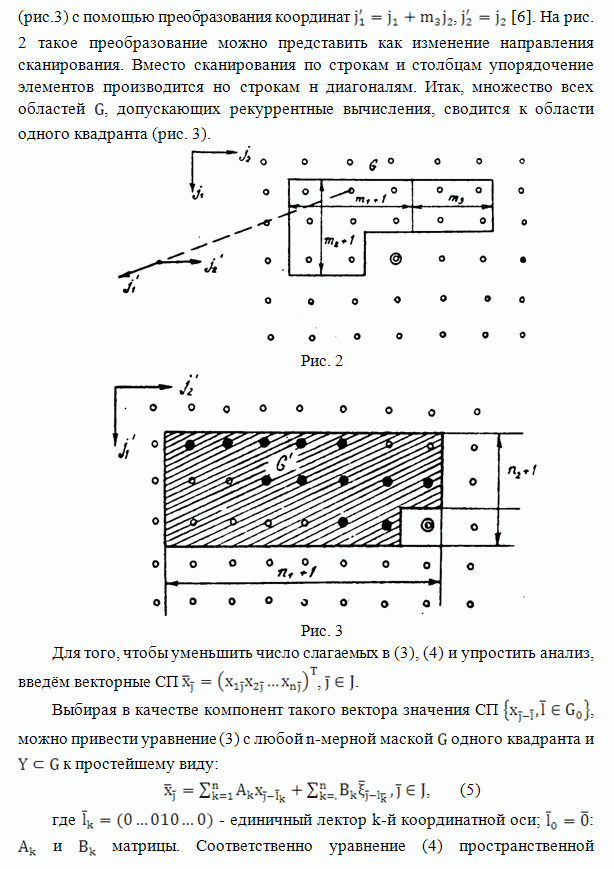
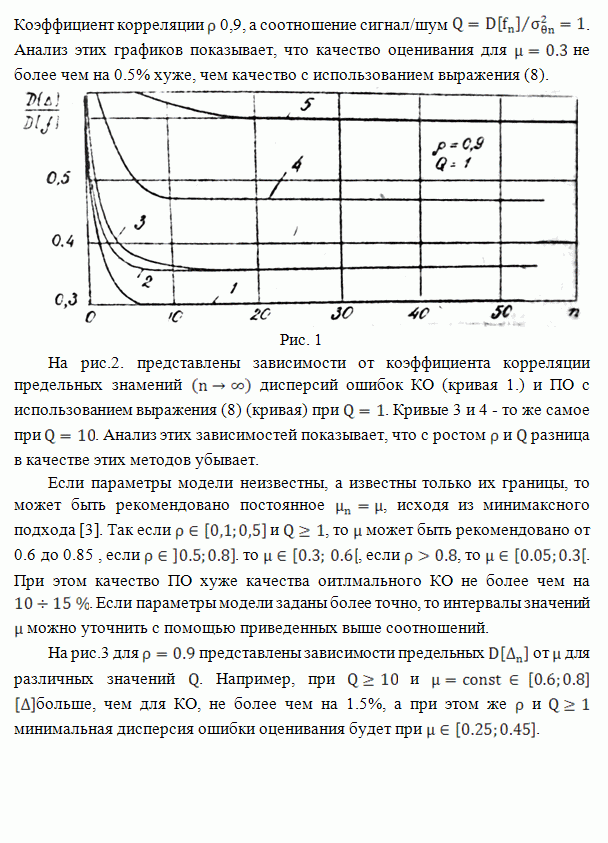
На рис.1 приведены графики для сравнительного анализа оптимальной калмановской
фильтрации и предложенных алгоритмов. На этом рисунке кривая 1 представляет
значения дисперсий ошибок калмановского оценивания (КО) в зависимости от номера
n отсчета, кривая 2 - значения дисперсий ошибок
псевдоградиентного оценивания (ПО) с использованием выражения (8), кривая 3
соответствует случаю ПО с ![]() ,
кривая 4 - ПО с
,
кривая 4 - ПО с ![]() и
кривая 5 - ПО с
и
кривая 5 - ПО с ![]() .
Коэффициент корреляции
.
Коэффициент корреляции ![]() 0,9, а
соотношение сигнал/шум
0,9, а
соотношение сигнал/шум ![]() .
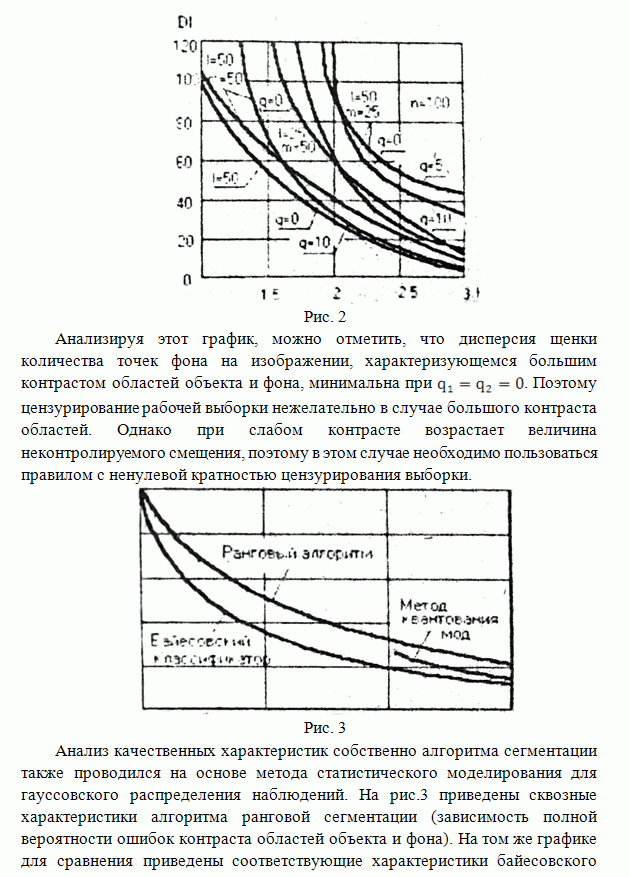
Анализ этих графиков показывает, что качество оценивания для
.
Анализ этих графиков показывает, что качество оценивания для ![]() не
более чем на 0.5% хуже, чем качество с использованием выражения (8).
не
более чем на 0.5% хуже, чем качество с использованием выражения (8).

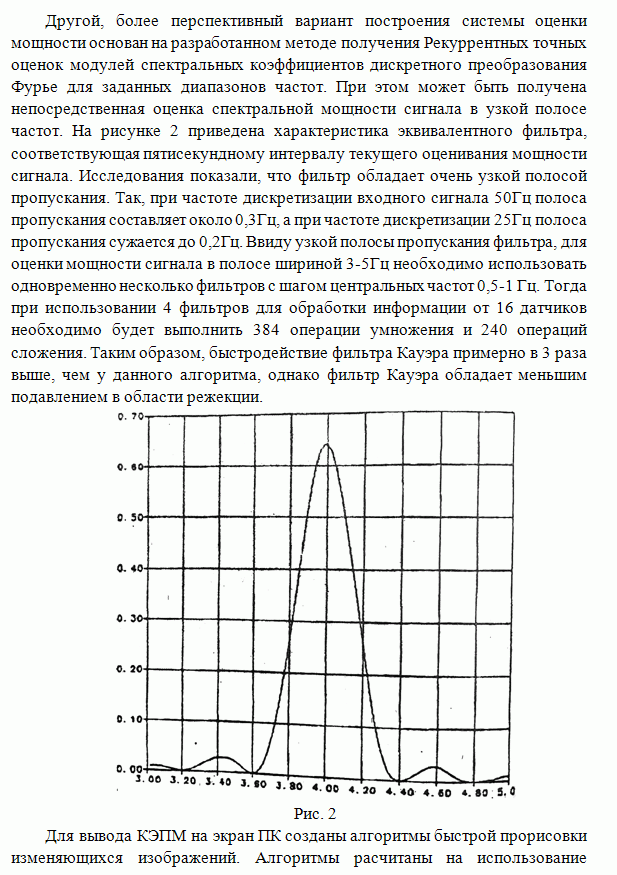
Рис. 1
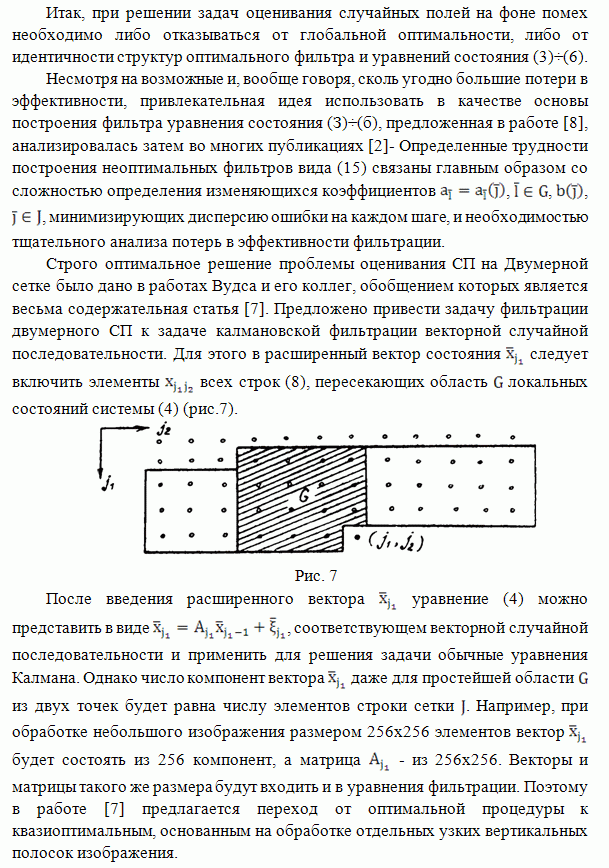
Ha
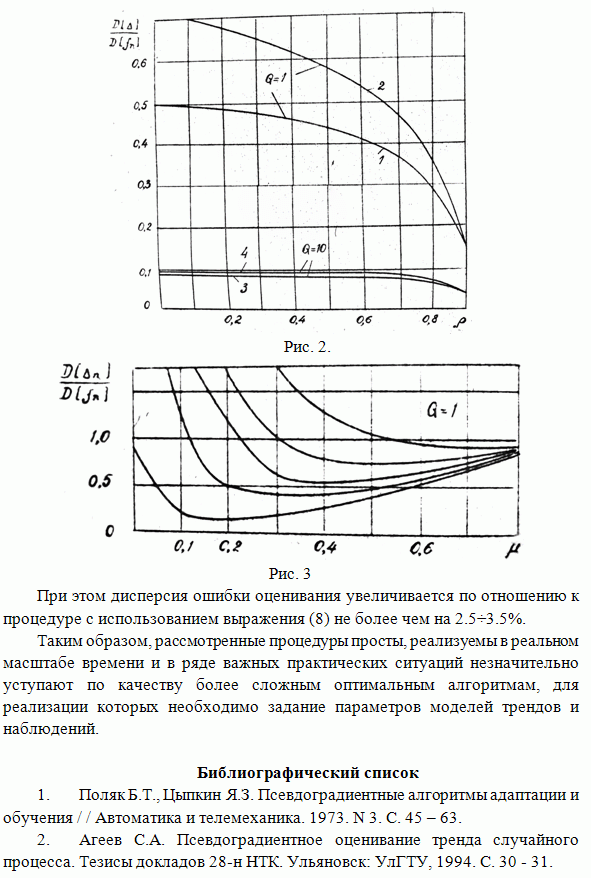
рис.2. представлены зависимости от коэффициента корреляции предельных знамений ![]() дисперсий
ошибок КО (кривая 1.) и ПО с использованием выражения (8) (кривая) при
дисперсий
ошибок КО (кривая 1.) и ПО с использованием выражения (8) (кривая) при ![]() .
Кривые 3 и 4 - то же самое при
.
Кривые 3 и 4 - то же самое при ![]() .
Анализ этих зависимостей показывает, что с ростом
.
Анализ этих зависимостей показывает, что с ростом ![]() и
и ![]() разница
в качестве этих методов убывает.
разница
в качестве этих методов убывает.
Если
параметры модели неизвестны, а известны только их границы, то может быть
рекомендовано постоянное ![]() , исходя
из минимаксного подхода [3]. Так если
, исходя
из минимаксного подхода [3]. Так если ![]() и
и ![]() , то
, то ![]() может
быть рекомендовано от 0.6 до 0.85 , если
может
быть рекомендовано от 0.6 до 0.85 , если ![]() . то
. то ![]() , если
, если ![]() , то
, то ![]() . При
этом качество ПО хуже качества оптимального КО не более чем на
. При
этом качество ПО хуже качества оптимального КО не более чем на ![]() . Если
параметры модели заданы более точно, то интервалы значений
. Если
параметры модели заданы более точно, то интервалы значений ![]() можно
уточнить с помощью приведенных выше соотношений.
можно
уточнить с помощью приведенных выше соотношений.
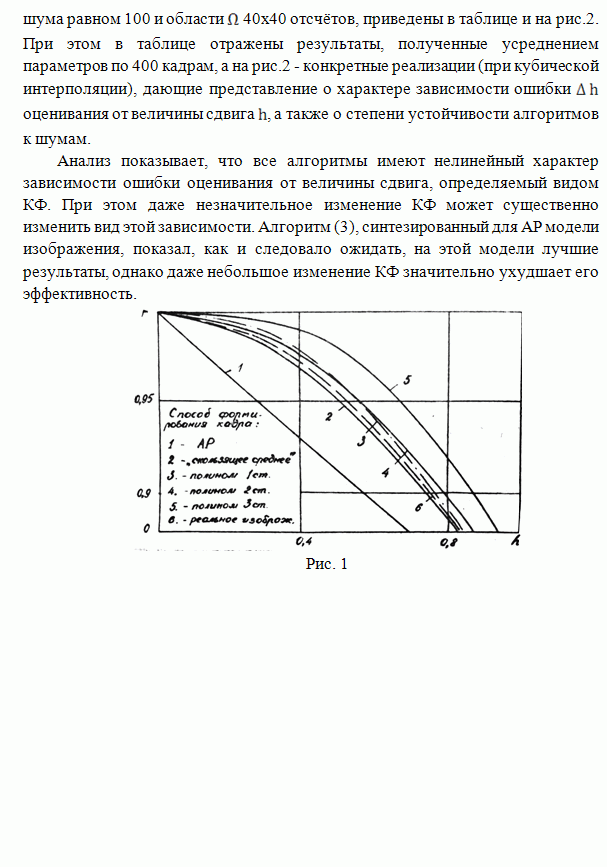
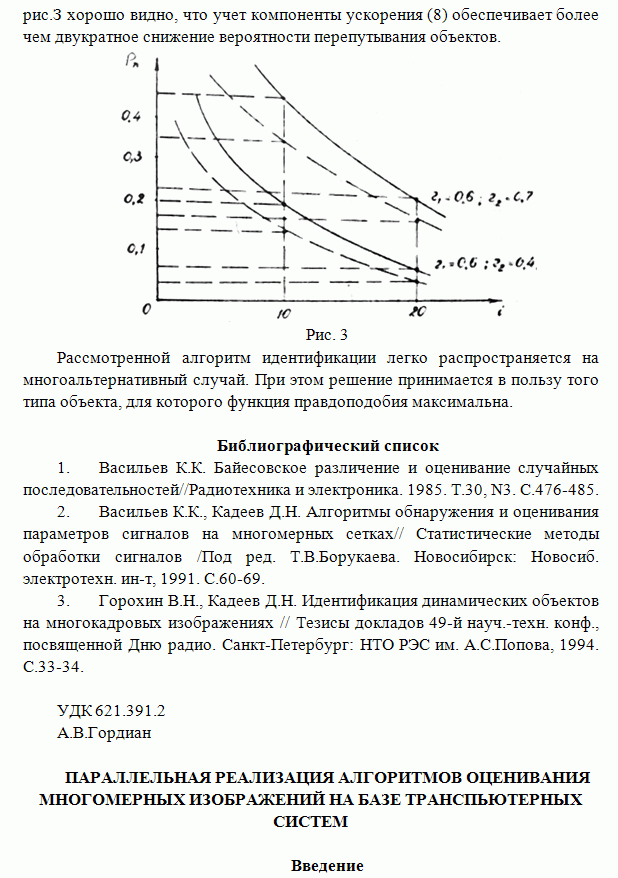
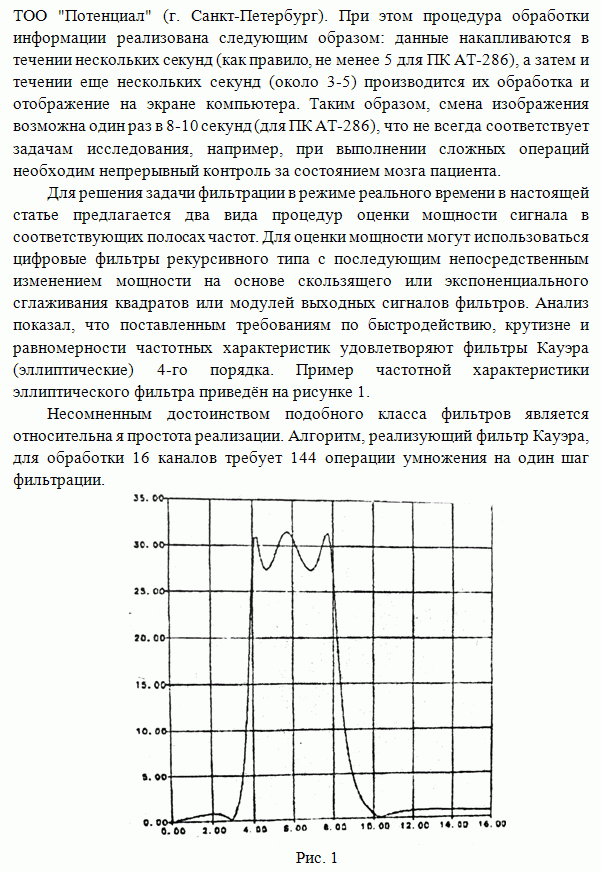
На рис.3
для ![]() представлены
зависимости предельных
представлены
зависимости предельных ![]() от
от ![]() для
различных значений
для
различных значений ![]() .
Например, при
.
Например, при ![]() и
и ![]()
![]() больше,
чем для КО, не более чем на 1.5%, а при этом же
больше,
чем для КО, не более чем на 1.5%, а при этом же ![]() и
и ![]() минимальная
дисперсия ошибки оценивания будет при
минимальная
дисперсия ошибки оценивания будет при ![]() .
.

Рис. 2.

Рис. 3
При этом дисперсия ошибки оценивания увеличивается по отношению к процедуре с использованием выражения (8) не более чем на 2.5÷3.5%.
Таким образом, рассмотренные процедуры просты, реализуемы в реальном масштабе времени и в ряде важных практических ситуаций незначительно уступают по качеству более сложным оптимальным алгоритмам, для реализации которых необходимо задание параметров моделей трендов и наблюдений.
Библиографический список
1. Поляк Б.Т., Цыпкин Я.З. Псевдоградиентные алгоритмы адаптации и обучения / / Автоматика и телемеханика. 1973. N 3. С. 45 – 63.
2. Агеев С.А. Псевдоградиентное оценивание тренда случайного процесса. Тезисы докладов 28-н НТК. Ульяновск: УлГТУ, 1994. С. 30 - 31.
3. Уилкс С., Математическая статистика. М.: Наука, 1967. 632 С.
| << Предыдущий параграф |
- МЕТОДЫ ПРЕДСТАВЛЕНИЯ И ОБРАБОТКИ СЛУЧАЙНЫХ ПОЛЕЙ (предисловие редколлегии)
- КАУЗАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ ПОЛЕЙ НА МНОГОМЕРНЫХ СЕТКАХ
- ГИББСОВСКИЕ СЛУЧАЙНЫЕ ПОЛЯ КАК ВЕРОЯТНОСТНЫЕ МОДЕЛИ ИЗОБРАЖЕНИЙ НА НИЖНЕМ УРОВНЕ ВЫЧИСЛИТЕЛЬНОГО ЗРЕНИЯ
- ОЦЕНКА МЕЖКАДРОВОГО СДВИГА ИЗОБРАЖЕНИЙ
- КЛАССИФИКАЦИЯ АЭРОКОСМИЧЕСКИХ ИЗОБРАЖЕНИЙ ПРИ РАЗЛИЧНОМ УРОВНЕ АПРИОРНОЙ ИНФОРМАЦИИ
- РАНГОВАЯ СЕГМЕНТАЦИЯ БИНАРНЫХ ИЗОБРАЖЕНИЙ
- ДВУХЭТАППЫЙ АЛГОРИТМ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ С ПРОИЗВОЛЬНЫМИ ОДНОМЕРНЫМИ СПЕКТРАЛЬНО-КОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ
- СПЕКТР ДВУМЕРНОЙ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ, НАБЛЮДАЕМОЙ В ОБЛАСТИ ОГРАНИЧЕННОЙ ПРОТЯЖЕННОСТИ
- ПСЕВДОГРАДИЕНТНЫЕ АЛГОРИТМЫ СТАБИЛИЗАЦИИ ПОРОГА ОБНАРУЖЕНИЯ
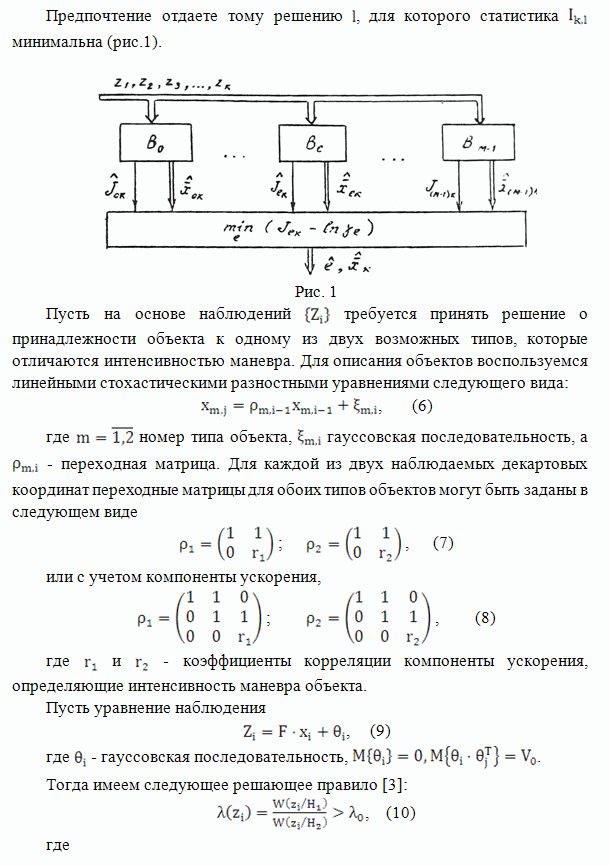
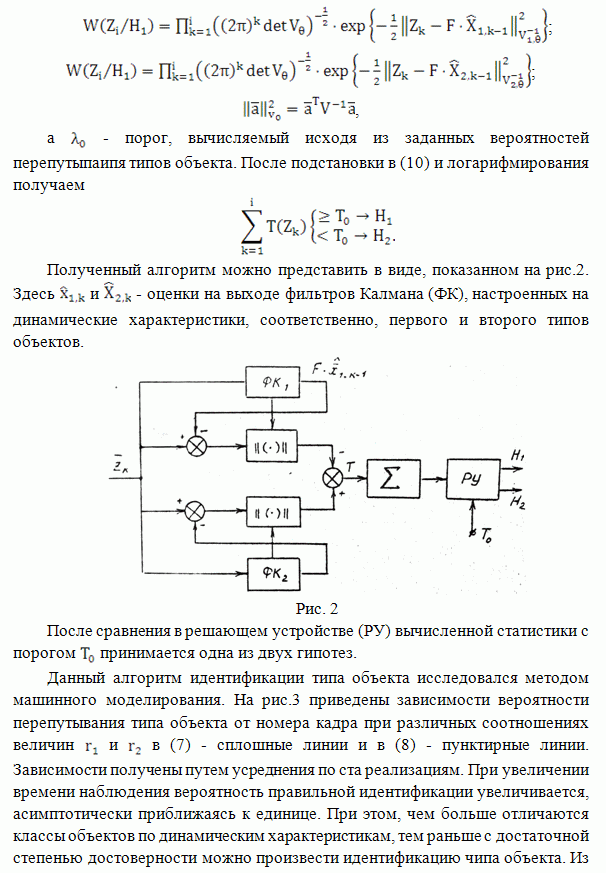
- ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ ПРИ ТРАЕКТОРНОЙ ОБРАБОТКЕ
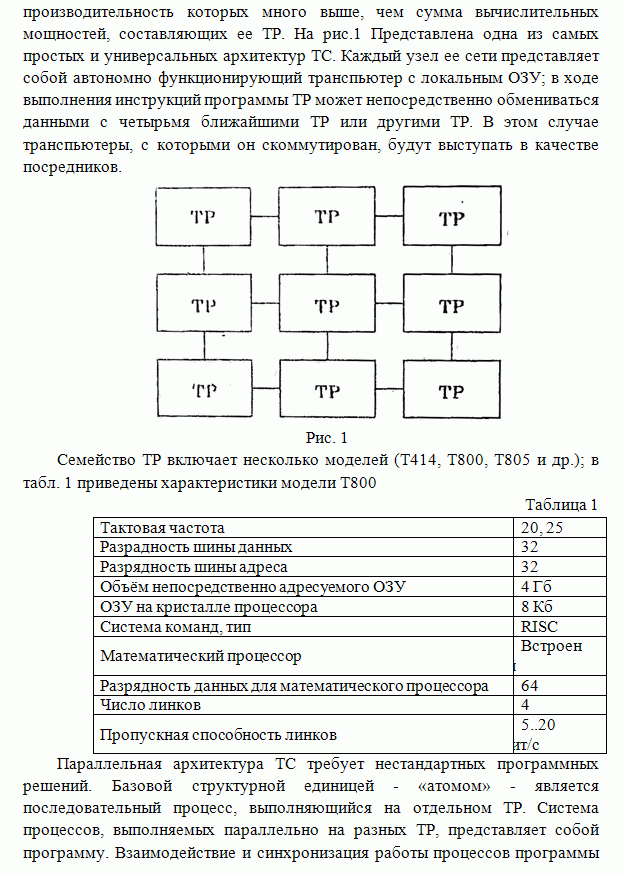
- ПАРАЛЛЕЛЬНАЯ РЕАЛИЗАЦИЯ АЛГОРИТМОВ ОЦЕНИВАНИЯ МНОГОМЕРНЫХ ИЗОБРАЖЕНИЙ НА БАЗЕ ТРАНСПЬЮТЕРНЫХ СИСТЕМ
- ПСЕВДОГРАДИЕНТНАЯ ФИЛЬТРАЦИЯ СТОХАСТИЧЕСКОГО ТРЕНДА
- ПРИМЕНЕНИЕ СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ С МАЛЫМИ ВЫЧИСЛИТЕЛЬНЫМИ ЗАТРАТАМИ
- КОМПЬЮТЕРНЫЙ ЭЛЕКТРОЭНЦЕФАЛОГРАФ