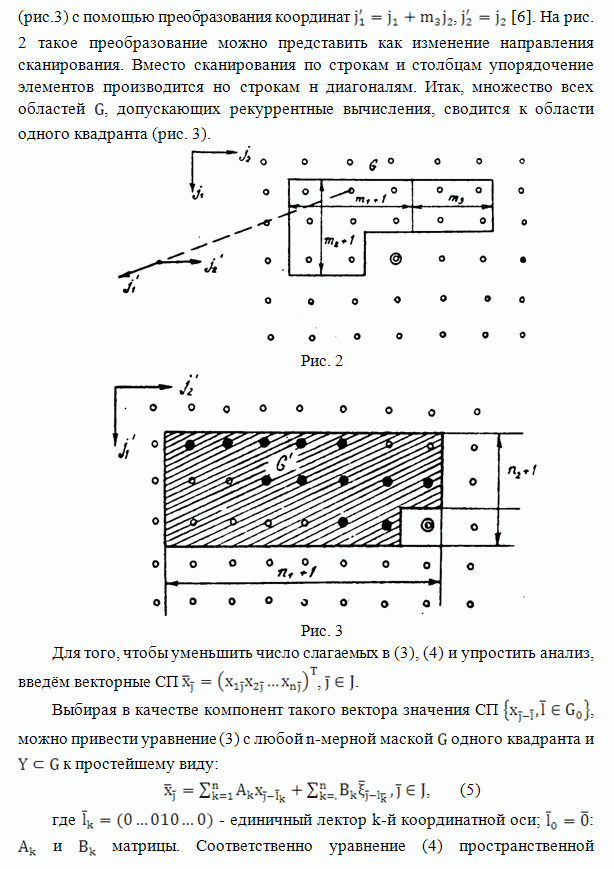
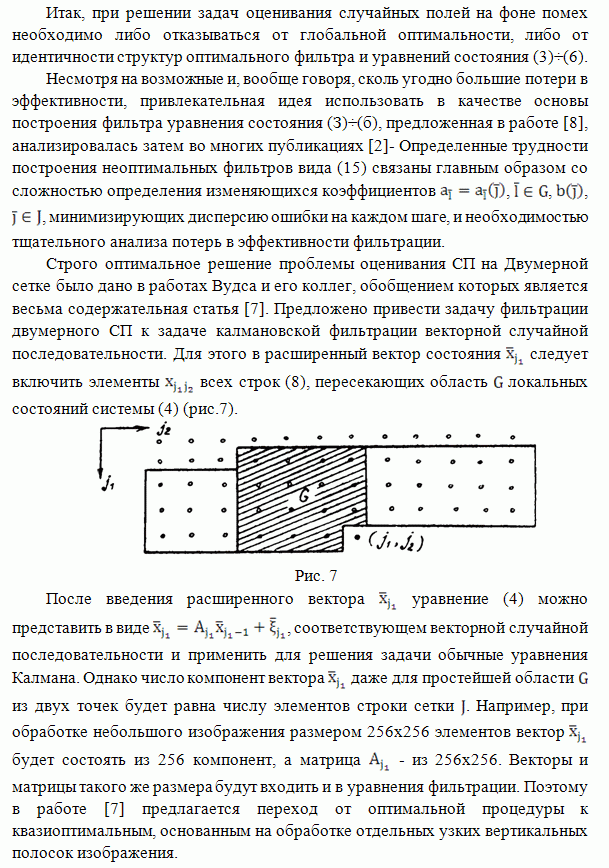
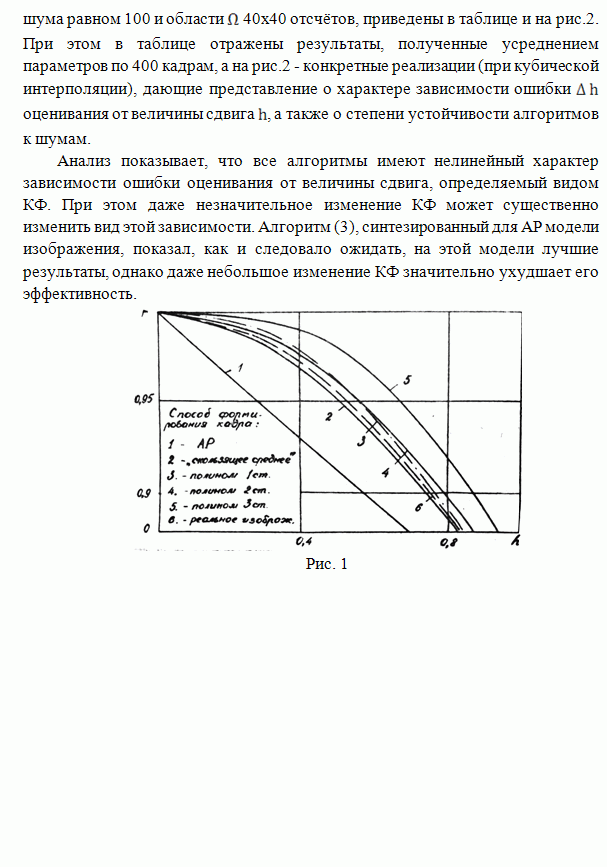
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
УДК
621.391
И.С.Грузман
ДВУХЭТАППЫЙ АЛГОРИТМ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ С ПРОИЗВОЛЬНЫМИ ОДНОМЕРНЫМИ СПЕКТРАЛЬНО-КОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ
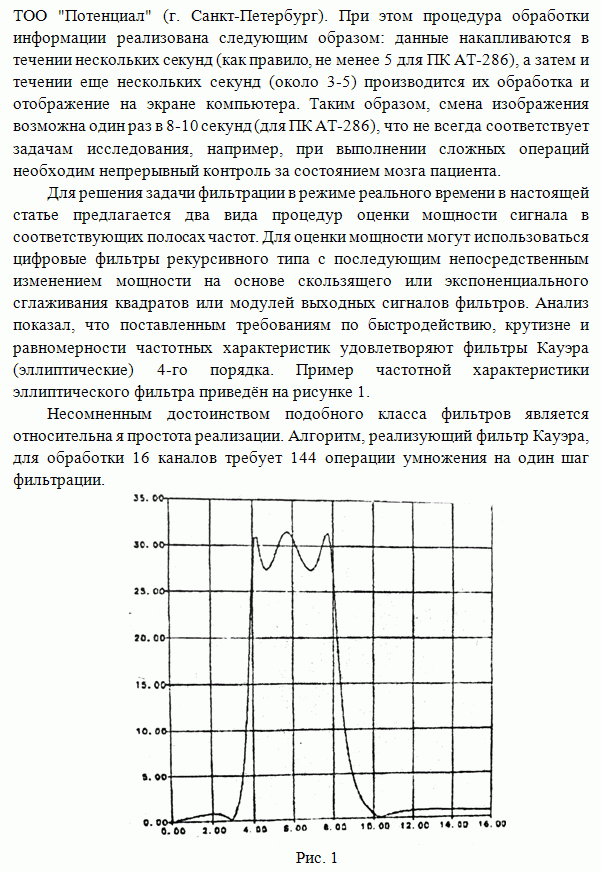
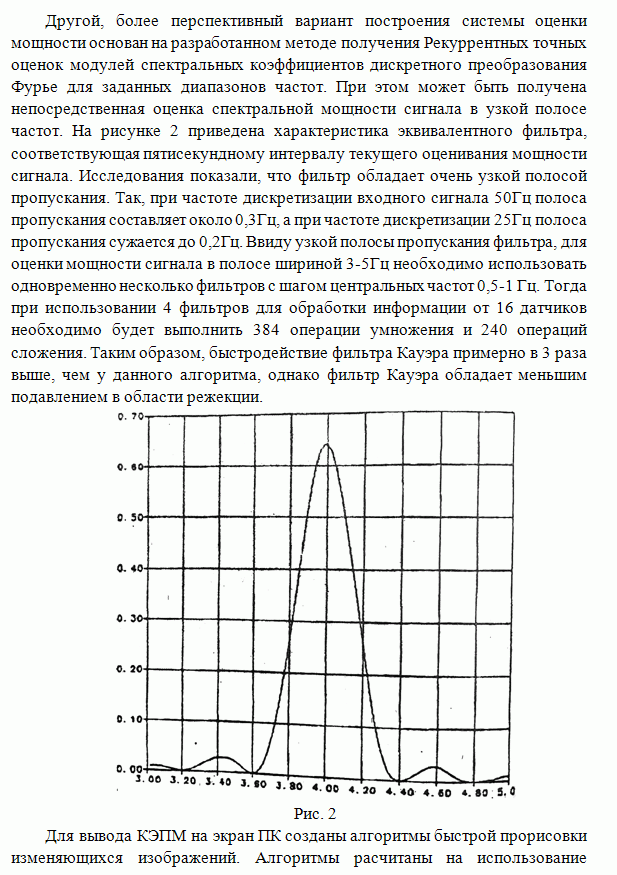
В ряде алгоритмов линейной обработки изображении используют двумерное преобразование Фурье. При обработке изображений больших размеров выполнение двумерных спектральных преобразований становится малоэффективным (по затратам машинного времени и ресурсам оперативной памяти). Поэтому возникает задача разработки алгоритмов, которые использовали бы одномерные алгоритмы фильтрации для восстановления изображений. В работах [1.2] предложен двухэтапный метод линейной фильтрации марковских полей, наблюдаемых на фоне аддитивной гауссовской помехи. При построении двухэтапной оценки используются лишь данные, расположенные на вертикальных и горизонтальных лучах, расходящихся из текущей точки фильтрации, что позволяет свести задачу двумерной фильтрации к совокупности Одномерных.
Ниже
предлагается подход к синтезу двухэтапного некаузального алгоритма фильтрации
изображения ![]() , наблюдаемого
на фоне аддитивного гауссовского шума и
, наблюдаемого
на фоне аддитивного гауссовского шума и ![]() . Наблюдаемое
изображение
. Наблюдаемое
изображение
![]() .
.
Взаимно
независимые двумерные поля ![]() и
и ![]() описываются
разделимыми по координатам корреляционными функциями (КФ)
описываются
разделимыми по координатам корреляционными функциями (КФ)
![]() и
и
![]() ,
,
где ![]() и
и ![]() -
дисперсии полей
-
дисперсии полей ![]() ,
, ![]() ,
, ![]() ,
, ![]() - произвольные
нормированные одномерные корреляционные функции полей, соответственно, по
вертикали и горизонтали.
- произвольные
нормированные одномерные корреляционные функции полей, соответственно, по
вертикали и горизонтали.
Двухэтапная
линейная оценка изображения ![]() , использующая
данные, расположенные на строке и столбце, имеет вид
, использующая
данные, расположенные на строке и столбце, имеет вид
![]() , (1)
, (1)
где ![]() и
и ![]() -
импульсные характеристики горизонтального и вертикального одномерных фильтров,
соответственно. Определим
-
импульсные характеристики горизонтального и вертикального одномерных фильтров,
соответственно. Определим ![]() и
и ![]() из
условия минимума среднеквадратической ошибки оценивания
из
условия минимума среднеквадратической ошибки оценивания
![]() , (2)
, (2)
где ![]() -
операция усреднения по множеству реализаций. В соответствии с методом
ортогонального проецирования [3], ошибка должна быть ортогональна пространству
исходных данных, на которых базируется оценка, т.е.
-
операция усреднения по множеству реализаций. В соответствии с методом
ортогонального проецирования [3], ошибка должна быть ортогональна пространству
исходных данных, на которых базируется оценка, т.е.
![]() (3)
(3)
Подставляя (1) в (3) и проводя усреднение, получим
 (4)
(4)
где ![]() – КФ
наблюдаемого поля. Перейдя в частотную область и решив систему линейных
интегральных уравнений с вырожденными ядрами, получим амплитудно-частотные
характеристики (АЧХ) фильтров:
– КФ
наблюдаемого поля. Перейдя в частотную область и решив систему линейных
интегральных уравнений с вырожденными ядрами, получим амплитудно-частотные
характеристики (АЧХ) фильтров:
![]() , (5)
, (5)
![]() ,
,
где ![]() и
и ![]() – АЧХ
горизонтального и вертикального одномерных фильтров Винера [3], соответственно:
– АЧХ
горизонтального и вертикального одномерных фильтров Винера [3], соответственно:
![]() -
нормированные одномерные энергетические спектры оцениваемого и помехового
полей. Коэффициенты
-
нормированные одномерные энергетические спектры оцениваемого и помехового
полей. Коэффициенты ![]() удовлетворяют
решению системы линейных уравнений
удовлетворяют
решению системы линейных уравнений

![]() (6)
(6)
С учётом (5) уравнение оценки (1) можно привести к виду
 , (7)
, (7)
где ![]() и
и ![]() -
импульсные характеристики горизонтального и вертикального одномерных фильтров
Винера;
-
импульсные характеристики горизонтального и вертикального одномерных фильтров
Винера; ![]() и
и ![]() -
предварительные оптимальные одномерные оценки, получаемые при независимой
вертикальной и горизонтальной обработке наблюдаемого изображения.
-
предварительные оптимальные одномерные оценки, получаемые при независимой
вертикальной и горизонтальной обработке наблюдаемого изображения.
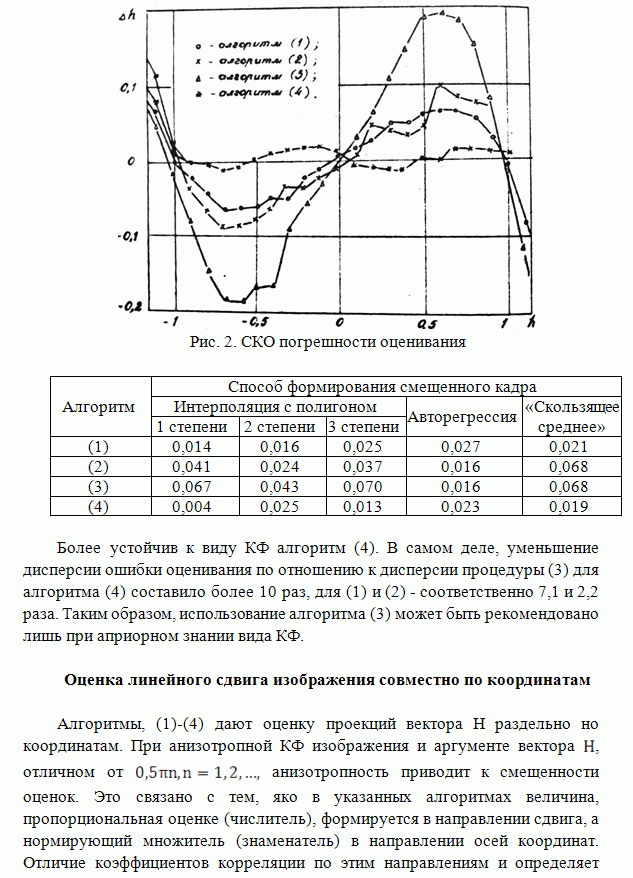
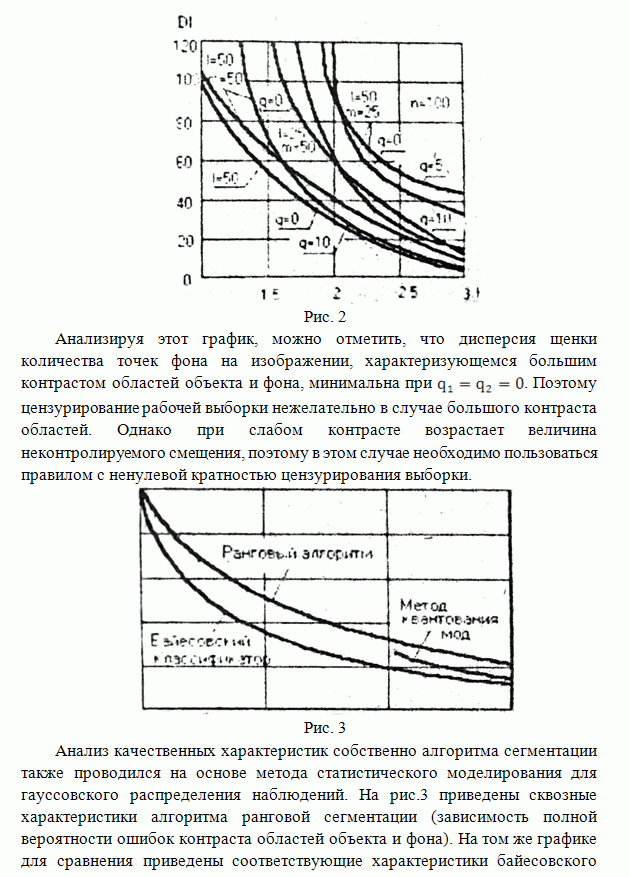
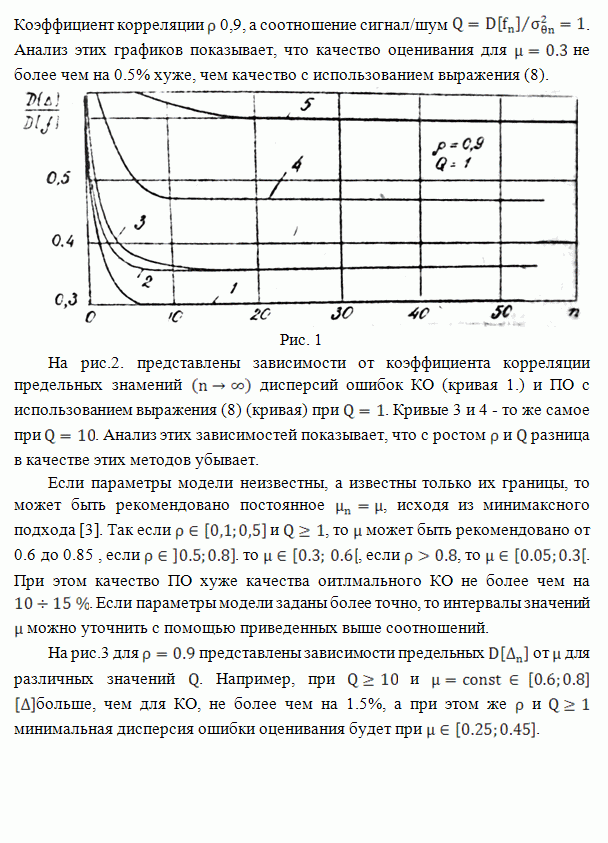
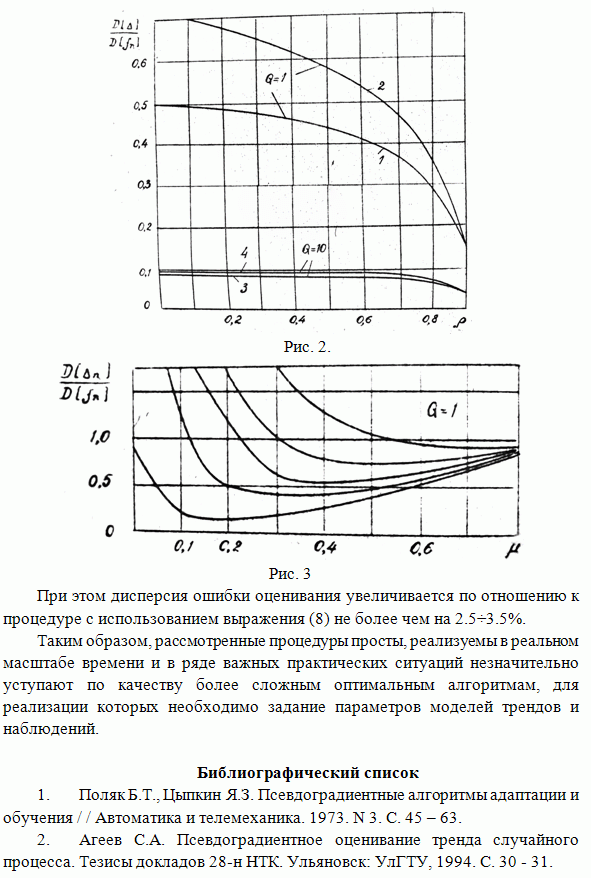
На
рисунке приведены зависимости относительной ошибки ![]() оценивания
гауссовского поля
оценивания
гауссовского поля ![]() с КФ
с КФ ![]() ,
наблюдаемого на фоне аддитивной помехи с КФ отношения сигнал/помеха
,
наблюдаемого на фоне аддитивной помехи с КФ отношения сигнал/помеха ![]() при
двух значениях
при
двух значениях ![]() .
Непрерывные кривые соответствуют двухэтапной оценке (1), пунктирные -
двумерному фильтру Винера. Анализ приведенных зависимостей показывает, что
двухэтапный фильтр незначительно проигрывает по ошибкам оценивания фильтру
Винера, однако для его реализации можно использовать одномерное преобразование
Фурье. Кроме того, полученная оценка может использоваться для определения
потенциальной точности двухэтапных линейных методов фильтрации.
.
Непрерывные кривые соответствуют двухэтапной оценке (1), пунктирные -
двумерному фильтру Винера. Анализ приведенных зависимостей показывает, что
двухэтапный фильтр незначительно проигрывает по ошибкам оценивания фильтру
Винера, однако для его реализации можно использовать одномерное преобразование
Фурье. Кроме того, полученная оценка может использоваться для определения
потенциальной точности двухэтапных линейных методов фильтрации.

Библиографический список
1. Спектор А.А. Двухэтапная фильтрация изображений при действии коррелированной помехи // Радиотехника. 1985. N9. C.718-726.
2. Спектор А.А. Двухэтапное оценивание неоднородности изображения, сформированного линейкой прием никои // Радиотехника. 1986. N 8. С.18-23.
| << Предыдущий параграф |
- МЕТОДЫ ПРЕДСТАВЛЕНИЯ И ОБРАБОТКИ СЛУЧАЙНЫХ ПОЛЕЙ (предисловие редколлегии)
- КАУЗАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ ПОЛЕЙ НА МНОГОМЕРНЫХ СЕТКАХ
- ГИББСОВСКИЕ СЛУЧАЙНЫЕ ПОЛЯ КАК ВЕРОЯТНОСТНЫЕ МОДЕЛИ ИЗОБРАЖЕНИЙ НА НИЖНЕМ УРОВНЕ ВЫЧИСЛИТЕЛЬНОГО ЗРЕНИЯ
- ОЦЕНКА МЕЖКАДРОВОГО СДВИГА ИЗОБРАЖЕНИЙ
- КЛАССИФИКАЦИЯ АЭРОКОСМИЧЕСКИХ ИЗОБРАЖЕНИЙ ПРИ РАЗЛИЧНОМ УРОВНЕ АПРИОРНОЙ ИНФОРМАЦИИ
- РАНГОВАЯ СЕГМЕНТАЦИЯ БИНАРНЫХ ИЗОБРАЖЕНИЙ
- ДВУХЭТАППЫЙ АЛГОРИТМ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ С ПРОИЗВОЛЬНЫМИ ОДНОМЕРНЫМИ СПЕКТРАЛЬНО-КОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ
- СПЕКТР ДВУМЕРНОЙ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ, НАБЛЮДАЕМОЙ В ОБЛАСТИ ОГРАНИЧЕННОЙ ПРОТЯЖЕННОСТИ
- ПСЕВДОГРАДИЕНТНЫЕ АЛГОРИТМЫ СТАБИЛИЗАЦИИ ПОРОГА ОБНАРУЖЕНИЯ
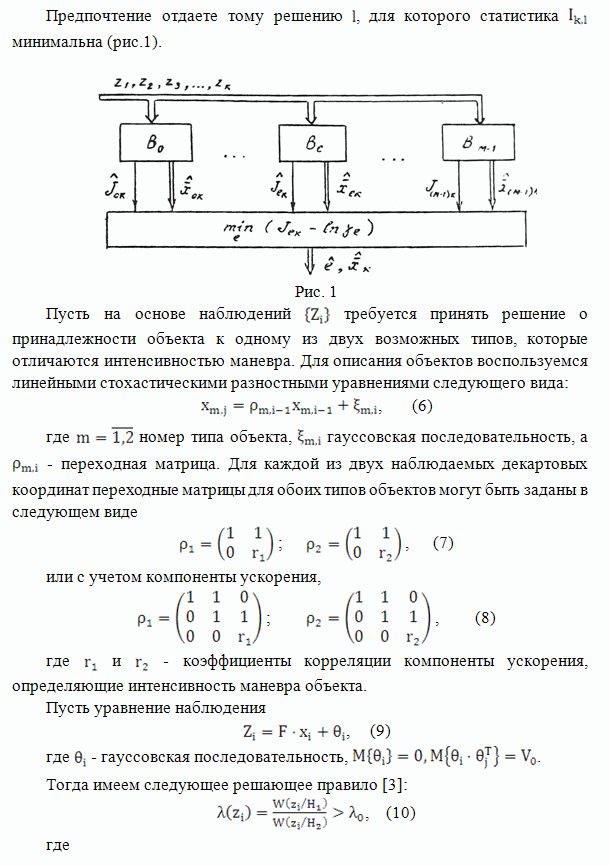
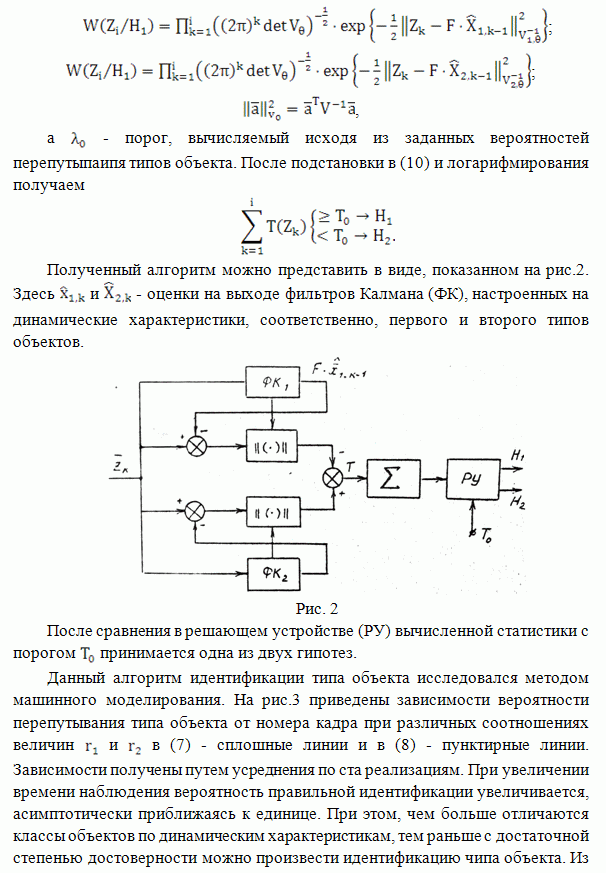
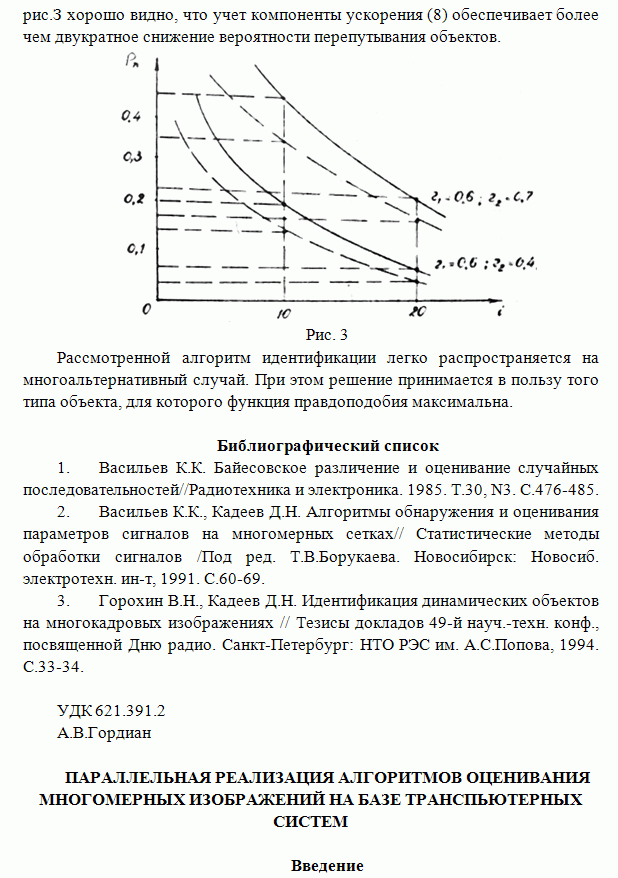
- ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ ПРИ ТРАЕКТОРНОЙ ОБРАБОТКЕ
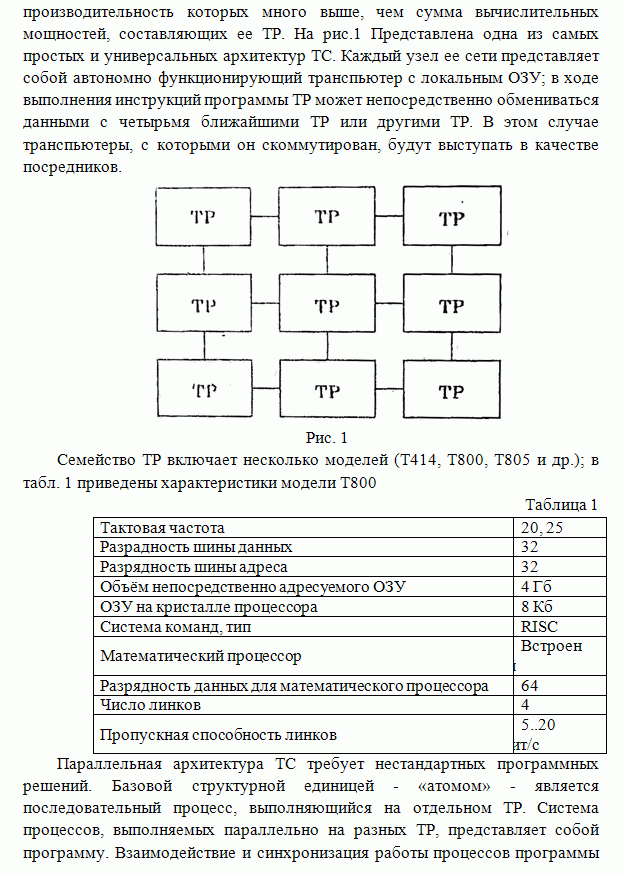
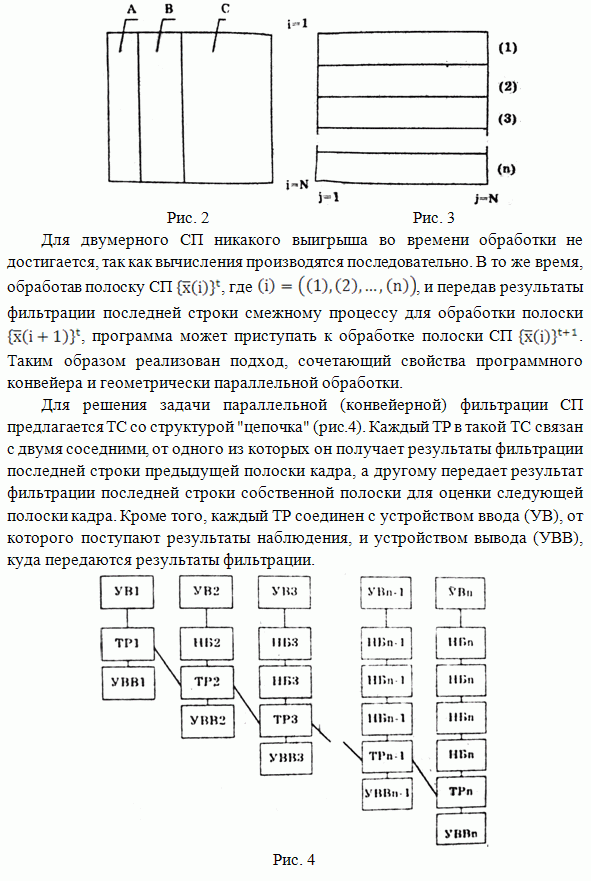
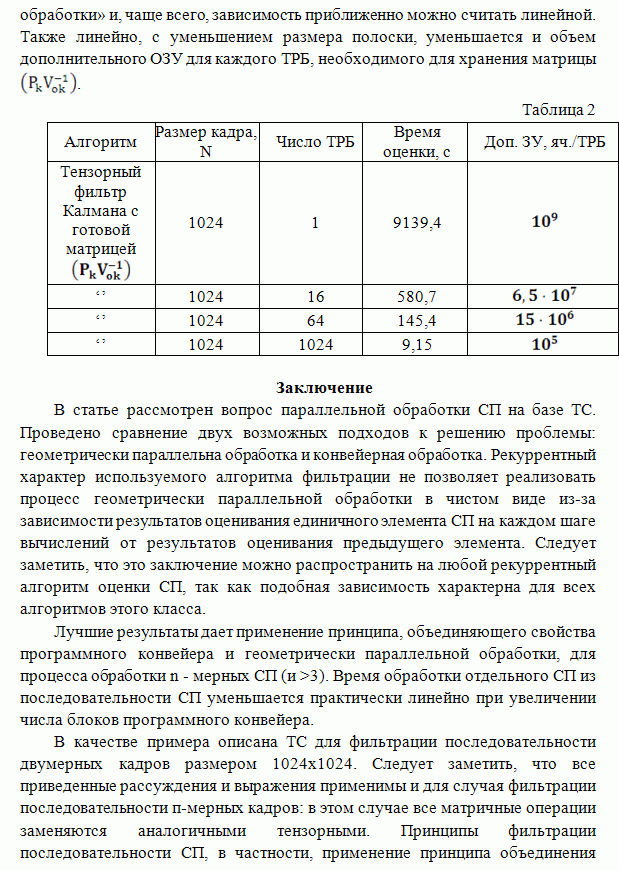
- ПАРАЛЛЕЛЬНАЯ РЕАЛИЗАЦИЯ АЛГОРИТМОВ ОЦЕНИВАНИЯ МНОГОМЕРНЫХ ИЗОБРАЖЕНИЙ НА БАЗЕ ТРАНСПЬЮТЕРНЫХ СИСТЕМ
- ПСЕВДОГРАДИЕНТНАЯ ФИЛЬТРАЦИЯ СТОХАСТИЧЕСКОГО ТРЕНДА
- ПРИМЕНЕНИЕ СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ С МАЛЫМИ ВЫЧИСЛИТЕЛЬНЫМИ ЗАТРАТАМИ
- КОМПЬЮТЕРНЫЙ ЭЛЕКТРОЭНЦЕФАЛОГРАФ