ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АНТИЧАСТИЦЫ

Согласно нерелятивистской квантовой механике, если частица, пребывающая в некотором состоянии попадет под влияние возмущающего потенциала U, то ее состояние изменится. Если положить то с точностью до фазового множителя амплитуда перехода в новое состояние определяется проекцией X на т. е.

Выражение представляет собой амплитуду, записанную в элегантной дираковской форме с использованием бракет векторов; впрочем, я не буду здесь часто применять эти обозначения. Условимся считать, что эта формула остается справедливой при переходе в релятивистскую область.

Предположим теперь, что состояние частицы возмущалось дважды — первый раз в момент времени а затем в момент времени нас будет интересовать амплитуда возврата в исходное состояние под влиянием второго возмущения. Обозначим через первое возмущение, действовавшее в момент времени а через возмущение в момент времени Нам нужно теперь записать результаты следующих процессов: рассеяния на потенциале эволюции состояния частицы в интервале времени от до и рассеяния на потенциале все это мы проделаем с помощью теории возмущений. Разумеется, самое простое, что может случиться, — это непосредственный переход из состояния опять в состояние с амплитудой Эта амплитуда определяет член низшего порядка ряда теории возмущений. Член следующего порядка малости отвечает процессу, при котором частица рассеивается на возмущении и переходит в некоторое промежуточное состояние с энергией в этом состоянии она пребывает в течение времени а затем рассеивается на возмущении обратно в состояние По всем промежуточным состояниям нужно просуммировать. Полная амплитуда перехода из состояния в исходное состояние будет

равна

(Для простоты я здесь считаю, что амплитуды первого порядка, отвечающие переходам из состояния обратно в равны нулю, т. е. что . Если в качестве промежуточных состояний использовать плоские волны и раскрыть выражения для амплитуд , то мы увидим, что

Здесь

и для частицы с массой . Множители с введены здесь с единственной

Рис. 1. Диаграммное представление вкладов прямого (а) и непрямого (б) переходов в полную амплитуду.

целью явно отразить релятивистские свойства, ибо величина представляет собой инвариантную плотность импульса. Графически данный процесс изображен на рис. 1.

Проанализируем полученное соотношение в некоторых специальных случаях. Я собираюсь сначала рассмотреть некоторые очень простые примеры, а затем перейду к более

общему случаю. Надеюсь, вы разберетесь в этих примерах, поскольку, осмыслив их, вы сразу же схватите суть дела; по крайней мере, ко мне понимание приходит именно таким путем.

Амплитуда перехода через промежуточное состояние отвечает рассеянию частицы из причем в промежуточном состоянии она имеет импульс и энергию Сейчас мы сделаем некое предположение, а именно, допустим, что все энергии строго положительны.

А вот теперь сюрприз: если оценить амплитуды для некоторых (можно даже допустить, что зависят от импульса ), то оказывается, что они не обращаются в нуль, когда находится вне светового конуса с вершиной в Вот что удивительно: если все энергии положительны, то волны, исходящие из некоторой точки, не смогут уместиться внутри светового конуса. Это вытекает из следующей математической теоремы.

Если функция представима в виде интеграла Фурье только по положительным частотам, т. е. если ее можно записать в виде

то она не может обращаться в нуль на конечных интервалах t, если только она тождественно не равна нулю. Я предпочел бы не останавливаться здесь на доказательстве этой теоремы, которое опирается на использование свойств функции

Вероятно, эта теорема вызовет у вас удивление, поскольку вы знаете, что можно взять функцию, обращающуюся в нуль на конечном интервале, и вычислить ее фурье-образ. Дело в том, что наряду с положительными частотами вы всегда будете получать и отрицательные. Я же настаиваю на том, что имеются только положительные частоты.

Чтобы использовать эту теорему в нашем случае, зафиксируем точки и представим интеграл по в виде интеграла по переменной . Этот интеграл будет совпадать по форме с интегралом (4), в котором значение равно нулю при зависит от . В нашем случае данная теорема применима непосредственно; мы видим, что амплитуда не может обращаться в нуль на любом конечном интервале времени. В частности, она не будет обращаться в нуль вне светового конуса с вершиной в Другими словами, будут существовать отличные от нуля амплитуды для частиц, движущихся

со скоростями больше скорости света, и никакая суперпозиция состояний с одними положительными энергиями не сможет исправить это положение.

Следовательно, если отвечает более позднему моменту времени, чем то в результирующую амплитуду будут вносить вклад частицы, которые движутся со скоростями больше скорости света и для которых точки разделены пространственноподобным интервалом.

Если события разделены пространственноподобным интервалом, то порядок их наступления зависит от выбора системы отсчета: если наблюдать эти события из системы отсчета, которая достаточно быстро движется относительно исходной, то момент будет предшествовать (рис. 2).

Как будут выглядеть эти события в новой системе отсчета? До наступления у нас будет иметься одна безмятежно движущаяся частица. В момент произойдет нечто очень странное, а именно: в точке на конечном расстоянии от исходной частицы возмущение приведет к рождению пары частиц, одна из которых будет, очевидно, двигаться вспять во времени. В момент исходная частица и та, что двигалась вспять во времени, исчезнут.

Рис. 2. Один и тот же процесс, наблюдаемый из различных систем отсчета: а — исходная система отсчета б — движущаяся система отсчета

Таким образом, теория относительности и требование положительности энергии заставляют нас допустить возможность рождения и аннигиляции пар, в которых одна из частиц движется вспять во времени. Чтобы понять, какой физический смысл имеет движение частицы вспять во времени, предположим, что у нее есть заряд. На рис. 2, б частица перемещается из точки в точку и переносит, скажем, положительный заряд из однако в точке частица оказывается раньше,

поэтому все выглядит так, будто отрицательный заряд переносится из в х.

Другими словами, порядок наступления событий зависит от выбора системы отсчета, и то, что одному кажется частицей, другому будет представляться как античастица. Фактически это и означает, что античастицы обязательно должны существовать.

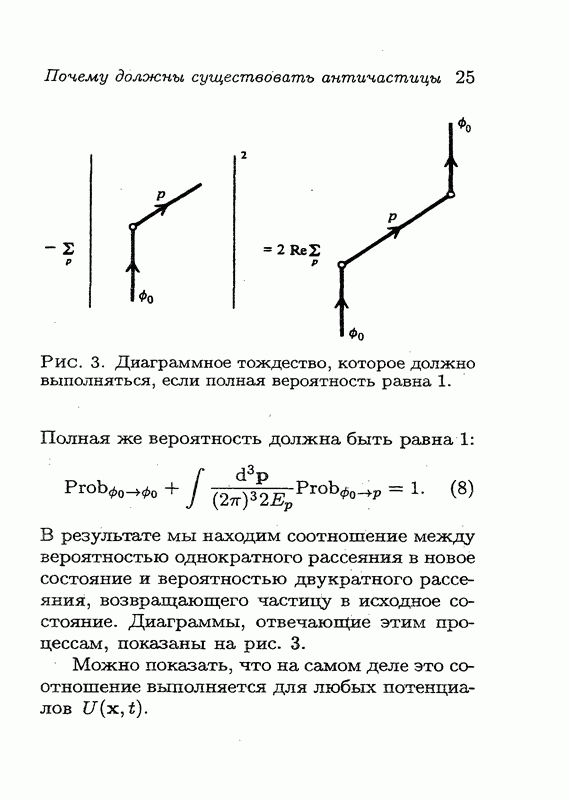
Подводя итог сказанному, можно утверждать следующее:

1) должны существовать античастицы, а также процессы рождения и уничтожения пар;

2) поведение античастиц определяется поведением обычных частиц.

Впоследствии мы тщательно проанализируем второе из этих утверждений, однако сейчас ограничимся следующими замечаниями. Если изменить на противоположные знаки координат х, у, z и времени t, то частица, первоначально двигавшаяся вперед во времени, окажется движущейся во времени вспять. Если обозначить через Р оператор пространственной инверсии, изменяющий знаки трех пространственных координат, через Т — операцию обращения времени, изменяющую направление его течения, и через С — оператор зарядового сопряжения, превращающий

частицы в античастицы и наоборот, то окажется, что действие операторов Р и Т на некоторое состояние приводит к тому же результату, что и действие оператора С, т. е. РТ — С.