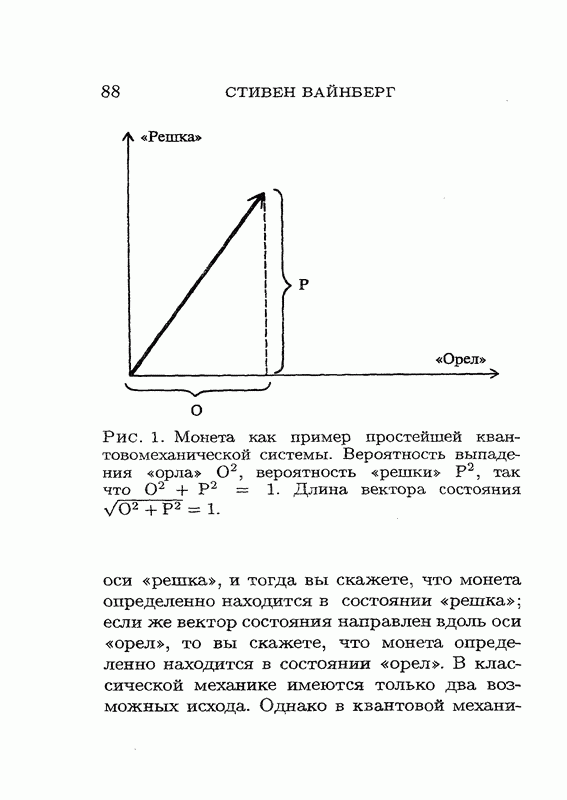
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
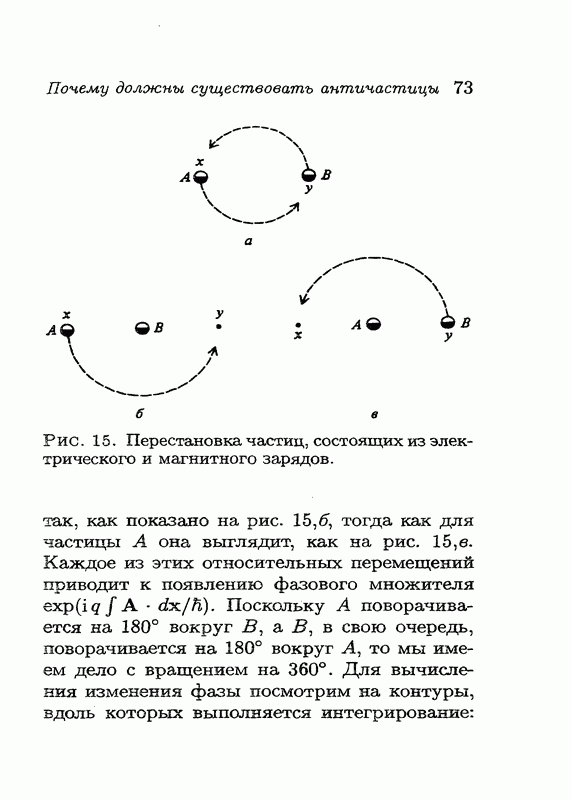
ОБРАЩЕНИЯ ВРЕМЕНИ
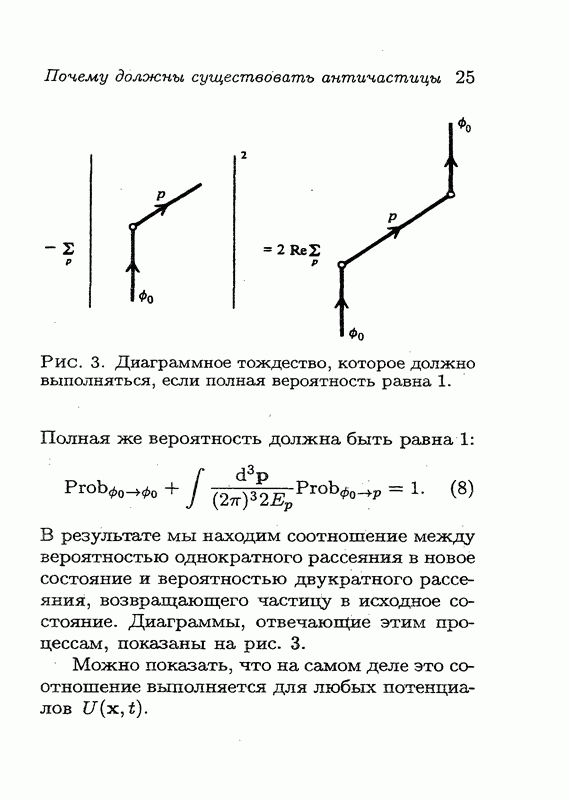
Почему так получается, что двукратное применение операции обращения времени к частице со спином  изменяет ее знак на противоположный? Ответ заключается в том, что двукратное действие Т эквивалентно пространственному вращению на 360°. Если дважды поменять направление оси
изменяет ее знак на противоположный? Ответ заключается в том, что двукратное действие Т эквивалентно пространственному вращению на 360°. Если дважды поменять направление оси  на противоположное, то получится поворот на 360°; в четырехмерном пространстве то же самое справедливо и в отношении оси t. Ниже я покажу, что это на самом деле верно (для этого мне даже не понадобится использовать какие-либо релятивистские соотношения между t и
на противоположное, то получится поворот на 360°; в четырехмерном пространстве то же самое справедливо и в отношении оси t. Ниже я покажу, что это на самом деле верно (для этого мне даже не понадобится использовать какие-либо релятивистские соотношения между t и  ). Как мы уже говорили, для частицы со спином
). Как мы уже говорили, для частицы со спином  поворот на 360° приводит к умножению на
поворот на 360° приводит к умножению на  и, таким образом,
и, таким образом,  Давайте покажем, что для частиц со спином
Давайте покажем, что для частиц со спином  действительно должно получаться
действительно должно получаться  . В табл. 1 приведены различные состояния и показано, как они изменяются после однократного и двукратного применения операции Т.
. В табл. 1 приведены различные состояния и показано, как они изменяются после однократного и двукратного применения операции Т.
Таблица 1. Результат обращения времени для различных состояний
(см. скан)
Первое состояние — это состояние, в котором частица находится в точке  с использованием дираковских обозначений оно записывается в виде
с использованием дираковских обозначений оно записывается в виде  Между символами
Между символами  находится индекс состояния или любой другой символ, обозначающий состояние; в данном случае это координата точки
находится индекс состояния или любой другой символ, обозначающий состояние; в данном случае это координата точки  в которой находится частица. Состояние частицы после обращения времени будет иметь вид
в которой находится частица. Состояние частицы после обращения времени будет иметь вид  т. е. ничего не произойдет, и частица останется на том же месте. С другой стороны, обращение времени для частицы в состоянии с импульсом
т. е. ничего не произойдет, и частица останется на том же месте. С другой стороны, обращение времени для частицы в состоянии с импульсом  переведет ее в состояние с импульсом
переведет ее в состояние с импульсом  ; повторное обращение времени вернет частицу обратно в состояние
; повторное обращение времени вернет частицу обратно в состояние 
Анализ состояния  показывает, что Т является так называемой антиунитарной операцией. Состояние
показывает, что Т является так называемой антиунитарной операцией. Состояние  можно представить в виде линейной комбинации, в которую состояния
можно представить в виде линейной комбинации, в которую состояния  для различных положений частицы входят с различными фазами. Чтобы получить состояние
для различных положений частицы входят с различными фазами. Чтобы получить состояние  , достаточно взять то же разложение
, достаточно взять то же разложение  в которое, однако, состояния входят с комплексно сопряженными фазовыми множителями. Следовательно, в общем случае
в которое, однако, состояния входят с комплексно сопряженными фазовыми множителями. Следовательно, в общем случае  т. е. при действии любого антиунитарного оператора вы должны сразу же заменить
т. е. при действии любого антиунитарного оператора вы должны сразу же заменить
коэффициенты на их комплексно сопряженные. Разумеется, при повторном применении Т вам опять понадобится вычислять комплексно сопряженные коэффициенты, но если вы разбираетесь в алгебре, то знаете, что это будет пустой тратой времени. Смотрите, что теперь получается. Состояние  было бы физически эквивалентным состоянию
было бы физически эквивалентным состоянию  если бы не эта дьявольская квантовая механика, из-за которой вечно получается путаница с фазами. В соответствии со сказанным
если бы не эта дьявольская квантовая механика, из-за которой вечно получается путаница с фазами. В соответствии со сказанным  фазовый множитель
фазовый множитель  причем этот множитель будет одинаковым для всех состояний, которые могут быть наложены на состояние
причем этот множитель будет одинаковым для всех состояний, которые могут быть наложены на состояние  и, таким образом, действие оператора ТТ не изменит результата интерференции состояний. Состояния с нулевым спином и спином
и, таким образом, действие оператора ТТ не изменит результата интерференции состояний. Состояния с нулевым спином и спином  не могут быть наложены друг на друга, поскольку между этими типами состояний есть фундаментальные различия; следовательно, суммарное изменение фазы в результате действия оператора ТТ может быть различным.
не могут быть наложены друг на друга, поскольку между этими типами состояний есть фундаментальные различия; следовательно, суммарное изменение фазы в результате действия оператора ТТ может быть различным.
Сейчас мы собираемся использовать следующий факт: если у нас есть состояние с некоторым угловым моментом  то
то  фазовый множитель
фазовый множитель  Для углового момента все должно выглядеть следующим образом: если объект вращается, то обращение
Для углового момента все должно выглядеть следующим образом: если объект вращается, то обращение
времени даст тот же объект, вращающийся в противоположном направлении. Например, поскольку Т действует как  то для углового момента
то для углового момента  будет
будет  т. е. действие оператора Т изменяет угловой момент на противоположный.
т. е. действие оператора Т изменяет угловой момент на противоположный.
Рассмотрим состояния с целочисленным спином. Среди них имеется состояние с нулевым угловым моментом, а именно  Однократное применение оператора Т к этому состоянию дает то же состояние
Однократное применение оператора Т к этому состоянию дает то же состояние  с некоторым фазовым множителем, повторное же применение Т вернет состояние к исходному
с некоторым фазовым множителем, повторное же применение Т вернет состояние к исходному  в силу антиунитарности Т. Таким образом, поскольку фаза должна быть одинаковой для всех интерферирующих состояний, то
в силу антиунитарности Т. Таким образом, поскольку фаза должна быть одинаковой для всех интерферирующих состояний, то  для состояний с целочисленным спином.
для состояний с целочисленным спином.
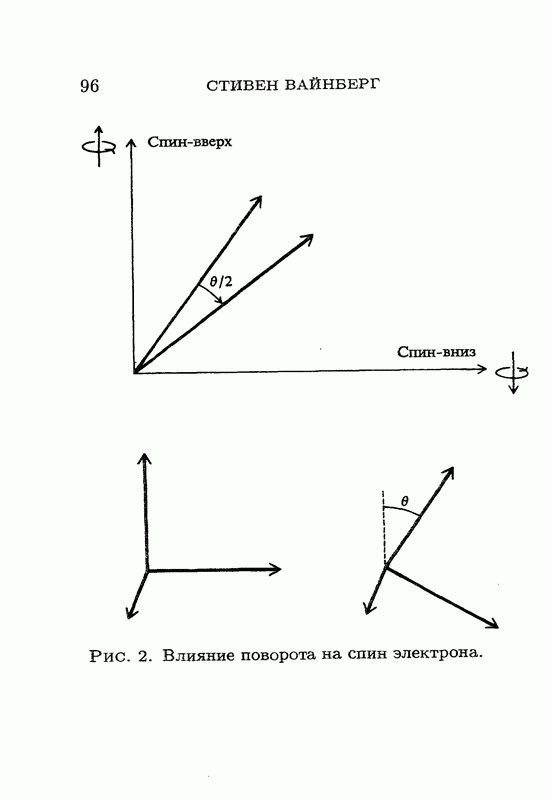
Чтобы разобраться в том, что происходит с полуцелым спином, рассмотрим простейший случай, когда спин равен Попробуем заполнить нашу таблицу для четырех специальных случаев: спин направлен параллельно оси  в прямом и в обратном направлениях,
в прямом и в обратном направлениях,  спин направлен параллельно оси
спин направлен параллельно оси  в прямом и в обратном направлениях:
в прямом и в обратном направлениях:  Элементарная теория спина объясняет нам, как два последних случая можно выразить
Элементарная теория спина объясняет нам, как два последних случая можно выразить
через базисные состояния  и
и  : состояние
: состояние  является результатом сложения базисных состояний в фазе, а
является результатом сложения базисных состояний в фазе, а  в противофазе. Физически обращение времени переводит состояние
в противофазе. Физически обращение времени переводит состояние  в состояние
в состояние  и наоборот. Точно так же при обращении времени из состояния
и наоборот. Точно так же при обращении времени из состояния  должно получиться состояние
должно получиться состояние  с точностью до фазового множителя.
с точностью до фазового множителя.
Для первой ячейки в таблице  с точностью до фазового множителя у нас должно получиться
с точностью до фазового множителя у нас должно получиться  . Легко проверить, что эта фаза может выбираться произвольно, и мы напишем
. Легко проверить, что эта фаза может выбираться произвольно, и мы напишем  Далее,
Далее,  должно быть равно
должно быть равно  с некоторым фазовым множителем. Мы не можем записать результат просто в виде
с некоторым фазовым множителем. Мы не можем записать результат просто в виде  поскольку при действии Т на состояние
поскольку при действии Т на состояние  ж), которое является результатом синфазного сложения
ж), которое является результатом синфазного сложения  вместо противофазного состояния
вместо противофазного состояния  умноженного на некоторое число, получилось бы опять синфазное состояние
умноженного на некоторое число, получилось бы опять синфазное состояние  , что лишено физического смысла. Чтобы произошло требуемое изменение фазы, мы обязаны положить
, что лишено физического смысла. Чтобы произошло требуемое изменение фазы, мы обязаны положить  т. е. взять противоположную по сравнению с
т. е. взять противоположную по сравнению с  фазу. Значит,
фазу. Значит,  и мы можем заполнить оставшиеся ячейки в таблице.
и мы можем заполнить оставшиеся ячейки в таблице.
Таким образом,  для спина и обращение времени всегда приводит к иному физическому состоянию; как легко показать, это справедливо для любого полуцелого спина j. Используя этот факт совместно с результатом для частиц с целочисленным спином, получаем, что ТТ эквивалентно полному повороту:
для спина и обращение времени всегда приводит к иному физическому состоянию; как легко показать, это справедливо для любого полуцелого спина j. Используя этот факт совместно с результатом для частиц с целочисленным спином, получаем, что ТТ эквивалентно полному повороту: 
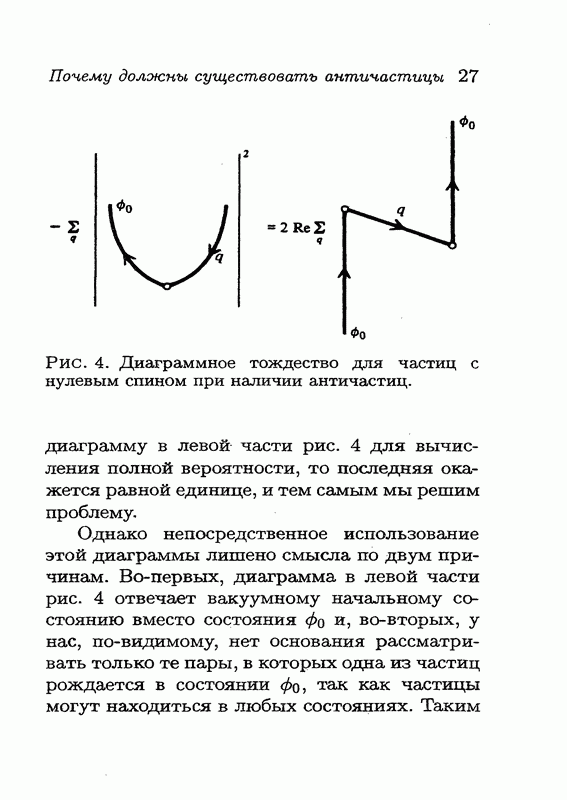
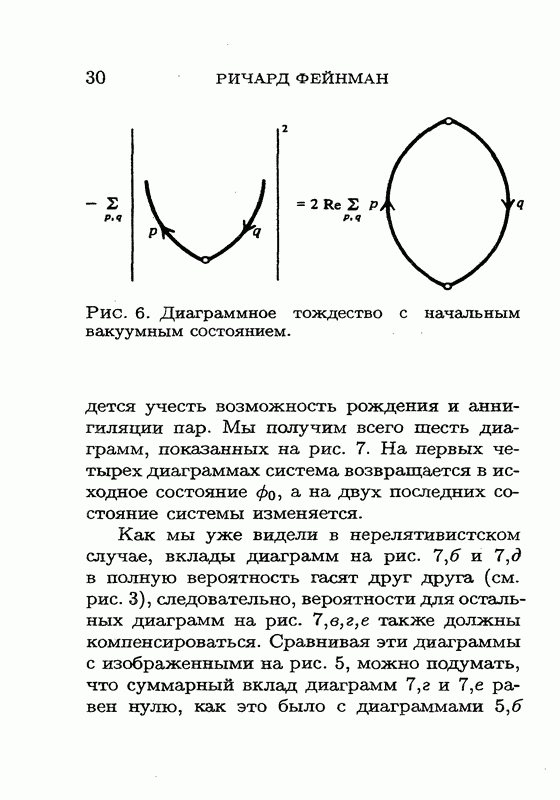
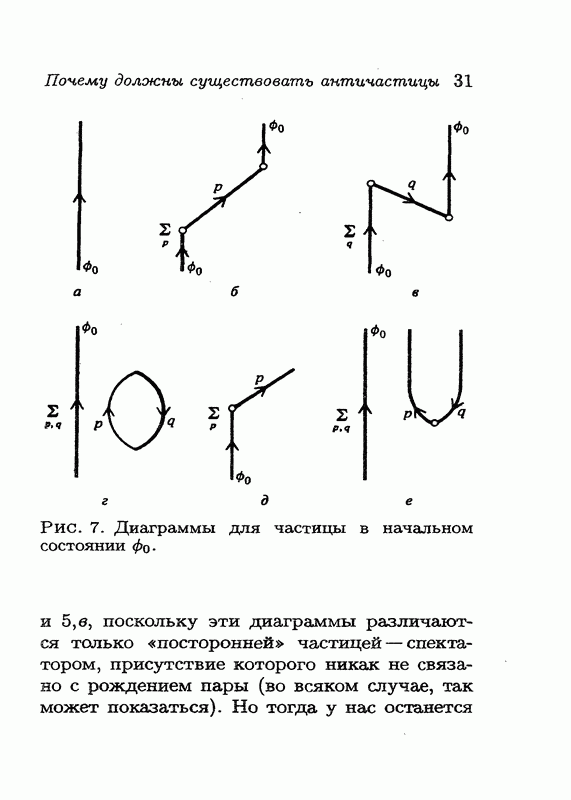
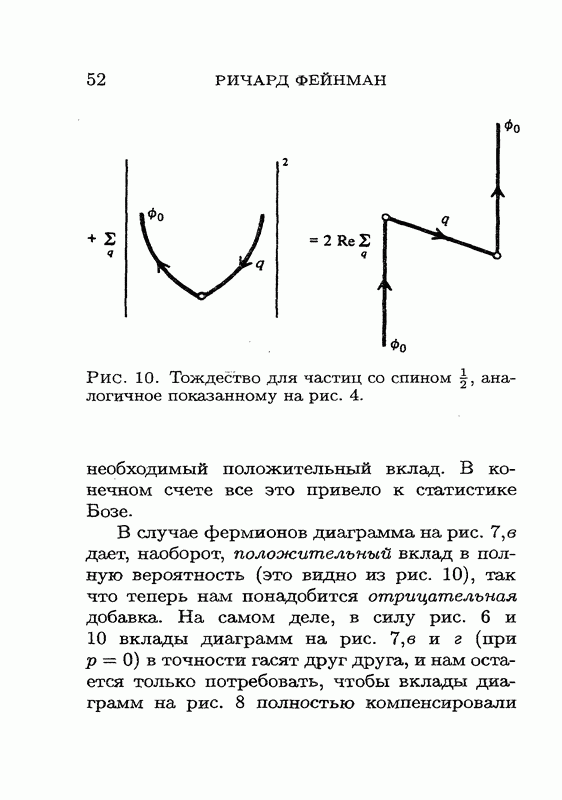
Мы наконец подошли к вопросу о знаке петли для частиц со спином Вы, наверное, еще помните, что в релятивистской квантовой теории потенциал приводит к рождению пар, поэтому вероятность того, что вакуумное состояние (т. е. состояние, в котором нет частиц) остается вакуумным, должна быть меньше единицы. Запишем амплитуду перехода из вакуумного состояния опять в вакуумное состояние в виде  где X — вклад всех замкнутых петель, показанных на рис. 6 справа. Величина X должна давать отрицательный вклад в вероятность того, что вакуумное состояние остается вакуумным; это следует из тождества на рис. 6, поскольку выражение в его левой части строго отрицательно.
где X — вклад всех замкнутых петель, показанных на рис. 6 справа. Величина X должна давать отрицательный вклад в вероятность того, что вакуумное состояние остается вакуумным; это следует из тождества на рис. 6, поскольку выражение в его левой части строго отрицательно.
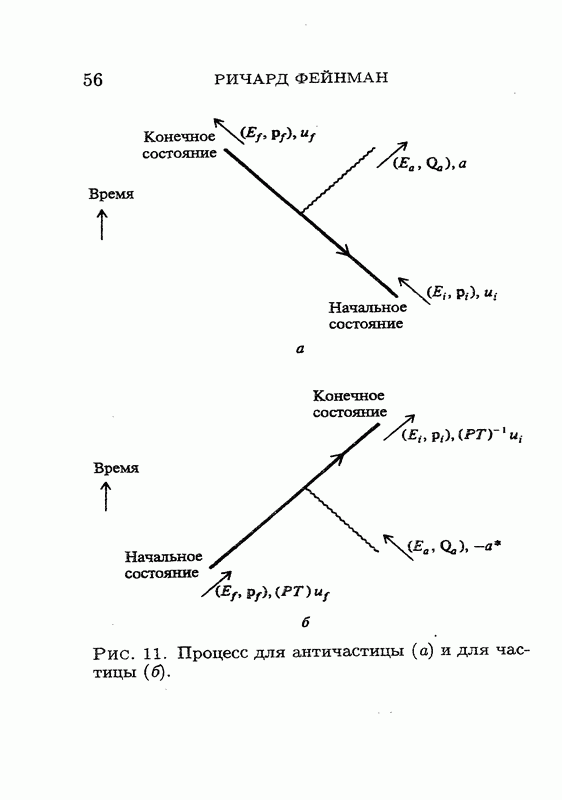
Рассмотрим петли, дающие вклад в X. Петля образуется электроном, который выходит из состояния, описываемого, скажем, дираковской волновой функцией и, обходит
петлю и возвращается в то же физическое состояние  мы же должны вычислить след получающегося произведения матриц, просуммировав диагональные элементы. Но здесь имеется одна тонкость: конечное физическое состояние могло оказаться повернутым на 360°, и мы действительно сталкиваемся с таким поворотом (или с эквивалентным ему преобразованием ТТ). Из какой бы системы отсчета вы ни наблюдали этот процесс, на определенном этапе электрон превратится в движущийся вспять во времени позитрон (одно Т), а затем превратится снова в электрон, движущийся вперед во времени (второе Т); таким образом, обойдя петлю, вы в конце концов придете к состоянию
мы же должны вычислить след получающегося произведения матриц, просуммировав диагональные элементы. Но здесь имеется одна тонкость: конечное физическое состояние могло оказаться повернутым на 360°, и мы действительно сталкиваемся с таким поворотом (или с эквивалентным ему преобразованием ТТ). Из какой бы системы отсчета вы ни наблюдали этот процесс, на определенном этапе электрон превратится в движущийся вспять во времени позитрон (одно Т), а затем превратится снова в электрон, движущийся вперед во времени (второе Т); таким образом, обойдя петлю, вы в конце концов придете к состоянию  (рис. 12).
(рис. 12).
Такой же оператор ТТ будет действовать и в случае бозонов (нулевой спин), однако при этом  так что здесь не возникнет никаких проблем. С бозонами все получается; вычисление для X дает отрицательный вклад. Однако для спина как мы только что показали, появляется дополнительный знак минус. Следовательно, чтобы обеспечить выполнение тождества на рис. 6, т. е. чтобы вклад X приводил к отрицательной добавке к вероятности, необходимо ввести дополнительное правило для частиц с полу целым спином, а именно,
так что здесь не возникнет никаких проблем. С бозонами все получается; вычисление для X дает отрицательный вклад. Однако для спина как мы только что показали, появляется дополнительный знак минус. Следовательно, чтобы обеспечить выполнение тождества на рис. 6, т. е. чтобы вклад X приводил к отрицательной добавке к вероятности, необходимо ввести дополнительное правило для частиц с полу целым спином, а именно,

Рис. 12. Петля для пары частица-античастица; показаны две операции обращения времени.
вычисляя вклад каждой одиночной петли, мы должны поставить еще один знак минус, чтобы компенсировать знак минус, который появляется из-за  Бели мы этого не сделаем, то не сможем правильно вычислить вероятность и не получим последовательной теории частиц со спином
Бели мы этого не сделаем, то не сможем правильно вычислить вероятность и не получим последовательной теории частиц со спином  Этот дополнительный знак минус связан со статистикой Ферми.
Этот дополнительный знак минус связан со статистикой Ферми.
Статистика Ферми для частиц со спином обусловлена общим правилом, согласно которому вы должны умножать результат для каждой замкнутой петли на —1 (см. рис. 9). Случаи, изображенные на рис. 9, а и б, различаются
знаком минус, поскольку на рис. 9, а имеется две петли, тогда как на рис. 9, 6 - только одна. Таким образом, рис. 9 говорит о том, что, поменяв две частицы местами, вы должны поставить знак минус, а это и есть статистика Ферми!
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПОЧЕМУ ДОЛЖНЫ СУЩЕСТВОВАТЬ АНТИЧАСТИЦЫ
- ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АНТИЧАСТИЦЫ
- ЧАСТИЦЫ С НУЛЕВЫМ СПИНОМ И СТАТИСТИКА БОЗЕ
- СООТНОШЕНИЕ МЕЖДУ ПОВЕДЕНИЕМ ЧАСТИЦ И АНТИЧАСТИЦ
- СПИН 1/2 И СТАТИСТИКА ФЕРМИ
- ОБРАЩЕНИЕ ВРЕМЕНИ И АНТИЧАСТИЦЫ
- ОБРАЩЕНИЯ ВРЕМЕНИ
- МАГНИТНЫЕ МОНОПОЛИ, СПИН И СТАТИСТИКА ФЕРМИ
- ЗАКЛЮЧЕНИЕ
- НА ПУТИ К ОКОНЧАТЕЛЬНЫМ ФИЗИЧЕСКИМ ЗАКОНАМ