| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СООТНОШЕНИЕ МЕЖДУ ПОВЕДЕНИЕМ ЧАСТИЦ И АНТИЧАСТИЦ
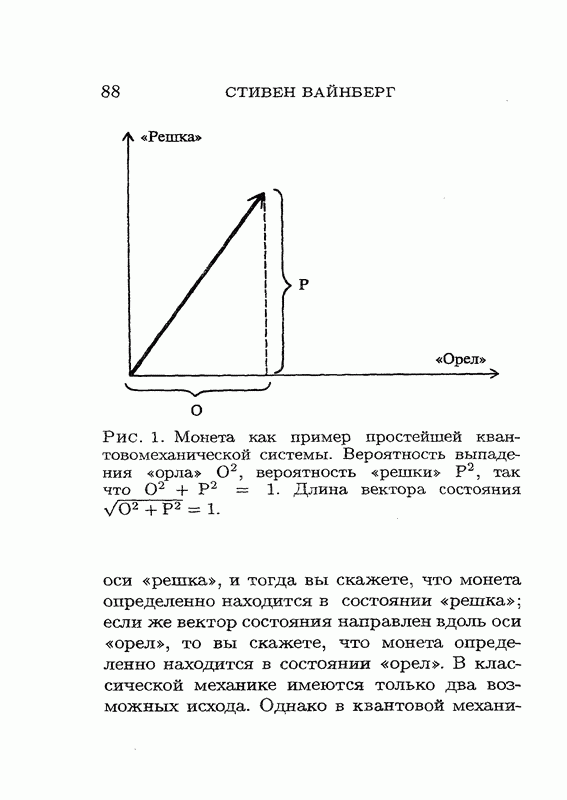
Прежде чем начать разговор о фермионах, мне хотелось бы вернуться назад и немного подробнее объяснить, как соотносится поведение частиц с поведением античастиц. Разумеется, поведение античастиц полностью определяется поведением соответствующих частиц. Рассмотрим это более подробно для простейшего случая нулевого спина и скалярного потенциала U. Мы уже знаем, что для  амплитуда
амплитуда
перехода свободной частицы массой  из
из  равна
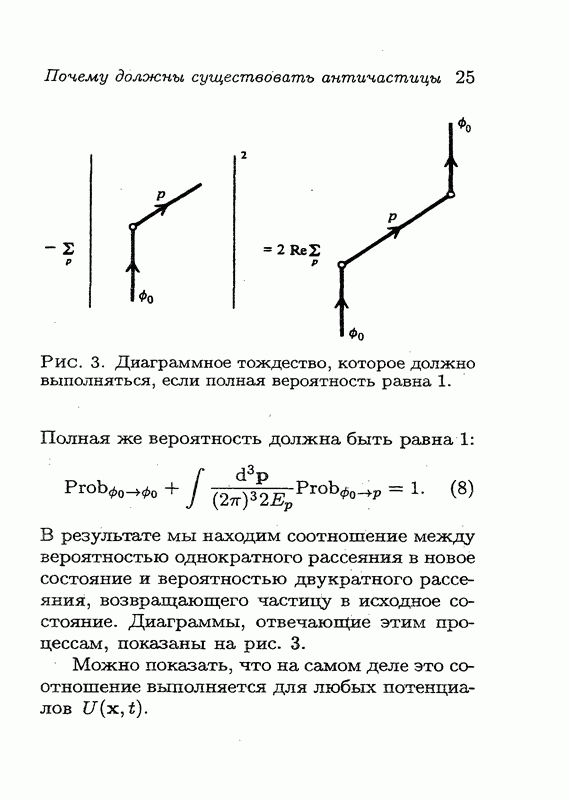
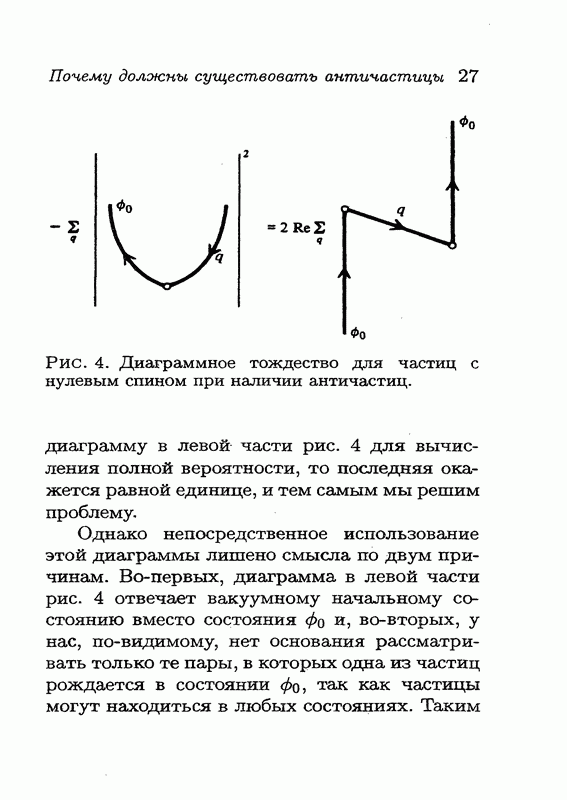
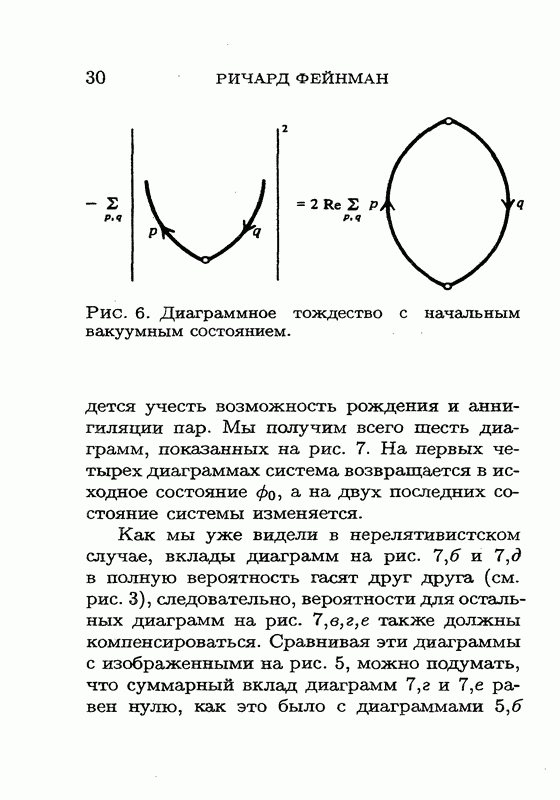
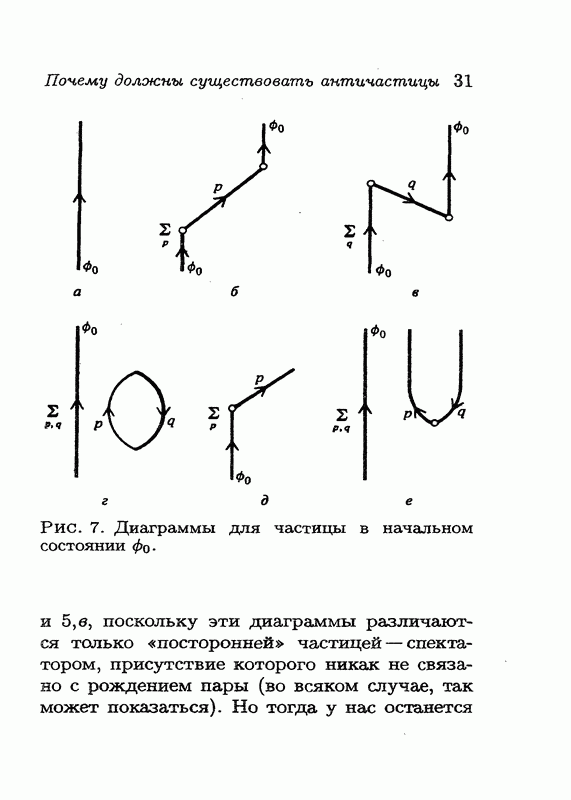
равна

Эта формула релятивистски ковариантна, поэтому для нулевого спина величины  в (5) можно считать постоянными. Нас интересует, какова будет амплитуда при
в (5) можно считать постоянными. Нас интересует, какова будет амплитуда при 
Для  и пространственноподобного интервала ответ прост: амплитуда по-прежнему равна
и пространственноподобного интервала ответ прост: амплитуда по-прежнему равна  Объясняется это следующим. Как мы уже знаем,
Объясняется это следующим. Как мы уже знаем,  справедлива для пространственноподобных интервалов при
справедлива для пространственноподобных интервалов при  Если наблюдать наш процесс из другой системы отсчета, то интервал по-прежнему будет пространственноподобным, однако может оказаться, что в такой системе отсчета
Если наблюдать наш процесс из другой системы отсчета, то интервал по-прежнему будет пространственноподобным, однако может оказаться, что в такой системе отсчета  Там мы получим ту же амплитуду, поскольку она не может зависеть от выбора системы координат; если же мы попытаемся выразить
Там мы получим ту же амплитуду, поскольку она не может зависеть от выбора системы координат; если же мы попытаемся выразить  в новой системе отсчета, то получим для
в новой системе отсчета, то получим для  в точности такую снсе формулу в силу ее релятивистской ковариантности. Итак, выражение для
в точности такую снсе формулу в силу ее релятивистской ковариантности. Итак, выражение для 
справедливо в области «абсолютно будущего» (верхняя полость светового конуса) и в области «абсолютно удаленного» (т. е. для событий, отстоящих от вершины конуса на пространственноподобный интервал). А как насчет области «абсолютно прошедшего»?
Здесь нам придется учесть, что при  волны по-прежнему будут распространяться только с положительными энергиями. Следовательно, в данной области мы сможем записать амплитуду в виде
волны по-прежнему будут распространяться только с положительными энергиями. Следовательно, в данной области мы сможем записать амплитуду в виде

где  — некоторая функция, вид которой нам еще предстоит определить. Причину изменения знака показателя экспоненты можно объяснить следующим образом. Волны испускаются из точки
— некоторая функция, вид которой нам еще предстоит определить. Причину изменения знака показателя экспоненты можно объяснить следующим образом. Волны испускаются из точки  и мы настаиваем на том, что они покидают источник, имея только положительные энергии (частоты). Другими словами, зависимость от времени должна иметь вид
и мы настаиваем на том, что они покидают источник, имея только положительные энергии (частоты). Другими словами, зависимость от времени должна иметь вид  где
где  Здесь
Здесь  интервал времени, прошедший с момента испускания волны; этот интервал должен быть положительным. При
интервал времени, прошедший с момента испускания волны; этот интервал должен быть положительным. При  волны существуют в течение времени
волны существуют в течение времени  а при
а при  они существуют в течение времени
они существуют в течение времени 
Таким образом, при  мы должны попытаться записать амплитуду в виде (10) и в области абсолютно прошедшего, и в области абсолютно удаленного. Это означает, что при
мы должны попытаться записать амплитуду в виде (10) и в области абсолютно прошедшего, и в области абсолютно удаленного. Это означает, что при  амплитуду можно вычислить в области абсолютно удаленного с помощью любого из выражений (9) или (10). Путем этих рассуждений можно сначала определить G в указанной области, а затем найти однозначное продолжение полученного выражения на произвольные времена
амплитуду можно вычислить в области абсолютно удаленного с помощью любого из выражений (9) или (10). Путем этих рассуждений можно сначала определить G в указанной области, а затем найти однозначное продолжение полученного выражения на произвольные времена 
Если  и события
и события  разделены пространственноподобным интервалом, то мы получим формулу (9), в которой суммирование ведется по отрицательным частотам. Вопрос в том, можно ли записать эту амплитуду в виде функции только положительных частот? В общем случае сделать этого нельзя. Поистине удивительно, что именно для данной релятивистски инвариантной функции найти такое представление оказывается возможным. Давайте выясним почему.
разделены пространственноподобным интервалом, то мы получим формулу (9), в которой суммирование ведется по отрицательным частотам. Вопрос в том, можно ли записать эту амплитуду в виде функции только положительных частот? В общем случае сделать этого нельзя. Поистине удивительно, что именно для данной релятивистски инвариантной функции найти такое представление оказывается возможным. Давайте выясним почему.
Прежде всего отметим, что при  функция
функция  вещественна. В этом случае экспоненциальный множитель просто равен
вещественна. В этом случае экспоненциальный множитель просто равен  его мнимая часть — нечетная функция, интегрируя ее в симметричных
его мнимая часть — нечетная функция, интегрируя ее в симметричных
пределах, мы получим нуль. Если же F вещественна при  то в силу релятивистской инвариантности она должна оставаться вещественной для любых событий
то в силу релятивистской инвариантности она должна оставаться вещественной для любых событий  разделенных пространственноподобным интервалом. В самом деле, движущийся наблюдатель должен получить такое же вещественное значение для амплитуды, хотя для него
разделенных пространственноподобным интервалом. В самом деле, движущийся наблюдатель должен получить такое же вещественное значение для амплитуды, хотя для него  Поскольку эта амплитуда вещественна, то она совпадает со своей комплексно сопряженной, в которую время входит с обратным знаком. Таким образом, амплитуда
Поскольку эта амплитуда вещественна, то она совпадает со своей комплексно сопряженной, в которую время входит с обратным знаком. Таким образом, амплитуда  совпадает с комплексно сопряженной амплитудой
совпадает с комплексно сопряженной амплитудой 

С этой формулой все в порядке: волны распространяются только с положительными энергиями. Полученное решение единственно, так как в силу теоремы (4) не существует функции вида (10), которая отличалась бы от него только в области абсолютно прошедшего. Итак, когда  предшествует
предшествует  в области абсолютно будущего, решение дается равенством (9); если
в области абсолютно будущего, решение дается равенством (9); если  предшествует
предшествует  в области
в области
абсолютно прошедшего, то решение дается равенством (11); в промежуточной области абсолютно удаленного, где события  разделены пространственноподобным интервалом, решение дается любым из соотношений (9) или (11) —в этой области обе формулы совпадают!
разделены пространственноподобным интервалом, решение дается любым из соотношений (9) или (11) —в этой области обе формулы совпадают!
Сначала мы рассмотрели, что происходит в одной области пространства-времени, а затем обобщили полученный результат на все остальные области, опираясь только на соображения релятивистской инвариантности. В этом нет никакой мистики. Если бы мы знали, что происходит хотя бы в одной области четырехмерного евклидова пространства, и при этом знали, как это нечто преобразуется при поворотах системы отсчета (здесь предполагается инвариантность), то мы могли бы как угодно повернуть нашу область и при этом абсолютно точно знали, что произойдет; действуя подобным образом, мы выяснили бы, что происходит в любом месте нашего четырехмерного евклидова пространства. Здесь же мы имеем дело с четырехмерным пространством Минковского  которое устроено немного иначе; впрочем, отличия не столь велики, и мы могли бы действовать тем же образом. Трудность с пространством
которое устроено немного иначе; впрочем, отличия не столь велики, и мы могли бы действовать тем же образом. Трудность с пространством
Минковского состоит в том, что в нем имеется «ничейная» полоса, нейтральная зона; находясь в ней, событие  оказывается вне светового конуса с вершиной в
оказывается вне светового конуса с вершиной в  преобразования Лоренца туда «не достают». Тем не менее, мы получили правильный ответ и в области абсолютно удаленного, воспользовавшись тем, что требование положительности энергий накладывает определенные ограничения на решения. Иначе говоря, изменяющая все знаки операция РТ по существу является релятивистским преобразованием, или, скорее, преобразованием Лоренца, продолженным на область абсолютно удаленного с помощью требования положительности энергий. Вот почему нет ничего удивительного в том, что релятивистская инвариантность столь важна.
преобразования Лоренца туда «не достают». Тем не менее, мы получили правильный ответ и в области абсолютно удаленного, воспользовавшись тем, что требование положительности энергий накладывает определенные ограничения на решения. Иначе говоря, изменяющая все знаки операция РТ по существу является релятивистским преобразованием, или, скорее, преобразованием Лоренца, продолженным на область абсолютно удаленного с помощью требования положительности энергий. Вот почему нет ничего удивительного в том, что релятивистская инвариантность столь важна.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПОЧЕМУ ДОЛЖНЫ СУЩЕСТВОВАТЬ АНТИЧАСТИЦЫ
- ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АНТИЧАСТИЦЫ
- ЧАСТИЦЫ С НУЛЕВЫМ СПИНОМ И СТАТИСТИКА БОЗЕ
- СООТНОШЕНИЕ МЕЖДУ ПОВЕДЕНИЕМ ЧАСТИЦ И АНТИЧАСТИЦ
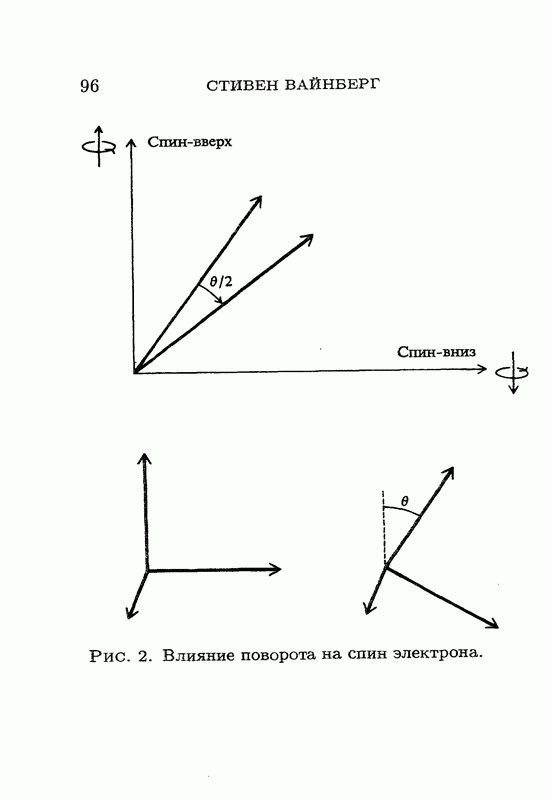
- СПИН 1/2 И СТАТИСТИКА ФЕРМИ
- ОБРАЩЕНИЕ ВРЕМЕНИ И АНТИЧАСТИЦЫ
- ОБРАЩЕНИЯ ВРЕМЕНИ
- МАГНИТНЫЕ МОНОПОЛИ, СПИН И СТАТИСТИКА ФЕРМИ
- ЗАКЛЮЧЕНИЕ
- НА ПУТИ К ОКОНЧАТЕЛЬНЫМ ФИЗИЧЕСКИМ ЗАКОНАМ