СПИН 1/2 И СТАТИСТИКА ФЕРМИ

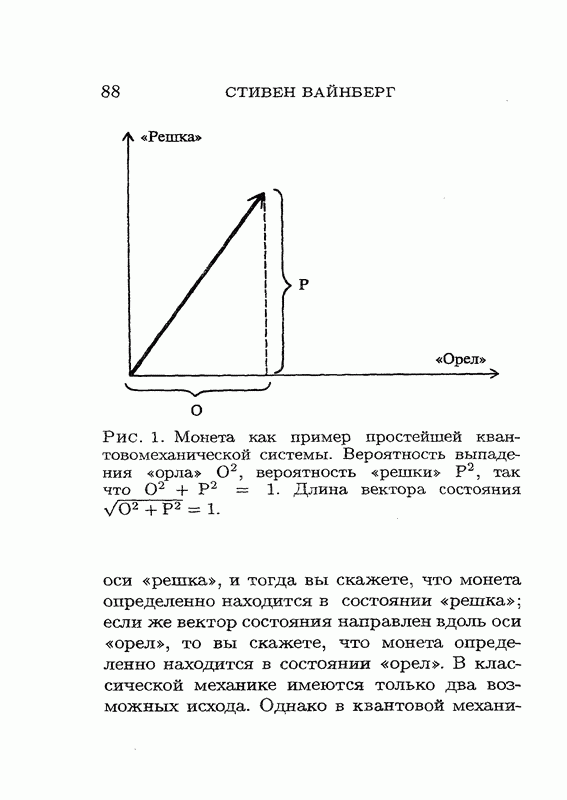
До сих пор спин считался равным нулю; теперь мне бы хотелось положить его равным и посмотреть, что из этого получится. Если имеется состояние со спином и вы совершите поворот, скажем, относительно оси z на угол , то фаза состояния изменится на . В теории групп имеется уйма методов доказательства

подобных штук; я не буду здесь на этом останавливаться, хотя это довольно приятное времяпрепровождение. Суть в том, что когда вы совершаете поворот на 360°, волновая функция умножается на Этот результат очень трудно осмыслить, и интуиция здесь не поможет. Как может поворот на 360° что-либо изменить? Сложнее всего нам надо будет следить за тем, был ли совершен поворот на 360° или нет, или, другими словами, надо ли писать знак минус или нет. Мы увидим, что появление загадочного знака минус у фермионов обусловлено именно таким незамеченным поворотом на 360°.

Дирак очень изящно продемонстрировал то, как полный поворот можно отличить от ситуации, в которой ничего не произошло В действительности только два полных поворота дают тот же результат, что и отсутствие вращения. Я вам сейчас покажу кое-что из того, что делают танцовщицы. Я собиралось повернуть этот стакан на полный оборот (см. серию снимков на рис. 9А) — запомните, в какую сторону

я это делаю — пока вы опять не увидите вот эту метку; вот я повернул его на 360°, но у меня возникли проблемы. Если я буду продолжать в том же духе — для этого потребуется немного мужества, если учесть обстоятельства — и не вывихну себе руку, то все встанет на свои места. Таким образом, два поворота равносильны тому, что ничего не произошло, но для одного поворота это не так, поэтому вам придется все время следить, был ли поворот; остальная часть этой лекции будет действовать вам на нервы из-за этих постоянных попыток отследить, был ли поворот или нет.

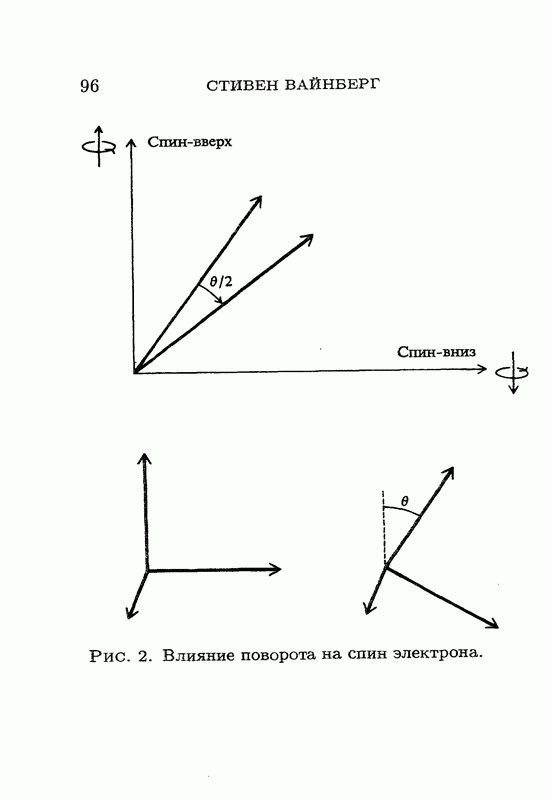
Чтобы у вас сложилось представление о структуре часто встречающихся здесь формул с половинными углами, я упомяну в качестве примера еще кое-что. Допустим, у вас есть электрон, и вы знаете, что проекция его спина на ось составляет Какова вероятность того, что измерение проекции спина на какое-либо другое направление, скажем, на ось , даст Если угол между этими двумя

Рис. 9А.

направлениями составляет , то ответ будет таков:

Давайте теперь посмотрим, что происходит в теории полуцелого спина с амплитудами для скалярного взаимодействия. Мы рассмотрим простое возмущение U, для которого спиновые составляющие амплитуд будут обусловлены

свойствами самих частиц, а не возмущения; это существенно упростит анализ. Мы выведем соотношения, сходные с полученной выше формулой с половинным углом, однако в них будут реально учтены релятивистские поправки. Итак, приступим.

Если у нас есть частица массой , то, как мы знаем, энергия и импульс удовлетворяют соотношению

где — разумеется, просто постоянная, и - абсолютная величина импульса. Из (13) вытекает, что если энергия Е задана, то импульс известен, и наоборот, так что здесь можно обойтись только одной переменной. С учетом сказанного соотношение (13) становится похожим на тригонометрическую формулу разница только в том, что здесь есть множитель и стоит знак минус. Чтобы выразить через одну переменную, вместо тригонометрических функций нужно использовать гиперболические. Если написать

то будут автоматически удовлетворять соотношению (13), здесь новая переменная — быстрота.

Предположим, что частица в состоянии с некоторым спином переходит под влиянием возмущения из состояния покоя в состояние с импульсом . В начальном состоянии -импульс был равен а в конечном где определены в (14). Амплитуда перехода частицы из начального состояния в конечное состояние дается формулой с половинными углами, аналогичной (12); с точностью до несущественного множителя она имеет вид

По аналогии с рассмотренным выше пространственным поворотом с точностью до несущественного множителя мы можем записать это выражение в форме

Эту амплитуду можно представить в релятивистски-ковариантной форме, если учесть, что где скалярное произведение

4-векторов. В результате амплитуда принимает вид

Преимущество релятивистски-ковариантной формы записи состоит в том, что амплитуда, полученная нами для частного случая, будет верна при любых Попробуем с помощью этого выражения найти амплитуду рождения пары. Положим, как и прежде, будем теперь считать, что Состояние с отрицательной энергией, разумеется, отвечает античастице. В данном случае и для амплитуды рождения пары мы находим

Используя эти результаты, мы продолжим наш разговор о полной вероятности для спина и увидим, что здесь нам придется столкнуться с принципом Паули. Поскольку рассмотрение данного вопроса во многом аналогично случаю нулевого спина, основное внимание я уделю только различиям между ситуациями с нулевым спином и спином

Если рассматривать начальное вакуумное состояние, то результаты для нулевого спина

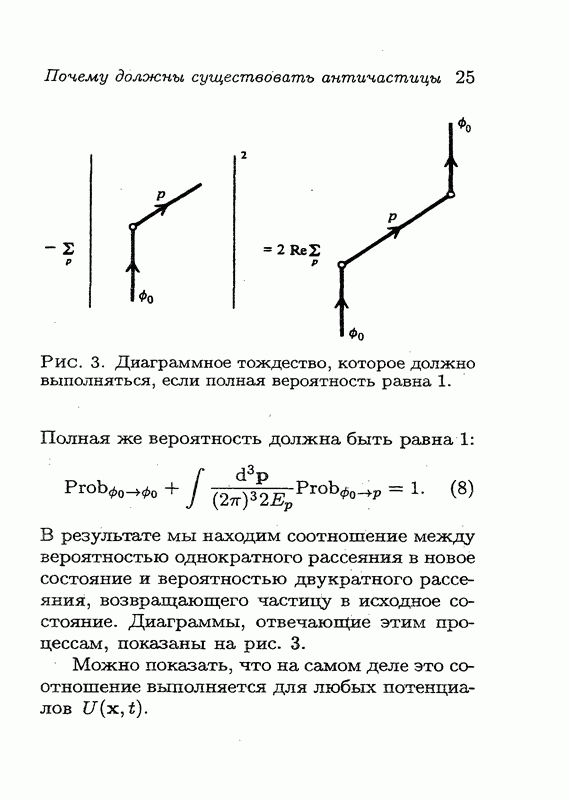
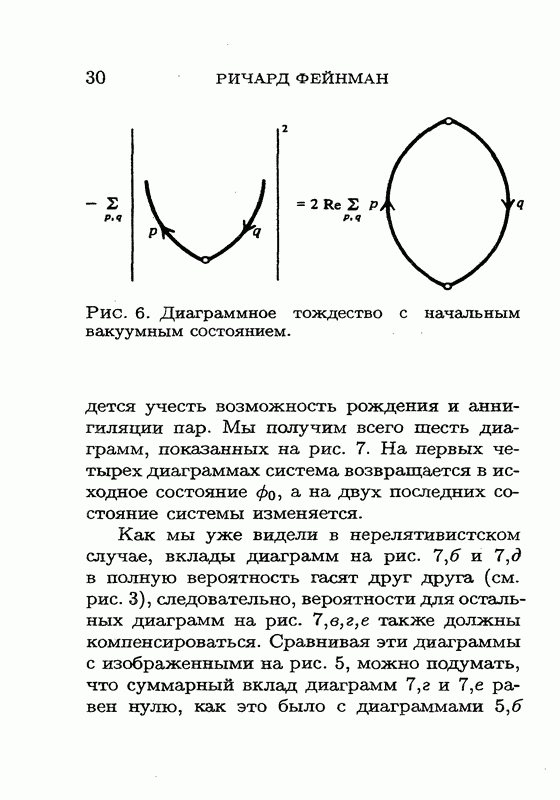
непосредственно обобщаются на наш случай, и мы получим такое же соотношение, как и на рис. 6.

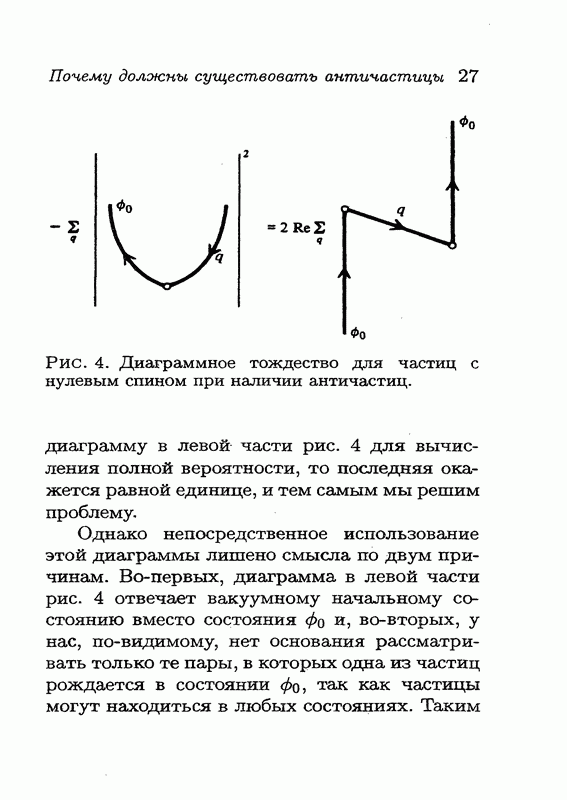
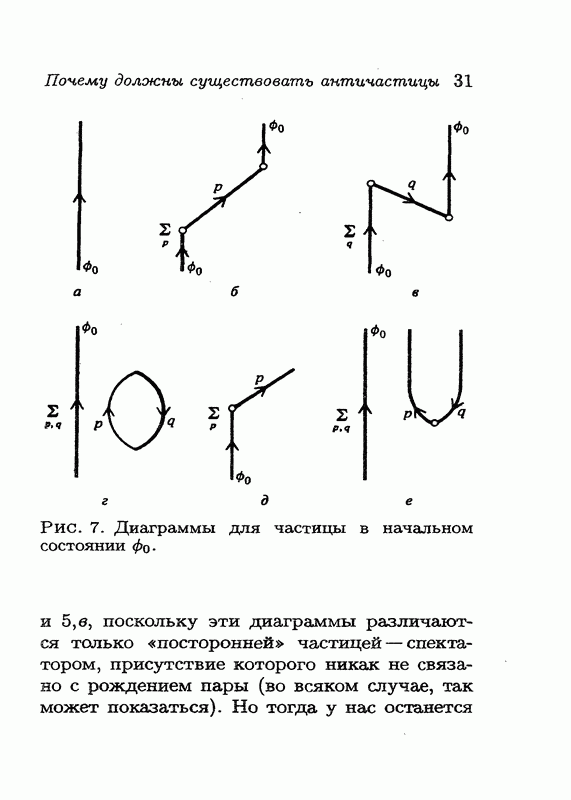
Рассмотрим теперь процесс, начальное условие для которого задается частицей в состоянии будем считать, что в этом состоянии частица покоится. Мы получим те же шесть диаграмм, что и на рис. 7, однако на этот раз амплитуды на этих диаграммах будут связаны между собой совершенно другими соотношениями.

Для вычисления полной вероятности нам потребуются вещественная часть амплитуд на рис. 7, б, в, г и квадрат модуля амплитуд на рис. 7, д и е. Начнем с процесса на рис. 7, б, в котором частица рассеивается в точке в состояние , затем движется до точки где испытывает еще одно рассеяние, возвращающее ее в состояние Из соотношения (17) видно, что каждый акт рассеяния приводит к появлению множителя , поэтому амплитуда процесса на рис. 7, б будет равна

причем знак минус здесь обусловлен множителями — i, появляющимися в каждой из вершин диаграммы.

Вероятность процесса на рис. 7, д дается квадратом модуля выражения (16); результат суммирования по импульсам показывает, что в силу (16) и (19) соотношение на рис. 3 будет справедливо и для частиц со спином

Теперь надо быть очень внимательными, чтобы получить правильное выражение для диаграммы на рис. 7, в. Это выражение содержит отрицательные частоты и должно совпадать с (19), когда события разделены пространственноподобным интервалом. Но (19), очевидно, совпадает с выражением которое, в свою очередь, равно в области абсолютно удаленного, так что амплитуда на рис. 7, в будет однозначно определяться равенством

Эта формула получена только на основе аналитических свойств амплитуды [таким же

способом было получено равенство (11)]; при ее выводе выражение (18) не использовалось, хотя можно было бы считать, что множитель возник из-за двух факторов Апары [см. (18)].

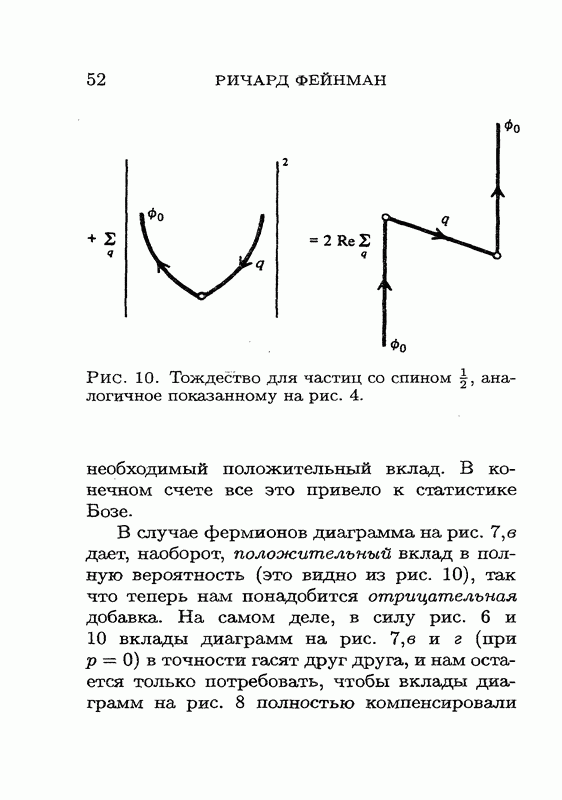
Здесь проявляется важное различие случаев нулевого спина и спина соотношение на рис. 4 неприменимо для фермионов. Мы теперь располагаем всем необходимым, чтобы убедиться в правильности этого вывода для частиц со спином Согласно (18), вероятность рождения пары (которая обязательно должна быть положительной) равна ; сравнивая этот результат с вещественной частью амплитуды (20) (равной произведению на амплитуду при нулевом спине), мы получим соотношение на рис. 10, которое из-за знака минус принципиально отличается от соотношения на рис. 4.

Вспомним теперь, что для бозе-частиц диаграмма на рис. 7, в давала отрицательный вклад в полную вероятность. Это означало, что должно было возникнуть нечто, дающее положительный вклад и тем самым сохраняющее общий баланс. Эту проблему можно решить, рассмотрев диаграммы 7, г и 7, е с р = 0 и диаграмму на рис. 7, в. Мы видели, что добавление обменной диаграммы (рис. 8) дает

Рис. 10. Тождество для частиц со спином , аналогичное показанному на рис. 4.

необходимый положительный вклад. В конечном счете все это привело к статистике Бозе.

В случае фермионов диаграмма на рис. 7, в дает, наоборот, положительный вклад в полную вероятность (это видно из рис. 10), так что теперь нам понадобится отрицательная добавка. На самом деле, в силу рис. 6 и 10 вклады диаграмм на рис. 7, в и г (при р = 0) в точности гасят друг друга, и нам остается только потребовать, чтобы вклады диаграмм на рис. 8 полностью компенсировали

друг друга — тогда полная вероятность будет равна единице.

Из сказанного ясно, что амплитуды, отвечающие диаграммам, в которых два фермиона поменялись местами, должны вычитаться. Это может быть верно только при следующем условии: если в некотором состоянии имеется частица- спектатор, то вероятность появления в том же состоянии другой частицы при рождении пары уменьшается для фермионов; если для бозонов амплитуда увеличивалась до 1 + 1 = 2, то для фермионов она падает до 1 - 1 = 0. Правило состоит в том, что если имеется частица в некотором состоянии, то при рождении пары в этом состоянии не может возникнуть другая частица; присутствие частицы не позволяет произойти тому, что вы ожидали, и величина вероятности изменяется в нужную сторону. Таким образом, мы на конкретном примере продемонстрировали связь спина со статистикой и, в частности, показали, что она должна быть разной для частиц с нулевым спином и спином Мы использовали теорию относительности и квантовую механику и получили соотношения, вытекающие из уравнения Дирака. Продолжим обсуждение этих вопросов, чтобы еще яснее представить себе, почему все это происходит.