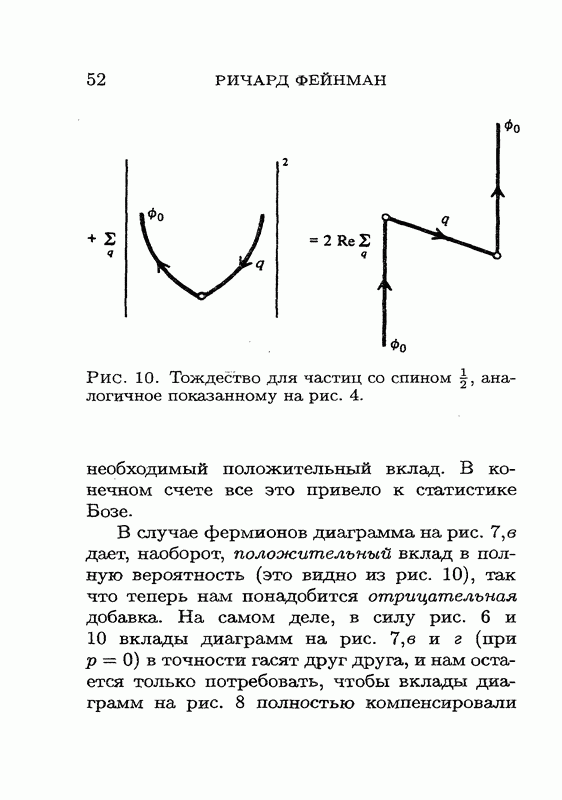
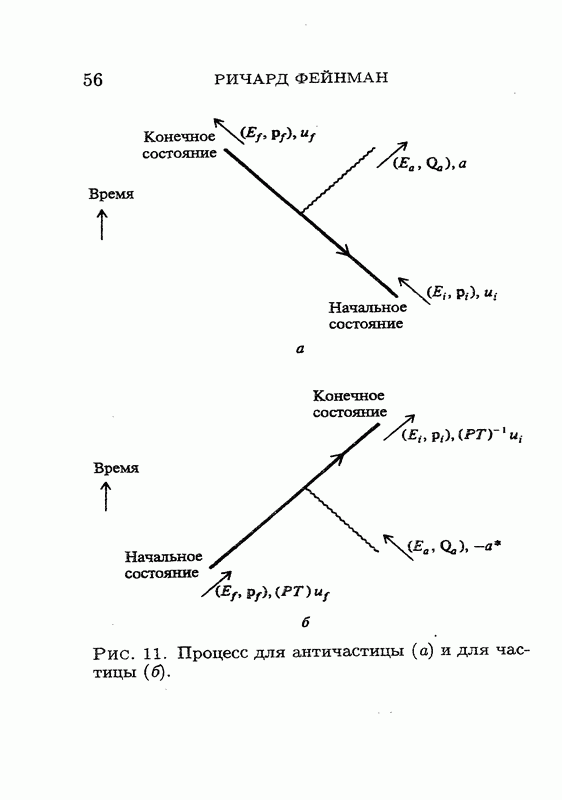
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
МАГНИТНЫЕ МОНОПОЛИ, СПИН И СТАТИСТИКА ФЕРМИ
Чтобы сделать еще более ясным соотношение между свойствами частиц по отношению к пространственным поворотам и их статистикой, мне бы хотелось привести в качестве примера объект со спином причем нам удастся выяснить, откуда у этого объекта берется угловой момент. Предположим, у нас имеется система из магнитного монополя и электрического заряда (рис. 13). Магнитный монополь был придуман Дираком, поэтому здесь будет уместно сказать о нем несколько слов. Подобно тому, как электрический заряд является источником электрического поля, магнитный монополь является источником магнитного поля. Хотя никто никогда не видел магнитного монополя, его легко себе представить. Если бы у вас был очень длинный стержневой магнит, то магнитное поле вблизи полюса такого

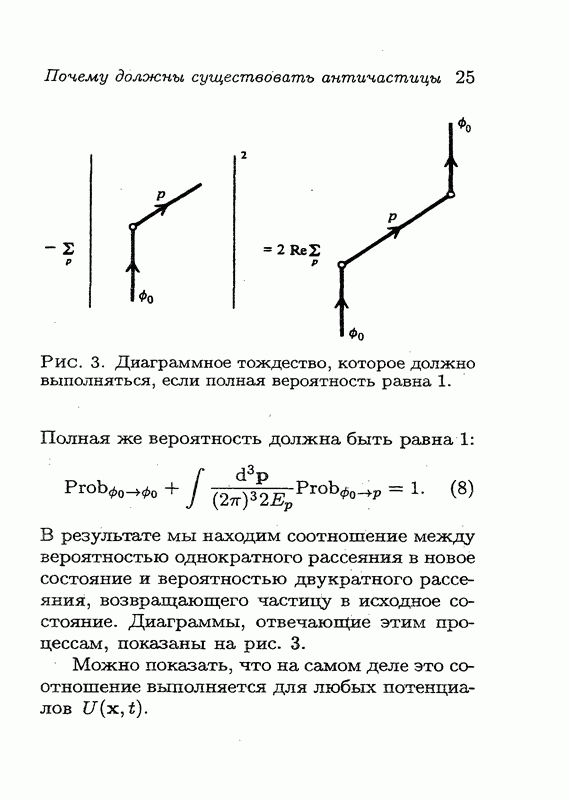
Рис. 13. Система из магнитного монополя  и электрического заряда
и электрического заряда 
магнита напоминало бы поле монополя, поскольку другой полюс находился бы очень далеко.
И все же представим себе, что у нас имеется магнитный монополь с магнитным зарядом  в присутствии обычного электрического заряда q. Будем считать, что обе частицы имеют нулевой спин, так что нам не придется учитывать их собственный угловой момент. Поскольку каждая из частиц находится в поле, создаваемом другой частицей, мы можем построить вектор Пойнтинга
в присутствии обычного электрического заряда q. Будем считать, что обе частицы имеют нулевой спин, так что нам не придется учитывать их собственный угловой момент. Поскольку каждая из частиц находится в поле, создаваемом другой частицей, мы можем построить вектор Пойнтинга  по обычным правилам. Интегрирование вектора Пойнтинга по объему дает импульс. Если проделать необходимые вычисления, то окажется,
по обычным правилам. Интегрирование вектора Пойнтинга по объему дает импульс. Если проделать необходимые вычисления, то окажется,
что наша система из двух частиц обладает угловым моментом (направленным вдоль прямой, соединяющей заряд и монополь), причем его величина не зависит от расстояния между частицами. Угловой момент можно вычислить различными способами, и я оставлю это в качестве упражнения. Оказывается, что он равен  .
.
В квантовой механике угловой момент квантуется. Как известно, разрешенные значения углового момента должны быть кратны (1/2) Н. Примем момент равным наименьшей разрешенной величине, т. е. положим  Таким образом, мы своими руками создали объект со спином
Таким образом, мы своими руками создали объект со спином  Теперь мы должны убедиться в том, что поворот на 360° изменяет фазовый множитель на (-1); посмотрим, так ли это.
Теперь мы должны убедиться в том, что поворот на 360° изменяет фазовый множитель на (-1); посмотрим, так ли это.
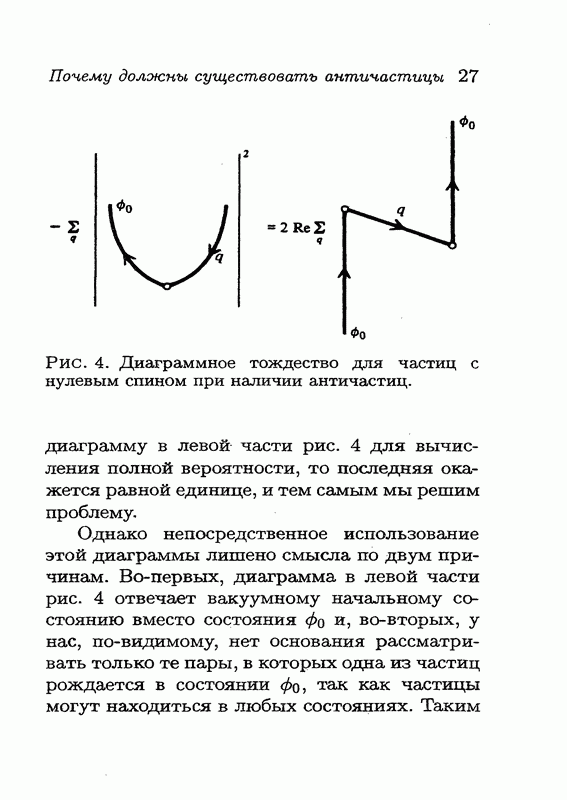
Допустим, что магнитный монополь закреплен, а электрический заряд совершает вокруг него оборот на 360° (рис. 14). Существует

Рис. 14. Поворот заряда q на 360° вокруг магнитного монополя.
известная теорема, которая утверждает следующее: если электрический заряд q движется в магнитном поле, то изменение фазы описывается множителем  , где
, где  криволинейный интеграл от векторного потенциала А вдоль траектории электрического заряда. (Эта теорема упомянута для устрашения!) В данном случае интеграл вычисляется по замкнутой окружности. Используя основы векторного анализа, преобразуем криволинейный интеграл от А по замкнутому контуру в поверхностный интеграл от магнитного поля В по натянутой на этот контур поверхности. Допустим, я преобразовал наш
криволинейный интеграл от векторного потенциала А вдоль траектории электрического заряда. (Эта теорема упомянута для устрашения!) В данном случае интеграл вычисляется по замкнутой окружности. Используя основы векторного анализа, преобразуем криволинейный интеграл от А по замкнутому контуру в поверхностный интеграл от магнитного поля В по натянутой на этот контур поверхности. Допустим, я преобразовал наш
криволинейный интеграл в интеграл от В по верхней полусфере. Поверхностный интеграл от В есть просто поток через данную поверхность. Величина полного потока магнитного поля монополя есть  т. е. интеграл от В по сфере, окружающей монополь, будет равен
т. е. интеграл от В по сфере, окружающей монополь, будет равен  Здесь же мы интегрируем по полусфере, поэтому результат вдвое меньше, т. е.
Здесь же мы интегрируем по полусфере, поэтому результат вдвое меньше, т. е.  Изменение полной фазы будет определяться фактором
Изменение полной фазы будет определяться фактором  подставив сюда
подставив сюда  , получим, что
, получим, что  , т. е. здесь все абсолютно правильно.
, т. е. здесь все абсолютно правильно.
Сейчас я должен сделать небольшое отступление. Мы вплотную подошли к одному факту, который в свое время был доказан Дираком, а именно: если бы во всей Вселенной существовал хотя бы один монополь, то величина электрического заряда квантовалась бы. Доказательство состоит примерно в следующем. Бели бы мы интегрировали не по верхней, а по нижней полусфере, то получили бы тот же самый результат. Однако в этом случае ориентация поверхности была бы противоположной по отношению к направлению обхода контура, и фазовый множитель был бы равен  что, впрочем, дало бы тот же результат (-1). Но заметьте, если бы заряд q не квантовался и не был кратен
что, впрочем, дало бы тот же результат (-1). Но заметьте, если бы заряд q не квантовался и не был кратен  то интегрирование
то интегрирование
по этим двум поверхностям дало бы различные результаты, и мы пришли бы к противоречию. Следовательно, существование магнитных монополей влечет квантование заряда. Судя по всему, заряд на самом деле квантуется, и на этом основании кое-кто верит в существование магнитных монополей.
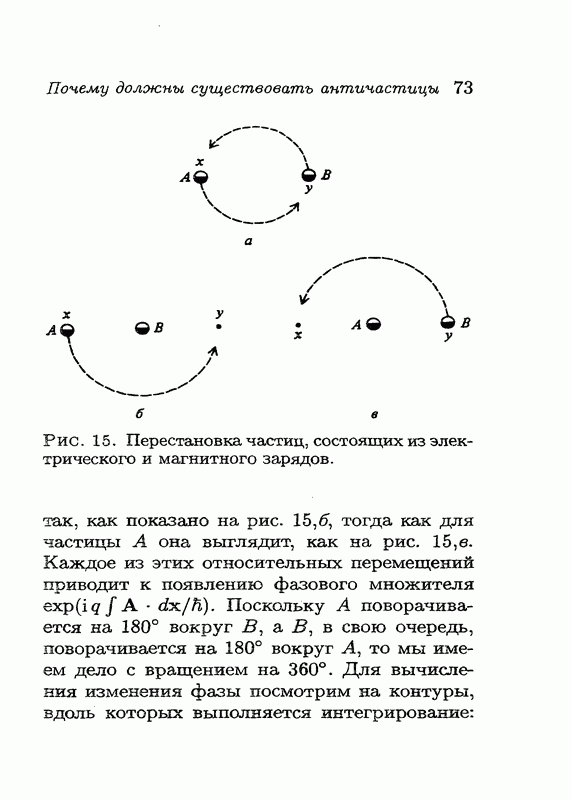
Предположим теперь, что у нас есть две такие составные частицы, каждая из которых обладает как электрическим, так и магнитным зарядом. Обозначим первую частицу через А, а вторую частицу, тождественную первой — через В. Пусть в исходном состоянии частица А находится в точке х, а частица В — в точке у (обе частицы считаются одинаково ориентированными). Что случится, если мы поменяем эти частицы местами? Давайте посмотрим.
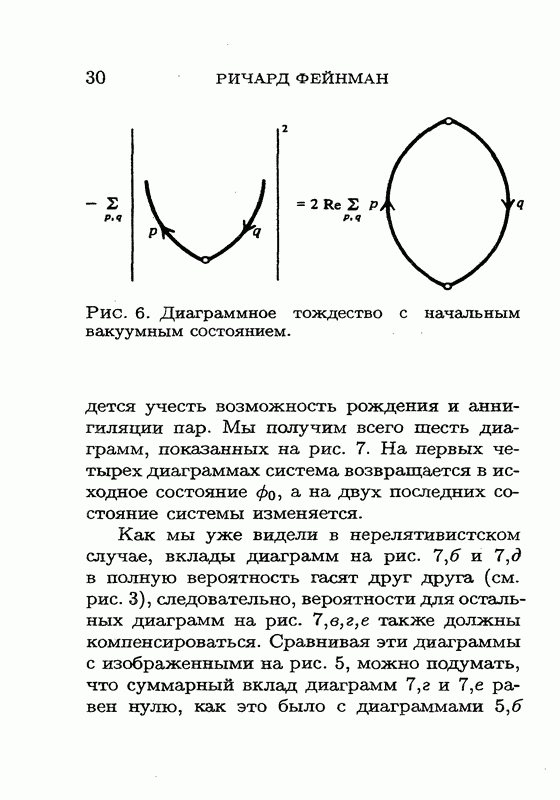
На рис. 15, а показано, как частицы меняются местами. Мы собираемся определить изменение фазы в результате этой процедуры. Причина изменения фазы обусловлена движением электрического заряда частицы А вокруг магнитного заряда частицы В и движением электрического заряда частицы В вокруг магнитного заряда частицы А. (Взаимное расположение электрического и магнитного зарядов внутри каждой из частиц не изменяется.) Для частицы В перестановка выглядит

Рис. 15. Перестановка частиц, состоящих из электрического и магнитного зарядов.
так, как показано на рис. 15, б, тогда как для частицы А она выглядит, как на рис. 15, в. Каждое из этих относительных перемещений приводит к появлению фазового множителя  Поскольку А поворачивается на 180° вокруг В, а В, в свою очередь, поворачивается на 180° вокруг А, то мы имеем дело с вращением на 360°. Для вычисления изменения фазы посмотрим на контуры, вдоль которых выполняется интегрирование:
Поскольку А поворачивается на 180° вокруг В, а В, в свою очередь, поворачивается на 180° вокруг А, то мы имеем дело с вращением на 360°. Для вычисления изменения фазы посмотрим на контуры, вдоль которых выполняется интегрирование:
на рис. 15, б интеграл вычисляется вдоль контура от точки  до точки у, а на рис. 15, в — от точки у до точки х. Эти интегралы дают в сумме криволинейный интеграл по замкнутому контуру вокруг монополя — такой же результат получается и при повороте на 360°. Как мы уже видели, в этом случае появляется множитель (-1). Разумеется, именно этого и следовало ожидать для статистики Ферми: множитель (-1) появляется всякий раз при перестановке частиц со спином (Мы считали, что составные частицы, т. е. заряд и монополь имеют нулевой спин и подчиняются статистике Бозе.)
до точки у, а на рис. 15, в — от точки у до точки х. Эти интегралы дают в сумме криволинейный интеграл по замкнутому контуру вокруг монополя — такой же результат получается и при повороте на 360°. Как мы уже видели, в этом случае появляется множитель (-1). Разумеется, именно этого и следовало ожидать для статистики Ферми: множитель (-1) появляется всякий раз при перестановке частиц со спином (Мы считали, что составные частицы, т. е. заряд и монополь имеют нулевой спин и подчиняются статистике Бозе.)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПОЧЕМУ ДОЛЖНЫ СУЩЕСТВОВАТЬ АНТИЧАСТИЦЫ
- ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АНТИЧАСТИЦЫ
- ЧАСТИЦЫ С НУЛЕВЫМ СПИНОМ И СТАТИСТИКА БОЗЕ
- СООТНОШЕНИЕ МЕЖДУ ПОВЕДЕНИЕМ ЧАСТИЦ И АНТИЧАСТИЦ
- СПИН 1/2 И СТАТИСТИКА ФЕРМИ
- ОБРАЩЕНИЕ ВРЕМЕНИ И АНТИЧАСТИЦЫ
- ОБРАЩЕНИЯ ВРЕМЕНИ
- МАГНИТНЫЕ МОНОПОЛИ, СПИН И СТАТИСТИКА ФЕРМИ
- ЗАКЛЮЧЕНИЕ
- НА ПУТИ К ОКОНЧАТЕЛЬНЫМ ФИЗИЧЕСКИМ ЗАКОНАМ