| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
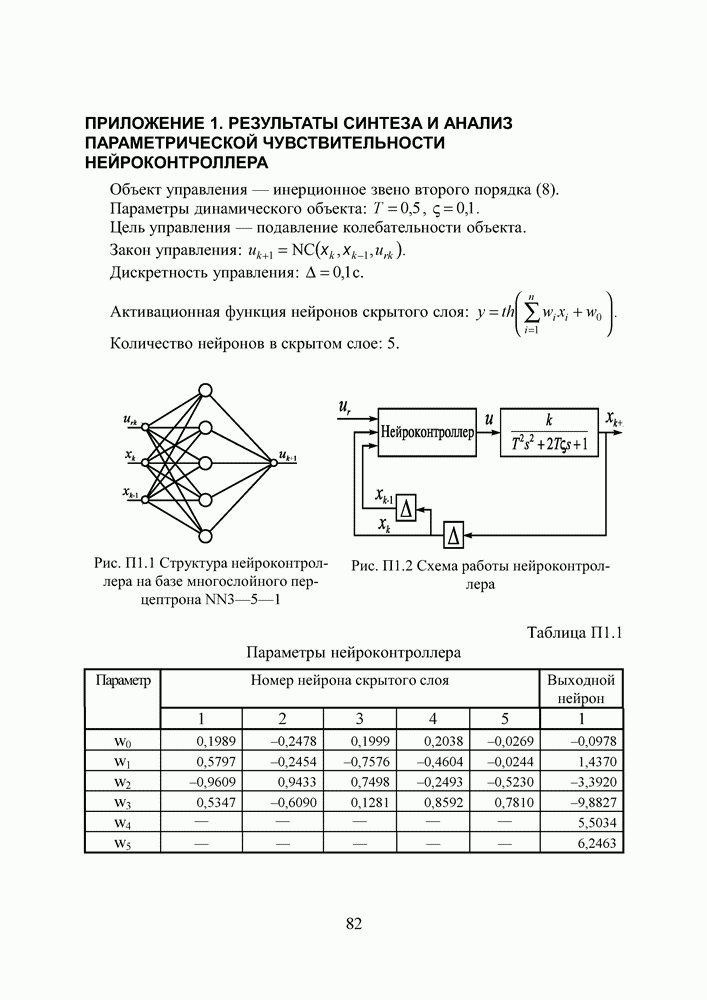
ПРИЛОЖЕНИЕ 3. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ ЭМУЛЯТОРА КОЛЕБАТЕЛЬНОГО ЗВЕНА С ЗАТУХАНИЕМ
Параметры динамического объекта  .
.
Закон предсказания: 
Шаг предсказания:  .
.
Глубина предсказания: 20 с.
Количество нейронов в скрытом слое: 8.

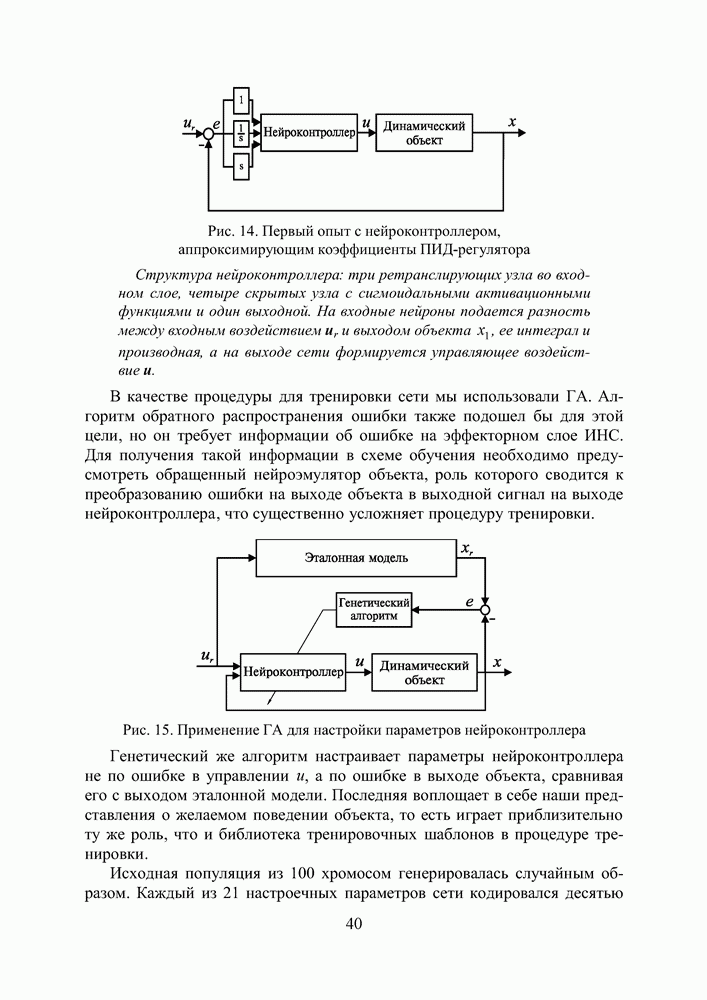
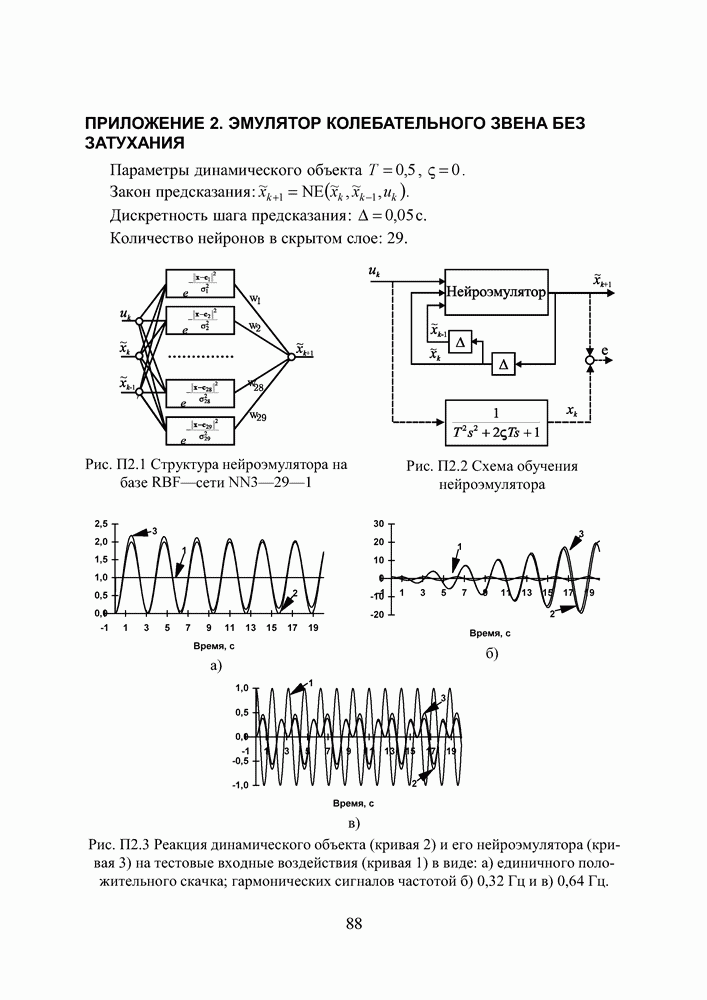
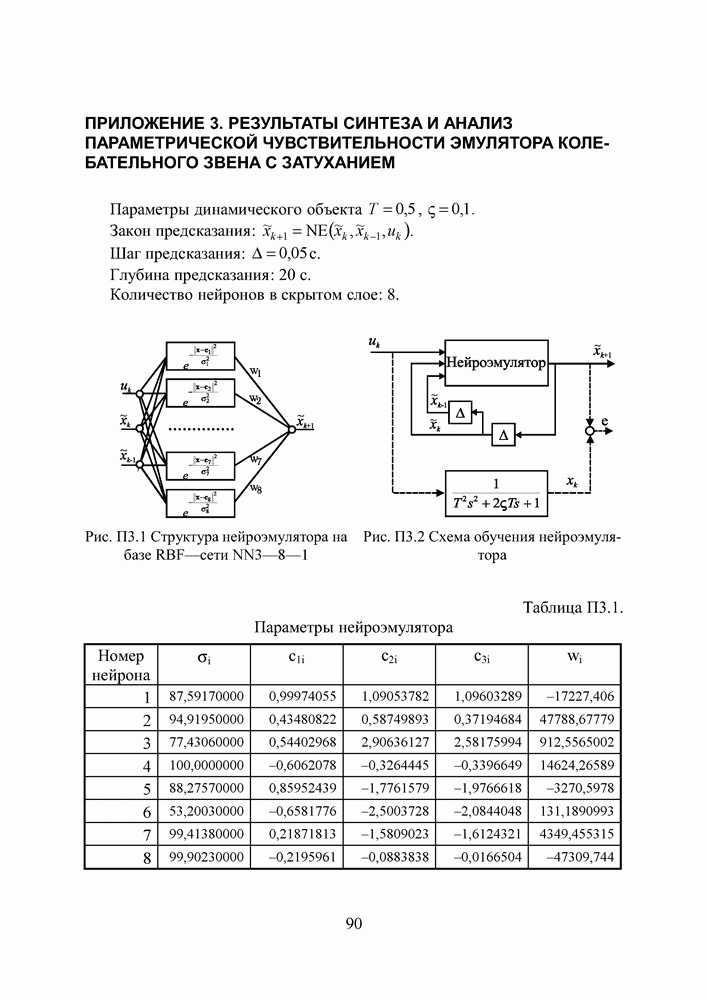
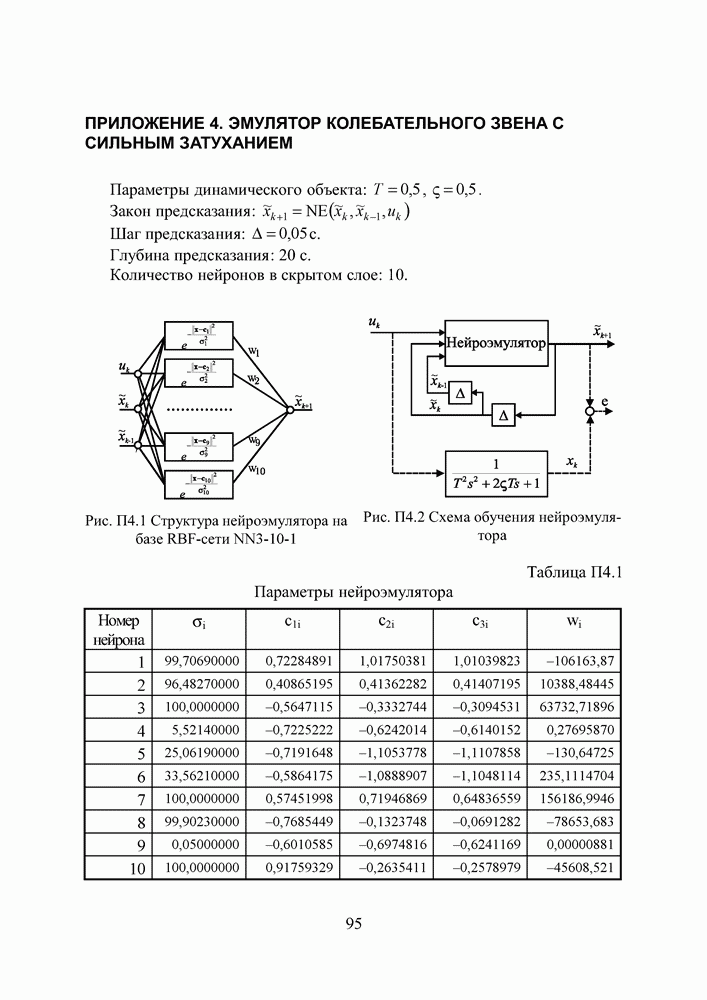
Рис. П3.1 Структура нейроэмулятора на базе RBF-сети 

Рис. П3.2 Схема обучения нейроэмулятора
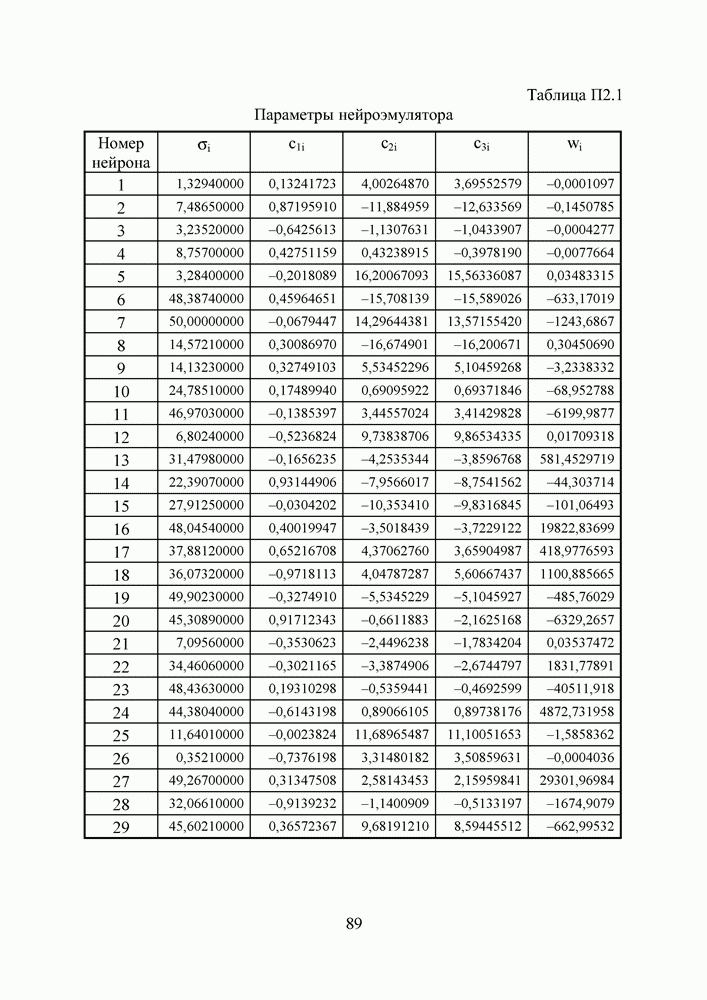
Таблица П3.1. (см. скан) Параметры нейроэмулятора

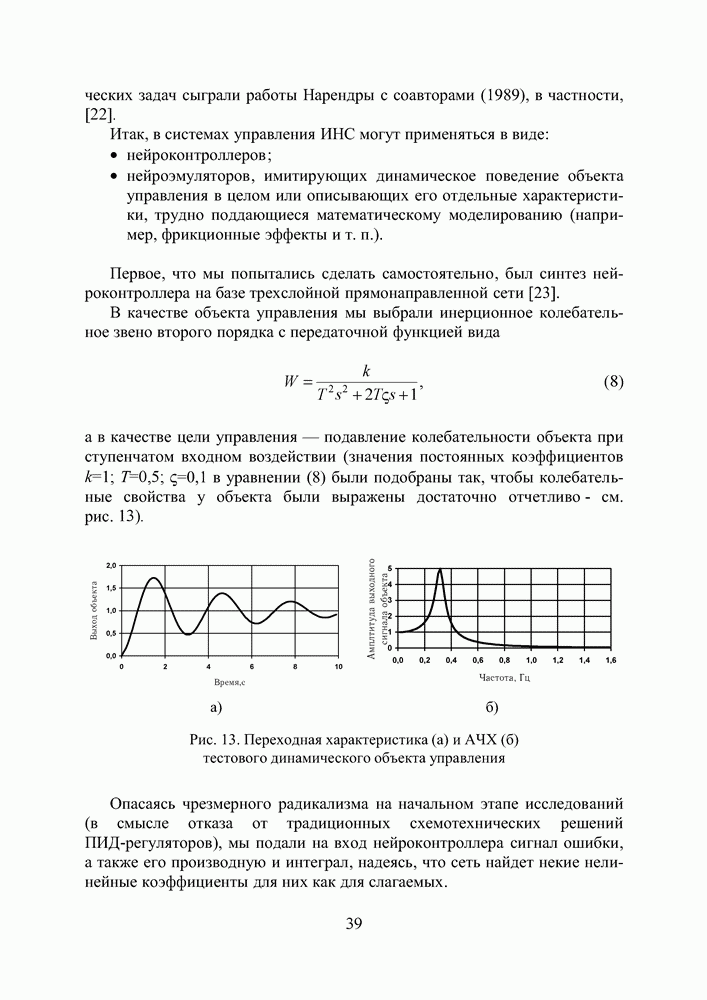
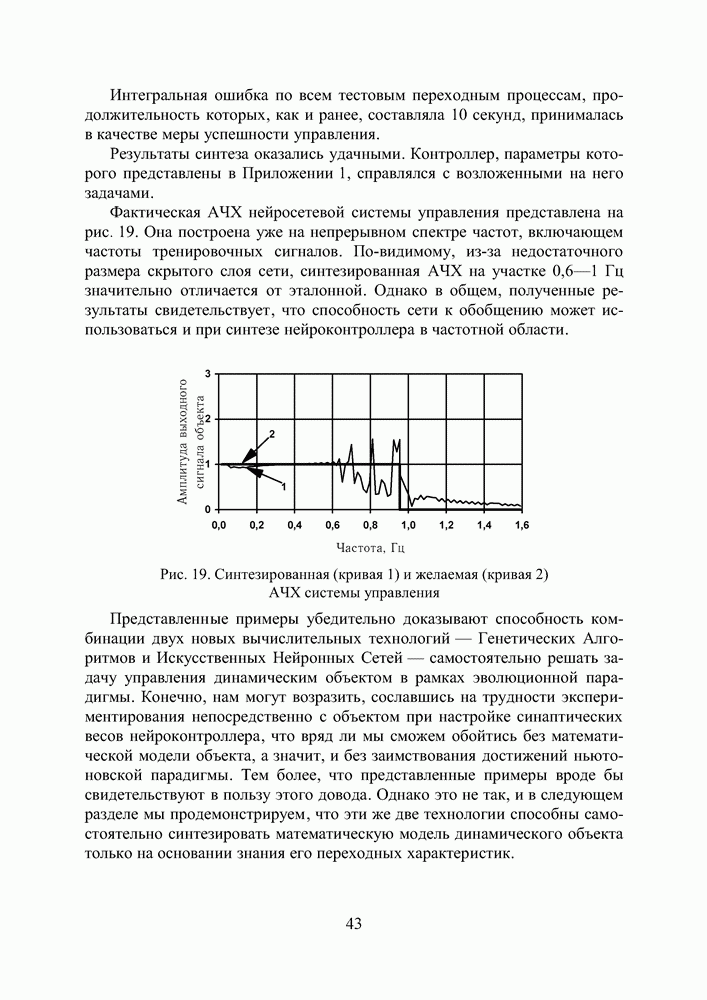
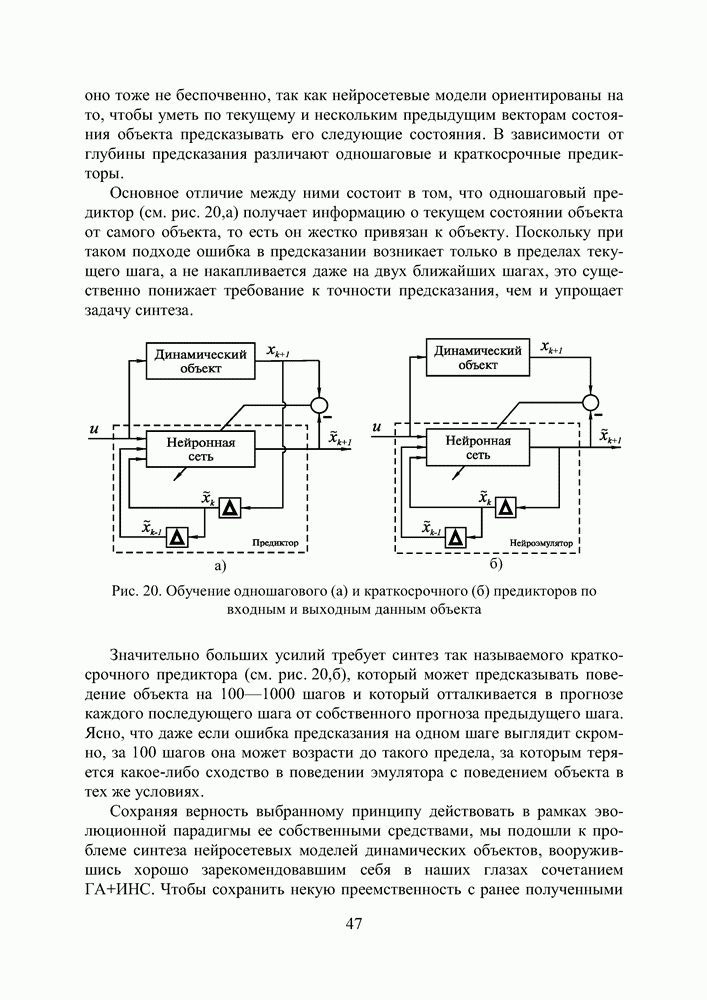
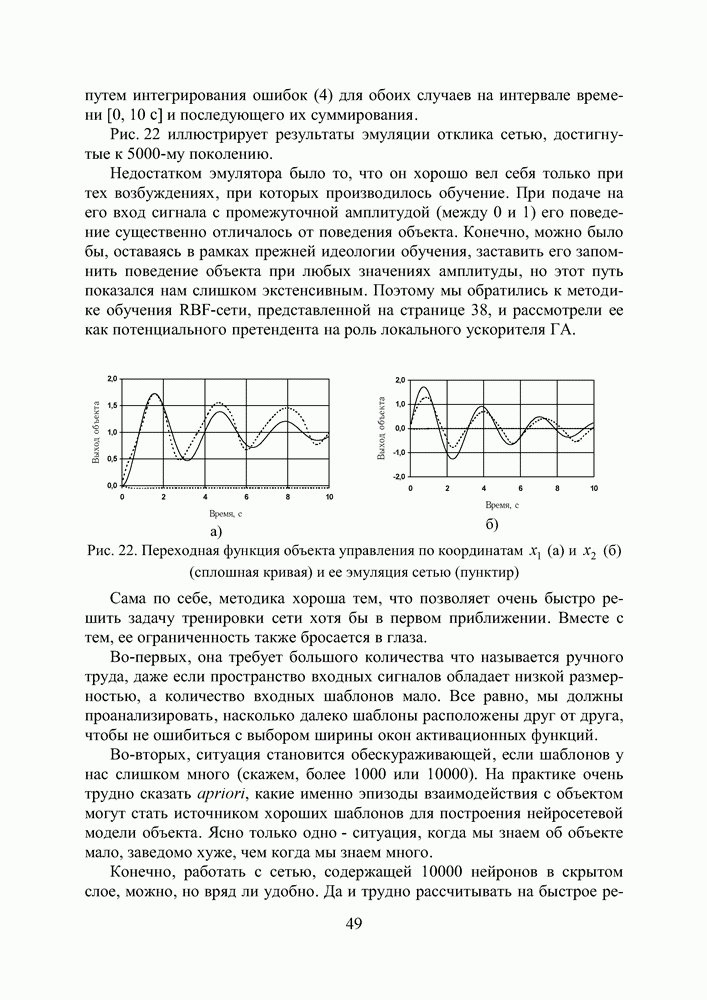
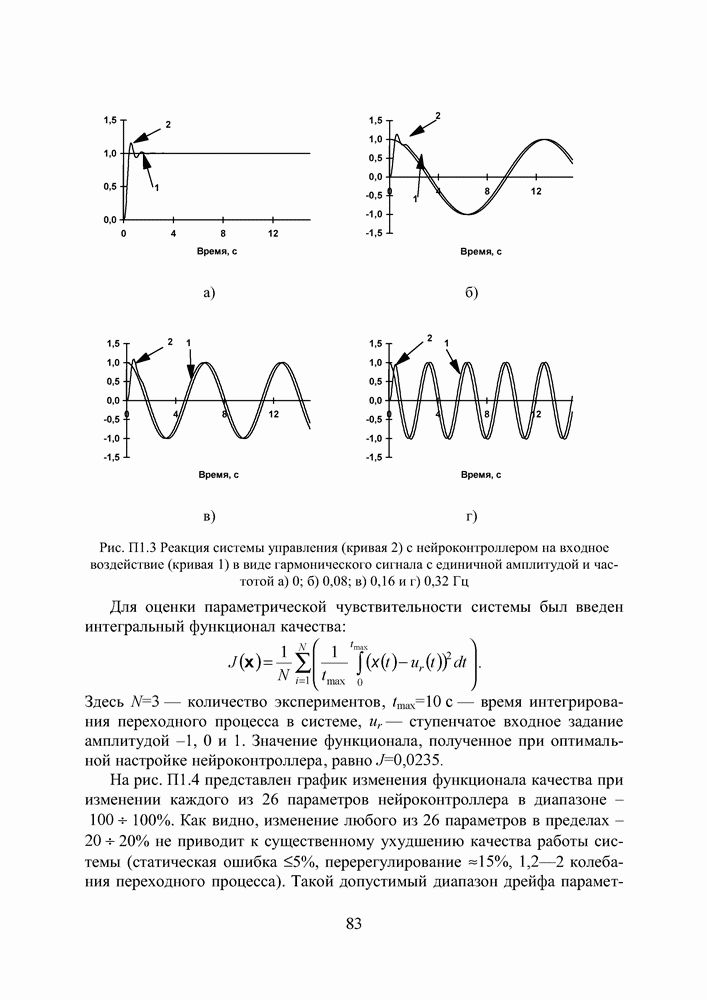
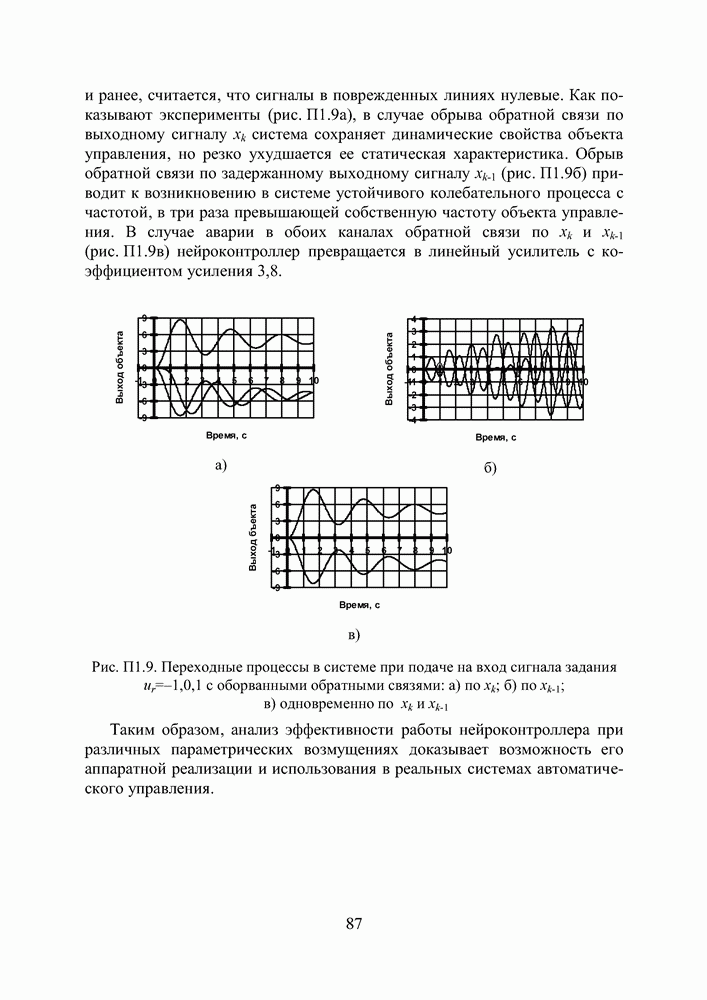
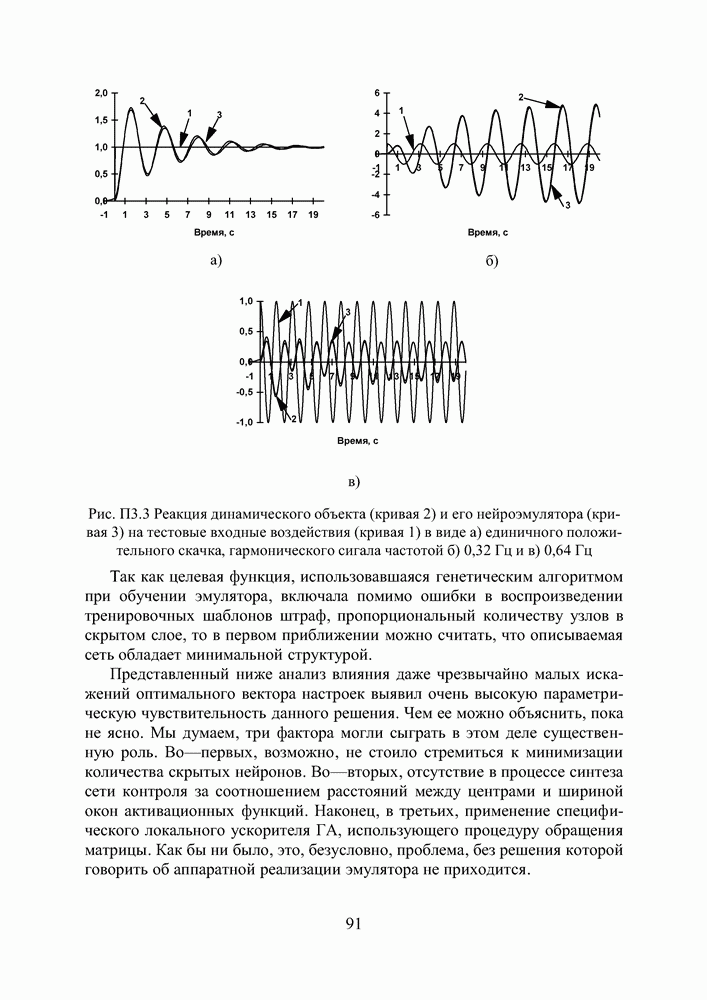
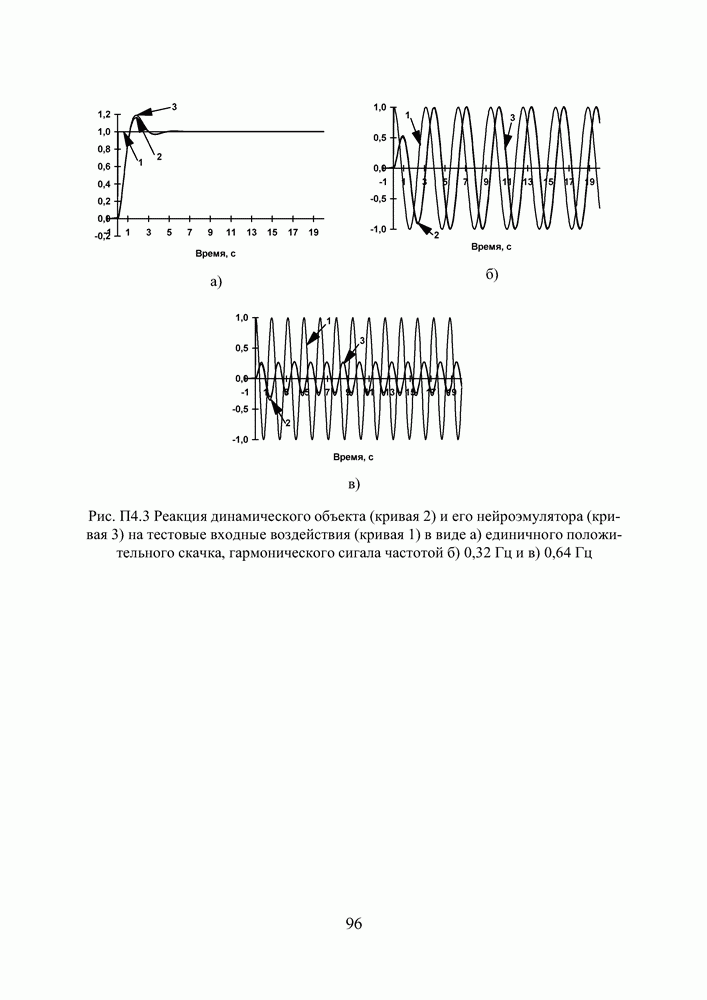
Рис. П3.3 Реакция динамического объекта (кривая 2) и его нейроэмулятора (кривая 3) на тестовые входные воздействия (кривая 1) в виде а) единичного положительного скачка, гармонического сигала частотой б) 0,32 Гц и в) 0,64 Гц
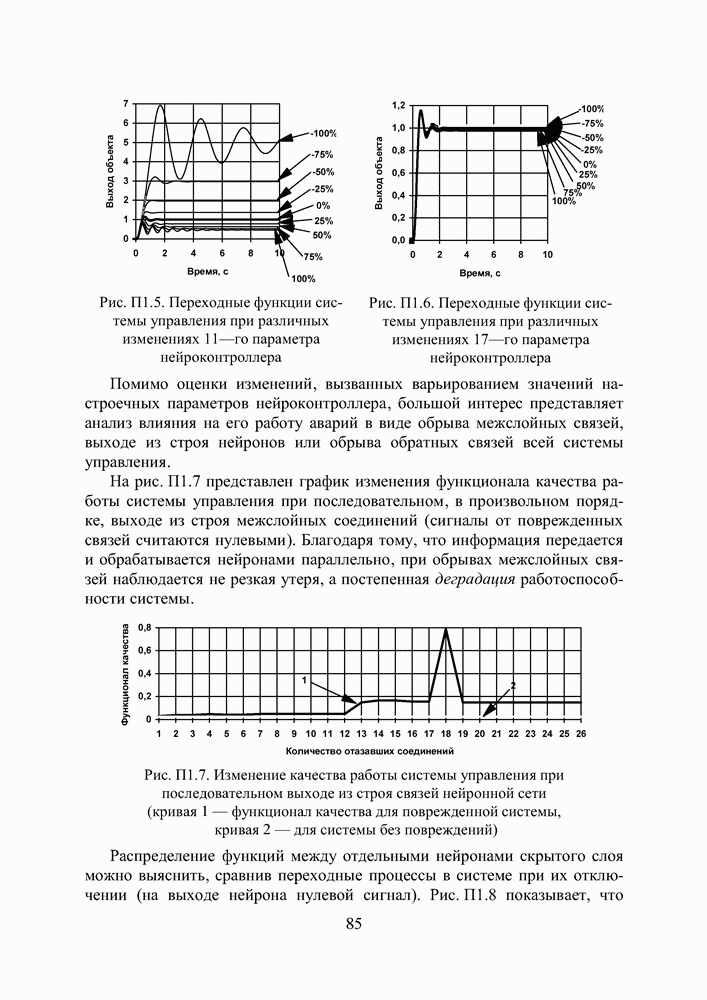
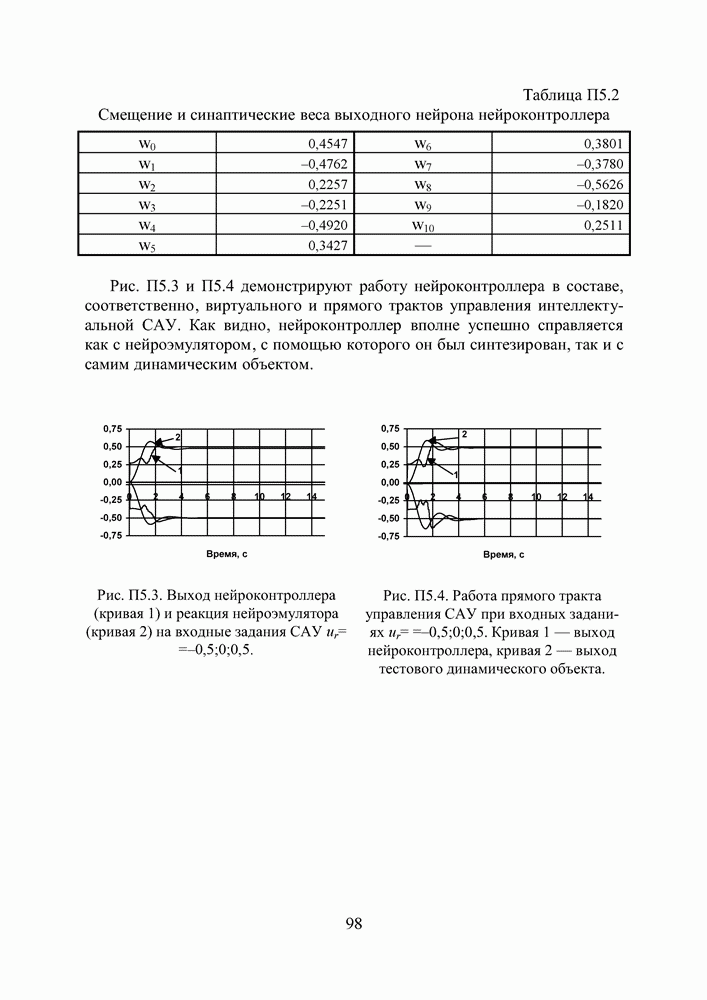
Так как целевая функция, использовавшаяся генетическим алгоритмом при обучении эмулятора, включала помимо ошибки в воспроизведении тренировочных шаблонов штраф, пропорциональный количеству узлов в скрытом слое, то в первом приближении можно считать, что описываемая сеть обладает минимальной структурой.
Представленный ниже анализ влияния даже чрезвычайно малых искажений оптимального вектора настроек выявил очень высокую параметрическую чувствительность данного решения. Чем ее можно объяснить, пока не ясно. Мы думаем, три фактора могли сыграть в этом деле существенную роль. Во—первых, возможно, не стоило стремиться к минимизации количества скрытых нейронов. Во—вторых, отсутствие в процессе синтеза сети контроля за соотношением расстояний между центрами и шириной окон активационных функций. Наконец, в третьих, применение специфического локального ускорителя ГА, использующего процедуру обращения матрицы. Как бы ни было, это, безусловно, проблема, без решения которой говорить об аппаратной реализации эмулятора не приходится.
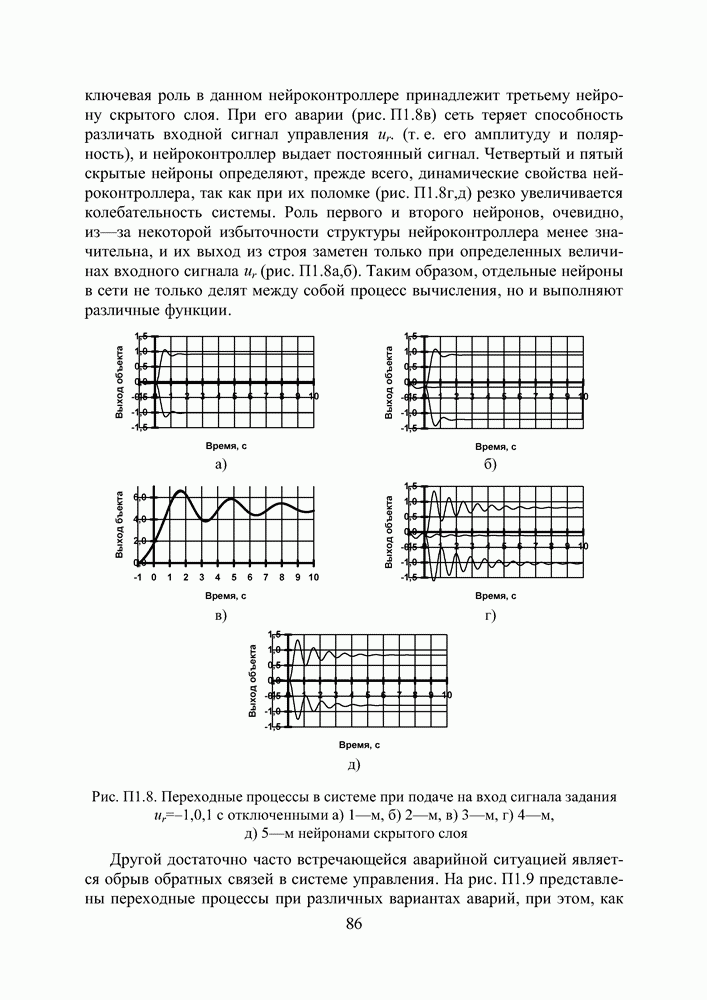
А) Изменение ширины окна активационной функции.
Реакции эмулятора на ступенчатое возбуждение, соответствующие различным искажениям параметра  демонстрирует рис. П3.4. Кривая 3 соответствует изменению параметра на 0,01% от оптимальной величины; при этом
демонстрирует рис. П3.4. Кривая 3 соответствует изменению параметра на 0,01% от оптимальной величины; при этом  Кривая 4 соответствует изменению параметра на 0,1%; при этом
Кривая 4 соответствует изменению параметра на 0,1%; при этом  Кривая 5 соответствует изменению параметра на 0,2%; при этом
Кривая 5 соответствует изменению параметра на 0,2%; при этом  Зависимость среднеквадратичной ошибки от изменения параметра
Зависимость среднеквадратичной ошибки от изменения параметра  приведена на рис. П3.5.
приведена на рис. П3.5.

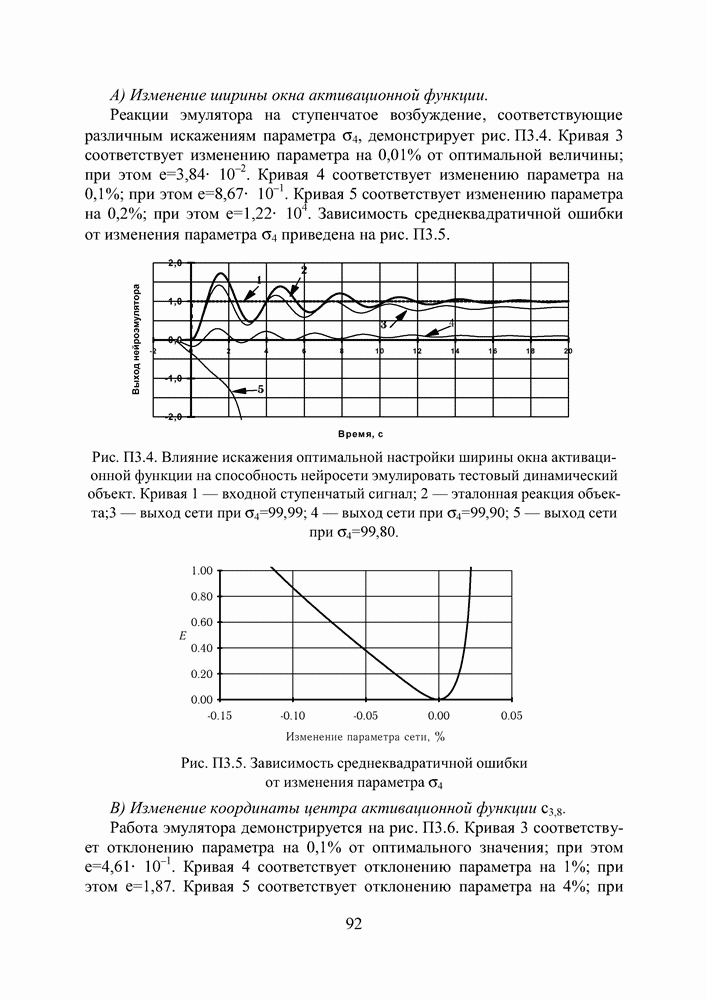
Рис. П3.4. Влияние искажения оптимальной настройки ширины окна активационной функции на способность нейросети эмулировать тестовый динамический объект. Кривая 1 — входной ступенчатый сигнал; 2 — эталонная реакция  — выход сети при
— выход сети при  — выход сети при
— выход сети при  — выход сети при
— выход сети при  .
.

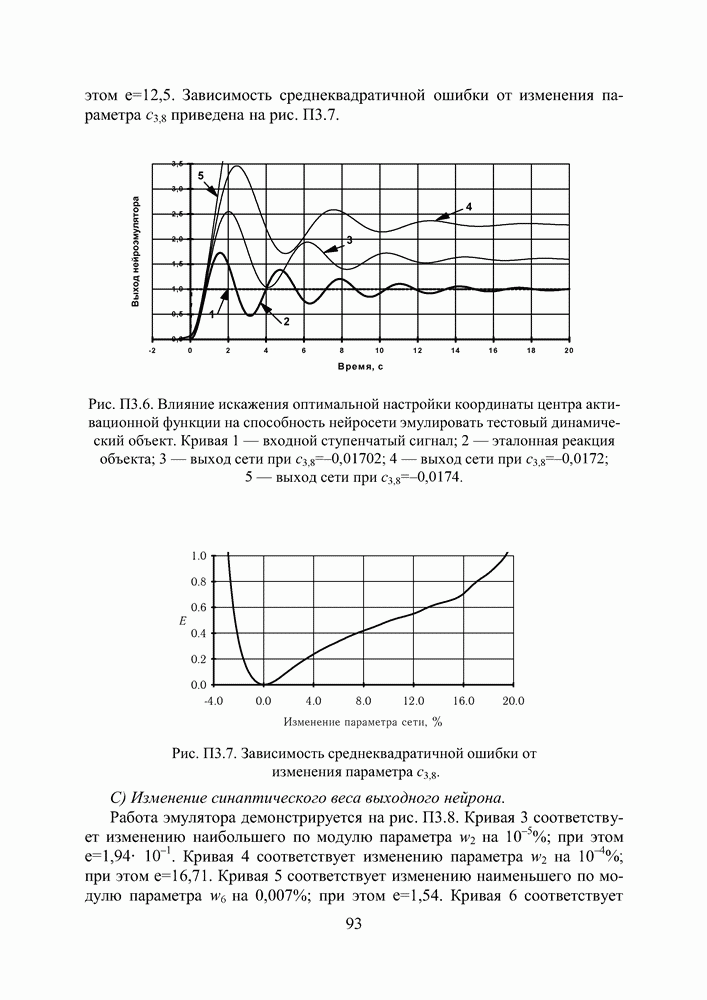
Рис. П3.5. Зависимость среднеквадратичной ошибки от изменения параметра 
В) Изменение координатыг центра активационной функции  .
.
Работа эмулятора демонстрируется на рис. П3.6. Кривая 3 соответствует отклонению параметра на 0,1% от оптимального значения; при этом  Кривая 4 соответствует отклонению параметра на 1%; при этом
Кривая 4 соответствует отклонению параметра на 1%; при этом  Кривая 5 соответствует отклонению параметра на 4%; при
Кривая 5 соответствует отклонению параметра на 4%; при
этом  . Зависимость среднеквадратичной ошибки от изменения параметра
. Зависимость среднеквадратичной ошибки от изменения параметра  приведена на рис. П3.7.
приведена на рис. П3.7.

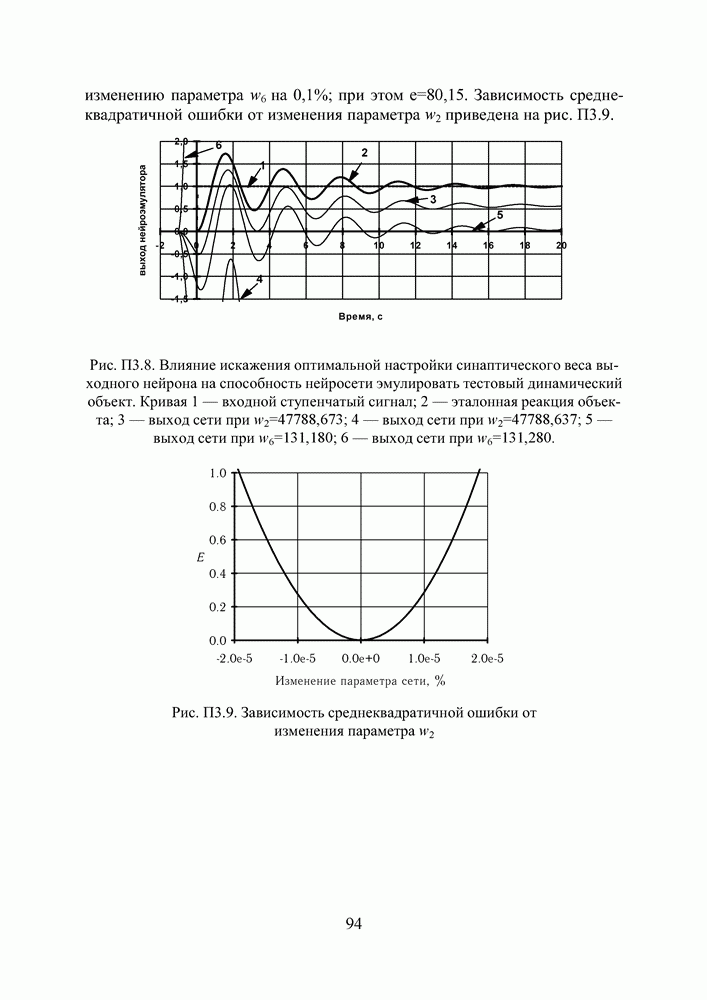
Рис. П3.6. Влияние искажения оптимальной настройки координаты центра активационной функции на способность нейросети эмулировать тестовый динамический объект. Кривая 1 — входной ступенчатый сигнал; 2 — эталонная реакция объекта; 3 — выход сети при  ; 4 — выход сети при
; 4 — выход сети при  ; 5 — выход сети при
; 5 — выход сети при  .
.

Рис. П3.7. Зависимость среднеквадратичной ошибки от изменения параметра 
С) Изменение синаптического веса выходного нейрона.
Работа эмулятора демонстрируется на рис. П3.8. Кривая 3 соответствует изменению наибольшего по модулю параметра  на
на  при этом
при этом  . Кривая 4 соответствует изменению параметра
. Кривая 4 соответствует изменению параметра  на
на  при этом
при этом  Кривая 5 соответствует изменению наименьшего по модулю параметра
Кривая 5 соответствует изменению наименьшего по модулю параметра  на
на  при этом
при этом  Кривая 6 соответствует
Кривая 6 соответствует
изменению параметра  на
на  при этом
при этом  Зависимость среднеквадратичной ошибки от изменения параметра
Зависимость среднеквадратичной ошибки от изменения параметра  приведена на рис. П3.9.
приведена на рис. П3.9.

Рис. П3.8. Влияние искажения оптимальной настройки синаптического веса выходного нейрона на способность нейросети эмулировать тестовый динамический объект. Кривая 1 — входной ступенчатый сигнал; 2 — эталонная реакция объекта; 3 — выход сети при  — выход сети при
— выход сети при  — выход сети при
— выход сети при  — выход сети при
— выход сети при 

Рис. П3.9. Зависимость среднеквадратичной ошибки от изменения параметра 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. О РАЗЛИЧНЫХ ТОЛКОВАНИЯХ ТЕРМИНА «ИНТЕЛЛЕКТУАЛЬНОСТЬ» В УПРАВЛЕНИИ
- 1. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 1.2. Генетические операторы
- 1.3. Преимущественное право размножения сильнейших
- 2. ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ
- 2.2. Становление и развитие ИНС
- 3. ГА+ИНС = НОВАЯ ПАРАДИГМА В УПРАВЛЕНИИ
- 4. ГА+ИНС = НОВАЯ ПАРАДИГМА В МОДЕЛИРОВАНИИ
- 5. СНОВА О ГЕНЕТИЧЕСКИХ АЛГОРИТМАХ
- 6. ВИРТУАЛЬНАЯ РЕАЛЬНОСТЬ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- ЗАКЛЮЧЕНИЕ
- ТЕРМИНОЛОГИЧЕСКИЙ СЛОВАРЬ
- ИМЕННОЙ СПИСОК
- СПИСОК ЛИТЕРАТУРЫ
- ПРИЛОЖЕНИЕ 1. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ НЕЙРОКОНТРОЛЛЕРА
- ПРИЛОЖЕНИЕ 2. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА БЕЗ ЗАТУХАНИЯ
- ПРИЛОЖЕНИЕ 3. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ ЭМУЛЯТОРА КОЛЕБАТЕЛЬНОГО ЗВЕНА С ЗАТУХАНИЕМ
- ПРИЛОЖЕНИЕ 4. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА С СИЛЬНЫМ ЗАТУХАНИЕМ
- ПРИЛОЖЕНИЕ 5. ВИРТУАЛЬНЫЙ ТРАКТ УПРАВЛЕНИЯ НА БАЗЕ НЕЙРОЭМУЛЯТОРА
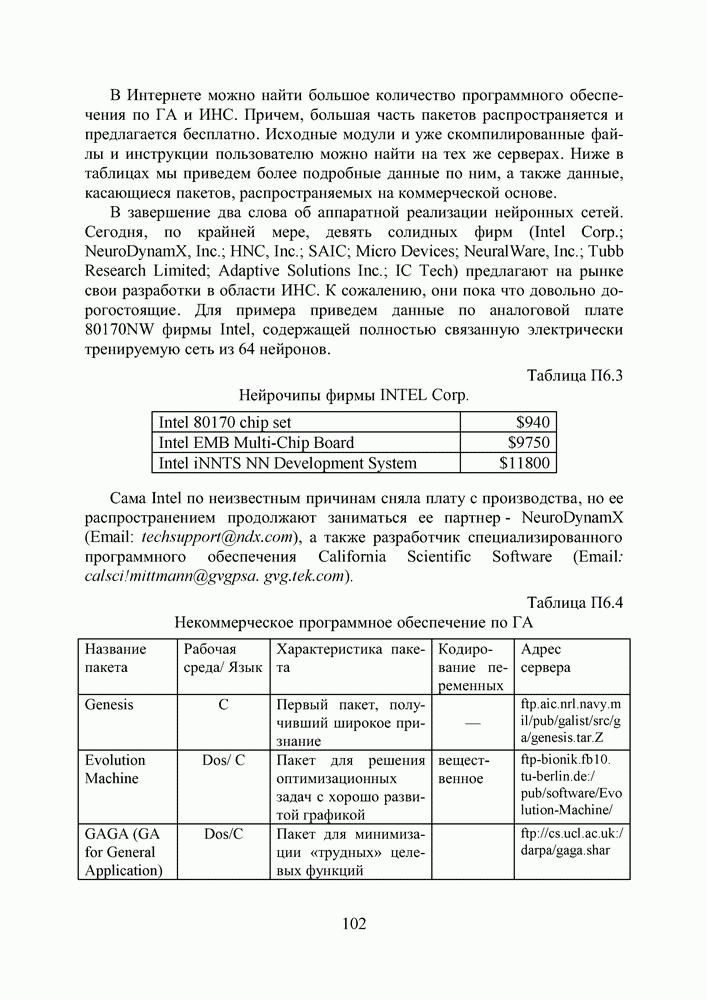
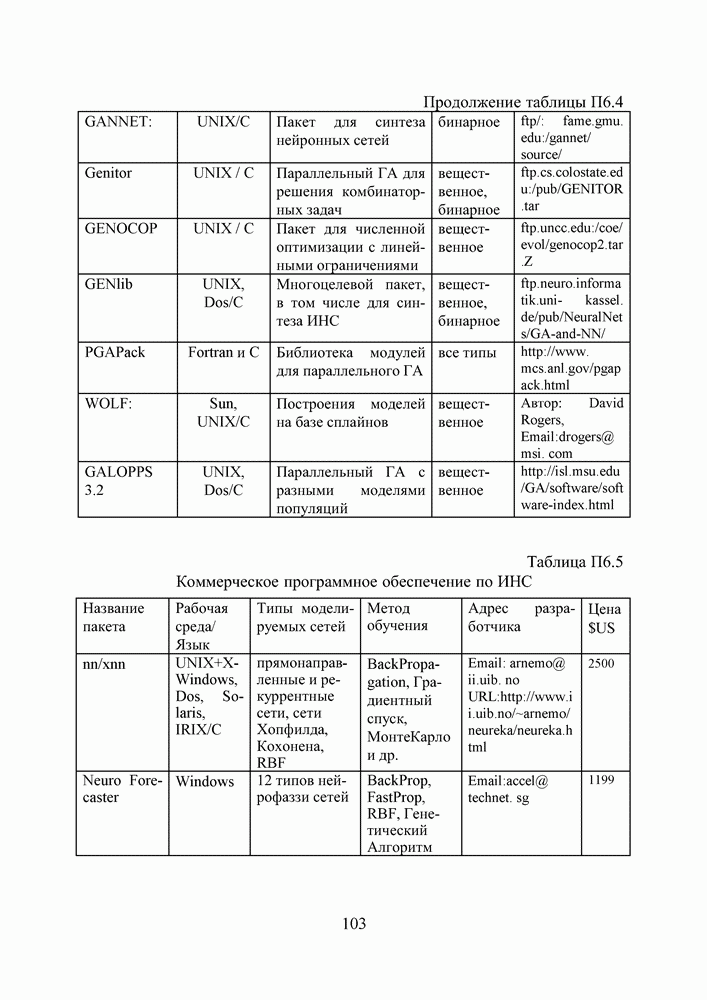
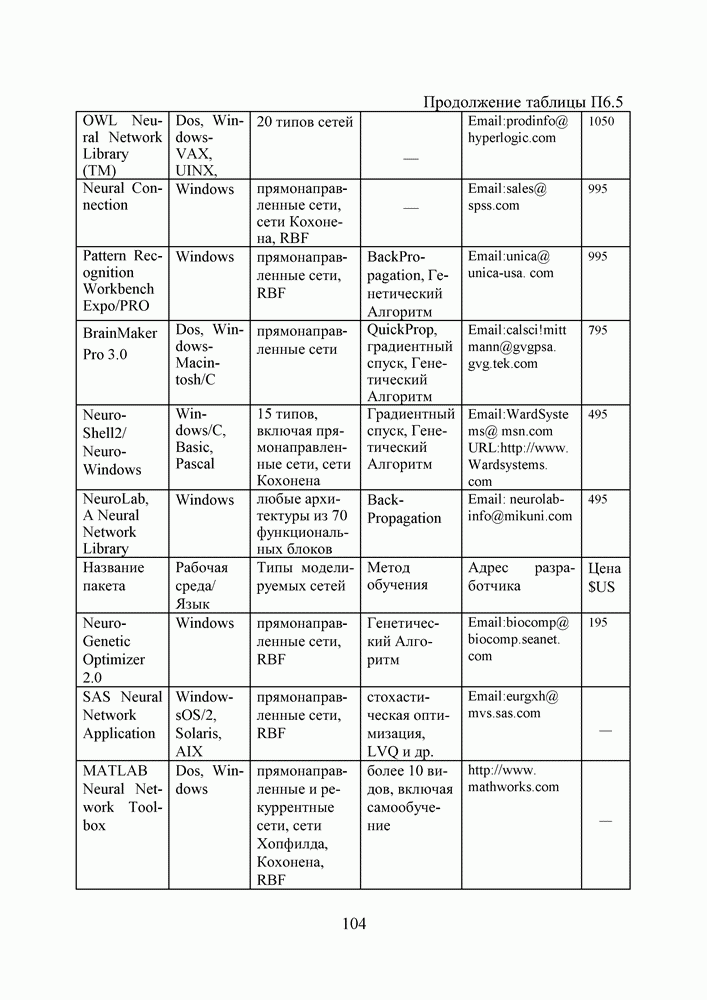
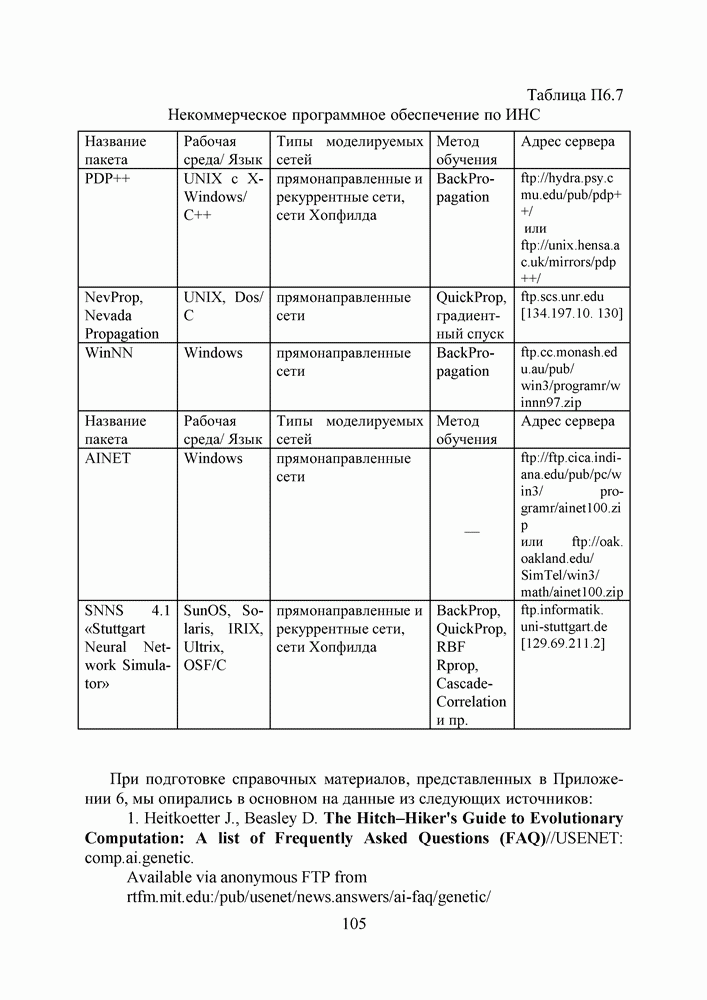
- ПРИЛОЖЕНИЕ 6. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ И ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ В ИНТЕРНЕТЕ