| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
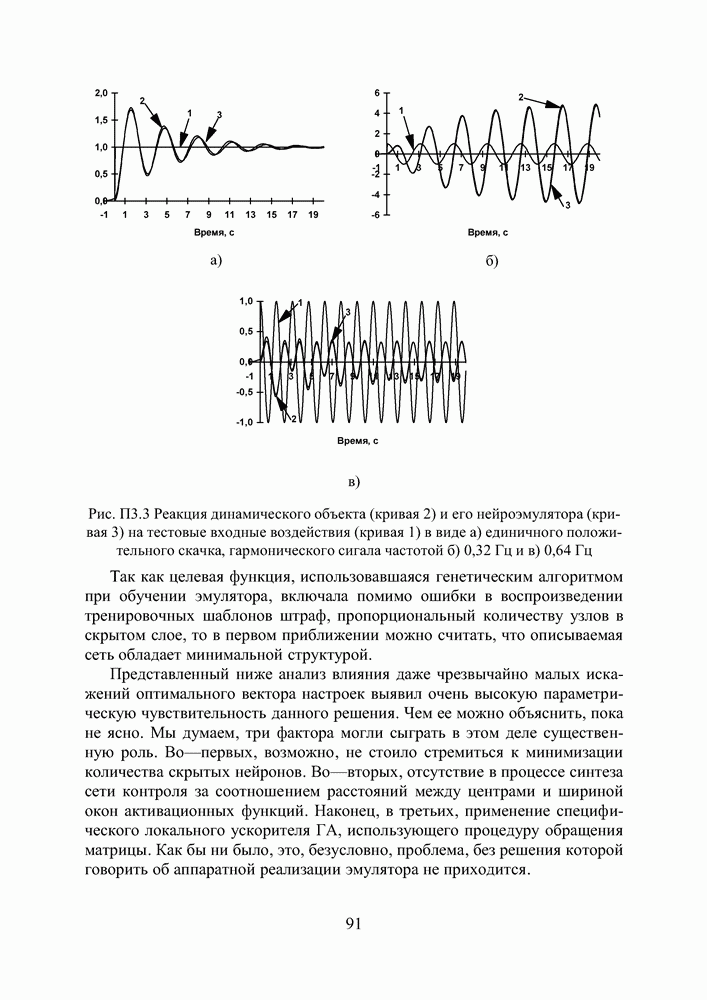
3. ГА+ИНС = НОВАЯ ПАРАДИГМА В УПРАВЛЕНИИ
Классические методы синтеза систем управления базируются на хорошо развитом аппарате интегро-дифференциального исчисления, созданном Ньютоном около трехсот лет назад. Нейронные сети представляют собой альтернативное, существующее всего несколько лет, направление в теории автоматического управления, предлагающее иной способ отражения и преобразования действительности, в котором можно обнаружить и сходные, и различные черты с классической парадигмой.
Проникновение дифференциальных уравнений в теорию автоматического регулирования связывают с именами Д. К. Максвелла (1831—1879) и И. А. Вышнеградского (1831—1895) [21]. Дело в том, что с момента построения Д. Уаттом паровой машины с центробежным регулятором скорости вращения (1784) и до середины второй половины прошлого века какая-либо теория регулирования просто отсутствовала. Однако, с ростом мощности паровых машин участились аварии, вызванные плохим качеством регулирования. И вот Максвелл и Вышнеградский почти одновременно и независимо друг от друга взялись за теоретический анализ этой системы. Оба использовали теорию малых колебаний, берущую начало от Ж. Л. Лагранжа. Записав уравнения Лагранжа для паровой машины и выразив в них фазовые переменные через возмущения относительно некоторых равновесных значений, Максвелл и Вышнеградский линеаризовали уравнения относительно возмущений и исследовали условия устойчивости состояния равновесия.
Так начался первый этап в развитии теории автоматического управления, этап расцвета классических методов анализа. Продолжался он довольно долго — до 40-х годов нашего века, но в содержательном отношении не отличался большим разнообразием подходов. Исследование устойчивости, а также качества переходных процессов продолжали оставаться основными задачами всего этого периода.
Термин «нейроуправление» впервые появился в работах Вербоса уже в 1976 году, однако решающую роль во внедрении ИНС в сферу управленческих
задач сыграли работы Нарендры с соавторами (1989), в частности, [22].
Итак, в системах управления ИНС могут применяться в виде:
• нейроконтроллеров;
• нейроэмуляторов, имитирующих динамическое поведение объекта управления в целом или описывающих его отдельные характеристики, трудно поддающиеся математическому моделированию (например, фрикционные эффекты и т. п.).
Первое, что мы попытались сделать самостоятельно, был синтез нейроконтроллера на базе трехслойной прямонаправленной сети [23].
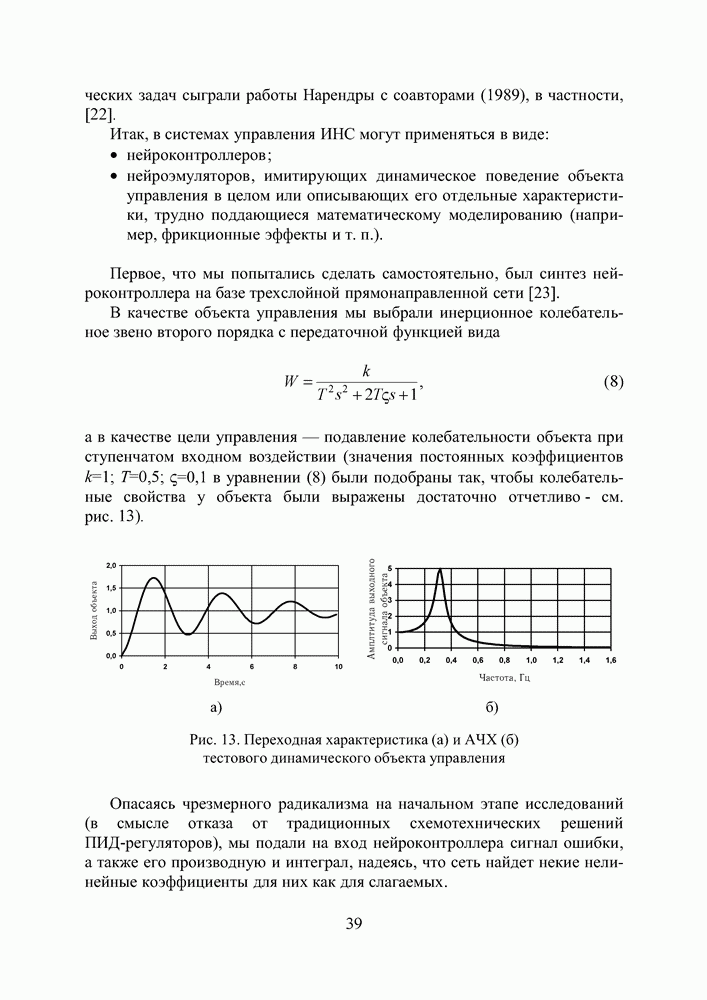
В качестве объекта управления мы выбрали инерционное колебательное звено второго порядка с передаточной функцией вида

а в качестве цели управления — подавление колебательности объекта при ступенчатом входном воздействии (значения постоянных коэффициентов  в уравнении (8) были подобраны так, чтобы колебательные свойства у объекта были выражены достаточно отчетливо - см. рис. 13).
в уравнении (8) были подобраны так, чтобы колебательные свойства у объекта были выражены достаточно отчетливо - см. рис. 13).

Рис. 13. Переходная характеристика (а) и АЧХ (б) тестового динамического объекта управления
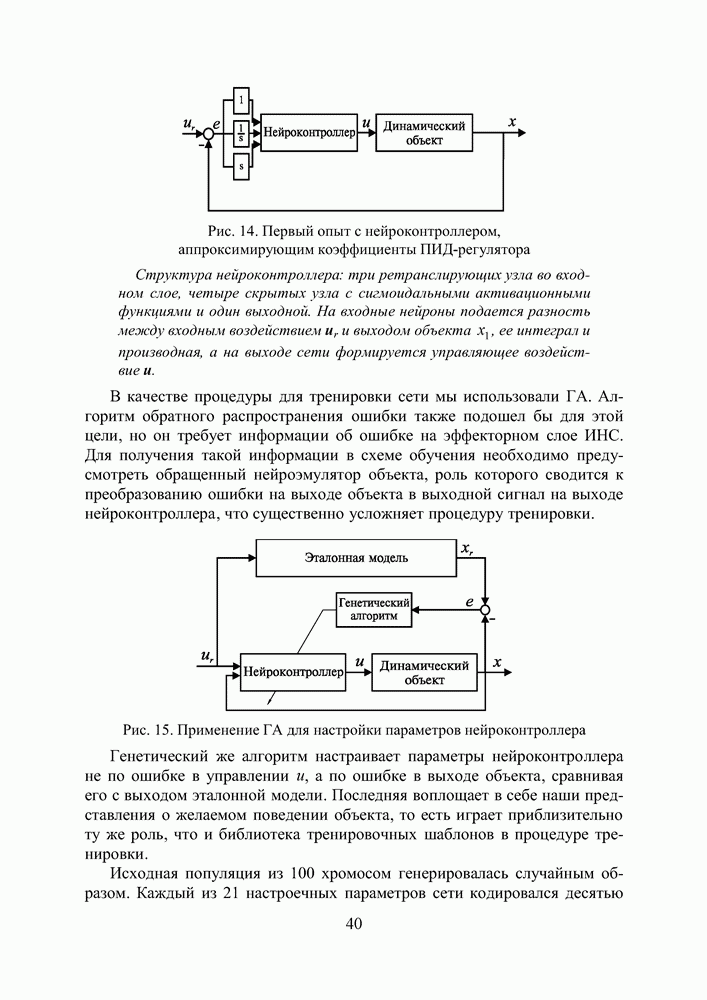
Опасаясь чрезмерного радикализма на начальном этапе исследований (в смысле отказа от традиционных схемотехнических решений ПИД-регуляторов), мы подали на вход нейроконтроллера сигнал ошибки, а также его производную и интеграл, надеясь, что сеть найдет некие нелинейные коэффициенты для них как для слагаемых.

Рис. 14. Первый опыт с нейроконтроллером, аппроксимирующим коэффициенты ПИД-регулятора
Структура нейроконтроллера: три ретранслирующих узла во входном слое, четыре скрытых узла с сигмоидальными активационными функциями и один выходной. На входные нейроныг подается разность между входным воздействием  и выюодом объекта
и выюодом объекта  ее интеграл и производная, а на выходе сети формируется управляющее воздействие
ее интеграл и производная, а на выходе сети формируется управляющее воздействие  .
.
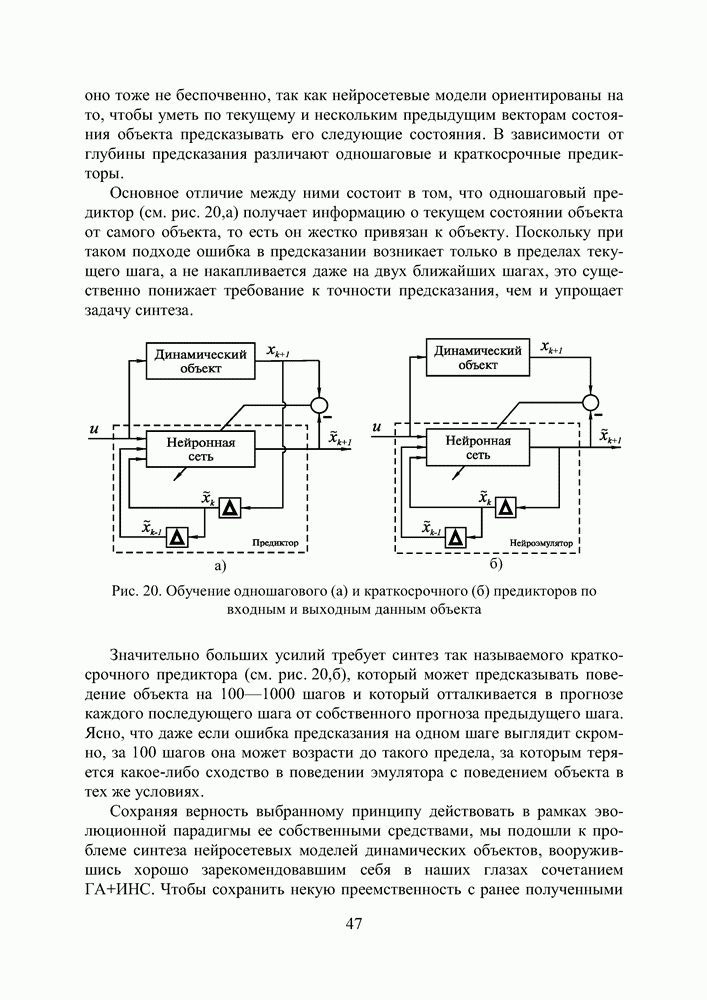
В качестве процедуры для тренировки сети мы использовали ГА. Алгоритм обратного распространения ошибки также подошел бы для этой цели, но он требует информации об ошибке на эффекторном слое ИНС. Для получения такой информации в схеме обучения необходимо предусмотреть обращенный нейроэмулятор объекта, роль которого сводится к преобразованию ошибки на выходе объекта в выходной сигнал на выходе нейроконтроллера, что существенно усложняет процедуру тренировки.

Рис. 15. Применение ГА для настройки параметров нейроконтроллера
Генетический же алгоритм настраивает параметры нейроконтроллера не по ошибке в управлении и, а по ошибке в выходе объекта, сравнивая его с выходом эталонной модели. Последняя воплощает в себе наши представления о желаемом поведении объекта, то есть играет приблизительно ту же роль, что и библиотека тренировочных шаблонов в процедуре тренировки.
Исходная популяция из 100 хромосом генерировалась случайным образом. Каждый из 21 настроечных параметров сети кодировался десятью
битами, таким образом, хромосома, кодирующая нейроконтроллер в целом, представляла собой 210-разрядную последовательность нолей и единиц. При том, что диапазон изменения каждого из параметров в пространстве  был принят от -1 до 1, десятиразрядное кодирование обеспечивало дискретность изменения параметра не хуже 0,002.
был принят от -1 до 1, десятиразрядное кодирование обеспечивало дискретность изменения параметра не хуже 0,002.
После декодирования хромосом в вектора переменных оценивалась способность каждого варианта сети следовать эталонной модели. Проверка осуществлялась путем последовательной подачи на управляющий вход нейроконтроллера единичного положительного, нулевого и единичного отрицательного входного воздействия и вычисления среднеквадратичной ошибки выходной координаты объекта на временном интервале до 10 секунд. Предварительно передаточная функция объекта управления преобразовывалась в систему обыкновенных дифференциальных уравнений в форме Коши

Интегрирование системы осуществлялось с постоянным шагом, равным 0,01 сек. Суммарная ошибка по всем трем переходным процессам принималась в качестве меры неудачности конструкции и использовалась далее в качестве количественного индекса для ранжирования особей в популяции.
Кривые переходных процессов для лучшего варианта из популяции на различных этапах поиска представлены на рис. 16.

Рис. 16. Лучшие из демонстрируемых популяцией нейроконтроллеров переходные процессы на выходе объекта управления в различные моменты работы ГА (задание — единичная ступенька): кривая 1 — начальная популяция, 2 — после 2000 поколений, 3 — после 4000 поколений, 4 — после 5000 поколений.
Как видно из этого рисунка, по мере работы алгоритма решения непрерывно улучшаются. Вектор переменных, найденный к 5000 поколению, обеспечивает вполне удовлетворительное решение поставленной задачи.
Рис. 17 иллюстрирует поведение объекта не только на тренировочных шаблонах, но и при промежуточных значениях амплитуды входного задания,
которое подтверждает универсальность аппроксимирующих свойств нейронных сетей.

Рис. 17. Переходные процессы в САУ с обученным нейроконтроллером при амплитудах входного задания -1, -0,5; 0; 0,5; 1 (снизу вверх)
Воодушевившись достигнутым результатом, мы усложнили задачу. На вход контроллера стали подавать не сигнал ошибки, его производную и интеграл, а просто выходную координату объекта на текущем и предыдущем шагах (единожды и дважды задержанный сигналы - см. рис. 18).

Рис. 18. Новая схема организации обратных связей по [22]
Подверглась изменениям и эталонная модель, которую сформировали теперь как требование к АЧХ канала управления [24]. В то время как сам объект обладает АЧХ с отчетливо выраженным резонансным пиком при частоте 0,32 Гц, нейроконтроллер должен научиться, с одной стороны, ограничивать резонансные колебания объекта, а с другой стороны, усиливать амплитуду вынужденных колебаний в пре- и пострезонансной областях, не внося при этом сдвиг фаз между выходными и входными колебаниями, а также подавлять колебания объекта при частотах, превышающих частоту среза желаемой АЧХ (кривая 2 на рис. 19).
На этот раз для контроллера опять была выбрана трехслойная сеть 3-10-1, т. е. с количеством нейронов в скрытом слое равным 10. Для определения пригодности сети на ее вход подавался фиксированный спектр гармонических колебаний различной амплитуды (в диапазоне 0,1-1) с частотами 0,16; 0,48; 0,80; 1,11 и 1,59 Гц.
Интегральная ошибка по всем тестовым переходным процессам, продолжительность которых, как и ранее, составляла 10 секунд, принималась в качестве меры успешности управления.
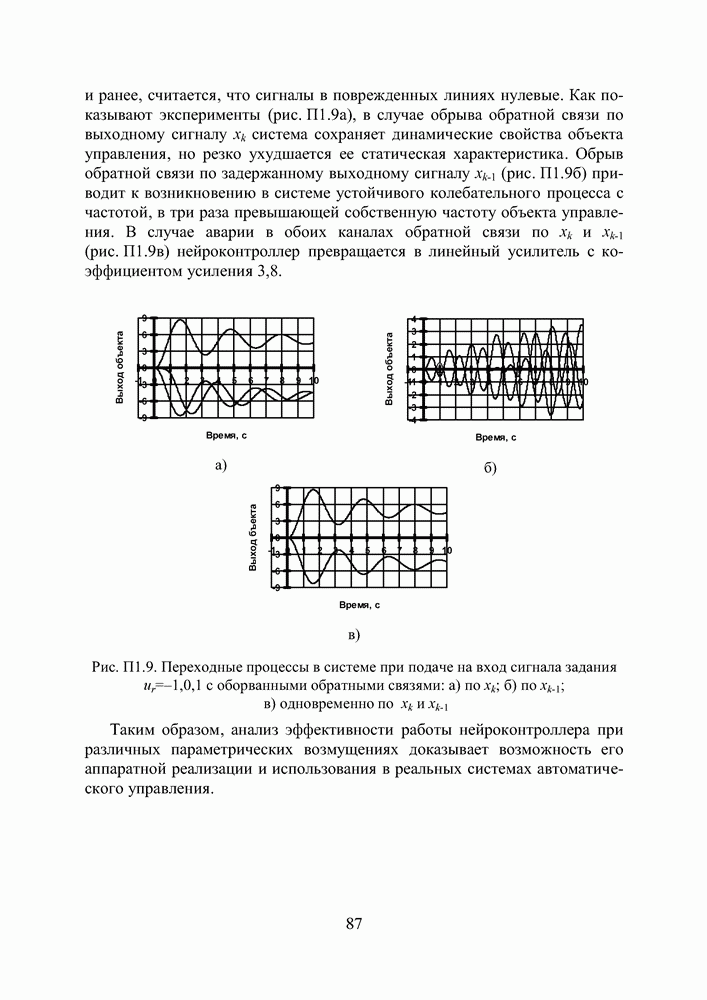
Результаты синтеза оказались удачными. Контроллер, параметры которого представлены в Приложении 1, справлялся с возложенными на него задачами.
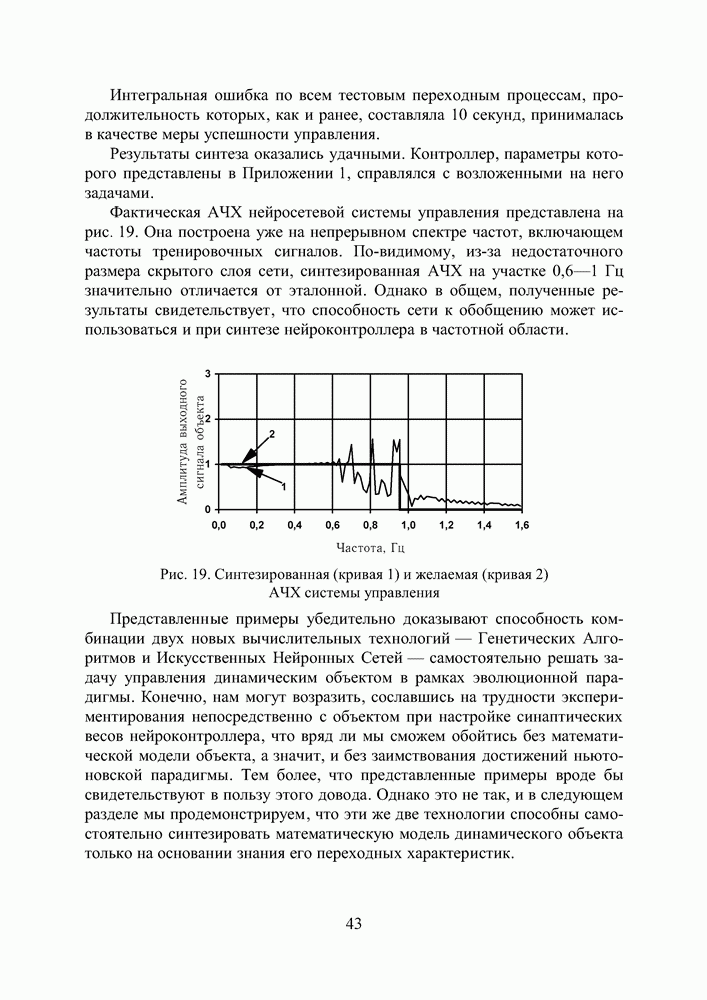
Фактическая АЧХ нейросетевой системы управления представлена на рис. 19. Она построена уже на непрерывном спектре частот, включающем частоты тренировочных сигналов. По-видимому, из-за недостаточного размера скрытого слоя сети, синтезированная АЧХ на участке 0,6-1 Гц значительно отличается от эталонной. Однако в общем, полученные результаты свидетельствует, что способность сети к обобщению может использоваться и при синтезе нейроконтроллера в частотной области.

Рис. 19. Синтезированная (кривая 1) и желаемая (кривая 2) АЧХ системы управления
Представленные примеры убедительно доказывают способность комбинации двух новых вычислительных технологий — Генетических Алгоритмов и Искусственных Нейронных Сетей — самостоятельно решать задачу управления динамическим объектом в рамках эволюционной парадигмы. Конечно, нам могут возразить, сославшись на трудности экспериментирования непосредственно с объектом при настройке синаптических весов нейроконтроллера, что вряд ли мы сможем обойтись без математической модели объекта, а значит, и без заимствования достижений ньютоновской парадигмы. Тем более, что представленные примеры вроде бы свидетельствуют в пользу этого довода. Однако это не так, и в следующем разделе мы продемонстрируем, что эти же две технологии способны самостоятельно синтезировать математическую модель динамического объекта только на основании знания его переходных характеристик.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. О РАЗЛИЧНЫХ ТОЛКОВАНИЯХ ТЕРМИНА «ИНТЕЛЛЕКТУАЛЬНОСТЬ» В УПРАВЛЕНИИ
- 1. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 1.2. Генетические операторы
- 1.3. Преимущественное право размножения сильнейших
- 2. ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ
- 2.2. Становление и развитие ИНС
- 3. ГА+ИНС = НОВАЯ ПАРАДИГМА В УПРАВЛЕНИИ
- 4. ГА+ИНС = НОВАЯ ПАРАДИГМА В МОДЕЛИРОВАНИИ
- 5. СНОВА О ГЕНЕТИЧЕСКИХ АЛГОРИТМАХ
- 6. ВИРТУАЛЬНАЯ РЕАЛЬНОСТЬ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- ЗАКЛЮЧЕНИЕ
- ТЕРМИНОЛОГИЧЕСКИЙ СЛОВАРЬ
- ИМЕННОЙ СПИСОК
- СПИСОК ЛИТЕРАТУРЫ
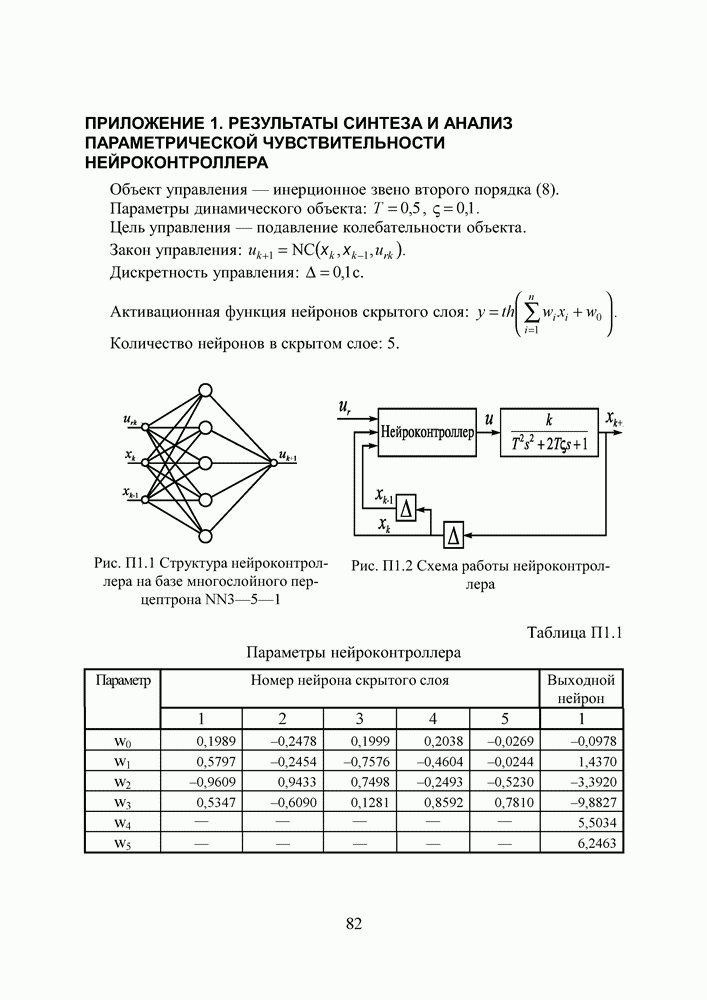
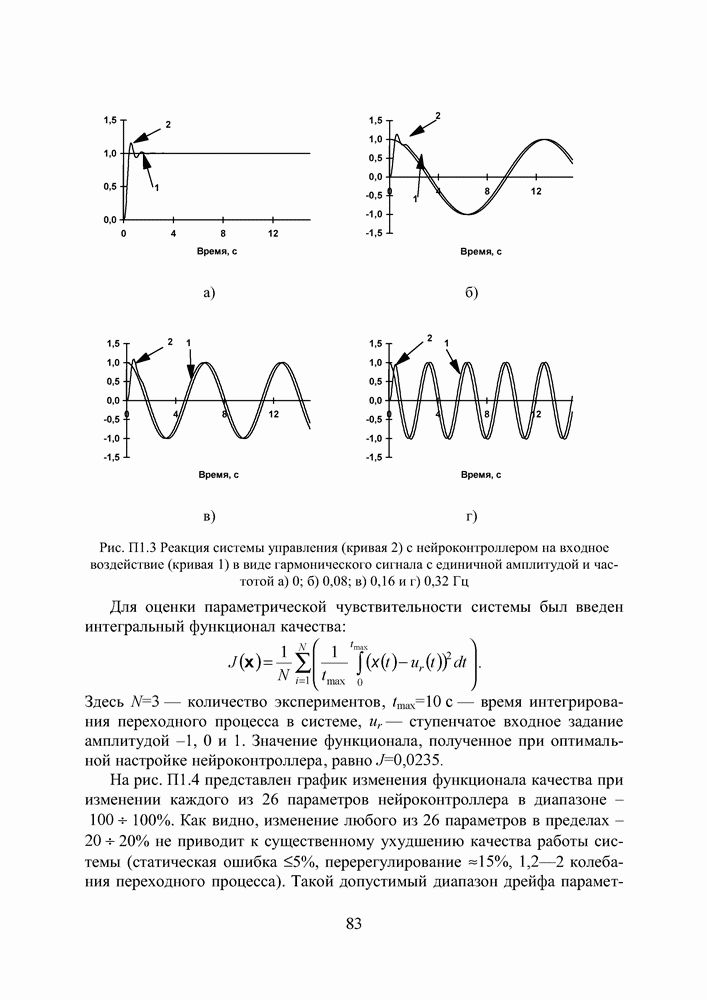
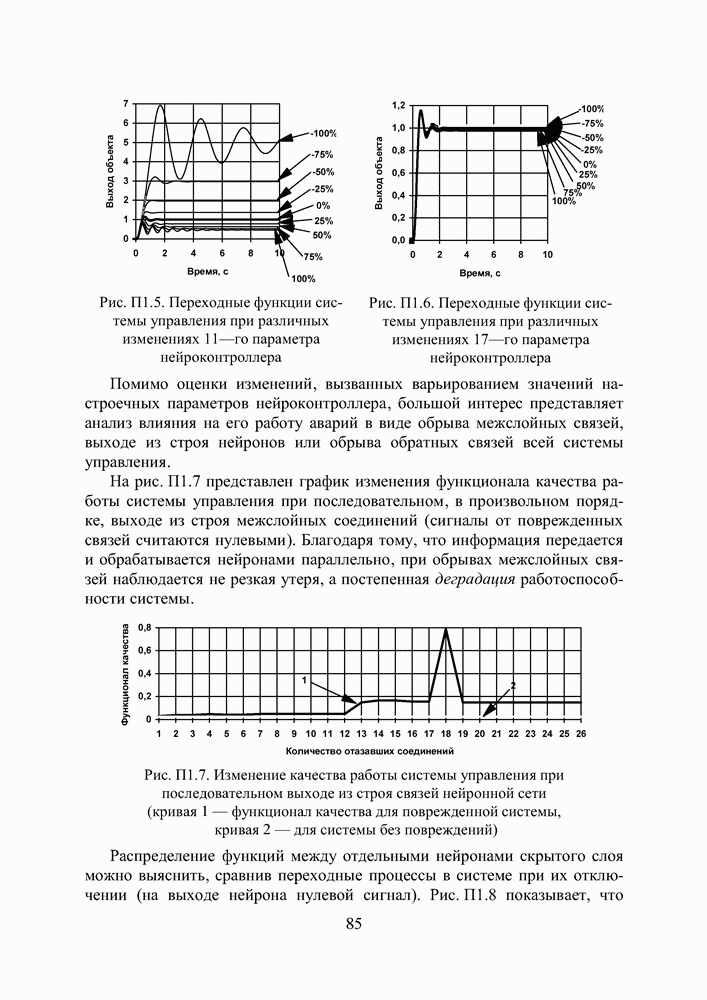
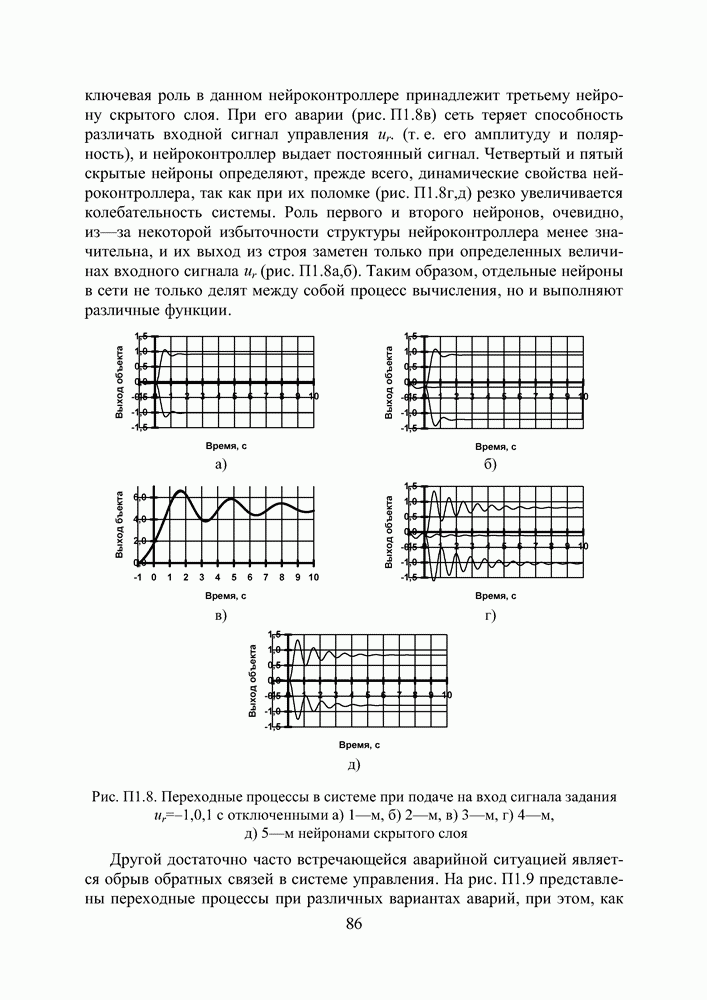
- ПРИЛОЖЕНИЕ 1. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ НЕЙРОКОНТРОЛЛЕРА
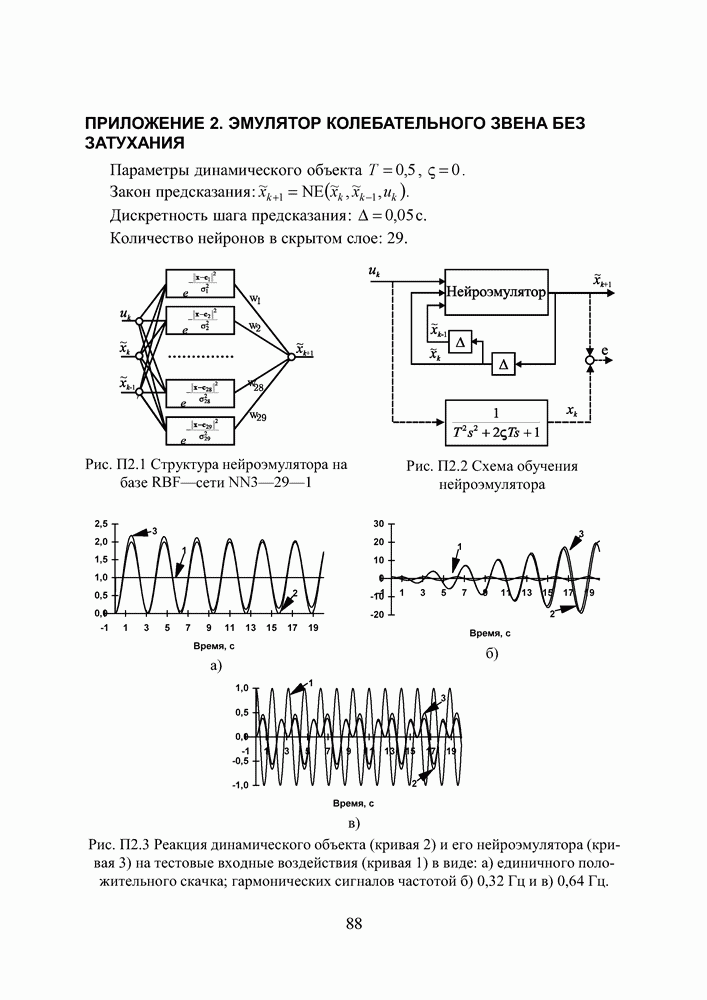
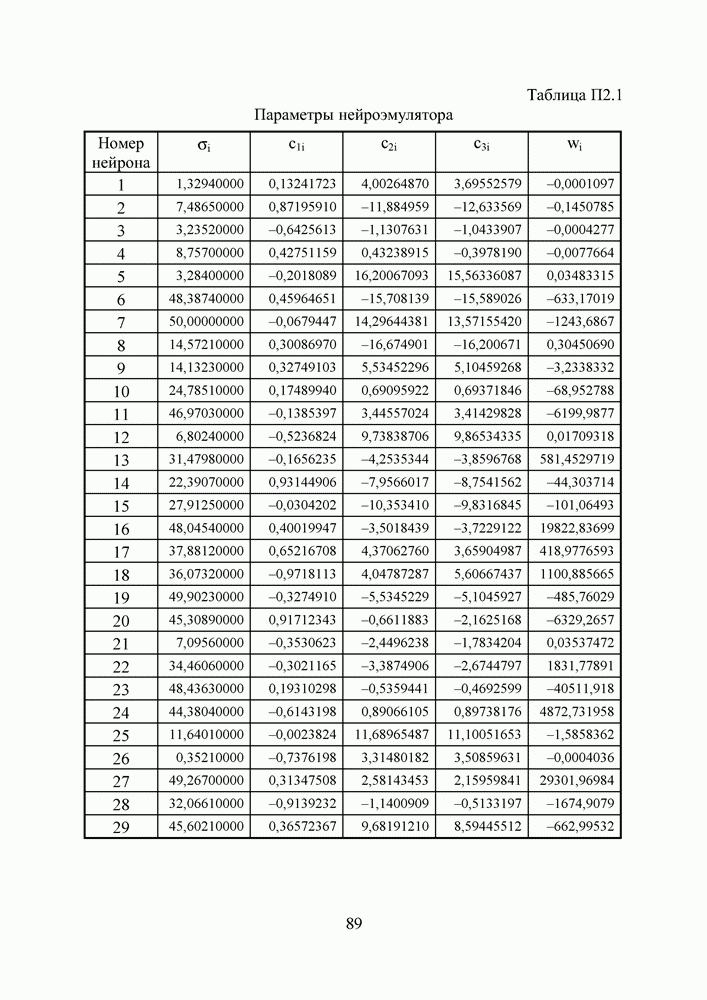
- ПРИЛОЖЕНИЕ 2. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА БЕЗ ЗАТУХАНИЯ
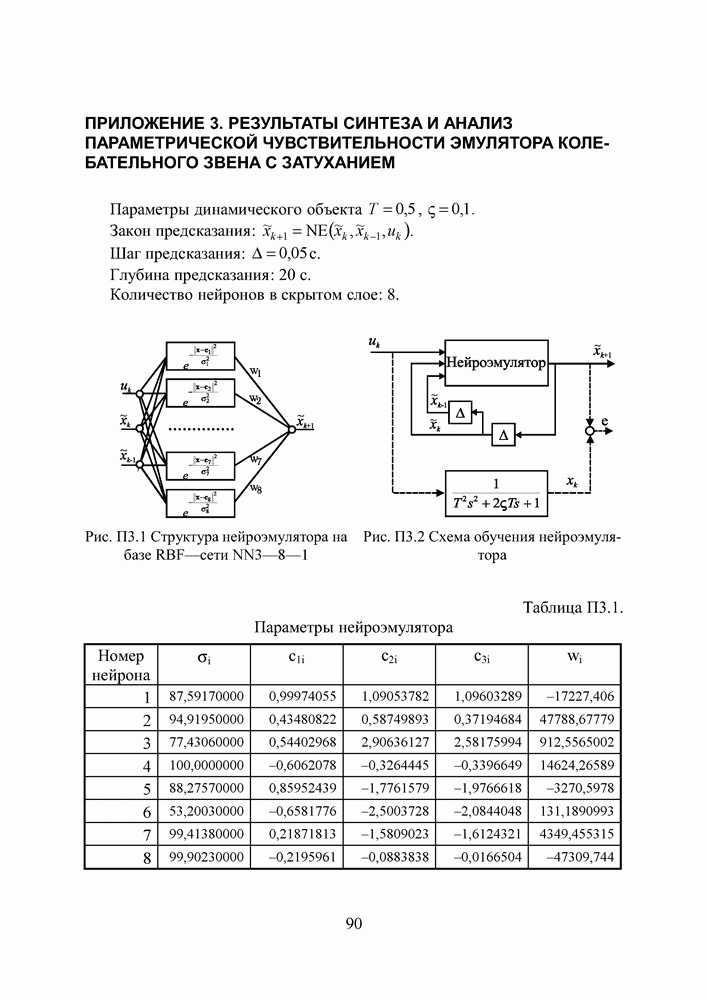
- ПРИЛОЖЕНИЕ 3. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ ЭМУЛЯТОРА КОЛЕБАТЕЛЬНОГО ЗВЕНА С ЗАТУХАНИЕМ
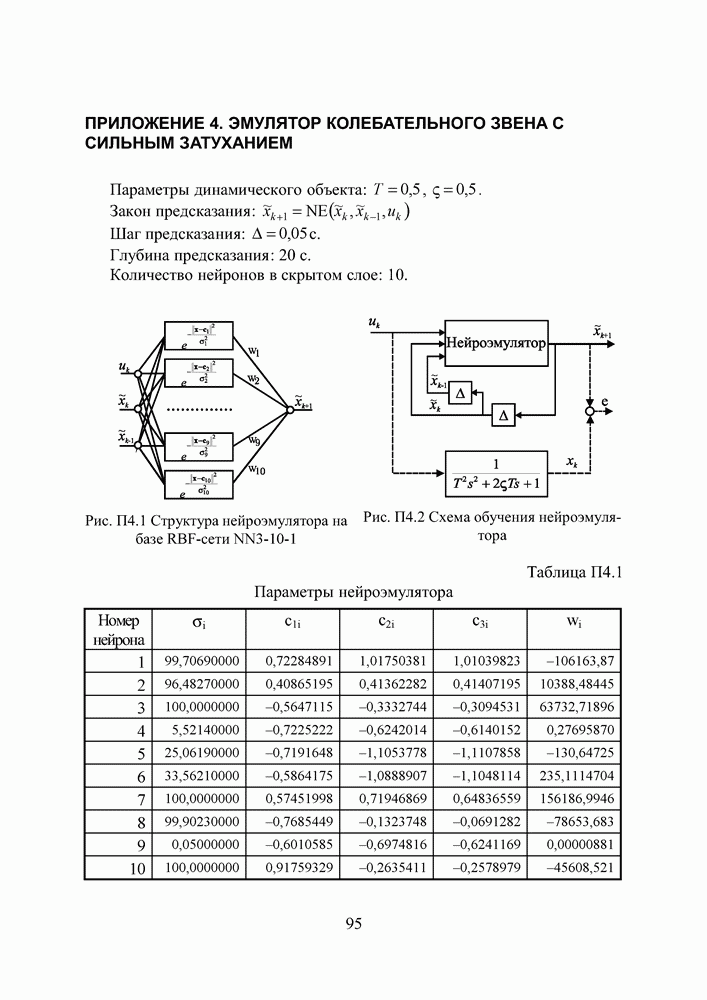
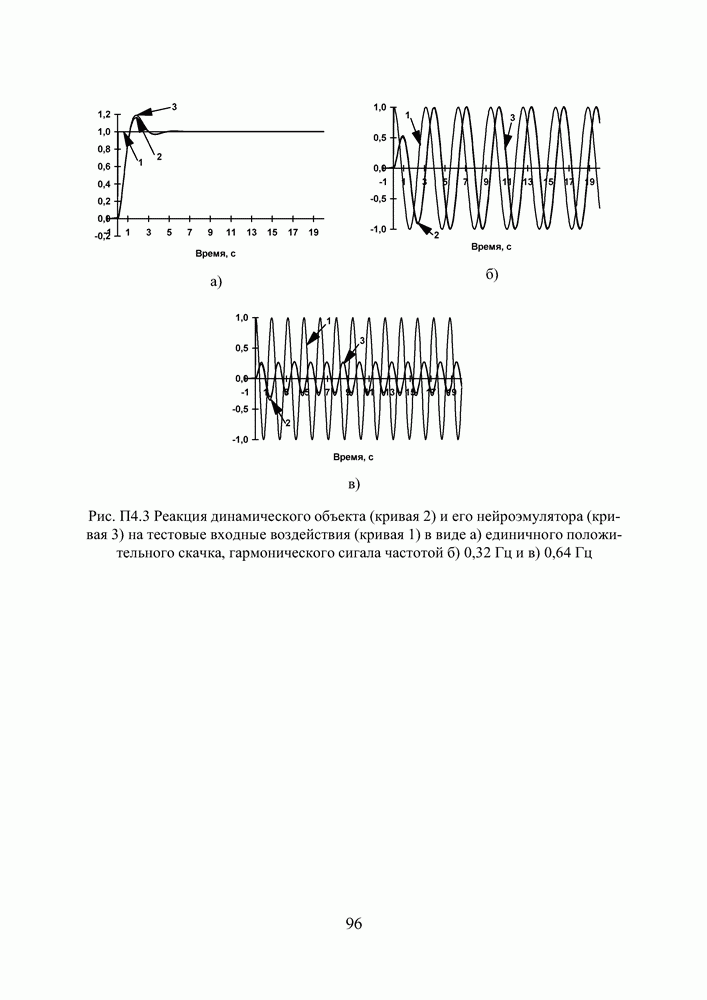
- ПРИЛОЖЕНИЕ 4. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА С СИЛЬНЫМ ЗАТУХАНИЕМ
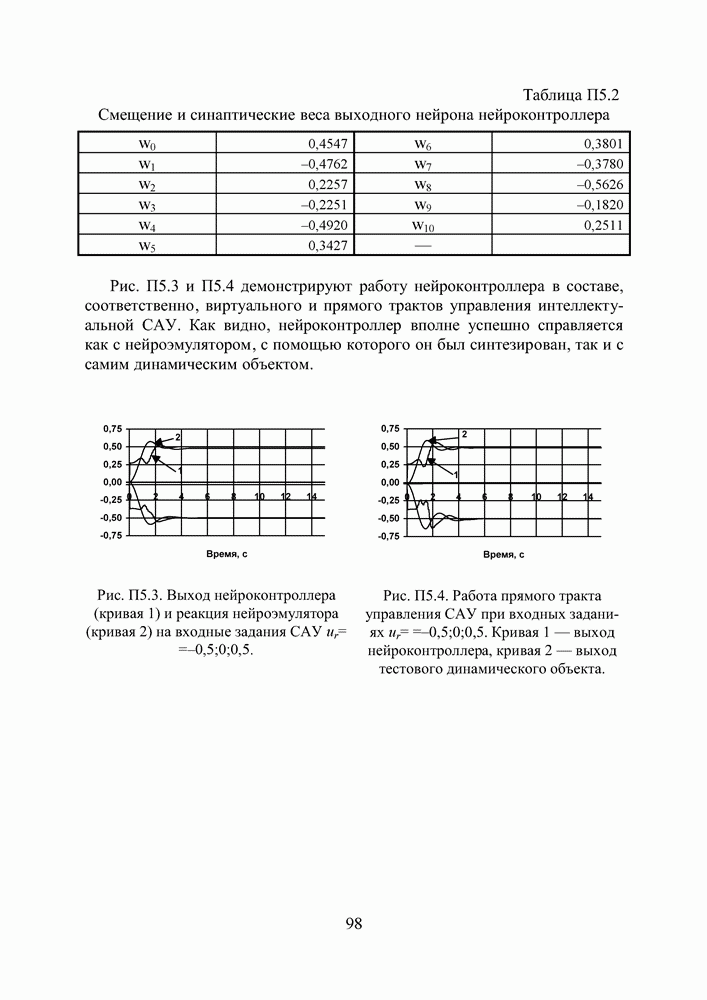
- ПРИЛОЖЕНИЕ 5. ВИРТУАЛЬНЫЙ ТРАКТ УПРАВЛЕНИЯ НА БАЗЕ НЕЙРОЭМУЛЯТОРА
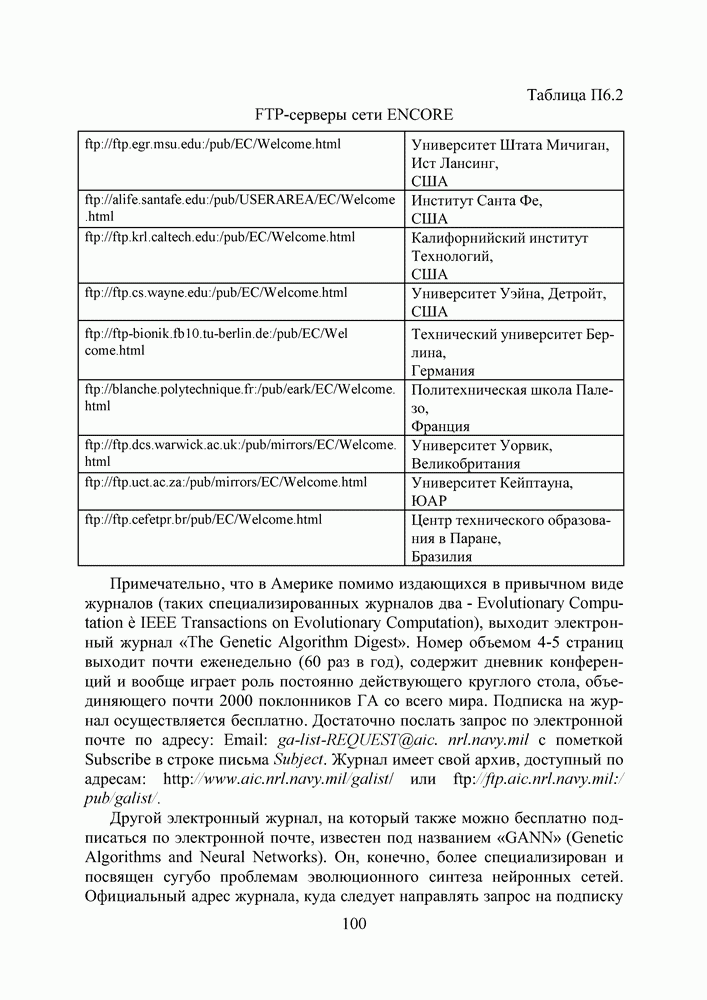
- ПРИЛОЖЕНИЕ 6. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ И ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ В ИНТЕРНЕТЕ