| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
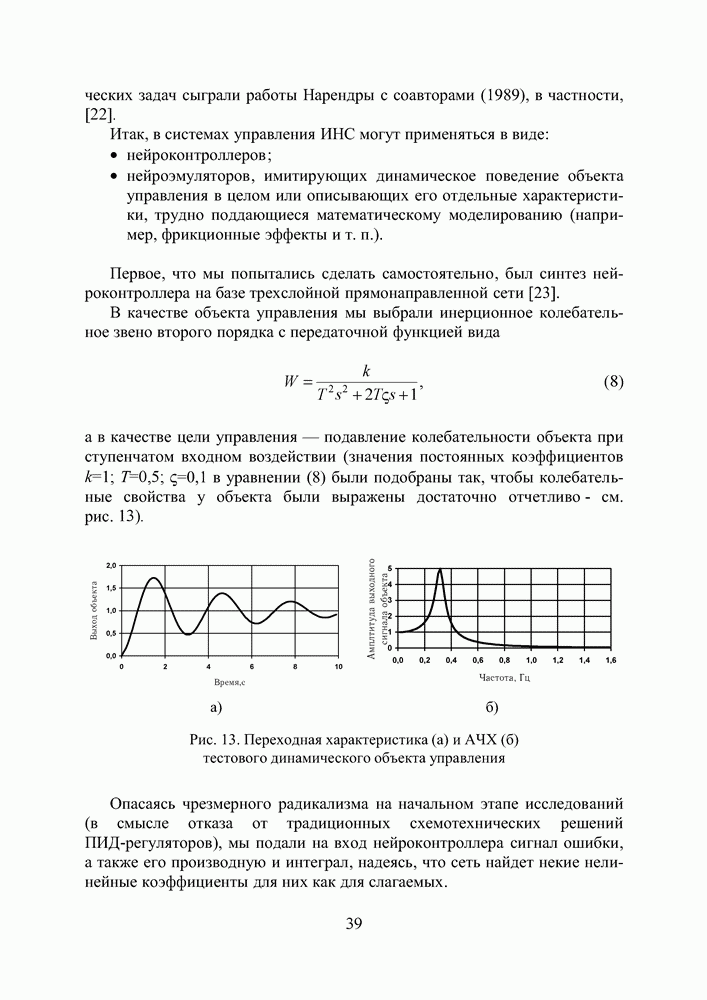
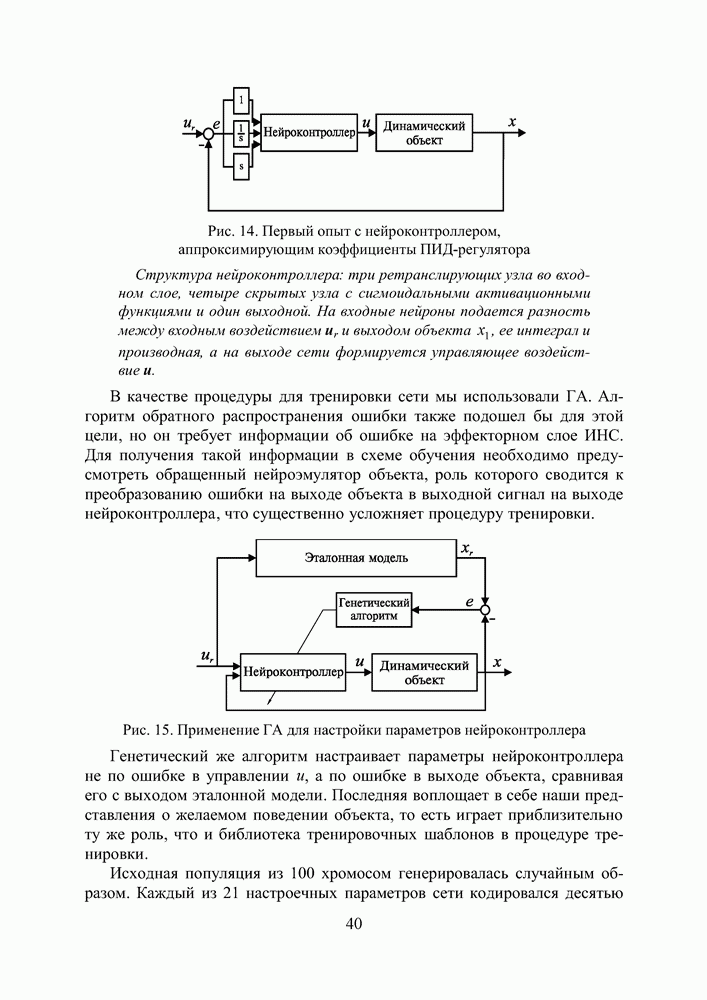
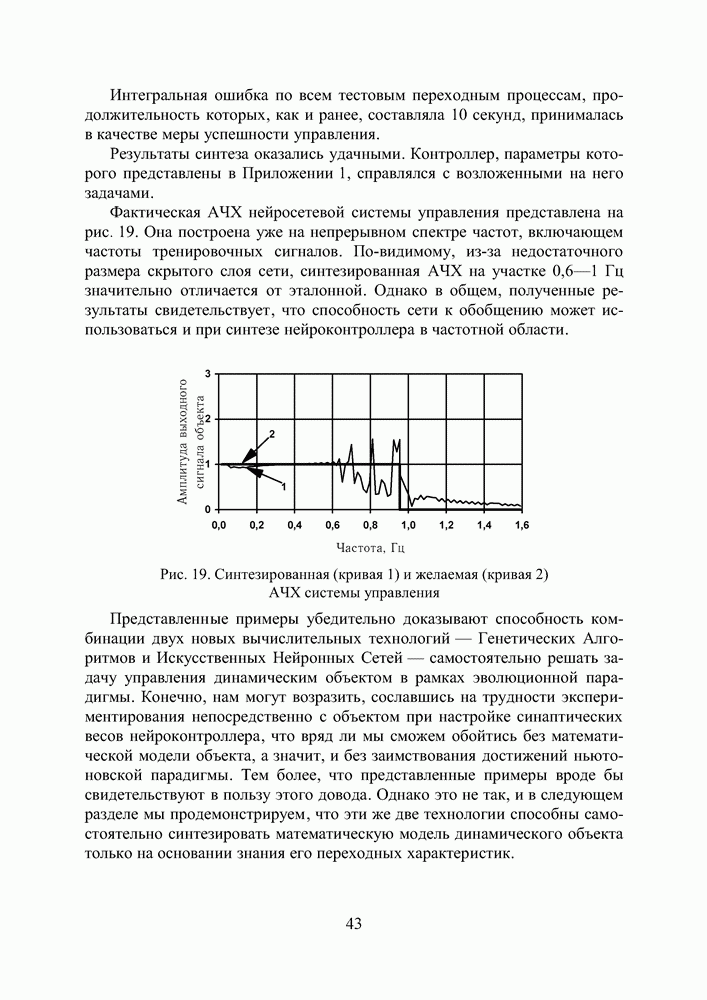
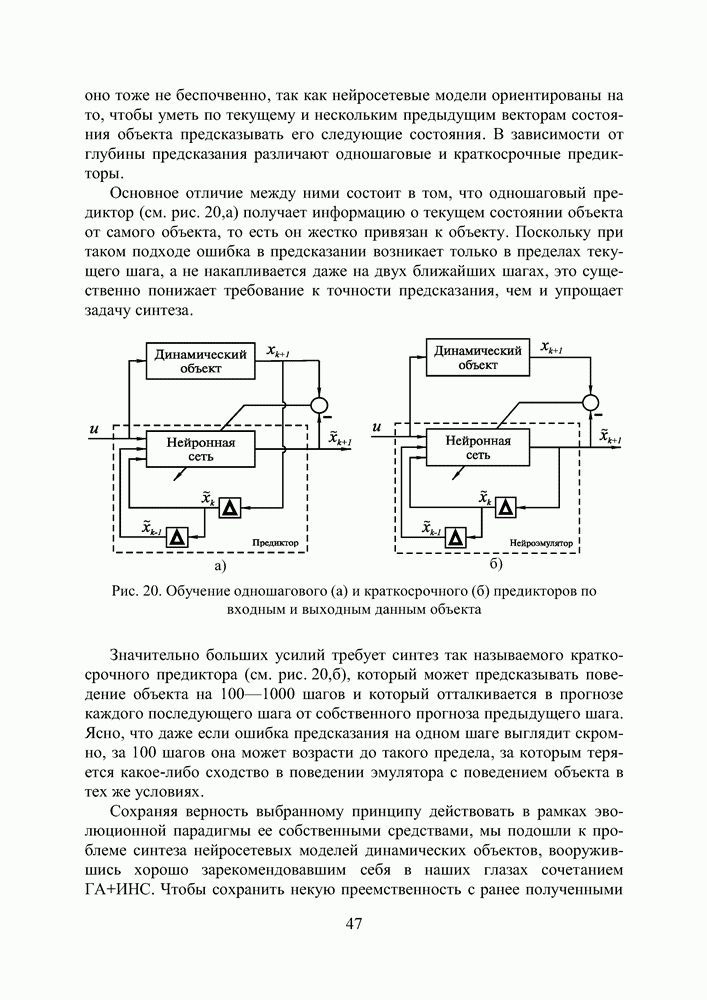
2.2. Становление и развитие ИНС
Наиболее емким представляется следующее определение ИНС как адаптивной машины, данное в [6]:
Искусственная нейронная сеть — это существенно параллельно распределенный процессор, который обладает способностью к сохранению и репрезентации опытного знания. Она сходна с мозгом в двух аспектах:
1. Знание приобретается сетью в процессе обучения;
2. Для сохранения знания используются силы межнейронных соединений, называемые также синаптическими весами.
История ИНС начинается в 1943, когда Маккаллок и Питтс предложили модель «порогового логического нейрона» и показали, что любая функция, которая может быть вычислена на электронно-вычислительной машине, может быть также вычислена сетью нейронов [7]. Сигналы  поступающие на вход нейрона, умножаются на весовые коэффициенты
поступающие на вход нейрона, умножаются на весовые коэффициенты  (синаптические веса). Далее они суммируются, и результирующий сигнал, сдвинутый на величину смещения
(синаптические веса). Далее они суммируются, и результирующий сигнал, сдвинутый на величину смещения 

подается на вход блока, реализующего активационную функцию нейрона.

Рис. 8. Модель нейрона
Традиционно активационная функция имеет ступенчатый вид, то есть сигнал на выходе нейрона y появляется лишь тогда, когда суммарное входное воздействие превышает некоторое критическое значение.

Рис. 9. Типы активационных функций нейронов
Хебб [8], изучая клеточные механизмы деятельности мозга, сформулировал правило обучения, которое увеличивает силу связи между пре- и постсинаптическим нейронами, если активность обоих совпадает во времени.
Другая концепция обучения в рамках более развитой архитектуры сети, названной перцептроном, была предложена и успешно применена для моделирования работы зрительного тракта Розенблаттом [9].
В своей самой простой версии многослойный перцептрон (см. рис. 10) представляет собой сеть с одним входным, одним выходным и одним или более внутренними или, как говорят, скрытыми слоями нейронов. Общей чертой для всех многослойных перцептронов является прямонаправленность сети, характеризующаяся передачей информации от входного слоя через К скрытых слоев к выходному слою. В стандартной топологии, узел  в слое
в слое  соединяется посредством весов
соединяется посредством весов  со всеми
со всеми  узлами предыдущего слоя
узлами предыдущего слоя  Здесь
Здесь  обозначают, соответственно, входной и выходной слои.
обозначают, соответственно, входной и выходной слои.

Рис. 10. Схема прямонаправленной слойной ИНС
Модифицированные версии могут иметь прямые связи между несмежными слоями, связи в пределах одного слоя, хаотичные связи между слоями вместо регулярных.
Входной слой перцептрона служит лишь для приема и ретрансляции входных сигналов на нейроны скрытого слоя. В скрытых слоях происходит основное нелинейное преобразование информации, а выходной слой осуществляет суперпозицию взвешенных сигналов последнего из скрытых слоев. В качестве нелинейности узлы скрытого слоя используют дифференцируемые сигмоидальные функции

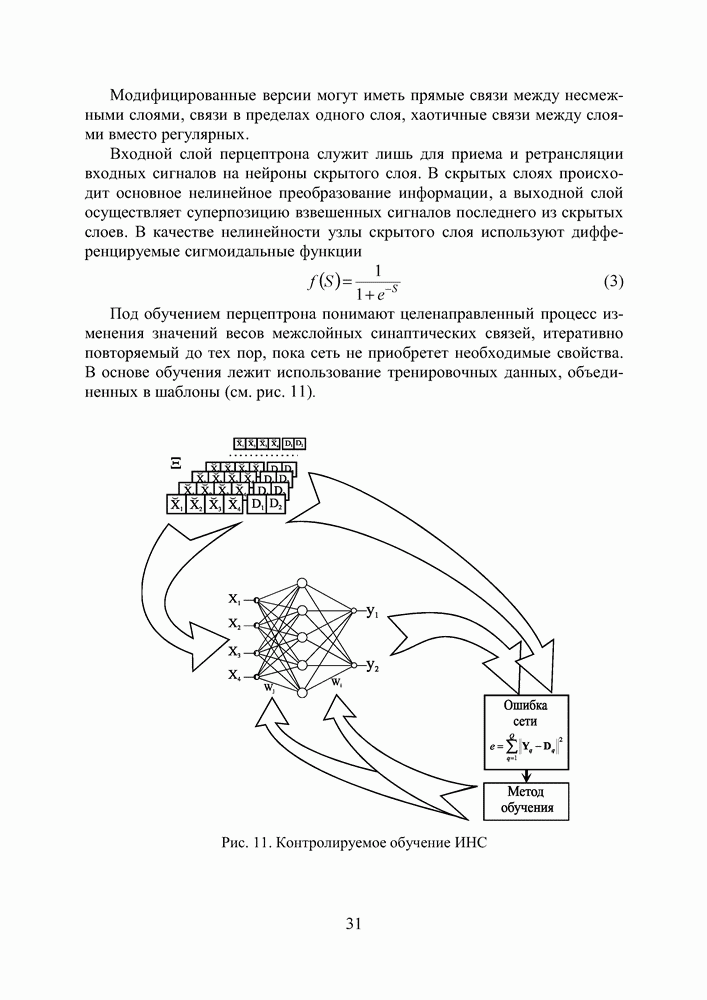
Под обучением перцептрона понимают целенаправленный процесс изменения значений весов межслойных синаптических связей, итеративно повторяемый до тех пор, пока сеть не приобретет необходимые свойства. В основе обучения лежит использование тренировочных данных, объединенных в шаблоны (см. рис. 11).
Рис. 11. (см. скан) Контролируемое обучение ИНС
Каждый шаблон  включает в себя вектор известных входных
включает в себя вектор известных входных
сигналов сети  и соответствующий ему вектор желаемых выходных сигналов
и соответствующий ему вектор желаемых выходных сигналов  . В процессе обучения на вход ИНС последовательно подаются данные из тренировочного набора шаблонов
. В процессе обучения на вход ИНС последовательно подаются данные из тренировочного набора шаблонов  после чего вычисляется ошибка между фактическим
после чего вычисляется ошибка между фактическим  и желаемым выходами сети
и желаемым выходами сети

Здесь под нормой  обычно понимают евклидово расстояние между векторами
обычно понимают евклидово расстояние между векторами  и
и 
Далее, с помощью определенного правила или алгоритма происходит такая модификация настроечных параметров сети, чтобы эта ошибка уменьшалась. Процесс повторяется до достижения сетью способности выполнять желаемый тип преобразования «вход-выход», заданного в неявном виде тренировочным набором шаблонов Н.
Благодаря обучению сеть приобретает способность правильно реагировать не только на шаблоны, предъявленные в процессе тренировки, но также хорошо справляться с другими наборами данных из допустимого пространства входов, которые она никогда не «видела» ранее. В этом смысле говорят, что ИНС обладает свойством обобщения (generalization).
Ошибка в обобщении, всегда имеющая место на выходе сети, имеет две составляющие. Первая из них обусловлена недостаточным качеством аппроксимации, выполняемой сетью конечных размеров. Вторая — вызвана неполнотой информации, предъявленной сети в процессе обучения, из-за ограниченного объема обучающей выборки.
У Розенблатта сила межслойных синаптических связей изменялась в зависимости от того, насколько точно выход перцептрона совпадал с выходным шаблоном, в соответствии со следующим правилом обучения. Веса связей увеличиваются, если выходной сигнал, сформированный принимающим нейроном, слишком слаб, и уменьшаются, если он слишком высокий. Однако, это простое правило минимизации ошибки применимо только к прямонаправленным сетям без скрытых слоев.
Несколько позже Минский и Пейперт выполнили глубокий анализ вычислительной мощности однослойного перцептрона.
Эффект их совместной книги «Персептроны» [10], предназначенной внести конструктивный вклад в теорию нейронных сетей, был для многих обескураживающим и привел к утрате интереса к нейронным сетям. Казалось, что если сети не могут реализовать даже XOR-функцию (логическая функция «исключающее ИЛИ», получившая с легкой руки авторов [10] статус теста при исследовании сравнительной эффективности тренировочных
Алгоритм обратного распространения ошибки
(см. скан)
процедур), их вычислительные способности слишком ограничены. Выход из этого положения — добавление скрытых слоев с нелинейными нейронами — был известен и тогда, однако не было ясности, как настроить веса у такой сети.
Настоящий прогресс был достигнут лишь после того, как Румельхарт, Хинтон и Вильямс в 1986 последовательно переоткрыли Алгоритм Обратного Распространения ошибки (АОР) [11, 12], впервые описанный Вербосом в 1974 году [13].
Уместно также вспомнить работы новосибирских ученых [14,15], независимо и одновременно с Румельхартом предложивших очень близкий к АОР Алгоритм Двойственного Функционирования для обучения нейронной сети. Хотя АОР рассеял пессимизм о возможности обучения многослойных сетей, он, тем не менее, не стал инструментом, который позволил бы решить коренной вопрос синтеза нейронных сетей — глобальную оптимизацию структуры и параметров сети. Инициализация начальных параметров сети осуществляется здесь случайным образом, а сам АОР, известный в статистике как метод стохастической аппроксимации, является по своей сути не более чем локальным методом и в силу этого не гарантирует окончания процесса обучения в точке глобального экстремума. Вместе с тем, не вызывает сомнений, что ошибка (4), используемая для оценки качества ИНС, является многоэкстремальной функцией параметров сети, поэтому для поиска ее минимума требуется, соответственно, глобальный метод.
Тем не менее, с появлением АОР интерес к нейронным сетям снова возродился. Нельзя игнорировать и тот факт, что к концу 80-х годов общая ситуация в мире науки существенно изменилась по сравнению с 60-тыми — прогресс в разработке персональных компьютеров существенно раздвинул границы численного экспериментирования, началась эра численных методов моделирования. Искусственные нейронные сети становятся массовым увлечением и через своих поклонников проникают в самые разные научные дисциплины.
Последние 10 лет ознаменовались двумя событиями, имеющими отношение к теме нашего исследования. Первое из них — появление RBF-сетей, поддающихся очень простой, не содержащей рекурсии, настройке [16]. Второе — применение ГА для тренировки сети произвольной архитектуры, содержащей любые комбинации активационных функций нейронов скрытого слоя [17].
Большое внимание уделялось также доказательству универсальности нейронных сетей для решения задач аппроксимации произвольной функции с любой степенью точности. В [18—19] это сделано для сетей перцептронного типа с сигмоидальными активационными функциями, в [20] — для RBF-сетей.
Рассмотрим процедуру тренировки RBF-сети (см. Рис.12), осуществляющей аппроксимацию функции, заданной в неявном виде набором шаблонов, как она описана в [16].
Пусть V — количество входов сети,  — количество нейронов скрытого слоя,
— количество нейронов скрытого слоя,  — количество выходов сети.
— количество выходов сети.
Предположим, что размер  набора тренировочных шаблонов Е не слишком велик и что шаблоны размещены достаточно разреженно в пространстве входных сигналов сети
набора тренировочных шаблонов Е не слишком велик и что шаблоны размещены достаточно разреженно в пространстве входных сигналов сети  .
.

Рис. 12. Классическая RBF-сеть
Сеть характеризуется тремя особенностями: 1) единственный скрытый слой; 2) только нейроныг скрытого слоя имеют нелинейную активационную функцию; 3) синаптические веса всех нейронов скрытого слоя равны единице.
Введем следующие обозначения:  — вектор координат центра активационной функции нейрона скрытого слоя;
— вектор координат центра активационной функции нейрона скрытого слоя;  — ширина окна активационной функции
— ширина окна активационной функции  нейрона скрытого слоя;
нейрона скрытого слоя;  — радиально-симметричная активационная функция нейрона скрытого слоя;
— радиально-симметричная активационная функция нейрона скрытого слоя;  — вес связи между
— вес связи между  нейроном выходного слоя и
нейроном выходного слоя и  нейроном скрытого слоя.
нейроном скрытого слоя.
Синтез и обучение сети включает в себя три этапа, объединенные следующим алгоритмом.
Алгоритм синтеза RBF-сети
(см. скан)
Ошибка аппроксимации в точках входного пространства, не совпадающих с центрами активационных функций, зависит от того, насколько удачно выбраны ширины окон, и адекватно ли количество тренировочных шаблонов сложности функционального преобразования.
К сожалению, процедура настройки синаптических весов является далеко не единственной и не последней проблемой, встречающейся при обучении сети. Куда как более сложным вопросом остается формирование набора тренировочных шаблонов, адекватно описывающего рассматриваемое функциональное преобразование. К этой проблеме мы еще вернемся в следующих разделах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. О РАЗЛИЧНЫХ ТОЛКОВАНИЯХ ТЕРМИНА «ИНТЕЛЛЕКТУАЛЬНОСТЬ» В УПРАВЛЕНИИ
- 1. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 1.2. Генетические операторы
- 1.3. Преимущественное право размножения сильнейших
- 2. ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ
- 2.2. Становление и развитие ИНС
- 3. ГА+ИНС = НОВАЯ ПАРАДИГМА В УПРАВЛЕНИИ
- 4. ГА+ИНС = НОВАЯ ПАРАДИГМА В МОДЕЛИРОВАНИИ
- 5. СНОВА О ГЕНЕТИЧЕСКИХ АЛГОРИТМАХ
- 6. ВИРТУАЛЬНАЯ РЕАЛЬНОСТЬ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- ЗАКЛЮЧЕНИЕ
- ТЕРМИНОЛОГИЧЕСКИЙ СЛОВАРЬ
- ИМЕННОЙ СПИСОК
- СПИСОК ЛИТЕРАТУРЫ
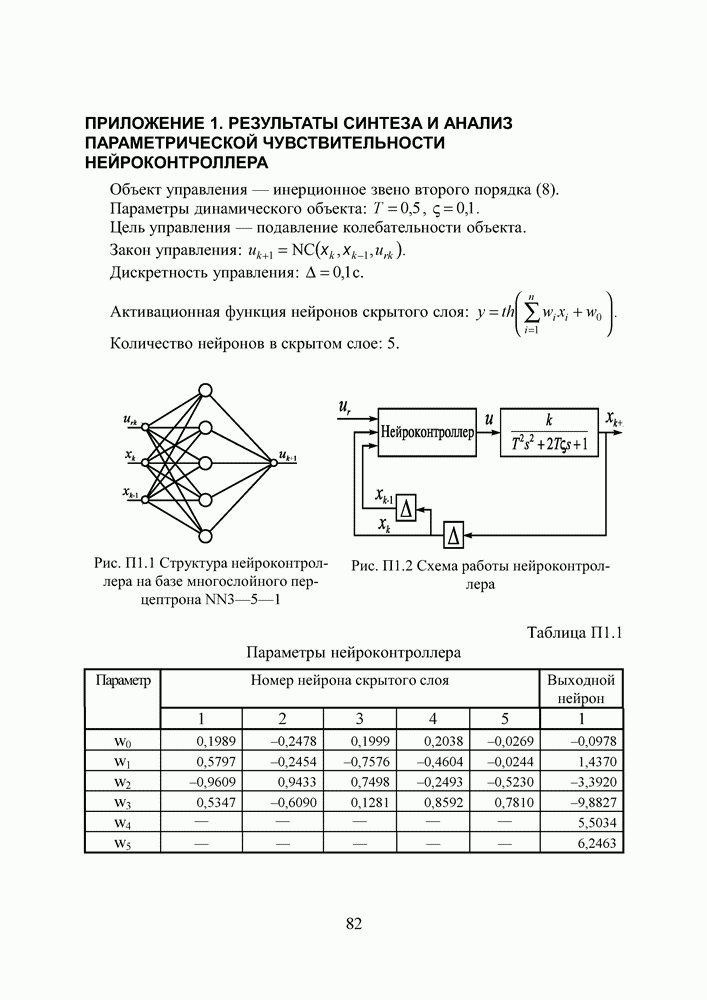
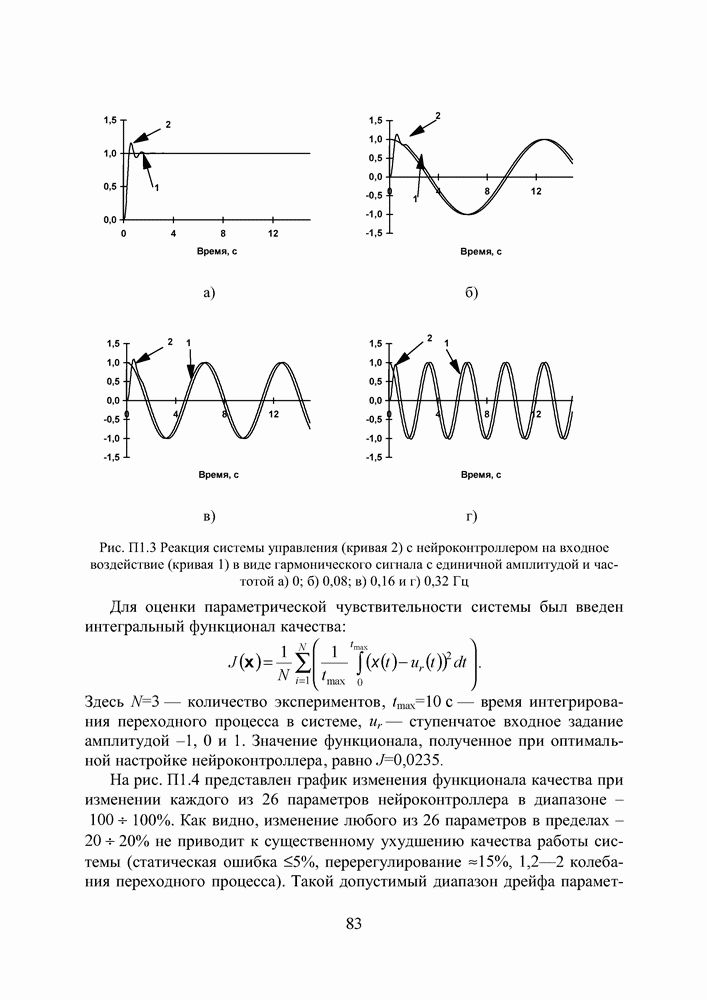
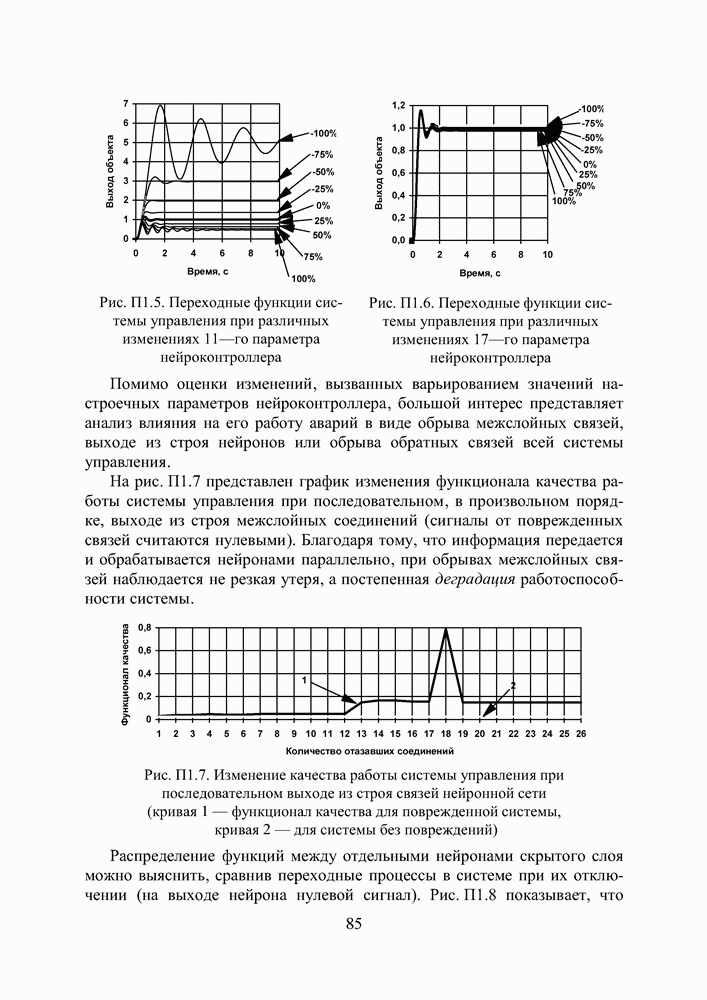
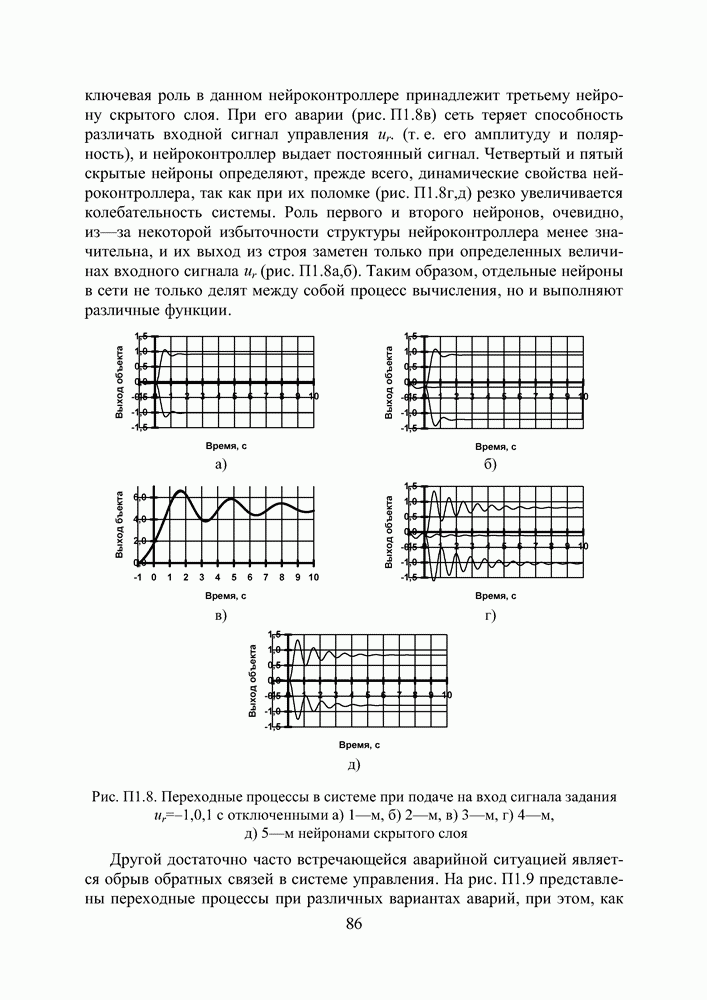
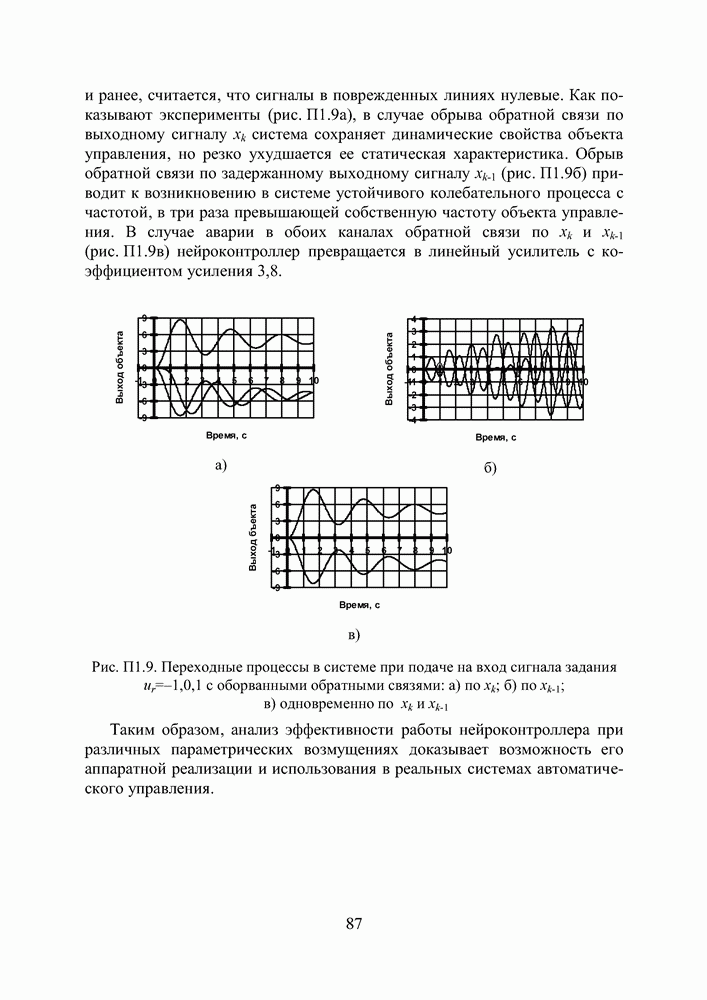
- ПРИЛОЖЕНИЕ 1. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ НЕЙРОКОНТРОЛЛЕРА
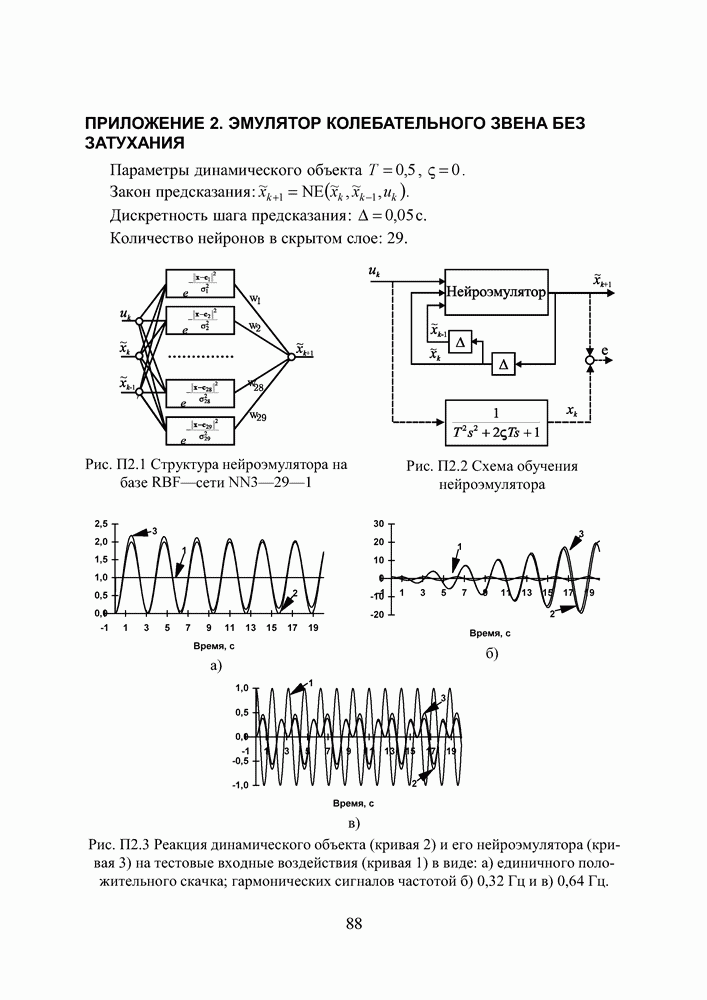
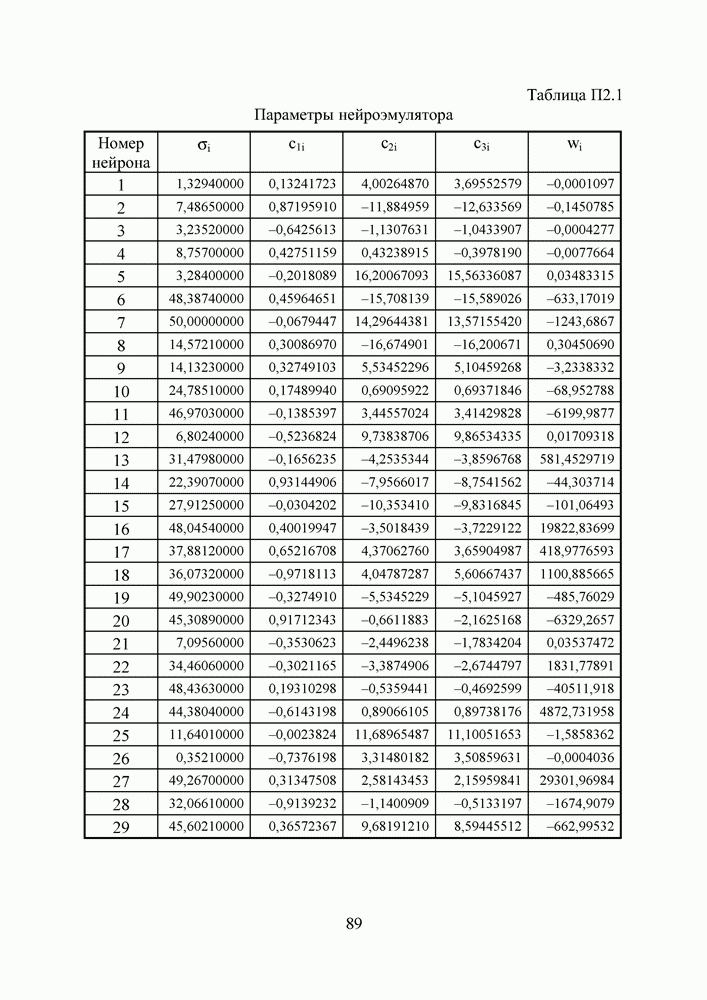
- ПРИЛОЖЕНИЕ 2. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА БЕЗ ЗАТУХАНИЯ
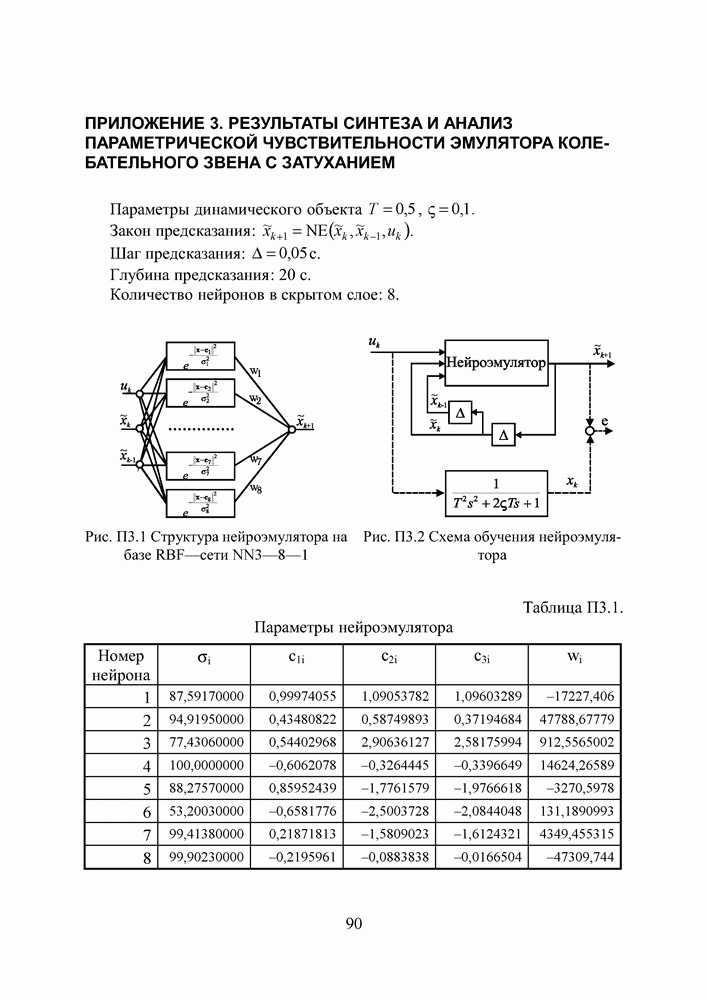
- ПРИЛОЖЕНИЕ 3. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ ЭМУЛЯТОРА КОЛЕБАТЕЛЬНОГО ЗВЕНА С ЗАТУХАНИЕМ
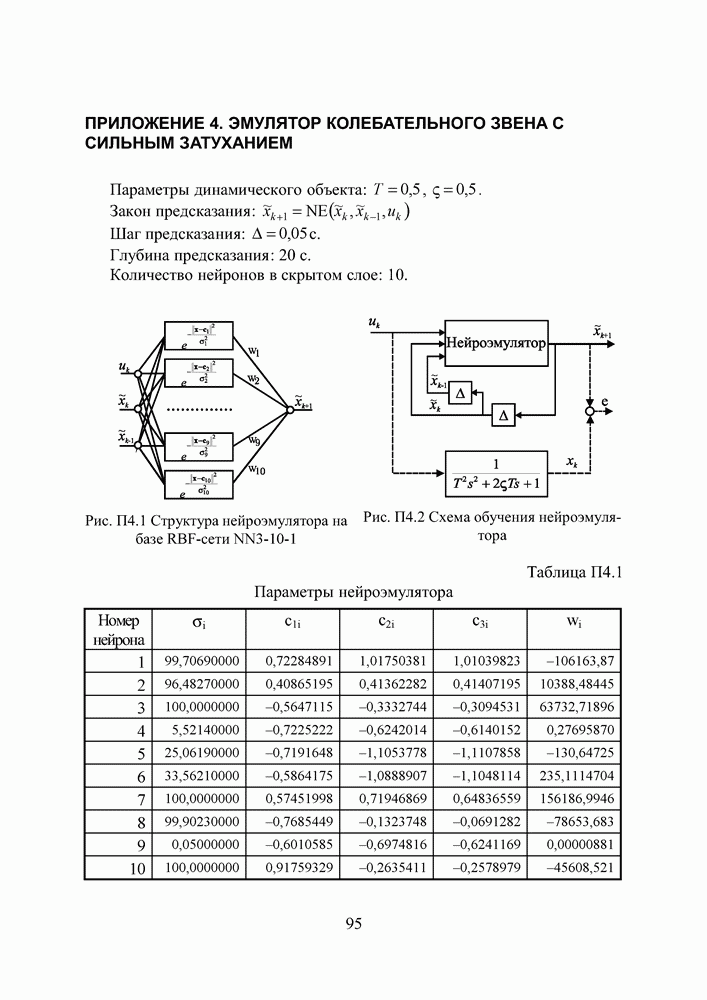
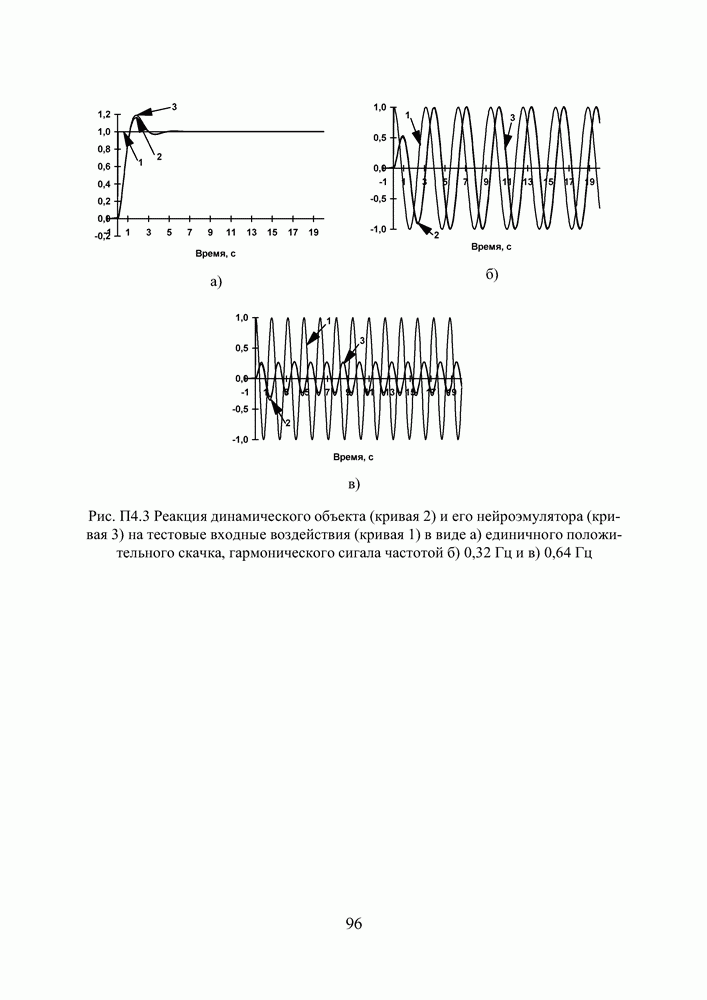
- ПРИЛОЖЕНИЕ 4. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА С СИЛЬНЫМ ЗАТУХАНИЕМ
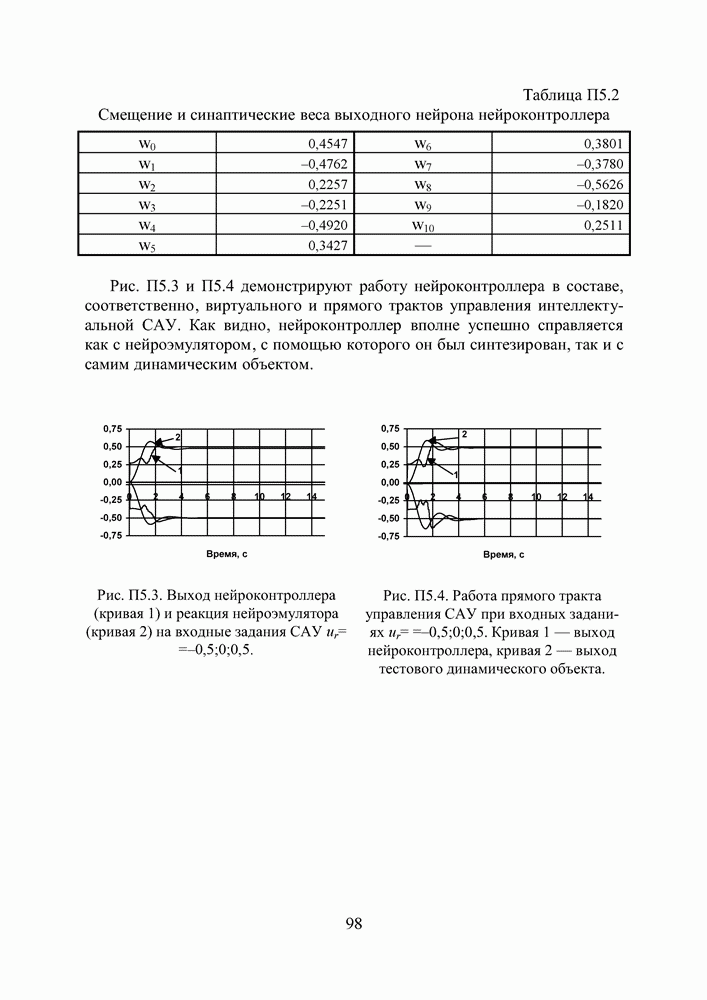
- ПРИЛОЖЕНИЕ 5. ВИРТУАЛЬНЫЙ ТРАКТ УПРАВЛЕНИЯ НА БАЗЕ НЕЙРОЭМУЛЯТОРА
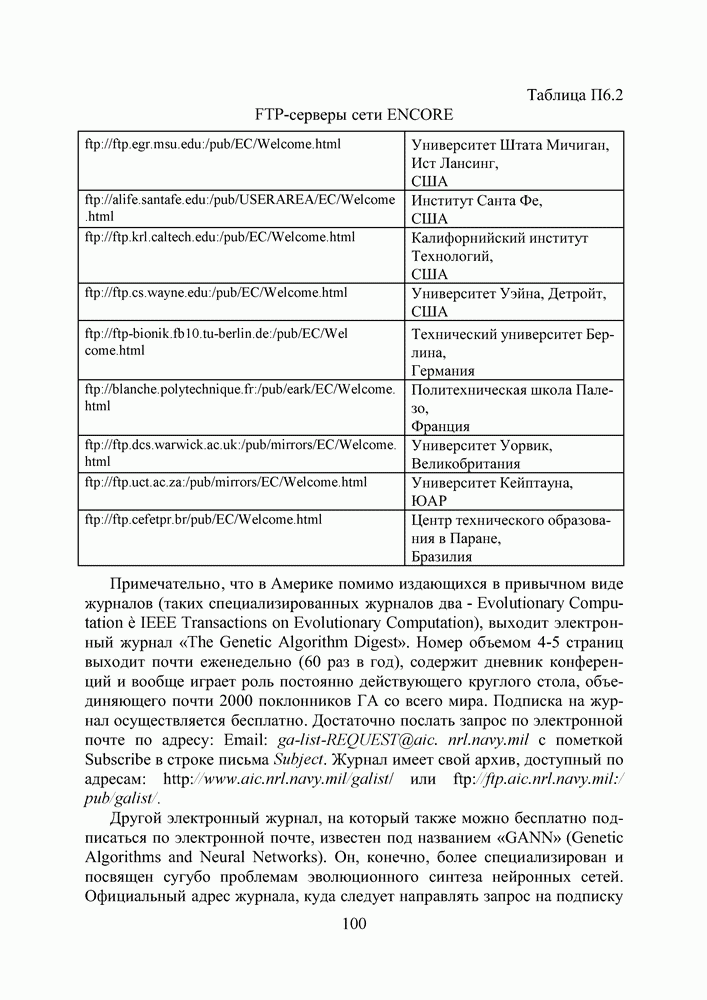
- ПРИЛОЖЕНИЕ 6. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ И ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ В ИНТЕРНЕТЕ