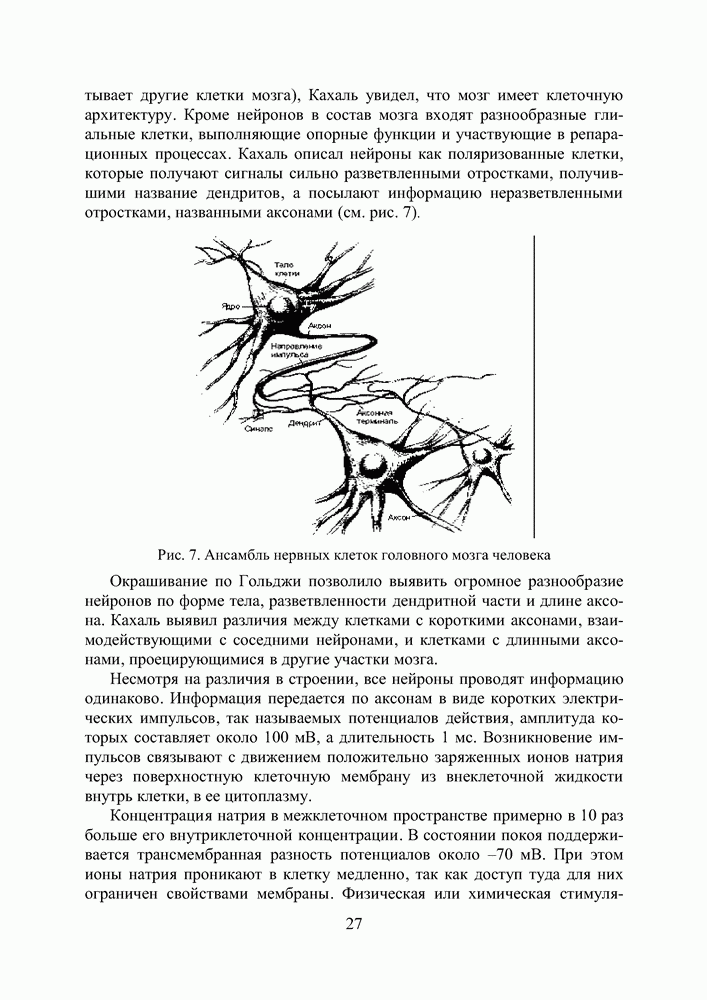
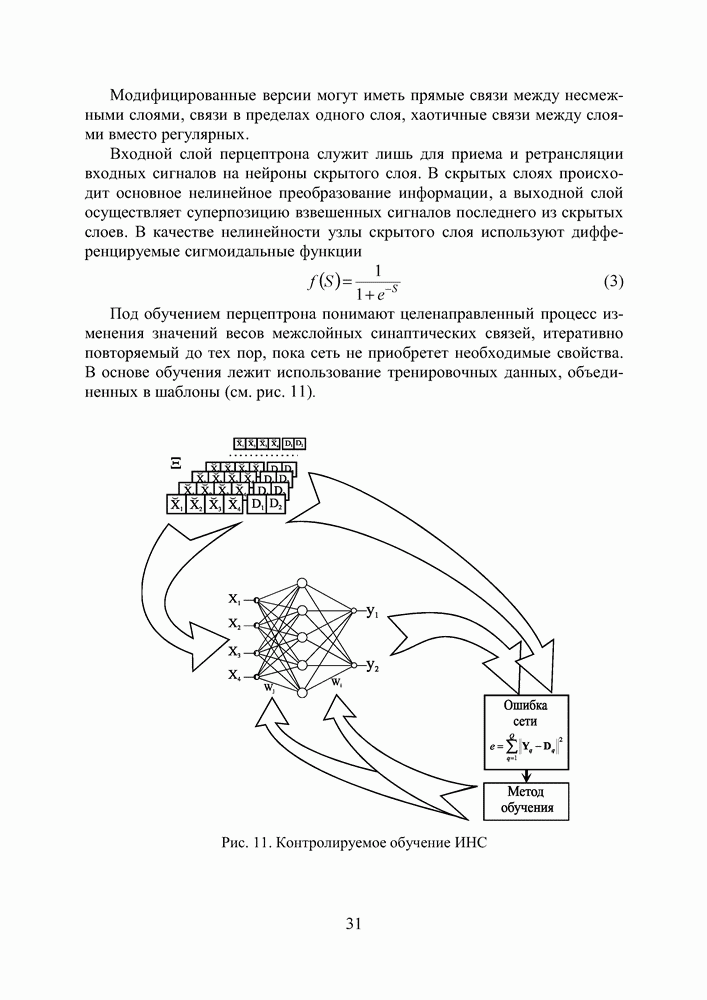
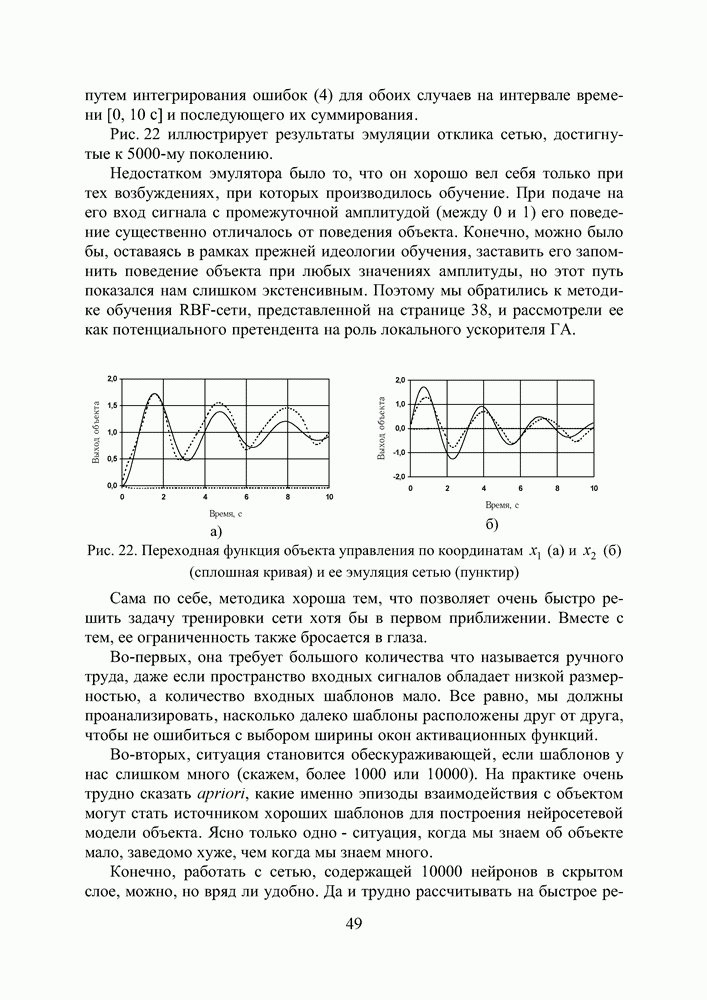
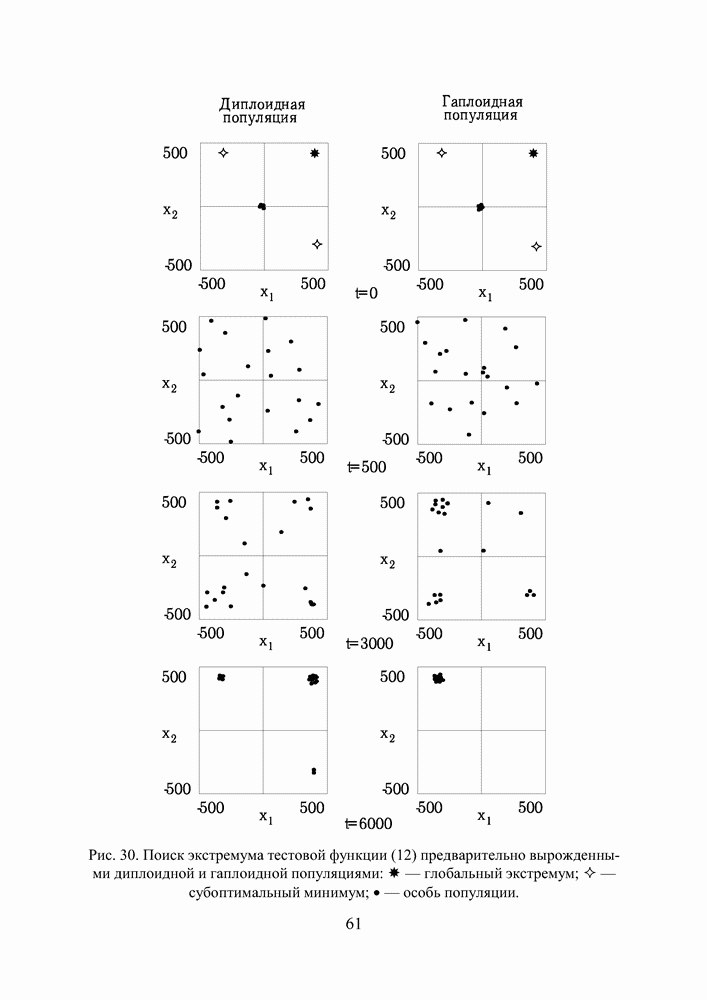
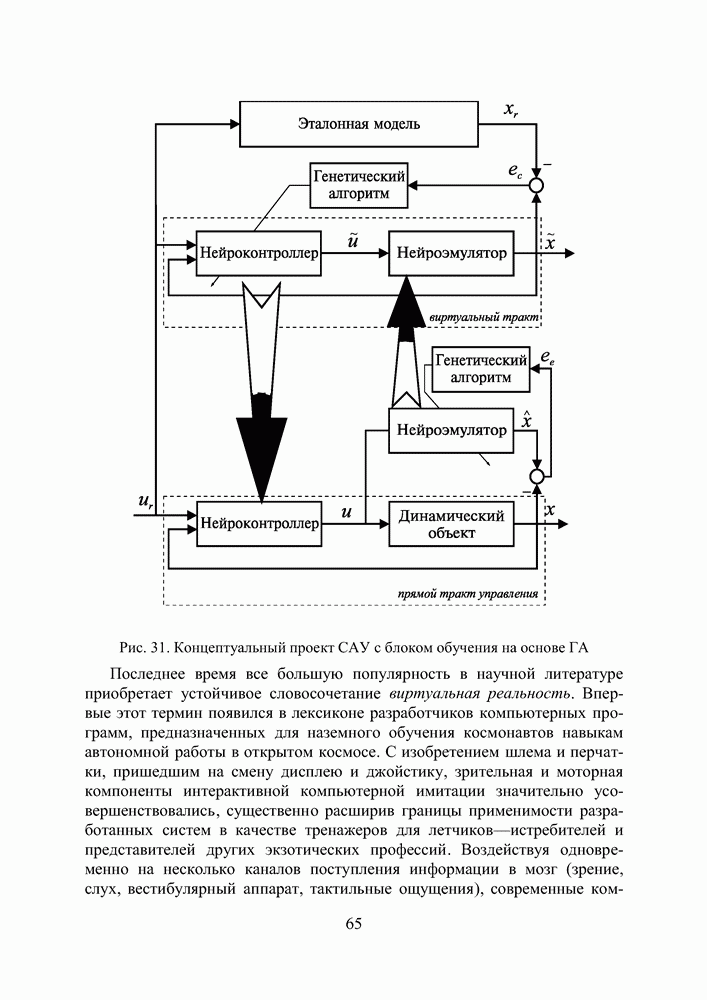
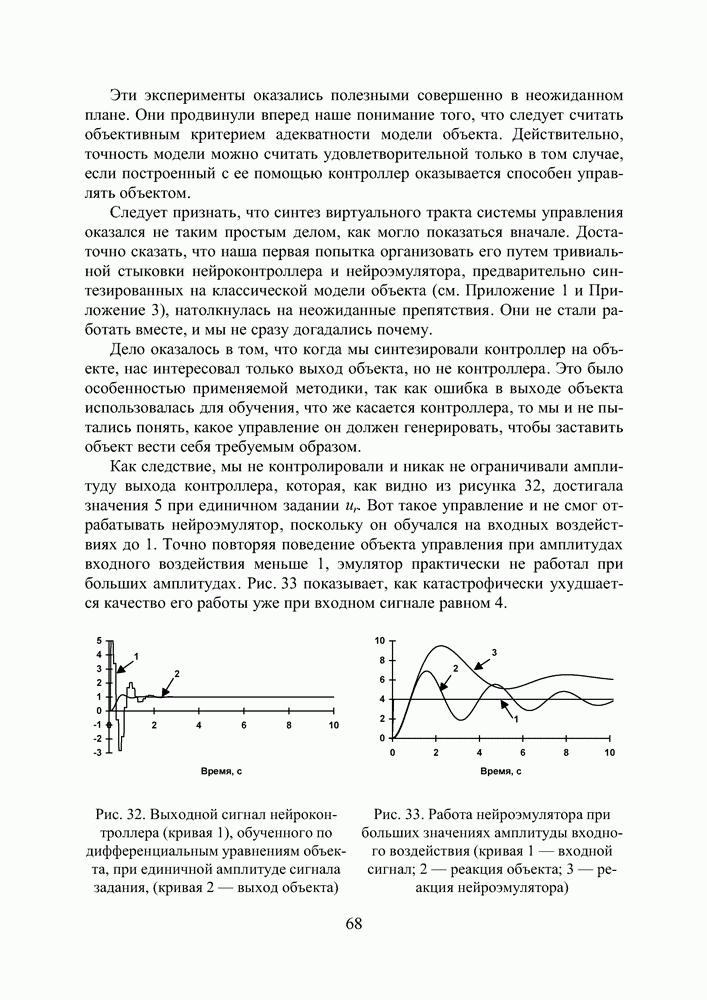
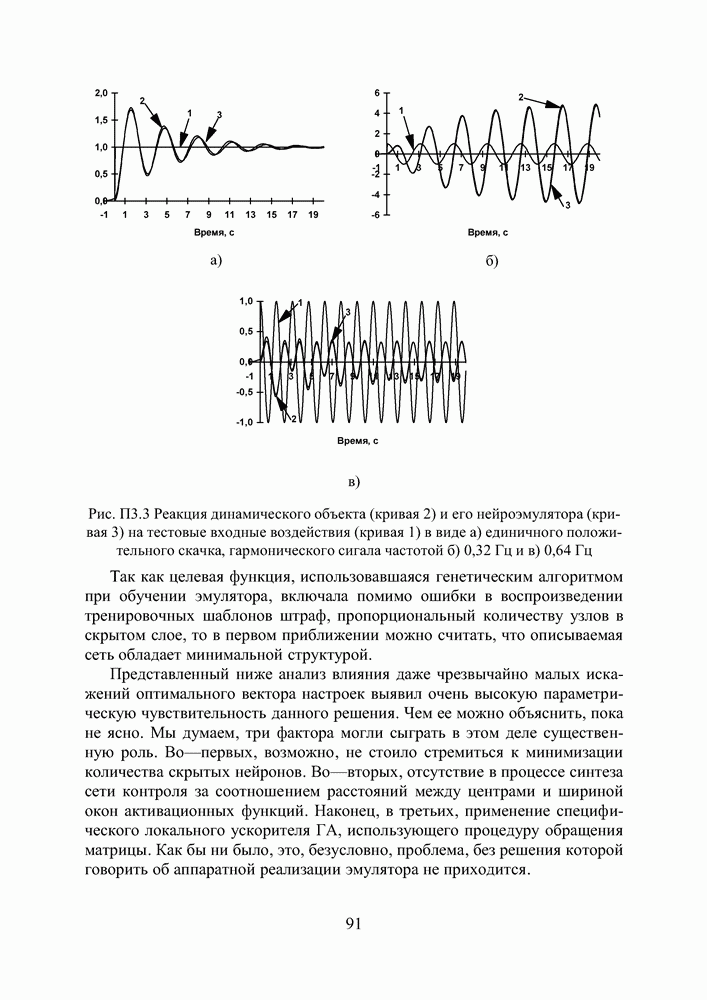
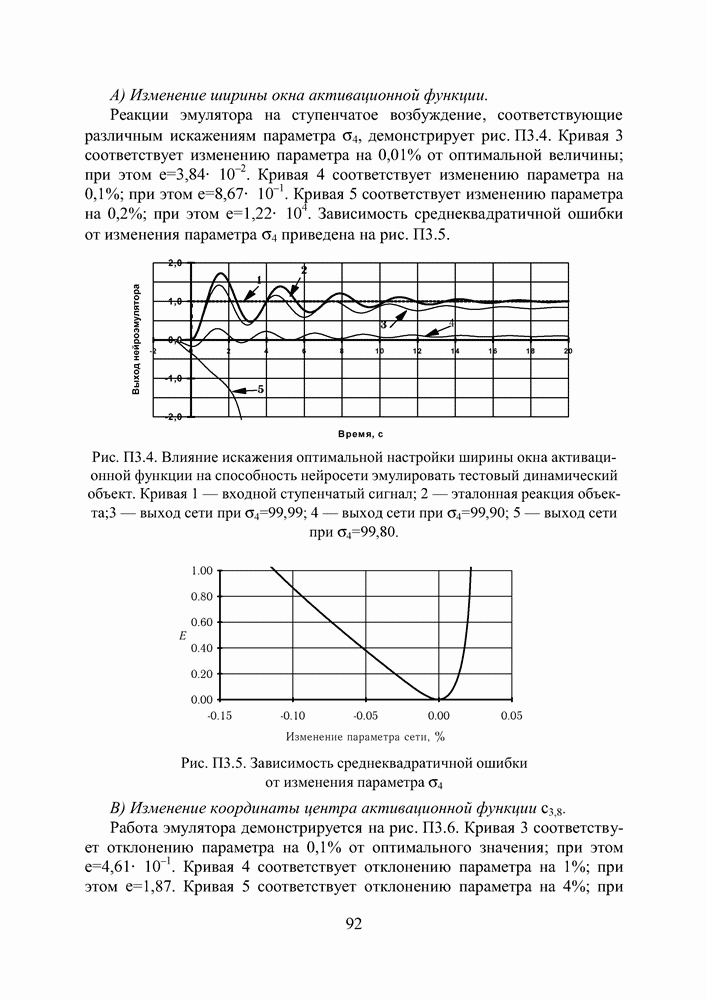
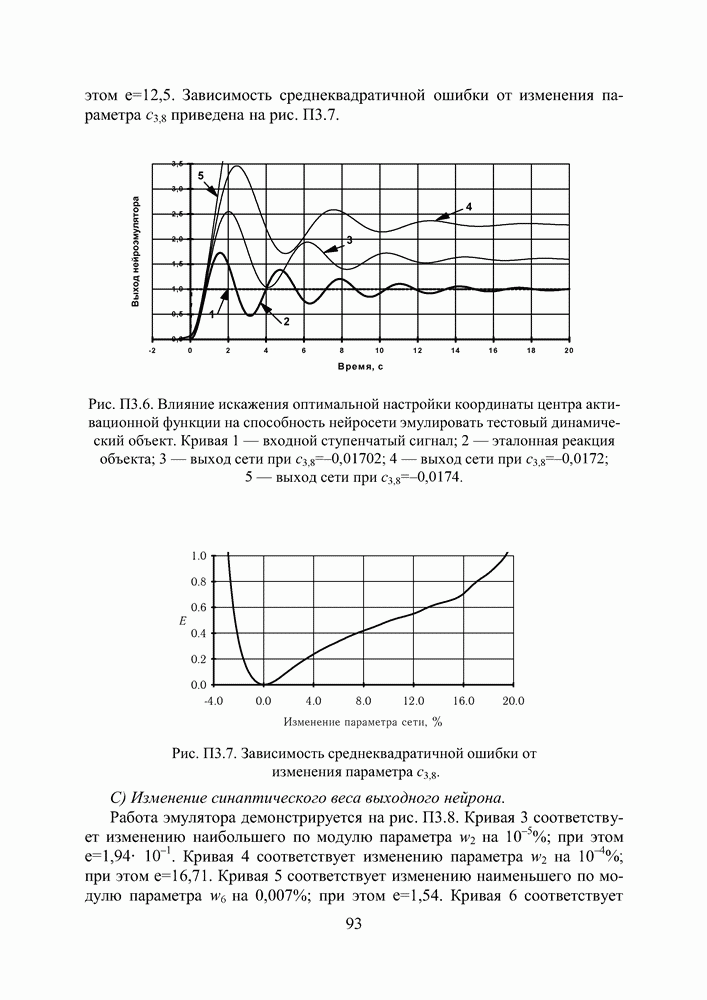
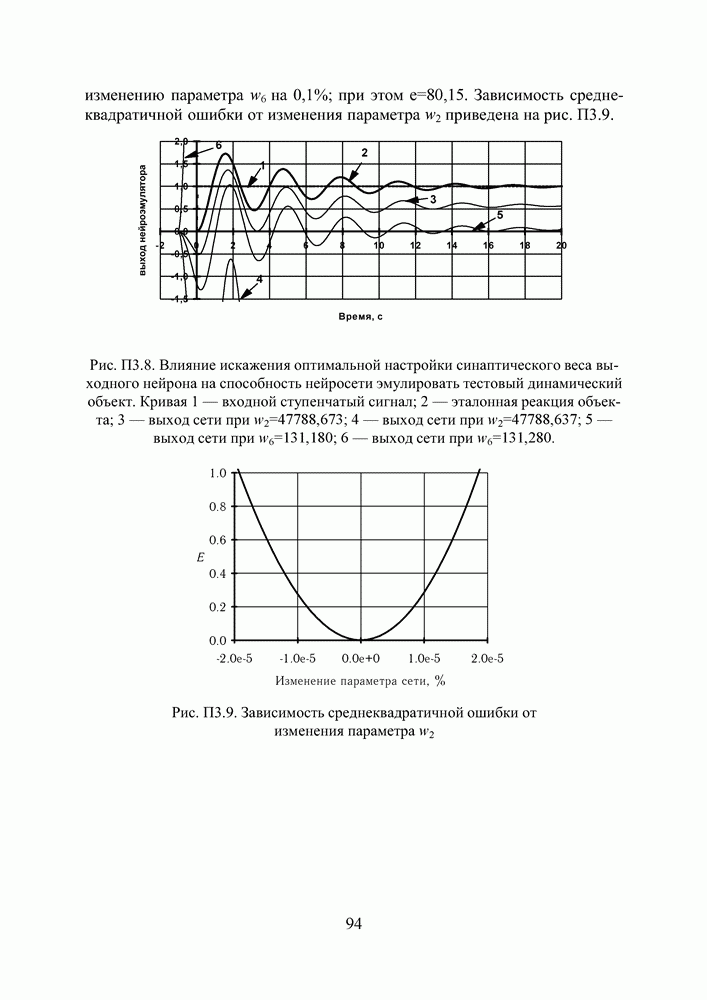
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
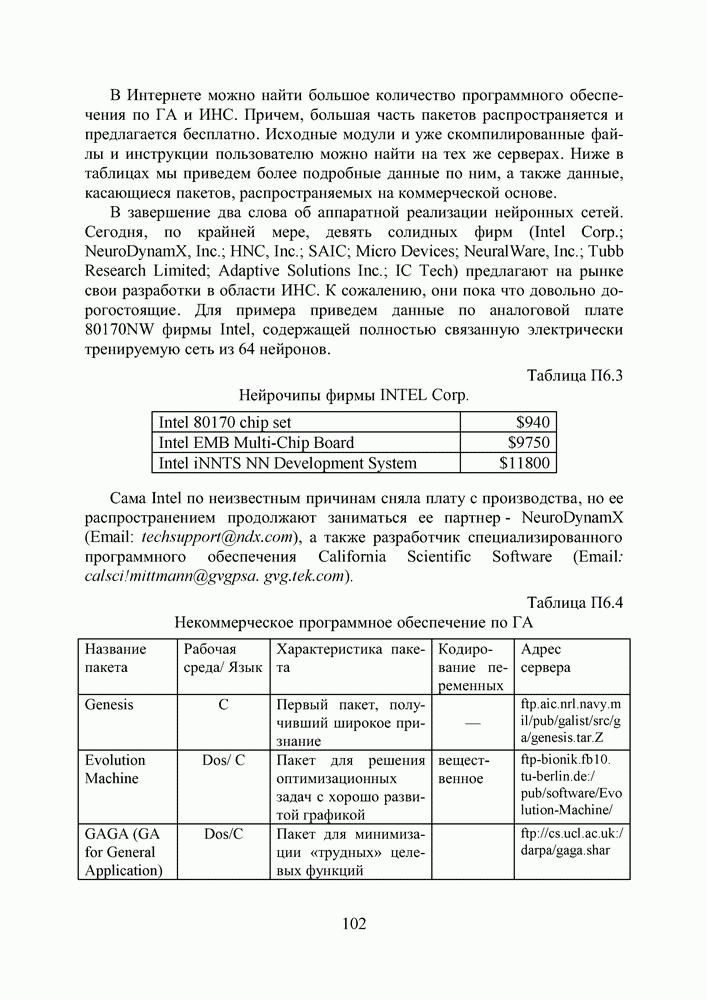
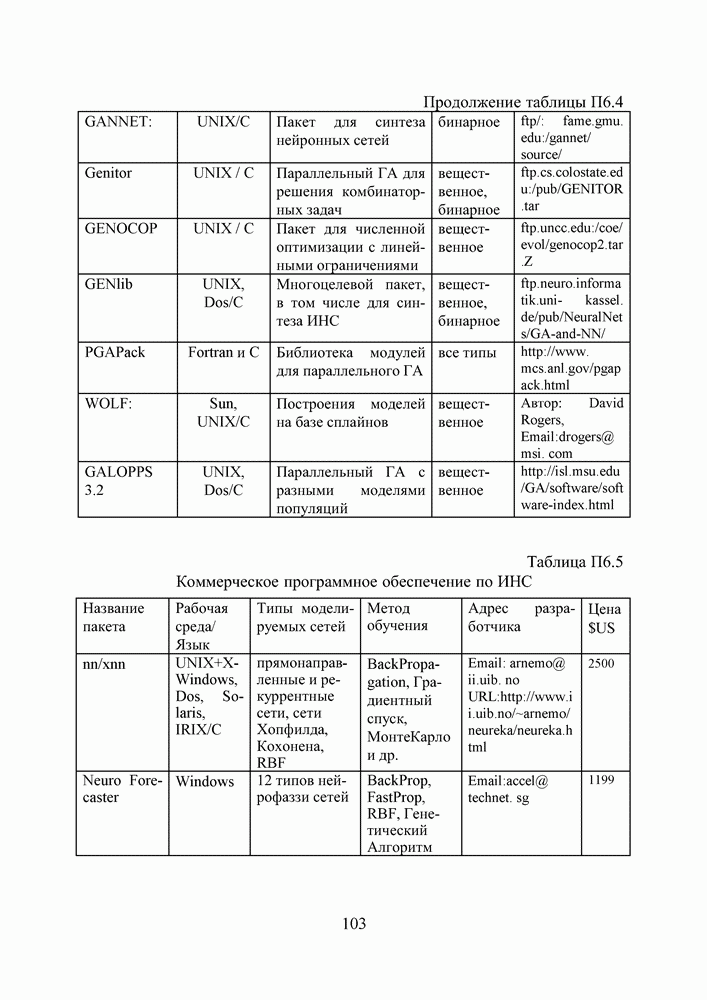
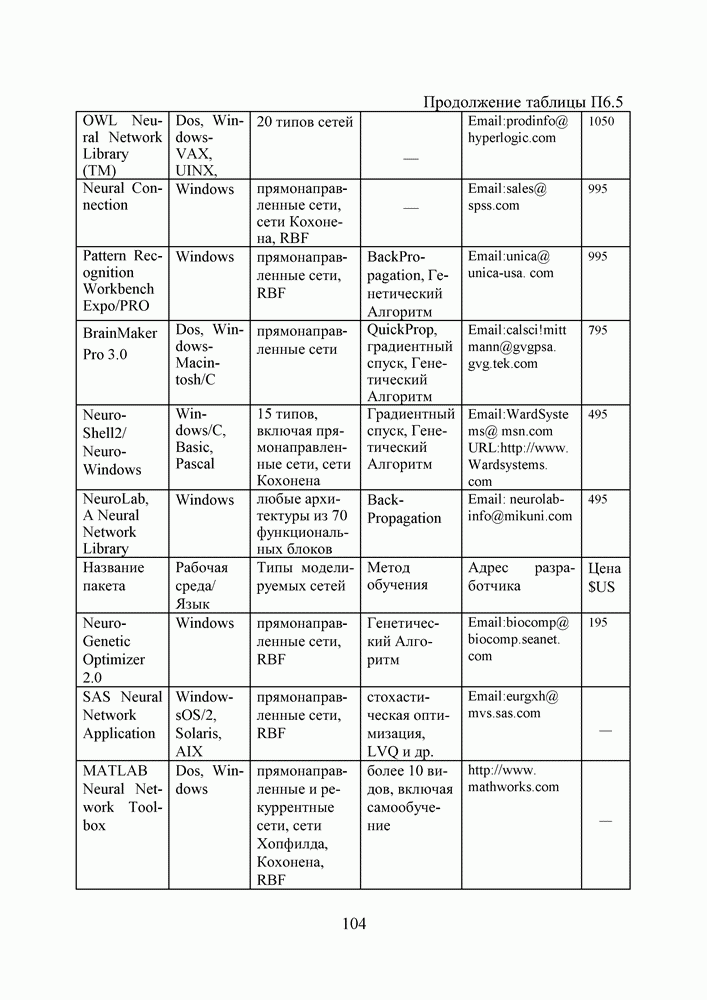
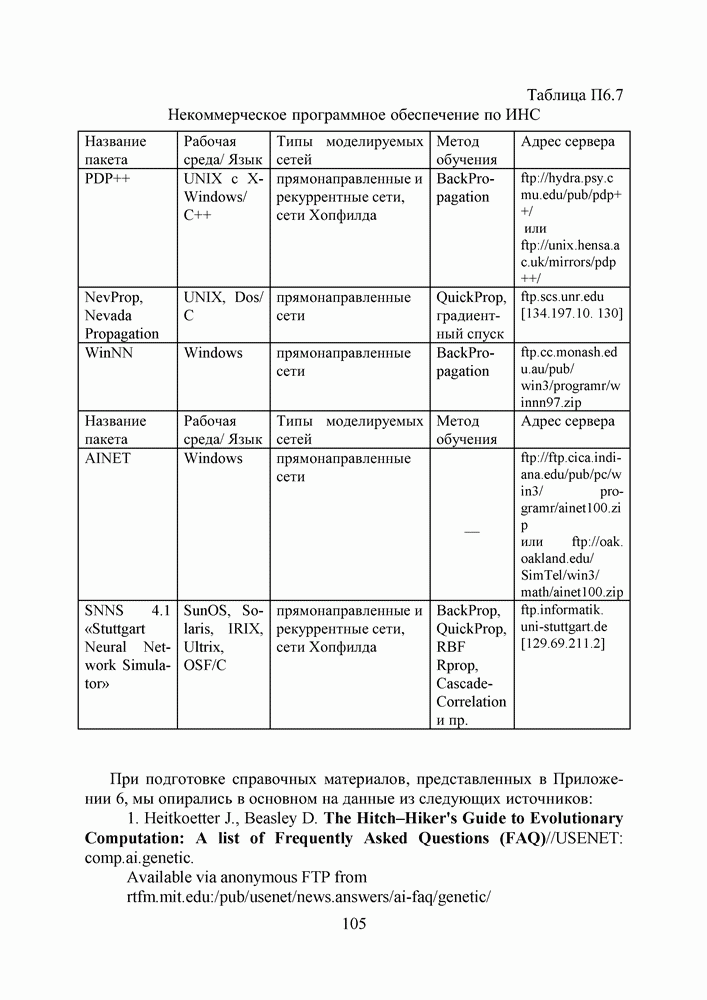
Современная библиография по генетическим алгоритмам давно перевалила за 9000 наименований и продолжает непрерывно увеличиваться. Однако, несмотря на такое обилие литературы, довольно трудно точно сформулировать, чем именно они являются — квинтэссенцией эволюционных перестроек в природных популяциях организмов, универсальным средством описания адаптаций в популяциях искусственных объектов, или мощной поисковой процедурой с претензиями на решение задач глобальной оптимизации.
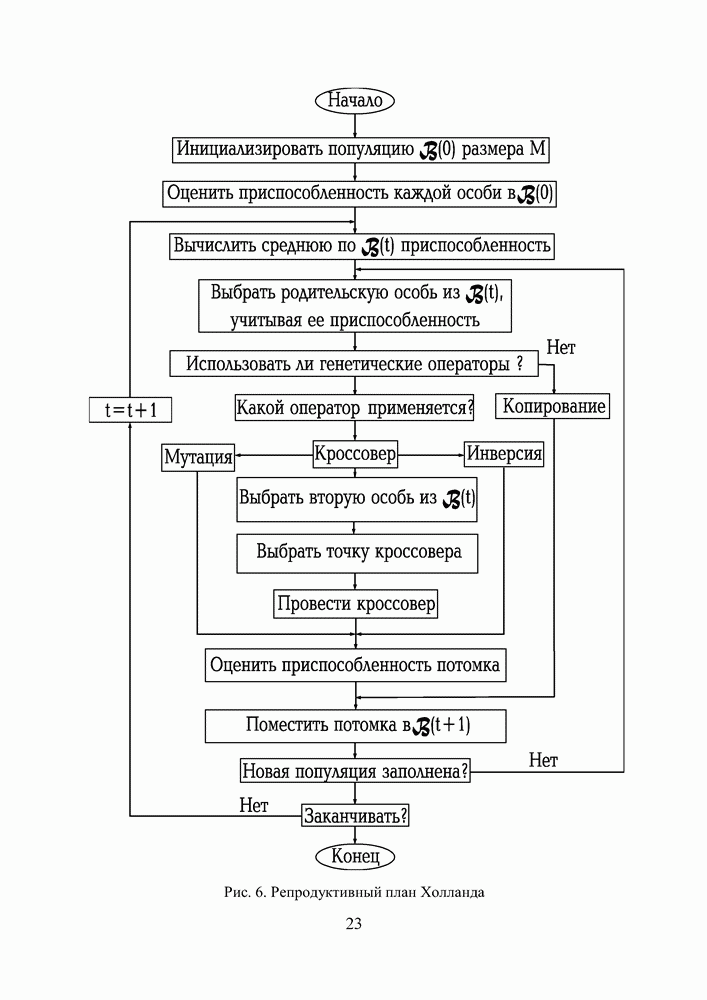
Мы намеренно начали этот раздел с сопоставления двух замечаний Дж. Холланда по поводу адаптации и оптимизации, сделанных им в предисловиях к первому и второму изданиям его знаменитой книги [1], положившей начало процессу распространения генетических алгоритмов в научных сообществах. Правда, генетическими они стали называться позднее, а в 1975 году Холланд называл их репродуктивными планами (reproductive plan) и рассматривал прежде всего как алгоритмы адаптации. Но то смещение акцентов в трактовке понятия адаптация, о котором он как бы вскользь говорит в предисловии 1992 года, очень точно, на наш взгляд, передает то состояние замешательства, которое мы ощущаем и сегодня, пытаясь, с одной стороны, дать достаточно общее и непротиворечивое определение адаптации, а с другой стороны, разграничить понятия адаптации и оптимизации, адаптации и эволюции, адаптации и обучения.
При дальнейшем изложении основных идей ГА мы не будем придерживаться стиля книги Холланда, а подойдем к ним как к процедуре глобальной оптимизации. Эта, хотя и несколько упрощенная по сравнению с холландовской, трактовка ГА вызвала сильный резонанс в литературе, и как показало время, вполне обоснованно. По большому счету, почти два десятилетия исследований ГА на тестовых многоэкстремальных функциях
ушли на доказательство именно этой грани могущества ГА, оставив в некоторой тени их выдающиеся адаптивные способности.
Итак, ГА базируются на теоретических достижениях синтетической теории эволюции, учитывающей микробиологические механизмы наследования признаков в природных и искусственных популяциях организмов, а также на накопленном человечеством опыте в селекции животных и растений.
Методологическая основа ГА зиждется на гипотезе селекции, которая в самом общем виде может быть сформулирована так: чем выше приспособленность особи, тем выше вероятность того, что в потомстве, полученном с ее участием, признаки, определяющие приспособленность, будут выражены еще сильнее. Поскольку ГА имеют дело с популяциями постоянной численности, особую актуальность здесь наравне с отбором в родители приобретает отбор на элиминирование. Стратегия элиминирования, призванная ответить на вопрос «От каких особей мы можем безболезненно отказаться?» составляет не менее важную компоненту современных ГА, чем стратегия отбора в родительскую группу. Чаще всего особи, обладающие низкой приспособленностью, не только не участвуют в генерации нового поколения, а элиминируются из популяции на текущем дискретном шаге (эпохе) эволюции.
Впрочем, сказанное справедливо не только для ГА, а для любого численного метода оптимизации. Сама идея оптимальности, как верно подмечено в [3], пришла в науку из биологии. Однако далеко не всегда мы отдаем себе отчет в том, сколь многие методические приемы оптимального проектирования имеют корни в селекционной практике и являются примером нашего не всегда осознанного подражания Природе.

Рис. 1. Двойственность задач селекции, обусловленная ограниченностью численности моделируемой популяции
Убедиться в справедливости сказанного не трудно, если попытаться взглянуть на процедуру численной оптимизации через призму гипотезы селекции (см. Рис.2).
Итак, обыкновенно проектирование начинают с формирования в поисковом пространстве области допустимых значений переменных и выбора в ней некоторых пробных точек.
Далее итеративно выполняют следующие действия. Сначала при помощи математической модели устройства производят отображение точек из поискового пространства на пространство критериев, что позволяет составить представление о рельефе поверхности критериев. Затем на основании полученной информации и в соответствии с выбранной поисковой стратегией осуществляют некоторые манипуляции с координатами точек в пространстве переменных, завершающиеся генерацией координат новых пробных точек.
Очерчивая в общих словах эту знакомую всем цепочку, отметим явно выраженный параллелизм между заложенной в ней идеологией поиска экстремума и тем, как решаются подобные по содержанию задачи в Природе, при адаптации популяций организмов к факторам окружающей среды.

Рис. 2. Циклическая структура процедуры численной оптимизации характеристик проекта
Большинство эвристических поисковых стратегий представляют собой довольно очевидные логические решающие правила, выведенные путем обобщения реального или умозрительного опыта обитания в трехмерном пространстве. Например, представим себе, что ночь застала нас врасплох и нам предстоит без фонарика двигаться по пересеченной местности, например, взобраться на вершину пологого холма. Ясно, что взяв в руки палку и ощупывая ею ближайшее окружение, мы получим требуемую информацию о локальном рельефе и будем двигаться в том направлении, в котором местность повышается, но не наоборот. Правильный выбор направления движения и величины шага гарантирует нам быстрый успех, если, конечно, поверхность холма гладкая, а не ухабистая.
Действительно, практикуемый способ описания технических объектов при помощи векторов переменных проектирования подразумевает символьное кодирование информации об объекте. Вектор переменных — даже не чертеж, то есть глядя на него и не зная правил кодирования, невозможно составить представление об объекте. В определенном смысле можно утверждать, что категория "вектор переменных проектирования" играет в технике ту же роль, что и категория "генотип" в биологии. Группируя ключевые параметры объекта в вектор переменных, мы, по существу, придаем им статус генетической информации. Именно генетической, потому что, с одной стороны, ее достаточно, для того, чтобы построить сам объект
(гипотетически — вырастить его), а во-вторых, она служит исходным материалом при генерации генотипов объектов следующего поколения.
А ведь именно такой смысл — генотипов потомков — имеют координаты упоминавшихся новых пробных точек. Подобно тому, как в Природе скрещивание организмов осуществляется на генетическом уровне, в процедуре оптимизации координаты новых пробных точек получаются как результат манипулирования координатами старых. Причем, и здесь незримо присутствует гипотеза селекции — в качестве родительских всегда выступают лучшие в фенотипическом отношении, а не произвольные точки (особи) из популяции потенциальных решений, неудачные же решения отбрасывают на текущем шаге (можно считать, что они вымирают).
Здесь мы подходим, наконец, к тому, что именно отличает ГА на фоне других численных методов оптимизации.
ГА заимствуют из биологии:
• понятийный аппарат;
• идею коллективного поиска экстремума при помощи популяции особей;
• способы представления генетической информации;
• способы передачи генетической информации в череде поколений (генетические операторы);
• идею о преимущественном размножении наиболее приспособленных особей (речь идет не о том, даст ли данная особь потомков, а о том, сколько будет у нее потомков).
1.1. Представление генетической информации
Подобно тому, как природный хромосомный материал представляет собой линейную последовательность различных комбинаций четырех нук-леотидов (А — аденин, Ц — цитозин, Т — тимин и Г — гуанин), вектора переменных в ГА также записывают в виде цепочек символов, используя двух-, трех- или четырехбуквенный алфавит. Для простоты изложения рассмотрим случай бинарного кодирования, используемый при моделировании эволюции гаплоидных популяций.
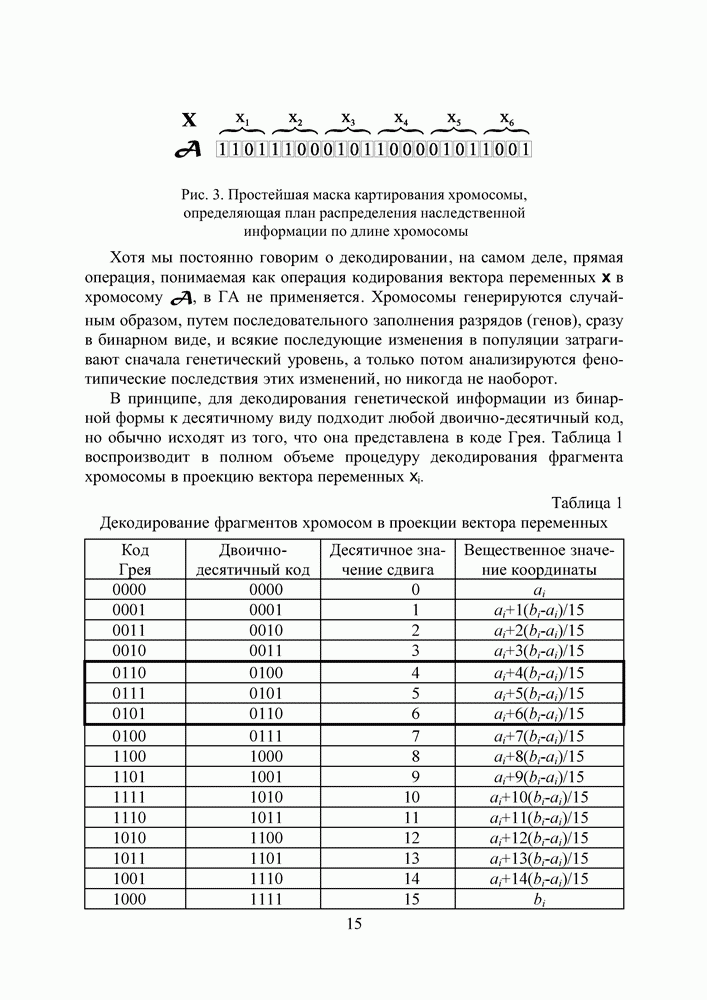
Итак, будем считать, что каждая переменная  кодируется определенным фрагментом хромосомы, состоящим из фиксированного количества генов (см. рис. 3). Все локусы хромосом диаллельны — то есть в любой позиции фрагмента может стоять как ноль, так и единица. Рядом стоящие фрагменты не отделяют друг от друга какими-либо маркерами, тем не менее, при декодировании хромосомы в вектор переменных на протяжении всего моделируемого периода эволюции используется одна и та же маска картирования.
кодируется определенным фрагментом хромосомы, состоящим из фиксированного количества генов (см. рис. 3). Все локусы хромосом диаллельны — то есть в любой позиции фрагмента может стоять как ноль, так и единица. Рядом стоящие фрагменты не отделяют друг от друга какими-либо маркерами, тем не менее, при декодировании хромосомы в вектор переменных на протяжении всего моделируемого периода эволюции используется одна и та же маска картирования.

Рис. 3. Простейшая маска картирования хромосомы, определяющая план распределения наследственной информации по длине хромосомы
Хотя мы постоянно говорим о декодировании, на самом деле, прямая операция, понимаемая как операция кодирования вектора переменных x в хромосому  в ГА не применяется. Хромосомы генерируются случайным образом, путем последовательного заполнения разрядов (генов), сразу в бинарном виде, и всякие последующие изменения в популяции затрагивают сначала генетический уровень, а только потом анализируются фено-типические последствия этих изменений, но никогда не наоборот.
в ГА не применяется. Хромосомы генерируются случайным образом, путем последовательного заполнения разрядов (генов), сразу в бинарном виде, и всякие последующие изменения в популяции затрагивают сначала генетический уровень, а только потом анализируются фено-типические последствия этих изменений, но никогда не наоборот.
В принципе, для декодирования генетической информации из бинарной формы к десятичному виду подходит любой двоично-десятичный код, но обычно исходят из того, что она представлена в коде Грея. Таблица 1 воспроизводит в полном объеме процедуру декодирования фрагмента хромосомы в проекцию вектора переменных  .
.
Таблица 1. (см. скан) Декодирование фрагментов хромосом в проекции вектора переменных
От кода Грея переходим к двоично-десятичному коду, а от него — к натуральным целым числам. Отношение полученного числа к максимальному числу, доступному для кодирования данным количеством разрядов фрагмента (по таблице 1 — число 15) и дает искомое значение сдвига переменной относительно левой границы  допустимого диапазона ее изменения, нормированного на ширину
допустимого диапазона ее изменения, нормированного на ширину  диапазона.
диапазона.
Из таблицы хорошо видно, почему код Грея имеет явные преимущества по сравнению с двоично-десятичным кодом, который при некотором стечении обстоятельств порождает своеобразные тупики для поискового процесса. В качестве примера рассмотрим любые три рядом стоящие строки из таблицы 1, например, кодирующие сдвиг в 4, 5 и 6 единиц.
Предположим, фрагменты хромосом, стоящие в пятой строке и кодирующие число 5, принадлежат оптимальному вектору, являющемуся решением некоторой задачи, а лучшая особь из текущей популяции содержит фрагмент хромосомы из строки 4. Такая ситуация благоприятна для обоих кодов. Достаточно выполнить всего одну операцию — заменить в четвертом разряде фрагмента 0 на 1 — и решение будет найдено. Более интересный случай получается, если лучшая особь содержит фрагмент из строки 6. Для кода Грея эта ситуация ничуть не сложнее предыдущей — замена 0 на 1 в третьем разряде опять приведет к успеху. В то же время двоично-десятичный код ставит нас в необходимость выполнить последовательно две операции — заменить 1 на 0 в третьем разряде и 0 на 1 в четвертом. С какой бы из них мы ни начали, результат не приблизит нас к решению (первый вариант замены переместит нас в четвертую строку, а второй — вообще в седьмую). А ведь это не самый худший пример — работать с сочетаниями 3-4, 7-8, 11-12 и т. д. строк в двоично-десятичном коде еще сложнее. Иначе говоря, если привлечь геометрические интерпретации, код Грея гарантирует, что две соседние, принадлежащие одному ребру, вершины гиперкуба  на котором осуществляется поиск, всегда декодируются в две ближайшие точки пространства вещественных чисел
на котором осуществляется поиск, всегда декодируются в две ближайшие точки пространства вещественных чисел  отстоящие друг от друга на одну дискрету точности. Двоично-десятичный код подобным свойством не обладает.
отстоящие друг от друга на одну дискрету точности. Двоично-десятичный код подобным свойством не обладает.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ. О РАЗЛИЧНЫХ ТОЛКОВАНИЯХ ТЕРМИНА «ИНТЕЛЛЕКТУАЛЬНОСТЬ» В УПРАВЛЕНИИ
- 1. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 1.2. Генетические операторы
- 1.3. Преимущественное право размножения сильнейших
- 2. ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ
- 2.2. Становление и развитие ИНС
- 3. ГА+ИНС = НОВАЯ ПАРАДИГМА В УПРАВЛЕНИИ
- 4. ГА+ИНС = НОВАЯ ПАРАДИГМА В МОДЕЛИРОВАНИИ
- 5. СНОВА О ГЕНЕТИЧЕСКИХ АЛГОРИТМАХ
- 6. ВИРТУАЛЬНАЯ РЕАЛЬНОСТЬ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- ЗАКЛЮЧЕНИЕ
- ТЕРМИНОЛОГИЧЕСКИЙ СЛОВАРЬ
- ИМЕННОЙ СПИСОК
- СПИСОК ЛИТЕРАТУРЫ
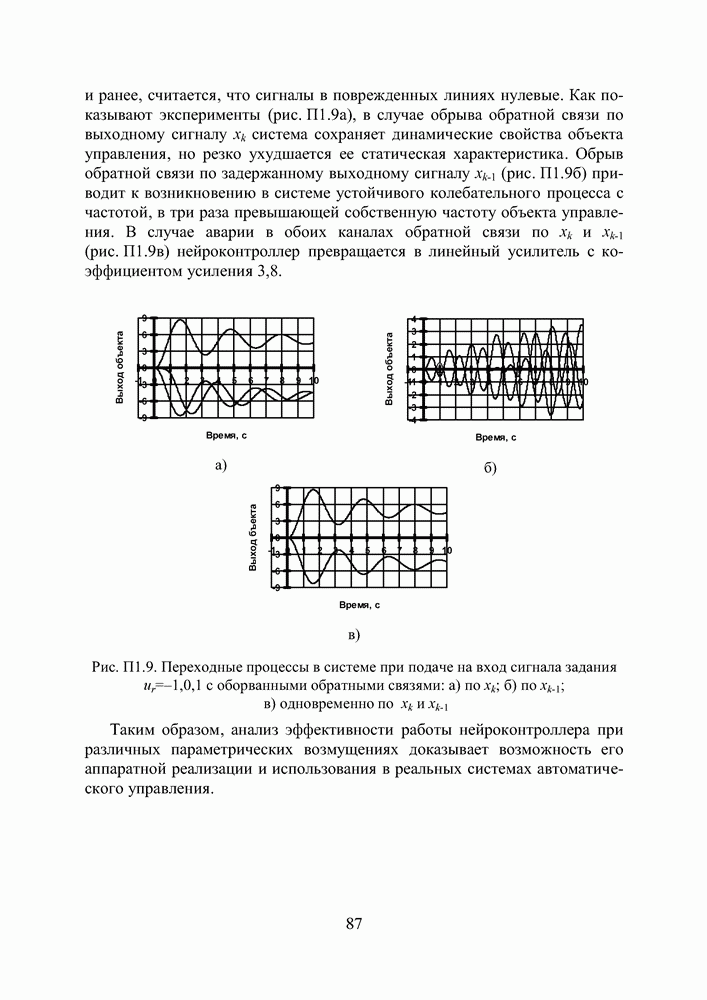
- ПРИЛОЖЕНИЕ 1. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ НЕЙРОКОНТРОЛЛЕРА
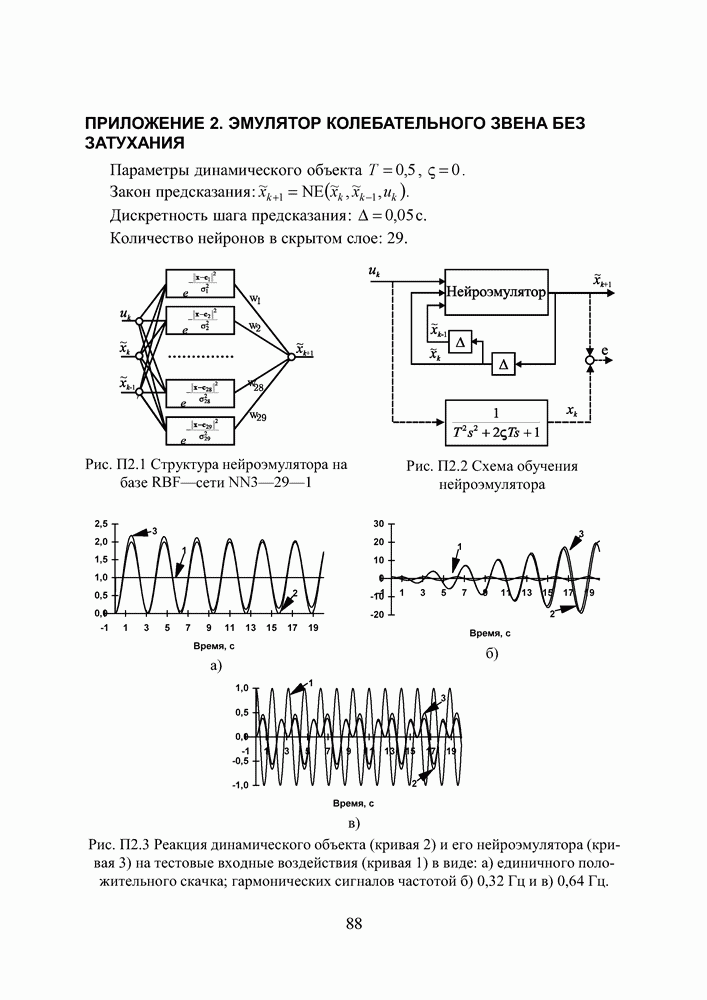
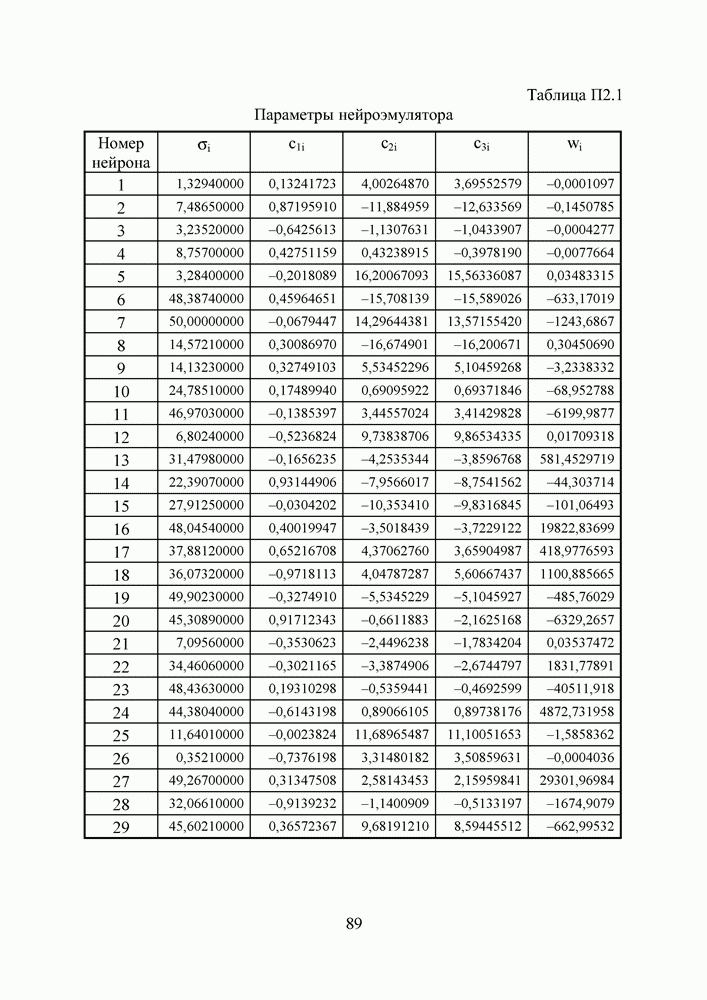
- ПРИЛОЖЕНИЕ 2. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА БЕЗ ЗАТУХАНИЯ
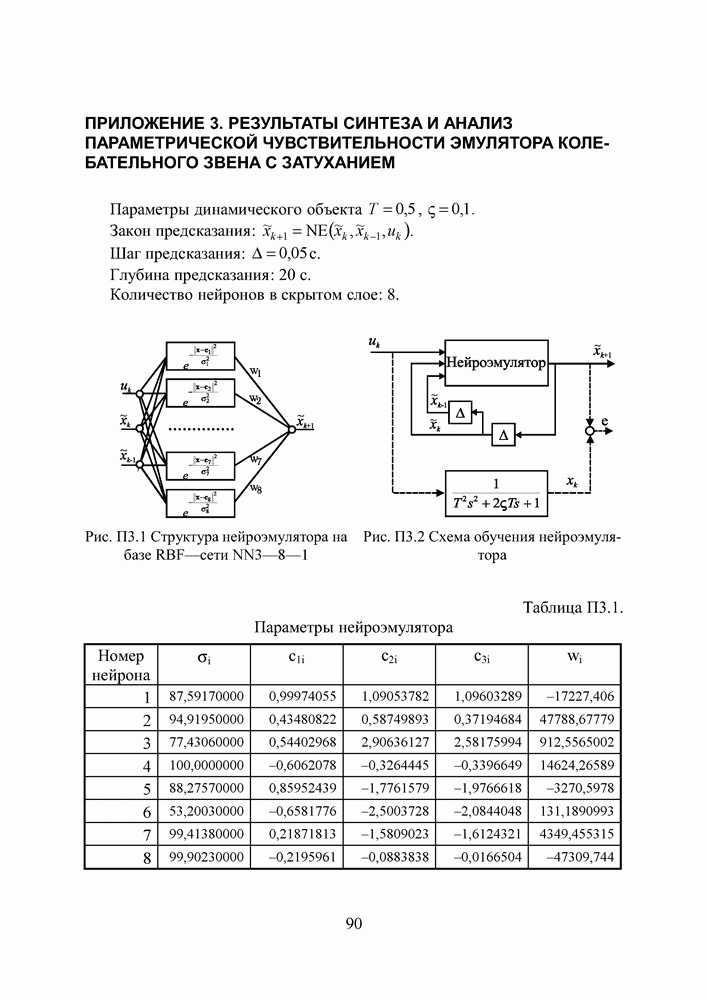
- ПРИЛОЖЕНИЕ 3. РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ ЭМУЛЯТОРА КОЛЕБАТЕЛЬНОГО ЗВЕНА С ЗАТУХАНИЕМ
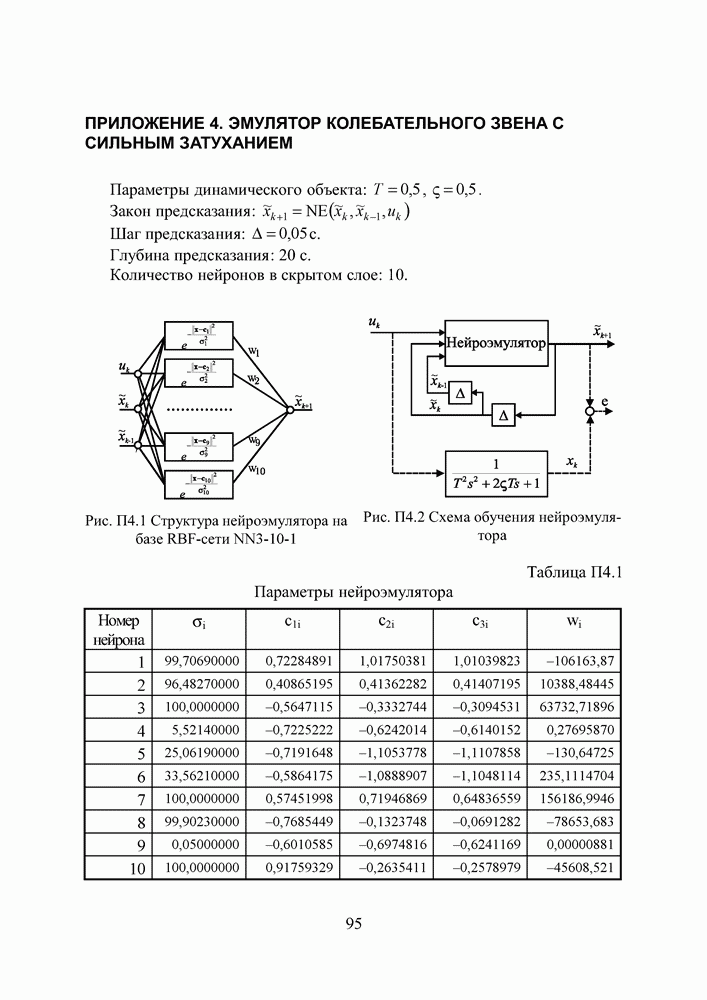
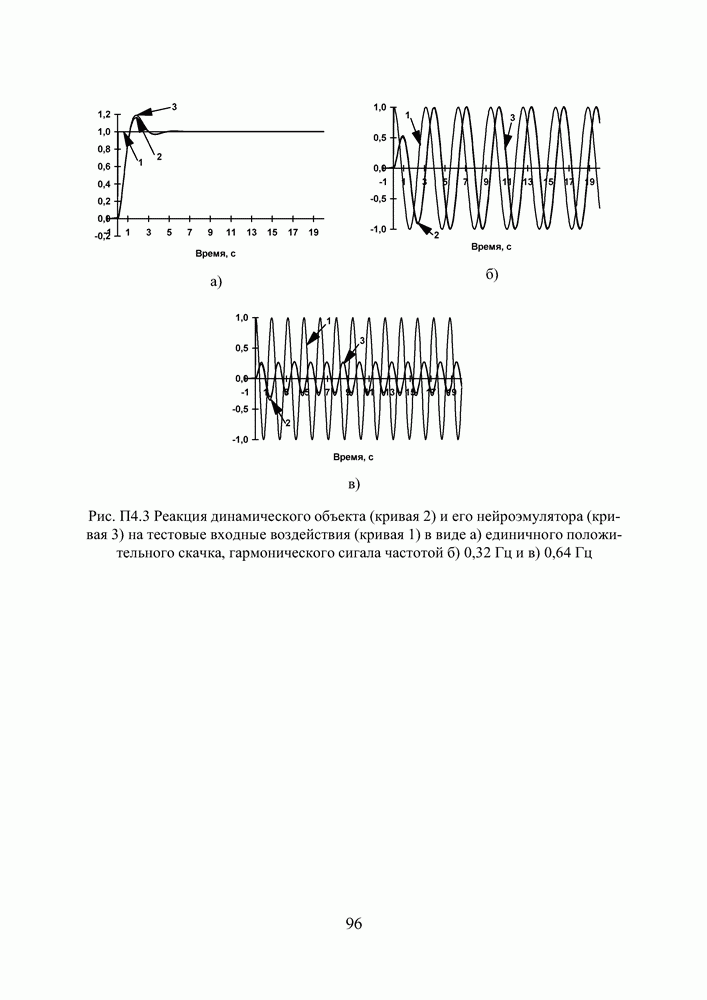
- ПРИЛОЖЕНИЕ 4. ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА С СИЛЬНЫМ ЗАТУХАНИЕМ
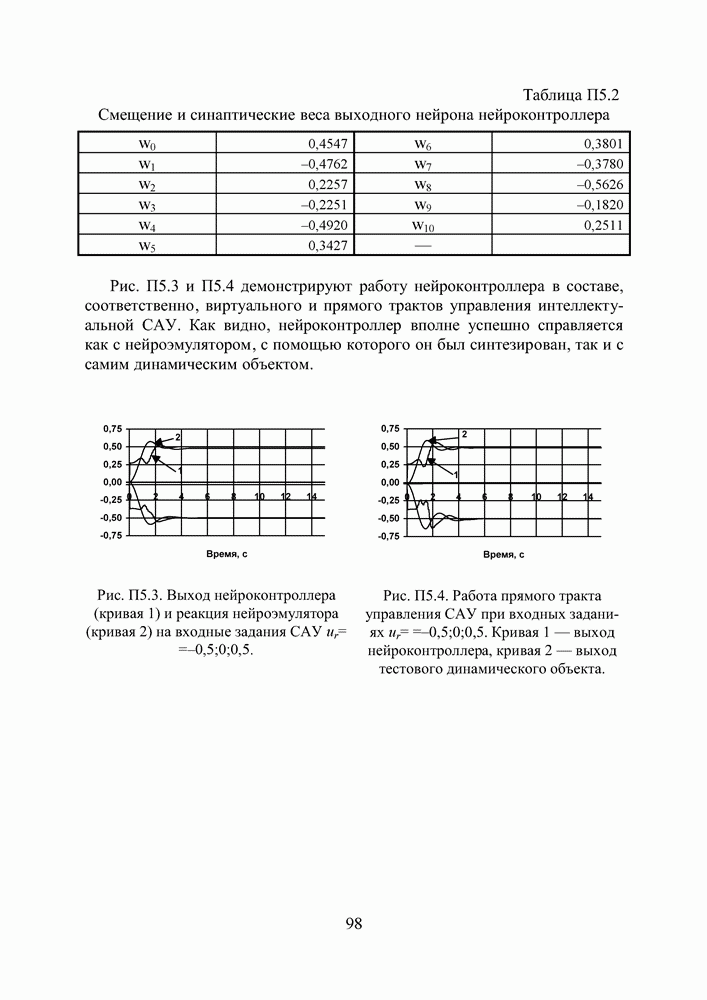
- ПРИЛОЖЕНИЕ 5. ВИРТУАЛЬНЫЙ ТРАКТ УПРАВЛЕНИЯ НА БАЗЕ НЕЙРОЭМУЛЯТОРА
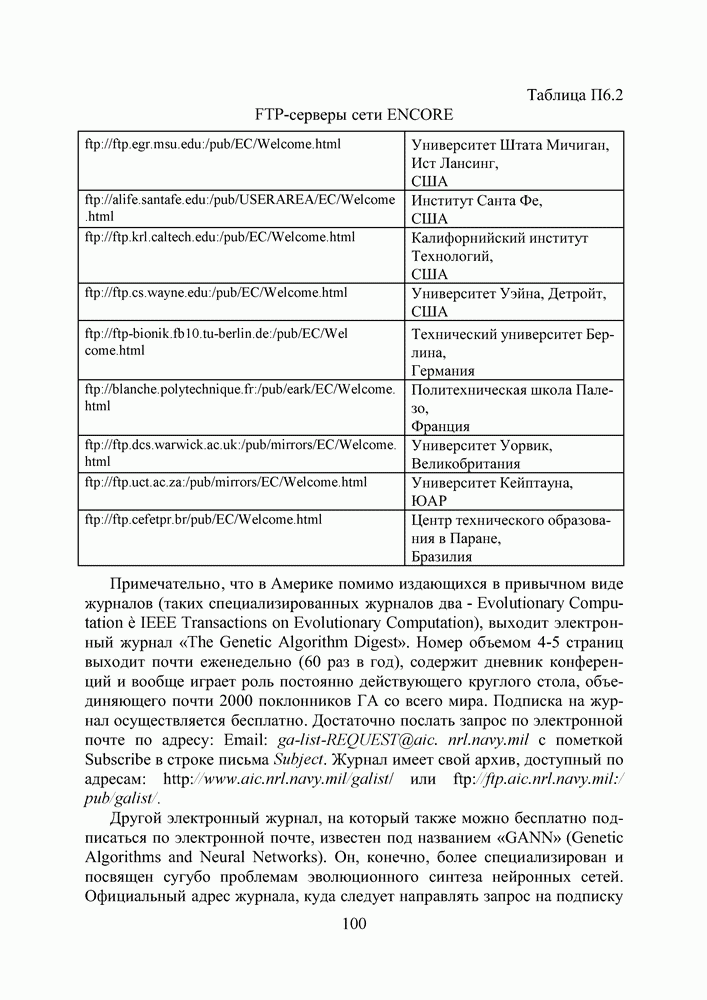
- ПРИЛОЖЕНИЕ 6. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ И ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ В ИНТЕРНЕТЕ