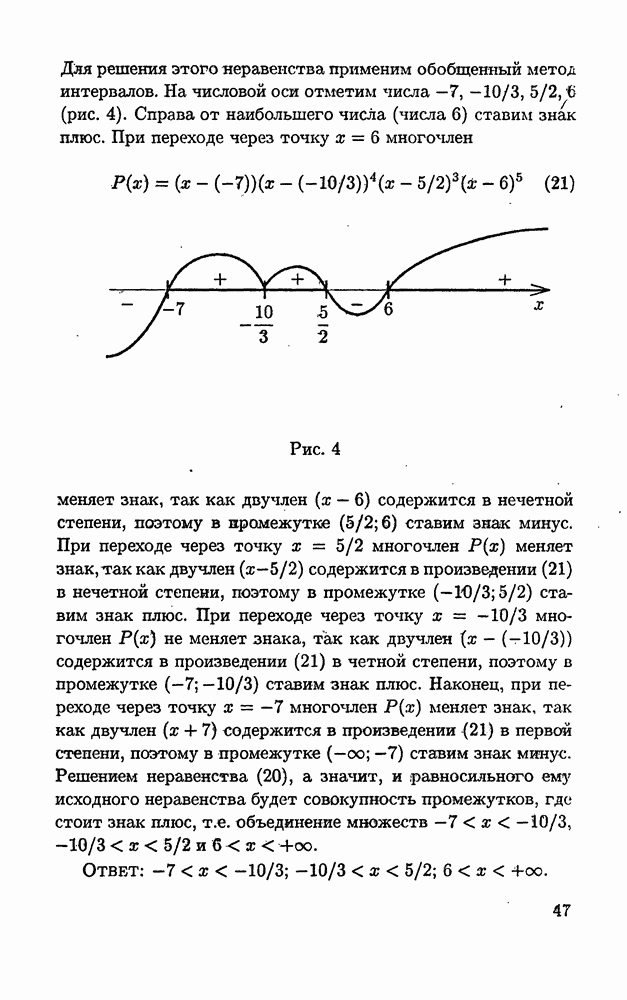
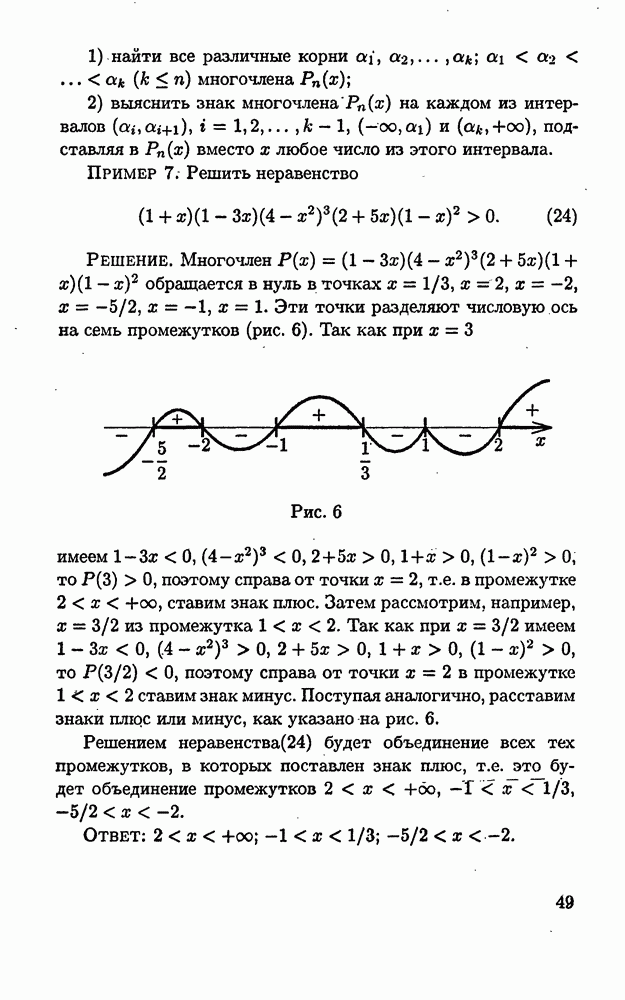
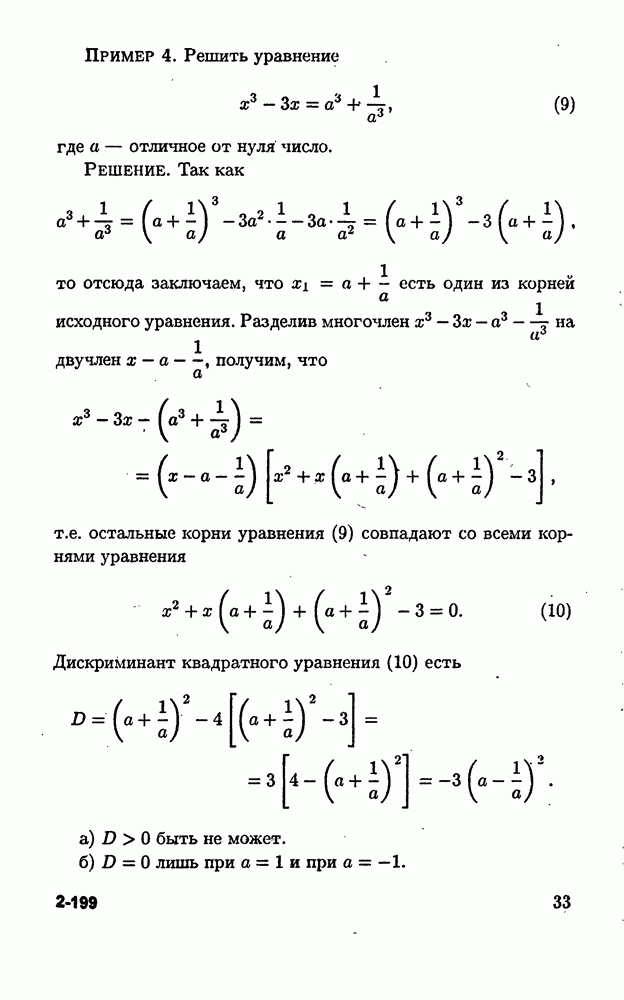| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
В этом параграфе рассматриваются уравнения и неравенства вида

При решении таких уравнений и неравенств надо учитывать, что их ОДЗ определяется из условий:
1) на ОДЗ все функции  имеют смысл;
имеют смысл;
2) на ОДЗ основания логарифмов, т.е. функции  должны удовлетворять условиям
должны удовлетворять условиям 
3) на ОДЗ функции, находящиеся под знаком логарифма, должны быть положительны, т.е. на ОДЗ должны выполняться неравенства 
2.2.1. Переход к числовому основанию.
Одним из основных способов решения уравнений и неравенств вида (1) и (2) является следующий.
1. Найти ОДЗ уравнения или неравенства.
2. Перейти в логарифмах к некоторому основанию а, где а — фиксированное число,  т.е. заменить уравнение (1) равносильным ему на ОДЗ уравнением
т.е. заменить уравнение (1) равносильным ему на ОДЗ уравнением

а неравенство  — равносильным ему на ОДЗ неравенством
— равносильным ему на ОДЗ неравенством

3. Решить полученное стандартное по внешнему виду уравнение (3) (или неравенство  на ОДЗ исходного уравнения
на ОДЗ исходного уравнения
(или неравенства) Его решения и будут решения исходного уравнения (или неравенства).
Заметим, что ОДЗ уравнений (1) и (3) и неравенств (2) и (4) совпадают, поэтому можно сразу переходить от уравнения (1) к уравнению (3) и неравенства (2) к неравенству (4) и решать их на своей ОДЗ.
Пример 1. Решить уравнение

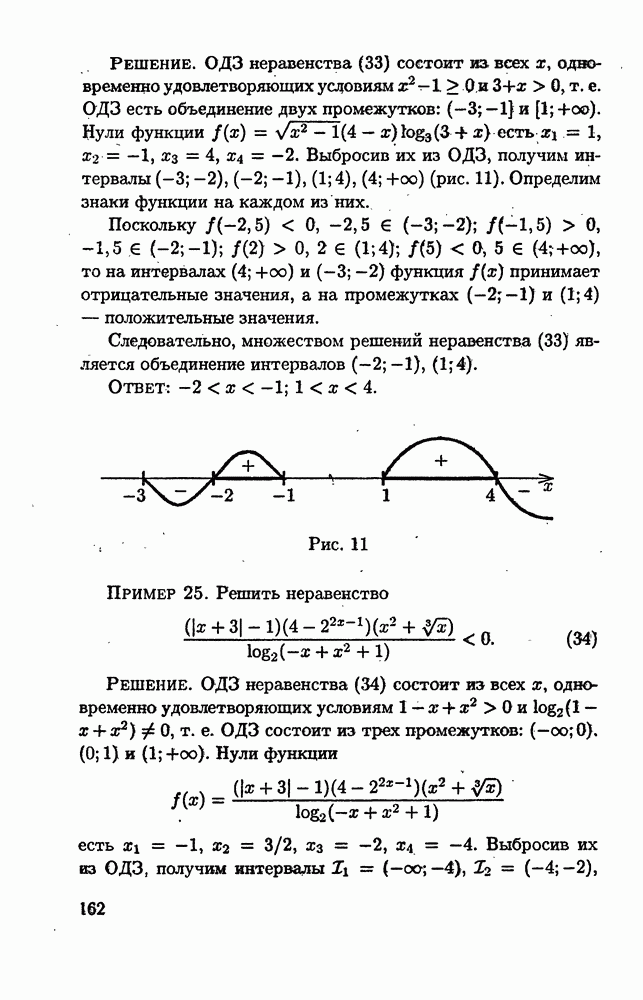
Решение. ОДЗ уравнения (5) состоит из всех х, одновременно удовлетворяющих условиям  т.е. ОДЗ состоит из двух промежутков
т.е. ОДЗ состоит из двух промежутков  Переходя в (5) к логарифмам по основанию, например, 2, получим уравнение
Переходя в (5) к логарифмам по основанию, например, 2, получим уравнение

равносильное уравнению (5) на ОДЗ. Поскольку для этих х имеем  то уравнение (6) можно записать в виде
то уравнение (6) можно записать в виде

или, так как на ОДЗ  , в виде
, в виде

Обозначим  через
через  тогда уравнение (7) можно переписать в виде
тогда уравнение (7) можно переписать в виде  Решения последнего уравнения есть
Решения последнего уравнения есть  Следовательно, уравнение (7) равносильно на ОДЗ исходного уравнения совокупности уравнений
Следовательно, уравнение (7) равносильно на ОДЗ исходного уравнения совокупности уравнений

Первое из уравнений этой совокупности не имеет решений, а решение второго уравнения есть  Это число принадлежит ОДЗ исходного уравнения и, следовательно, является единственным его решением.
Это число принадлежит ОДЗ исходного уравнения и, следовательно, является единственным его решением.
Ответ: 
Пример 2. Решить неравенство

Решение. ОДЗ неравенства (8) состоит из всех х, одновременно удовлетворяющих условиям  т.е. ОДЗ состоит из двух промежутков:
т.е. ОДЗ состоит из двух промежутков: 
Перейдем в логарифмах неравенства (8) к логарифмам по основанию, например, 2. В результате получим неравенство

равносильное исходному на его ОДЗ. Поскольку на ОДЗ исходного неравенства имеем  то неравенство (9) для этих х можно переписать в виде,
то неравенство (9) для этих х можно переписать в виде,

или в виде

или, наконец, в виде

Так как  , то на ОДЗ исходного неравенства
, то на ОДЗ исходного неравенства  следовательно,
следовательно,  Поэтому неравенство
Поэтому неравенство
(10) равносильно неравенству  Решения последнего неравенства есть все
Решения последнего неравенства есть все  Поскольку все
Поскольку все  входят в ОДЗ исходного неравенства, то все они являются его решениями. Ответ:
входят в ОДЗ исходного неравенства, то все они являются его решениями. Ответ: 
Отметим, что иногда при решении уравнений и неравенств вида (1) и (2) нецелесообразно переходить к некоторому постоянному основанию, так как это может сделать более громоздкой запись уравнения (или неравенства) и не облегчит процесс его решения.
Пример 3. Решить уравнение

Решение. Поскольку  то ОДЗ исходного уравнения состоит из всех
то ОДЗ исходного уравнения состоит из всех  одновременно удовлетворяющих условию
одновременно удовлетворяющих условию

т.е. ОДЗ состоит из двух промежутков:  . Легко видеть, что переход в логарифмах к некоторому основанию а приведет к громоздким выражениям. Поэтому поступим иначе: преобразуем уравнение на его ОДЗ. Исходное уравнение на своей ОДЗ равносильно уравнению
. Легко видеть, что переход в логарифмах к некоторому основанию а приведет к громоздким выражениям. Поэтому поступим иначе: преобразуем уравнение на его ОДЗ. Исходное уравнение на своей ОДЗ равносильно уравнению

т.е. уравнению

Обозначим  через
через  Тогда поскольку на ОДЗ
Тогда поскольку на ОДЗ

то уравнение (12) можно записать в виде  . Это уравнение имеет корни
. Это уравнение имеет корни  Следовательно, исходное
Следовательно, исходное
уравнение на своей ОДЗ равносильно совокупности двух уравнений:

Первое из этих уравнений равносильно на расматриваемой области  уравнению
уравнению

т.е. уравнению

Это уравнение имеет два корня:  из которых ни один не входит в рассматриваемую область, и поэтому не является решением исходного уравнения. Второе уравнение совокупности (13) равносильно на области
из которых ни один не входит в рассматриваемую область, и поэтому не является решением исходного уравнения. Второе уравнение совокупности (13) равносильно на области  , уравнению
, уравнению  решения которого есть
решения которого есть  Из этих значений только
Из этих значений только  входит в рассматриваемую область, и поэтому является единственным корнем исходного уравнения.
входит в рассматриваемую область, и поэтому является единственным корнем исходного уравнения.
Ответ:  .
.
2.2.2. Переход к основанию, содержащему неизвестную.
Иногда при решении уравнений и неравенств вида (1) и (2) переходят к логарифмам по другому основанию, содержащему х. При этом надо помнить, что может произойти сужение ОДЗ, а следовательно, и потеря корня. Поэтому при переходе в уравнении (или неравенстве) к логарифмам по некоторому основанию  содержащему
содержащему  вначале надо проверить, что
вначале надо проверить, что  для рассматриваемых х, а также проверить, не являются ли значения
для рассматриваемых х, а также проверить, не являются ли значения  при которых
при которых  решениями исходного уравнения, после чего уже переходить к основанию
решениями исходного уравнения, после чего уже переходить к основанию  но уже для тех
но уже для тех  для которых
для которых 
Пример 4. Решить уравнение

Решение. ОДЗ этого уравнения состоит из всех х, удовлетворяющих условиям 
Будем решать это уравнение, переходя к логарифмам по основанию х. Прежде чем сделать этот переход, проверим, является ли  корнем исходного уравнения. Подставляя 1 вместо х в уравнение (14), получаем, что
корнем исходного уравнения. Подставляя 1 вместо х в уравнение (14), получаем, что  есть его корень. Перейдя теперь в уравнении (14) к логарифмам по основанию х (учитывая, что
есть его корень. Перейдя теперь в уравнении (14) к логарифмам по основанию х (учитывая, что  получим уравнение
получим уравнение

равносильное исходному уравнению на множестве  Уравнение (15) для этих х можно переписать так:
Уравнение (15) для этих х можно переписать так:

Поскольку  для рассматриваемых
для рассматриваемых  то уравнение равносильно уравнению
то уравнение равносильно уравнению

или уравнению

имеющему единственный корень  Так как этот корень входит в рассматриваемое множество
Так как этот корень входит в рассматриваемое множество  то он и является решением исходного уравнения на этом множестве.
то он и является решением исходного уравнения на этом множестве.
Ответ: 
2.2.3. Уравнения вида
Уравнения

можно решать и таким способом:
1. Перейти от этих уравнений к их следствиям, т.е. от уравнения (17) к уравнению

а от уравнения (18) к совокупности уравнений

2. Решить уравнение (19) или совокупность уравнений (20).
3. Проверить, какие из найденных корней будут корнями исходного уравнения.
Пример 5. Решить уравнение

Решение. Уравнение

является следствием уравнения (21). Переписав уравнение (22) в виде  находим его корни
находим его корни  При
При  функция, находящаяся в основании логарифмов, принимает отрицательное значение
функция, находящаяся в основании логарифмов, принимает отрицательное значение  т.е.
т.е.  не удовлетворяет уравнению (21). При
не удовлетворяет уравнению (21). При  функция, находящаяся в основании логарифмов, принимает значение, большее нуля и не равное 1, так как
функция, находящаяся в основании логарифмов, принимает значение, большее нуля и не равное 1, так как  т.е.
т.е.  удовлетворяет уравнению (21).
удовлетворяет уравнению (21).
Ответ: 
Пример 6. Решить уравнение

Решение. Совокупность уравнений

является следствием уравнения (23). Ясно, что все решения первого уравнения совокупности (24) есть решения уравнения  т. е.
т. е.  При любом
При любом  функция
функция  равна 2, т.е. при этих
равна 2, т.е. при этих  основания логарифмов в уравнении (23) равны 2. Поэтому решениями уравнения (23) будут те
основания логарифмов в уравнении (23) равны 2. Поэтому решениями уравнения (23) будут те  к
к  для которых
для которых  Легко видеть, что только
Легко видеть, что только  удовлетворяет этому условию, а следовательно, является решением уравнения (23).
удовлетворяет этому условию, а следовательно, является решением уравнения (23).
Решения уравнения  есть
есть  Так как
Так как  Значит,
Значит,  удовлетворяет уравнению (23). Следовательно, решениями уравнения (23) являются
удовлетворяет уравнению (23). Следовательно, решениями уравнения (23) являются 
Ответ: 
2.2.4. Уравнения вида
Если в уравнении

 где
где  натуральное число, то следствием уравнения (25) является уравнение
натуральное число, то следствием уравнения (25) является уравнение

Если же  то следствием уравнения (25) является уравнение
то следствием уравнения (25) является уравнение

Уравнение вида (25) можно решать, следовательно, так:
1. Перейти от этого уравнения при натуральном  к уравнению (26), а при
к уравнению (26), а при  к уравнению (27).
к уравнению (27).
2. Решить уравнение (26) или уравнение (27).
3. Проверить, какие из найденных корней будут корнями исходного уравнения.
Замечание. Конечно, можно считать, что при любом действительном числе а следствием уравнения (25) является уравнение

но тогда надо уточнять, что понимается под функцией 
Пример 7. Решить уравнение

Решение. Уравнение

является следствием уравнения (28). Переписав уравнение (29) в виде  находим его корни
находим его корни  Легко видеть, что
Легко видеть, что  является корнем уравнения (28), а
является корнем уравнения (28), а  не является его корнем.
не является его корнем.
Ответ: 
Пример 8. Решить уравнение

Решение. Следствием уравнения (30) является уравнение  решения которого есть
решения которого есть  Ясно, что
Ясно, что  этих х уравнению (30) будут удовлетворять лишь
этих х уравнению (30) будут удовлетворять лишь 
Ответ: 
2.2.5. Неравенства вида
Согласно общему методу решения неравенств, содержащих неизвестную в основании логарифмов, неравенство

равносильно при  неравенству
неравенству

которое можно переписать в виде

Последнее неравенство равносильно совокупности систем неравенств

или совокупности систем неравенств

Поэтому неравенство вида (31) можно решать следующим образом:
1. Перейти от неравенства (31) к равносильной совокупности неравенств (32).
2. Решить совокупность неравенств (32), ее решения и будут решениями неравенства (31).
Пример 9. Решить неравенство

Решение. Неравенство (33) равносильно совокупности двух систем неравенств:


Система (34) равносильна совокупности двух систем:

из которых первая не имеет решений, а решения второй составляют промежуток 
Система (35) равносильна совокупности систем неравенств

Решения первой системы этой совокупности есть множество  а вторая система решений не имеет.
а вторая система решений не имеет.
Следовательно, решениями исходного неравенства являются все х из объединения двух промежутков 
Ответ: 
Процесс решения неравенства вида (31) иногда оформляют следующим образом:
1. Находят ОДЗ неравенства (31).
2. Разбивают ОДЗ неравенства (31) на два множества  — та часть ОДЗ, где
— та часть ОДЗ, где  — та часть ОДЗ, где
— та часть ОДЗ, где 
3. На  решают неравенство
решают неравенство  равносильное на
равносильное на  исходному неравенству.
исходному неравенству.
3. На  решают неравенство
решают неравенство  равносильное на
равносильное на  исходному неравенству.
исходному неравенству.
Объединяя решения, найденные на  получают все решения исходного неравенства.
получают все решения исходного неравенства.
Пример 10. Решить неравенство

Решение. ОДЗ неравенства (36] пределяется из условий  т.е. ОДЗ состоит из двух промежутков
т.е. ОДЗ состоит из двух промежутков 
а) Пусть  Для этих х исходное неравенство равносильно неравенству
Для этих х исходное неравенство равносильно неравенству

Так как  для рассматриваемых
для рассматриваемых  то неравенство (37) равносильно неравенству
то неравенство (37) равносильно неравенству  ), котрое можно записать в виде
), котрое можно записать в виде

Решениями неравенства (38) являются все х из промежутка  Из этих х условию
Из этих х условию  удовлетворяют х из промежутка
удовлетворяют х из промежутка 
Следовательно, в случае а) решения исходного неравенства составляют промежуток 
б) Пусть  Для этих х исходное неравенство равносильно неравенству
Для этих х исходное неравенство равносильно неравенству

Так как  для рассматриваемых
для рассматриваемых  то неравенство (39) равносильно неравенству
то неравенство (39) равносильно неравенству  , которое можно записать в виде
, которое можно записать в виде

Решениями неравенства (40) являются все  из двух промежутков
из двух промежутков  Ни одно из этих х не удовлетворяет условию
Ни одно из этих х не удовлетворяет условию 
Следовательно, в случае б) исходное неравенство не имеет решений.
Поэтому решениями неравенства (36) являются х из промежутка 
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
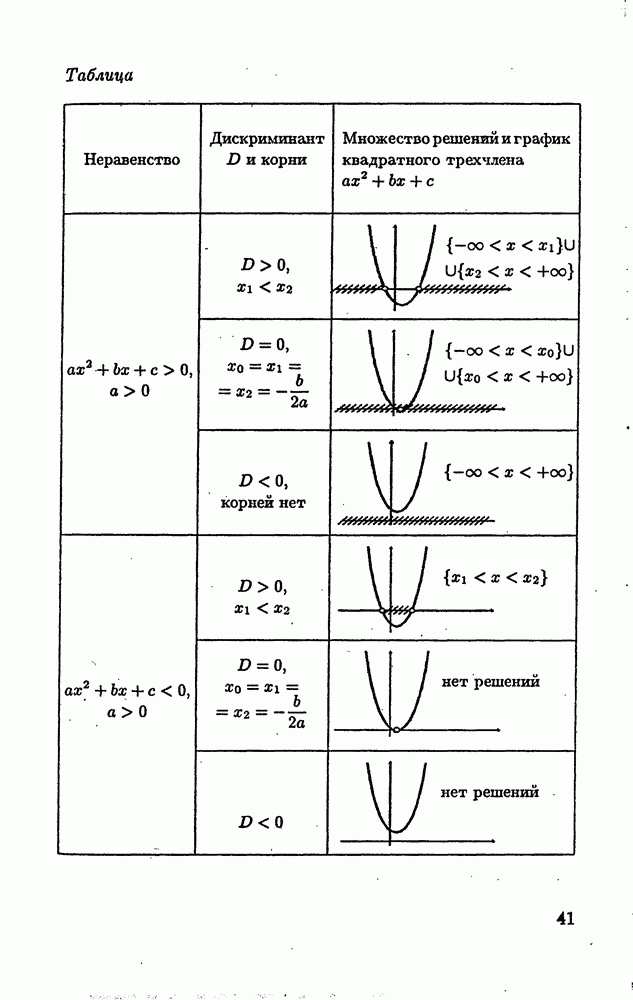
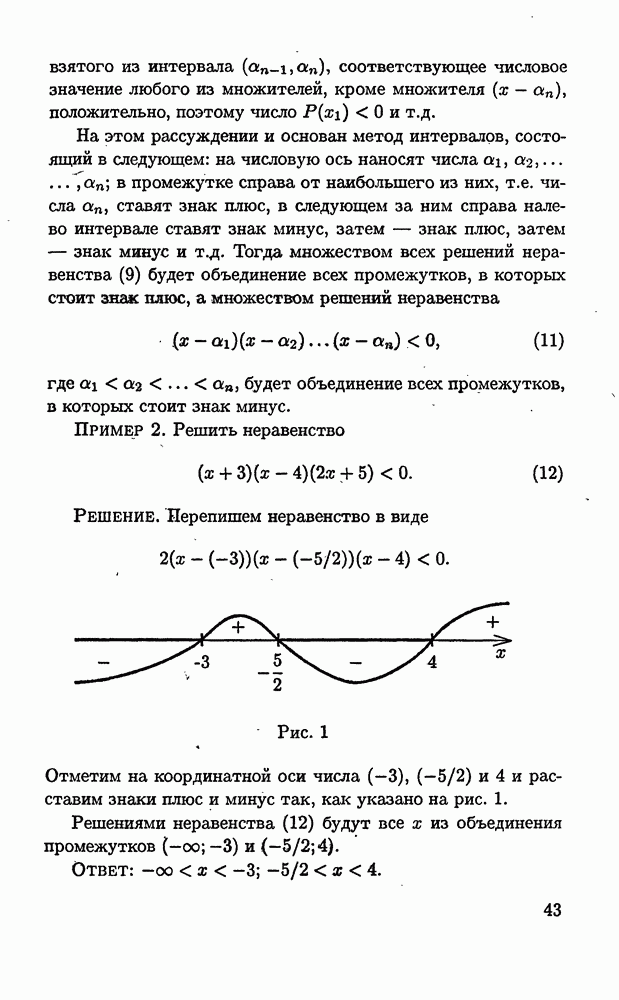
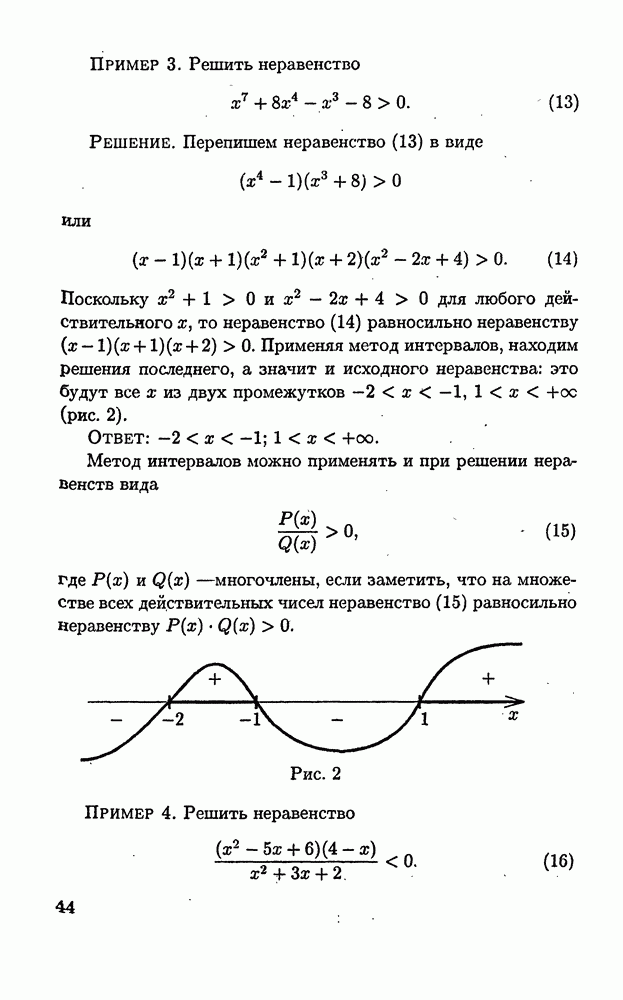
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.