| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
В этой главе рассматриваются алгебраические уравнения степени т.е. уравнения вида

и алгебраические неравенства степени  т.е. неравенства вида
т.е. неравенства вида

и

где  — многочлен степени
— многочлен степени  т.е.
т.е.

При решении алгебраических уравнений и неравенств часто приходится разлагать многочлен  на множители, поэтому § 1.1 посвящен этому вопросу.
на множители, поэтому § 1.1 посвящен этому вопросу.
§ 1.1. Разложение многочлена на множители
Разложить многочлен на множители — это значит представить его в виде произведения двух или нескольких многочленов. В этом параграфе приводятся некоторые методы
разложения многочленов в произведение множителей первой и второй степени, поскольку знания такого разложения достаточно для решения алгебраических уравнений и неравенств.
1.1.1. Вынесение общего множителя.
Если все члены многочлена имеют общий множитель, то, вынося его за скобки, получим разложение многочлена на множители.Пример 1. Разложить на множители многочлен

Решение. Все члены данного многочлена содержат общий множитель х. Вынося его за скобки, получим разложение данного многочлена на множители

1.1.2. Применение формул сокращенного умножения.
Иногда многочлен  можно разложить на множители, используя формулы сокращенного умножения:
можно разложить на множители, используя формулы сокращенного умножения:

Пример 2. Разложить на множители многочлен

Решение. Применяя формулу  имеем
имеем 

Пример 3. Разложить на множители многочлен

Решение. Применяя формулу  имеем
имеем

1.1.3. Выделение полного квадрата.
Иногда многочлен можно разложить на множители, если воспользоваться сначала методом выделения полного квадрата, а затем, как правило, формулой разности квадратов.
Пример 4. Разложить на множители многочлен

Решение. Выделяя полный квадрат, а затем применяя формулу разности квадратов, имеем 
1.1.4. Группировка.
Этот способ применяется чаще всего в сочетании со способом вынесения за скобки общего множителя. Суть его состоит в перегруппировке слагаемых в многочлене и дальнейшего объединения в группы таким образом, чтобы после вынесения (если это можно) общего множителя из каждого слагаемого в данной группе в скобке получилось выражение, являющееся в свою очередь общим множителем для каждой группы.
Пример 5. Разложить на множители многочлен

Решение. Объединим в одну группу первое и второе слагаемые, а в другую — третье и четвертое слагаемые. Тогда имеем  Вынося из первой скобки множитель
Вынося из первой скобки множитель  а из второй скобки
а из второй скобки  получаем
получаем  Наконец, вынося за скобку общий множитель
Наконец, вынося за скобку общий множитель  получаем, что
получаем, что  и, наконец, вынося
и, наконец, вынося  скобки множитель
скобки множитель  получим, что
получим, что

1.1.5. Метод неопределенных коэффициентов.
Суть этого метода состоит в том, что заранее предполагается вид множителей — многочленов, на которые разлагается данный многочлен. Этот метод опирается на следующие утверждения:
1) два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях 
2) любой многочлен третьей степени разлагается в произведение линейного и квадратного множителей;
3) любой многочлен четвертой степени разлагается в произведение двух многочленов второй степени.
Пример 6. Разложить на множители многочлен

Решение. Будем искать многочлены  такие, что справедливо тождественное равенство
такие, что справедливо тождественное равенство

Правую часть этого равенства можно записать в виде

Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства (1), получаем систему равенств
для нахождения 

Легко видеть, что этим равенствам удовлетворяют числа  а это означает, что многочлен
а это означает, что многочлен  разлагается на множители
разлагается на множители  .
.
1.1.6. Подбор корня многочлена по его старшему и свободному коэффициентам.
Иногда при разложении многочлена на множители бывают полезными следующие утверждения:
1) если многочлен  , с целыми коэффициентами имеет рациональный корень
, с целыми коэффициентами имеет рациональный корень  — несократимая дробь,
— несократимая дробь,  то
то  — делитель свободного члена
— делитель свободного члена  — делитель старшего коэффициента
— делитель старшего коэффициента 
2) если каким-либо образом подобран корень  многочлена
многочлена  степени
степени  то многочлен
то многочлен  можно представить в виде
можно представить в виде  где
где  — многочлен степени
— многочлен степени 
Многочлен  можно найти либо делением многочлена
можно найти либо делением многочлена  на двучлен
на двучлен  “столбиком”, либо соответствующей группировкой слагаемых многочлена и выделением из них множителя
“столбиком”, либо соответствующей группировкой слагаемых многочлена и выделением из них множителя  либо методом неопределенных коэффициентов.
либо методом неопределенных коэффициентов.
Пример 7. Разложить на множители многочлен

Решение. Поскольку коэффициент при  равен 1, то рациональные корни данного многочлена, если они существуют.
равен 1, то рациональные корни данного многочлена, если они существуют.
являются делителями числа  т.е. могут быть целыми числами
т.е. могут быть целыми числами  . Обозначим данный многочлен через
. Обозначим данный многочлен через  Так как
Так как  , то числа
, то числа  не являются корнями многочлена
не являются корнями многочлена  . Поскольку
. Поскольку  то
то  является корнем многочлена
является корнем многочлена  значит, данный многочлен делится на двучлен
значит, данный многочлен делится на двучлен  Поэтому
Поэтому

Следовательно,  Так как
Так как  , то
, то  .
.
1.1.7. Метод введения параметра.
Иногда при разложении многочлена на множители помогает метод введения параметра. Суть этого метода поясним на следующем примере. Пример 8. Разложить на множители многочлен

Решение. Рассмотрим многочлен с параметром а.

который при  превращается в заданный многочлен. Запишем этот многочлен как квадратный трехчлен относительно а:
превращается в заданный многочлен. Запишем этот многочлен как квадратный трехчлен относительно а:

Так как корни этого квадратного относительно а трехчлена есть  то справедливо равенство
то справедливо равенство 
 Следовательно, многочлен
Следовательно, многочлен  разлагается на множители
разлагается на множители  т.е.
т.е.

1.1.8. Метод введения новой неизвестной.
В некоторых случаях путем замены выражения  входящего в многочлен
входящего в многочлен  через
через  молено получить многочлен относительно у, который уже легко разложить на множители. Затем после замейы у на
молено получить многочлен относительно у, который уже легко разложить на множители. Затем после замейы у на  получаем разложение на множители многочлена
получаем разложение на множители многочлена 
Пример 9. Разложить на множители многочлен

РЕШЕНИЕ. Преобразуем данный многочлен следующим образом:

Обозначим  через у. Тогда имеем
через у. Тогда имеем

Поэтому

Пример 10. Разложить на множители многочлен

Решение. Обозначим  через у. Тогда
через у. Тогда 

1.1.9. Комбинирование различных методов.
Часто при разложении многочлена на множители приходится применять последовательно несколько из рассмотренных выпке методов.
Пример 11. Разложить на множители многочлен

Решение. Применяя группировку, перепишем многочлен в виде

Применяя к первой скобке метод выделения полного квадрата, имеем

Применяя формулу полного квадрата, можно теперь записать, что

Наконец, применяя формулу разности квадратов, получим, что

| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
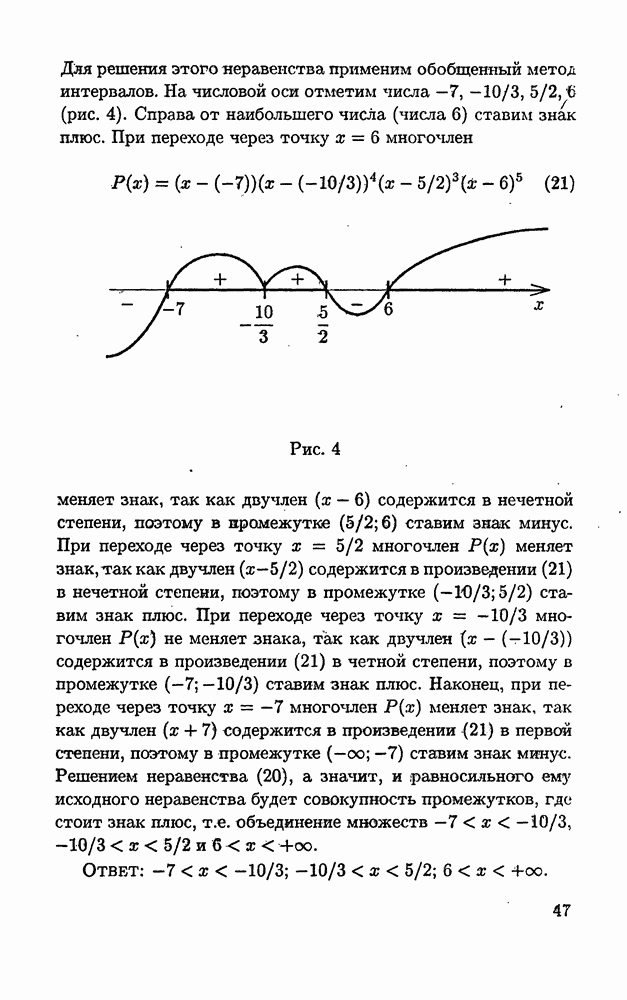
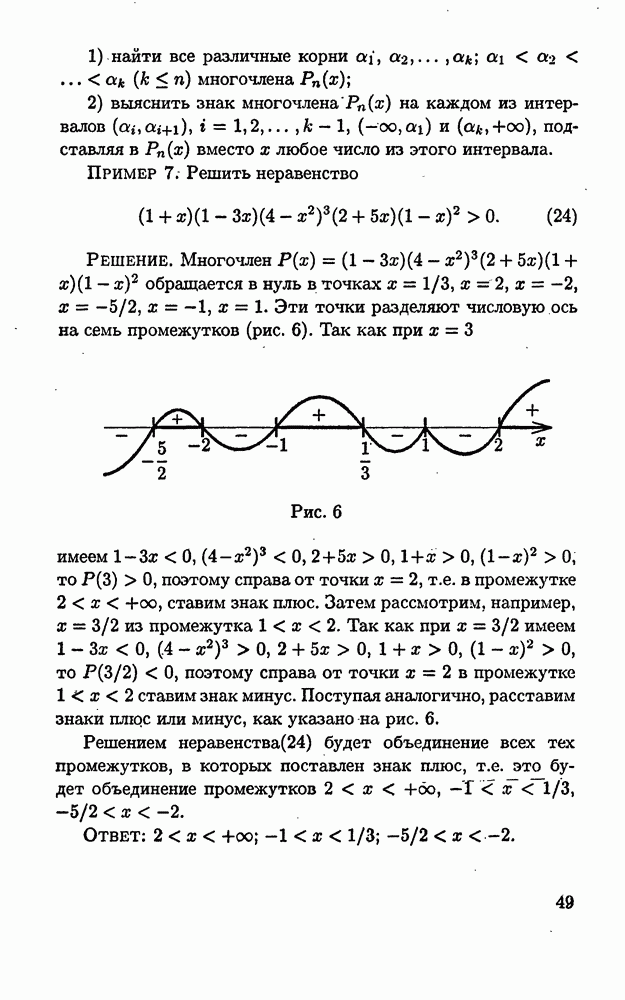
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.