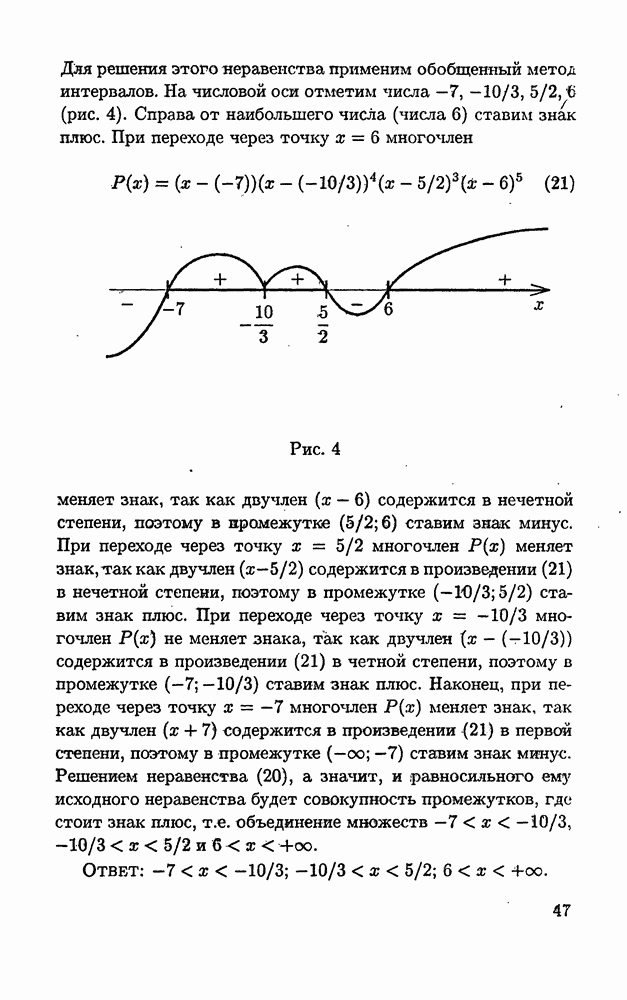
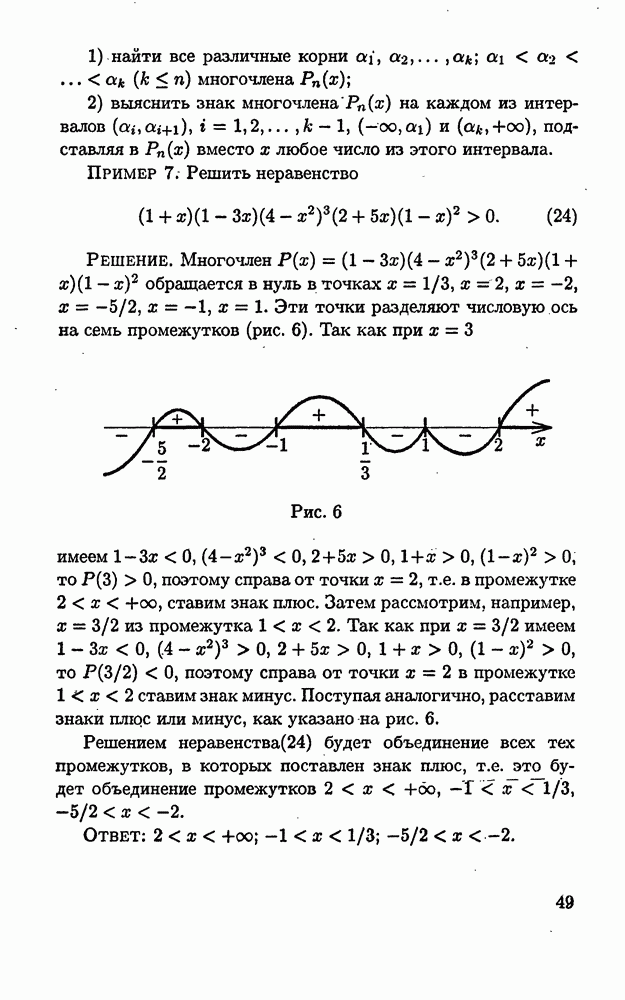
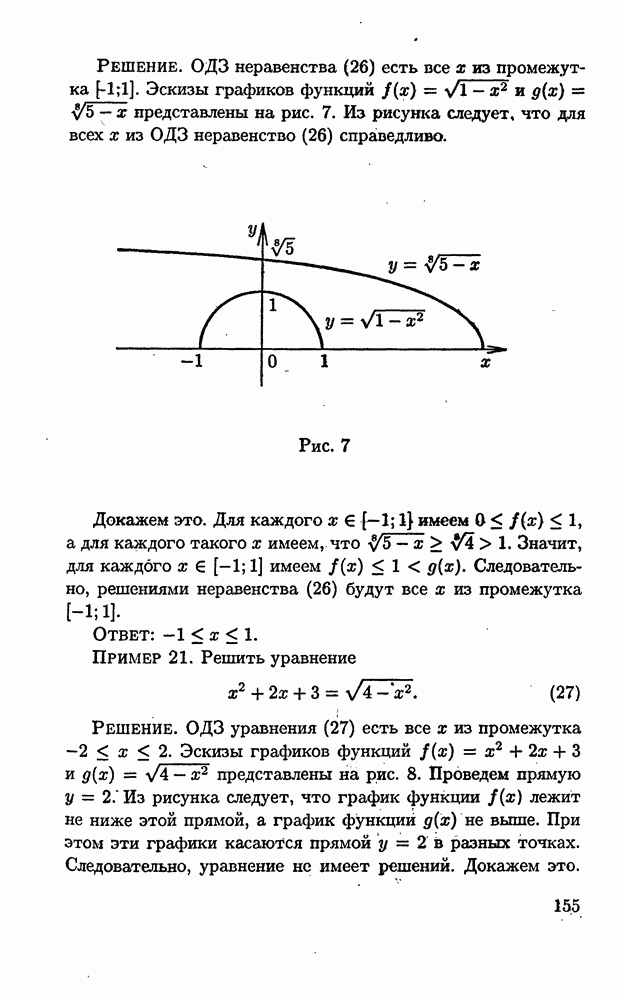
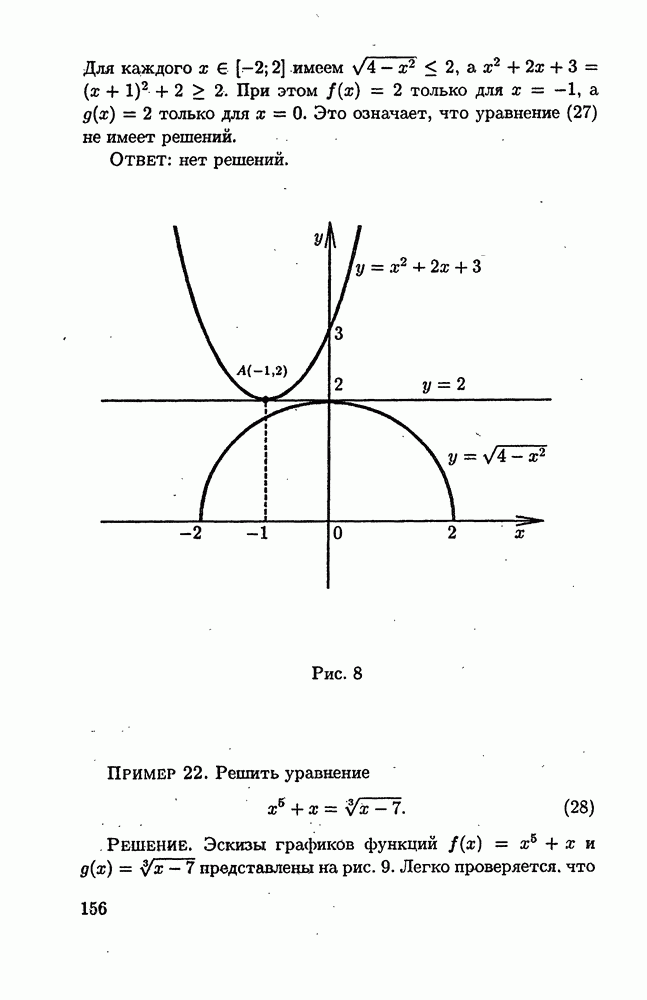
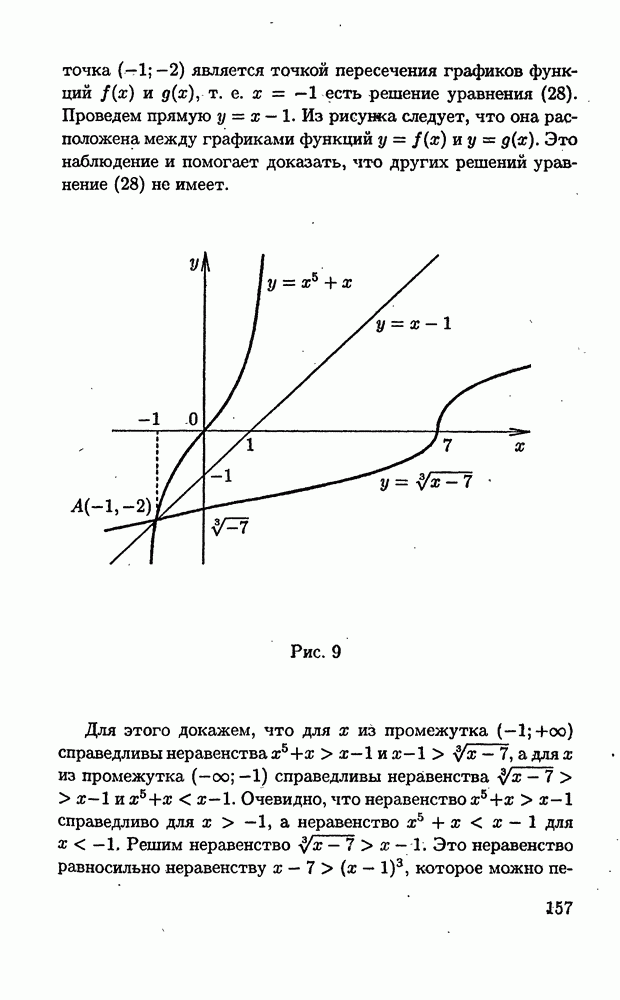
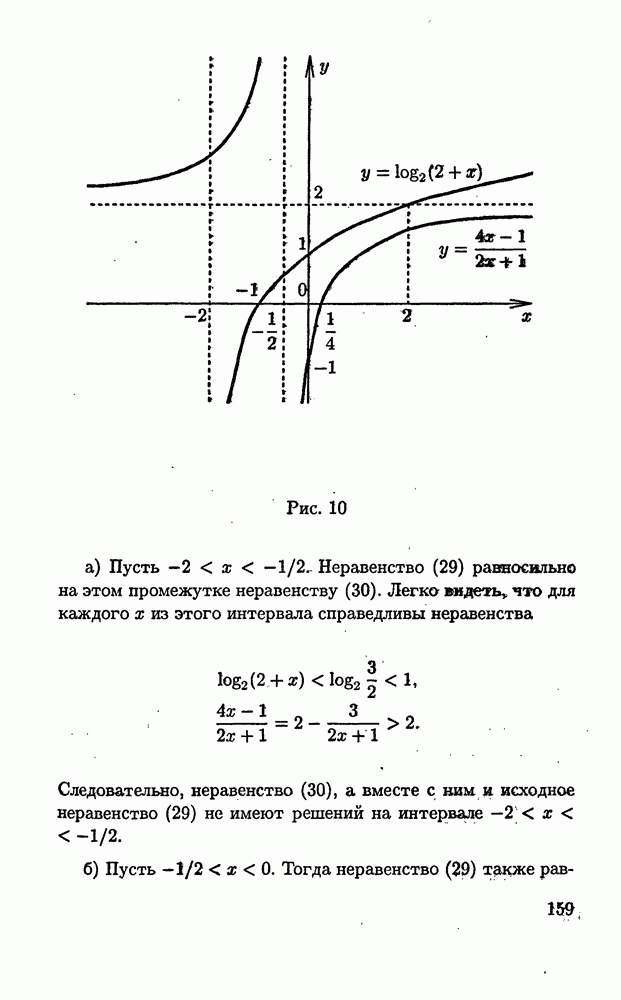
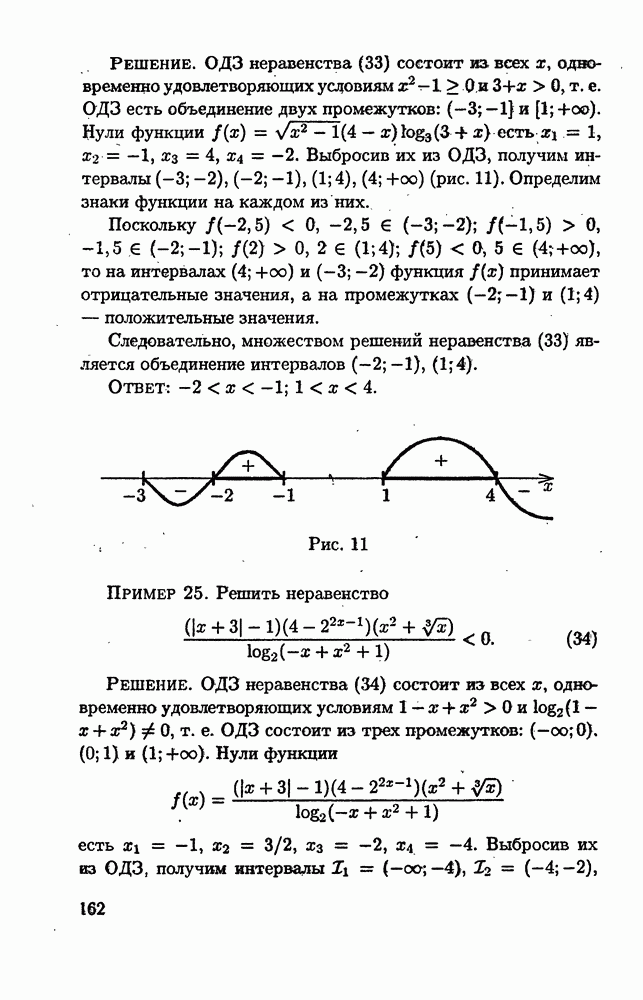
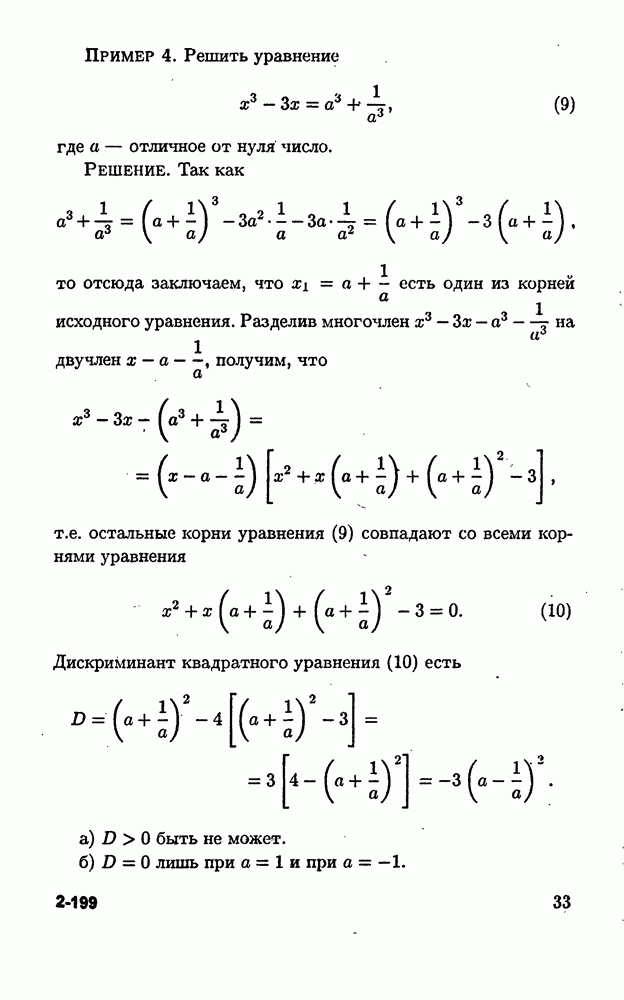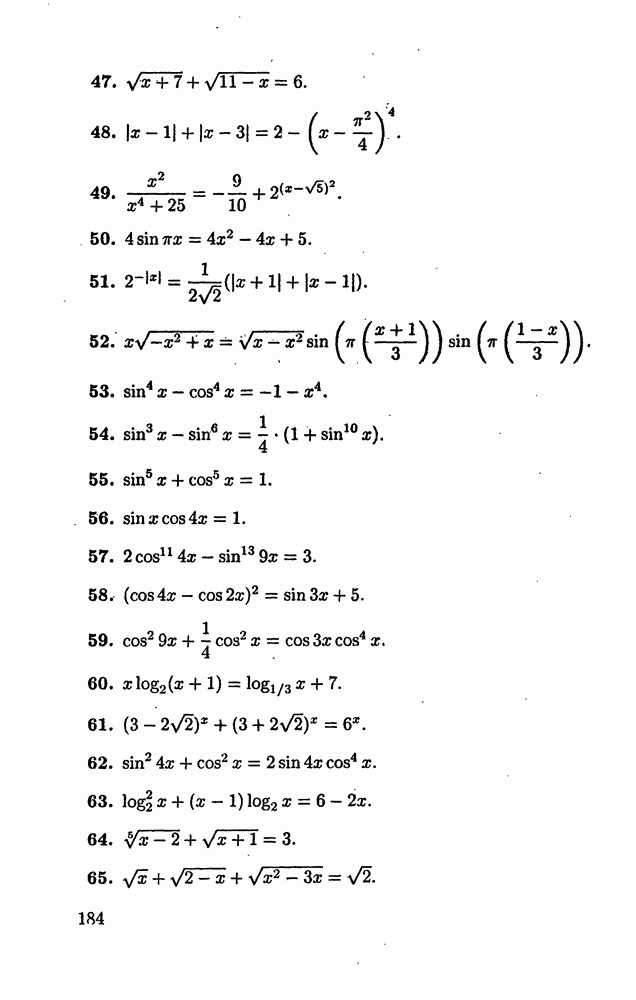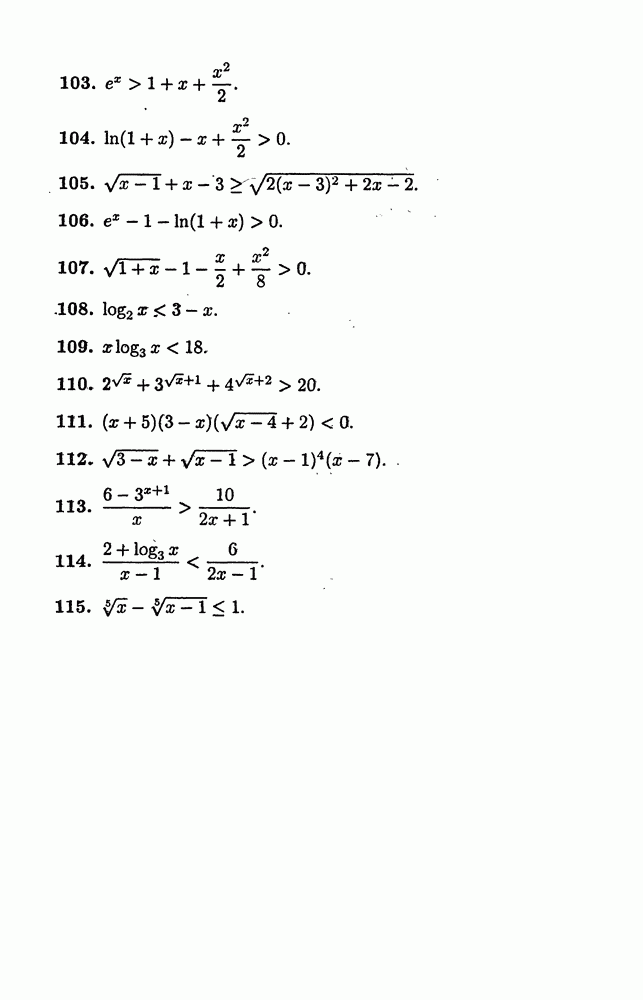| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
Если дано уравнение

то заменой неизвестной  оно сначала сводится к уравнению
оно сначала сводится к уравнению

а потом после нахождения всех решений уравнения (II)

сводится к решению совокупности уравнений

Этот прием достаточно хорошо известен, и поэтому в этой главе ему уделяется мало внимания. В основном в этой главе рассматриваются замены неизвестных для различных частных случаев уравнений, не записанных в виде (I).
§ 3.1. Алгебраические уравнения
3.1.1. Понижение степени уравнения.
Некоторые алгебраические уравнения заменой в них некоторого многочлена
одной буквой могут быть сведены к алгебраическим уравнениям, степень которых меньше степени исходного уравнения и решение которых проще.
Пример 1. Решить уравнение

Решение. Обозначим  через
через  , тогда уравнение (1) можно переписать в виде
, тогда уравнение (1) можно переписать в виде  Последнее уравнение имеет корни
Последнее уравнение имеет корни  Следовательно, уравнение (1) равносильно совокупности уравнений
Следовательно, уравнение (1) равносильно совокупности уравнений  Решения первого уравнения этой совокупности есть
Решения первого уравнения этой совокупности есть  Решения второго уравнения есть
Решения второго уравнения есть  Решениями уравнения (1) являются
Решениями уравнения (1) являются 
Ответ: 
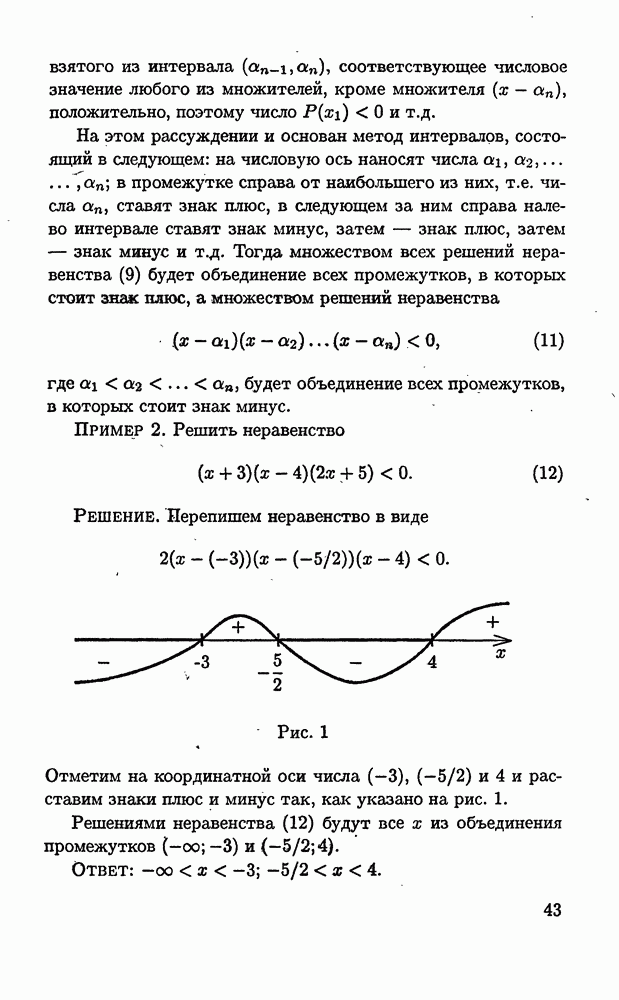
Пример 2. Решить уравнение

Решение. Умножив обе части уравнения на 12 и обозначив  через
через  получим уравнение
получим уравнение  Переписав это уравнение в виде
Переписав это уравнение в виде

и обозначив  через
через  перепишем уравнение (3) в виде
перепишем уравнение (3) в виде  Последнее уравнение имеет корни
Последнее уравнение имеет корни  Поэтому получаем, что уравнение (3) равносильно совокупности двух уравнений
Поэтому получаем, что уравнение (3) равносильно совокупности двух уравнений  Решения этой совокупности уравнений есть
Решения этой совокупности уравнений есть  т.е. уравнение
т.е. уравнение  равносильно совокупности уравнений
равносильно совокупности уравнений

Решениями совокупности (4) являются  они и являются решениями уравнения (2).
они и являются решениями уравнения (2).
Ответ: 
3.1.2. Уравнения вида
Уравнение

где  — данные числа, можно свести к биквадратному уравнению с помощью замены неизвестной
— данные числа, можно свести к биквадратному уравнению с помощью замены неизвестной

т. е. замены

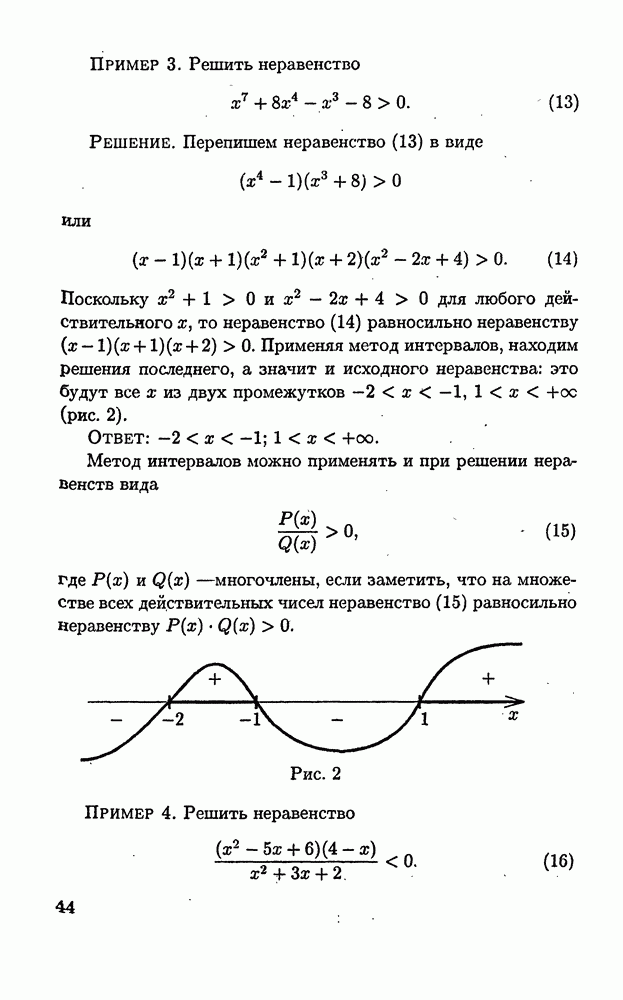
Пример 3. Решить уравнение

Решение. Обозначим  через у, т. е. сделаем замену переменных
через у, т. е. сделаем замену переменных  или
или  Тогда уравнение (6) можно переписать в виде
Тогда уравнение (6) можно переписать в виде  или применяя формулу (а
или применяя формулу (а  в виде
в виде

Поскольку корни квадратного уравнения  есть
есть  то решения уравнения (7) есть решения совокупности уравнений
то решения уравнения (7) есть решения совокупности уравнений  Эта совокупность уравнений имеет два решения
Эта совокупность уравнений имеет два решения  Следовательно, решения уравнения (6) есть
Следовательно, решения уравнения (6) есть 
Ответ: 
3.1.3. Уравнения вида
Уравнение

где числа  таковы, что
таковы, что  заменой неизвестных
заменой неизвестных

сводится к биквадратному уравнению.
Пример 4. Решить уравнение

Решение. Сделаем замену неизвестных

т.е.  или
или  Тогда уравнение (9) можно переписать в виде
Тогда уравнение (9) можно переписать в виде  т.е. в виде
т.е. в виде

Биквадратное уравнение (10) имеет два корня:  Следовательно, уравнение (9) также имеет два корня:
Следовательно, уравнение (9) также имеет два корня: 
Ответ: 
3.1.4. Уравнения вида
Уравнение

где  не имеет корня
не имеет корня  поэтому, разделив уравнение (11) на
поэтому, разделив уравнение (11) на  получим равносильное ему уравнение
получим равносильное ему уравнение

которое после замены неизвестной  перепишется в виде квадратного уравнения, решение которого не представляет трудностей.
перепишется в виде квадратного уравнения, решение которого не представляет трудностей.
Пример 5. Решить уравнение

Решение. Так как  не является корнем уравнения (12), то, разделив его на
не является корнем уравнения (12), то, разделив его на  получим равносильное ему уравнение
получим равносильное ему уравнение

Делая замену неизвестной  получим уравнение
получим уравнение  которое имеет два корня:
которое имеет два корня:  Следовательно, исходное уравнение (12) равносильно совокупности уравнений
Следовательно, исходное уравнение (12) равносильно совокупности уравнений

Эта совокупность имеет два корня:  Ответ:
Ответ: 
Замечание. Уравнение вида

у которого  всегда можно привести к виду (11) и, более того, считая
всегда можно привести к виду (11) и, более того, считая  к виду
к виду

3.1.5, Уравнения вида
Уравнение

где числа  таковы, что
таковы, что  можно переписать, перемножив первую скобку со второй, а третью с четвертой, в виде
можно переписать, перемножив первую скобку со второй, а третью с четвертой, в виде

т.е. уравнение (13) теперь записано в виде (11), и его решение можно проводить так же, как решение уравнения (11).
Пример 6. Решить уравнение

Решение. Уравнение (14) имеет вид (13), поэтому перепишем его в виде

или в виде

Так как  не есть решение этого уравнения, то, разделив его обе части на
не есть решение этого уравнения, то, разделив его обе части на  получим равносильное исходному уравнение
получим равносильное исходному уравнение  Делая замену переменных
Делая замену переменных  получаем квадратное уравнение
получаем квадратное уравнение  решения которого есть
решения которого есть  Следовательно, исходное уравнение (14) равносильно совокупности уравнений
Следовательно, исходное уравнение (14) равносильно совокупности уравнений

Решения первого уравнения этой совокупности есть 

второе уравнение этой совокупности решений не имеет. Итак, исходное уравнение имеет корни 
Ответ:

3.1.6. Уравнения вида
Уравнение

где числа  таковы, что а
таковы, что а  не имеет корня
не имеет корня  поэтому, разделив уравнение (15) на
поэтому, разделив уравнение (15) на  получим равносильное ему уравнение
получим равносильное ему уравнение

которое после замены неизвестной  перепишется в виде квадратного уравнения, решение которого не представляет трудностей.
перепишется в виде квадратного уравнения, решение которого не представляет трудностей.
Пример 7. Решить уравнение

Решение. Так как  не является корнем уравнения (16), то, разделив обе его части на
не является корнем уравнения (16), то, разделив обе его части на  получим уравнение
получим уравнение

равносильное уравнению (16). Сделав замену неизвестной  уравнение (17) перепишем в виде
уравнение (17) перепишем в виде 

Квадратное уравнение (18) имеет два корня:  Поэтому уравнение (17) равносильно совокупности уравнений
Поэтому уравнение (17) равносильно совокупности уравнений

Совокупность уравнений (19) имеет четыре корня:  . Они будут корнями уравнения (16).
. Они будут корнями уравнения (16).
Ответ: 
3.1.7. Уравнения вида
Пусть многочлен  обладает свойством: для некоторого фиксированного числа а справедливо тождественное равенство
обладает свойством: для некоторого фиксированного числа а справедливо тождественное равенство  Тогда
Тогда  показать, что существует многочлен
показать, что существует многочлен  такой, что справедливо тождественное равенство
такой, что справедливо тождественное равенство  при этом многочлен
при этом многочлен  должен быть четной степени.
должен быть четной степени.
Поэтому уравнение  можно переписать в этом
можно переписать в этом  степень которого меньше степени уравнения
степень которого меньше степени уравнения 
Для решения таких уравнений можно поступить следующим образом: сначала сделать замену неизвестной  тогда получим алгебраическое уравнение той же степени
тогда получим алгебраическое уравнение той же степени  что и уравнение
что и уравнение  но уже содержащее только четные степени у. Делая затем замену неизвестной
но уже содержащее только четные степени у. Делая затем замену неизвестной  получим алгебраическое уравнение уже степени к.
получим алгебраическое уравнение уже степени к.
Пример 8. Решить уравнение

Решение. Рассмотрим многочлен

Поскольку легко проверить, что  то уравнение (20) есть уравнение рассматриваемого вида. Сделаем замену неизвестной
то уравнение (20) есть уравнение рассматриваемого вида. Сделаем замену неизвестной  или
или  тогда уравнение (20) перепишется в виде
тогда уравнение (20) перепишется в виде

Так как  то, подставляя эти выражения в левую часть уравнения (21) и раскрывая четвертые степени по формуле
то, подставляя эти выражения в левую часть уравнения (21) и раскрывая четвертые степени по формуле

получим, что уравнение (21) перепишется в виде

Уравнение (22) имеет два корня:  Следовательно, исходное уравнение имеет также два корня
Следовательно, исходное уравнение имеет также два корня 
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
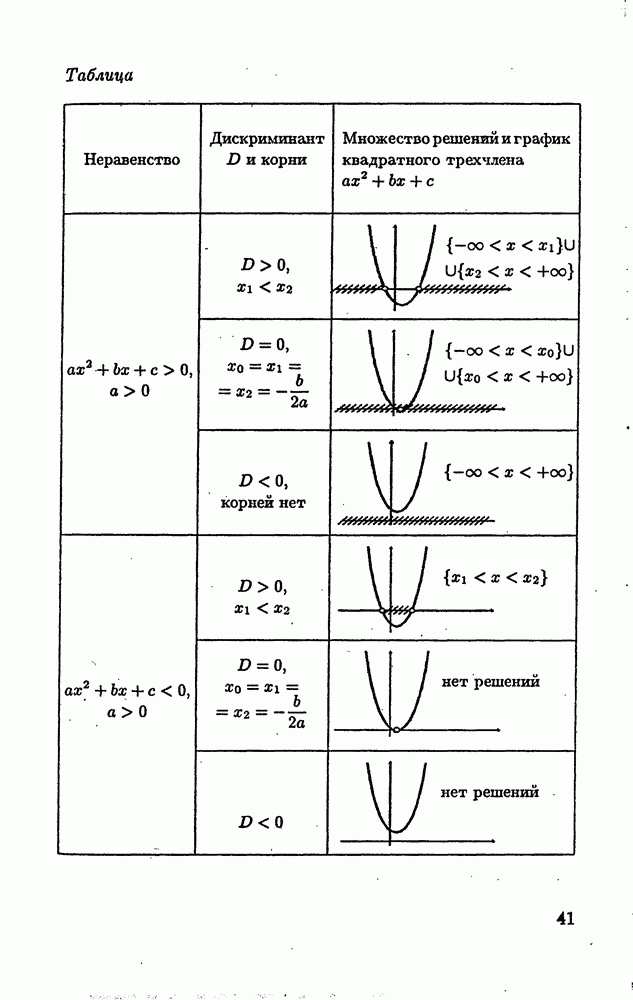
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.