| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
4.2.1. Уравнения вида
Уравнения вида

равносильны системе уравнений

Пример 1. Решить уравнение

Решение. Перепишем уравнение (4) в виде

откуда очевидно, что уравнение (5) равносильно системе уравнений

Первое уравнение этой системы имеет единственное решение  которое не удовлетворяет второму уравнению системы (6). Следовательно, система (6) не имеет решений.
которое не удовлетворяет второму уравнению системы (6). Следовательно, система (6) не имеет решений.
Ответ: нет решений.
Пример 2. Решить уравнение

Решение. Перепишем уравнение (7) в виде

Это уравнение равносильно системе уравнений

Решение первого из этих уравнений есть  Проверка показывает, что это число также является и решением второго уравнения системы (8). Следовательно,
Проверка показывает, что это число также является и решением второго уравнения системы (8). Следовательно,  является решением исходного уравнения (7).
является решением исходного уравнения (7).
Ответ: 
Отметим, что к системе (3) сводится и ряд других уравнений. Приведем пример.
ПРИМЕР 3. Решить уравнение

РЕШЕНИЕ. Для любых  справедливы неравенства
справедливы неравенства

Поэтому уравнение (9) равносильно системе уравнений

имеющей единственное решение 
Ответ: 
4.2.2. Неравенства вида
Решениями неравенств вида

являются все  из их ОДЗ, за исключением тех
из их ОДЗ, за исключением тех  которые являются решениями системы уравнений
которые являются решениями системы уравнений

Пример 4. Решить неравенство

Решение. ОДЗ неравенства (13) есть все  Для нахождения решений неравенства (13) надо исключить из его ОДЗ
Для нахождения решений неравенства (13) надо исключить из его ОДЗ
все решения системы уравнений

Эта система имеет единственное решение  следовательно, решениями неравенства (13) являются все
следовательно, решениями неравенства (13) являются все  кроме
кроме 
Ответ: 
Пример 5. Решить неравенство

Решение. ОДЗ неравенства (14) есть все  Перепишем неравенство (14) в виде
Перепишем неравенство (14) в виде

Для любого х справедливы неравенства

Поэтому неравенство (14) не выполняется лишь для таких  что одновременно
что одновременно

Следовательно, решениями исходного неравенства (14) являются все  кроме
кроме 
Ответ: 
Отметим, что к системе (12) сводятся иногда и другие неравенства.
Пример 6. Решить неравенства

Решение. ОДЗ неравенства (15) являются все х, удовлетворяющие условию  т. е. ОДЗ есть все
т. е. ОДЗ есть все  На ОДЗ справедливы неравенства
На ОДЗ справедливы неравенства

Поэтому неравенство (15) выполняется для всех х из ОДЗ, кроме тех, которые удовлетворяют системе уравнений.

Решениями второго уравнения этой системы являются  Из них первому уравнению удовлетворяет только
Из них первому уравнению удовлетворяет только  Итак, решениями данного неравенства (15) являются все х из промежутка
Итак, решениями данного неравенства (15) являются все х из промежутка 
Ответ: 
4.2.3. Использование ограниченности функций.
Если при решении уравнения

удается показать, что для всех  из некоторого множества М справедливы неравенства
из некоторого множества М справедливы неравенства  то на множестве М уравнение (16) равносильно системе уравнений
то на множестве М уравнение (16) равносильно системе уравнений

Пример 7. Решить уравнение

Решение. Перепишем это уравнение в виде

Очевидно, что для любых действительных х имеем

Следовательно, уравнение (18) равносильно системе уравнений

Эта система уравнений не имеет решений, поэтому исходное уравнение также не имеет решений.
Ответ: нет решений.
Пример 8. Решить уравнение

Решение. ОДЗ уравнения (19) являются все действительные числа х. Для любых х имеем

Следовательно, уравнение (19) равносильно системе уравнений

Решения второго уравнения системы (20) есть  Из этих значений первому уравнению удовлетворяет только
Из этих значений первому уравнению удовлетворяет только
 которое, следовательно, является единственным решением исходного уравнения.
которое, следовательно, является единственным решением исходного уравнения.
Ответ: 
Пример 9. Решить уравнение

Решение. Поскольку  то уравнение (21) можно переписать в виде
то уравнение (21) можно переписать в виде  или в виде,
или в виде,

Поскольку для любого действительного х имеем  то уравнение (22) равносильно системе уравнений
то уравнение (22) равносильно системе уравнений

Система (23) равносильна совокупности систем уравнений

Решения первой из этих систем есть  второй
второй  Все эти решения и будут решениями исходного уравнения.
Все эти решения и будут решениями исходного уравнения.
Ответ: 
4.2.4. Использование свойств синуса и косинуса.
Решение большого количества тригонометрических уравнений может быть сведено к решению систем уравнений. Примерами таких уравнений могут служить следующие:

где  — данные действительные числа,
— данные действительные числа,  — данные натуральные числа. При решении таких уравнений используется следующее свойство синуса: если для некоторого числа
— данные натуральные числа. При решении таких уравнений используется следующее свойство синуса: если для некоторого числа  справедливо строгое неравенство
справедливо строгое неравенство  то такое число
то такое число  не может быть корнем ни одного из уравнений (25). Аналогично, при решении уравнений
не может быть корнем ни одного из уравнений (25). Аналогично, при решении уравнений

используется свойство косинуса: если для некоторого числа  справедливо строгое неравенство
справедливо строгое неравенство  то такое число
то такое число  не может быть корнем ни одного из этих уравнений.
не может быть корнем ни одного из этих уравнений.
Пример 10. Решить уравнение

Ршшшё. Если  — решение уравнения (26), то либо
— решение уравнения (26), то либо  либо
либо  Действительно, если бы
Действительно, если бы  то из уравнения (26) следовало бы, что
то из уравнения (26) следовало бы, что  что, естественно, невозможно. Но если
что, естественно, невозможно. Но если  то из уравнения (26) следует, что
то из уравнения (26) следует, что  если
если  то
то  Следовательно, любое решение уравнения (26) является решением совокупности двух систем уравнений:
Следовательно, любое решение уравнения (26) является решением совокупности двух систем уравнений:

Легко видеть, что любое решение системы (27) и любое решение системы (28) есть решение уравнения (26). Следовательно, уравнение (26) равносильно совокупности систем уравнений (27) и (28). Решим эти системы.
Первое уравнение системы (27) имеет решения

Все они удовлетворяют второму уравнению этой системы, т. е. являются решениями системы (27).
Первое уравнение системы (28) имеет решения

Ни одно из этих чисел не удовлетворяет второму уравнению этой системы. Поэтому система (28) не имеет решений.
Итак, решения исходного уравнения (26) совпадают с решениями системы (27).
Ответ: 
Пример 11. Решить уравнение

Решение. Если  есть решение уравнения (29), то
есть решение уравнения (29), то  ибо в противном случае было бы справедливо неравенство
ибо в противном случае было бы справедливо неравенство  что невозможно. Но если
что невозможно. Но если  то из уравнения (29) следует, что
то из уравнения (29) следует, что  Поэтому любое решение уравнения (29) является решением системы уравнений:
Поэтому любое решение уравнения (29) является решением системы уравнений:

Легко видеть, что любое решение системы (30) есть решение уравнения (29). Следовательно, уравнение (29) равносильно системе уравнений (30).
Первое уравнение системы (30) имеет решеншг

Все они удовлетворяют второму уравнению системы (30), т. е. являются решениями уравнения (29).
Ответ: 
Пример 12. Решить уравнение

Решение. Если  — решение уравнения (31), то
— решение уравнения (31), то  (в противном случае
(в противном случае  что невозможно). Но тогда
что невозможно). Но тогда  Следовательно; любое решение уравнения (31) есть решение системы уравнений
Следовательно; любое решение уравнения (31) есть решение системы уравнений

Легко видеть, что любое решение системы (32) есть решение уравнения (31). Поэтому уравнение (31) равносильно системе (32).
Первое уравнение системы (32) имеет решения

Найдем те из этих решений, которые будут удовлетворять второму уравнению системы (32). Это будут те  для каждого из которых найдется число
для каждого из которых найдется число  такое, что будет справедливо равенство
такое, что будет справедливо равенство

Перепишем равенство (33) в виде

Поскольку к  целые числа, то равенство (34) справедливо лишь тогда, когда
целые числа, то равенство (34) справедливо лишь тогда, когда  но тогда
но тогда  Итак, решениями системы (32) являются
Итак, решениями системы (32) являются  где
где 
Ответ: 
4.2.5. Использование числовых неравенств.
Иногда, применяя то или иное числовое неравенство к одной из частей уравнения (неравенства), его можно заменить равносильной ему системой уравнений. Примером такого неравенства является неравенство между средним арифметическим и средним геометрическим  где
где  — неотрицательные числа, причем равенство здесь возможно лишь при
— неотрицательные числа, причем равенство здесь возможно лишь при  Часто бывает полезно пользоваться следствиями из этих неравенств, например,
Часто бывает полезно пользоваться следствиями из этих неравенств, например,  при
при  причем
причем  тогда и только тогда, когда
тогда и только тогда, когда  или
или  при
при  причем
причем  тогда и только тогда, когда
тогда и только тогда, когда 
Пример 13, Решить уравнение

Решение. ОДЗ этого уравнения есть все действительные числа. Переписав левую часть уравнения (35) в виде

замечаем, что она не меньше четырех, как сумма двух взаимно обратных положительных величин, и только при  она равна четырем. В то же время правая часть при
она равна четырем. В то же время правая часть при  также равна четырем, а для всех
также равна четырем, а для всех  меньше, четырех. Следовательно,
меньше, четырех. Следовательно,  есть единственное решение уравнения (35). Ответ:
есть единственное решение уравнения (35). Ответ: 
Пример 14. Решить уравнение

Решение. Докажем, что для любых положительных чисел
а и  справедливо неравенство
справедливо неравенство

В самом деле, применяя неравенство о среднем арифметическом и среднем геометрическом сначала к числам  , а затем к числам
, а затем к числам  имеем
имеем 

откуда
Поскольку на ОДЗ уравнения (36) имеем  то, применяя неравенство (37), получаем, что для любого такого х левая часть уравнения (36) не меньше 4. В то же
то, применяя неравенство (37), получаем, что для любого такого х левая часть уравнения (36) не меньше 4. В то же

время на ОДЗ уравнения (36)  Следовательно, уравнение (36) равносильно системе уравнений
Следовательно, уравнение (36) равносильно системе уравнений

Из последнего уравнения системы (38) находим его решения  Подставляя эти значения в первое уравнение системы (38), получаем, что они являются его решениями. Следовательно,
Подставляя эти значения в первое уравнение системы (38), получаем, что они являются его решениями. Следовательно,  являются решениями исходного уравнения (36).
являются решениями исходного уравнения (36).
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
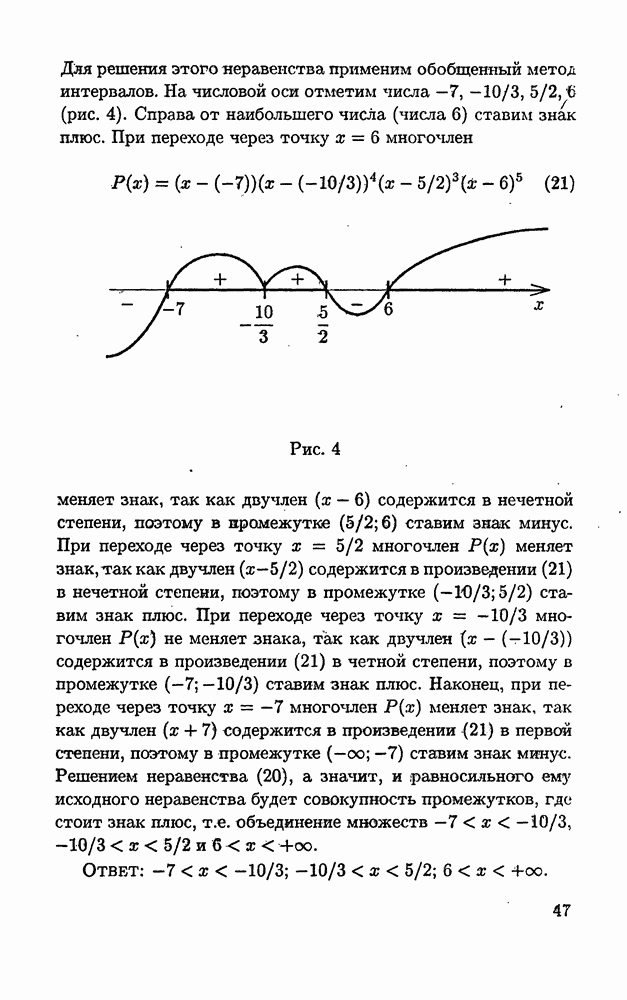
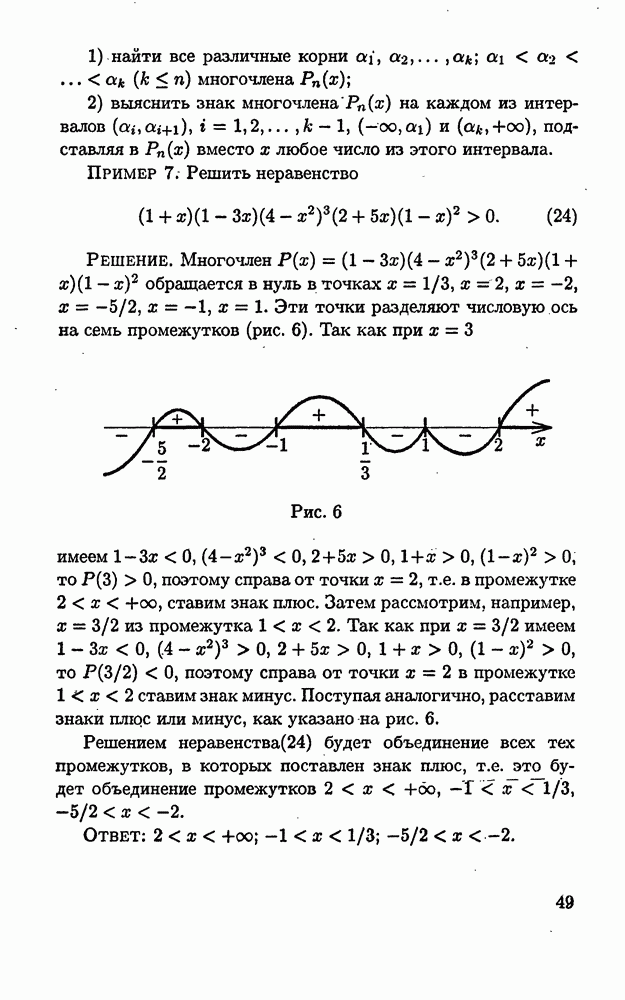
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.