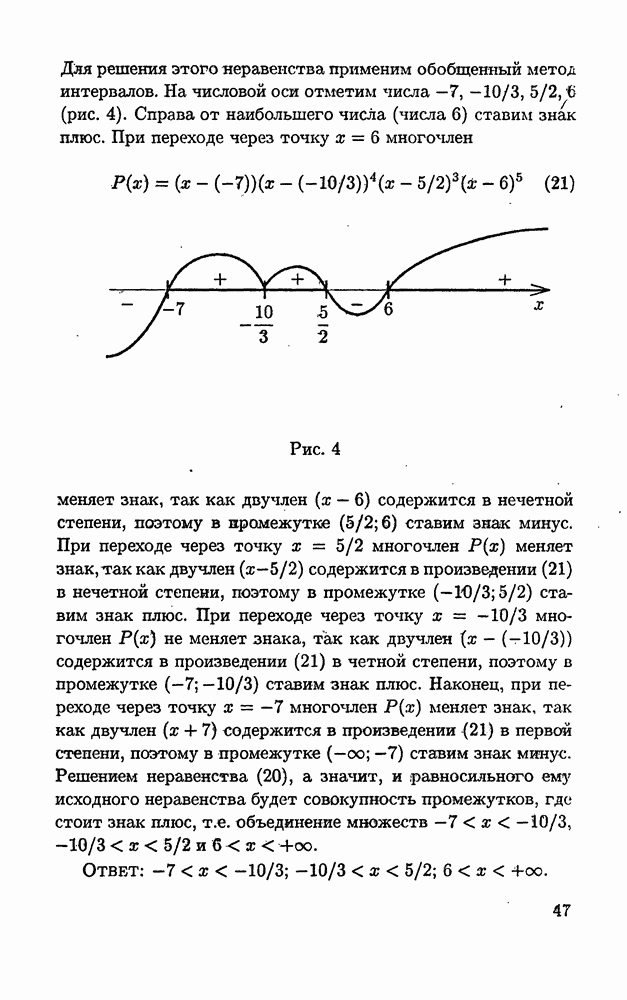
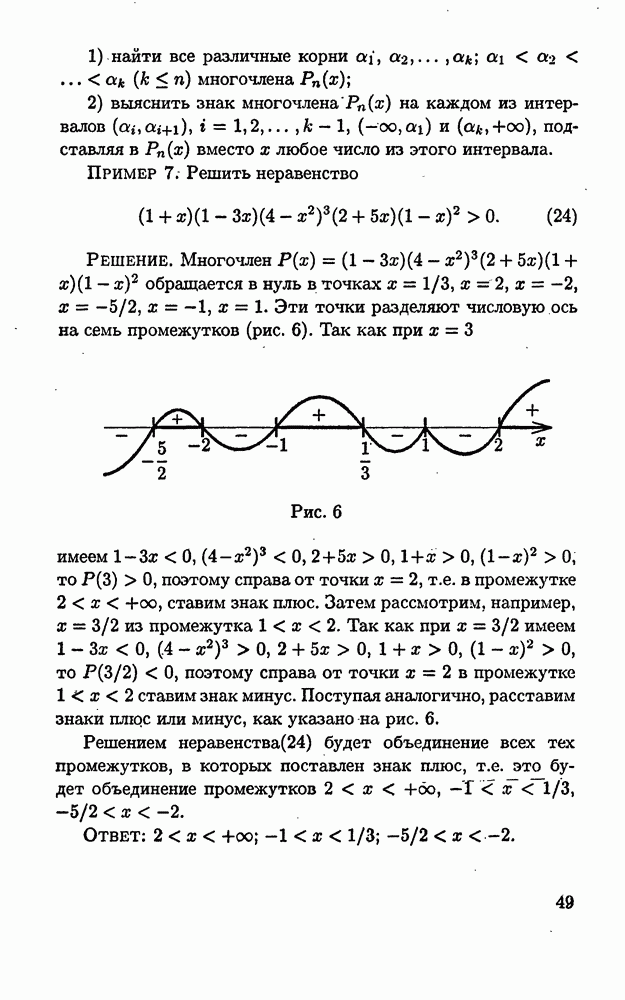
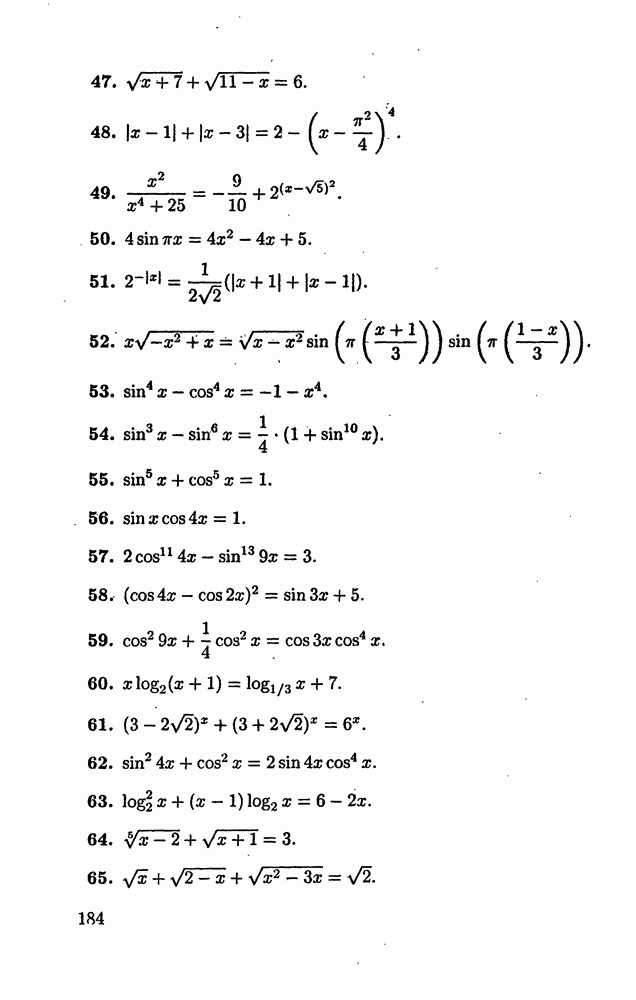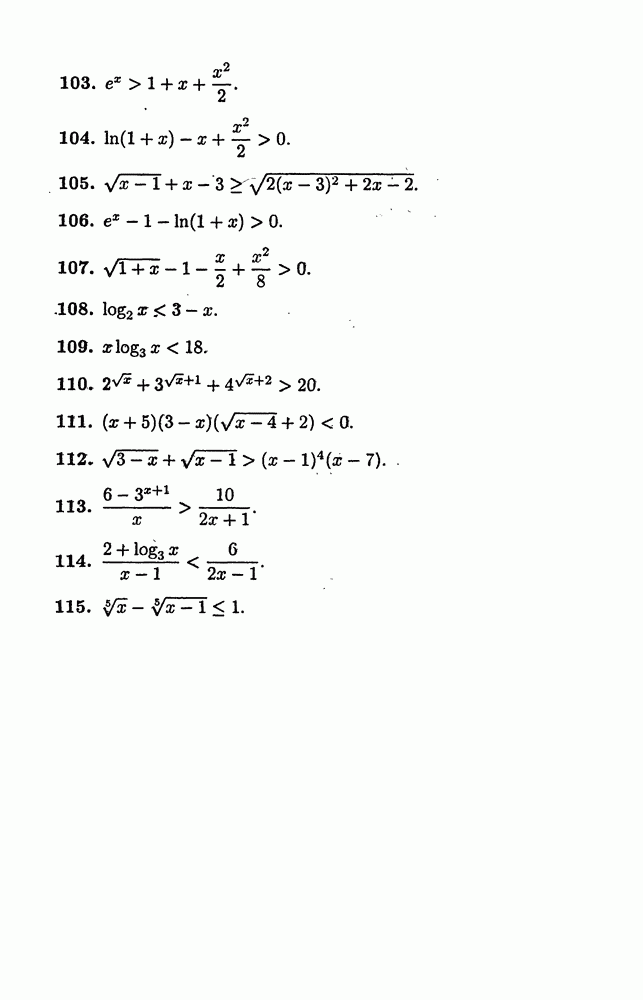| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
2.4.1. Раскрытие знаков модулей.
Основной метод решения уравнений и неравенств, содержащих модули, состоит в следующем: надо разбить ОДЗ уравнения или неравенства на множества, на каждом из которых каждое из выражений, находящихся под знаком модуля, сохраняет знак. На каждом таком множестве уравнение или неравенство записывается без знака модуля и затем решается на этом множестве. Объединение решений, найденных на всех этих множествах - частях ОДЗ уравнения или неравенства, составляет множество всех его решений.
Пример 1. Решить уравнение

Решение. ОДЗ уравнения состоит из всех действительных х. Разобьем ОДЗ на два промежутка:

а) Пусть  тогда
тогда  и уравнение (1) запишется на этом множетве так:
и уравнение (1) запишется на этом множетве так:

Это уравнение превращается в верное числовое равенство для любого действительного  т.е. его решениями являются все действительные х. Из них условию
т.е. его решениями являются все действительные х. Из них условию  удовлетворяют все х из промежутка
удовлетворяют все х из промежутка  Они и являются решениями уравнения (1) в случае а).
Они и являются решениями уравнения (1) в случае а).
б) Пусть  тогда
тогда  уравнение (1) запишется на этом множетве так:
уравнение (1) запишется на этом множетве так:

или

Решения этого уравнения есть  Из этих значений условию
Из этих значений условию  удовлетворяют только
удовлетворяют только  Итак, решения уравнения (1) есть
Итак, решения уравнения (1) есть  и все
и все  из промежутка
из промежутка 
Ответ: 
Пример 2. Решить неравенство

Решение. ОДЗ неравенства состоит из всех х, удовлетворяющих условию  Так как функции
Так как функции  меняют знак на области
меняют знак на области  проходя через точку
проходя через точку  то разобьем ОДЗ на два промежутка:
то разобьем ОДЗ на два промежутка: 
а) Если  то
то  Поэтому неравенство (3) запишется для этих
Поэтому неравенство (3) запишется для этих  в виде
в виде

т. е.

Решения этого неравенства есть  Все эти
Все эти  удовлетворяют условию
удовлетворяют условию  значит, являются решениями исходного неравенства (3).
значит, являются решениями исходного неравенства (3).
б) Если  то
то  Поэтому неравенство (3) перепишется в виде
Поэтому неравенство (3) перепишется в виде

т.е. в виде  Решения этого неравенства составляют два промежутка:
Решения этого неравенства составляют два промежутка: 
Из этих  условию
условию  удовлетворяют все
удовлетворяют все  из промежутка
из промежутка  поэтому все они являются решениями неравенства (3). Множеством всех решений исходного
поэтому все они являются решениями неравенства (3). Множеством всех решений исходного
неравенства (3) будет объединение решений, найденных в случаях а) и б).
Ответ: 
2.4.2. Уравнения вида
Уравнение

можно решать основным методом. Однако в некоторых случаях полезно уравнение (4) решать следующим образом:
1. Найти ту часть ОДЗ уравнения (4), где 
2. На этой области уравнение (4) равносильно совокупности двух уравнений

Решения этой совокупности, принадлежащие рассматриваемой области, и дадут решение уравнения (4).
Пример 3. Решить уравнение

Решение. ОДЗ этого уравнения есть все действительные х. Очевидно, что на ОДЗ, т.е. для любого действительного х,

Поэтому уравнение (5) равносильно совокупности уравнений

и

Первое уравнение решений не имеет, а второе равносильно уравнению  имеющему единственный корень
имеющему единственный корень 
Ответ: 
2.4.3. Неравенства вида
Неравенство

можно решать основным способом. Однако, иногда бывает полезно заменить неравенство (6) равносильной ему системой неравенств

Пример 4. Решить неравенство

Решение. Данное неравенство равносильно системе неравенств

которую можно переписать в виде

Решения первого неравенства системы (8) составляют промежуток  решения второго составляют промежуток
решения второго составляют промежуток  Следовательно, решения системы неравенств (8), а значит, и исходного неравенства (7) составляют промежуток
Следовательно, решения системы неравенств (8), а значит, и исходного неравенства (7) составляют промежуток 
Ответ: 
2.4.4. Неравенства вида
Неравенство

можно решать основным способом. Однако иногда бывает полезно разбить ОДЗ неравенства (9) на две части иначе, а именно:
1. Найти область, где  Все х из этой области дают решение неравенства (9).
Все х из этой области дают решение неравенства (9).
2. Найти область, где  и на ней рассмотреть неравенство
и на ней рассмотреть неравенство

Объединение найденных решений и дает все решения неравенства (9).
Пример 5. Решить неравенство

Решение. ОДЗ неравенства (10) состоит из всех действительных 
а) Найдем те х, для которых

Перепишем неравенство (11) в виде

Ясно, что никакое х из промежутка  не является решением неравенства (12). Пусть
не является решением неравенства (12). Пусть  для этих х неравенство (12) равносильно неравенству
для этих х неравенство (12) равносильно неравенству

Решения неравенства (13) составляют два промежутка:  . Из этих х условию
. Из этих х условию  удовлетворяют лишь х из промежутка —
удовлетворяют лишь х из промежутка — 
Следовательно, решениями неравенства (11) являются все  из промежутка
из промежутка  все эти х являются решениями исходного неравенства (10).
все эти х являются решениями исходного неравенства (10).
б) Теперь на множестве  рассмотрим неравенство
рассмотрим неравенство

Неравенство (14) можно переписать в виде

Ясно, что  не есть решение неравенства (15). Для любого
не есть решение неравенства (15). Для любого  левая часть неравенства (15) отрицательна, а правая положительна, следовательно, среди
левая часть неравенства (15) отрицательна, а правая положительна, следовательно, среди  нет решений неравенства (15). Для любого
нет решений неравенства (15). Для любого  левая часть неравенства (15) положительна, а правая отрицательна, следовательно, любое из этих а? является решением неравенства (15).
левая часть неравенства (15) положительна, а правая отрицательна, следовательно, любое из этих а? является решением неравенства (15).
Из этих х в множество  входят все х из промежутка
входят все х из промежутка  Все они являются решениями исходного неравенства (10).
Все они являются решениями исходного неравенства (10).
Объединяя решения, найденные в пунктах а) и б), получаем решения исходного неравенства.
Ответ:  .
.
2.4.5. Уравнения и неравенства вида
Уравнение

и неравенство

можно решать согласно общему методу. Однако иногда бывает полезно заменить уравнение (16) уравнением  т.е. уравнением
т.е. уравнением  равносильным ему на его ОДЗ, а неравенство (17) неравенством
равносильным ему на его ОДЗ, а неравенство (17) неравенством 
 т. е. неравенством
т. е. неравенством  равносильным ему на его ОДЗ.
равносильным ему на его ОДЗ.
Пример 6. Решить неравенство

Решение. ОДЗ этого неравенства есть все действительные х. Неравенство (18) равносильно неравенству

которое можно переписать в виде  Решением этого неравенства является любое действительное х кроме
Решением этого неравенства является любое действительное х кроме  В самом деле, для любого
В самом деле, для любого  принадлежащего промежутку
принадлежащего промежутку  , имеем
, имеем  поэтому
поэтому  для любого такого х. Для любого
для любого такого х. Для любого  принадлежащего промежутку
принадлежащего промежутку  имеем
имеем  поэтому
поэтому  В силу четности функции
В силу четности функции  получаем, что все
получаем, что все  также являются решениями неравенства. Очевидно, что
также являются решениями неравенства. Очевидно, что  неравенству не удовлетворяет.
неравенству не удовлетворяет.
Ответ: 
Пример 7. Решить уравнение

Решение. ОДЗ уравнения (19) есть все действительные  Возведя обе части уравнения в квадрат, получим уравнение
Возведя обе части уравнения в квадрат, получим уравнение

равносильное исходному. Это уравнение можно переписать в виде  откуда следует, что оно равносильно совокупности уравнений
откуда следует, что оно равносильно совокупности уравнений

и

Так как  и дискриминант квадратного трехчлена
и дискриминант квадратного трехчлена  отрицателен, то уравнение (20) имеет единственный корень
отрицателен, то уравнение (20) имеет единственный корень  Поскольку
Поскольку  то решения уравнения (21) есть
то решения уравнения (21) есть 
Итак, исходное уравнение имеет четыре корня: 
Ответ: 
2.4.6. Использование свойств абсолютной величины.
При решении уравнений и неравенств с модулем иногда бывает полезно решать их не по основному методу, а применять различные свойства абсолютных величин действительных чисел.
Пример 8. Решить уравнение

Решение. Обозначим  через а и
через а и  через
через  Тогда уравнение (22) можно записать в виде
Тогда уравнение (22) можно записать в виде

Из свойств абсолютной величины вытекает, что равенство (23) возможно тогда и только тогда, Когда одновременно  Поэтому исходное уравнение (22) равносильно системе неравенств
Поэтому исходное уравнение (22) равносильно системе неравенств

Решение этой системы неравенств, а значит, и исходного уравнения есть 
Ответ: 
Пример 9. Решить уравнение

Решение. ОДЗ уравнения (24) есть все  кроме
кроме  Поскольку для любого х из ОДЗ
Поскольку для любого х из ОДЗ

то уравнение (24) можно переписать так:

Обозначим  через а и
через а и  через
через  тогда уравнение
тогда уравнение

(25) можно переписать так:

Из свойств абсолютной величины вытекает, что равенство (26) имеет место тогда и только тогда, когда

Это означает, что решения уравнения (24) совпадают с реше ниями неравенства
Решениями неравенства (27), а значит, и исходного уравнения, являются  и все х из промежутка
и все х из промежутка 
Ответ: 
Пример 10. Решить неравенство

Решение. Для любого  имеем
имеем  поэтому
поэтому  а это означает, что ни одно из
а это означает, что ни одно из  не является решением неравенства (28).
не является решением неравенства (28).
Для любого  имеем
имеем  ипоэтому
ипоэтому  а это означает, что ни одно
а это означает, что ни одно  также не является решением неравенства (28).
также не является решением неравенства (28).
Для любого х из промежутка  имеем
имеем  поэтому
поэтому  Следовательно,
Следовательно,  а это означает, что ни одно х из промежутка
а это означает, что ни одно х из промежутка  не является решением неравенства (28).
не является решением неравенства (28).
Итак, неравенство (28) не имеет решений.
Ответ: решений нет.
Задачи
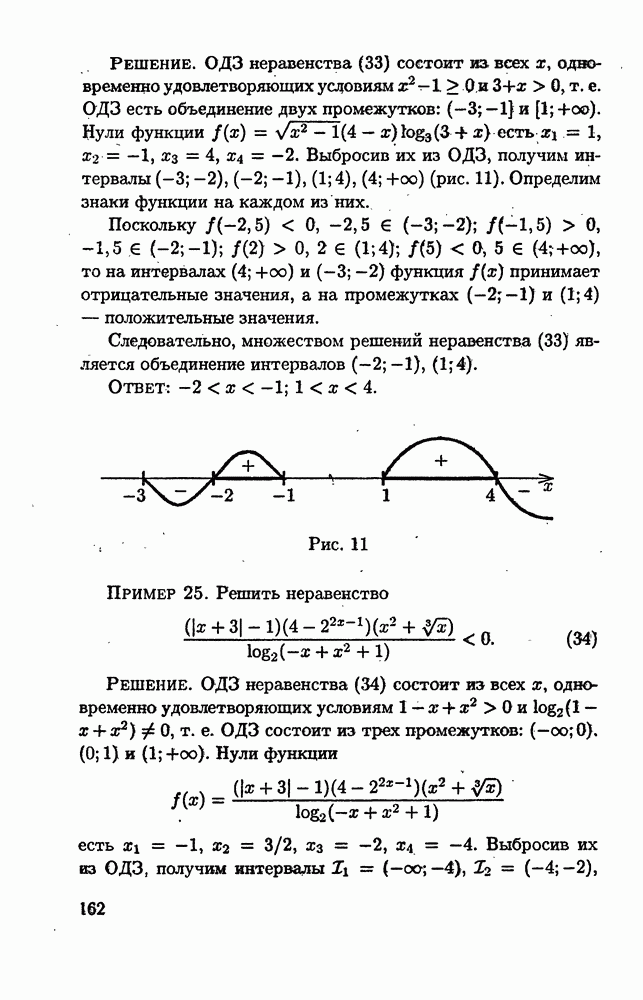
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.