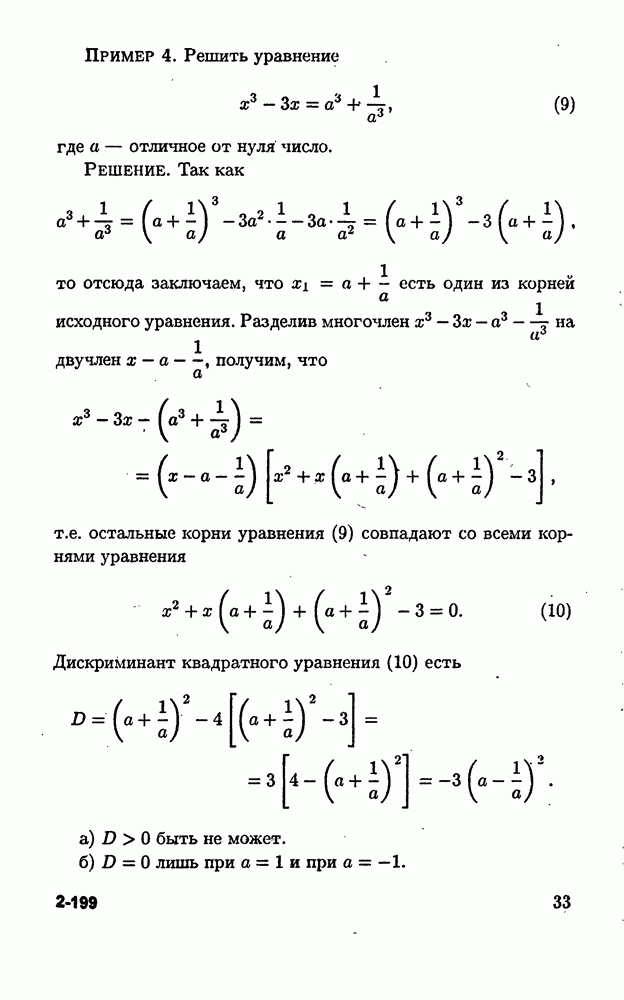| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.2. Простейшие способы решения алгебраических уравнений
В случае  уравнение (I) обычно записывается в виде
уравнение (I) обычно записывается в виде

и называется уравнением первой степени. Уравнение (1) имеет единственный корень 
В случае  уравнение (I) обычно записывается в виде
уравнение (I) обычно записывается в виде

и называется квадратным уравнением.
Хорошо известно, что если дискриминант  квадратного трехчлена
квадратного трехчлена  с:
с:
а) отрицателен, то уравнение (2) не имеет корней;
 положителен, то уравнение (2) имеет два различных корня
положителен, то уравнение (2) имеет два различных корня

в) равен нулю, то уравнение (2) имеет единственный кореш»  Иногда в этом случае говорят, что уравнение (2) имеет два совпадающих корня
Иногда в этом случае говорят, что уравнение (2) имеет два совпадающих корня  Легко видеть, что они также отыскиваются по формулам (3).
Легко видеть, что они также отыскиваются по формулам (3).
При  существуют формулы для нахождения корней алгебраических уравнений третьей и четвертой степеней, однако в силу их громоздкости они применяются редко.
существуют формулы для нахождения корней алгебраических уравнений третьей и четвертой степеней, однако в силу их громоздкости они применяются редко.
В общем случае не существует формул для нахождения корней любого алгебраического уравнения более высокой степени, чем четыре. Тем не менее достаточно часто приходится решать алгебраические уравнения степени большей, чем два.
Если многочлен  записан в виде произведения многочленов первой и второй степени, то уравнение
записан в виде произведения многочленов первой и второй степени, то уравнение  равносильно
равносильно
совокупности соответствующих уравнений первой и второй степени, формулы решения которых приведены выше.
Пример 1. Решить уравнение

Решение. Данное уравнение равносильно совокупности уравнений  Решение первого из этих уравнений есть
Решение первого из этих уравнений есть  Решения второго уравнения есть
Решения второго уравнения есть  Следовательно, решения исходного уравнения есть
Следовательно, решения исходного уравнения есть 
Ответ: 
Если многочлен  имеет степень большую, чем 2, и не разложен на множители первой и второй степени, то его сначала надо каким-либо способом разложить на такие множители, а затем заменить уравнение
имеет степень большую, чем 2, и не разложен на множители первой и второй степени, то его сначала надо каким-либо способом разложить на такие множители, а затем заменить уравнение  равносильной ему совокупностью уравнений.
равносильной ему совокупностью уравнений.
Приведем решения некоторых алгебраических уравнений  основанныена разложении его левой части — многочлена
основанныена разложении его левой части — многочлена  — на множители методами, изложеннными в предыдущем параграфе.
— на множители методами, изложеннными в предыдущем параграфе.
ПРИМЕР 2. Решить уравнение

Решение. Поскольку

то данное уравнение равносильно совокупности двух уравнений

Второе уравнение этой совокупности решений не имеет, решения первого есть  Эти числа и являются решениями уравнения (4).
Эти числа и являются решениями уравнения (4).
Отвшч 
Пример 3. Решить уравнение

Решение. Будем искать многчлены  такие, что справедливо тождественное равенство
такие, что справедливо тождественное равенство

Тогда, приравнивал коэффициенты при одинаковых степенях неизвестного х в левой и правой частях этого равенства, имеем систему равенств

Этой системе равенств удовлетворяют числа  Поэтому справедливо разложение многочлена на множители:
Поэтому справедливо разложение многочлена на множители:

откуда следует, что исходное уравнение равносильно совокупности уравнений

Эта совокупность имеет единственное решение  Ответ:
Ответ: 
Пример 4. Решить уравнение

Решение. Поскольку коэффициенты многочлена — целые числа и старший коэффициент равен 1, то рациональные корни многочлена, если они есть, могут быть только среди чисел
 . Легко проверить, что
. Легко проверить, что  есть корень многочлена. Значит, данный многочлен делится на
есть корень многочлена. Значит, данный многочлен делится на  Произведем деление многочлена
Произведем деление многочлена  на двучлен
на двучлен  “столбиком”:
“столбиком”:

Следовательно,  и исходное уравнение равносильно совокупности уравнений
и исходное уравнение равносильно совокупности уравнений  откуда получаем, что решения исходного уравнения есть
откуда получаем, что решения исходного уравнения есть 
Ответ: 
Пример 5. Решить уравнение

Решение. Обозначим  и рассмотрим уравнение с параметром:
и рассмотрим уравнение с параметром: 
Рассматривая это уравнение как квадратное относительно а, разложим его левую часть на множители

Значит, уравнение (5) равносильно совокупности уравнений

Множество решений первого уравнения есть

Множество решений второго уравнения есть

Следовательно, исходное уравнение имеет четыре корня: 
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
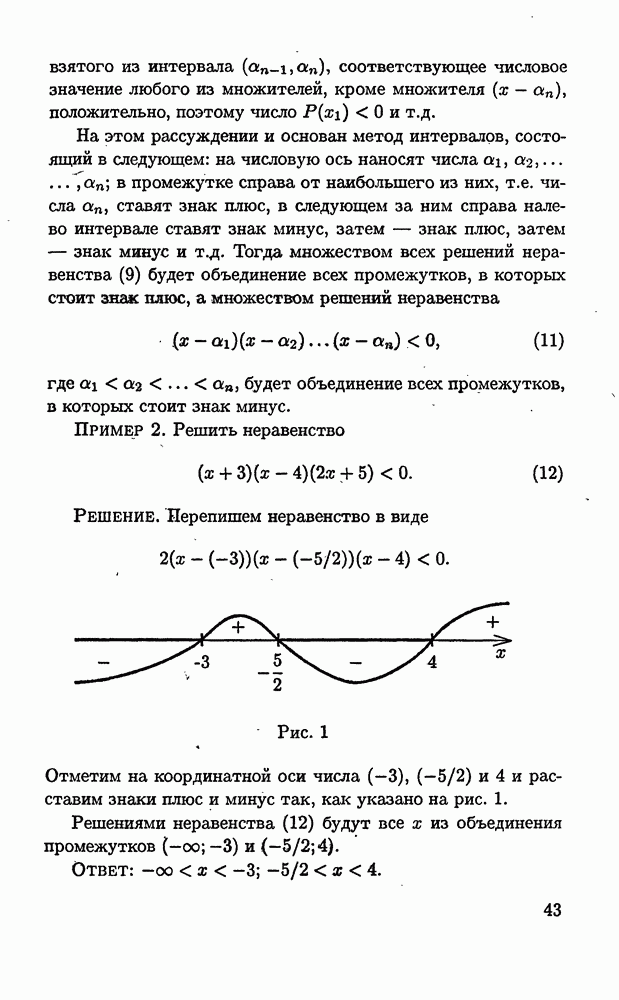
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.