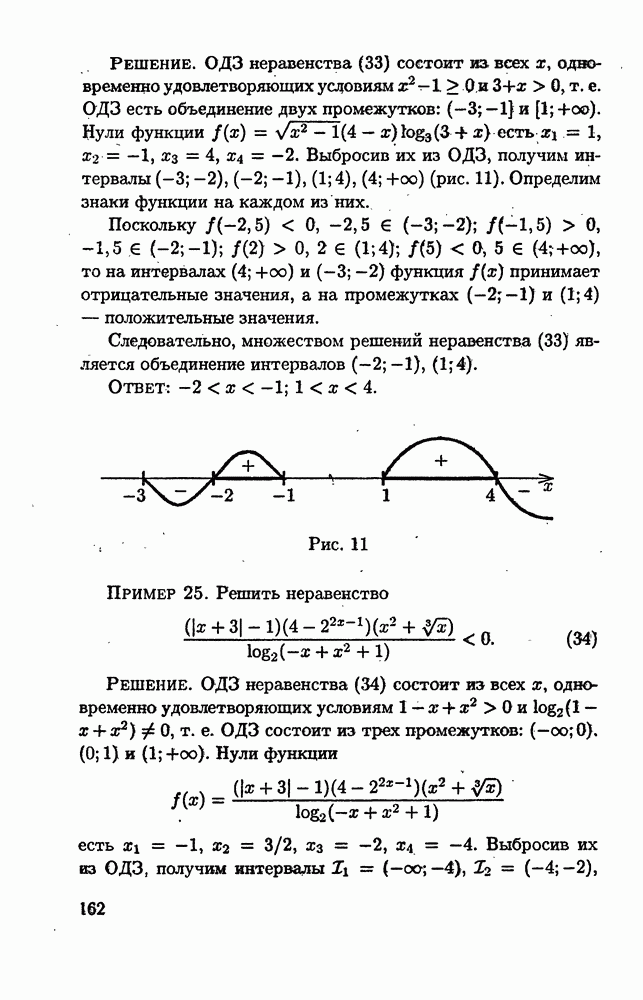
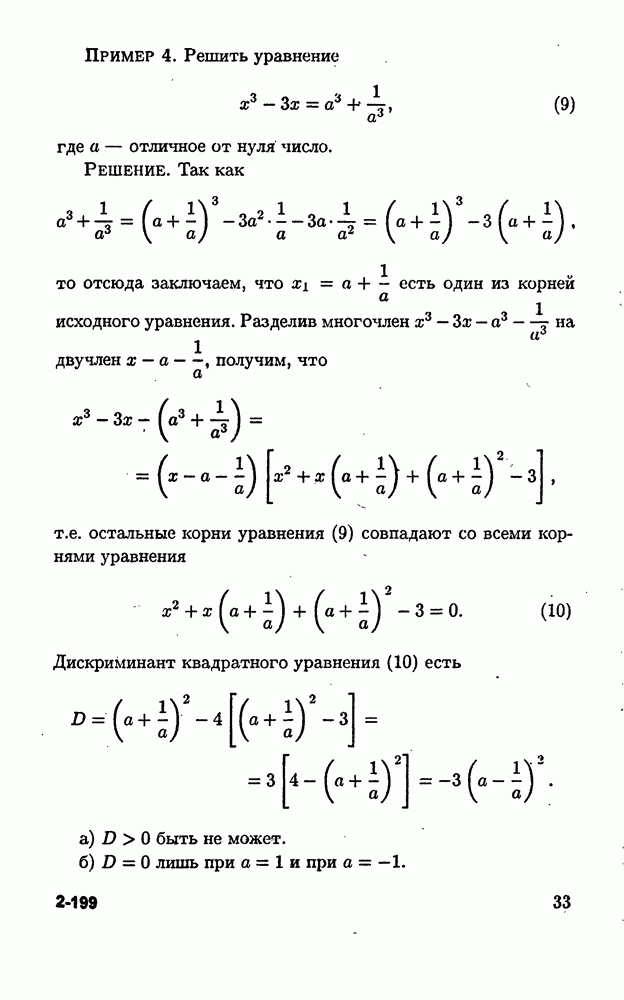| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.4. Некоторые искусственные способы решения алгебраических уравнений
В этом параграфе будут приведены некоторые нестан дартные способы решения; алгебраических уравнений.
1.4.1. Умножение уравнения на функцию.
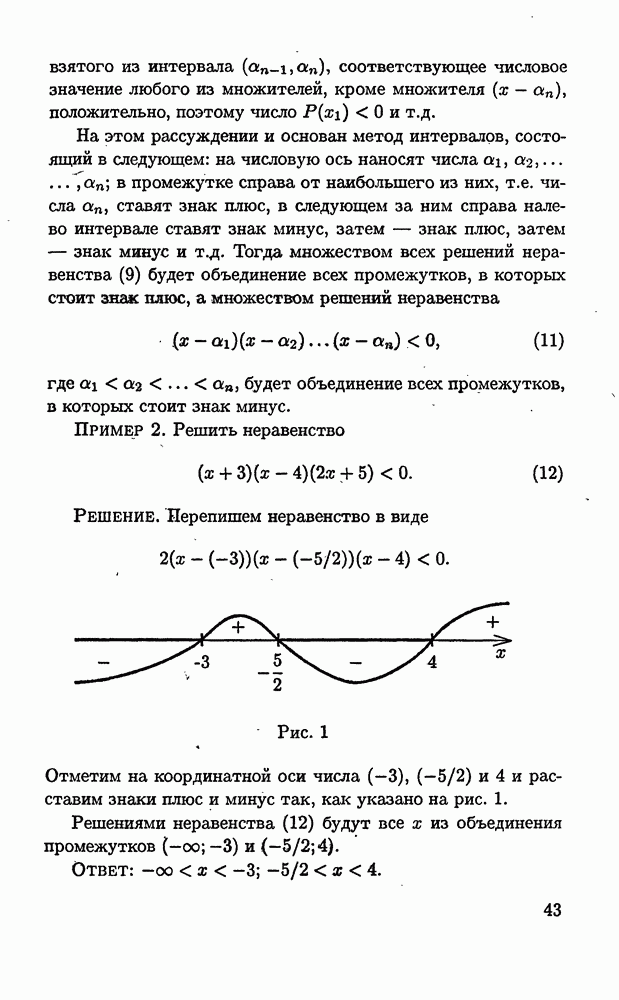
Иногда решение алгебраического уравнения существенно облегчается, если умножить обе его части на некоторую функцию - многочлен от неизвестной. При этом надо помнить, что возможно появление лишних корней - корней многочлена, на который умножали уравнение. Поэтому надо либо умножать на многочлен, не имеющий корней, и получать равносильное уравнение, либо умножать на многочлен, имеющий корни, и тогда каждый из таких корней надо обязательно подставить в исходное уравнение и установить, является ли это число его корнем. Пример 1. Решить уравнение

Решение:. Умножив обе части уравнения на многочлен  не имеющий корней, получим уравнение
не имеющий корней, получим уравнение

равносильное уравнению (1). Уравнение (2) можно записать в виде

Ясно, что уравнение (3) не имеет действительных корней, поэтому и уравнение (1) их не имеет.
Ответ: нет решений.
Пример 2. Решить уравнение

Решение. Умножив обе части уравнения на многочлен  получим уравнение
получим уравнение

являющееся следствием уравнения (4), так как уравнение (5) имеет корень  не являющийся корнем уравнения (4).
не являющийся корнем уравнения (4).
Уравнение  есть симметрическое уравнение четвертой степени. Поскольку
есть симметрическое уравнение четвертой степени. Поскольку  не является корнем уравнения (5), то разделив обе его части на
не является корнем уравнения (5), то разделив обе его части на  и перегруппировав его члены, получим уравнение равносильное уравнению (5). Обозначив
и перегруппировав его члены, получим уравнение равносильное уравнению (5). Обозначив  перепишем
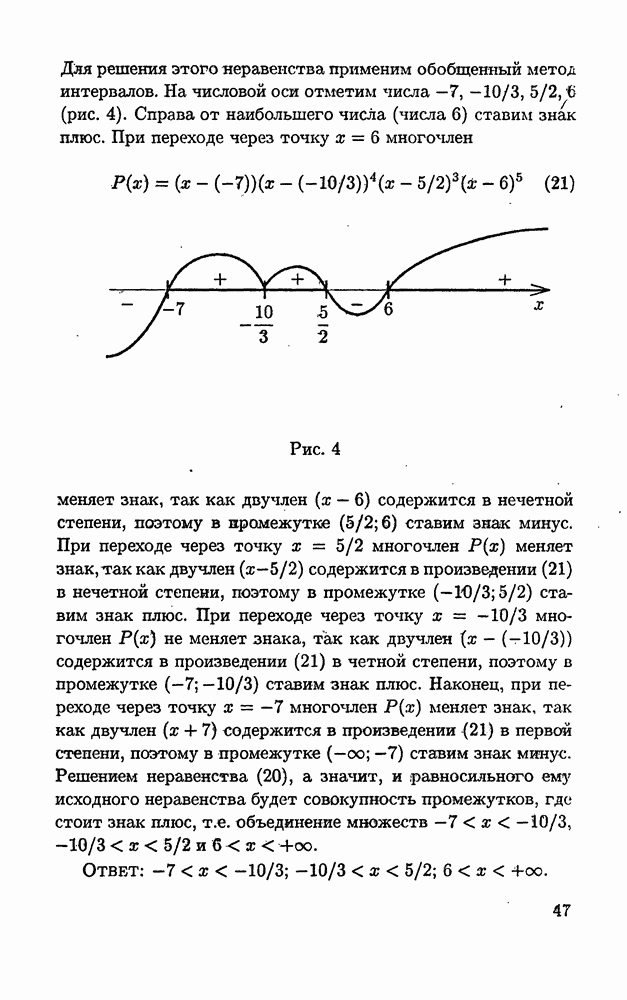
перепишем

уравнение (6) в виде

Уравнение (7) имеет два корня:  Поэтому уравнение (6) равносильно совокупности уравнений
Поэтому уравнение (6) равносильно совокупности уравнений

Решив каждое из этих уравнений, найдем четыре корня уравнения (6), а тем самым и уравнения 

Так как корень  является посторонним для уравнения (4). то отсюда получаем, что уравнение (4) имеет три корня:
является посторонним для уравнения (4). то отсюда получаем, что уравнение (4) имеет три корня: 
ОТВЕТ 
Замечание. Прием, рассмотренный в примере 2, можно применять к уравнениям, которые после умножения на некоторый многочлен превращаются в возвратные или симметрические уравнения.
Например, таким образом можно решать уравнения вида

где  с
с  . В самом деле умножив это уравнение на многочлен
. В самом деле умножив это уравнение на многочлен  получим симметрическое уравнение четвертой степени, среди корней которого содержится и корень
получим симметрическое уравнение четвертой степени, среди корней которого содержится и корень  Отметим, что этот корень может быть посторонним корнем для уравнения (8).
Отметим, что этот корень может быть посторонним корнем для уравнения (8).
1.4.2. Угадывание корня уравнения.
Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения..
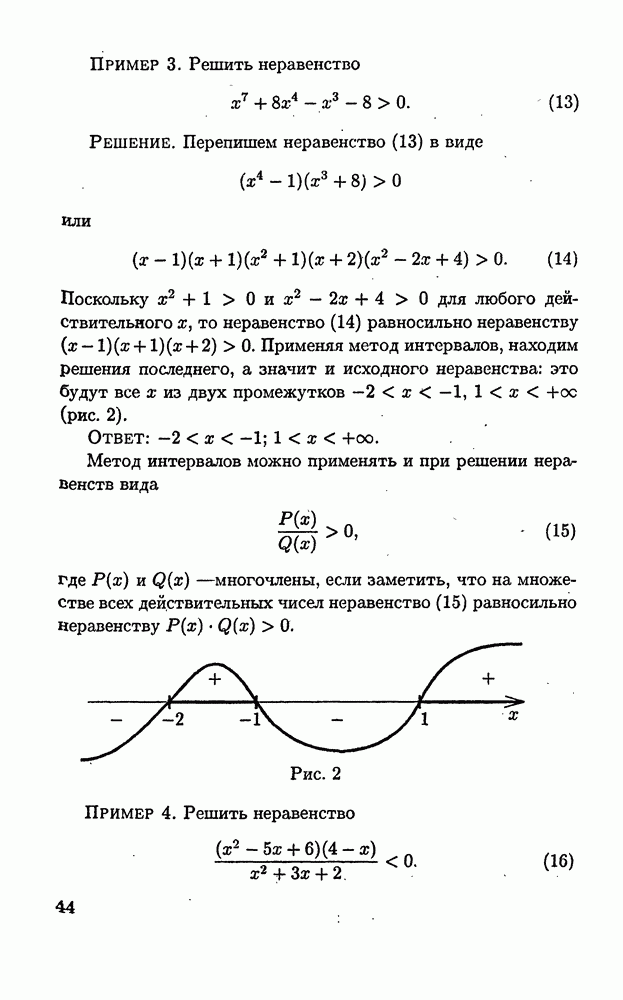
Пример 3. Решить уравнение

Решение. Из внешнего вида этого уравнения очевидно, что  есть его корень. Для нахождения остальных корней преобразуем многочлен
есть его корень. Для нахождения остальных корней преобразуем многочлен

Так как многочлен  не имеет корней, то исходное уравнение имеет единственный корень
не имеет корней, то исходное уравнение имеет единственный корень 
Ответ: 
Пример 4. Решить уравнение

где а — отличное от нуля число.
Решение. Так как

то отсюда заключаем, что  есть один из корней исходного уравнения. Разделив многочлен
есть один из корней исходного уравнения. Разделив многочлен  на двучлен
на двучлен  получим, что
получим, что

т.е. остальные корни уравнения (9) совпадают со всеми корнями уравнения

Дискриминант квадратного уравнения (10) есть

а) D > 0 быть не может.
б)  лишь при
лишь при 
Итак, уравнение (10) не имеет корней при  имеет единственный корень
имеет единственный корень  при
при  и единственный корень
и единственный корень  при
при  Добавляя еще один корень
Добавляя еще один корень  находим все корни исходного уравнения.
находим все корни исходного уравнения.
Ответ: при  два корня
два корня 
при  два корня
два корня 
при  один корень
один корень 
Пример 5. Решить уравнение

где  — данные числа.
— данные числа.
Решение. Из внешнего вида уравнения очевидно, что  является корнем.
является корнем.
Для нахождения остальных корней уравнения перенесем все его члены в одну сторону и разложим полученный многочлен на множители. Тогда получим, что уравнение (11) можно записать в виде

Уравнение (12) равносильно совокупности уравнений

Первое уравнение совокупности  имеет единственный корень
имеет единственный корень  а второе уравнение имеет решения в зависимости от дискриминанта:
а второе уравнение имеет решения в зависимости от дискриминанта:
а) если  то будет два корня,
то будет два корня,
б) если  то будет один корень,
то будет один корень,
в) если  то корней лет.
то корней лет.
Отсюда легко находятся корни уравнения (11).
Ответ: при 
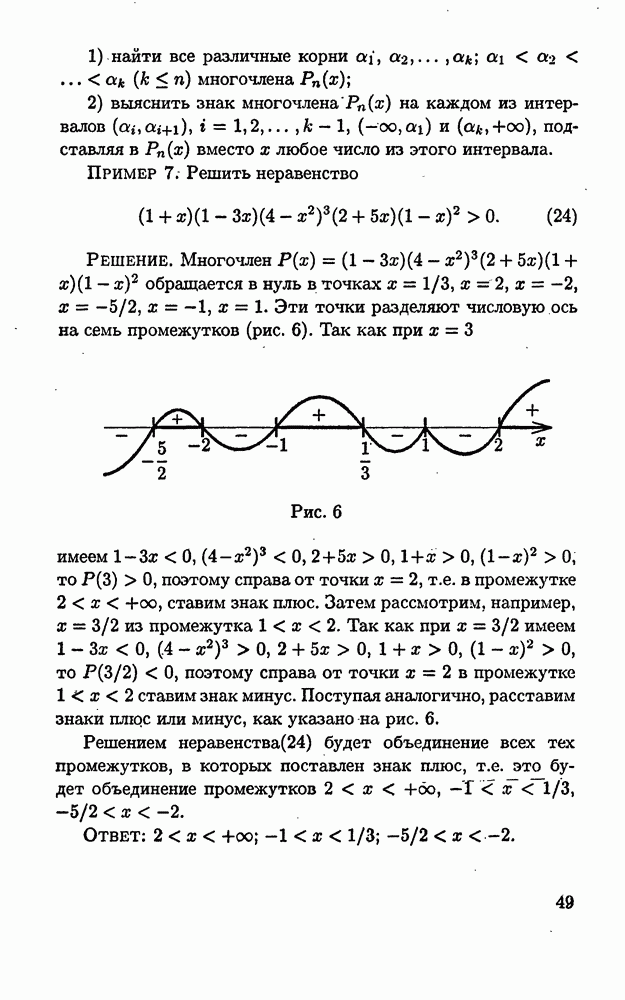
Пример 6. Решить уравнение

Решение. Легко заметить, что  являются решениями этого уравнения. После раскрытия скобок это уравнение перепишется как квадратное. А это означает, что оно может иметь не более двух корней. Так как два корня этого уравнения найдены, то тем самым оно и решена.
являются решениями этого уравнения. После раскрытия скобок это уравнение перепишется как квадратное. А это означает, что оно может иметь не более двух корней. Так как два корня этого уравнения найдены, то тем самым оно и решена.
Ответ: 
1.4.3. Использование симметричности уравнения.
Иногда внешний вид уравнения — некоторая его симметричность — подсказывает способ решения уравнения.
Пример 7. Решить уравнение

Решение. Очевидно, что внешний вид уравнения подсказывает. что один из корней уравнения (14) есть  Однако для нахождения остальных корней этого уравнения прием, предложенный а предыдущем пункте (разложение многочлена на множители), здесь мало поможет. Перепишем уравнение (14) в несколько ином виде.
Однако для нахождения остальных корней этого уравнения прием, предложенный а предыдущем пункте (разложение многочлена на множители), здесь мало поможет. Перепишем уравнение (14) в несколько ином виде.
Поскольку справедливы тождественные равенства

то уравнение (14) молено переписать так:

Теперь очевидно, что если  — корень уравнения (15), то
— корень уравнения (15), то  также корень уравнения (15), поскольку
также корень уравнения (15), поскольку

Покажем, что если  есть корень уравнения (14), то
есть корень уравнения (14), то  также есть корень этого уравнения.
также есть корень этого уравнения. 
Действительно, так как

то отсюда и вытекает это утверждение.
Итак, если  — корень уравнения (14), то оно имеет еще корни
— корень уравнения (14), то оно имеет еще корни

т.е. уравнение (14) имеет корни

Поскольку уравнение (14) есть алгебраическое уравнение шестой степени, то оно имеет не более шести корней. Таким образом, мы нашли все корни уравнения (14).
Ответ: 
1.4.4. Использование суперпозиции функций.
Иногда можно найти корень уравнения, если заметить, что функция, находящаяся в одной из частей уравнения, является суперпозицией некоторых более простых функций.
Пример 8. Решить уравнение

Решение. Обозначим  , тогда уравнение (16) можно переписать в виде
, тогда уравнение (16) можно переписать в виде  Теперь очевидно, что если
Теперь очевидно, что если  — корень уравнения
— корень уравнения  то
то  и корень уравнения
и корень уравнения  Корни уравнения
Корни уравнения  есть
есть  Следовательно, и уравнение (16) имеет эти корни. Переписав уравнение (16) в виде
Следовательно, и уравнение (16) имеет эти корни. Переписав уравнение (16) в виде

и разделив многочлен  на многочлен
на многочлен  получим, что уравнение (17) можно записать в виде
получим, что уравнение (17) можно записать в виде  Следовательно, корнями уравнения (16) наряду с
Следовательно, корнями уравнения (16) наряду с  являются также корни уравнения
являются также корни уравнения  т.е. числа
т.е. числа 
Ответ: 
1.4.5 Исследование уравнения на промежутках действительной оси.
Иногда решения уравнения можно найти, исследуя его на разных числовых промежутках. Пример 9. Решить уравнение

Решение. Перепишем уравнение в виде  или, используя формулу разности
или, используя формулу разности

в виде

Отсюда видно, что один из корней данного уравнения есть  Докажем, что уравнение
Докажем, что уравнение

решений не имеет.
Разобьем числовую ось на промежутки 
Для любого х из промежутка  имеем, что левая часть уравнения (19) положительна, поэтому на этом промежутке уравнение решений не имеет.
имеем, что левая часть уравнения (19) положительна, поэтому на этом промежутке уравнение решений не имеет.
Поскольку

то для любого х из промужутка  этот многочлен положителен. Это означает, что на промежутке
этот многочлен положителен. Это означает, что на промежутке  уравнение (19) также не имеет решений.
уравнение (19) также не имеет решений.
Поскольку

то для любого х из промежутка  этот многочлен по ложителен. Следовательно, и на промежутке
этот многочлен по ложителен. Следовательно, и на промежутке  уравнение (19) не имеет решений.
уравнение (19) не имеет решений.
Итак, данное уравнение (19) имеет единственное решение 
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
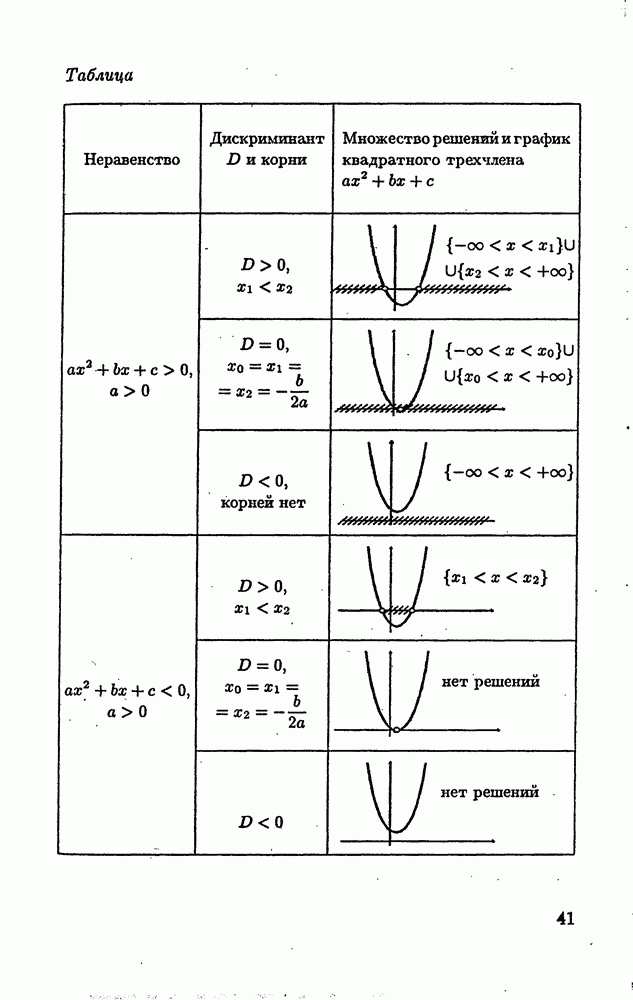
- § 1.5. Решение алгебраических неравенств
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.