| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Расстояние как интеграл
Обсудим теперь обратную проблему. Пусть вместо таблицы
расстояний нам дана таблица скоростей в различные моменты времени, начиная с
нуля. В табл. 8.4 представлена зависимость скорости падающего шара от времени.
Аналогичную таблицу можно составить и для машины, если записывать показания
спидометра через каждую минуту или полминуты. Но можно ли, зная скорость машины
в любой момент времени, вычислить расстояние, которое ею было пройдено? Эта
задача обратна той, которую мы только что рассмотрели. Как же решить ее, если
скорость машины непостоянна, если она то ускоряется до ![]() , то замедляется, затем
где-то останавливается у светофора и т.д.? Сделать это нетрудно. Нужно
использовать ту же идею и выражать полное расстояние через бесконечно малые его
части. Пусть в первую секунду скорость будет
, то замедляется, затем
где-то останавливается у светофора и т.д.? Сделать это нетрудно. Нужно
использовать ту же идею и выражать полное расстояние через бесконечно малые его
части. Пусть в первую секунду скорость будет ![]() , тогда по формуле
, тогда по формуле ![]() можно вычислить
расстояние, пройденное за эту секунду. В следующую секунду скорость будет
несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние,
пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на
интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца
пути. В результате мы получим много маленьких отрезков, которые в сумме дадут
весь путь. Таким образом, путь является суммой скоростей, умноженных на
отдельные интервалы времени, или
можно вычислить
расстояние, пройденное за эту секунду. В следующую секунду скорость будет
несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние,
пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на
интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца
пути. В результате мы получим много маленьких отрезков, которые в сумме дадут
весь путь. Таким образом, путь является суммой скоростей, умноженных на
отдельные интервалы времени, или ![]() , где греческая буква
, где греческая буква ![]() (сигма) означает
суммирование. Точнее, это будет сумма скоростей в некоторые моменты времени,
скажем
(сигма) означает
суммирование. Точнее, это будет сумма скоростей в некоторые моменты времени,
скажем ![]() умноженные
на
умноженные
на ![]() :
:
![]() , (8.6)
, (8.6)
причем каждый последующий момент ![]() находится по правилу
находится по правилу ![]() . Но расстояние, полученное этим методом, не будет точным, поскольку
скорость за время
. Но расстояние, полученное этим методом, не будет точным, поскольку
скорость за время ![]() все же изменяется. Выход из этого
положения заключается в том, чтобы брать все меньшие и меньшие интервалы
все же изменяется. Выход из этого
положения заключается в том, чтобы брать все меньшие и меньшие интервалы ![]() , т. е. разбивать
время движения на все большее число все меньших отрезков. В конце концов мы
придем к следующему, теперь уже точному выражению для пройденного пути:
, т. е. разбивать
время движения на все большее число все меньших отрезков. В конце концов мы
придем к следующему, теперь уже точному выражению для пройденного пути:
![]() . (8.7)
. (8.7)
Таблица 8.4 Скорость падающего шара
|
|
|
|
0 |
0 |
|
1 |
10 |
|
2 |
20 |
|
3 |
30 |
|
4 |
40 |
Математики придумали для этого предела, как и для дифференциала,
специальный символ. Значок ![]() превращается в
превращается в ![]() , напоминая о том, что интервал
времени сколь угодно мал, а знак суммирования превращается в
, напоминая о том, что интервал
времени сколь угодно мал, а знак суммирования превращается в ![]() — искаженное большое
— искаженное большое
![]() , первая
буква латинского слова «Summa». Этот значок назван интегралом.
Таким образом, мы пишем
, первая
буква латинского слова «Summa». Этот значок назван интегралом.
Таким образом, мы пишем
![]() , (8.8)
, (8.8)
где ![]() — скорость в момент
— скорость в момент ![]() . Сама же операция
суммирования этих членов называется интегрированием. Она противоположна
операции дифференцирования в том смысле, что производная этого интеграла равна
. Сама же операция
суммирования этих членов называется интегрированием. Она противоположна
операции дифференцирования в том смысле, что производная этого интеграла равна ![]() , так что один
оператор
, так что один
оператор ![]() «уничтожает»
другой (
«уничтожает»
другой (![]() ).
Это дает возможность получать формулы для интегралов путем обращения формул для
дифференциалов: интеграл от функции, стоящей в правой колонке табл.8.3, будет
равен функции, стоящей в левой колонке. Дифференцируя все виды функций, вы сами
можете составить таблицу интегралов.
).
Это дает возможность получать формулы для интегралов путем обращения формул для
дифференциалов: интеграл от функции, стоящей в правой колонке табл.8.3, будет
равен функции, стоящей в левой колонке. Дифференцируя все виды функций, вы сами
можете составить таблицу интегралов.
Любая функция, заданная в аналитическом виде, т. е. выражающаяся через комбинацию известных нам функций, дифференцируется очень просто — вся операция выполняется чисто алгебраически, и в результате мы всегда получаем какую-то известную функцию. Однако интеграл не от всякой функции можно записать в аналитическом виде. Разумеется, для каждого частного интеграла всегда сначала пытаются найти такую функцию, которая, будучи продифференцирована, давала бы функцию, стоящую после знака интеграла (она называется подынтегральной). Однако это не всегда удается сделать. В таких случаях интеграл вычисляют просто суммированием, т. е. вычисляют суммы типа (8.6) со все меньшими и меньшими интервалами, пока не получат результате достаточной точностью.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
- § 3. Случайные блуждания
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
- § 5. Численное решение уравнений
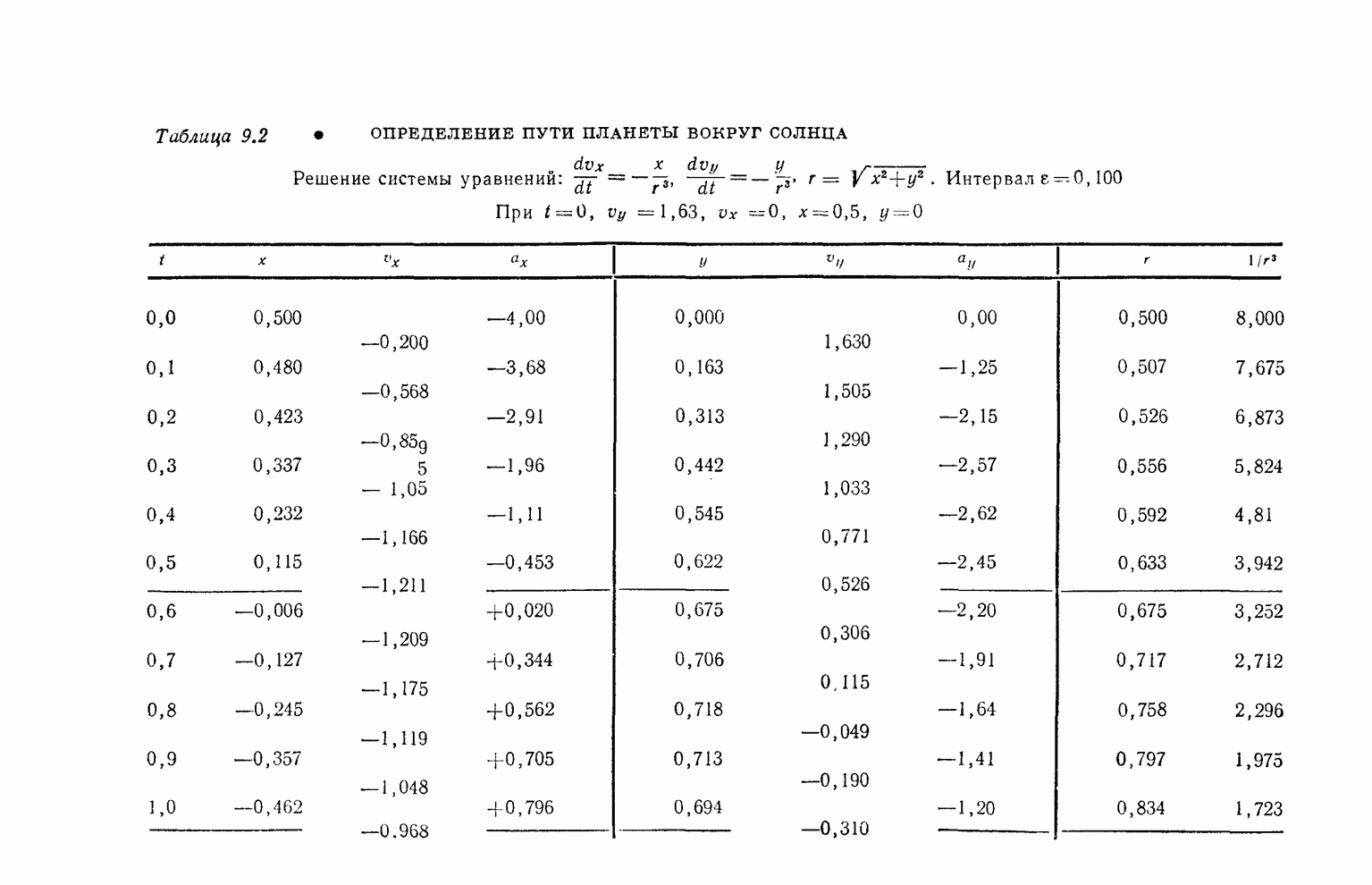
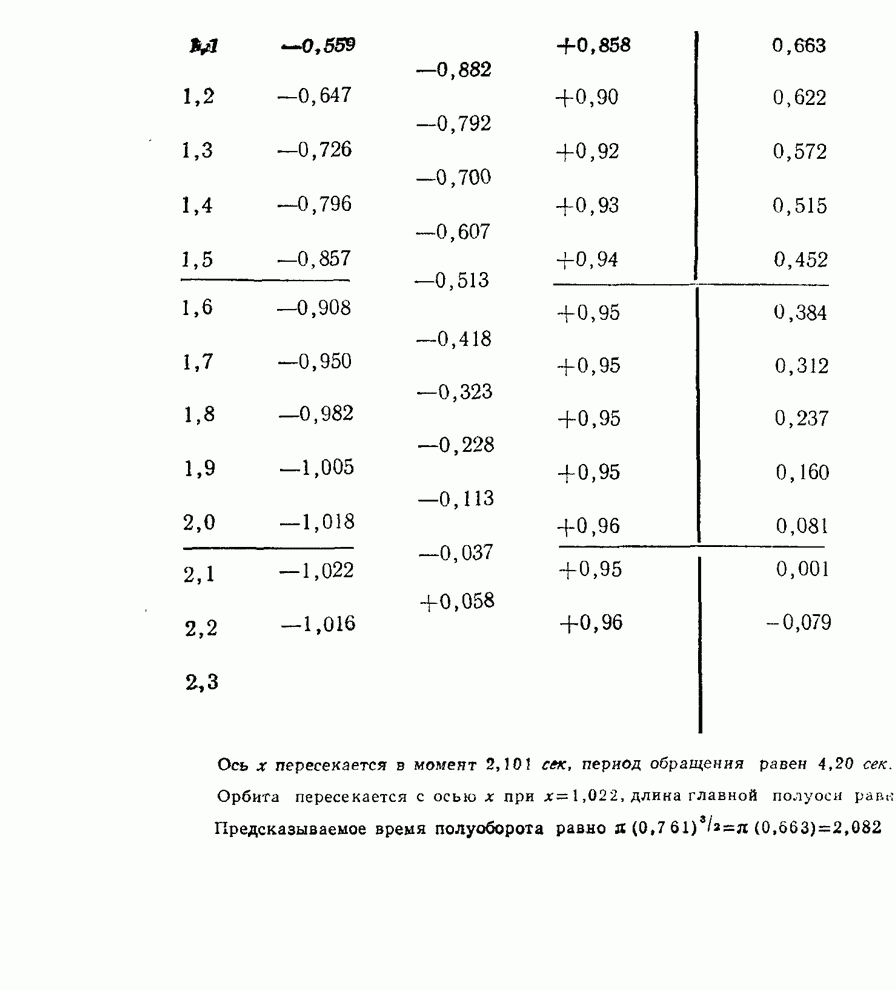
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля