| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Скорость
Хотя мы примерно представляем себе, что такое
«скорость», однако здесь есть одна очень важная тонкость. Заметьте, что древние
греки так и не смогли до конца разобраться в проблеме скорости. Тонкость, о
которой идет речь, дает себя знать, когда пытаешься точно определить, что же
подразумевается под понятием «скорость». Этот вопрос был камнем преткновения
для древних греков, и потребовалось открытие новой области математики, помимо
геометрии и алгебры, которые были известны и грекам, и арабам, и вавилонянам.
Попробуйте-ка с помощью одной лишь алгебры решить следующую задачу. Воздушный
шар надувается таким образом, что его объем увеличивается со скоростью ![]() . С какой
скоростью увеличивается его радиус, когда объем шара достигает
. С какой
скоростью увеличивается его радиус, когда объем шара достигает ![]() ? Задачи такого
рода были неразрешимы для древних греков. Кроме того, их сбивали с толку
многочисленные «парадоксы». Вот один из них, придуманный Зеноном, который
хорошо показывает, насколько была сложна в то время проблема скорости движения.
«Предположим,— говорит он, — что Ахиллес бегает в десять раз быстрее черепахи.
Но тем не менее он никогда не перегонит ее. Действительно, пусть в начале состязания
черепаха находилась в 100метрах впереди Ахиллеса. Тогда ко времени, когда
Ахиллес пробежит эти 100метров, черепаха окажется в 10метрах впереди него.
Пробежав и эти 10метров, Ахиллес увидит черепаху в 1метре впереди себя. За то
время, пока он пробежит этот метр, черепаха пройдет 10сантиметров и так далее
до бесконечности. Следовательно, в любой момент черепаха будет впереди
Ахиллеса, и он никогда не сможет перегнать ее». В чем здесь ошибка? Конечный
интервал времени можно разделить на бесконечное число частей точно так же, как
и конечный отрезок длины, если последовательно делить его пополам. Но бесконечное
число этапов до того места, где Ахиллес поравняется с черепахой, вовсе не
означает бесконечное количество времени. Этот пример хорошо показывает, с
какими трудностями приходилось сталкиваться в проблеме определения скорости.
? Задачи такого
рода были неразрешимы для древних греков. Кроме того, их сбивали с толку
многочисленные «парадоксы». Вот один из них, придуманный Зеноном, который
хорошо показывает, насколько была сложна в то время проблема скорости движения.
«Предположим,— говорит он, — что Ахиллес бегает в десять раз быстрее черепахи.
Но тем не менее он никогда не перегонит ее. Действительно, пусть в начале состязания
черепаха находилась в 100метрах впереди Ахиллеса. Тогда ко времени, когда
Ахиллес пробежит эти 100метров, черепаха окажется в 10метрах впереди него.
Пробежав и эти 10метров, Ахиллес увидит черепаху в 1метре впереди себя. За то
время, пока он пробежит этот метр, черепаха пройдет 10сантиметров и так далее
до бесконечности. Следовательно, в любой момент черепаха будет впереди
Ахиллеса, и он никогда не сможет перегнать ее». В чем здесь ошибка? Конечный
интервал времени можно разделить на бесконечное число частей точно так же, как
и конечный отрезок длины, если последовательно делить его пополам. Но бесконечное
число этапов до того места, где Ахиллес поравняется с черепахой, вовсе не
означает бесконечное количество времени. Этот пример хорошо показывает, с
какими трудностями приходилось сталкиваться в проблеме определения скорости.
Чтобы еще яснее представить себе эти трудности, вспомним старую шутку, которую вы наверняка слышали. Вы помните, что автомобиль, о котором мы говорили в начале этой лекции, был остановлен полицейским. Он подходит к машине и говорит: «Мадам (ибо за рулем была женщина), Вы нарушили правила уличного движения. Вы ехали со скоростью 90 километров в час». Женщина отвечает: «Простите, это невозможно. Как я могла делать 90 километров в час, если я еду всего лишь 7 минут!» Как бы вы ответили на месте полицейского? Конечно, если вы действительно настоящий полицейский, то такими хитростями вас не запутаешь. Вы бы твердо сказали: «Мадам, оправдываться будете перед судьей!» Но предположим, что у вас нет такого выхода. Вы хотите честно доказать нарушительнице ее вину и пытаетесь объяснить ей, что означает скорость 90 км/час. Как это сделать? Вы скажете: «Я имел в виду, мадам, что если бы вы продолжали ехать таким же образом, то через час Вы бы проехали 90 километров». «Да, но я ведь затормозила и остановила машину,— может ответить она,— так что теперь-то я уж никак не могла бы проехать 90километров в час».
Аналогичная проблема возникает и в случае падающего шарика. Предположим, что мы хотим определить его скорость через 3 сек, если бы он двигался таким же образом. Но что означает «двигался таким же образом»? Сохранял бы ускорение, двигался быстрее, что ли? Конечно, нет! Сохранял бы ту же самую скорость. Но ведь это как раз то, что мы пытаемся определить! Если бы шарик продолжал двигаться «таким же образом», то он падал бы так же, как падает. Так что нужно придумать что-то лучшее для определения скорости. Что же все-таки должно сохраняться? Нарушительница могла бы вам еще ответить и так: «Если бы я продолжала ехать, как ехала, еще час, то налетела бы на стену в конце улицы!» В общем, как видите, полицейский оказался бы в очень трудном положении, пытаясь объяснить, что он имел в виду.
Многие физики думают, что единственным определением
любого понятия является способ его измерения. Но тогда при объяснении вы должны
прибегнуть к прибору, измеряющему скорость. «Смотрите,— скажете вы в этом
случае, — ваш спидометр показывает 60». «Мой спидометр сломан и давно не работает»,—
ответит она. Но достаточно ли этого, чтобы поверить, что машина не двигалась?
Мы полагаем, что как-то нужно было бы определять скорость и без помощи спидометра.
Только при этих условиях можно сказать, что спидометр не работает, что он
сломан. Это было бы абсурдным, если бы скорость не имела смысла без спидометра.
Очевидно, что понятие «скорость» не зависит от спидометра. Спидометр нужен
только для того, чтобы измерять се. Давайте посмотрим, нельзя ли придумать лучшее
определение понятия «скорость». Вы скажете: «Разумеется, мадам, если бы вы
ехали таким же образом в течение часа, то налетели бы на стену, но за 1 секунду
вы бы проехали 25 метров, так что вы делали 25 метров в секунду, и если бы продолжали ехать таким же образом, то в следующую секунду опять
проехали бы 25 метров, а стена стоит гораздо дальше». «По правила запрещают
делать 90 километров в час, а не 25 метров в секунду». «Да ведь это то же самое, что и 90 километров в час»,— ответите вы. А если это то же самое, то к чему
тогда все длинные разговоры о ![]() ? В действительности же падающий шар
не может двигаться одинаковым образом даже 1 сек, так как он постоянно ускоряется,
и, следовательно, нужно определить скорость как-то точнее.
? В действительности же падающий шар
не может двигаться одинаковым образом даже 1 сек, так как он постоянно ускоряется,
и, следовательно, нужно определить скорость как-то точнее.
Но теперь мы, кажется, находимся на правильном пути, который
приводит нас вот к чему. Если бы машина продолжала двигаться таким же образом
следующую тысячную долю часа, то она прошла бы тысячную долю 90 км. Другими словами, нет никакой необходимости ехать целый час с той же быстротой, достаточно
какого-то момента. Это означает, что за какой-то момент времени машина проходит
такое же расстояние, как я идущая с постоянной скоростью 90 им час. Наши рассуждении
о ![]() , возможно,
и правильные; мы отмечаем, сколько машина прошла в следующую секунду, и если
получается расстояние 25 .и, то это означает, что скорость достигает
, возможно,
и правильные; мы отмечаем, сколько машина прошла в следующую секунду, и если
получается расстояние 25 .и, то это означает, что скорость достигает ![]() .
.
Другими словами, можно определить скорость следующим образом. Определяем расстояние, которое было пройдено за очень малый отрезок времени, и, разделив его на этот отрезок времени, получаем скорость. Однако этот отрезок должен быть как можно меньше, и чем меньше, тем лучше, потому что в этот период могут произойти снова изменения. Смешно, например, для падающего тела в качестве такого отрезка принять час. Принять в качестве отрезка секунду, может быть, удобно для автомобиля, так как за секунду его скорость изменяется не слишком сильно, но этот отрезок велик для падающего тела. Таким образом, чтобы вычислить скорость более точно, нужно брать все меньшие и меньшие интервалы времени. Если на миллионную долю секунды мы разделим расстояние, которое было пройдено в течение этого времени, то получим расстояние в секунду, т. е. как раз то, что мы понимаем под скоростью. Именно это нужно было сказать нашей нарушительнице, т. е. дать то определение скорости, которое мы и будем использовать.
Такое определение содержит некую новую идею, которая была недоступна грекам в ее общей форме.
Она заключается в том, чтобы малые расстояния разделить
на соответствующие малые отрезки времени и посмотреть, что произойдет с
частным, если отрезок времени брать все меньше и меньше (иными словами, брать
предел отношения пройденного расстояния к интервалу времени при неограниченном
уменьшении последнего). Впервые эта идея была высказана независимо Ньютоном и
Лейбницсм и явилась основой новой области математики — дифференциального
исчисления. Оно возникло в связи с описанием движения, и первым его приложением
был ответ па вопрос: «Что означает ![]() ?»
?»
Попытаемся теперь точнее определить скорость. Пусть за
некоторое малое время ![]() машина или какое-то другое тело
прошли малое расстояние
машина или какое-то другое тело
прошли малое расстояние ![]() ; тогда скорость
; тогда скорость ![]() определяется как
определяется как
![]() ,
,
причем точность будет тем больше, чем меньше ![]() . Математики
записывают это следующим образом:
. Математики
записывают это следующим образом:
![]() , (8.3)
, (8.3)
т. е. скорость есть предел отношения ![]() при
при ![]() , стремящемся к нулю. Для
нашей машины-нарушительницы невозможно точно вычислить скорость, так как
таблица неполная. Ее положение известно нам только через интервалы 1 мин. Приближенно,
конечно, можно сказать, что в течение седьмой минуты, например, она шла со средней
скоростью
, стремящемся к нулю. Для
нашей машины-нарушительницы невозможно точно вычислить скорость, так как
таблица неполная. Ее положение известно нам только через интервалы 1 мин. Приближенно,
конечно, можно сказать, что в течение седьмой минуты, например, она шла со средней
скоростью ![]() ,
однако о ее скорости в конце шестой минуты ничего сказать невозможно. Может
быть, она ускорялась и скорость с
,
однако о ее скорости в конце шестой минуты ничего сказать невозможно. Может
быть, она ускорялась и скорость с ![]() в начале шестой минуты возросла до
в начале шестой минуты возросла до ![]() в конце ее, а
может быть, она двигалась иначе. Мы не знаем этого точно, так как у нас нет
детальной записи ее движения между шестой и седьмой минутами. Только когда
таблица будет пополнена бесконечным числом данных, из нее можно будет
действительно вычислить скорость. Если, однако, нам известна полная
математическая формула, как, например, в случае падающего тела [уравнение
(8.1)], то можно подсчитать скорость. Ведь по формуле можно найти положение
тела в любой момент времени.
в конце ее, а
может быть, она двигалась иначе. Мы не знаем этого точно, так как у нас нет
детальной записи ее движения между шестой и седьмой минутами. Только когда
таблица будет пополнена бесконечным числом данных, из нее можно будет
действительно вычислить скорость. Если, однако, нам известна полная
математическая формула, как, например, в случае падающего тела [уравнение
(8.1)], то можно подсчитать скорость. Ведь по формуле можно найти положение
тела в любой момент времени.
В качестве примера давайте найдем скорость падающего
шара через ![]() после
начала падения. Один способ — это посмотреть по табл. 8.2, что происходило с
шариком на пятой секунде. В течение этой секунды он прошел
после
начала падения. Один способ — это посмотреть по табл. 8.2, что происходило с
шариком на пятой секунде. В течение этой секунды он прошел ![]() , так что, казалось бы, он
падал со скоростью
, так что, казалось бы, он
падал со скоростью ![]() . Однако это неверно, поскольку
скорость его все время изменялась. Конечно, в среднем в течение этой секунды
она составляла
. Однако это неверно, поскольку
скорость его все время изменялась. Конечно, в среднем в течение этой секунды
она составляла ![]() ,
но в действительности шар ускорялся и в конце пятой секунды падал быстрее
,
но в действительности шар ускорялся и в конце пятой секунды падал быстрее ![]() . Наша задача
состоит в том, чтобы определить скорость точно. Сделаем это следующим образом.
Нам известно, где шарик находился через
. Наша задача
состоит в том, чтобы определить скорость точно. Сделаем это следующим образом.
Нам известно, где шарик находился через ![]() . За
. За ![]() он прошел расстояние
он прошел расстояние ![]() . К моменту
. К моменту ![]() общее расстояние,
которое прошел шарик, составит, согласно уравнению (8.1),
общее расстояние,
которое прошел шарик, составит, согласно уравнению (8.1), ![]() . Таким образом, за
дополнительную десятую долю секунды он проходит
. Таким образом, за
дополнительную десятую долю секунды он проходит ![]() . А поскольку
. А поскольку ![]() за
за ![]() то же самое, что и
то же самое, что и ![]() , то это и будет
его скорость. Однако это все еще не совсем точно. Для нас совершенно неважно,
будет ли это скорость в момент
, то это и будет
его скорость. Однако это все еще не совсем точно. Для нас совершенно неважно,
будет ли это скорость в момент ![]() , или в момент
, или в момент ![]() , или где-то посредине.
Наша задача вычислить скорость точно через
, или где-то посредине.
Наша задача вычислить скорость точно через ![]() , а этого мы пока не сделали.
Придется улучшить точность и взять теперь на тысячную долю больше
, а этого мы пока не сделали.
Придется улучшить точность и взять теперь на тысячную долю больше ![]() , т. е. момент
, т. е. момент ![]() . Полное
расстояние, пройденное за это время, составляет
. Полное
расстояние, пройденное за это время, составляет
![]() .
.
Следовательно, в последнюю тысячную долю секунды шарик
проходит ![]() ,
и если разделить это число на
,
и если разделить это число на ![]() , то получим скорость
, то получим скорость ![]() . Это уже очень
близко, но все же еще не точно. Однако теперь уже ясно, как поступить, чтобы
найти скорость точно. Удобнее решать эту задачу в несколько более общем виде.
Пусть требуется найти скорость в некоторый момент времени
. Это уже очень
близко, но все же еще не точно. Однако теперь уже ясно, как поступить, чтобы
найти скорость точно. Удобнее решать эту задачу в несколько более общем виде.
Пусть требуется найти скорость в некоторый момент времени ![]() (например,
(например, ![]() ). Расстояние,
которое пройдено к моменту
). Расстояние,
которое пройдено к моменту ![]() (назовем его
(назовем его ![]() ), будет
), будет ![]() (в нашем случае
(в нашем случае ![]() ). Чтобы
определить расстояние, мы задавали вопрос: где окажется тело спустя время
). Чтобы
определить расстояние, мы задавали вопрос: где окажется тело спустя время ![]() (небольшой
добавок), или
(небольшой
добавок), или ![]() ?
Новое положение тела будет
?
Новое положение тела будет ![]() . (Это расстояние больше того
расстояния, которое шарик прошел за
. (Это расстояние больше того
расстояния, которое шарик прошел за ![]() сек, т. е. больше
сек, т. е. больше ![]() ). Назовем это
расстояние
). Назовем это
расстояние ![]() (небольшой
добавок), или
(небольшой
добавок), или ![]() .
Если теперь вычесть из него расстояние, пройденное к моменту
.
Если теперь вычесть из него расстояние, пройденное к моменту ![]() , то получим
, то получим ![]() — то дополнительное
расстояние, которое шарик прошел за добавочное время
— то дополнительное
расстояние, которое шарик прошел за добавочное время ![]() , т. е.
, т. е. ![]() . Так что в первом
приближении скорость будет равна
. Так что в первом
приближении скорость будет равна
![]() (8.4)
(8.4)
Теперь мы уже знаем, что нужно делать, чтобы получить
скорость точно в момент ![]() : нужно брать отрезок е все меньше и
меньше, т. е. устремлять его к нулю. Таким путем из уравнения (8.4) получим
: нужно брать отрезок е все меньше и
меньше, т. е. устремлять его к нулю. Таким путем из уравнения (8.4) получим
![]() .
.
В нашей задаче ![]() , следовательно, скорость равна
, следовательно, скорость равна ![]() . Это и есть
нужный ответ. Раньше, когда
. Это и есть
нужный ответ. Раньше, когда ![]() бралось равным 0,1 и
бралось равным 0,1 и ![]() , получалась
несколько большая величина, чем
, получалась
несколько большая величина, чем ![]() , но теперь мы видим, что в
действительности она в точности равна
, но теперь мы видим, что в
действительности она в точности равна ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
- § 3. Случайные блуждания
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
- § 5. Численное решение уравнений
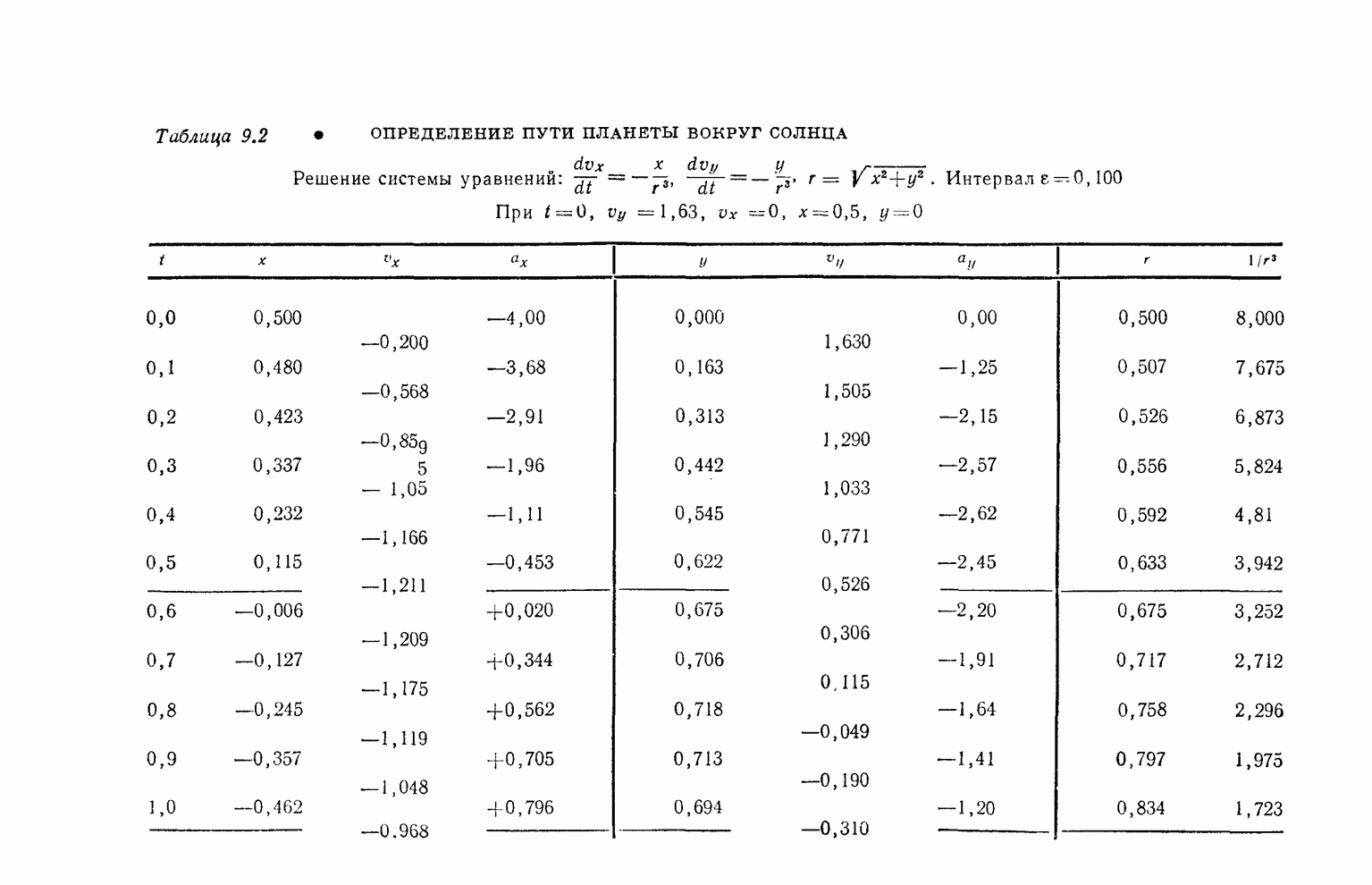
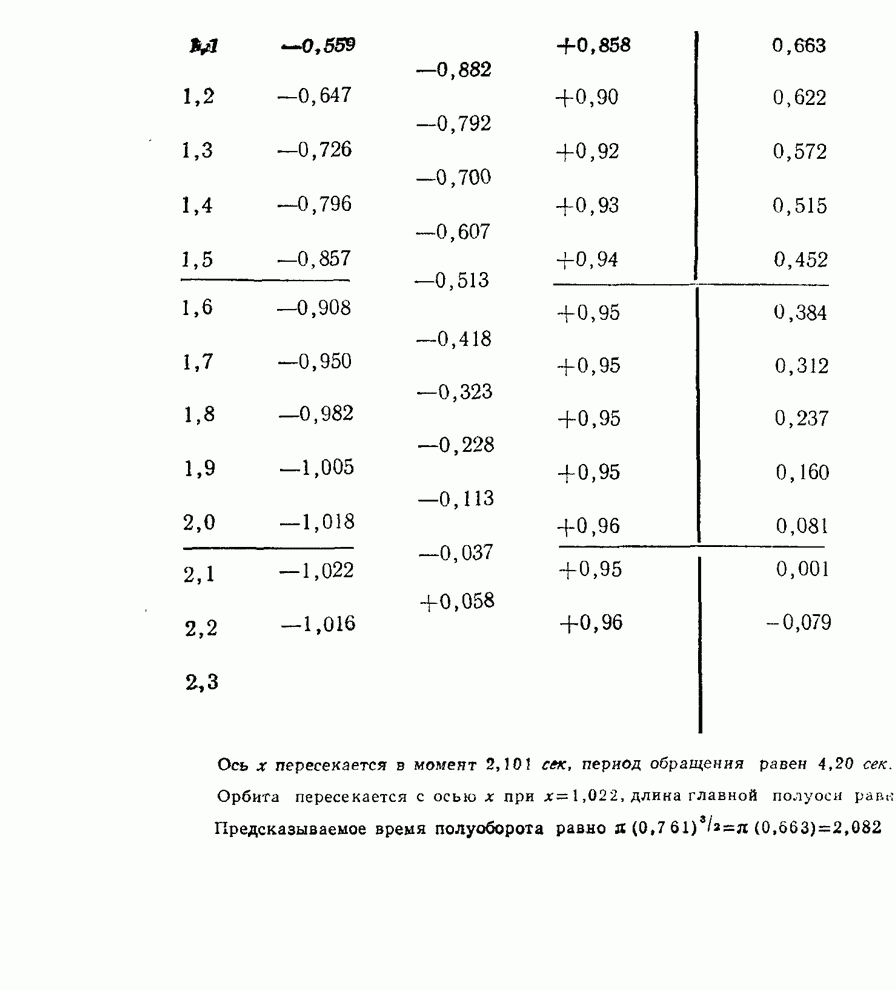
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля