| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Переносы начала
Мы ограничим наше рассмотрение законами механики, которую достаточно хорошо изучили. В предыдущих главах мы установили, что законы механики можно свести к трем справедливым для любой частицы уравнениям:
![]() (11.1)
(11.1)
Это
означает, что существует такой способ измерения расстояний ![]() и
и ![]() вдоль трех взаимно
перпендикулярных осей и сил вдоль этих направлений, при котором определяемые
уравнениями (11.1) законы верны. Расстояния должны отсчитываться от некоторого
начала, но где следует расположить это начало? Ньютон сказал нам только, что
такая точка, от которой можно начать отсчет, существует; может быть, это центр
Вселенной, и при измерении расстоянии от нее его законы верны. Но мы можем
немедленно показать, что незачем искать центр Вселенной, ибо безразлично, какую
точку взять за начало координат. Иными словами, предположим, что имеются два
человека — Джо, который выбрал начало своей системы координат в какой-то точке,
и Мик, который построил систему координат, параллельную первой, но принял за
начало другую точку (фиг. 11.1), расположенную на расстоянии
вдоль трех взаимно
перпендикулярных осей и сил вдоль этих направлений, при котором определяемые
уравнениями (11.1) законы верны. Расстояния должны отсчитываться от некоторого
начала, но где следует расположить это начало? Ньютон сказал нам только, что
такая точка, от которой можно начать отсчет, существует; может быть, это центр
Вселенной, и при измерении расстоянии от нее его законы верны. Но мы можем
немедленно показать, что незачем искать центр Вселенной, ибо безразлично, какую
точку взять за начало координат. Иными словами, предположим, что имеются два
человека — Джо, который выбрал начало своей системы координат в какой-то точке,
и Мик, который построил систему координат, параллельную первой, но принял за
начало другую точку (фиг. 11.1), расположенную на расстоянии ![]() по оси
по оси ![]() в его системе.
Когда Джо определяет положение произвольной точки в пространстве, он находит
три ее координаты:
в его системе.
Когда Джо определяет положение произвольной точки в пространстве, он находит
три ее координаты: ![]() и
и ![]() (обычно мы опускаем ось
(обычно мы опускаем ось ![]() , ибо ее трудно
изобразить на нашем чертеже). В системе Мика эта точка будет иметь другое
значение
, ибо ее трудно
изобразить на нашем чертеже). В системе Мика эта точка будет иметь другое
значение ![]() (чтобы
отличить его, введем обозначение
(чтобы
отличить его, введем обозначение ![]() ) и, вообще говоря, другое значение
) и, вообще говоря, другое значение ![]() хотя в нашем
примере они численно равны. Таким образом, мы имеем
хотя в нашем
примере они численно равны. Таким образом, мы имеем
![]() (11.2)
(11.2)

Фигура 11.1. Две параллельные координатные системы.
Чтобы
сделать наш анализ полным, нужно знать, какие силы измеряет Мик. Если сила
действует вдоль произвольной линии, то под силой вдоль направления ![]() мы понимаем
некоторую часть общей силы, которая равна произведению величины силы на косинус
угла между направлением силы и осью
мы понимаем
некоторую часть общей силы, которая равна произведению величины силы на косинус
угла между направлением силы и осью ![]() . Легко видеть, что Мик получит те же
проекции силы, какие получил Джо, т. е. мы имеем систему уравнений
. Легко видеть, что Мик получит те же
проекции силы, какие получил Джо, т. е. мы имеем систему уравнений
![]() (11.3)
(11.3)
Уравнения (11.2) и (11.3) определяют соотношения между величинами, используемыми Джо и Миком.
Теперь поставим вопрос так: если Джо знает законы Ньютона, то будут ли они верны, когда их попробует использовать Мик? Имеет ли значение выбор начала координат? Другими словами, предположим, что уравнения (11.1) верны, а (11.2) и (11.3) определяют соотношения между измеряемыми величинами; верно ли, что
 (11.4а)
(11.4а)
 (11.4б)
(11.4б)
 (11.4в)
(11.4в)
Чтобы
проверить эти уравнения, дважды продифференцируем выражение для ![]() по времени.
Прежде всего
по времени.
Прежде всего
![]()
Предположим
теперь, что начало системы координат, которой пользуется Мик, фиксировано (не
движется) относительно системы координат Джо, т. е. ![]() постоянна и
постоянна и ![]() ; таким образом,
получаем
; таким образом,
получаем
![]()
и, следовательно,
![]()
Если предположить, что измеряемые Джо и Миком массы равны, то уравнение (11.4а) принимает вид
![]()
Таким
образом, произведения массы на ускорение одинаковы у обоих друзей. Можно
получить и формулу для ![]() Использовав (11.1), мы обнаружим
Использовав (11.1), мы обнаружим
![]()
Следовательно, законы механики, с точки зрения Мика, точно такие же: он пишет законы Ньютона в других координатах, и эти законы оказываются верными. Это означает, что центра Вселенной нет и законы движения выглядят одинаково, с какого бы места они ни наблюдались.
Верно и такое утверждение: если в каком-либо месте установить устройство с каким-то механизмом, то и в любом другом месте это устройство будет работать одинаково. Почему? Потому что любая машина, которую изучает Мик, подчиняется тем же уравнениям, которые описывают работу машины, контролируемой Джо. Поскольку уравнения одинаковы, то и явления одни и те же. Таким образом, доказательство того, что аппарат в новом месте будет работать так же, как на прежнем, сводится к доказательству, что отнесенные к новой точке пространства уравнения воспроизводят себя. Поэтому мы говорим, что законы физики симметричны относительно перемещений в пространстве, симметричны в том смысле, что законы не изменяются при перемещениях начала системы координат. Конечно, каждый интуитивно знает, что это верно, но интересно и полезно обсудить математику этого явления.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
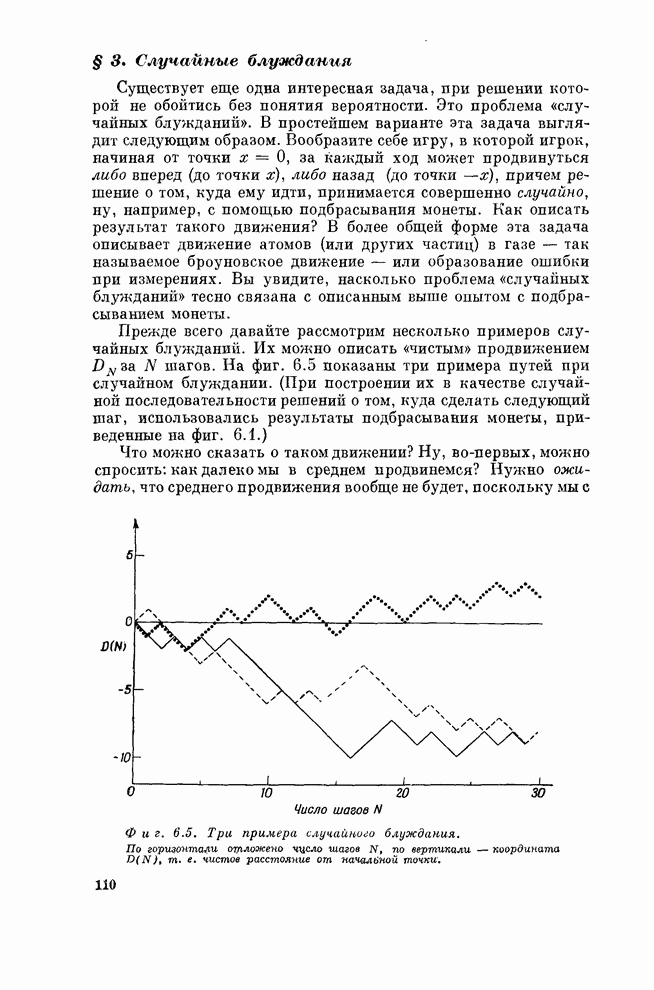
- § 3. Случайные блуждания
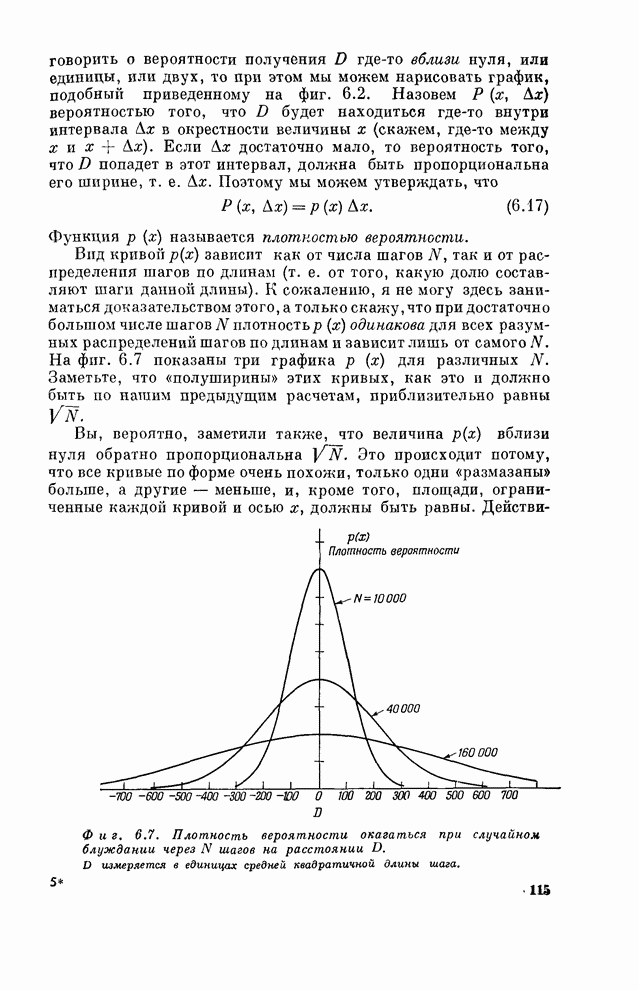
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
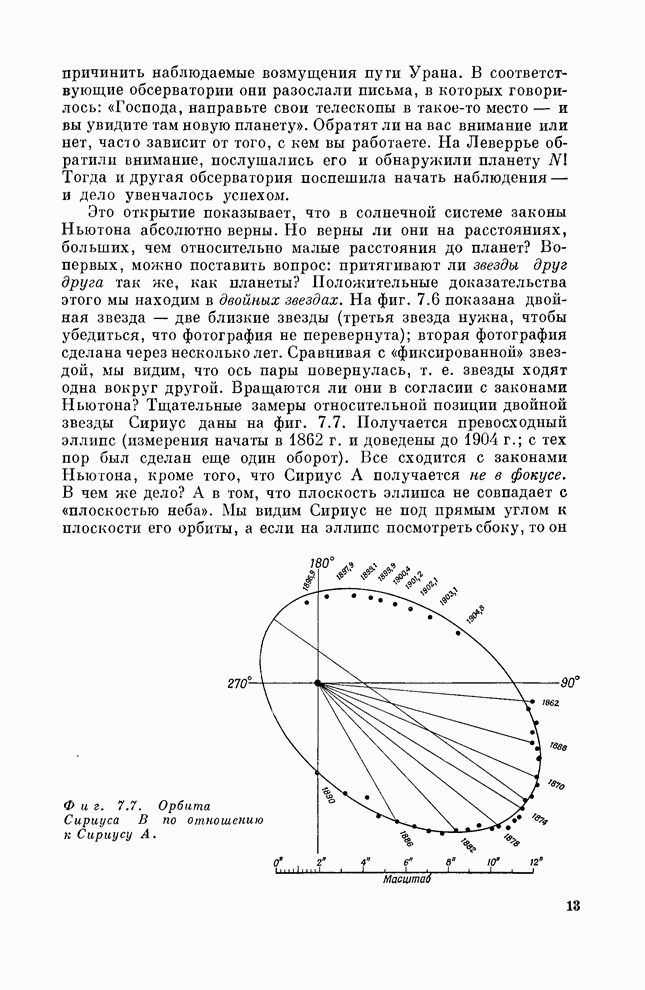
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
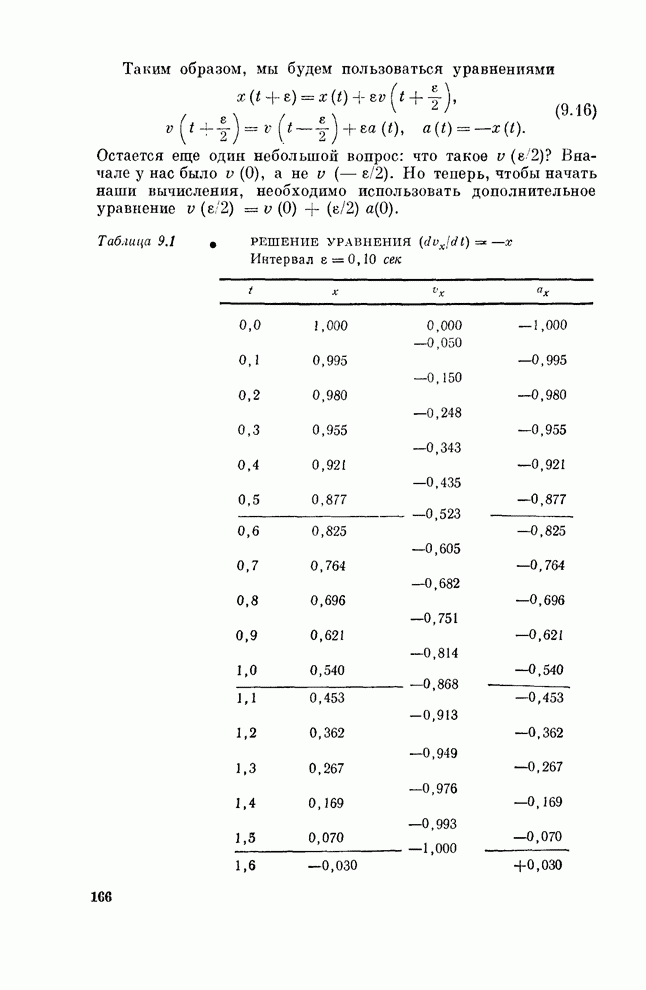
- § 5. Численное решение уравнений
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля