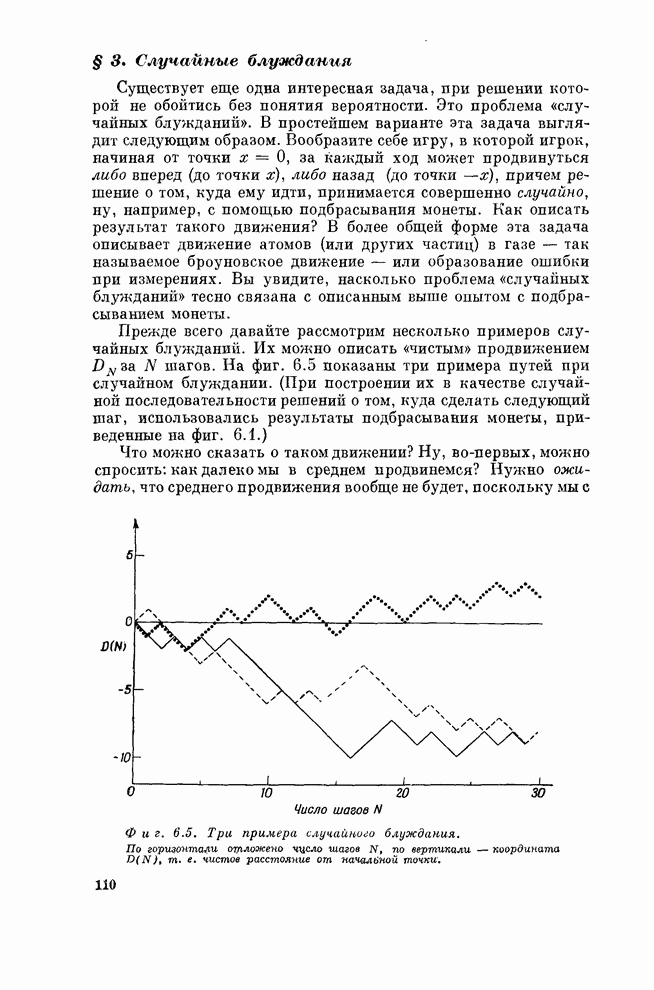
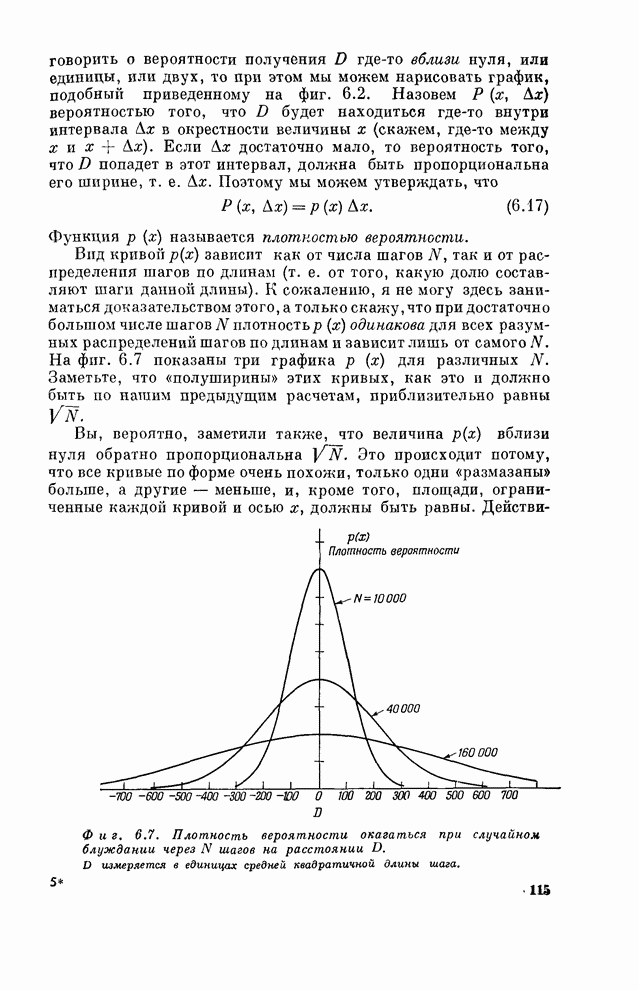
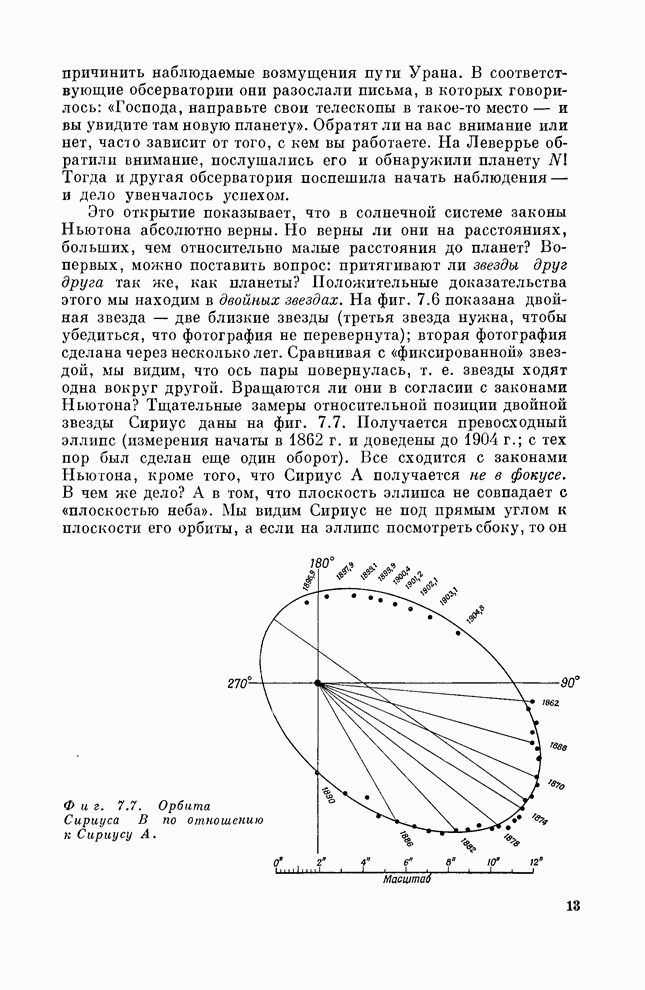
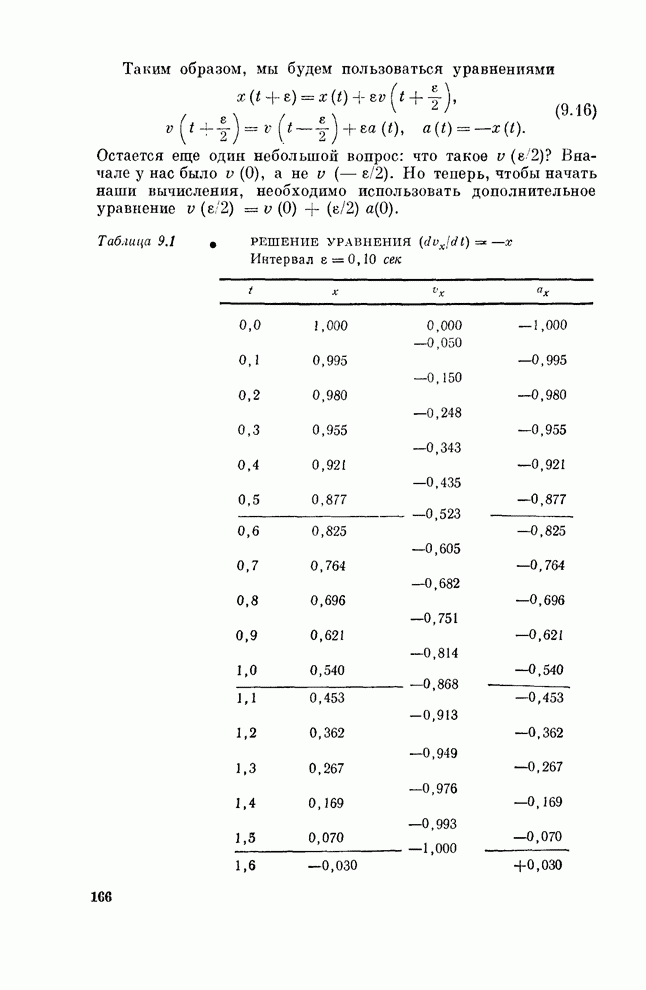
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Импульс все-таки сохраняется!
Можно экспериментально проверить наши предположения о том, что, во-первых, покоящиеся два тела с равной массой, разорванные взрывом, полетят в разные стороны с равной скоростью и, во-вторых, что два тела, обладающие равными скоростями и массами, при соударении и слипании останавливаются. Такую проверку можно сделать с помощью замечательного устройства — воздушного желоба (фиг. 10.1). В этом устройстве нет никаких трущихся деталей — вопрос, который очень беспокоил Галилея. Он не мог поставить эксперимента со скользящими телами, ибо они не скользили свободно, но с помощью чудесного желоба мы можем теперь избавиться от трения. Наши тела будут лететь без помех, а скорость их, согласно предвидению Галилея, будет оставаться постоянной. Ото достигается тем, что тело поддерживается воздушной подушкой, а поскольку трение о воздух очень мало, то тело планирует практически с постоянной скоростью, если на него но действуют никакие силы. Возьмем сначала два скользящих бруска, вес или массы которых с большой точностью равны друг другу (практически измеряется вес, но он, как вы знаете, пропорционален массе), и поместим между ними небольшой взрыватель в закрытом цилиндре (фиг. 10.2). Всю эту систему устанавливаем в центре желоба и электрической искрой поджигаем взрыватель. Что же произойдет? Если массы брусков одинаковы, то они, разлетевшись в стороны, одновременно достигнут концов желоба. Там они отскакивают от ограничителей, сталкиваются и слипаются в центре, точно в том же месте, откуда разлетелись (фиг. 10.3). Это интересный опыт. И в действительности происходит все так, как мы рассказали.

Фигура 10.1. Воздушный желоб (вид с торца).

Фигура 10.2. Продольный разрез скользящего бруска, скрепленного со взрывным цилиндром.

Фигура 10.3 Схема эксперимента с равными массами.
Теперь
па очереди проблема посложнее. Допустим, мы имеем две массы, причем одна
движется со скоростью у, а другая стоит на месте. Затем первая ударяет по
второй и они слипаются. Что произойдет дальше? Образуется одно тело с массой ![]() , которое как-то
будет двигаться. Но с какой скоростью? Вот в чем вопрос. Чтобы ответить на
него, предположим, что мы едем вдоль желоба на автомобиле. Все законы физики
должны при этом выглядеть точно так же, как и прежде, когда мы стояли на месте.
Мы начали с того, что если столкнуть два тела с равными массами и одинаковыми
скоростями
, которое как-то
будет двигаться. Но с какой скоростью? Вот в чем вопрос. Чтобы ответить на
него, предположим, что мы едем вдоль желоба на автомобиле. Все законы физики
должны при этом выглядеть точно так же, как и прежде, когда мы стояли на месте.
Мы начали с того, что если столкнуть два тела с равными массами и одинаковыми
скоростями ![]() то
после слипания они
останавливаются. А теперь представьте, что в это время мы катим на автомобиле
со скоростью
то
после слипания они
останавливаются. А теперь представьте, что в это время мы катим на автомобиле
со скоростью ![]() .
Какую же картину мы увидим? Ясно, что одно из тел, поскольку оно все время
летит рядом с автомобилем, будет казаться нам неподвижным. Второе же, которое
движется навстречу со скоростью
.
Какую же картину мы увидим? Ясно, что одно из тел, поскольку оно все время
летит рядом с автомобилем, будет казаться нам неподвижным. Второе же, которое
движется навстречу со скоростью ![]() покажется нам несущимся с удвоенной
скоростью
покажется нам несущимся с удвоенной
скоростью ![]() (фиг.
10.4). Наконец, образовавшееся после соударения и слипания тело будет казаться
нам летящим со скоростью
(фиг.
10.4). Наконец, образовавшееся после соударения и слипания тело будет казаться
нам летящим со скоростью ![]() . Отсюда мы делаем вывод, что если
тело, летящее со скоростью
. Отсюда мы делаем вывод, что если
тело, летящее со скоростью ![]() ударяется о покоящееся тело той же
массы и прилипает к нему, то образовавшееся тело будет двигаться со скоростью
ударяется о покоящееся тело той же
массы и прилипает к нему, то образовавшееся тело будет двигаться со скоростью ![]() или (что
математически то же самое) тело со скоростью
или (что
математически то же самое) тело со скоростью ![]() , ударяясь о покоящееся тело тон же
массы и прилипая к нему, образует тело, движущееся со скоростью
, ударяясь о покоящееся тело тон же
массы и прилипая к нему, образует тело, движущееся со скоростью ![]() . Заметьте, что
если умножить массы тел на их скорости и сложить их, то получим одинаковый
результат как до столкновения
. Заметьте, что
если умножить массы тел на их скорости и сложить их, то получим одинаковый
результат как до столкновения ![]() , так и после
, так и после ![]() . Вот как обстоит дело,
если тело, обладающее скоростью
. Вот как обстоит дело,
если тело, обладающее скоростью ![]() , столкнется с телом, находящимся в
покое.
, столкнется с телом, находящимся в
покое.

Фигура 10.4. Неупругое соударение равных масс.
Точно таким же образом можно определить, что произойдет, когда сталкиваются два одинаковых тела, каждое из которых движется с произвольной скоростью.
Пусть
одно тело летит со скоростью ![]() , а другое — со скоростью
, а другое — со скоростью ![]() в том же
направлении
в том же
направлении ![]() .
Какова будет их скорость после соударения? Давайте снова сядем в машину и поедем,
скажем, со скоростью
.
Какова будет их скорость после соударения? Давайте снова сядем в машину и поедем,
скажем, со скоростью ![]() . Тогда одно из тел будет казаться
нам стоящим на месте, а второе — налетающим на него со скоростью
. Тогда одно из тел будет казаться
нам стоящим на месте, а второе — налетающим на него со скоростью ![]() . Эта ситуация уже
знакома нам, и мы знаем, что после соударения скорость нового тела по отношению
к машине будет равна
. Эта ситуация уже
знакома нам, и мы знаем, что после соударения скорость нового тела по отношению
к машине будет равна ![]() . Что же касается действительной
скорости относительно земли, то ее можно найти, прибавив скорость автомобиля:
. Что же касается действительной
скорости относительно земли, то ее можно найти, прибавив скорость автомобиля: ![]() или
или ![]() (фиг. 10.5).
Обратите внимание, что снова
(фиг. 10.5).
Обратите внимание, что снова
![]() (10.6)
(10.6)

Фигура 10.5. Другой случай неупругого соударения равных масс.
Таким образом, принцип относительности Галилея помогает нам разобраться в любом соударении равных масс. До сих пор мы рассматривали движение в одном измерении, однако на основе его становится ясным многое из того, что будет происходить в более сложных случаях соударения: нужно только пустить автомобиль не вдоль направления движения тел, а под каким-то углом. Принцип остается тем же самым, хотя детали несколько усложняются.
Чтобы
экспериментально проверить, действительно ли тело, летящее со скоростью ![]() после
столкновения с покоящимся телом той же массы, образует новое тело, летящее со
скоростью
после
столкновения с покоящимся телом той же массы, образует новое тело, летящее со
скоростью ![]() ,
проделаем на нашей замечательной установке следующий опыт. Поместим в желоб три
тела с одинаковыми массами, два из которых соединены цилиндром со взрывателем,
а третье находится вблизи одного из них, хотя и несколько отделено от него. Оно
снабжено клейким амортизатором, так что прилипает к тому телу, которое ударяет
его. В первое мгновение после взрыва мы имеем два объекта с массами
,
проделаем на нашей замечательной установке следующий опыт. Поместим в желоб три
тела с одинаковыми массами, два из которых соединены цилиндром со взрывателем,
а третье находится вблизи одного из них, хотя и несколько отделено от него. Оно
снабжено клейким амортизатором, так что прилипает к тому телу, которое ударяет
его. В первое мгновение после взрыва мы имеем два объекта с массами ![]() , движущимися со
скоростью
, движущимися со
скоростью ![]() каждое.
В последующее мгновение одно из тел сталкивается с третьим и образует новое
тело с массой
каждое.
В последующее мгновение одно из тел сталкивается с третьим и образует новое
тело с массой ![]() ,
которое, как мы полагаем, должно двигаться со скоростью
,
которое, как мы полагаем, должно двигаться со скоростью ![]() . Но как проверить, что
скорость его действительно
. Но как проверить, что
скорость его действительно ![]() ? Для этого мы вначале установим тела
таким образом, чтобы расстояния до концов желоба относились как 2:1, так что
первое тело, которое продолжает двигаться со скоростью
? Для этого мы вначале установим тела
таким образом, чтобы расстояния до концов желоба относились как 2:1, так что
первое тело, которое продолжает двигаться со скоростью ![]() , должно пролететь за тот
же промежуток времени вдвое большее расстояние, чем скрепившиеся два других
тела (с учетом, конечно, того малого расстояния
, должно пролететь за тот
же промежуток времени вдвое большее расстояние, чем скрепившиеся два других
тела (с учетом, конечно, того малого расстояния ![]() , которое второе тело прошло до
столкновения с третьим). Если мы правы, то массы
, которое второе тело прошло до
столкновения с третьим). Если мы правы, то массы ![]() и
и ![]() должны достичь концов желоба
одновременно; так оно и происходит на самом деле (фиг. 10.6).
должны достичь концов желоба
одновременно; так оно и происходит на самом деле (фиг. 10.6).

Фигура 10.6. Экспериментальная проверка того
факта, что масса ![]() , ударяя со скоростью
, ударяя со скоростью ![]() массу
массу ![]() , образует тело с
массой
, образует тело с
массой ![]() и
скоростью
и
скоростью ![]() .
.
Следующая
проблема, которую мы должны решить: что получится, если тела имеют разные
массы. Давайте возьмем массы ![]() и
и ![]() и устроим между ними взрыв. Что
произойдет тогда? С какой скоростью полетит масса
и устроим между ними взрыв. Что
произойдет тогда? С какой скоростью полетит масса ![]() , если масса
, если масса ![]() летит со скоростью
летит со скоростью ![]() ? Фактически нам
нужно повторить только что проделанный эксперимент, но с пулевым зазором между
вторым и третьим телом. Разумеется, что при этом мы получим тот же результат —
скорости тел с массами
? Фактически нам
нужно повторить только что проделанный эксперимент, но с пулевым зазором между
вторым и третьим телом. Разумеется, что при этом мы получим тот же результат —
скорости тел с массами ![]() и
и ![]() должны быть со ответственно равны
должны быть со ответственно равны ![]() и
и ![]() . Итак, при
разлете тел с массами
. Итак, при
разлете тел с массами ![]() и
и ![]() получается тот же результат, что и
при симметричном разлете двух тел с массами
получается тот же результат, что и
при симметричном разлете двух тел с массами ![]() с последующим неупругим соударением
одного из этих тел с третьим, масса которого тоже равна
с последующим неупругим соударением
одного из этих тел с третьим, масса которого тоже равна ![]() . Более того, отразившись
от концов, каждое из этих тел будет лететь с почти той же скоростью, но,
конечно, в обратном направлении, и после неупругого соударения они
останавливаются.
. Более того, отразившись
от концов, каждое из этих тел будет лететь с почти той же скоростью, но,
конечно, в обратном направлении, и после неупругого соударения они
останавливаются.
Перейдем
теперь к следующему вопросу. Что произойдет, если тело с массой ![]() и скоростью
и скоростью ![]() столкнется с
покоящимся телом с массой
столкнется с
покоящимся телом с массой ![]() ? Воспользовавшись принципом
относительности Галилея, можно легко ответить на этот вопрос. Попросту говоря,
нам нужно опять садиться в машину, идущую со скоростью
? Воспользовавшись принципом
относительности Галилея, можно легко ответить на этот вопрос. Попросту говоря,
нам нужно опять садиться в машину, идущую со скоростью ![]() (фиг. 10.7), и наблюдать
за только что описанным процессом. Скорости, которые мы при этом увидим, будут
равны
(фиг. 10.7), и наблюдать
за только что описанным процессом. Скорости, которые мы при этом увидим, будут
равны


Фигура 10.7. Неупругое соударение между
телами с массами ![]() и
и ![]()
После
соударения масса ![]() покажется нам движущейся со
скоростью
покажется нам движущейся со
скоростью ![]() .
Таким образом, мы получили, что отношение скоростей до и после соударения равно
3:1, т. е. образовавшееся тело с массой
.
Таким образом, мы получили, что отношение скоростей до и после соударения равно
3:1, т. е. образовавшееся тело с массой ![]() будет двигаться в три раза
медленней. И в этом случае снова выполняется общее правило: сумма произведений
массы на скорость остается той же как до, так и после соударения:
будет двигаться в три раза
медленней. И в этом случае снова выполняется общее правило: сумма произведений
массы на скорость остается той же как до, так и после соударения: ![]() равно
равно ![]() . Вы видите, как
постепенно шаг за шагом устанавливается закон сохранения импульса.
. Вы видите, как
постепенно шаг за шагом устанавливается закон сохранения импульса.
Итак, мы
рассмотрели столкновение одного тела с двумя. Используя те же рассуждения,
можно предсказать результаты столкновения одного тела с тремя телами, двух тел
с тремя телами и т. д. На фиг. 10.8 как раз показан случай разлета масс ![]() и
и ![]() из состояния
покоя.
из состояния
покоя.

Фигура 10.8. Разлет тел с массами ![]() и
и ![]() .
.
В каждом из этих случаев выполняется одно и то же правило: масса первого тела, умноженная на его скорость, плюс масса второго тела, умноженная на его скорость, равны произведению полной массы на скорость ее движения. Все это — примеры сохранения импульса. Итак, начав с простого случая симметричных равных масс, мы установили закон сохранения для более сложных случаев. В сущности это можно сделать для любого рационального отношения масс, а поскольку любое число может быть со сколь угодно большой точностью заменено рациональным, то закон сохранения импульса справедлив для любых масс.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
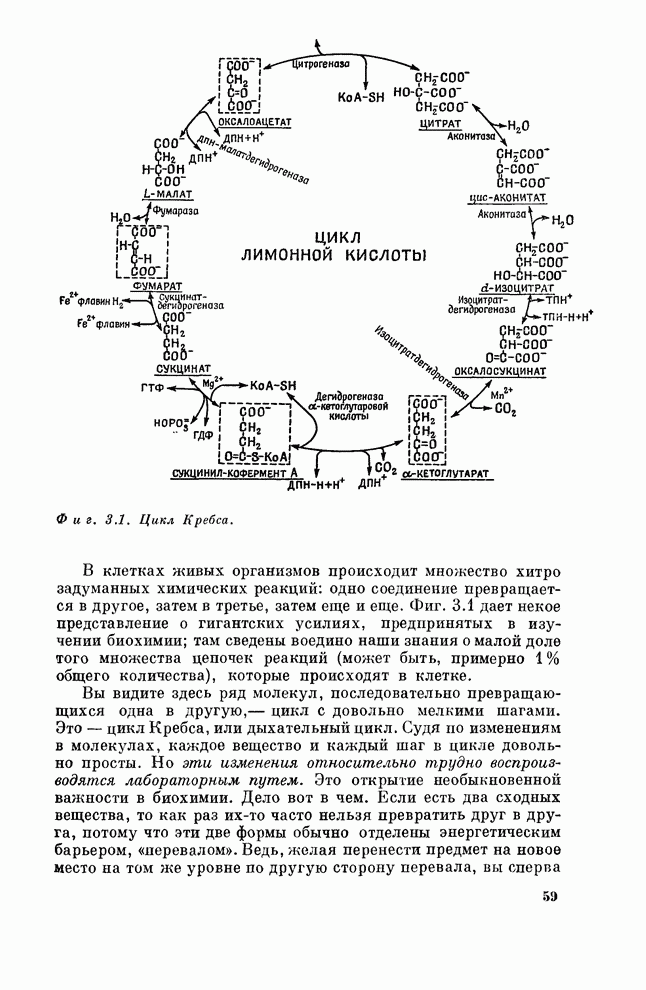
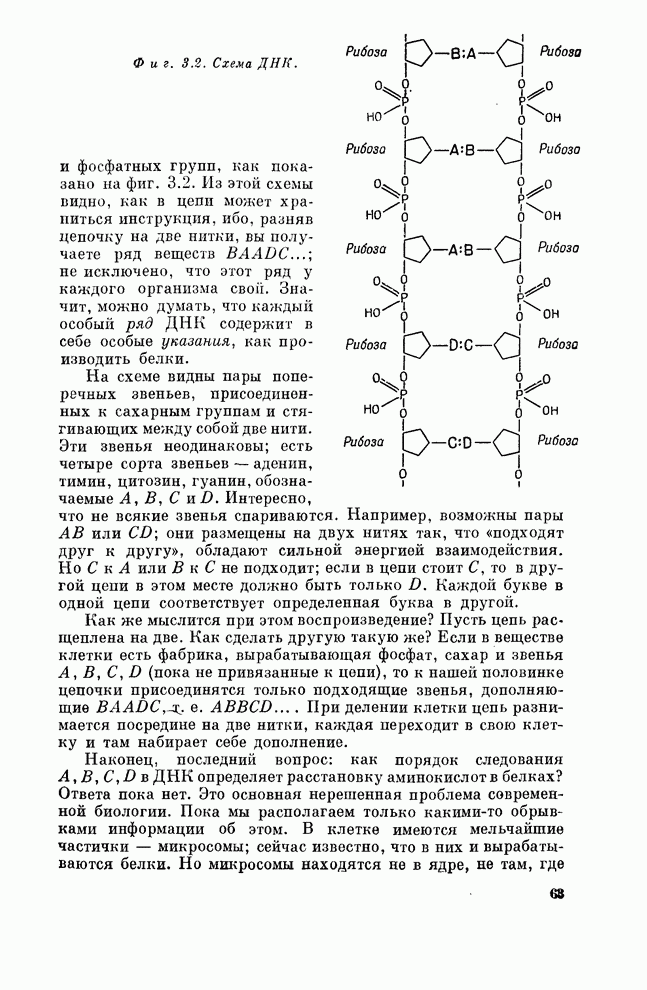
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
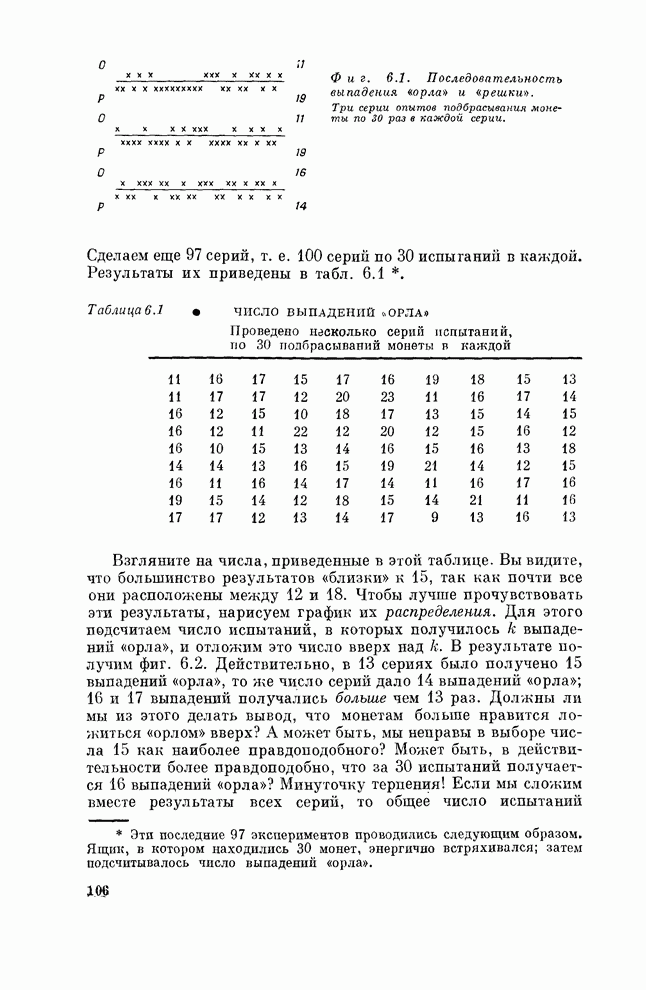
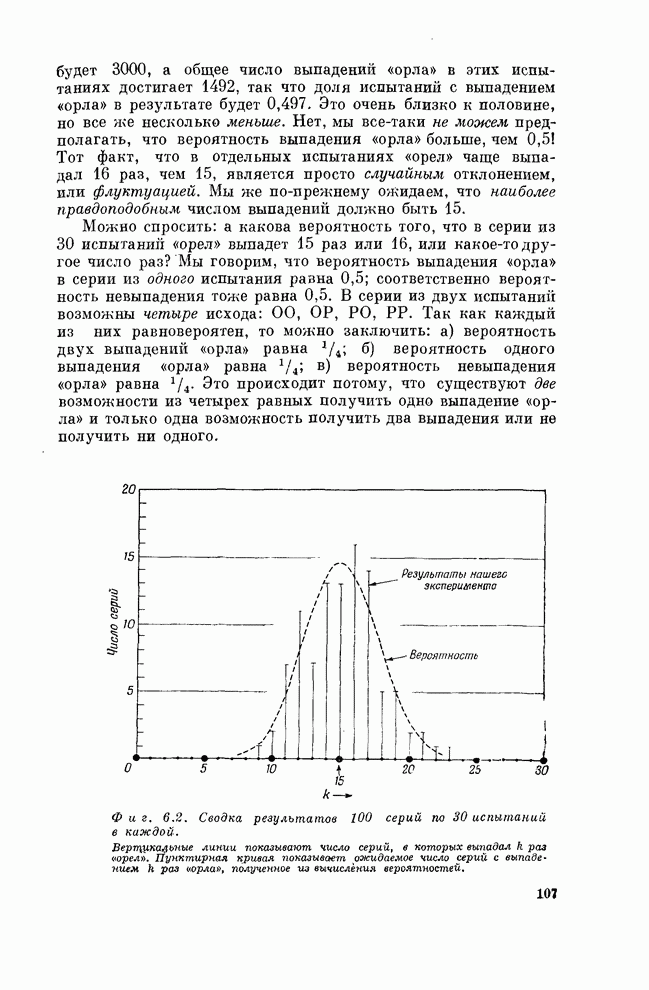
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
- § 3. Случайные блуждания
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
- § 5. Численное решение уравнений
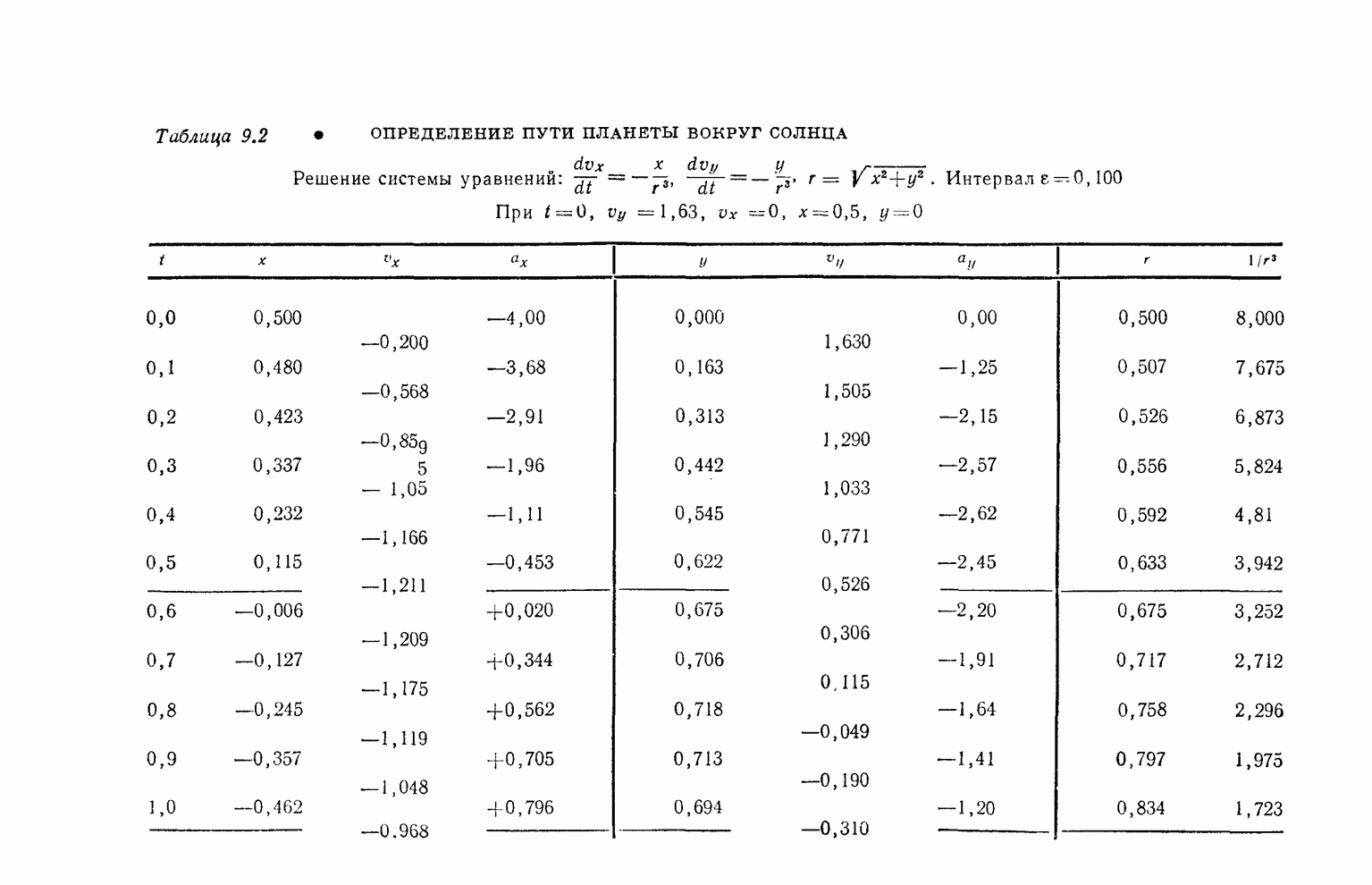
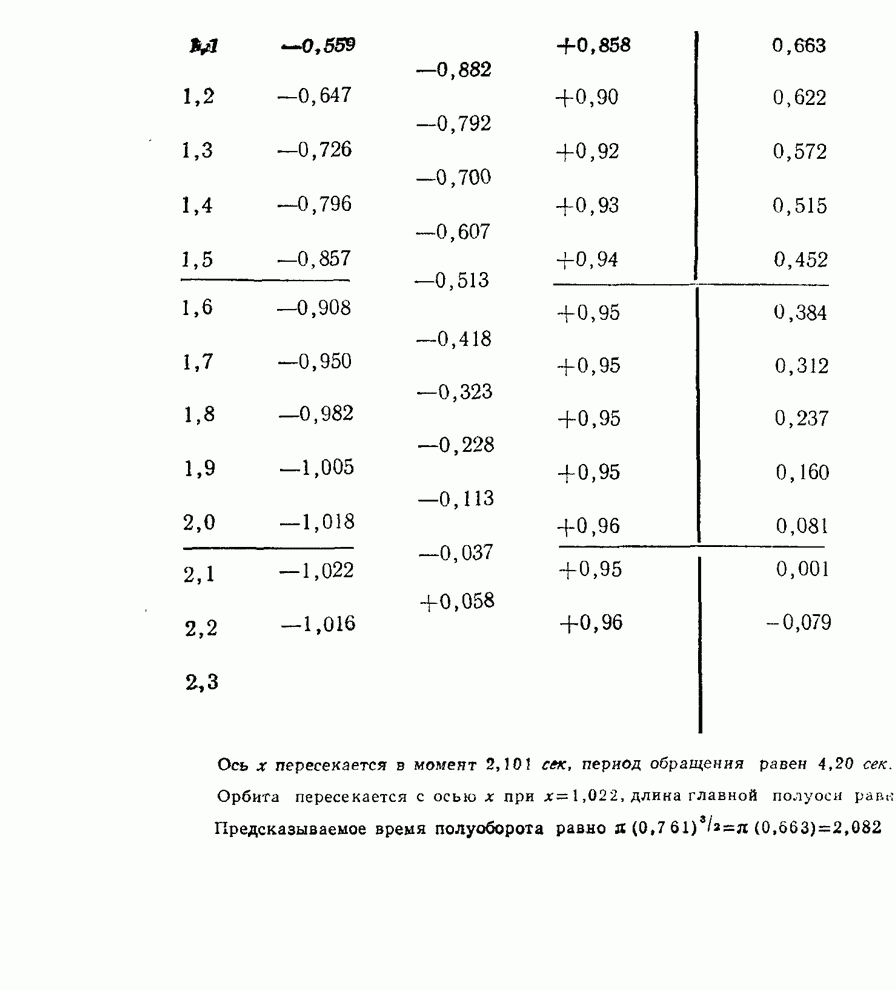
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля